1 Introduction

Robotic systems have gained significant popularity due to their capacity for automating processes, extending beyond industrial environments to encompass domestic services and medical applications [1, 2]. Owing to the growing complexity of tasks executed by robots, an expanding array of sensors is now employed within robotic systems, consequently leading to elevated costs [3, 4]. In response, numerous research groups have undertaken initiatives to investigate alternatives for efficient sensor signal processing [5, 6] or the adoption of strategies aimed at reducing the number of sensors through the use of observers [7, 8].

It is well known that robot manipulators are highly non-linear and coupled systems that are exposed to different types of perturbations, including unmodeled dynamics, friction, unknown payloads and interaction forces [9]. Such disturbances have the potential to significantly impact the performance of control systems, particularly when using non-robust control approaches [10,11,12]. A commonly employed technique for enhancing the robustness of control systems involves compensating for disturbances by incorporating an additional term to estimate the lumped perturbations within any nominal control framework.

Disturbance observers can be categorized into two main groups: the linear disturbance observers (LDOBs) and the nonlinear disturbance observers (NDOBs) [13]. In these techniques, the process begins with the reconstruction of the robot’s inverse dynamics through the measurement of its motion. Subsequently, this reconstructed dynamic information is subtracted from the known forces/torques applied to the robot. Next, the resulting residue is processed using a linear filter in LDOBs or a non-linear filter in NDOBs, ultimately yielding estimates of the unknown forces/torques or lumped disturbances [14].

Recently, the research in the field of disturbance estimators has shifted its focus towards NDOBs due to their enhanced performance when applied to nonlinear systems, outperforming LDOBs. The structure of dynamic equations permits the classification of NDOBs into two broad categories: basic and those based on sliding modes [15,16,17]. While sliding-mode based observers do achieve convergence in finite time, the tuning process is more intricate compared to the basic approach because it necessitates the selection of a greater number of gain parameters [12, 18]. Furthermore, the common occurrence of chattering in sliding-mode NDOBs adds complexity to their analysis. To address this phenomenon, second-order sliding mode NDOBs were introduced, albeit at the cost of increasing the number of parameters that need to be tuned [2]. In an effort to circumvent the complexity associated with the structure and tuning procedures of sliding-mode-based NDOBs, this work has opted for the basic approach.

Numerous disturbance observer techniques have been introduced in the robotics and mechatronics literature, as detailed in references [13, 19, 20]. Such observers serve a dual purpose, not only for rejecting perturbations but also for estimating and controlling interaction forces in both industrial and medical robotic applications. To mitigate the expenses associated with robotic systems for interaction tasks, there have been proposals to employ virtual force sensors based on disturbance estimators as a substitute for the conventional F/T sensors [21, 22]. Despite the variety of proposed solutions, Mohammadi’s basic scheme [23] remains a frequently employed and referenced approach. This can be attributed to its versatile formulation suitable for applications with diverse kinematic structures, characterized by a lack of restrictions on the number of degrees of freedom (DOF). Moreover, it eliminates the requirement for measuring joint acceleration and offers straightforward tuning, however, it is necessary to compute the inverse of the inertia matrix [24, 25]. For example, in [26] this NDOB is employed to estimate end-effector forces and torques within an admittance-controlled wheeled mobile manipulator, facilitating mobility assistance while obviating the necessity for an expensive F/T sensor. In [11], instead of using F/T sensors in a non-linear teleoperation control system, which is susceptible to variable time delays, Mohammadi’s NDOB serves as a virtual F/T sensor for both the master and slave robots. On the other hand, in [15], the NDOB is employed to estimate and compensate model uncertainties and external disturbances in an underwater multilateral teleoperation system. In [10], Mohammadi’s NDOB is combined with a finite time controller that leads to a robust tracking control structure.

When formulating an NDOB for force/torque estimation in joint space, the requirement for the inverse of the Jacobian matrix arises. Therefore, in [27], a Cartesian NDOB inspired by Mohammadi’s observer is introduced to circumvent this calculation. This NDOB is employed to estimate external forces within a nonlinear teleoperation system that is controlled by an adaptive force-position controller. Some other studies focus on estimating external forces and torques using Kalman Filters, which are designed according to the robot’s dynamic equations. Typically, such research presents experimental results, yet they often lack a formal convergence analysis, such as a Lyapunov stability analysis [28, 29]. While the generalized momentum observer (GMOB) is an alternative technique designed for estimating disturbances and can also be applied to estimate external torques. Its implementation does not necessitate the measurement of joint accelerations. However, it assumes that velocity is a measurable variable. A distinctive feature of GMOB is that it eliminates the need for calculating the inverse of the inertia matrix [30, 31].

In contrast to schemes based on Mohammadi’s NDOB, certain disturbance observers are designed to incorporate supplementary information related to the robot’s motion, such as motor currents. For instance, in [21, 32], the authors present an application of force control using a virtual sensor for a 7-DOF robot equipped with both position and motor current sensors. Other force estimators are devised for implementation in robots equipped with torque sensors in all joints. For example, in [33], the authors introduce an estimator for external torque that exclusively relies on motor-side information, employing torque residual equations as the basis.

Given the escalating complexity of robotic tasks involving human–robot interaction and collaboration, there is an imperative need for control systems that prioritize both security and stability. Additionally, there is a growing demand for more accessible robotic systems capable of executing intricate tasks with minimal sensor reliance. Consequently, the central focus of this work is on addressing as primary challenge: the development of a virtual F/T sensor for robots equipped with only position sensors.

Mohammadi’s NDOB structure necessitates the measurement of joint velocity for its practical implementation, rendering it unsuitable for robotic systems equipped solely with joint position sensors. In practical applications, the estimation of velocity-dependent dynamic terms becomes necessary through numerical methods. However, this modification lacks formal analysis to guarantee the convergence of estimation errors [30]. This paper introduces an innovative structure that enhances the basic Mohammadi’s NDOB by eliminating the requirement for joint velocity measurements. The proposed structure incorporates an auxiliary subsystem for estimating joint velocity through filtering of robot joint positions, a key element integrated into the convergence analysis, supported by an appropriate Lyapunov function. To the best of our knowledge, no similar approach has been presented to date with a structure as straightforward and easily tunable as the one proposed in this study. Hence, our proposal holds both theoretical and practical significance, which can be succinctly summarized through the following key points:

  • It estimates both external contact or friction forces and the robot joint velocity.

  • The observer convergence is underpinned by a rigorous stability analysis following the Lyapunov framework.

  • The observer architecture requires solely the measurement of joint positions and the simple tuning of a limited number of parameters.

  • Experimental validation affirms that the observer’s performance is comparable to other state-of-the-art schemes, despite having a simpler structure and requiring fewer sensors.

2 Preliminaries

In this paper, scalars, vectors and matrices are represented as \(x \in {\mathbb {R}}\), \(\varvec{y}\in {\mathbb {R}}^n\) and \(\varvec{A}\in {\mathbb {R}}^{n \times m}\), respectively. The origin of \({\mathbb {R}}^n\) is denoted by \({\varvec{0}}_n\), while the \(n \times n\) identity matrix is represented as \(\varvec{I}_n\). The Euclidean norm of vectors and the induced norm of matrices are denoted by \(\left\| {\varvec{y}}\right\| =\sqrt{\varvec{y}^T\varvec{y}}\) and \(\left\| {\varvec{A}}\right\| =\sqrt{\lambda _{\textrm{max}}\left\{ {\varvec{A}^T \varvec{A}}\right\} }\), respectively, where \(\lambda _{\textrm{max}}\left\{ {\varvec{A}^T \varvec{A}}\right\} \) represents the maximum eigenvalue of matrix \(\varvec{A}^T \varvec{A}\).

2.1 Dynamic modeling of serial rigid robotic manipulators

The dynamic model of a robot arm establishes the relationship between the generalized joint torques exerted by the actuators and its motion. This relationship is described in terms of the positions, velocities, and accelerations of the robot’s joints. It is important to note that this model does not necessarily assume that the robot is equipped with velocity and acceleration sensors. However, the presence of these sensors may be necessary for the implementation of certain control algorithms and disturbance observers. Consider the Euler–Lagrange formulation for the dynamic model of a n-DOF serial rigid robot manipulator in contact with the environment given by [34]

$$\begin{aligned} \varvec{M}(\varvec{q})\ddot{\varvec{q}}\ +\varvec{h}(\varvec{q},\dot{\varvec{q}})+ \varvec{f}(\dot{\varvec{q}})= \varvec{\tau }- \varvec{\tau }_e \end{aligned}$$
(1)

where \(\varvec{h}(\varvec{q},\dot{\varvec{q}})= \varvec{C}(\varvec{q},\dot{\varvec{q}})\dot{\varvec{q}}+ \varvec{g}(\varvec{q})\nonumber \); \(\varvec{q}, \dot{\varvec{q}}, \ddot{\varvec{q}}\in {\mathbb {R}}^n\) are the joint position, velocity and acceleration vectors, respectively; \(\varvec{M}(\varvec{q})\in {\mathbb {R}}^{n \times n}\) is the inertia matrix, and \(\varvec{f}(\dot{\varvec{q}})\), \(\varvec{C}(\varvec{q},\dot{\varvec{q}})\dot{\varvec{q}}\), \(\varvec{g}(\varvec{q})\), \(\varvec{\tau }\), \(\varvec{\tau }_e\) are vectors of joint friction, Coriolis and centrifugal forces, gravitational forces, generalized control torques, and external contact torques, respectively. Subsequently, we denote \(\dot{\varvec{M}}(\varvec{q},\dot{\varvec{q}})\) as the rate of change of \(\varvec{M}(\varvec{q})\).

Assumption 1

Let \(D_{\varvec{q}}\) denote the set of all attainable joint positions, representing the finite workspace of a physical robot. In order to consider robots with both revolute and prismatic joints, which cannot extend infinitely, we assume that \(D_{\varvec{q}}\) is a bounded set.

Assumption 2

It is a known fact that electronic drives cannot deliver infinite energy to the actuators, thereby constraining the robot’s motion. Consequently, we assume that both the speed and acceleration of the manipulator fall within the following bounded sets

$$\begin{aligned} \dot{\varvec{q}}\in D_{\dot{\varvec{q}}}= & {} \left\{ {\dot{\varvec{q}}\in {\mathbb {R}}^n: \left\| {\dot{\varvec{q}}}\right\| \le \left\| {\dot{\varvec{q}}}\right\| _{\textrm{max}} }\right\} \end{aligned}$$
(2)
$$\begin{aligned} \ddot{\varvec{q}}\in D_{\ddot{\varvec{q}}}= & {} \left\{ {\ddot{\varvec{q}}\in {\mathbb {R}}^n: \left\| {\ddot{\varvec{q}}}\right\| \le \left\| {\ddot{\varvec{q}}}\right\| _{\textrm{max}} }\right\} \end{aligned}$$
(3)

The following properties of the dynamic model (1) are useful for further analysis [35, 36].

Property 1

The inertia matrix \(\varvec{M}(\varvec{q})\) is symmetric, positive definite and bounded, that is,

$$\begin{aligned} \varvec{M}(\varvec{q})= & {} \varvec{M}(\varvec{q})^T >0 \\ \mu _m \varvec{I}_n\le & {} \varvec{M}(\varvec{q})\le \mu _M \varvec{I}_n \end{aligned}$$

for some constants \(\mu _M \ge \mu _m > 0\).

Property 2

The matrix \(\varvec{C}(\varvec{q},\dot{\varvec{q}})\) is upper bounded as \(\left\| {\varvec{C}(\varvec{q},\dot{\varvec{q}})}\right\| \le C_b(\dot{\varvec{q}}) \left\| {\dot{\varvec{q}}}\right\| \), where \(C_b(\dot{\varvec{q}})\) is a scalar function. For a robot with all revolute joints, \(C_b(\dot{\varvec{q}})\) can be replaced by a non-negative constant defined as \(\gamma = \text {sup}_{\varvec{q}\in D_{\varvec{q}}} \left\{ {C_b(\dot{\varvec{q}})}\right\} \) and recalling Assumption 2, it is observed that

$$\begin{aligned} \left\| {\varvec{C}(\varvec{q},\dot{\varvec{q}})}\right\| \le \gamma \left\| {\dot{\varvec{q}}}\right\| _{\textrm{max}} \end{aligned}$$
(4)

Property 3

The matrices \(\dot{\varvec{M}}(\varvec{q},\dot{\varvec{q}})\) and \(\varvec{C}(\varvec{q},\dot{\varvec{q}})\) are related in such a way that

$$\begin{aligned} \dot{\varvec{M}}(\varvec{q},\dot{\varvec{q}})= \varvec{C}(\varvec{q},\dot{\varvec{q}})+ \varvec{C}^T (\varvec{q}, \dot{\varvec{q}}) \end{aligned}$$
(5)

therefore, by considering (4) and (5) we obtain

$$\begin{aligned} \left\| {\dot{\varvec{M}}(\varvec{q},\dot{\varvec{q}})}\right\| \le 2 \gamma \left\| {\dot{\varvec{q}}}\right\| _{\textrm{max}} \end{aligned}$$
(6)

A simple procedure to explicitly obtain the value of \(\gamma \) for robots with only revolute joints is presented in [36]. Consider appropriate constants \(\bar{M}_i\) such that \(\left\| {\frac{\partial \varvec{M}(\varvec{q})}{\partial q_i}}\right\| \le \bar{M}_i\), \(i=1,\ldots ,n\), for all \(\varvec{q}\in {\mathbb {R}}^n\), then \(\gamma \) is computed as

$$\begin{aligned} \gamma = \frac{3}{2} \sum \limits _{i = 1}^n \bar{M}_i \end{aligned}$$
(7)

2.2 NDOB for robot manipulators with velocity sensors

This section reviews the structure of the well-known NDOB proposed by Mohammadi et al. [23].

Assumption 3

Let \(\hat{\varvec{M}}(\varvec{q})\) and \(\hat{\varvec{h}}(\varvec{q},\dot{\varvec{q}})\) be the estimates of actual \(\varvec{M}(\varvec{q})\) and \(\varvec{h}(\varvec{q},\dot{\varvec{q}})\), respectively, while \(\Delta \varvec{M}\) and \(\Delta \varvec{h}\) are the corresponding additive uncertainties present in the robot model such that

$$\begin{aligned} \varvec{M}(\varvec{q})= & {} \hat{\varvec{M}}(\varvec{q})+ \Delta \varvec{M}\nonumber \\ \varvec{h}(\varvec{q},\dot{\varvec{q}})= & {} \hat{\varvec{h}}(\varvec{q},\dot{\varvec{q}})+ \Delta \varvec{h}\end{aligned}$$
(8)

By substituting the Eqs. (8) in (1), the system that reconstructs the robot dynamics is obtained as follows

$$\begin{aligned} \hat{\varvec{M}}(\varvec{q})\ddot{\varvec{q}}+ \hat{\varvec{h}}(\varvec{q},\dot{\varvec{q}})= \varvec{\tau }+ \varvec{\tau }_d \end{aligned}$$
(9)

where \(\varvec{\tau }_d\) represents the lumped disturbance vector defined as

$$\begin{aligned} \varvec{\tau }_d = -\varvec{\tau }_e - \varvec{f}(\dot{\varvec{q}})-\Delta \varvec{M}\ddot{\varvec{q}}-\Delta \varvec{h}\end{aligned}$$
(10)

Moreover, the estimate of inertia matrix \(\hat{\varvec{M}}(\varvec{q})\) and its rate of change \(\dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\) satisfy the following properties:

Property 4

The estimate of inertia matrix \(\hat{\varvec{M}}(\varvec{q})\) is symmetric, positive definite and bounded, that is,

$$\begin{aligned} \hat{\varvec{M}}(\varvec{q})= \hat{\varvec{M}}(\varvec{q})^T >0 \nonumber \\ \sigma _m \varvec{I}_n \le \hat{\varvec{M}}(\varvec{q})\le \sigma _M \varvec{I}_n \end{aligned}$$
(11)

for some constants \(\sigma _M \ge \sigma _m > 0\).

Property 5

The matrix \(\dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\) is upper bounded as

$$\begin{aligned} \left\| {\dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})}\right\| \le \zeta \end{aligned}$$
(12)

for some constant \(\zeta >0\). Note that, under Assumptions 1 and 2, this property is not only valid for robots with only revolute joints, but also for robots with prismatic joints.

2.2.1 Disturbance observer structure

In order to estimate the lumped disturbance vector \(\hat{\varvec{\tau }}_d\), Mohammadi et al. [23] proposed the following system

$$\begin{aligned} \dot{\varvec{z}}= & {} -\varvec{L}(\varvec{q})\varvec{z}+ \varvec{L}(\varvec{q})\left[ \hat{\varvec{h}}(\varvec{q},\dot{\varvec{q}})- \varvec{\tau }-\varvec{p}(\dot{\varvec{q}})\right] \end{aligned}$$
(13)
$$\begin{aligned} \hat{\varvec{\tau }}_d= & {} \varvec{z}+ \varvec{p}(\dot{\varvec{q}})\end{aligned}$$
(14)

where

$$\begin{aligned} \varvec{L}(\varvec{q})= & {} \varvec{X}^{-1} \hat{\varvec{M}}^{-1}(\varvec{q})\end{aligned}$$
(15)
$$\begin{aligned} \varvec{p}(\dot{\varvec{q}})= & {} \varvec{X}^{-1} \dot{\varvec{q}}\end{aligned}$$
(16)
$$\begin{aligned} \hat{\varvec{h}}(\varvec{q},\dot{\varvec{q}})= & {} \hat{\varvec{C}}(\varvec{q},\dot{\varvec{q}})\dot{\varvec{q}}+ \varvec{g}(\varvec{q})\end{aligned}$$
(17)

with \(\varvec{X}\) being an invertible matrix, while \(\varvec{L}(\varvec{q})\) and \(\varvec{p}(\dot{\varvec{q}})\) satisfy \(\frac{d}{dt} \varvec{p}(\dot{\varvec{q}})= \varvec{L}(\varvec{q})\hat{\varvec{M}}(\varvec{q})\ddot{\varvec{q}}\).

To ensure convergence and complete the design of the NDOB, it is suggested to find a constant matrix \(\varvec{\Gamma }>0\) such that

$$\begin{aligned} \varvec{X}+ \varvec{X}^T - \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\ge \varvec{\Gamma }\end{aligned}$$
(18)

The disturbance estimation error defined as \(\Delta \varvec{\tau }_d= \varvec{\tau }_d -\hat{\varvec{\tau }}_d\), whose dynamics is given by

$$\begin{aligned} \dot{\Delta } \varvec{\tau }_d= \dot{\varvec{\tau }}_d- \varvec{L}(\varvec{q})\Delta \varvec{\tau }_d\end{aligned}$$
(19)

where \(\dot{\varvec{\tau }}_d\) is the rate of change of the lumped disturbance vector. Also, two scenarios related with \(\dot{\varvec{\tau }}_d\) are considered for convergence analysis:

Case 1

Fast-varying disturbances. The rate of change of the lumped disturbance vector is bounded, i.e. \( \left\| {\dot{\varvec{\tau }}_d}\right\| \le k\) for some constant \(k>0\). In this case, the disturbance tracking error converges with an exponential rate \(\beta _{M1}\) defined as

$$\begin{aligned} \beta _{M1} = \frac{(1-\theta ) \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} }{2 \sigma _M \left\| {\varvec{X}}\right\| ^2} \end{aligned}$$

to the ball with radius \(2 k \sigma _M \left\| {\varvec{X}}\right\| ^2 / \left( \theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \right) \) where \(0 \le \theta \le 1\).

Case 2

Slow-varying disturbances. The rate of change of the lumped disturbance acting on the manipulator is negligible in comparison with the error dynamics (19), hence \(\dot{\varvec{\tau }}_d\approx {\varvec{0}}_n \). In this case, the disturbance tracking error converges asymptotically to zero with minimum exponential rate \(\beta _{M2}\) defined as

$$\begin{aligned} \beta _{M2} = \frac{\lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} }{2 \sigma _M \left\| {\varvec{X}}\right\| ^2} \end{aligned}$$

In addition, an optimal design for \(\varvec{Y}= \varvec{X}^{-1}\) can be obtained as follows

$$\begin{aligned} \varvec{Y}_{M\text {optimal}} = \frac{1}{2} \left[ \zeta + 2 \beta _{M2} \sigma _M \right] \varvec{I}_n \end{aligned}$$

Observe that the NDOB structure presented in (13), (14) implies that the robot is equipped with position and velocity sensors. In the next section, a NDOB for robots without velocity and acceleration sensors is presented.

3 NDOB without velocity and acceleration measurements

The main disadvantage of the NDOB reviewed in Sect. 2.2 is the need for velocity measurements [23]. In practical applications, velocity and acceleration sensors are often absent in many robotic systems. Nevertheless, it is feasible to adapt the disturbance observer (13), (14) to eliminate the necessity for velocity measurement. To achieve this, we introduce the following velocity estimator

$$\begin{aligned} \dot{\varvec{v}}_c= & {} - \varvec{A}_v \left[ \varvec{v}_c + \varvec{A}_v \varvec{q}\right] \nonumber \\ \varvec{v}= & {} \varvec{v}_c + \varvec{A}_v \varvec{q}\end{aligned}$$
(20)

where \(\varvec{v}\) is the estimate of joint velocity \(\dot{\varvec{q}}\), while \(\varvec{A}_v\) is a constant diagonal, positive definite matrix. Note that the auxiliary subsystem (20) gives rise to the so-called dirty derivative of \(\dot{\varvec{q}}\) [37, 38], where each of its components passes through a first-order low-pass filter. This practice is common in order to limit high-frequency gains, resulting in an approximated causal derivative operator.

Now, in order to establish a system that, like in Eq. (9), reconstructs the robot dynamics without requiring velocity measurements, consider the rate of change of the estimated velocity \(\dot{\varvec{v}}\) such that

$$\begin{aligned} \hat{\varvec{M}}(\varvec{q})\dot{\varvec{v}}+ \hat{\varvec{h}}(\varvec{q},\varvec{v})= \varvec{\tau }+ \varvec{\tau }_d \end{aligned}$$
(21)

where \(\hat{\varvec{h}}(\varvec{q},\varvec{v})= \hat{\varvec{C}}(\varvec{q},\varvec{v})\varvec{v}+ \varvec{g}(\varvec{q})\). Therefore, the modified disturbance observer that does not need velocity or acceleration measurements takes the following form

$$\begin{aligned} \dot{\varvec{z}}= & {} -\varvec{L}(\varvec{q})\varvec{z}+ \varvec{L}(\varvec{q})\left[ \hat{\varvec{h}}(\varvec{q},\varvec{v})- \varvec{\tau }-\varvec{p}(\varvec{v})\right] \end{aligned}$$
(22)
$$\begin{aligned} \hat{\varvec{\tau }}_d= & {} \varvec{z}+ \varvec{p}(\varvec{v})\end{aligned}$$
(23)

where \(\varvec{L}(\varvec{q})\) was defined in (15) and \(\varvec{p}(\varvec{v})\) is given by

$$\begin{aligned} \varvec{p}(\varvec{v})= \varvec{X}^{-1} \varvec{v}\end{aligned}$$
(24)

with \(\varvec{X}\in {\mathbb {R}}^{n \times n}\) being an invertible matrix. In this case, observe that the terms \(\varvec{L}(\varvec{q})\) and \(\varvec{p}(\varvec{v})\) are related as follows \(\frac{d}{dt} \varvec{p}(\varvec{v})= \varvec{L}(\varvec{q})\hat{\varvec{M}}(\varvec{q})\dot{\varvec{v}}\).

Before performing the convergence analysis for NDOB (22)-(23), the dynamics of estimation errors shall be studied.

3.1 Dynamics of estimation errors

The estimation error vector \(\varvec{e}\in {\mathbb {R}}^{2n}\) contains the perturbation and velocity estimation errors and it is defined as

$$\begin{aligned} \varvec{e}= \left[ \begin{array}{c}\varvec{e}_d\\ \varvec{e}_v\end{array}\right] \end{aligned}$$
(25)

where the perturbation estimation error \(\varvec{e}_d\in {\mathbb {R}}^n\) is given by

$$\begin{aligned} \varvec{e}_d= \varvec{\tau }_d - \hat{\varvec{\tau }}_d\end{aligned}$$
(26)

while the velocity estimation error \(\varvec{e}_v\in {\mathbb {R}}^n\) is

$$\begin{aligned} \varvec{e}_v= \dot{\varvec{q}}- \varvec{v}\end{aligned}$$
(27)

Note that \(\varvec{e}_d\) is equivalent to \(\Delta \varvec{\tau }_d\) previously defined in Sect. 2.2.

Now, the rate of change of \(\varvec{e}_d\) is analyzed. Taking the time derivative of (26), we obtain that

$$\begin{aligned} \dot{\varvec{e}}_d= & {} \dot{\varvec{\tau }}_d- \dot{\hat{\varvec{\tau }}}_d\\= & {} \dot{\varvec{\tau }}_d- \left[ \dot{\varvec{z}}+ \frac{d}{dt} \varvec{p}(\varvec{v})\right] \\= & {} \dot{\varvec{\tau }}_d- \left\{ {-\varvec{L}(\varvec{q})\varvec{z}+ \varvec{L}(\varvec{q})\left[ \hat{\varvec{h}}(\varvec{q},\varvec{v})- \varvec{\tau }-\varvec{p}(\varvec{v})\right] }\right\} - \frac{d}{dt} \varvec{p}(\varvec{v})\\= & {} \dot{\varvec{\tau }}_d- \varvec{L}(\varvec{q})\left[ \varvec{\tau }_d - \hat{\varvec{\tau }}_d\right] \end{aligned}$$

therefore,

$$\begin{aligned} \dot{\varvec{e}}_d= \dot{\varvec{\tau }}_d- \varvec{L}(\varvec{q})\varvec{e}_d\end{aligned}$$
(28)

which retains the same structure as Eq. (19) used in the NDOB with velocity measurements.

On the other hand, taking the time derivative of (27)

$$\begin{aligned} \dot{\varvec{e}}_v= \ddot{\varvec{q}}- \dot{\varvec{v}}\end{aligned}$$
(29)

and observe that

$$\begin{aligned} \dot{\varvec{v}}= & {} \dot{\varvec{v}}_c+ \varvec{A}_v \dot{\varvec{q}}\\= & {} - \varvec{A}_v \left[ \varvec{v}_c + \varvec{A}_v \varvec{q}\right] + \varvec{A}_v \dot{\varvec{q}}\\= & {} \varvec{A}_v \left[ \dot{\varvec{q}}- \varvec{v}\right] \end{aligned}$$

therefore,

$$\begin{aligned} \dot{\varvec{e}}_v= \ddot{\varvec{q}}- \varvec{A}_v \varvec{e}_v\end{aligned}$$
(30)

3.2 Stability and convergence analysis

The analysis of estimation error behavior for the proposed NDOB encompasses two scenarios, previously referred to as Cases 1 and 2. While the same Lyapunov candidate function is utilized for both cases, distinct conditions regarding the rate of perturbation change in its time derivative are taken into account.

Assumption 4

For the fast-varying disturbances case, it is assumed that the rate of change of the lumped disturbance is bounded as \(\left\| {\dot{\varvec{\tau }}_d}\right\| \le k_d\), for some constant \(k_d>0\).

Assumption 5

For the slow-varying disturbances case, it is assumed that the rate of change is negligible in comparison with error dynamics, that is, \(\dot{\varvec{\tau }}_d\approx {\varvec{0}}_n\).

Assumption 6

For both slow and fast-varying disturbances cases, it is assumed that

  1. 1.

    It is possible to find a constant, positive definite matrix \(\varvec{\Gamma }\) that satisfies Inequality (18).

  2. 2.

    From Assumption 2, there is a constant \(k_a>0\) that upper bounds the acceleration such that

    $$\begin{aligned} \left\| {\ddot{\varvec{q}}}\right\| \le k_a \left\| {\varvec{e}_v}\right\| \end{aligned}$$
    (31)

3.2.1 Fast-varying disturbances

To assess the behavior of estimation errors, consider the following Lyapunov candidate function

$$\begin{aligned} w\left( \varvec{e}_d,\varvec{e}_v\right) = \left[ \varvec{X}\varvec{e}_d\right] ^T \hat{\varvec{M}}(\varvec{q})\left[ \varvec{X}\varvec{e}_d\right] + \frac{1}{2}\varvec{e}_v^T\varvec{e}_v\end{aligned}$$
(32)

Note that according to Property 4, \(w\left( \varvec{e}_d,\varvec{e}_v\right) \) is a positive definite function. Also, by considering two positive constants \(\varepsilon _{11}\) and \(\varepsilon _{12}\) given by

$$\begin{aligned} \varepsilon _{11}&\buildrel \Delta \over = \text {min} \left\{ { \sigma _m \lambda _{\textrm{min}}\left\{ {\varvec{X}^T \varvec{X}}\right\} , \frac{1}{2}}\right\} \end{aligned}$$
(33)
$$\begin{aligned} \varepsilon _{12}&\buildrel \Delta \over = \text {max} \left\{ { \sigma _M \left\| {\varvec{X}}\right\| ^2 , \frac{1}{2}}\right\} \end{aligned}$$
(34)

and from (25) that

$$\begin{aligned} \left\| {\varvec{e}}\right\| ^2= & {} \left\| {\left[ \begin{array}{c}\varvec{e}_d\\ \varvec{e}_v\end{array}\right] }\right\| ^2 = \varvec{e}_d^T \varvec{e}_d\nonumber \\{} & {} + \varvec{e}_v^T \varvec{e}_v= \left\| {\varvec{e}_d}\right\| ^2 + \left\| {\varvec{e}_v}\right\| ^2 = \left\| {\left[ \begin{array}{c}\left\| {\varvec{e}_d}\right\| \\ \left\| {\varvec{e}_v}\right\| \end{array}\right] }\right\| ^2 \end{aligned}$$
(35)

it is obtained that \(w\left( \varvec{e}_d,\varvec{e}_v\right) \) can be upper- and lower bounded as follows

$$\begin{aligned} \varepsilon _{11} \left\| {\varvec{e}}\right\| ^2 \le w\left( \varvec{e}_d,\varvec{e}_v\right) \le \varepsilon _{12} \left\| {\varvec{e}}\right\| ^2 \end{aligned}$$
(36)

Appendix 1 shows in detail how it was obtained.

Now, taking the time derivative of \(w\left( \varvec{e}_d,\varvec{e}_v\right) \) we have that

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right)= & {} \dot{\varvec{e}}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{e}_d+ \varvec{e}_d^T \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\varvec{e}_d\nonumber \\{} & {} + \varvec{e}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\dot{\varvec{e}}_d+ \varvec{e}_v^T \dot{\varvec{e}}_v\end{aligned}$$
(37)

where, from (15) and (28), \(\dot{\varvec{e}}_d= \dot{\varvec{\tau }}_d-\varvec{X}^{-1}\hat{\varvec{M}}^{-1}(\varvec{q})\varvec{e}_d\). Therefore, considering that \(\dot{\varvec{e}}_v\) is given by (30) then

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right)= & {} \left[ \dot{\varvec{\tau }}_d-\varvec{X}^{-1}\hat{\varvec{M}}^{-1}(\varvec{q})\varvec{e}_d\right] ^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{e}_d\nonumber \\{} & {} + \varvec{e}_d^T \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\varvec{e}_d\nonumber \\{} & {} + \varvec{e}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\left[ \dot{\varvec{\tau }}_d-\varvec{X}^{-1}\hat{\varvec{M}}^{-1}(\varvec{q})\varvec{e}_d\right] \nonumber \\{} & {} + \varvec{e}_v^T \left[ \ddot{\varvec{q}}- \varvec{A}_v \varvec{e}_v\right] \nonumber \\= & {} \dot{\varvec{\tau }}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{e}_d-\varvec{e}_d^T \left[ \hat{\varvec{M}}^{-1}(\varvec{q})\right] ^T\nonumber \\{} & {} \left[ \varvec{X}^{-1} \right] ^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{e}_d\nonumber \\{} & {} + \varvec{e}_d^T \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\varvec{e}_d+ \varvec{e}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\dot{\varvec{\tau }}_d\nonumber \\{} & {} - \varvec{e}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{X}^{-1}\hat{\varvec{M}}^{-1}(\varvec{q})\varvec{e}_d\nonumber \\{} & {} + \varvec{e}_v^T \ddot{\varvec{q}}- \varvec{e}_v^T \varvec{A}_v \varvec{e}_v\nonumber \\= & {} \varvec{e}_d^T \left[ \varvec{X}+ \varvec{X}^T - \varvec{X}^T \hat{\varvec{M}}^{-1}(\varvec{q})\varvec{X}\right] \varvec{e}_d\nonumber \\{} & {} + \dot{\varvec{\tau }}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{e}_d\nonumber \\{} & {} + \varvec{e}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\dot{\varvec{\tau }}_d+ \varvec{e}_v^T \ddot{\varvec{q}}- \varvec{e}_v^T \varvec{A}_v \varvec{e}_v\end{aligned}$$
(38)

In order to demonstrate that \(\dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \) is negative definite, consider Assumptions 4 and 6, as well as the following positive constant

$$\begin{aligned} \varepsilon _{2} \buildrel \Delta \over = \text {min} \left\{ { \left( 1-\theta \right) \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} , \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} - k_a}\right\} > 0 \end{aligned}$$
(39)

with \(\theta \in \left( 0,1\right) \) and \(\lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} > k_a\). Then, from (18)

$$\begin{aligned} \varvec{e}_d^T \left[ \varvec{X}+ \varvec{X}^T - \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\right] \varvec{e}_d\ge \varvec{e}_d^T \varvec{\Gamma }\varvec{e}_d&\ge \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 \nonumber \\ \qquad \Longrightarrow - \varvec{e}_d^T \left[ \varvec{X}+ \varvec{X}^T - \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\right] \varvec{e}_d&\le - \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 \end{aligned}$$
(40)

also, note that according to Property 4

$$\begin{aligned} \dot{\varvec{\tau }}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\varvec{e}_d+ \varvec{e}_d^T \varvec{X}^T \hat{\varvec{M}}(\varvec{q})\varvec{X}\dot{\varvec{\tau }}_d\le & {} 2 \sigma _M \left\| {\dot{\varvec{\tau }}_d}\right\| \left\| {\varvec{X}}\right\| ^2 \left\| {\varvec{e}_d}\right\| \nonumber \\\le & {} 2 \sigma _M k_d \left\| {\varvec{X}}\right\| ^2 \left\| {\varvec{e}_d}\right\| \end{aligned}$$
(41)

while from (31)

$$\begin{aligned} \varvec{e}_v^T \ddot{\varvec{q}}\le \left\| {\varvec{e}_v}\right\| \left\| {\ddot{\varvec{q}}}\right\| \le k_a \left\| {\varvec{e}_v}\right\| ^2 \end{aligned}$$
(42)

and as \(\varvec{A}_v\) is a positive definite diagonal matrix

$$\begin{aligned} - \varvec{e}_v\varvec{A}_v \varvec{e}_v\le - \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} \left\| {\varvec{e}_v}\right\| ^2 \end{aligned}$$
(43)

Then, from inequalities (40) to (43), \(\dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \) is upper bounded by

$$\begin{aligned}{} & {} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \\{} & {} \quad \le -\lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 + 2 \sigma _M k_d \left\| {\varvec{X}}\right\| ^2 \left\| {\varvec{e}_d}\right\| \\{} & {} \qquad - \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} \left\| {\varvec{e}_v}\right\| ^2 + k_a \left\| {\varvec{e}_v}\right\| ^2 \\{} & {} \quad \le -\left( 1-\theta \right) \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 - \left( \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} - k_a \right) \left\| {\varvec{e}_v}\right\| ^2 \\{} & {} \qquad - \left( \theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 -2 \sigma _M k_d \left\| {\varvec{X}}\right\| ^2 \left\| {\varvec{e}_d}\right\| \right) \\{} & {} \quad \le - \left[ \begin{array}{c}\left\| {\varvec{e}_d}\right\| \\ \left\| {\varvec{e}_v}\right\| \end{array}\right] ^T \varvec{Q}_{2} \left[ \begin{array}{c}\left\| {\varvec{e}_d}\right\| \\ \left\| {\varvec{e}_v}\right\| \end{array}\right] - w_2\left( \varvec{e}_d\right) \end{aligned}$$

where

$$\begin{aligned} \varvec{Q}_{2}= & {} \left[ \begin{array}{cc} \left( 1-\theta \right) \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} &{} 0 \\ 0 &{} \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} - k_a \end{array}\right] \\ w_2\left( \varvec{e}_d\right)= & {} \theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 - 2 \sigma _M k_d \left\| {\varvec{X}}\right\| ^2 \left\| {\varvec{e}_d}\right\| \end{aligned}$$

Therefore

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \le - \varepsilon _2 \left\| {\varvec{e}}\right\| ^2 <0, \qquad \forall \left\| {\varvec{e}_d}\right\| \ge \frac{2 k_d \sigma _M \left\| {\varvec{X}}\right\| ^2}{\theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} } \end{aligned}$$
(44)

Now, according to (36), it can be observed that \(w\left( \varvec{e}_d,\varvec{e}_v\right) / \varepsilon _{12} \le \left\| {\varvec{e}}\right\| ^2\) thus

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \le -\frac{\varepsilon _{2}}{\varepsilon _{12}} w\left( \varvec{e}_d,\varvec{e}_v\right) , \qquad \forall \left\| {\varvec{e}_d}\right\| \ge \frac{2 k_d \sigma _M \left\| {\varvec{X}}\right\| ^2}{\theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} } \end{aligned}$$

and then

$$\begin{aligned} w(t) \le w(0) \exp \left( -\frac{\varepsilon _{2}}{\varepsilon _{12}} t \right) , \qquad \forall \left\| {\varvec{e}_d}\right\| \ge \frac{2 k_d \sigma _M \left\| {\varvec{X}}\right\| ^2}{\theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} } \end{aligned}$$
(45)

Also, from (36) we have that \(\left\| {\varvec{e}}\right\| ^2 \le w(t)/\varepsilon _{11}\) thereby

$$\begin{aligned} \left\| {\varvec{e}}\right\| ^2 \le \frac{w(0)}{\varepsilon _{11}} \exp \left( -\frac{\varepsilon _{2}}{\varepsilon _{12}} t \right) , \qquad \forall \left\| {\varvec{e}_d}\right\| \ge \frac{2 k_d \sigma _M \left\| {\varvec{X}}\right\| ^2}{\theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} } \end{aligned}$$

that is,

$$\begin{aligned}{} & {} \left\| {\varvec{e}}\right\| \le \sqrt{\frac{w(0)}{\varepsilon _{11}}} \exp \left( -\frac{\varepsilon _{2}}{2\varepsilon _{12}} t \right) , \\{} & {} \forall \left\| {\varvec{e}_d}\right\| \ge \frac{2 k_d \sigma _M \left\| {\varvec{X}}\right\| ^2}{\theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} }, \; t>0 \end{aligned}$$

Therefore, according to the uniform ultimate boundedness theorems [39], the tracking error is globally uniformly ultimately bounded. Moreover, the perturbation estimation error converges with an exponential rate of \(\varepsilon _{2}/\left( 2\varepsilon _{12}\right) \) to the ball with radius \(2 k_d \sigma _M \left\| {\varvec{X}}\right\| ^2/\left( \theta \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \right) \), \(\forall \varvec{e}_d(0) \in {\mathbb {R}}^2\), where \(0<\theta <1\). While the velocity estimation error will be bounded for any initial condition \(\varvec{e}_v(0)\).

3.2.2 Slow-varying disturbances

Consider again the Lyapunov candidate function (32) and its time derivative (38), as well as the following positive constant

$$\begin{aligned} \varepsilon _{3} \buildrel \Delta \over = \text {min} \left\{ {\lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} ,\lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} - k_a}\right\} > 0 \end{aligned}$$
(46)

with \(\lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} > k_a\).

According to Assumption 5, it can be observed that Eq. (38) is simplified as follows

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right)= & {} \varvec{e}_d^T \left[ \varvec{X}+ \varvec{X}^T - \varvec{X}^T \hat{\varvec{M}}^{-1}(\varvec{q})\varvec{X}\right] \varvec{e}_d\nonumber \\{} & {} + \varvec{e}_v^T \ddot{\varvec{q}}- \varvec{e}_v^T \varvec{A}_v \varvec{e}_v\end{aligned}$$
(47)

Now, according to Assumption  6 and inequalities (40), (42) and (43), we obtain that

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right)\le & {} -\lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \left\| {\varvec{e}_d}\right\| ^2 - \left( \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} - k_a \right) \left\| {\varvec{e}_v}\right\| ^2 \\\le & {} - \left[ \begin{array}{c}\left\| {\varvec{e}_d}\right\| \\ \left\| {\varvec{e}_v}\right\| \end{array}\right] ^T \varvec{Q}_{3} \left[ \begin{array}{c}\left\| {\varvec{e}_d}\right\| \\ \left\| {\varvec{e}_v}\right\| \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} \varvec{Q}_{3} = \left[ \begin{array}{cc} \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} &{} 0 \\ 0 &{} \lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} - k_a \end{array}\right] \end{aligned}$$

Therefore

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \le - \varepsilon _3 \left\| {\varvec{e}}\right\| ^2 <0 \end{aligned}$$
(48)

Note that \(\dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \) is negative definite for all \(\varvec{e}\in {\mathbb {R}}^{2n}\). Therefore, the disturbance and velocity estimation errors asymptotically converge to zero as time tends to infinity, for all \(\varvec{e}\in {\mathbb {R}}^{2n}\). In order to compute the convergence rate, from (36) it can be observed that \(w\left( \varvec{e}_d,\varvec{e}_v\right) / \varepsilon _{12} \le \left\| {\varvec{e}}\right\| ^2\), hence

$$\begin{aligned} \dot{w}\left( \varvec{e}_d,\varvec{e}_v\right) \le -\frac{\varepsilon _{3}}{\varepsilon _{12}} w\left( \varvec{e}_d,\varvec{e}_v\right) \end{aligned}$$

and then

$$\begin{aligned} w(t) \le w(0) \exp \left( -\frac{\varepsilon _{3}}{\varepsilon _{12}} t \right) \end{aligned}$$
(49)

Again, from (36) we have that \(\left\| {\varvec{e}}\right\| ^2 \le w(t)/\varepsilon _{11}\), thus

$$\begin{aligned} \left\| {\varvec{e}}\right\| ^2 \le \frac{w(0)}{\varepsilon _{11}} \exp \left( -\frac{\varepsilon _{3}}{\varepsilon _{12}} t \right) \end{aligned}$$

that is,

$$\begin{aligned} \left\| {\varvec{e}}\right\| \le \sqrt{\frac{w(0)}{\varepsilon _{11}}} \exp \left( -\frac{\varepsilon _{3}}{2\varepsilon _{12}} t \right) , \qquad t>0 \end{aligned}$$

Therefore, the minimum convergence rate of the estimation error is

$$\begin{aligned} \beta = \frac{\varepsilon _{3}}{2\varepsilon _{12}} \end{aligned}$$
(50)

where \(\varepsilon _{12}\) and \(\varepsilon _{3}\) were defined in (34) and (46), respectively.

3.3 Aspects to consider for implementing the proposed NDOB

While we have analyzed the convergence of estimation errors, there remain practical issues that require attention to finalize the NDOB design. In the subsequent analyses, please take into account the rate of convergence as defined in Eq. (50), as typically, there is limited prior information available regarding the perturbations [23].

3.3.1 Velocity estimator

Note that from the velocity estimator (20), the following transfer function [37] (in the frequency domain) is obtained for its i-th element

$$\begin{aligned} v_i = \frac{a_{vi} s }{s+a_{vi}} q_i =\frac{a_{vi} }{s+a_{vi}} \dot{q}_i \end{aligned}$$

whose maximum gain is 1. Therefore, \(\left\| {\varvec{v}}\right\| \) tends to \(\left\| {\dot{\varvec{q}}}\right\| \) after the transient period. Considering the definition of \(\varvec{e}_v\) in (27), we obtain that \(\left\| {\varvec{e}_v}\right\| = \left\| {\dot{\varvec{q}}-\varvec{v}}\right\| \) and consequently \(\left\| {\varvec{e}_v}\right\| \le \left\| {\dot{\varvec{q}}}\right\| + \left\| {\varvec{v}}\right\| \), thus \(\left\| {\varvec{e}_v}\right\| \le 2 \left\| {\dot{\varvec{q}}}\right\| \). While when considering Inequality (31), \(\left\| {\ddot{\varvec{q}}}\right\| \le k_a \left\| {\varvec{e}_v}\right\| \le 2 k_a \left\| {\dot{\varvec{q}}}\right\| \). Then, according to Assumption 2

$$\begin{aligned} k_a \ge \frac{\left\| {\ddot{\varvec{q}}}\right\| _{\textrm{max}}}{2\left\| {\dot{\varvec{q}}}\right\| _{\textrm{max}}} \end{aligned}$$

On the other hand, concerning the definition of \(\varepsilon _{3}\), it is feasible to design \(\varvec{\Gamma }= \gamma _o \varvec{I}_n\) and \(\varvec{A}_v =a_v \varvec{I}_n\) to satisfy \(\lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} > k_a\) and \(\lambda _{\textrm{min}}\left\{ {\varvec{A}_v}\right\} -k_a > \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \). Then, the constant \(a_v\) can be selected as

$$\begin{aligned} a_v = \alpha _v \left( \gamma _o + k_a \right) \end{aligned}$$

with \(k_a = \left\| {\ddot{\varvec{q}}}\right\| _{\textrm{max}}/ \left( 2\left\| {\dot{\varvec{q}}}\right\| _{\textrm{max}}\right) \) and \(\alpha _v>1\). The procedure for calculating the value of \(\gamma _o\) will be explained in the following section.

3.3.2 Gain of the NDOB

To align with the definition of \(\varepsilon _{12}\), one can choose \(\varvec{Y}= \varvec{X}^{-1} = y \varvec{I}_n\) such as \(\sigma _M \left\| {\varvec{X}}\right\| ^2 <1/2\). Based on the analysis presented in the preceding section, it is obtained that the minimum convergence rate for the NDOB is given by \(\beta = \lambda _{\textrm{min}}\left\{ {\varvec{\Gamma }}\right\} \), then

$$\begin{aligned} \gamma _o = \beta \end{aligned}$$
(51)

Furthermore, pre- and post-multiplying (18) by \(\varvec{Y}^T\) and \(\varvec{Y}\), respectively, we obtain that

$$\begin{aligned} \varvec{Y}^T \left[ \varvec{X}+ \varvec{X}^T - \varvec{X}^T \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\varvec{X}\right] \varvec{Y}\ge & {} \varvec{Y}^T \varvec{\Gamma }\varvec{Y}\\ \varvec{Y}^T + \varvec{Y}- \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\ge & {} \varvec{Y}^T \varvec{\Gamma }\varvec{Y}\\ \varvec{Y}^T + \varvec{Y}- \varvec{Y}^T \varvec{\Gamma }\varvec{Y}\ge & {} \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\end{aligned}$$

Note that Property 5 implies that \(\dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\le \zeta \varvec{I}_n\) for some constant \(\zeta >0\). Then, \(\varvec{Y}\) can be designed to satisfy \(\varvec{Y}^T + \varvec{Y}- \varvec{Y}^T \varvec{\Gamma }\varvec{Y}\ge \zeta \varvec{I}_n \ge \dot{\hat{\varvec{M}}}(\varvec{q},\dot{\varvec{q}})\) and so

$$\begin{aligned} \left( \varvec{Y}^T + \varvec{Y}- \zeta \varvec{I}_n \right) - \varvec{Y}^T \varvec{\Gamma }\varvec{Y}\ge & {} {\varvec{0}}_n \\ \left[ \left( y \varvec{I}_n\right) ^T + y \varvec{I}_n - \zeta \varvec{I}_n \right] - \left[ y \varvec{I}_n\right] ^T \left[ \gamma _o \varvec{I}_n\right] \left[ y \varvec{I}_n\right]\ge & {} {\varvec{0}}_n \\ \left[ 2y - \zeta - y^2 \gamma _o \right] \varvec{I}_n\ge & {} {\varvec{0}}_n \\ 2y - \zeta - y^2 \gamma _o\ge & {} 0 \end{aligned}$$

thus, according to (51)

$$\begin{aligned} 2y - \zeta \ge y^2 \beta \end{aligned}$$
(52)

Now, because \(\sigma _M \left\| {\varvec{X}}\right\| ^2 < 1/2\) then \(\sigma _M/y^2 \le 1/2\), therefore

$$\begin{aligned} y \ge \frac{1}{2} \left( \zeta + 2 \sigma _M \beta \right) \end{aligned}$$

Note that \(\left\| {\varvec{L}(\varvec{q})}\right\| \le \left\| {\varvec{Y}}\right\| \left\| {\hat{\varvec{M}}^{-1}(\varvec{q})}\right\| \), i.e., the observer gain is proportional to \(\left\| {\varvec{Y}}\right\| \). Then, a high NDOB gain amplifies sensitivity to disturbances caused by measurement noise, leading to its amplification. From this perspective, it is advisable to choose the smallest possible NDOB gain so that

$$\begin{aligned} \varvec{Y}_{\textrm{optimal}} = \frac{1}{2} \left[ \zeta + 2 \beta \sigma _M \right] \varvec{I}_n \end{aligned}$$
(53)

where, as previously defined, \(\zeta \) and \(\sigma _M\) are constants that depend on the robot’s dynamic parameters and maximum joint velocities. With this, the NDOB design procedure is concluded.

4 Simulation results

The initial validation of the proposed NDOB was conducted by simulating a robot-environment interaction task. The numerical simulation was executed using Matlab r2021b, employing the ODE45 function.

We performed a comparative analysis, assessing the performance of our proposal against Mohammadi’s scheme [23] and the GMOB approach [31]. To regulate the robot-environment interaction task, the following stiffness controller [40] was used

$$\begin{aligned} \varvec{\tau }= \varvec{J}^T \left[ \varvec{K}_p \tanh \left( \bar{\varvec{x}}\right) - \varvec{K}_v \dot{\varvec{x}} \right] + \varvec{g}(\varvec{q})\end{aligned}$$
(54)

where \(\bar{\varvec{x}} = \varvec{x}_d - \varvec{x}\), with \(\varvec{x}_d\) and \(\varvec{x}\) representing the desired and actual posture of the robot end-effector in task space, respectively. \(\varvec{J}\) is the analytic Jacobian matrix, \(\varvec{g}(\varvec{q})\) is the gravity vector of the robot, while \(\varvec{K}_p\) and \(\varvec{K}_v\) are the proportional and damping gain matrices, respectively. Since the controller was originally designed without a velocity estimator, the task-space velocity is computed as \(\dot{\varvec{x}}= \varvec{J}\dot{\varvec{q}}\).

It is worth noting that the control gains remained consistent with those outlined in [40]. This choice was made to solely evaluate the performance of the disturbance observers, hence \(\varvec{K}_p=\text {diag}\left\{ {750, 1750, 850}\right\} \) and \(\varvec{K}_v=\text {diag}\left\{ {15, 15, 45}\right\} \).

4.1 Robot model

The robotic platform utilized in numerical simulations is a 3-DOF anthropomorphic robot manipulator. The corresponding direct kinematics mapping \(\varvec{x}(\varvec{q})=\left[ \begin{array}{c} x_1, x_2, x_3 \end{array}\right] ^T\) and the elements of Jacobian matrix are given by

$$\begin{aligned} x_1= & {} \left( d_2+d_3 \right) c_{1} - l_2 s_{1} s_{2} - l_3 s_{1} \left( c_{2} s_{3} +s_{2} c_{3} \right) \\ x_2= & {} \left( d_2+d_3 \right) s_{1} + l_2 c_{1} s_{2} + l_3 c_{1} \left( c_{2} s_{3} + s_{2} c_{3} \right) \\ x_3= & {} - l_2 c_{2} - l_3 c_{2,3} \\ J_{11}= & {} - \left( d_2 + d_3 \right) s_{1} - l_2 c_{1} s_{2} - l_3 c_{1} \left( c_{2} s_{3} + s_{2} c_{3} \right) \\ J_{12}= & {} - l_2 s_{1} c_{2} + l_3 s_{1} \left( s_{2} s_{3} - c_{2} c_{3} \right) \\ J_{13}= & {} l_3 s_{1} \left( s_{2} s_{3} - c_{2} c_{3}\right) \\ J_{21}= & {} \left( d_2 + d_3 \right) c_{1} - l_2 s_{1} s_{2} - l_3 s_{1} \left( c_{2} s_{3} + s_{2} c_{3} \right) \\ J_{22}= & {} l_2 c_{1} c_{2} + l_3 c_{1} \left( c_{2} c_{3} - s_{2} s_{3} \right) \\ J_{23}= & {} l_3 c_{1} \left( c_{2} c_{3} -s_{2} s_{3}\right) \\ J_{31}= & {} 0 \\ J_{32}= & {} l_2 s_{2} + l_3 s_{2,3} \\ J_{33}= & {} l_3 s_{2,3} \end{aligned}$$

where \(s_i = \sin (q_i)\), \(c_i = \cos (q_i)\), \(s_{2,3} =\sin (q_2+q_3)\) and \(c_{2,3} = \cos (q_2+q_3)\), while \(d_2=0.15\) m, \(d_3=0.1\) m, \(l_2=0.45\) m, and \(l_3=0.45\) m.

The dynamic model of the robot manipulator and its nominal parameters were reported in [41], and their corresponding numerical values are presented in Table 1. The model has the following structure

$$\begin{aligned}{} & {} \underbrace{\left[ \begin{array}{ccc} M_{11} &{} M_{12} &{} M_{13} \\ M_{12} &{} M_{22} &{} M_{23} \\ M_{13} &{} M_{23} &{} M_{33} \end{array}\right] }_{\varvec{M}(\varvec{q})} \ddot{\varvec{q}} + \underbrace{\left[ \begin{array}{ccc} C_{11} &{} C_{12} &{} C_{13} \\ C_{21} &{} C_{22} &{} C_{23} \\ C_{31} &{} C_{32} &{} C_{33} \end{array}\right] }_{\varvec{C}(\varvec{q},\dot{\varvec{q}})} \dot{\varvec{q}}+ \underbrace{\left[ \begin{array}{c} g_1 \\ g_2 \\ g_3 \end{array}\right] }_{\varvec{g}(\varvec{q})} + \underbrace{\left[ \begin{array}{c}f_1 \\ f_2 \\ f_3 \end{array}\right] }_{\varvec{f}(\dot{\varvec{q}})}\\{} & {} \quad = \varvec{\tau }- \underbrace{\left[ \begin{array}{ccc} J_{11} &{} J_{12} &{} J_{13} \\ J_{21} &{} J_{22} &{} J_{23} \\ J_{31} &{} J_{32} &{} J_{33} \\ \end{array}\right] ^{T}}_{\varvec{J}^T(\varvec{q})}\varvec{f}_e\end{aligned}$$

where

$$\begin{aligned} M_{11}= & {} \rho _{1} + \rho _{2} c_{2}^2 + \rho _{3} s_{22} + \rho _{4} s_{22,23} + \rho _{5} c_{2,3}^2 \nonumber \\{} & {} + 2 l_{2} \left( \rho _{6} s_{2} s_{2,3} +\rho _{7} s_{2} c_{2,3} \right) \nonumber \\ M_{12}= & {} \rho _{8} c_{2,3} + \rho _{9} s_{2,3} + \rho _{10} c_{2} +\rho _{11} s_{2} \nonumber \\ M_{13}= & {} \rho _{8} c_{2,3} + \rho _{9} s_{2,3} \nonumber \\ M_{22}= & {} \rho _{12} + 2 l_{2} \left( \rho _{6} c_3 - \rho _{7} s_3 \right) \nonumber \\ M_{23}= & {} \rho _{13} + l_{2} \left( \rho _{6} c_3 - \rho _{7} s_3 \right) \nonumber \\ M_{33}= & {} \rho _{13} \nonumber \\ C_{11}= & {} \dot{q}_{2} \left( \rho _{3} c_{22} -\frac{\rho _{2}}{2} s_{22} \right) \nonumber \\{} & {} + \left( \dot{q}_{2} +\dot{q}_{3} \right) \left( \rho _{4} c_{22,23} -\frac{\rho _{5}}{2} s_{22,23} \right) \nonumber \\{} & {} + l_{2} \left( \dot{q}_{2} +\frac{1}{2} \dot{q}_{3} \right) \left( \rho _{6} s_{22,3} + \rho _{7} c_{22,3} \right) \nonumber \\{} & {} -\frac{l_{2}}{2} \dot{q}_{3} \left( \rho _{6} s_3 + \rho _{7} c_3 \right) \nonumber \\ C_{12}= & {} \dot{q}_{1} \left[ \rho _{3} c_{22} -\frac{\rho _{2}}{2} s_{22} + \rho _{4} c_{22,23} -\frac{\rho _{5}}{2} s_{22,23}\right. \nonumber \\{} & {} \qquad \left. + l_{2} \left( \rho _{6} s_{22,3} + \rho _{7} c_{22,3} \right) \right] \nonumber \\{} & {} +\dot{q}_{2} \left( \rho _{11} c_{2} - \rho _{10} s_{2} \right) +\left( \dot{q}_{2} + \dot{q}_{3} \right) \left( \rho _{9} c_{2,3} -\rho _{8} s_{2,3} \right) \nonumber \\ C_{13}= & {} \dot{q}_{1} \left[ \rho _{4} c_{22,23} -\frac{\rho _{5}}{2} s_{22,23} +\frac{l_{2}}{2} \right. \nonumber \\{} & {} \qquad \left. \left[ \rho _{6} \left( s_{22,3} - s_3 \right) +\rho _{7} \left( c_{22,3} - c_3 \right) \right] \right] \nonumber \\{} & {} +\left( \dot{q}_{2} + \dot{q}_{3} \right) \left( \rho _{9} c_{2,3} - \rho _{8} s_{2,3} \right) \nonumber \\ C_{21}= & {} \dot{q}_{1} \left[ \frac{\rho _{2}}{2} s_{22} -\rho _{3} c_{22}- \rho _{4} c_{22,23}+\frac{\rho _{5}}{2} s_{22,23} \right. \nonumber \\{} & {} \qquad \left. - l_{2} \left( \rho _{6} s_{22,3} + \rho _{7} c_{22,3} \right) \right] \nonumber \\ C_{22}= & {} - l_{2} \dot{q}_{3} \left( \rho _{6} s_3 + \rho _{7} c_3 \right) \nonumber \\ C_{23}= & {} -l_{2} \left( \dot{q}_{2} + \dot{q}_{3} \right) \left( \rho _{6} s_3 + \rho _{7} c_3 \right) \nonumber \\ C_{31}= & {} \dot{q}_{1} \left[ \frac{\rho _{5}}{2} s_{22,23} - \rho _{4} c_{22,23}+\frac{l_{2}}{2} \right. \nonumber \\{} & {} \qquad \left. \left[ \rho _{6}\left( s_3 - s_{22,3} \right) + \rho _{7} \left( c_3 - c_{22,3} \right) \right] \right] \nonumber \\ C_{32}= & {} \dot{q}_{2} l_{2} \left( \rho _{6} s_3 + \rho _{7} c_3 \right) \nonumber \\ C_{33}= & {} 0 \nonumber \\ g_1= & {} 0 \nonumber \\ g_2= & {} \rho _{14} s_{2} + \rho _{15} c_{2} + g \left( \rho _{6} s_{2,3} + \rho _{7} c_{2,3} \right) \nonumber \\ g_3= & {} g \left( \rho _{6} s_{2,3} + \rho _{7} c_{2,3} \right) \nonumber \\ f_1= & {} \rho _{16} \dot{q}_{1}+\rho _{17} \textrm{sgn}(\dot{q}_{1}) \nonumber \\ f_2= & {} \rho _{18} \dot{q}_{2}+\rho _{19} \textrm{sgn}(\dot{q}_{2}) \nonumber \\ f_3= & {} \rho _{20} \dot{q}_{3}+\rho _{21} \textrm{sgn}(\dot{q}_{3}) \end{aligned}$$
(55)

with \(s_{2} = \sin (q_2)\), \(c_{2} = \cos (q_2)\), \(s_{3} = \sin (q_3)\), \(c_{3} = \cos (q_3)\), \(s_{22} = \sin (2q_2)\), \(c_{22} = \cos (2q_2)\), \(s_{2,3} = \sin (q_2+q_3)\), \(c_{2,3} = \cos (q_2+q_3)\), \(s_{22,3} = \sin (2q_2+q_3)\), \(c_{22,3} = \cos (2q_2+q_3)\), \(s_{22,23} = \sin (2q_2+2q_3)\), \(c_{22,23} = \cos (2q_2+2q_3)\). Whereas \(\varvec{f}_e\) denotes the external force applied to the robot end-effector and \(g=9.81\) m/s\({}^2\) is the acceleration of gravity.

Table 1 Nominal parameters of the dynamic model
Full size table

The robot actuators have as torque limit values \(\tau _{\textrm{max}} = \left[ \begin{array}{c} 50, 150, 15\end{array}\right] ^T\) Nm, for the base, shoulder and elbow joints, respectively. Moreover, the maximum values of velocity and acceleration are \(\dot{\varvec{q}}_{\textrm{max}} = \left[ \begin{array}{c}2\pi , \pi , 4\pi \end{array}\right] ^T\)rad/s and \(\ddot{\varvec{q}}_{\textrm{max}} = \left[ \begin{array}{c}520.833333, 1056.338028, 1250\end{array}\right] ^T\) rad/s\({}^2\), respectively. Thus, inequalities (11) and (12) are satisfied with \(\sigma _M = 5.116525\) kg m\({}^2\) and \(\zeta =167.048302\) kg m\({}^2\)/s, respectively.

4.2 Configuration of the interaction task

The interaction task is depicted in Fig. 1, where the robot is required to interact with an inclined plane. The stiffness of the plane in the normal direction is 2000 N/m. The origin of this plane, known as user frame in industrial robotics, is represented as \(x_p y_p z_p\) and it is located at \(\left[ \begin{array}{c}0.5, 0.35, -\,0.49\end{array}\right] ^T\) m from the world reference frame \(x_0 y_0 z_0\). The orientation is established through a sequence of successive rotations X–Z–X, with angles of 30, 90, and 20 degrees, respectively. Then, the position of the robot end-effector relative to the user frame is computed as follows

$$\begin{aligned} \left[ \begin{array}{c} x_{pe 1} \\ x_{pe 2} \\ x_{pe 3} \\ 1 \\ \end{array}\right] = \varvec{H}_e^{-1} \left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ 1 \\ \end{array}\right] \end{aligned}$$
(56)

where

$$\begin{aligned} \varvec{H}_e = \left[ \begin{array}{cccc} 0 &{} -0.940 &{} 0.342 &{} 0.50 \\ 0.866 &{} -0.171 &{} -0.470 &{} 0.35 \\ 0.5 &{} 0.296 &{} 0.814 &{} -0.49 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] \end{aligned}$$
(57)

The robot’s motion commences with the initial joint configuration \(\varvec{q}(0)=\left[ \begin{array}{c}-\,10, 110, -\,75\end{array}\right] ^T\) degrees. Consequently, the robot end-effector is initially situated at \(\varvec{x}(0)=\left[ \begin{array}{c}0.364, 0.627, -\,0.215 \end{array}\right] ^T\) m and needs to reach the target position \(\varvec{x}_d=\left[ \begin{array}{c}0.321, 0.626, -\,0.28 \end{array}\right] ^T\) m. Whereas the initial joint velocity is \(\dot{\varvec{q}}(0)=\left[ \begin{array}{c}0,0,0 \end{array}\right] \) rad/s.

Fig. 1
figure 1

Graphical representation of the interaction task. The reference frame at the robot’s origin is denoted as \(x_0 y_0 z_0\), while \(x_p y_p z_p\) represents the coordinate frame attached to the plane (user frame)

Full size image

4.3 Configuration of the observers

In order to compare the performance of both NDOBs and considering that \(\varvec{Y}_{M\text {optimal}} = \varvec{Y}_{\textrm{optimal}}\), the convergence rate was set as \(\beta = \beta _{M2} = 8\). Then,

$$\begin{aligned} \varvec{Y}_{\textrm{optimal}} = 124.456 \varvec{I}_n \end{aligned}$$

and \(\gamma _o = 8\). In addition, taking into account the maximum velocity values and choosing \(\alpha _v=20\), we have that \(k_a = 59.648\) and \(a_v = 1352.953\), therefore

$$\begin{aligned} \varvec{A}_v = 1352.953 \varvec{I}_n \end{aligned}$$

Furthermore, for ensuring swift convergence in velocity estimation and enhancing the observer’s response, it is advisable to choose an appropriate initial condition for the auxiliary variable \(\varvec{v}_c\) and set the initial velocity to zero, such that \(\varvec{v}_c(0)=-\varvec{A}_v \varvec{q}(0)\).

On the other hand, the GMOB [31] can be formulated to estimate the disturbance torque, which can be modeled either as the external torque or as the sum of friction and external torque. In the first scenario,

$$\begin{aligned} \dot{\varvec{\Gamma }} = \varvec{\tau }- \hat{\varvec{C}}^T(\varvec{q},\dot{\varvec{q}})\dot{\varvec{q}}- \varvec{g}(\varvec{q})- \varvec{f}(\dot{\varvec{q}})+ \hat{\varvec{\tau }}_d\end{aligned}$$
(58)

where

$$\begin{aligned} \hat{\varvec{\tau }}_d= \varvec{L}\left[ \varvec{p}(t) -\varvec{p}(0) - \varvec{\Gamma }\right] \end{aligned}$$
(59)

with \(\varvec{p}= \varvec{M}(\varvec{q})\dot{\varvec{q}}\) representing the generalized momentum of the robot manipulator and \(\varvec{L}\) being a user-designed diagonal, definite positive matrix. The tuning of \(\varvec{L}\) aims to strike a balance between the desired bandwidth and noise amplification. While in the second scenario,

$$\begin{aligned} \dot{\varvec{\Gamma }} = \varvec{\tau }- \hat{\varvec{C}}^T(\varvec{q},\dot{\varvec{q}})\dot{\varvec{q}}- \varvec{g}(\varvec{q})+ \hat{\varvec{\tau }}_d\end{aligned}$$
(60)

To assess its performance relative to NDOBs, \(\varvec{L}\) was selected as

$$\begin{aligned} \varvec{L}= 28.003 \varvec{I}_n \end{aligned}$$

with \(\varvec{\Gamma }(0) = -\varvec{p}(0)\) as initial condition.

4.4 Results

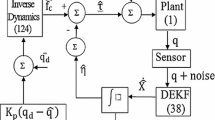
To optimize simulation time, the traditional friction model is approached as a continuous function denoted by \(f(\dot{q}_i) = f_{vi} \dot{q}_{i} + f_{ci} \tanh (10^{4}\dot{q}_{i})\), where \(f_{vi}\) and \(f_{ci}\) represent the i-th viscous and Coulumb friction coefficients, respectively. The block diagram in Fig. 2 represents how both the controller and the proposed NDOB were implemented. Please note that while the controller necessitates the robot’s joint velocity for its implementation, the proposed NDOB solely relies on the estimated velocity \(\varvec{v}\).

Fig. 2
figure 2

Block diagram illustrating the implementation of the proposed NDOB and the stiffness controller

Full size image

Figure 3 illustrates a comparative graph between the robot’s actual velocity and its estimation obtained through the proposed scheme. It is evident that the velocity estimation error undergoes a transient phase lasting approximately 0.5 s before gradually converging to a stable state, approaching zero.

Fig. 3
figure 3

Components of joint velocity and velocity estimation error, respectively

Full size image

The results of disturbance estimation are shown in Figs. 4 and 5. The estimation error behaviors are notably similar among the three observers. The proposed scheme holds the advantage of not necessitating velocity measurements.

Fig. 4
figure 4

Components of disturbance torque, where the subscript ‘m’ corresponds to results obtained with Mohammadi’s observer, while the subscript ‘g’ indicates results obtained with the GMOB

Full size image
Fig. 5
figure 5

Components of the disturbance estimation error, where the subscript ‘m’ corresponds to results obtained with Mohammadi’s observer, while the subscript ‘g’ indicates results obtained with the GMOB

Full size image

Additionally, assuming that unmodeled dynamics is negligible, Fig. 6 presents the estimate of contact force given by \(\hat{\varvec{f}_e}=\left[ \varvec{J}^T(\varvec{q})\right] ^{-1} \varvec{\tau }_e\), where \(\varvec{\tau }_e=-\hat{\varvec{\tau }_d}-\varvec{\tau }_{\textrm{fric}}\) with \(\varvec{\tau }_{\textrm{fric}}\) representing the friction torque for each observer, i.e., \(\varvec{f}(\dot{\varvec{q}})\) and \(\varvec{f}(\varvec{v})= \left. \varvec{f}(\dot{\varvec{q}})\right| _{\dot{\varvec{q}}=\varvec{v}} \), respectively. It can be observed that the force estimation behavior is nearly identical across all schemes.

Fig. 6
figure 6

Components of the estimated contact force, where the subscript ‘m’ corresponds to results obtained with Mohammadi’s observer, while the subscript ‘g’ indicates results obtained with the GMOB

Full size image

To assess the effectiveness of the disturbance estimator within a stiffness control scheme, we present the controller results in Fig. 7. It is evident that the position error components have a stable behavior. However, achieving the desired position is unattainable due to contact with the surface. Nevertheless, the system exhibits stable behavior. Consequently, during contact, priority is directed towards force regulation, as further illustrated in Fig. 7.

On the other hand, both the proposed observer and Mohammadi’s scheme can be adapted to enhance contact force estimation. This adaptation involves incorporating friction torques into the observer structure while excluding them from the perturbations. The formulation of this modified NDOB is detailed in [26]. Therefore, the corresponding modifications are \(\hat{\varvec{h}}(\varvec{q},\dot{\varvec{q}})= \hat{\varvec{C}}(\varvec{q},\dot{\varvec{q}})\dot{\varvec{q}}+ \varvec{g}(\varvec{q})+ \varvec{f}(\dot{\varvec{q}})\) and \(\hat{\varvec{h}}(\varvec{q},\varvec{v})= \hat{\varvec{C}}(\varvec{q},\varvec{v})\varvec{v}+ \varvec{g}(\varvec{q})+ \varvec{f}(\varvec{v})\) for Mohammadi’s NDOB and our proposal, respectively. It is important to emphasize that demonstrating the validity of the presented convergence analysis for both modified observers requires no extensive effort.

Fig. 7
figure 7

Position error components and normal contact force with respect to the user frame

Full size image
Fig. 8
figure 8

Components of disturbance torque in the case of the modified observers, where the subscript ‘m’ corresponds to results obtained with Mohammadi’s observer, while the subscript ‘g’ indicates results obtained with the GMOB

Full size image

Figures 8 and 9 depict the results of disturbance estimation, while Fig. 10 illustrates the contact force estimation for the modified structures with \(\hat{\varvec{f}_e}=-\left[ \varvec{J}^T(\varvec{q})\right] ^{-1} \hat{\varvec{\tau }_d}\). Observing the results, it becomes evident that incorporating the friction term into the observer structure yields an enhancement in the accuracy of contact force estimation. Furthermore, all components exhibit a convergence pattern similar to that obtained with the original scheme.

Fig. 9
figure 9

Components of the disturbance estimation error in the case of the modified observers, where the subscript ‘m’ corresponds to results obtained with Mohammadi’s observer, while the subscript ‘g’ indicates results obtained with the GMOB

Full size image

Lastly, Table 2 presents a numerical comparison of the root mean square (RMS) values for perturbation and contact force estimation errors, respectively. The force estimation error is defined as the difference between the actual and estimated contact force, i.e., \(\varvec{e}_{fe}= \varvec{f}_e- \hat{\varvec{f}_e}\). It is evident that Mohammadi’s NDOB yields slightly superior results in disturbance and contact force estimation. However, RMS values are very similar and the proposed observer holds the advantage of not requiring velocity measurements for its implementation. Furthermore, a more accurate estimate of the contact force is achieved using the modified structure for all disturbance observers.

To provide a comprehensive perspective, it is noteworthy to consider the findings from pertinent studies that employ alternative disturbance estimation techniques, such as Kalman filters and sliding mode schemes, as referenced in [2, 29, 32, 33]. In these studies, the reported results reveal instantaneous estimation errors of up to 5 Nm in external torques and 5 N in external forces, which surpass the errors observed in our proposed approach. Moreover, in certain cases, the implementation of these techniques necessitates a greater number of sensors. Furthermore, it’s worth noting that these results lack a quantitative assessment and are exclusively presented in graphical form. Regarding the remaining referenced studies [12, 16,17,18, 21, 28], they neither include comparative plots illustrating the estimated versus actual external force/torque nor provide a comprehensive performance evaluation. In some instances, the sole discernible advantage lies in a faster convergence rate.

Fig. 10
figure 10

Components of the estimated contact force in the case of the modified observers, where the subscript ‘m’ corresponds to results obtained with Mohammadi’s observer, while the subscript ‘g’ indicates results obtained with the GMOB

Full size image
Table 2 RMS values for the errors in disturbance and contact force estimation
Full size table

5 Experimental results

A series of experimental tests were conducted to validate the effective performance of the proposed scheme in a practical two-dimensional interaction task. To corroborate the simulation results obtained earlier, a comparative analysis was conducted, evaluating both the original and modified estimation schemes described previously, in the context of an interaction task regulated by the same controller (54). The control gains were selected as \(\varvec{K}_p=\text {diag}\left\{ {90, 90}\right\} \) and \(\varvec{K}_v=\text {diag}\left\{ {60, 60}\right\} \).

The experimental test involved directing the robot’s end-effector to interact with a solid, flat surface (a wooden wall covered with a styrofoam plate) positioned within the robot workspace, as illustrated in Fig. 11. The robot commences its motion from a stationary position with joint configuration \(\varvec{q}(0)=[45,-\,58]\) degrees. Consequently, the initial location of the robot end-effector is at \(\varvec{x}(0)=[0.486, -\,0.134]\) meters. As the robot starts moving, it endeavors to reach the target position \(\varvec{x}(0)=[0.638, -\,0.314]\) meters; however, it collides with the wooden structure before achieving this goal.

Fig. 11
figure 11

Experimental robotic platform

Full size image

5.1 Robot model and configuration of the NDOB

The experimental platform comprises a 2-DOF parallelogram SCARA-type robot manipulator. It is actuated using Sureservo systems, specifically the SVM-220B servomotor with a torque limit of 9.4 Nm and the SVA-2300 servoamplifier configured in torque mode. Joint positions are acquired using quadrature encoders with a resolution of 10,000 pulses per revolution. The control algorithm operates at a 2 ms cycle on an STM32F407 Discovery board. To assess the performance of the disturbance estimators, an ATI multi-axis force/torque sensor model Gamma was affixed to the robot end-effector, calibrated with a maximum force of 130 N and a maximum torque of 10 Nm about each axis.

The direct kinematic model \(\varvec{x}(\varvec{q}) = [x_1,x_2]^T\) and the elements of the Jacobian matrix are given by

$$\begin{aligned} x_1= & {} L_1 \sin {q_1} + L_2 \cos {q_2} \nonumber \\ x_2= & {} L_1 \cos {q_1} + L_2 \sin {q_2} \nonumber \\ J_{11}= & {} L_1 \cos {q_1} \nonumber \\ J_{12}= & {} -L_2 \sin {q_2} \nonumber \\ J_{21}= & {} -L_1 \sin {q_1} \nonumber \\ J_{22}= & {} L_2 \cos {q_2} \end{aligned}$$
(61)

where \(L_1=0.35\) m and \(L_2=0.45\) m. Figure 12 shows the kinematic diagram of the robot.

Fig. 12
figure 12

Kinematic diagram of the experimental robotic platform

Full size image

On the other hand, the dynamic model of the robot has the following structure

$$\begin{aligned} \underbrace{\left[ \begin{array}{cc}M_{11} &{} M_{12} \\ M_{12} &{} M_{22} \end{array}\right] }_{\varvec{M}(\varvec{q})} \ddot{\varvec{q}} + \underbrace{\left[ \begin{array}{cc}0 &{} C_{12} \\ C_{21} &{} 0 \end{array}\right] }_{\varvec{C}(\varvec{q},\dot{\varvec{q}})} \dot{\varvec{q}}+ \underbrace{\left[ \begin{array}{c}f_1 \\ f_2 \end{array}\right] }_{\varvec{f}(\dot{\varvec{q}})} = \varvec{\tau }- \underbrace{\left[ \begin{array}{cc}J_{11} &{} J_{12} \\ J_{21} &{} J_{22} \end{array}\right] ^T }_{\varvec{J}^T(\varvec{q})}\varvec{f}_e\end{aligned}$$

with

$$\begin{aligned} M_{11}=\, & {} \varrho _1 \nonumber \\ M_{12}=\, & {} \varrho _2 \sin {(q_1+q_2)} + \varrho _3 \cos {(q_1+q_2)} \nonumber \\ M_{21}=\, & {} \varrho _2 \sin {(q_1+q_2)} + \varrho _3 \cos {(q_1+q_2)} \nonumber \\ M_{22}=\, & {} \varrho _4 \nonumber \\ C_{12}=\, & {} \dot{q}_2 \left[ \varrho _2 \cos {(q_1+q_2)} - \varrho _3 \sin {(q_1+q_2)} \right] \nonumber \\ C_{21}=\, & {} \dot{q}_1 \left[ \varrho _2 \cos {(q_1+q_2)} - \varrho _3 \sin {(q_1+q_2)} \right] \nonumber \\ f_{1}=\, & {} f_{v1} \, \dot{q}_1 + f_{c1}\tanh \left( r_1 \dot{q}_1 \right) + b_{12} \left( \dot{q}_1+ \dot{q}_2 \right) \nonumber \\ f_{2}=\, & {} f_{v2} \, \dot{q}_2 + f_{c2}\tanh \left( r_2 \dot{q}_2 \right) + b_{12} \left( \dot{q}_1+ \dot{q}_2 \right) \end{aligned}$$
(62)

where \(\varvec{f}_e\) denotes the external forces applied to the end-effector. The nominal inertial and friction parameters are presented in Table 3.

Table 3 Nominal parameters of dynamic model (experimental robot)
Full size table

As previously stated, the actuators are subject to the following torque limit values \(\tau _{\textrm{max}}=[9.4,9.4]^T\) Nm, while the maximum velocity and acceleration values are \(\dot{\varvec{q}}_{\textrm{max}}=[7,7]^T\) rad/s and \(\ddot{\varvec{q}}_{\textrm{max}}=[21.45,21.45]^T\) rad/s\({}^2\), respectively. Thus, inequalities (11) and (12) are satisfied with \(\sigma _M = 0.74841\) kg m\({}^2\) and \(\zeta =17.574574\) kg m\({}^2\)/s, respectively.

The convergence rate of the NDOB was configured as \(\beta =5.629\), then \(\varvec{Y}_{\textrm{optimal}} = 13 \varvec{I}_n\) and \(\gamma _0 =5.629\). Considering the maximum velocity values and selecting \(\alpha _v=22.714\), we have that \(k_a=1.532\) and \(a_v=162.65\), then \(\varvec{A}_v=162.65 \varvec{I}_n\).

5.2 Results

The experimental results for the proposed disturbance estimation schemes are presented in Figs. 13, 14, 15 and 16 and Table 4. The behavior of the position error is illustrated at the top of Fig. 13, where initially it attempts to converge to the desired position before stabilizing at the location of the wooden barrier. In addition, the bottom part of Fig. 13 illustrates that the disturbance increases as the robot interacts with the environment. Consequently, for the first approximately 600 ms, the perturbation is primarily attributed to friction and unmodeled dynamics.

In this paper, our primary interest lies in utilizing the disturbance estimation scheme as a replacement for force/torque sensors in interaction controllers. Hence, Fig. 14 presents comparative graphs depicting the components of the robot-environment contact force. It is evident that the estimated forces exhibit a behavior very similar to that of the measured forces. However, the estimates display a smoother response, as they are less susceptible to noise caused by vibrations, as observed in the measured forces. This sensitivity is associated with the rate of change of the interaction forces and the tuning of the observer, as elucidated in Sect. 3.3.2.

On the other hand, Fig. 15 depicts the position errors and the disturbances estimated using the modified scheme. Regarding the position errors, their behavior closely resembles that depicted in Fig. 13. However, when it comes to perturbation torques, slight discrepancies become apparent. These differences arise because the modified scheme attempts to compensate for friction by incorporating it as a component of the known dynamics.

Fig. 13
figure 13

Components of position error and estimated disturbance torques using the original proposed observer

Full size image
Fig. 14
figure 14

Components of the measured and estimated contact force, respectively, as obtained through the original proposed observer

Full size image
Fig. 15
figure 15

Components of position error and estimated disturbance torques using the proposed modified observer

Full size image
Fig. 16
figure 16

Components of the measured and estimated contact force, respectively, as obtained through the proposed modified observer

Full size image

The comparison between the behavior of measured forces and those estimated using the modified scheme is illustrated in Fig. 16. It can be observe that there exist only minor deviations in the transient response when compared to the behavior of the original scheme (refer to Fig. 14). Consequently, it became essential to calculate the RMS value of the force error \(\varvec{e}_{fe}\) to more accurately gauge the enhancement in contact force estimation, as demonstrated in Table 4.

Table 4 RMS values for the errors in contact force estimation
Full size table

6 Conclusion

This paper has introduced a nonlinear disturbance observer for serial robot manipulators. This estimation scheme is applicable to robot kinematic configurations without any restrictions on the number of degrees of freedom. The proposed observer accomplishes velocity estimation through a linear auxiliary subsystem, making it suitable for implementation without the necessity of velocity and acceleration measurements, and allowing for straightforward tuning. Moreover, the convergence of perturbation and joint-velocity estimations is theoretically substantiated by a formal stability analysis in the Lyapunov sense.

The practical effectiveness of our proposed observer was validated through numerical simulations and experimental tests involving robot-environment interaction tasks. In this validation process, we compared the performance of our proposal with the classic scheme introduced by Mohammadi et al. and the generalized momentum observer. The results of this comparative analysis demonstrate that our proposed scheme offers a practical advantage: it can be applied even in robots lacking velocity sensors. Furthermore, the achieved results are comparable to those obtained with state-of-the-art schemes, which are still widely utilized in various robotic applications. The estimation of force/torque during robot-environment interaction is effectively achieved using the proposed perturbation observer. The results show an improvement when friction is incorporated as part of the known robot dynamics, even in the presence of uncertainty, as observed in the experimental tests.

In future research, it will be crucial to design force or impedance control schemes that incorporate these observers into their structure while minimizing sensor requirements. Specifically, it would be desirable for the scheme to rely solely on joint position sensors to enhance cost-effectiveness. Additionally, efforts should be directed towards conducting stability and convergence analyses for the complete closed-loop system, encompassing the robot dynamics, controller, and observer.

Another important aspect to consider is the development of robot-environment interaction control schemes that do not rely on force/torque sensors while taking into account the torque and speed capabilities of the robot’s actuators. These schemes should operate safely within the robot drive system’s operational limits, with a particular focus on enhancing safety in tasks involving human–robot interaction. One approach could involve utilizing control structures based on saturation functions, for instance.