1 Introduction

The advantages of Residue Number System (RNS) such as carry-free operation, modularity and fault tolerance have made it attractive in applications like cryptography, digital signal processing (DSP) and communication systems [1,2,3,4]. Several three-, four- or more-moduli sets have been described in literature. They use powers-of-two-related moduli of the form 2u, 2u + 1, 2u − 1, 2v + 3, 2v − 3. In addition, other three-moduli sets that use consecutive numbers as moduli also have been investigated, viz., {2m − 1, 2m, 2m + 1} [5] and {2m, 2m + 1, 2m + 2} [6], the latter using two moduli that have a common factor. The moduli sets {2α − 1, 2α, 2α + 1} [7,8,9,10,11,12] and {2β−1 − 1, 2β − 1, 2β} [13,14,15,16] are special cases of these two-moduli sets. Note that the moduli set {2β−1 − 1, 2β − 1, 2β} is obtained by removing the common factor from one of the two even moduli 2β − 2 and 2β in the moduli set {2β − 2, 2β − 1, 2β} to make the moduli relatively prime. The moduli set {2α − 1, 2α+γ, 2α + 1} has been also investigated to give a variable dynamic range (DR) using the additional degree of freedom γ where 0 ≤ γ ≤ α. [17]. This gives an increment of DR by γ bits over the moduli set {2α − 1, 2α, 2α + 1} with a resolution of 1 bit. On the other hand, the moduli set {2m − 1, 2m, 2m + 1} also offers several other options for realizing a desired DR through proper choice of m. As an illustration, the DRs of the popular moduli set starting from α = 3, 4 and 5 are, respectively, 504, 4080 and 32736. The choice of variable γ leads to the DRs that are 1008, 2016, 4032, etc. In the case of {2m − 1, 2m, 2m + 1} starting from m = 3, 4, 5, 6, 7, etc. the DRs are 210, 504, 990, 1716, 2730, 5814, 7980, etc.

Premkumar [5] suggested the three-moduli set M1 {2m − 1, 2m, 2m + 1} and several reverse converters for M1 have been reported in the literature [5, 18,19,20,21]. The first reverse converter for M1 is presented in [5] using CRT. Later, two reverse converters were presented using a modification of CRT for reducing the modulo reduction complexity [18]. Reverse converters for this moduli set using New CRT II [22] also have been investigated [19]. More recently, improved reverse converters for this moduli set using CRT have been presented [20, 21]. However, these converters can be considered to be similar to a Mixed Radix Conversion (MRC)-type design. The intermediate digits derived, however, are not amenable for facilitating comparison since one of the intermediate digits can be negative. It is interesting to note that MRC technique has not been explored for the moduli set M1. It is well known that MRC technique facilitates easy comparison of two RNS numbers as well as scaling by one modulus or product of two moduli [2]. In this paper, we consider the MRC technique for reverse conversion. Several architectures will be described that take advantage of the simper multiplicative inverses in order to arrive at designs with hardware requirement/conversion time trade-off. All the proposed architectures are compared to the state-of-the-art reverse converters reported earlier for the moduli set M1 in the literature as well as two representative four-moduli sets {2n − 1, 2n, 2n + 1, 2n+1 − 1} and {2n − 1, 2n, 2n + 1, 2n+1 + 1} regarding hardware requirement and conversion time.

In section 2, background material has been given in brief. The proposed MRC-based reverse converter architectures are presented in section 3. The performance evaluation and comparison of the proposed converters with converters for M1 reported earlier and implementation results are provided in section 4. Comparison with converters for two representative four-moduli sets is also presented in section 4. The concluding remarks are given in section 5.

2 Background material

The two popular approaches used for the reverse conversion process in RNS are Chinese Remainder Theorem (CRT) and MRC. In CRT, we compute decoded binary number X as

$$ X = \left( {\mathop \sum \limits_{i = 1}^{j} x_{i} M_{i} \left( {\frac{1}{{M_{i} }}} \right)_{{m_{i} }} } \right)\bmod \, M $$
(1)

where M is the product of all moduli mi, Mi = M/mi and xi are the given residues defined such that xi = X mod mi. Note that \( y = \left( {\frac{1}{a}} \right)_{b} \) is known as a multiplicative inverse of a with respect to modulus b defined such that remainder of the computation (a × y)/b is 1. The main advantage of CRT is the parallel computation of various terms in (1) corresponding to the given residues followed by the summation of various terms mod M.

In MRC for three-moduli set {m1, m2, m3}, the decoded number X corresponding to residues (x1, x2, x3) is obtained as

$$ X = U_{3} m_{2} m_{1} + U_{2} m_{1} + U_{1} $$
(2)

where the mixed radix digits Ui (i = 1, 2, 3) are computed as follows:

$$ U_{1} = x_{1} ,\;\;U_{2} = \left( {\left( {x_{2} - x_{1} } \right)\left( {\frac{1}{{m_{1} }}} \right)_{{m_{2} }} } \right)\bmod \, m_{2} , $$
(3a)
$$ U_{3} = \left( {\left( {\left( {\left( {x_{3} - U_{1} } \right)\left( {\frac{1}{{m_{1} }}} \right)_{{m_{3} }} } \right)_{{m_{3} }} - U_{2} } \right)\left( {\frac{1}{{m_{2} }}} \right)_{{m_{3} }} } \right)\bmod \,m_{3} . $$
(3b)

Since MRC is a sequential process, in each step a single mixed radix digit is determined. The next step is to compute X in (2). Note that the cumbersome modulo M reduction needed in the case of CRT in (1) is not needed in MRC since 0 ≤ X < M. In the present paper, we use MRC technique for deriving various reverse converters.

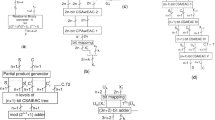
In the implementation of MRC, we need modulo subtractors for computing (xj − xk) mod mi. They use structures similar to cost-effective (CE) and high-speed (HS) modulo adders [2]. We can use the HS architecture of figure 1a in which we compute T1 = (xj − xk) and T2 = (xj − xk + mi) using two parallel adders and based on the sign of T1 we select either T1 or T2 using a 2:1 multiplexer (2:1 MUX). Note that one’s complement of xk and a carry input of 1 are added to obtain two’s complement of xk. Thus the hardware requirement is two k-bit carry-propagate adders (CPA1 and CPA2), one k-bit carry-save adder (CSA1) and one k-bit 2:1 MUX where \( k = { \log }_{2} \left( {2m + 1} \right) \). The computation time is (k + 1)ΔFA + ΔMUX where ΔFA and ΔMUX are delays of a full adder and a 2:1 MUX, respectively. We denote this block as MODSUBA.

Figure 1
figure 1

Architecture of (a) MODSUBA, (b) MODSUBB, (c) MODSUBC and (d) MODMUL (modulo multiplier (H × m) mod (2m − 1)).

Full size image

Note, however, in the case of mj = 2m − 1, mk = 2m + 1, for computing (xj − xk) mod mj for xj = 0, xk = 2m, two consecutive additions of mj are needed since 0 − 2m + (2m − 1) = − 1 and −1 mod (2m − 1) is (2m − 2). Instead, we compute T3 = (xj − xk) or T4 = (xj − xk + 2m − 1) and one among T3, T4 and T5 = 2m − 2 can be selected using a 3:1 MUX based on the sign of T3 and T4 as shown in the MODSUBB block in figure 1b. The computation time, however, is about the same as that of MODSUBA.

The CE version of a modulo subtractor (MODSUBC block) can be realized as shown in figure 1c, in which we compute T6 = (xj − xk) followed by T7 = (T6 + mj) using two adders and based on the sign of T6, we select either T6 or T7 using a 2:1 MUX. Thus the hardware requirement is two k-bit CPAs (CPA5 and CPA6) and one k-bit 2:1 MUX. The computation time needed is (2k)ΔFA + ΔMUX.

The implementation of (H × m) mod (2m − 1) is also needed in the proposed reverse converter architectures. This can be carried out by considering H = 2Y + h0, where Y is the word formed by (k − 1)-bit MSBs of the k-bit word H and h0 is the LSB of H, as

$$ \left( {H \times m} \right) \bmod \left( {2m - 1} \right) = \left( {2Y \times m + h_{0} \times m} \right) \bmod \left( {2m - 1} \right) = \left( {Y + h_{0} \times m} \right) \bmod \left( {2m - 1} \right). $$
(4)

Note that Y is at most Hmax/2 = (2m − 2)/2 = m − 1, in which case h0 = 0, thus making Y + ho × m = m − 1. In the other cases, Hmax/2 < m − 1 and even if h0 = 1, (Y + hom) ≤ (m − 2) + m = 2m − 2 < 2m − 1. Thus, (H × m) mod (2m − 1) can be realized by adding Y with hom (obtained by enabling m by ho using (k − 1) two-input AND gates) using CPA8 as shown in the MODMUL block of figure 1d. Note that m is available as (k − 1) most significant bits of m2 = 2m.

3 Proposed RNS-to-binary converters

In this section, we present new RNS-to-binary converters for the three-moduli set M1 {2m − 1, 2m, 2m + 1} using MRC technique. The MRC algorithm for the three-moduli set M1 is shown in figure 2. The various multiplicative inverses needed in the computation are as follows:

$$ a = \left( {\frac{1}{2m + 1}} \right)_{2m} = 1, $$
(5a)
$$ b = \left( {\frac{1}{2m + 1}} \right)_{2m - 1} = m, $$
(5b)
$$ c = \left( {\frac{1}{2m}} \right)_{2m - 1} = 1. $$
(5c)

They can be verified to be true since (2m + 1) × a = 1 mod 2m, ((2m + 1) × b) mod (2m − 1) = 1 and (2m) × c = 1 mod (2m − 1). We denote the residues corresponding to the three-moduli m1 = 2m − 1, m2 = 2m and m3 = 2m + 1 as (x1, x2, x3) and binary number corresponding to this residue set as X. The DR is M = 2m(4m2 − 1). The implementation of the MRC algorithm of figure 2 using various multiplicative inverses Eq. (5a)–(5c) is presented in figure 3. This converter is denoted as D6.

Figure 2
figure 2

Conventional MRC for M1.

Full size image
Figure 3
figure 3

Architecture of MRC-based converter D6 for M1.

Full size image

The computation of (x2 − x3) mod 2m can be carried out using CE version of a modulo subtractor MODSUBC of figure 1c to obtain intermediate result UA*. The mixed radix digit UA is thus already available as UA* since a is 1 (see Eq. (5a)).

The computation of UB* = (x1 − x3) mod (2m − 1) can be realized using MODSUBB block shown in figure 1b. Next, the intermediate result UB is computed from UB* by performing multiplication with b modulo (2m − 1) in modulo multiplier block shown in figure 1d since b is m (see Eq. (5b)). Next, the modulo subtraction (UB − UA) mod (2m − 1) can be carried out using MODSUBA block to obtain UC*. The mixed radix digit UC is thus already available as UC* since c is 1 (see Eq. (5c)).

The last stage in the converter computes X using Eq. (2) as

$$ X = \left( {x_{3} + U_{\text{A}} m_{3} } \right) + U_{\text{C}} m_{2} m_{3} . $$
(6)

Here the first term (x3 + UAm3) is computed using a (k × k)-bit merged array multiplier MULT1 that multiplies two inputs UA and m3 and adds a third input x3 in the carry save portion of the multiplier [23]. The second term UCm2m3 in Eq. (6) is computed using a (2k × k)-bit array multiplier MULT2. Thus the decoded integer can be obtained using 3k-bit CPA9 as shown in BLOCK1 of figure 3.

The design D6 is based on conventional MRC that requires sequential modulo reductions in the modulus m1 channel to obtain the mixed radix digits. We explore techniques to reduce the number of cascaded modulo reductions next. For this purpose, we choose an ordering of moduli different from that shown in figure 2. The various multiplicative inverses needed for this approach shown in figure 4 are as follows:

$$ e = \left( {\frac{1}{2m}} \right)_{2m + 1} = - 1, $$
(7a)
$$ f = \left( {\frac{1}{2m}} \right)_{2m - 1} = 1, $$
(7b)
$$ g = \left( {\frac{1}{2m + 1}} \right)_{2m - 1} = m. $$
(7c)

The correctness of Eq. (7a)–(7c) can be easily verified.

Figure 4
figure 4

MRC for three-moduli set M1.

Full size image

The architecture of the converter D7 following figure 4 is shown in figure 5. The mixed radix digit P can be computed as (x2 − x3) + tm3 since e = − 1 (see Eq. (7a)) where if x2 ≥ x3, t is 0, else t is 1. Note that (x2 − x3) + tm3 is computed using MODSUBC block (see figure 5 with xj = x2 and xk = x3 and mi = m3). The sign bit of the result (the output of CPA5 in MODSUBC block in figure 1c) is considered as t.

Figure 5
figure 5

Architecture of the MRC-based converter D7 for M1.

Full size image

Next, we consider computation of the mixed radix digit Q. We compute (x1 − x2) but we defer modulo m1 reduction since the multiplicative inverse f with which we need to multiply mod m1 is unity (see Eq. (7b)). Next, unlike in conventional MRC, we subtract ((x2 − x3) + tm3) from (x1 − x2) to obtain the intermediate result:

$$ Q^{*} = \left( {x_{3} - 2x_{2} + x_{1} - tm_{3} } \right) \bmod \, m_{1} = \left( {x_{3} - 2x_{2} + x_{1} - 2t} \right) \bmod \,m_{1} . $$
(8)

Note that in the second equality, we have used the fact m3 mod m1 = 2. The subtraction of ((x2 − x3) + tm3) instead of P has the advantage that t is available before P is available, saving one k-bit CPA delay.

The computation of Eq. (8) requires addition of x3, x1, (2x2)2C (realized as addition of one’s complement of 2x2 and carry input of 1) and t × (2)2C (two’s complement of 2 enabled by t) using CSA3 and CSA4 followed by a modulo m1 adder. The maximum positive and minimum negative values of (x3 − 2x2 + x1 − 2t) are (4m − 4) and (−4m + 2), respectively. The maximum positive value occurs when x1 = (2m − 2) and x3 = 2m and since x2 < x3 in this case, t = 1, thus making the maximum positive value (4m − 4). On the other hand, when x1 = x3 = 0 and for all x2 values, t = 0, yielding the minimum negative value −2(2m − 1) = − 4m + 2. Hence, for modulo m1 reduction of the sum of the outputs S4 and C4 of CSA4, at most addition of m1 or 2m1 or subtraction of m1 (addition of two’s complement of m1) is needed. This can be realized using a HS version of a parallel-type modulo m1 adder that uses a 4:1 MUX to select the correct result Q* as shown in figure 5. The CPA10 computes sum T9 = C4 + S whereas the CSA5 followed by CPA11 computes T8 = C4 + S − m1, CSA6 followed by CPA12 computes T10 = C4 + S + m1 and CSA7 followed by CPA13 computes T8 = C4 + S + 2m1. Note that one’s complement of m1 is added with a carry input of Ci = 1 inserted in the free LSB of CARRY vector C5. The correct result Q* is selected using a 4:1 MUX as shown in BLOCK2 of figure 5. Next, the multiplication of Q* with g (= m) (see figure 5) is carried out to obtain the mixed radix digit Q using MODMUL block shown in figure 1d with H = Q*. We next compute X as

$$ X = x_{2} + Pm_{2} + Qm_{2} m_{3} $$
(9)

using BLOCK3 (similar to BLOCK1 in figure 3). This uses multipliers MULT3 and MULT4 of sizes k × k and 2k × k, respectively, followed by CPA14. Note that MULT3 is a merged multiplier.

In the design of reverse converters following figure 4, we can notice that the computation of mixed radix digit Q is the critical path. Hence we present some alternate designs for computing the mixed radix digit Q employing two different methods for mod m1 reduction of sum of C4 and S4 in figure 5 to obtain Q*. In the design shown in figure 6a, we first add C4 and S 4 in CPA15 to obtain T12. Note that CPA15 has a carry input of 1 to realize two’s complement of 2x2. We reduce the result T12 mod m1 using one ADD/SUB unit realized by CPA16 and k exclusive-OR gates and one adder adding 2m1 using CPA17. The correct result is selected using a 3:1 MUX based on the sign bits of outputs of CPA16 and CPA17. Note that the exclusive-OR gates invert the bits of m1 to facilitate subtraction and a carry input Ci = s′ is added where s is the sign bit of T12. This block can be used in the architecture of converter D7 in figure 5 in place of BLOCK2 to realize converter D8.

Figure 6
figure 6

Alternative designs for replacing BLOCK2 in converter D7 for computation of Q* (a) for converter D8 and (b) for converter D9.

Full size image

In an alternative converter design D9, we use a binary-to-RNS converter to reduce T12 mod m1 as shown in figure 6b. Since T12 is (k + 2)-bit wide, based on the two MSB bits, we add a constant W to the k-bit LSBs of T12. Denoting x = 2k mod m1 it can be seen that the two MSBs correspond to the four values before mod m1 reduction: 00b → 0, 01b → 2k = x, 10b → −2k+1, 11b → −2k. (Note that b indicates binary representation and (k + 1)th bit is sign bit of T12)). Thus, using a 4:1 MUX, appropriate value among these can be selected and added with k LSBs of T12 and reduced mod m1 using CPA18, CSA8, CPA19 and 2:1 MUX to obtain Q*. Note that the sum of W and word corresponding to k LSBs of T12 is at most (2k − 1) so that a single subtraction of modulus m1 (addition of (m1)1C with a carry input of 1 to CPA19) is sufficient to obtain Q* as shown in figure 6b.

Next, we consider realizing the computation of Q* and multiplication with m in a single block, instead of the cascade designs considered in figures 5 and 6. In the design D10, to determine the mixed radix digit Q, we need to compute [m × ((x3 − 2x2 + x1 − 2t) mod m1)] mod m1 = (mx3 + mx1 − x2 − t) mod m1 in one step. Note that (m × 2x2) and (m × 2t) are reduced modulo m1 as x2 and t, respectively, since (2m) mod x1 = 1. We consider x3 = 2x3H + x30 and x1 = 2x1H + x10 where x3H and x1H are the words formed by the most significant (k − 1) bits of x3 and x1, respectively. The computation of (mx3 + mx1) can be realized by adding m × x30, m × x10, x3H and x1H since (2m × x3H) mod m1 = x3H and (2m × x1H) mod m1 = x1H. Note that −x2 − t is realized as (x2)1C + (1 − t) = (x2)1C + t′ where t′ is inverted bit t. Thus, we need to compute (m × x30 + m×x10 + x3H + x1H + x21C + t′) mod m1 to obtain Q. Note that m × x30 and m × x10 can be obtained using a pair of (k − 1) AND gates enabled by x30 and x10, respectively, as shown in figure 7.

Figure 7
figure 7

Architecture for the computation of mixed radix digit Q in D10.

Full size image

The five operands can be added using three-level CSA tree (CSA9–CSA11) and CPA20 followed by a mod m1 adder. Note that the maximum positive and minimum negative values of the result of CPA20 are (4m − 4) and (−2m + 1), respectively. Hence, at most a single addition or subtraction of modulus m1 is sufficient to obtain Q. Hence, a modulo m1 adder using an ADD/SUB unit formed by CPA21, k exclusive-OR gates and a 2:1 MUX is used to compute Q.

4 Performance evaluation and comparison

The hardware requirement and conversion time for the various reverse converters described in [5, 18, 19, 21] for the moduli set M1 along with the proposed reverse converters have been presented in table 1. Note that FA, HA, AND and w:1 MUX stand for a full adder, half adder, two-input AND gate and w:1 multiplexer, respectively. The notations L1 and L2 are used to represent 2k × k and k × k multipliers, respectively, and LiM (for i = 1, 2) is used to represent merged multiplier [23]. Note that the hardware requirement of L1 and L2 is (2k2 − 2k)FA and (k2 − k)FA, respectively, considering that an array multiplier using (k − 2) carry save levels followed by a CPA is used and the delay of L1 and L2 is (3k − 2)ΔFA and (2k − 2)ΔFA, respectively.

Table 1 Comparison of hardware requirement and conversion time of various reverse converters for the three- and four-moduli sets M1–M3.
Full size table

The converter D1 due to Premkumar [5] uses CRT. It needs five two-input adders, three 2k × k multipliers each of the range 4m2 and 5 numbers of 3k-bit 2:1 MUXs. Premkumar et al [18] suggested two converters D2 (Architecture A) and D3 (Architecture B) later by simplifying the conventional CRT. In this method, the modulo M reduction needed in [5] is simplified as modulo (m1 × m3) reduction. This converter needs one 2k × k and another k × k multiplier of the range 4m2 and 2m, respectively. Architecture A (D2) presented in [18] needs seven two-input adders and 6k-bit 2:1 MUXs whereas another Architecture B (D3) presented in [18], which is a HS version, needs nine adders and 5k-bit 2:1 MUXs. In the converter D4 for M1 proposed by Wang et al [19] based on new CRT II technique, we need one 2k × k multiplier and one k × k multiplier, a few adders and a few comparators. The recent converter D5 for M1 due to Gbolagade et al [21] is based on the modification of CRT. It realizes modulo m1 reduction using several MUXs and comparators and it needs one 2k × k multiplier and one k × k multiplier. The hardware requirement and conversion time for these five converters D1–D5 are presented as first five entries in table 1. The proposed converters are presented as D6–D10 in table 1.

Among all the converters using two multipliers L1 and L2 for the moduli set M1, converter D5 needs the least area and D4 needs the highest area. However, it may be noted that the area of multipliers L1 and L2 has quadratic dependence on k and hence, for large k, the area of the multipliers dominates the total area. All the converters need similar conversion time except converters D2, D3, D8 and D9. The converters D2 and D3 need larger conversion time than converters D8 and D9. The m and n values needed for realizing DRs ranging from 8-bit to 64-bit for various moduli sets are presented in table 2. As an illustration, m = 21 for 16-bit DR of M1 implies use of the moduli set {41,42,43}. We have also considered the three reverse converters D11–D13 for the four-moduli set M2 {2n − 1, 2n, 2n + 1, 2n+1 − 1} [24,25,26] and two reverse converters D14 and D15 for the four-moduli set M3 {2n − 1, 2n, 2n + 1, 2n+1 + 1} [25, 27] for the purpose of comparison. Note that they use the efficient RNS to binary converters for the three-moduli set {2n − 1, 2n, 2n + 1} [9,10,11,12] followed by a two-moduli MRC to include the fourth modulus. The hardware resource and conversion time requirements in terms of basic gates for the proposed reverse converters along with the converters for M1–M3 are also presented using unit-gate model [28] in table 3 for the general case and for the six standard DRs in table 4. Note that the equivalent number of gates for full adder, half adder, 2:1 MUX, EXOR/EXNOR, AND and OR gates is considered as 7, 3, 3, 2, 1 and 1 and the delays are considered as 4Δg, 2Δg, 2Δg, 2Δg, Δg and Δg, respectively, where Δg is unit-gate delay.

Table 2 Values of ‘m’ and ‘n’ to be considered for various DRs of M1–M3.
Full size table
Table 3 Hardware requirement and delay estimation based on unit gate model for various three- and four-moduli set reverse converters.
Full size table
Table 4 Area and delay comparison for 8-, 16-, 24-, 32-, 48- and 64-bit DR three- and four-moduli set reverse converters using unit gate model.
Full size table

From table 4, it can be observed that for all the standard DRs, among the considered three- and four-moduli sets the design D12 is preferable regarding lower hardware resource requirement and the converter D13 needs least conversion time among all the converters. Among the converters D5–D10 for moduli set M1, the proposed converter D10 needs the lowest hardware resources for DR 8 and 16 bits whereas converter D5 is better for 24-, 32-, 48- and 64-bit DRs. Regarding conversion time, for all considered standard DRs, D5 and D10 are better than other converters D6–D9. It can also be observed that the proposed converters D6–D10 need less conversion time than converters D14 and D15 for all the considered standard DRs.

The proposed converters D6–D10 as well as design D5 [21] were implemented using Cadence (Version 14.20), Compiler: RC 14.25 and synthesized using the Cadence Encounter tool using 180-nm technology. The post place and route results of area, conversion time and power dissipation for all these designs for DRs of 8, 16, 24, 32, 48 and 64 bits are presented in table 5.

Table 5 ASIC implementation results of various reverse converters for the three-moduli set M1.
Full size table

Regarding hardware requirements, for 8- and 64-bit DRs, the design D5 is superior to the converters D6–D10 and the design D6 outperforms converters D5 and D7–D10 for 16-, 24-, 32- and 48-bit DRs. For 16-bit D7 and D8 and for 32-bit and 48-bit DR, converter D8 require less hardware resources than D5. The converter D9 is preferable compared with D5 regarding area for 16-, 24-, 32- and 48-bit DRs.

Regarding conversion time, for 8, 32 and 64 bits, D5 performs better than D6–D10 and for 16-, 24- and 48-bit DRs, D6 outperforms converters D5 and D7–D10. The converter D7 also requires less conversion time than D5 for 16-bit DR.

Regarding power dissipation, 8-, 32-, 48- and 64-bit DRs, the converter D5 is superior than D6–D10 and for 16-bit DR, the converters D6, D7, D9 and D10 outperform converter D5. For 24-bit DR, the converter D7 needs less power dissipation than D5, D6 and D8–D10. Among the proposed converters, for 8-bit DR, the converter D6 is preferable and for 16- and 32-bit DRs, the converter D10 is superior to the other converters regarding power dissipation. For 24-, 48- and 64-bit DRs, the converter D7 needs least power dissipation compared with other proposed converters.

5 Conclusions

In this paper we have presented RNS-to-binary converters for the moduli set {2m−1, 2m, 2m + 1} using MRC technique. All the proposed converters were evaluated based on the hardware resource requirement as well as conversion time with all converters described in literature for the moduli set {2m−1, 2m, 2m + 1}. The proposed converters have also been compared to two four-moduli reverse converters. All the proposed converters are implemented and compared to the area-efficient converter [21] for M1 regarding area and conversion time for different DRs. The proposed converters also need less conversion time than reverse converters for some four-moduli sets. The proposed converters for M1 were shown to be better than some of the other converters regarding area and conversion time while having the advantage of availability of mixed radix digits.