Reverse Conversion Using Core Function, CRT and Mixed Radix Conversion

Abstract

In this paper, residue number system (RNS) to binary number system conversion using core function is compared with techniques using Chinese remainder theorem (CRT) and mixed radix conversion (MRC). The cause of inaccuracy of core function for comparison, sign detection and scaling is analyzed. In spite of the inaccuracy in estimating the exact core, the application of core function for RNS to binary conversion is shown to be accurate. Since not much attention has been given to the use of core function in designing reverse converters, reverse converters using core function has been explored for some moduli sets for which other techniques such as CRT and MRC also have been found to lead to complicated designs. Reverse converters for two three-moduli sets {$2^{n}, 2^{n}-1, 2^{n+1}-1\}$ and {$2m-1, 2m, 2m+1\}$ using core function and for one four-moduli set {$2^{n}-3, 2^{n}-1, 2^{n}+1, 2^{n}+3\}$ are presented and compared with earlier available designs using other techniques regarding hardware requirement and conversion time trade-offs. State-of-the-art models for ROM and combinational logic have been used to perform realistic estimate of area and conversion time. It has been shown that designs using core function may be preferable over other designs in some cases.

1 Introduction

Several techniques have been described in the literature for residue number system (RNS) to binary number system conversion [6, 29, 35, 37] which are based on Chinese remainder theorem (CRT) [37], mixed radix conversion (MRC) [37], core function [1, 2, 4, 5, 15, 16, 23, 24, 27, 28, 43], new Chinese remainder theorems I, II (new CRTs) [40], mixed radix CRT [14], quotient function [20] and more recent diagonal function [9, 18, 19, 31]. The performance of other operations needed in a RNS-based processor such as scaling, sign detection, comparison and error correction is also dependent on the efficiency of RNS to binary conversion.

Akushkii et al. [4] have introduced the core function whose purpose is to obtain positional information from a residue encoded number (i.e., the position in the dynamic range). Application of core function for residue to binary conversion, scaling and sign detection has been studied by several researchers [1, 2, 5, 15, 16, 23, 24, 27, 28, 43]. Hardware implementations also have been described in the literature [27, 43]. However, the application of core function for residue to binary conversion has not received much attention as compared to application of other residue to binary conversion techniques.

In this paper, we will revisit the concept of core function and derive the relationship between the reverse conversion techniques based on core function, CRT and MRC. We show that core function can be used for exact residue to binary conversion even though it is not accurate for scaling, sign detection and comparison. We provide an insight into the reasons for inaccuracy of the core function for being used for residue number comparison, sign detection and scaling in RNS. In addition, the design of reverse converters using core function for two three-moduli sets {$2^{n}, 2^{n}-1, 2^{n+1}-1\}$ [8], $\{2m+1, 2m, 2m-1\}$ [3, 21, 22, 32, 33] and one four-moduli set $\{2^{n}-1, 2^{n}+1, 2^{n}-3, 2^{n}+3\}$ [7, 11, 26, 34] is investigated in order to bring out the trade-offs involved in hardware requirements and conversion time.

In Sect. 2, we review the concepts of the core function and RNS to binary conversion using core function. We compare the core function-based RNS to binary conversion with CRT and MRC in Sect. 3. The reverse conversion architectures using core function for two three-moduli sets $\{2^{n}, 2^{n}-1, 2^{n+1}-1\}$ [8], $\{2m, 2m-1, 2m+1\}$ [3, 21, 22, 32, 33] and one four-moduli set $\{2^{n}-1, 2^{n}+1, 2^{n}-3, 2^{n}+3\}$ [7, 11, 26, 34] are presented in Sect. 4. In Sect. 5, the proposed converters are compared regarding hardware requirements and conversion time with other reverse converters proposed in the literature for the moduli sets considered in this paper. Since some of the converters proposed in this paper and other converters described in the literature have used ROMs together with combinational logic, we use state-of-the-art models for ROMs as well as combinational logic for evaluation of various converters. Section 6 concludes the brief.

2 Core Function and RNS to Binary Conversion

Consider the RNS using the moduli set $\{m_{1}, m_{2}, m_{3}, \ldots , m_{k}\}$ with a dynamic range $M=\prod _{i=1}^k {m_i }$ and given residues ($r_{1}, r_{2}, r_{3}, \ldots , r_{k})$. The residues $r_{i}$ corresponding to a given number X such that 0 $\le X \le$ ($M-1$) are defined as X mod $m_{i}$ and are also represented as ${(X)}_{m_i }$. We need to choose first a constant C(M) as the core. It can be the largest modulus in the RNS or product of two or more moduli. As in the case of CRT, we define various $B_{i }$as

$$\begin{aligned} B_{i}= M_i {\left( {\frac{1}{ M_i}} \right) }_{ m_i} \end{aligned}$$

(1)

where $M _{i}=M/m _{i}$ and ${\left( {\frac{1}{M_i }} \right) }_{m_i }$is the multiplicative inverse of $M _{i}$ mod $m _{i}$ satisfying the requirement that ${\bigg ( {{\big ( {\frac{1}{M_i }} \big )}_{m_i } M_i } \bigg )\bmod \left( {m_i } \right) } =1$. We next need to compute weights $w _{i}$ defined as

$$\begin{aligned} w_i = \left( {{\left( {\frac{1}{M_i }} \right) }_{m_i } C(M)} \right) \bmod _{m_i} \end{aligned}$$

(2a)

The weights also need to satisfy the condition

$$\begin{aligned} C(M)=\sum _{i=1}^k {M\frac{w_i }{m_i }} \end{aligned}$$

(2b)

thereby necessitating that some weights be negative. The weights are next used to compute the core function C(X) of a given number X as

$$\begin{aligned} C(X)=\left( {X\frac{C(M)}{M}-\sum _{i=1}^K {\frac{w_i }{m_i }r_i } } \right) \bmod C(M) \end{aligned}$$

(3)

Note that the core values $C(B_{i})$ corresponding to the input $B_{i}$ can be seen from (3) to be

$$\begin{aligned} C(B_i )=\frac{B_i C(M)}{M}-\frac{w_i }{m_i } \end{aligned}$$

(4)

since the residue $r_{i}$ corresponding to $B_{i}$ mod $m_{i}$ is 1 and residues of $B_{i }$ corresponding to all other moduli are zero. Note that various $C(B_{i})$ values are constants for a chosen moduli set. From (2) and (4), it can be seen that $C(B_{i}) < C(M)$ since $B_{i }< M$.

The residue to binary conversion corresponding to residues ($r_{1} , r_{2} , r_{3} ,\ldots , r_{k})$ is carried out by first determining the core function C(X) of the given number X as

$$\begin{aligned} C(X)=\left( {\sum _{i=1}^k{r_i C(B_i )} } \right) \bmod C(M)=\sum _{i=1}^k{r_i C(B_i )} -\alpha C(M) \end{aligned}$$

(5)

where $\alpha$ is known as the rank function defined by CRT. Note that (5) is known as CRT for core function. Next X can be computed by rewriting (3) as

$$\begin{aligned} X={\left( {\frac{M}{C(M)}\left( {C(X)+\sum _{i=1}^k {\frac{w_i }{m_i }r_i } } \right) } \right) }_M \end{aligned}$$

(6)

The important property of C(X) is that the term $X\frac{C(M)}{M}$ in (3) monotonically increases with X with some furriness due to the second term in (3) [15]. In general, for choice of C(M) typically of same value as one modulus, the range of C(X) for $0<X <M$ gets smaller and the second term in (3) causes significant errors and hence, accurate comparison of two numbers using core function or sign detection is difficult.

The main advantage claimed for using the core function is that the constants $C(B_{i})$ involved in computing the core function following (5) are small since they are less than C(M). However, in order to simplify or avoid the cumbersome division by C(M) needed in (6), it has been suggested that C(M) be chosen as a power of two or one modulus or product of two or more moduli.

The following example illustrates the procedure of computing core and reverse conversion using core function.

Example 1

Consider the moduli set {3, 5, 7, 11}. Let us choose $C(M) = 11$. Then, $M = 1155, M _{1}= 385, M _{2 }= 231, M _{3}= 165$ and $M _{4 }= 105$. The values of ${\left( {\frac{1}{M_i }} \right) }_{m_i }$ are 1, 1, 2, 2. Thus, $B_i =M_i {\left( {\frac{1}{M_i }} \right) }_{m_i }$ are 385, 231, 330, 210. The $w _{i}$ can be found from (2a) as $-1, 1, 1, 0$. It can be verified that (2b) is satisfied:

$C(M) = -1\times 385+1\times 231+1\times 165 = 11$. Next, we find following (4), $C(B_{1}) = 4, C(B_{2}) = 2, C(B_{3}) = 3$ and $C(B_{4}) = 2$. Consider the residues (1, 2, 3, 8). Then, we find from (5), $C(X) = (1\times 4+2\times 2+3\times 3+8\times 2) \bmod 11 = 0$. Next, X can be found from (6) as $X={\left( {105\left( {0+\frac{1\times -1}{3}+\frac{2\times 1}{5}+\frac{3\times 1}{7}} \right) } \right) }_{1155} =52$.

3 Comparison with CRT, MRC and Mixed Radix CRT

It is interesting to note from (3) that the value of the core function C(X) corresponding to a given number X for a chosen C(M) actually represents the approximate quotient resulting from the division of that number X by M / C(M). We use CRT to explain this point and show the relationship between core function, mixed radix digit computation and CRT. The use of CRT yields the binary number corresponding to the given residues as

$$\begin{aligned} X=r_1 B_1 +r_2 B_2 +r_3 B_3 +\cdots +r_k B_k -\alpha M \end{aligned}$$

(7)

where $B_{i}$ is given by (1). Multiplying both sides of (7) with C(M) / M, we have

$$\begin{aligned} {C}'(X)=X\frac{C(M)}{M}=\frac{C(M)}{M}\left( {r_1 B_1 +r_2 B_2 +r_3 B_3 +\cdots +r_k B_k } \right) -\alpha C(M) \end{aligned}$$

(8)

Substituting (4) in (5) and the resulting C(X) value in (6), we obtain

$$\begin{aligned} X= & {} \frac{M}{C(M)}{\left( {\sum _{i=1}^k {\left( {r_i \left( {\frac{B_i C(M)}{M}-\frac{w_i }{m_i }} \right) -\alpha C(M)} \right) +\sum _{i=1}^k {\frac{r_i w_i }{m_i }} } } \right) } \nonumber \\= & {} \sum _{i=1}^k {\left( {r_i B_i } \right) } -\alpha M \end{aligned}$$

(9)

Note that any choice of $w_{i}$ will yield correct decoding. However, since $\frac{B_i C(M)}{M}$ can be a mixed fraction for all moduli except the one chosen as C(M), choice of $\frac{w_i }{m_i }$ suitably will yield an integer value for the terms $r_i \left( {\frac{B_i C(M)}{M}-\frac{w_i }{m_i }} \right)$. Note that ${C}'(X)={\left( {\sum _{i=1}^k {\left( {\frac{r_i B_i C(M)}{M}} \right) } } \right) }_{C(M)}$ will give the correct quotient $X\frac{C(M)}{M}$, whereas C(X) computed from (5) gives an approximate quotient. Thus, using C(X) computed from (5) for comparison of two numbers by comparing core function values, for sign detection and scaling, leads to inaccuracies. If C(M) is chosen as one modulus (i.e., $C(M)=m_{i})$, then $X\frac{C(M)}{M}$ corresponds to the highest mixed radix digit. We consider the following example given by Burgess [15] in order to illustrate the difference between core function and mixed radix digit in the case of choosing one modulus as core function.

Example 2

The residues given are (7, 4, 2, 22, 16) in the moduli set {13, 17, 19, 29, 31} corresponding to the number 3,004,567. We consider $C(M) = 31$. The multiplicative inverses ${\left( {\frac{1}{M_i }} \right) }_{m_i}$ are (3, 16, 14, 12, 21), respectively. From (8) and (1), we have

$$\begin{aligned} {\left( {X\frac{C(M)}{M}} \right) }_{C(M)}= & {} {\left( {\left\lfloor {\sum _{i=1}^k {\frac{C(M)r_i }{m_i }{\left( {\frac{1}{M_i }} \right) }_{m_i } } } \right\rfloor } \right) }_{C(M)} \\= & {} {\left( {\left\lfloor {7\times 7\frac{2}{13}+4\times 29\frac{3}{17}+2\times 22\frac{16}{19}+22\times 12\frac{24}{29}+16\times 21} \right\rfloor } \right) }_{31} \\= & {} {\left( {\left\lfloor {830.67391} \right\rfloor } \right) }_{31} =24 \end{aligned}$$

The use of core function yields $C(M) = 27$ for all the three methods given by Burgess [15]. The reason is that it estimates the sum of rounded weighted values ($7\times 7+4\times 29+2\times 23+22\times 13+16\times 21)\bmod 31 = 833\bmod 31 = 27$.

Core function yields approximate mixed radix digit when C(M) is chosen as one modulus. Conventional mixed radix conversion can give the exact value of all mixed radix digits which is sequential in computation. Bi and Gross technique [14] termed as mixed radix CRT facilitates exact parallel computation of mixed radix digits but involves cumbersome division operations. Sign detection and comparison involve sequential comparison of mixed radix digits starting from the highest digit. It is interesting to note that direct highest mixed radix digit computation was described for the moduli set $\{2^{n}-1, 2^{n}, 2^{n}+1, 2^{n+1}-1\}$ in [38].

4 Implementation Architectures for Reverse Converters Using Core Function

The implementation of the reverse converter using core function follows (5) and (6). It can be seen that the maximum value of C(X) is $C(M)-1$. The magnitudes of the terms $\frac{w_i r_i }{m_i }$ are always less than $w_{i}$ since 0 $\le r_{i} \le (m_{i}-1)$. Some of the $w_{i}$ values may be negative. Considering in the worst case all $w_{i}$ values are positive, the maximum possible value of X in (6) can be $\frac{M}{C(M)}\left( {C(M)-1+\sum _{i=1}^k {\left| {w_i } \right| } } \right)$ [15]. Thus, depending on the $w_{i}$ values of the chosen moduli set, the range of X before reduction mod M needs to be estimated (which can be larger than that of M) so that the needed modulo M reduction can be carried out to obtain the decoded X value.

The values of $C(M), w_{i,} C(B_{i})$ and expression for C(X) for four powers-of-two-related three-moduli sets M1 $\{2^{n}, 2^{n}-1, 2^{n}+1\}$ [12, 17, 30, 39, 41], M2 $\{2^{n}, 2^{n}-1, 2^{n+1}-1\}$ [8], M3 $\{2^{n}, 2^{n}-1, 2^{n-1}-1\}$ [10, 25] M4 $\{2m, 2m-1, 2m+1\}$ [3, 21, 22, 32, 33] are presented in Table 1 for illustration. We consider reverse conversion using core function for moduli sets M2 and M4 in detail next.

Table 1 Core function computation for few three-moduli sets

4.1 Moduli Set M2 $\{2^{n}, 2^{n}-1, 2^{n+1}-1\}$

In the case of the moduli set $\{m_{1}, m_{2}, m_{3}\} = \{2^{n}, 2^{n}-1, 2^{n+1}-1\}$, choosing $C(M_{a}) = 2^{n}$, where $M_{a} = 2^{n}(2^{n}-1)(2^{n+1}-1$), the decoded number following (6) and using the expressions for $C(B_{i})$ from Table 1 is given as

$$\begin{aligned} X= & {} \left( {\frac{M}{C(M)}C(X)+w_2 {r_2 m}_3 +w_3 {r_3 m}_2 } \right) \bmod M_a \nonumber \\= & {} \left[ \left( 2^n -1\right) \left( 2^{n+1} -1\right) C(X)+r_2 \left( 2^{n+1} -1\right) \right. \nonumber \\&-\left. 2r_3 (2^n -1)\right] \bmod \left( {2^n (2^n -1)(2^{n+1} -1)} \right) \end{aligned}$$

(10)

The core function C(X) can be computed from Table 1 as

$$\begin{aligned} C(X)={\left( {r_1 C(B_1 )+r_2 C(B_2 )+r_3 C(B_3 )} \right) }_{2^n } ={\left( {r_1 +r_2 -2r_3 } \right) }_{2^n } \end{aligned}$$

(11)

Note that (11) can be computed using a 4-input n-bit adder and ignoring the carry bit. As an illustration for the $n = 5$ case, the four 5-bit words to be added are $r_{14} r_{13} r_{12} r_{11} r_{10} ,r_{24} r_{23} r_{22} r_{21} r_{20} ,\overline{r_{33} } \overline{r_{32} } \overline{r_{31} } \overline{r_{30} } 1,00001$. Note that the $-2r_{3}$ term is realized by left shifting $r_{3}$ by one bit and one’s complementing the n LSBs and ignoring the MSB due to mod($2^{n}$) reduction and adding ‘1’. Next these four words need to be added, and carry can be ignored to obtain C(X) (denoted as $C_{n}$ hereafter). This needs one CSA stage of n full-adders followed by a n-bit CPA as shown in Fig. 1a. Next, the computation in (10) (before modular reduction) can be carried out by the addition of the words in the bit matrix for the case $n = 5$ shown in Fig. 2 where the bars indicate inverted bits (the top row indicates the bit position).

Fig. 1

RNS to binary converters using core function. a for the moduli set $\{2^{n}, 2^{n}-1, 2^{n+1}-1\}$, b for the moduli set $\{2m, 2m-1, 2m+1\}$

Fig. 2

Bit matrix for the final adder for reverse converter for the moduli set $\{2^{n}, 2^{n}-1, 2^{n+1}-1\}$

We have considered $-2^{n}C(X), -2^{n+1}C(X), -r_{2}, -2^{n+1}r_{3}$, respectively, as $2^{n}(2^{n}-1-C(X)), 2^{n+1}(2^{n}-1-C(X)), (2^{n}-1-r_{2})$ and $2^{n+1}(2^{n+1}-1-r_{3})$ needing a correction term to be added. The overall correction term Z that needs to be added is $Z=M-2^n (2^n -1)-2^{n+1} (2^n -1)-(2^n -1)-2^{n+1} (2^{n+1} -1)$. Note that in effect M has been added so that the result is always positive. Note that the maximum and minimum values of (10) are ($2^{2n}-2^{n}-1)(2^{n+1}-1)$ and -($2^{n+2}-4)(2^{n}-1$). However, one mod M subtraction will be required if the result of addition of all words such as those in Fig. 2 in the general n case exceeds $M_{a}$. The complete architecture is presented in Fig. 1a. The carry-save-adder tree for adding the various bits in the five words in Fig. 1 needs $(5n+2)\text {FA}+(2n-1)\text {HA}$, and the CPA following it needs ($3n+1)\text {FA}$ and ($3n+1$)-bit $\hbox {A}_{2:1\,\mathrm{MUX}}$ where FA, HA and $\hbox {A}_{2:1\,\mathrm{MUX}}$ stand for full-adder, half-adder and 2:1 multiplexer, respectively. The computation time for this stage is ($4+2(3n+1))\tau _{FA}$ where $\tau _{FA}$ is delay of a full-adder. The overall hardware and conversion time requirements are ($10n+3)\hbox {FA}+(2n-1)\hbox {HA} +(3n+1)\hbox {A}_{2:1\,\mathrm{MUX}}$ and ($7n+7)\tau _{FA}$.

4.2 Moduli Set M4 {2m+1, 2m, 2m-1}

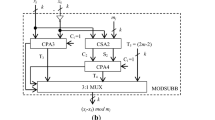
We next consider reverse conversion for the moduli set $\{m_{1}, m_{2}, m_{3}\} = \{2m+1, 2m, 2m-1\}$ using core function. We select $C(M_{b}) = 2m$ in this case where the dynamic range of this RNS is $M_{b} = 2m(4m^{2}-1)$. The decoded number can be written following (6) and using $C(B_{i})$ values from Table 1, as

$$\begin{aligned} X= & {} \left[ (4m^2 -1){(mr_1 -r_2 +(m+1)r_3 )}_{2m} +m(2m-1)r_1 \right. \nonumber \\&+\,\left. (1-m)(2m+1)r_3 \right] \bmod (2m(4m^2 -1)) \end{aligned}$$

(12)

An architecture for computation of (12) is presented in Fig. 1b. Note that ($mr_{1}+mr_{3})$ mod (2m) is realized by enabling m when ($r_{10}\, \hbox {exor} \,r_{30}$) is ‘1’ where $r_{10}$ and $r_{30}$ are the least significant bits of $r_{1}$ and $r_{3}$, respectively. Note also that $m(2m-1)r_1 +(1-m)(2m+1)r_3$ is realized as $(r_1 -r_3 )(2m^2 -m)+r_3$. Denoting $q = \hbox {log}_{2}(2m+1)$, this architecture needs one multiplier ($q-$ bit $\times 2q-$ bit), one ($q+1$)-bit subtractor, one mod (2m) adder (q-bit) and one mod ($2m (4m^{2}-1$)) adder (3q-bit) in the critical path. One q-bit subtractor and a ($q+1$)-bit $\times (2q-1$)-bit multiplier are in a parallel path. Note that the maximum and minimum values of X in (12) before reduction are $(6m^{2}-1)(2m-1)$ and $(4m^{2}-2m-2)(1-m)$, respectively, and hence, one mod $M_{b}(= 2m(4m^{2}-1))$ addition or subtraction needs to be carried out.

4.3 Moduli Set M5 $\{2^{n}-1, 2^{n}+1, 2^{n}-3, 2^{n}+3\}$

We consider the three cases of choosing $C _{1}(M _{c}) = 2^{n}-1, C _{2}(M _{c}) = (2^{n}-1)(2^{n}+1)$ and $C _{3}(M _{c})= (2^{n}-1)(2^{2n}-9)$ where the dynamic range of this RNS is $M _{c} = (2^{2n}-1)(2^{2n}-9)$. The first two choices permit easy reduction in the respective core values $C _{1}(X)$ mod $C _{1}(M _{c})$ and $C _{2}(X)$ mod $C _{2}(M _{c})$. The third choice involves difficult reduction in $C _{3}(X)$ mod $C _{3}(M _{c})$ but simplifies the computation of the final decoded word. Defining $m _{1} = 2^{n}-1, m _{2 }= 2^{n}+1, m _{3 }= 2^{n}-3$ and $m _{4} = 2^{n}+3$, the various multiplicative inverses needed in (1) for this moduli set are as follows:

$$\begin{aligned} {\left( {\frac{1}{M_1 }} \right) }_{m_1 }= & {} {\left( {-\frac{1}{16}} \right) }_{2^n -1} =2^n -1-2^{n-4} , {\left( {\frac{1}{M_2 }} \right) }_{m_2 } ={\left( {\frac{1}{16}} \right) }_{2^n +1} \nonumber \\= & {} 2^n +1-2^{n-4} , {\left( {\frac{1}{M_3 }} \right) }_{m_3 } ={\left( {\frac{1}{48}} \right) }_{2^n -3} =\frac{k(2^n -3)+1}{48} \end{aligned}$$

(13a)

where $k = 11$ for n even and $k = 43$ for n odd,

$$\begin{aligned} {\left( {\frac{1}{M_4 }} \right) }_{m_4 } ={\left( {-\frac{1}{48}} \right) }_{2^n +3} =\frac{{k}'(2^n +3)-1}{48} \end{aligned}$$

(13b)

where $k' = 43$ for n even and $k' = 11$ for n odd.

We denote the three cases of choosing cores as $(2^{n}-1), (2^{2n}-1)$ and $(2^{n}-1)(2^{2n}-9)$, respectively, as Case I, Case II and Case III.

4.3.1 Case I

Choosing $C_{1}(M) = 2^{n}-1$, in this case, the various $w_{i}$ and $C_{1}(B_{i})$ values can be found for the case n even as follows:

$$\begin{aligned}&w_1 =0,\quad w_2 =2^{n-3}, \quad w_3 =\left( {\frac{40-13\times 2^n }{24}} \right) ,w_4 =\frac{5(2^n +3)+1}{12}\nonumber \\&C_1 (B_1 )=C_1 (B_2 )=2^n -2^{n-4} -1, \quad C_1 (B_3 )=\frac{11(2^n -3)+1}{48}+1,\nonumber \\&\quad C_1 (B_4 )=\frac{43(2^n +3)-193}{48} \end{aligned}$$

(14)

For the case n odd, we have

$$\begin{aligned}&w_1 =0,\quad w_2 =2^{n-3},\quad w_3 =-\left( {\frac{5(2^n -3)-1}{24}} \right) ,\quad w_4 =\frac{(2^n +4)}{12}\nonumber \\&C_1 (B_1)=C_1 (B_2 )=2^n -2^{n-4} -1,\quad C_1 (B_3)=\frac{43(2^n -3)+97}{48},\nonumber \\&\quad C_1 (B_4 )=\frac{11(2^n +3)-49}{48} \end{aligned}$$

(15)

For reverse conversion following (6), we need to compute

$$\begin{aligned} X= & {} \left[ C _{1}(X)\left( 2^{2n}-9\right) \left( 2^{n}+1\right) + w _{2} m _{3} m _{4} r _{2}+w _{3} m _{2} m _{4} r _{3}\right. \nonumber \\&+\left. _{ } w _{4} m _{2} m _{3} r _{4} \right] {\mathrm{mod}} \left( \big (2 ^{2n} -1\big )\big (2 ^{2n} -9\big )\right) \end{aligned}$$

(16)

after computing $C_{1}(X)$ from (5) using the $C_{1}(B_{i})$ values from (14) and (15) for n even and odd, respectively. Note that the maximum positive value of X before reduction mod $M_{c}$ in (16) can be >M $_{c}$ or negative thus needing one addition or subtraction of $M_{c}$ for performing modulo reduction in (16).

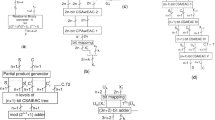
The typical $C _{1}(B _{i})$ and $w _{i}$ values in the case $C _{1}(M _{c}) = 2^{n}-1$ for $n = 5,6,7$ and 8 are presented in Table 2. Since the $C _{1}(B _{i})$ and $w _{i}$ values cannot be expressed as simple sum of terms of the form $2^{z}$, it is preferable to use read-only memory (ROM) to obtain ($r _{i} C _{1}(B _{i})$)$\mod C _{1}(M _{c})$ as shown in Fig. 3a. The ROM1 and ROM3 are of size $2^{n} \times n$ bits, and ROM2 and ROM4 are of size $2^{n+1} \times n$ bits. Next, the output words of ROM1, ROM2, ROM3 and ROM4 need to be added mod ($2^{n}-1$) using two n-bit CSA stages with end-around-carry (EAC) (CSA1 and CSA2) followed by a n-bit CPA with EAC (CPA1) as shown in Fig. 3a (note that C and S stand for carry and sum vectors). Next, corresponding to given $r _{2}, r _{3}$ and $r _{4}$ using ROMs ROM5, ROM6 and ROM7, the 4n-bit values $u=w _{2} m _{3} m _{4} r _{2}, v=w _{3} m _{2} m _{4} r _{3}, w =w _{4} m _{2} m _{3} r _{4 }$ can be obtained as shown in Fig. 3a. These ROMs are of size $2^{n+1} \times (3n), 2^{n} \times (4n), 2^{n+1} \times (4n)$, respectively. Note that the bit width of the ROM 5 is less since the multiplier $w _{2}$ is $2^{n-3}$ and can be obtained by appending n-3 zero bits as LSBs to the word read from the ROM5. The weighting of $C _{1}(X)$ with $(2^{2n}-9)(2^{n}+1)$ and addition with the three terms obtained from ROMs ROM5, ROM6 and ROM7 can be carried out by mapping the bits of $C _{1}(X)$ denoted as $c _{1,j}$ and the three ROM outputs as shown in the bit matrix in Fig. 3b. The bit mapping 1 block in Fig. 3a performs this function. Note that dashes $(')$ indicate inverted bits. The addition is performed using a four-level CSA tree 1 needing $(10n-2)\hbox {FA}+(4n+1)$ XNOR/OR +4HA. The CSA tree 1 is followed by a mod $M_{c}$ adder 1 using two cascaded 4n-bit CPAs each needing $4n\hbox {FA}$. The second CPA stage performs optional addition or subtraction of $M_{c}$.

4.3.2 Case II

In this case, the $C_{2}(B_{i})$ values will be bounded by the chosen $C_{2}(M_{c}) = 2^{2n}-1$. The various $w_{i}$ and $C_{2}(B_{i})$ values for the case n even are as follows:

$$\begin{aligned} w_1= & {} 0,w_2 =0,w_3 =\left( {\frac{-2^n +4}{6}} \right) ,w_4 =\frac{2^n +2}{6} \nonumber \\ C_2 (B_1 )= & {} (2^n -2^{n-4} -1)(2^n +1),C_2 (B_2 )=(2^n -2^{n-4} +1)(2^n -1),\nonumber \\ C_2 (B_3 )= & {} (2^n +3)\left( {\frac{11(2^n -3)+1}{48}} \right) +2,\nonumber \\ C_2 (B_4 )= & {} (2^n -3)\left( {\frac{43(2^n +3)-1}{48}} \right) +7 \end{aligned}$$

(17)

Table 2 $C_{1}(B_{i}), C_{2}(B_{i})$ and $w_{i}$ values for both cases $C_{1}(M_{c}) = 2^{n}-1$ and $C_{2}(M_{c}) = 2^{2n}-1$ for moduli set M5

Fig. 3

Reverse conversion method I for moduli set M5. a architecture, and b bit matrix corresponding to computation of X (primes indicate inverted bits.) (LSBs are shown in the top figure, and MSBs are shown in the bottom figure)

For the case n odd, we have

$$\begin{aligned} w_1= & {} 0,w_2 =0,w_3 =\frac{2^n -2}{6},w_4 =-\left( {\frac{2^n +4}{6}} \right) \nonumber \\ C_2 (B_1 )= & {} \left( 2^n -2^{n-4} -1\right) (2^n +1),C_2 (B_2 )=\left( 2^n -2^{n-4} +1\right) (2^n -1),\nonumber \\ C_2 (B_3 )= & {} (2^n +3)\left( {\frac{43(2^n -3)+1}{48}} \right) +7, \nonumber \\ C_2 (B_4 )= & {} (2^n -3)\left( {\frac{11(2^n +3)-1}{48}} \right) +2 \end{aligned}$$

(18)

For reverse conversion following (6), we need to compute

$$\begin{aligned} X = \left[ C _{2}(X) \left( 2 ^{2n} -9\right) + w _{3} m _{4} r _{3}+_{ } w _{4} m _{3} r _{4} \right] {\mathrm{mod}} M _{c} \end{aligned}$$

(19)

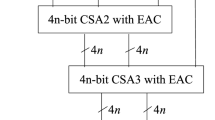
after computing $C _{2}(X)$ from (5) using $C _{2}(B _{i})$ values from (17) and (18) for n even and odd, respectively. Note that in this case also, the maximum positive value of X before reduction mod $M _{c}$ in (19) is >M $_{c}$ and can be negative also thus needing one addition or subtraction of $M _{c}$. The typical $C _{2}(B _{i})$ and $w _{i}$ values in the case $C _{2}(M _{c}) = 2^{2n}-1$ for $n = 5,6,7$ and 8 are also presented in Table 2. Since the $C _{2}(B _{i})$ and $w _{i}$ values cannot be expressed as simple sum of terms of the form $2^{z}$, it is preferable to use read-only memory (ROM) to obtain ($r _{i} C _{2}(B _{i})$)$\mod C _{2}(M _{c})$ values from ROM8, ROM9, ROM10 and ROM11. The ROMs ROM8 and ROM10 are of size $2^{n} \times 2n$ bits and ROM9 and ROM11 are of size $2^{n+1} \times (2n)$ bits. Next, the ROM output words need to be added mod ($2^{2n}-1$) using two 2n-bit CSA stages with EAC (CSA3 and CSA4) followed by a 2n-bit CPA with end-around-carry (CPA2) as shown in Fig. 4a. Next, corresponding to given $r _{3}$ and $r _{4}$ using ROMs ROM12 and ROM13, the values $s=w _{3} m _{4} r _{3}, t= w _{4} m _{3} r _{4 }$ can be obtained as shown in Fig. 4a. These are of size $2^{n} \times (3n)$ and $2^{n+1} \times (3n)$, respectively. The weighting of $C _{2}(X)$ with ($2^{2n}-9$) and addition with the two terms obtained from ROMs ROM12 and ROM13 can be carried out by mapping the bits of $C _{2}(X)$ denoted as $c _{2,j}$ and the outputs of ROM12 and ROM13 as shown in the bit matrix in Fig. 4b. The bit mapping block 2 in Fig. 4a performs this function. Note that dashes $(')$ indicate inverted bits. The addition is performed using a three-level CSA tree 2 needing ($5n+1)\hbox {FA}+(2n-2)\hbox {XNOR/OR}+(2n-2)\hbox {HA}$. The CSA tree 2 is followed by a mod $M _{c}$ adder 2 using two cascaded 4n-bit CPAs needing each $4n\hbox {FA}$. The second stage performs optional addition or subtraction of $M _{c}$.

Fig. 4

Reverse conversion method II for moduli set M5. a architecture, and b bit matrix corresponding to computation of X (primes indicate inverted bits.) (LSBs are shown in the top figure, and MSBs are shown in the bottom figure)

4.3.3 Case III

We next consider the case with core chosen as product of all moduli except $m_{2}$. Thus, we choose $C_{3}(M) = (2^{n}-1)(2^{n}-3)(2^{n}+3)$. In this case, note that only $w_{4}$ exists. Using the core value $C_{3}(M)$, we can find $w_{4}$ from (2a) as 1:

$$\begin{aligned} {w_i} =\left( {{\left( {\frac{1}{{(2}^n -1)(2^{2n} -9)}} \right) }_{2^n +1} {(2}^n -1)(2^{2n} -9)} \right) \bmod ({(2}^n +1)=1 \end{aligned}$$

(20)

The remaining $w_{i}$ for $i = 1, 2, 3$ are zero. The various $C(B_{i})$ values can be next obtained as

$$\begin{aligned} C_3 (B_1 )= & {} {(2}^n -2^{n-4} -1){(2}^{2n} -9),C_3 (B_2 )=\frac{k(2^n -3)+1}{48}(2^n -1)(2^n +3), \nonumber \\ C_3 (B_3 )= & {} 15\times 2^{3n-4} -7\times 2^{2n-3} -137\times 2^{n-4} +8,\nonumber \\ C_3 (B_4 )= & {} \frac{{k}'(2^n +3)-1}{48}(2^n -1)(2^n -3) \end{aligned}$$

(21)

where k and $k'$ for n even and odd are as defined in (13). Next from (21), the core can be found from (5) as

$$\begin{aligned} C_3 (X)={\left( {r_1 C_3 (B_1 )+r_2 C_3 (B_2 )+r_3 C_3 (B_3 )+r_4 C_3 (B_4 )} \right) }_{{(2}^n -1)(2^{2n} -9)} \end{aligned}$$

(22)

and the decoded number is obtained as

$$\begin{aligned} X= C_{3}(X)(2^{n}+1)+ r_{2} \end{aligned}$$

(23)

Note that no final mod M reduction is needed in this case. The typical $C _{3}(B _{i})$ and $w _{i}$ values in the case $C _{3}(M _{c}) = (2^{n}-1)(2^{2n}-9)$ for $n = 5, 6, 7$ and 8 are presented in Table 3. The reverse converter following (22) and (23) is presented in Fig. 5a. Note that ROM14, ROM15, ROM16 and ROM 17 can be used to obtain, respectively, the four 3n-bit words $r _{i} \times C _{3}(B _{i})$ for $i = 1,2,3$ and 4. Note that the ROMs 14 and ROM 15 are $2^{n} \times 3n$ bits and ROMs 16 and 17 are $2^{n+1} \times 3n$ bits. The output words of the ROMs are added using 3n-bit CSAs CSA5 and CSA6 followed by a modulo (($2^{2n}-9)(2^{n}-1$)) adder using a ($3n+2$)-bit CPA and a ($3n+2$)-bit 2:1 MUX to obtain $C _{3}(X)$. Note that an addition followed by two consecutive subtractions may be needed for the modulo reduction to obtain $C _{3}(X)$. Next, X can be computed using (23) by adding the three 3n-bit words shown in Fig. 5b.

Table 3 Hardware requirement and conversion time of various converters for three-moduli sets

Note that $C_{3}(X)$ is the 3n-bit word $c_{3,3n-1} c_{3,3n-2},\ldots ,c_{3,1}, c_{3,0}$. The addition of these words using a CSA7 followed by CPA3 needs ($3n+1$) FAs and ($3n-1$) HAs after simplification due to the reason that several bits are zero.

Fig. 5

Reverse conversion method III. a Architecture and b bit matrix corresponding to computation of X (primes indicate inverted bits)

It is interesting to note that most reverse converter implementations based on CRT obtained by subtracting one residue from the CRT sum and dividing by the corresponding modulus or those reverse converters based on new CRT I compute X similar to (23). The decoded number in new CRT I [40] can be obtained as

$$\begin{aligned} X=r_2 +m_2 {\big ({(x_3 -x_2 )a+m_3 b(x_4 -x_3 )+m_3 m_4 c(x_1 -x_4 )} \big )}_{M_2 } \end{aligned}$$

(24a)

where

$$\begin{aligned} a={\left( {\frac{1}{m_2 }} \right) }_{m_1 m_3 m_4 } , \quad b={\left( {\frac{1}{m_2 m_3 }} \right) }_{m_1 m_4 } {\mathrm{and}} \quad c={\left( {\frac{1}{m_2 m_3 m_4 }} \right) }_{m_1 } \end{aligned}$$

(24b)

Note that a, b and c can be obtained as

$$\begin{aligned} a= & {} 2^{3n-4} -2^{2n-3} -7\times 2^{n-4} +1,\nonumber \\ b= & {} \frac{(2^{n+2} -\alpha )(2^n -1)(2^n +3)-1}{2^{n+2} }, {\mathrm{and}} \,c=2^n -2^{n-4} -1 \end{aligned}$$

(24c)

where $\alpha$ is such that b is an integer. For $n = 8, \alpha = 171$. Substituting these a, b and c values in (24a) and collecting terms of $r _{1}, r _{2}$, $r _{3}$ and $r _{4}$, the multiplier of $m _{2}$ in (24a) can be seen to be $C _{3}(X)$. Thus, if we choose core C(M) as the product of all moduli except one modulus, e.g., $m _{a}$, denoting the decoded number as $X=d\left( {\frac{M}{m_a }} \right) +r_a$, the core value C(X) is the MRC digit d. For all other choices of C(M), C(X), it is approximate value of $X\left( {\frac{C\left( M \right) }{M}} \right)$.

4.4 Additional Remarks

We wish to point out that the values of $w_{i}$ and $C(B_{i})$ can be easily obtained from the CRT expansion itself. This can be seen by dividing the CRT expansion by M/C(M) and observing the coefficients of $r_{i}$ which are mixed fractions. These can be rounded or truncated depending on the fractional part being greater than 0.5 or less than 0.5. This yields the $C(B_{i})$ values and $w_{i}$ values since $C(B_{i})+w_{i}$ has to be same as the coefficient of $r_{i}$ in ‘scaled’ CRT expansion given in (8).

Consider the four-moduli set $\hbox {M5} = \{2^{n}-1, 2^{n}+1, 2^{n}-3, 2^{n}+3\}= \{255,257,253,259\}$ for $n = 8$. Let the core chosen be $C(M) = 255$. Note that the ${\left( {\frac{1}{M_i }} \right) }_{m_i }$ values are 239, 241, 58 and 232, respectively, for $i = 1, 2, 3$ and 4 from (13a). The CRT expansion yields after division by $M _{c}/C _{1}(M _{c}) = 257\times 253\times 259$,

$$\begin{aligned} \frac{X}{257\times 253\times 259}=239r_1 +239\frac{32}{257}r_2 +58\frac{116}{253}r_3 +228\frac{108}{259}r_4 \end{aligned}$$

Note that truncation or rounding of the coefficients of $r _{2}, r _{3}$ and $r _{4}$ can be performed. The numerators of the fractions are the various $w _{i}$ values. One or more of these can be chosen as ($m _{i}-w _{i}$) and corresponding integer part of the weight of $m _{i}$ be incremented by 1 so as to meet the condition (2b). Thus, we have $C(B _{1})=C(B _{2}) = 239, C(B _{3}) = 59, C(B _{4}) = 228$ and $w _{1 } = 0, w _{2 }= 32, w _{3 }= -137, w _{4 }= 108$. It may be verified that (2b) is satisfied: $32\times 255\times 253\times 259-137\times 255\times 257\times 259+108\times 255\times 257\times 253 = 255$. Considering the given residues {1, 2, 3, 4}, the core value can be obtained as 21 and the decoded number is $X= 21\times 257\times 253\times 259+2\times 32\times 253\times 259- 3\times 137\times 257\times 259 +4 \times 108\times 257\times 253 = 358{,}574{,}626$.

5 Comparison with Earlier Designs

In this section, hardware requirements as well as conversion times of the proposed converters for the two three-moduli sets M2 and M4 and four-moduli set M5 are evaluated. The total resource requirements of proposed converter in terms of full-adders, half-adders, gates such as exclusive ORs and the conversion time in terms of full-adder delay are presented in Table 3 as entry D4 for moduli set M2. The corresponding resource requirement and conversion time for designs reported in the literature in [8] for moduli set M2 are also presented in Table 3 as entries D1–D3. The technique used for reverse conversion in each of these converters is also given in Table 3. The design converter I (entry D1) is based on mixed radix conversion, whereas the converters II (D2) and III (D3) designs are based on CRT. The design D3 uses ROM, whereas the converters D1 and D2 need only combinational logic.

The recently described converter D6 [22] for the three-moduli set M4 based on a modification of CRT has been shown to be area-efficient over the previous designs [3] and [21]. Note, however, that the authors in [22] did not give the area in terms of basic logic elements and described only an FPGA implementation. We consider the use of array multipliers for both $2n\times n$ multiplier as well as $n\times n$ multiplier where $n=\hbox {log}_2 \left( {2m+1} \right)$. We also consider that 5:1 MUX is realized as a three-level cascade of 2:1 multiplexers (MUX) (first level containing two 2:1 MUXes, second level 2:1 MUX combining the outputs of these two MUXes and a third level combining the fifth input with the output of the second level 2:1 MUX). The total hardware and conversion time requirements thus computed are presented as entry D6 in Table 3 for this converter, whereas the corresponding requirements for the proposed converter are presented in entry D5 in Table 3.

We have also considered state-of-the-art models for gates in terms of transistors [13] for more realistic estimate of the performance. The transistors needed for various gates and arithmetic cells are 20, 10, 8, 6, 4 and 2 for a full-adder, half-adder and 2:1 multiplexer/XOR/NOR logic elements, AND/OR, NAND/NOR and NOT gates, respectively. Note that two-input gates have been considered in the above estimation. Since some of the converters (converter III (entry D3) for moduli set M2 and converters entries 4–7, 9, 10 for moduli set M5) need ROM, we need to estimate the number of transistors needed for ROM. We use the model used by earlier authors [36] and [42]. Denoting the ROM requirements as $\theta \times \gamma$ bits implying $\theta = 2^{n}$ locations each $\gamma$ bit-wide, the number of transistors $A_\mathrm{ROM}$ required for implementing the ROM and access time $D_\mathrm{ROM}$ are given as

$$\begin{aligned} A_\mathrm{ROM }=\theta \times { \gamma }+2 ^{a}(a +1)+2 ^{b}(b +2) \gamma +(2 ^{b} +1){ \gamma } \end{aligned}$$

(25a)

and

$$\begin{aligned} D_\mathrm{ROM} =\left( {1+2\hbox {log}_2 a+2\hbox {log}_2 \left( {b+1} \right) +b} \right) \Delta _g \end{aligned}$$

(25b)

where $\Delta _{g}$ is the delay of a simple 2-input gate, $a=\lceil \hbox {log}_2 \theta \rceil$ and $b=\lfloor \hbox {log}_2 \theta \rfloor$. Note that design entry 3 of Table 3 needs 10($2n+1$) ROM bits, whereas we have considered 16($2n+1$) bits thus implying $\theta = 16, a = 4, b = 4$ and $\gamma = 2n+1$. Thus, the number of transistors needed can be obtained from (24a) as 10 ($2n+1)+16\times (4+1)+16\times (4+2)\times (2n+1)+(16+1)\times (2n+1)$ or $246n+203$. The ROM access time for various a and b values obtained from (24b) is presented in Table 4. The delays of various logic elements in terms of $\Delta _{g}$ (a two-input gate delay) are, respectively, [26] for full-adder, half-adder, 2:1 MUX/XOR/XNOR, AND/OR, NAND/NOR and NOT as 4, 2, 2, 1, 1 and 0. The total number of transistors and the conversion time needed for all the three-moduli set converters using the models for ROM and various gates obtained from Table 3 are presented in Table 5. The area in terms of number of transistors for all the three-moduli converters for $n =3$–32 is presented in Table 6. The plots showing the area in number of transistors and conversion times for all the designs for Moduli set M2 are presented in Fig. 6a, b and for moduli set M4 in Fig. 6c, d, respectively.

Table 4 ROM access time for different memory address ranges (2$^{\alpha })$

Table 5 Hardware requirements (number of transistors) and Conversion time of three-moduli converters

Table 6 Area (number of transistors) for three-moduli sets

Fig. 6

a Transistor requirement for moduli set M2, b conversion time of designs for moduli et M2, c transistor requirement, d conversion time for moduli set M4 for three-moduli reverse converters or various values of n

Table 7 Hardware and conversion time comparison of converters for four-moduli set M5

Table 6 shows that among the converters for the moduli set M2, converter D1 using MRC needs the lowest number of transistors, whereas the proposed design D4 based on core function needs less area than the converters D2 and D3 based on CRT and more area than the converter D1 using MRC. The conversion time of the proposed converter design 4 is more than that of D1. The converters D2 and D3 need much lower conversion time than the converter I using MRC. It can be concluded that the D1 using MRC is preferable for low area and low conversion time than the proposed design. Considering the two converters for the moduli set M4 in Table 6, it can be seen that the converter based on core function D5 needs more area and conversion time than converter D6 for $n>$3. For n increasing from 5 to 32, the area increases from 2 to 28 % and the conversion time increases from 8 to 18 %.

Table 8 Hardware requirements (number of transistors) and conversion times of converters for moduli set M5

Fig. 7

a Transistor requirement for all designs and b conversion times for reverse converters for moduli set M5 for various values of n

We next consider the reverse converters for the four-moduli set M5. The converter proposed in [34] uses new CRT II by considering pairs of moduli $\{2^{n}-3, 2^{n}+1\}$ and $\{2^{n}-1, 2^{n}+3\}$ in first level using MRC to obtain two intermediate numbers followed by a second level also using MRC to obtain the final number. This design uses large size ROMs together with combinational logic. The ROM model needs $a=\lceil \hbox {log}_2 \left( {2^{n+4}+16} \right) \rceil$ and $b=\lfloor \hbox {log}_2 \left( {2^{n+4}+16} \right) \rfloor$ [26]. The hardware and conversion time requirements in terms of basic components are presented in entry D1 in Table 7. Converters for this moduli set using two-level MRC (same as new CRT II for four-moduli RNS) and CRT are described in [11] which can be realized as cost-effective or high-speed versions. Note that the high-speed designs realize modulo addition ($A+B$) mod $m_{i}$ by computing $A+B$ and $A+B-m_{i}$ using two adders in parallel and based on the sign bit of the result of the computation of ($A+B-m_{i}$), the correct output among $A+B$ and $A+B-m_{i}$ is selected. The two-level MRC-based designs use same pairs of moduli as in [34] but use Montgomery algorithm to implement two-moduli MRC algorithm using combinational logic. The cost-effective and high-speed versions of these converters are presented as entries D2 and D3 in Table 7. The designs using conventional MRC using ROM for both high-speed and cost-effective versions are presented as entries D4 and D5 in Table 7. In both these designs, three levels of table look-up are needed. The hardware and conversion time requirements of CRT-based implementation using ROM for both high-speed and cost-effective versions are presented as entries D6 and D7 in Table 7. Note that the designs 4–7 need $2^{n}$ locations for each ROM thus needing $a=b=n$. In the designs using CRT (entry 6 and entry 7), only one level of table look-up is needed. The recent design of Jaberipur and Ahmadifar [26] uses combinational logic only and uses different pairing of moduli in the first level $\{2^{n}-1, 2^{n}+1\}$ and $\{2^{n}-3, 2^{n}+3\}$ from that in [34] and [11]. The hardware and conversion time of this converter are presented as entry D8 in Table 7. Finally, the hardware and conversion time of the three converters based on core function using $C_{1}(M_{c}) = 2^{n}-1, C_{2}(M_{c}) = 2^{2n}-1$ and $C_{3}(M_{c}) = (2^{n}-1)(2^{2n}-9)$ are presented as entries D9–D11 in Table 7. The corresponding count of the number of transistors needed taking into account the component and ROM models described before for all the eleven designs for various values of n are presented in Table 8 for moduli set M5 together with the corresponding conversion times. The plots showing the area in number of transistors and the conversion times for all the eleven converters are presented in Fig. 7a, b.

Figure 7a and Tables 7 and 8 show that among the converters based on core function, the choice of core as one modulus (D9) leads to lower conversion time, whereas the choice of core as product of three moduli (D11) leads to less area. The converter D8 [26] using two-level MRC needs lower hardware requirements and conversion times than the proposed three converters based on core function. The designs D2 and D3 need less area than all the other converters. It can be concluded that the converter D8 exhibits the best performance—low area and low conversion time. The proposed converters D9–D11 need less conversion time than the designs D2, D3 and D5 using MRC and 6 using CRT. Among these, for n values below 16, the converter 8 needs least area. The conventional MRC-based designs D4 and D5, CRT-based designs D6 and D7, and core function-based designs D9–D11 exhibit fast increase in hardware requirements with increase in n. This results because of the large ROM requirement due to the complicated structure of the various multiplicative inverses.

It is relevant to assess the various RNS to binary conversion methods. The MRC-based converters need ($k-1$) steps for a k-moduli RNS. Each step needs several modulo subtractions followed by modulo multiplication with multiplicative inverses. In the case of moduli of the type $2^{x}-1$, the modulo subtraction can be simplified using adders with EAC. In the case of general moduli ($2^{x}\pm a)$, the modulo subtractions need cost-effective or high-speed modulo adders. In the case of moduli sets needing simple multiplicative inverses having only few ‘’1” bits (many bits may be zero), the multiplications mod $m_{i}$ when $m_{i}$ is $2^{x}-1$, the partial products are obtained by circular left shift which can be added using CSA tree followed by a CPA with EAC. In the case of modulus $2^{x}\pm a$, other techniques need to be used where the MSB bits of the partial products (bits beyond x bits) need to be reduced and added with LSB bits of all partial products leading to increase in hardware as well as computation time. In the case of general moduli, the modulo multiplication with the multiplicative inverses may need ROMs. Next parallel multiplications of the MRC digits $d_{i}$ with constants such as $m_{1}, m_{1} m _{2}, m _{1}m_{2} m _{3},\ldots , m_{1}m_{2}m_{3}\ldots m_{k-1}$ and final addition of all the products needs to be carried out for evaluating the final decoded number:

$$\begin{aligned} X=d _{0}+d _{1} m _{1}+d _{2} m _{1} m _{2}+d _{3} m _{1} m _{2} m _{3} +\cdots + d _{n-1} m _{1} m _{2} m _{3} \ldots m _{n-1}\nonumber \\ \end{aligned}$$

(26)

In case of powers-of-two-related moduli sets, the weighting with these various constants (products of moduli) can be carried out by having few partial product terms. Using multiple level CSA and CPA, the addition of all these terms can be obtained. In the case of general moduli sets, multipliers of various operand bit lengths (since word lengths of the various constants are different) will be required to multiply the constants with the MRC digits obtained and final addition needs to be performed using a CSA tree and CPA to obtain X. The advantage of MRC is that final modulo reduction is not needed.

All other techniques of RNS to binary conversion CRT, new CRT II and core function use some form of CRT. We consider CRT for three different cases. In the first case where no modulus of the form $2^{k}$ is present, the various $M_{i}r_{i}(1/M_{i})$ mod $m_{i }$ can be computed in parallel and the sum S of these is reduced modulo M. This technique, however, needs mod M reduction in a large number S. Alternatively, the various $M_{i }(r_{i}(1/M_{i})$ mod $m_{i})$mod $m_{i}$ can be computed and the results added in a modulo M adder. For a k moduli RNS, in the first case the sum of the various terms S needs subtraction of a large multiple of M and the latter case needs subtraction of at most $(k-1)M$. Thus, the reduction in result modulo M is area- and time-consuming even if the simpler latter option is chosen. In the second technique, subtracting one of the residues $r_{j}$ corresponding to one modulus $m_{j}$ from the CRT summation and dividing by $m_{j}$, the modulo reduction is simplified to a smaller size word $M/m_{j}$. The result $X_{H}$ needs final multiplication with $m_{j}$ and addition of $r_{j}$ in a final adder. In case one modulus is of the form $2^{x}$, the final result can be obtained by concatenating the result and $r_{i }$ without needing additional hardware. In some moduli sets, $M/2^{x}$ of the form ($2^{\alpha }-1$), so that the modulo $M/2^{x}$ reduction can be easily carried out using end-around-carry operations to obtain the MSBs $X_{H}$ of the decoded word. This advantage is enjoyed by the moduli sets $\{2^{n}, 2^{n}+1, 2^{n}-1\}$, $\{2^{n}, 2^{n}-1,2^{n}+1,2^{2n}+1\}$, $\{2^{n},2^{n}-1,2^{n}+1,2^{n}-2^{n+1/2}+1,2^{n}+2^{n+1/2}+1\}$, $\{2^{n}, 2^{2n}-1,2^{2n}+1\}$. In the third case, e.g., moduli sets M2, M3 having one modulus of the type $2^{x}$ but with the product of the other moduli not of the form ($2^{\alpha } -1$), e.g., moduli set M2, M3 and M4, we need the difficult reduction modulo a large number $M/2^{x}$. This increases the conversion time and needs more hardware. In the general case like moduli set M5, new CRT II can be used needing only modulo ($M/m_{a}$) reduction where $m_{a}$ is any one modulus in the moduli set. In this case, reduction modulo $M/m_{a}$ needs to be carried out, but a final adder following (23) will be needed.

The use of core function for RNS to binary conversion aims to reduce the magnitude of CRT summation <($k-1$)M so that the multiple of M that needs to be subtracted to perform reduction mod M can be reduced. The sum consists of two parts [see (6)] a first part dependent on the core C(X) and the second part dependent on some of the given residues $r_{i}$ and weights $w_{i}$ and moduli $m_{i}$. The choice of core of the form $2^{z}-1$ or $2^{z}$ will simplify modulo reduction to obtain the core C(X) from (5). The various $C(B_{i})$ are less than C(M), and if they are in simple form, multiplication with residues $x_{i }$ can be carried out by shifting/complementing operations and reduction modulo C(M) can be simplified. However, if the core C(M) is not of the two forms, the computation of C(X) needs reduction modulo C(M) which leads to more hardware and conversion time. The computation of the second part in (6) needs multipliers. Since one of the weights is negative, the final result can be negative as well in which case, the modulo reduction to obtain X needs addition of M. The core function-based reverse conversion needs invariably a final modulo M adder irrespective of whether one modulus is of the form $2^{x}$ or not. The choice of C(M) as one modulus or product of more moduli leads to requirement of different size multipliers and adders in the two parallel paths leading to area/conversion time trade-offs.

Thus, the choice of a particular technique MRC, CRT, new CRT II or core function depends on the structure of the moduli, the simplicity of multiplicative inverses, the simplicity of products of all moduli and/or simplicity of $C(B_{i})$ values. For general moduli sets where all the advantages of easy modular operations exist, CRT-based methods or variations such as new CRT II and core function may be attractive as evidenced by several interesting solutions. The choice of MRC is preferable in cases where the area and conversion time needed for final reduction mod M or mod $M/2^{k}$ needed in CRT or simplified CRT or core function-based conversion is compensated by the sequential computation of the mixed radix digits and weighted summation of the MRC digits. MRC facilitates comparison of numbers based on mixed radix digits without needing final conversion, though in a sequential manner. In the case of general moduli sets, all the techniques of reverse conversion need to be explored to arrive at an acceptable solution.

6 Conclusion

It has been shown that core function can be derived from CRT and is an approximate version of CRT scaled by one modulus or product of several moduli. In the case of choice of one modulus as ore, it has been shown that core function evaluates the mixed radix digit approximately. It has been shown that the reverse conversion using core function is exact and leads to new architectural options which need to be explored for possible area–time trade-offs for any moduli set chosen. Three-moduli sets for which RNS to binary conversion is more difficult than for the popular three-moduli set $\{2^{n}-1, 2^{n}, 2^{n}+1\}$ are considered for evaluation of the efficiency of reverse conversion using core function. The possible area (number of transistors) and conversion times trade-offs have been discussed taking into account realistic models for various logic gates as well as ROM. The choice of core as one modulus or product of two and three moduli is also studied for the four-moduli set M5 to bring out the trade-offs between area and conversion time. Just as the computation of mixed radix digit alone cannot give the exact location of the given RNS number in the dynamic range of the RNS to facilitate comparison or sign detection, core value alone cannot be accurately used for comparison or sign detection except in the case when core is product of all but one moduli. Accurate comparison and sign detection can be performed after reverse conversion only.