Reverse Converters for the Moduli Set {$2^{n}, 2^{n-1}-1,2^{n}-1, 2^{n+1}-1\}(n\,\hbox {Even})$

Abstract

In this paper, two residue number system (RNS) to binary converters for the moduli set {$2^{n}, 2^{n-1}-1,2^{n}-1, 2^{n+1}-1\}$ for (n even) are presented. One of them uses a two-level conversion, in which, in the first level, two pairs of moduli are considered to obtain two intermediate decoded numbers. A second-level converter obtains the final decoded number corresponding to these two intermediate decoded numbers. Both levels use mixed radix conversion. The second proposed RNS to binary converter uses the conventional MRC of the four-moduli set. The proposed converters are compared with previously reported conversion techniques for this moduli set and converters for other four, five and eight moduli sets for realizing similar dynamic ranges regarding hardware requirement and conversion time. The hardware resource requirement (A), conversion time (T), AT and $AT^{2}$ trade-offs are discussed to bring out the relative advantages of various converters. The proposed converters have been shown to need less hardware or less conversion time than the other some of the reported converters for this moduli set. It has been shown by detailed comparison that converters using conjugate moduli and vertical extension generally exhibit better performance (lower hardware /lower conversion time) than those using no vertical extension, while needing differing word lengths of various moduli. These, however, need slightly complex multipliers/adders in the $(2^{n} +1)$ channel. Implementation results on FPGA of the proposed converters for few dynamic ranges also have been presented.

1 Introduction

The residue number system (RNS) using three or more moduli of the form $2^{a}, 2^{b}-1, 2^{c}+1$ has attracted considerable attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33, 35,36,37,38,39,40] . In view of the relative difficulty of operations using moduli of the form $(2^{c}+1)$ as compared to moduli of the form $2^{a}, 2^{b}-1$, designers have considered moduli sets with moduli of the form $2^{a}$ and $2^{b}-1$ with a and b values as close as possible so that all moduli processors have about the same word length. The modulo addition, modulo subtraction, modulo multiplication are known to be easy for such moduli. A b-bit modulo addition ($u+v)$ mod $(2^{b}-1)$ where u and v are b-bit numbers can be performed by a b-bit adder adding u and v with end-around-carry (EAC). A b-bit modulo subtraction, i.e., ($u-v)$ mod $(2^{b}-1)$ can be carried out by addition of u with one’s complement of v in a b-bit adder with EAC. The operation ($u\times v)$ mod $(2^{b}-1)$ can be easily carried out by rewriting the bits of the partial products in the higher bit positions in lower bit positions by using the periodic property of such moduli: $2^{k+b}x_{i}$ mod $(2^{b}-1) = 2^{k}x_{i}$ and adding the reduced b-bit partial products using a carry-save adder tree followed by a b-bit adder with EAC. Scaling $x_{i}$ by $2^{k}$ mod $(2^{b}-1)$ can be achieved by left circular left of $x_{i}$ by k bits.

Only two four-moduli sets M1 {$2^{n}, 2^{n-1}-1, 2^{n}-1, 2^{n+1}-1$} [12, 13, 33], M2 {$2^{k}, 2^{n-1}-1, 2^{n}-1, 2^{n+1}-1$} [39] with n even, have been described in the literature which use one modulus of the form $2^{\alpha }$ and other three moduli of the form $(2^{\beta }-1)$. Esmaeildoust et al. [12] have recently presented two designs of RNS to binary converters for the moduli set M1. These were realized using two-moduli RNS {$M_{\mathrm{a}}, 2^{n-1}-1$}, where $M_{{a}}$ is the three-moduli set {$2^{n}, 2^{n}-1, 2^{n+1}-1$} [2]. They have used mixed radix conversion (MRC) for the two-moduli RNS and employing three converters proposed for the three-moduli subset $M_{a}$ [2]; they have described six RNS to binary converters. Taheri et al. [33] have described a two-stage RNS to binary converter for this moduli set. In the first stage, the reverse conversion for the moduli set $M_{b} \{2^{n-1}-1, 2^{n}-1, 2^{n+1}-1$} is carried out using MRC. The second stage uses MRC for the composite moduli set {$M_{b}, 2^{n}$}. However, they avoid the final addition in the MRC-based converter in the first stage in order to reduce the conversion time. The moduli set M1{$2^{n}, 2^{n-1}-1, 2^{n}-1, 2^{n+1}-1$} has been suggested by Schinianaikis et al. for use in ECC processors with $n = 64$ [13]. They have used MRC to obtain mixed radix digits. However, in their application, these MRC digits are used to perform base extension to another moduli set using Horner’s rule. The last stage needed in MRC-based RNS to binary conversion was not investigated. In [39], using modulus $2^{k}$ in place of $2^{n}$ in the moduli set M1, the MRC technique has been used to realize a RNS to binary converter. In this paper, we propose one RNS to binary converter based on two-level conversion technique and also extend the mixed radix conversion technique considered in [13] to realize another RNS to binary converter. In Sect. 2, we present the background material needed for this paper. The detailed derivation of the two proposed converters together with the architectures needed for their realization is presented in Sect. 3 in detail. In Sect. 4, the proposed converters are compared regarding hardware requirement and conversion time with earlier described designs of converters for this moduli set in [12, 33]. The proposed designs are also compared with converters for other moduli sets using four or more moduli considering their design for similar dynamic range. These are $\hbox {M3} \{2^{n}, 2^{n}-1, 2^{n}+1, 2^{n+1}-1)$ [4, 6, 15, 35] (n even), $\hbox {M4} \{2^{n}, 2^{n}-1, 2^{n}+1, 2^{n-1}-1\}$ [6] (n even), $\hbox {M5} \{2^{n}, 2^{n}-1, 2^{n}+1, 2^{n+1}+1\}$ (n odd) [4, 5, 29], M6 {$2^{n}, 2^{n}-1, 2^{n}+1, 2^{n-1}+1\}$ (n odd) [19], $\hbox {M7}\{2^{n}, 2^{n}-1, 2^{n}+1, 2^{n+1}-1, 2^{n-1}-1\}$ [8], $\hbox {M8}\{2^{n}, 2^{n}-1, 2^{n}+1, 2^{2n+1}-1\}$ [17, 30], $\hbox {M9} \{2^{2n}, 2^{n}-1, 2^{n}+1, 2^{2n+1}-1\}$ [30], $\hbox {M10}\{2^{n}, 2^{n}-1, 2^{n}+1, 2^{2n}+1\}$ [7], $\hbox {M11}\{2^{2n}, 2^{n}-1, 2^{n}+1, 2^{2n}+1\}$ [17] and $\hbox {M12} \{2^{n-5}-1, 2^{n-3}-1, 2^{n-3}+1$, $2^{n-2}+1, 2^{n-1}-1, 2^{n-1}+1, 2^{n}, 2^{n}+1\}$ [26]. Implementation results of the two proposed converters on FPGA for few n values are also presented. In Sect. 5, we conclude the paper.

2 Background Material

A residue number system uses l moduli {$m_{1}, m_{2},m_{3}, m_{4}, \ldots , m_{l}$} and has a dynamic range $D=m_{1}\times m_{2}\times m_{3}\times \cdots \times m_{l}$, thus being capable of representing uniquely all the numbers X between 0 and D-1 using the residues {$x_{1}, x_{2}, x_{3}, \ldots , x_{l}$} where X mod $m_{i}=x_{i}$ for i= 1, 2,..., l. The process of obtaining the binary number X corresponding to given residues {$x_{1}, x_{2}, x_{3}, \ldots , x_{l}$} is known as reverse conversion and can be carried out by several techniques [1, 18, 28, 32] and most popular among these are based on using Chinese remainder theorem (CRT) [1] and mixed radix conversion (MRC) [1]. In the classical MRC technique, (l-1) sequential steps are required to compute the various mixed radix digits $d_{i}$ for$i =1,2,\ldots , l-1$ defined as

$$\begin{aligned} X=\mathop x\nolimits _1 +\mathop d\nolimits _1 \mathop m\nolimits _1 +\mathop d\nolimits _2 \mathop m\nolimits _1 \mathop m\nolimits _2 +\cdots +\mathop d\nolimits _{l-1} \mathop m\nolimits _1 \mathop m\nolimits _2 \mathop m\nolimits _3 \ldots \mathop m\nolimits _{l-1} \end{aligned}$$

(1)

In the jth step, the mixed radix digit $d_{j-1}$ determined in the ($j-1$)th step is subtracted from the residues of other moduli $m_{k}$ where $k=j+1, j+2,\ldots , l$ and multiplied with the multiplicative inverses $\mathop {\left( {\frac{1}{\mathop m\nolimits _j }} \right) }\nolimits _{\mathop m\nolimits _k }$. Note that $\mathop {w=\left( {\frac{1}{y}} \right) }\nolimits _z$is the multiplicative inverse of y with respect to modulus z defined such that w $\times$ y = 1 mod z.

MRC can be carried out in $\left\lceil {\mathop {\log }\nolimits _2 l} \right\rceil$ steps also considering several pairs of moduli in each step for an l-moduli RNS. In the first step (considering $l = \hbox {even}$, i.e., even number of moduli without loss of generality), the pairs can be chosen as {$m_{1}, m_{2}\}, \{m_{3}, m_{4}\}, \ldots , \{m_{l-1}, m_{l}$}. Mixed radix conversion can be used for each pair {$m_{g}, m_{g+1}$} to obtain the intermediate decoded numbers $X_{g,g+1}$ as

$$\begin{aligned} \mathop {\mathop X\nolimits _{g,g+1} =\mathop x\nolimits _g +\mathop m\nolimits _g \left( {\mathop {(\mathop x\nolimits _{g+1} -\mathop x\nolimits _g )}\nolimits _{\mathop m\nolimits _{g+1} } \mathop {\left( {\frac{1}{\mathop m\nolimits _g }} \right) }\nolimits _{\mathop m\nolimits _{g+1} } } \right) }\nolimits _{\mathop m\nolimits _{g+1} } \end{aligned}$$

(2)

Each of the next steps considers pairs of residues corresponding to the composite moduli (e.g., in second step composite moduli are of the form $(m_{g}{\times m}_{g+1}))$ and computes the decoded numbers. Evidently, the size of the operands (composite moduli as well residues corresponding to these moduli) increases progressively from first step to last step. We consider the application of the classical MRC as well as two-level MRC techniques in this paper.

3 Proposed RNS to Binary Converters for the Four-Moduli Set

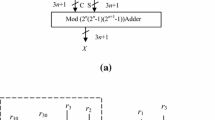
We first denote the moduli as $m_{1 }= 2^{n}, m_{2} = 2^{n-1}-1, m_{3} = 2^{n}-1, m_{4} = 2^{n+1}-1$ with n even and the corresponding residues as $x_{1}, x_{2}, x_{3}$ and $x_{4}$, respectively. It can be easily verified that the moduli are mutually prime. This moduli set has a dynamic range $M=m_{1}\times m_{2}\times m_{3}\times m_{4} = (2^{4n}+7\times (2^{2n-1}-2^{3n-1})-2^{n})$. We describe two RNS to binary converters in the next two subsections.

3.1 Two-Level MRC-Based Converter

We consider the two pairs of moduli {$2^{n}, 2^{n-1}-1\}$ and {$2^{n}-1, 2^{n+1} -1$} in the first level and use MRC on the pairs of respective residues to obtain the two intermediate numbers $X_{12}$ and $X_{34}$. In the second level, we use MRC for the residues ($X_{12}, X_{34})$ in the composite two-moduli set {$M_{12}, M_{34}$} where $M_{12}=m_{1}\times m_{2} = 2^{n}(2^{n-1}-1)$ and $M_{34}=m_{3}\times m_{4} = (2^{n}-1)(2^{n+1}-1)$ to obtain X(Fig. 1). Note that other pairings of moduli in the first level are also possible. The resulting composite moduli sets are {$M_{13}, M_{24}$} and {$M_{14}, M_{23}$}. One of the multiplicative inverse needed in the first level for the pairing {$M_{13}, M_{24}$} is not simple power of 2 thus making modulo multiplication with the multiplicative inverse expensive in hardware and time. The multiplicative inverses needed in the first level are simple for the set {$M_{14}, M_{23}$} which are 2 and -2 (see “Appendix”). In the second level, MRC needs multiplicative inverses which have more number of bits which are 1 in the case of pairing {$M_{13}, M_{24}$}, thus making the modulo multiplication operation with the multiplicative inverse complex. The multiplicative inverses needed in the second level, while using the pairing {$M_{14}, M_{23}$} has only (n/2) +1 bits which are “1,” whereas in case of using {$M_{12}, M_{34}$}, the partial products are n/2 (see “Appendix”).

Fig. 1

Two-level mixed radix conversion

Fig. 2

a Block computing $X_{12}$, b block computing $X_{34}$, c block for computing T and d block for obtaining final decoded word X

3.1.1 Computation of $X_{12}$

It can be seen that $X_{12}$ can be obtained from $x_{1}$ and $x_{2}$ following ( 2) as

$$\begin{aligned} \mathop {\mathop X\nolimits _{12} =\mathop x\nolimits _1 +\mathop m\nolimits _1 \left( {ab} \right) }\nolimits _{\mathop m\nolimits _2 } =\mathop {\mathop x\nolimits _1 +\mathop 2\nolimits ^n \left( {ab} \right) }\nolimits _{\mathop 2\nolimits ^{n-1} -1}, \end{aligned}$$

(3)

where $\mathop {a=\left( {\mathop x\nolimits _2 -\mathop x\nolimits _1 } \right) }\nolimits _{\mathop 2\nolimits ^{n-1} -1}$and $b=\mathop {\left( {\frac{1}{\mathop 2\nolimits ^n }} \right) }\nolimits _{\mathop 2\nolimits ^{n-1} -1} =\mathop 2\nolimits ^{n-2}$. Since the word lengths of $x_{1}$ and $x_{2}$ are different, $x_{1}$ needs to be written as $x_{1}=x_{12}2^{n-1}+x_{11}$ where $x_{11}=x_{1,n-2}x_{1,n-3} \ldots x_{1,1}x_{1,0}$ and $x_{12} = 00 \ldots 0 x_{1,n-1}$ are ($n-1$)-bit words. One’s complements $x_{11,1C}$ and $x_{12,1C}$ of these two words $x_{11}$ and $x_{12}$ need to be added to $x_{2}$ mod ($2^{n-1}-1$) for computing a. A ($n-1$)-bit carry-save adder (CSA) stage (CSA1) followed by a ($n-1$)-bit carry-propagate adder (CPA) (Adder 1 in Fig. 2a) both with end-around carry (EAC) will be required. Since ($n-2$) bits of the word $x_{12,1C}$ are “1,” the hardware requirements of the CSA stage are 1 full-adder (FA) and ($n-2$) EXNOR/OR pairs of gates. Thus, totally, this stage needs n full-adders and ($n-2$) EXNOR/OR pairs. The computation time is ($2n-1)D_{FA}$ where $D_{FA}$ is the delay of a full-adder since the EAC adder exhibits twice the delay of a ($n-1$)-bit adder. Next, the multiplication mod ($2^{n-1}-1$) with the multiplicative inverse $b = 2^{n-2}$ can be realized by circular left shift of a by ($n-2$) bits. The ($n-1$)-bit result $p=\mathop {\left( {ab} \right) }\nolimits _{\mathop 2\nolimits ^{n-1} -1}$can be concatenated with $x_{1}$ as n LSBs to yield a $(2n-1)$-bit word $X_{12}$ following (3). The architecture for computing $X_{12}$ is presented in Fig. 2a.

3.1.2 Computation of $X_{34}$

We next consider evaluation of $X_{34}$. Using MRC for the moduli set {$m_{3}, m_{4}$}, we have

$$\begin{aligned} \mathop X\nolimits _{34} =\mathop x\nolimits _3 +\mathop m\nolimits _3 \mathop {(cd)}\nolimits _{\mathop m\nolimits _4 } =\mathop x\nolimits _3 +(\mathop 2\nolimits ^n -1)\mathop {(cd)}\nolimits _{\mathop 2\nolimits ^{n+1} -1}, \end{aligned}$$

(4)

where $\mathop {c=\left( {\mathop x\nolimits _4 -\mathop x\nolimits _3 } \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1}$. It can be easily verified that the multiplicative inverse of $m_{3}$ with respect to $m_{4}$ is

$$\begin{aligned} \mathop {d=\mathop {\left( {\frac{1}{\mathop m\nolimits _3 }} \right) }\nolimits _{\mathop m\nolimits _4 } =\left( {\frac{1}{\mathop 2\nolimits ^n -1}} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =\mathop {(-2)}\nolimits _{\mathop 2\nolimits ^{n+1} -1}. \end{aligned}$$

(5)

The computation of $\mathop {c=\left( {\mathop x\nolimits _4 -\mathop x\nolimits _3 } \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1}$needs a $(n+1)$-bit CPA (Adder 2 in Fig. 2b) with EAC adding $x_{4}$ and one’s complement of $x^\prime _{3}$ where $x^\prime _{3 }$ is obtained by prepending $x_{3}$ with one zero bit as most significant bit (MSB). The multiplication using the multiplicative inverse d mod $(2^{n+1}-1)$ for obtaining $q=\mathop {(cd)}\nolimits _{\mathop 2\nolimits ^{n+1} -1}$can be realized by one-bit circular left shift of c and taking one’s complement. Next computation of $X_{34}$ from (4) can be carried out by adding the two $(2n+1)$-bit words $q2^{n}+x_{3}$ and two’s complement of q:

$$\begin{aligned} \begin{array}{lr} q_{n }q_{n-1} \ldots q_{2 }q_{1}q_{0 }x_{3,n-1}\ldots x_{3,1}x_{3,0}&{}\\ 1 1 {\ldots }1 1 q'_{n}q'_{n-1 }{\ldots } q'_{1 }q'_{0}&{}\\ &{}1 \end{array} \end{aligned}$$

(Note that $q 2^{n}+x_{3}$ is obtained by concatenating qas $(n+1)$ bit MSB word with $x_{3})$. Note also that the primes indicate inverted bits. (Since the result is always positive, the adder can be $(2n+1)$-bit; sign bit of the two’s complement word need not be considered). The addition of these words needs a $(2n+2)$-bit CPA (Adder 3 in Fig. 2b) which can be simplified taking into account the fact that n bits in one of the words are 1. The hardware requirements are n full-adders and $(n+1)$ pairs of exclusive-NOR (XNOR) and OR gates. Thus, the total hardware requirements for computing $X_{34}$ is $(2n+1)$ full-adders and $(n+1)$ EXNOR/OR pairs of gates. The computation time is ($4n+3)D_{FA}$.

3.1.3 Computation of X

The computation of the final result X uses mixed radix conversion corresponding to the residues ($X_{12}, X_{34})$ for the moduli set {$M_{12}, M_{34}$}:

$$\begin{aligned} \mathop {X=\mathop X\nolimits _{34} +\mathop M\nolimits _{34} \left( {ef} \right) }\nolimits _{\mathop M\nolimits _{12} }, \end{aligned}$$

(6)

where $\mathop {e=\left( {\mathop X\nolimits _{12} -\mathop X\nolimits _{34} } \right) }\nolimits _{\mathop M\nolimits _{12} }$ and

$$\begin{aligned} f=\mathop {\left( {\frac{1}{\mathop M\nolimits _{34} }} \right) }\nolimits _{\mathop M\nolimits _{12} } =\frac{\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^{n+1} +3}{3}=\mathop 2\nolimits ^{n+1} \left( {\frac{\mathop 2\nolimits ^{n-2} -1}{3}} \right) +1. \end{aligned}$$

(7)

Note that $\left( {\frac{\mathop 2\nolimits ^{n-2} -1}{3}} \right) =\frac{\mathop 2\nolimits ^{n-2} -1}{\mathop 2\nolimits ^2 -1}=\mathop 2\nolimits ^{n-4} +\mathop 2\nolimits ^{n-6} +\cdots +4+1$ for $n \quad \ge$ 6 and for n = 4, $\left( {\frac{\mathop 2\nolimits ^{n-2} -1}{3}} \right) =1$. Hence, $\left( {\frac{\mathop 2\nolimits ^{n-2} -1}{3}} \right)$has ($n-2$)/2 bits which are “1.” Thus, fhas n/2 bits which are “1” leading to n/2 partial products which are left-shifted versions of e. As an illustration, for n = 4, 6, 8, 10, we have $\mathop {f=\left( {\frac{1}{\mathop M\nolimits _{34} }} \right) }\nolimits _{\mathop M\nolimits _{12} } =33, 641, 10753, 174081$ having 2, 3, 4 and 5 bits which are “1.” The proof for (7) is as follows:

We need to find f such that ($f \quad \times \quad M_{34})$ = 1 mod $M_{12}$ or

$$\begin{aligned} f\times (\mathop 2\nolimits ^{2n+1} -3\times \mathop 2\nolimits ^n +1)=1\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n ) \end{aligned}$$

(8a)

which is same as

$$\begin{aligned} f\times (\mathop 2\nolimits ^n +1)=1\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n ) \end{aligned}$$

(8b)

after mod ($2^{2n-1}-2^{n}$) reduction. Multiplying (8b) both sides by ($2^{n}-4$), we have

$$\begin{aligned} f\times (-\mathop 2\nolimits ^n -4)=(\mathop 2\nolimits ^n -4)\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n ). \end{aligned}$$

(8c)

Adding (8b) and (8c), we have

$$\begin{aligned} f\times (-3)=(\mathop 2\nolimits ^n -3)\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n ) \end{aligned}$$

(8d)

or

$$\begin{aligned} f=\left( {\frac{3-\mathop 2\nolimits ^n }{3}} \right) \bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )=\left( {\frac{\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^{n+1} +3}{3}} \right) . \end{aligned}$$

(8e)

We consider next computation of e. The word lengths of $X_{12}$ and $X_{34}$ are $2n-1$ and $(2n+1)$ bits, respectively. Since mod $M_{12}$ where $M_{12} = (2^{2n-1}-2^{n})$ operation is required, we consider the $(2n+1)$-bit word $X_{34}$ as $X_{34H}2^{2n-1}+X_{34L}$, where $X_{34L}$ is a $(2n-1)$-bit word $x_{34,2n-2}x_{34,2n-3 } \ldots x_{34,0}$ and $X_{34H}$ is a 2-bit word $x_{34,2n}x_{34,2n-1}$. We next note that $2^{2n-1}$ mod $(2^{2n-1}-2^{n}) = 2^{n}$. Thus, we have

$$\begin{aligned} (X_{34}) \hbox { mod } (2^{2n-1}-2^{n})= & {} (X_{34H}2^{2n-1}+X_{34L}) \hbox { mod } (2^{2n-1}-2^{n})\nonumber \\= & {} (X_{34H}2^{n}+X_{34L}) \hbox { mod } (2^{2n-1}-2^{n}). \end{aligned}$$

(9)

Next, the $(n+2)$-bit word $X_{34H}2^{n}$ is prepended with $(n-3)$ number of “0” bits to make it a $(2n-1)$ bit word $X^\prime _{34H}$. Thus, e can be computed as

$$\begin{aligned} e= & {} {\left( { X_{12} - X_{34} } \right) }_{ M_{12} } \nonumber \\= & {} \left( { X_{12} + X_{34L,1C} +{ {{X}'}_{34H,} }_{1C} +{C}'} \right) _{ M_{12} }, \end{aligned}$$

(10)

where 1C indicates one’s complement. Note that a correction term $C' = 2^{2n-1}-3\times 2^{n}+2$ needs to be added to take care of one’s complementing operation of $X_{34L}$ and $X_{34H}$ and mod $(2^{2n-1}-2^{n})$ reduction in (10):

$$\begin{aligned}&\mathop X\nolimits _{34L,1C} +\mathop {\mathop {{X}'}\nolimits _{34H,} }\nolimits _{1C} +\mathop 2\nolimits ^{2n-1} -3\times \mathop 2\nolimits ^n +2=(\mathop 2\nolimits ^{2n-1} -1-\mathop X\nolimits _{34L} )\nonumber \\&\qquad +\,(\mathop 2\nolimits ^{2n-1} -1-\mathop {\mathop 2\nolimits ^n X}\nolimits _{34H} )+\mathop 2\nolimits ^{2n-1} -3\times \mathop 2\nolimits ^n +2 \nonumber \\&\quad = (-\mathop X\nolimits _{34} )\bmod \mathop M\nolimits _{12}. \end{aligned}$$

(11)

Note that $\mathop X\nolimits _{12} +\mathop X\nolimits _{34L,1C} +\mathop {\mathop {{X}'}\nolimits _{34H,} }\nolimits _{1C} +{C}'$ in (10) can exceed $M_{12}$ when $X_{12 }$ is maximum (= $2^{2n-1}-2^{n}-1$) and $X_{34} = 0$ and can be at most $(2^{2n-1}-2^{n}-1) + 2(2^{2n-1}-1) + 2^{2n-1}-3\times 2^{n }+ 2 = 2^{2n+1}-2^{n+2} -1$. The terms $\mathop X\nolimits _{12} ,\mathop X\nolimits _{34L,1C} ,\mathop {\mathop {{X}^\prime }\nolimits _{34H,} }\nolimits _{1C}$ can be added using a CSA stage (CSA2) needing 2 FA and $(2n-3)$ pairs of XNOR/AND gates since $(2n-3)$ bits are “1” in $X_{34H,1C}$ (Fig. 2c). Next, $C^\prime = 2^{2n-1}-3\times 2^{n}+2 = 2^{n}(2^{n-1}-3)+2$ can be added with the SUM and CARRY output vectors of this CSA2 in another level of CSA (CSA3) comprising nHA (where HA stands for half-adder) and ($n-1$) XNOR/OR pairs since $C'$ contains n bits which are zeros and ($n-1$) bits which are “1.” These two CSA levels generate two carry bits $C_{x}$ and $C_{y}$ which are added using a HA to obtain carry $C_{a}$ and sum $S_{a }$bits of weights 2$^{2n}$ and 2$^{2n-1}$. These can be reduced mod $(2^{2n-1}-2^{n})$ using the relation $(\mathop C\nolimits _a \mathop 2\nolimits ^{2n} +\mathop S\nolimits _a \mathop 2\nolimits ^{2n-1} )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )=\mathop C\nolimits _a \mathop 2\nolimits ^{n+1} +\mathop S\nolimits _a \mathop 2\nolimits ^n$.

This implies adding $C_{a}$ and $S_{a}$ at the $(n+1)$th and nth bit positions in another level of CSA (CSA4) needing $(n-3)$HA and 2FA. This is followed by a modulo $(2^{2n-1}-2^{n})$ Adder 1 which needs two cascaded $(2n-1)$-bit CPAs. Thus, the CSAs in Fig. 2c need 4FA+$(2n-3)$HA+(3n-4)XNOR/OR pairs of gates and the two CPAs need (4n-2)FA. The total time needed for computing e is (4n+1)$D_{FA}$.

The computation of $\mathop {T=\left( {ef} \right) }\nolimits _{\mathop M\nolimits _{12} }$needed in (6) requires mod $(2^{2n-1}-2^{n})$ reduction in the n / 2 partial products (PPs) $T_{i}$ which are left-shifted versions of e. Some of these PPs $\mathop \textit{PP}\nolimits _i =e\mathop f\nolimits _i \mathop 2\nolimits ^i$ where $f_{i}$ is the ith bit of fwhich is “1,” extend beyond (2$n-$1) bits up to (4n-4) bits. Hence, denoting PP $_{i}$ = PP $_{i2}$ 2$^{3n-2}$+PP $_{i1}$ 2$^{2n-1}$+PP $_{i0}$, we have

$$\begin{aligned} (\mathop \textit{PP}\nolimits _i )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )= & {} (\mathop \textit{PP}\nolimits _{i2} \mathop 2\nolimits ^{3n-2} +\mathop \textit{PP}\nolimits _{i1} \mathop 2\nolimits ^{2n-1} +\mathop \textit{PP}\nolimits _{i0} )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )\nonumber \\ {}= & {} \mathop {(PP}\nolimits _{i2} \mathop 2\nolimits ^n +\mathop \textit{PP}\nolimits _{i1} \mathop 2\nolimits ^n +\mathop \textit{PP}\nolimits _{i0} )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n ) \end{aligned}$$

(12)

since $(\mathop \textit{PP}\nolimits _{i1} \mathop 2\nolimits ^{2n-1} )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )=\mathop \textit{PP}\nolimits _{i1} \mathop 2\nolimits ^n$ and $(\mathop \textit{PP}\nolimits _{i2} \mathop 2\nolimits ^{3n-2} )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )=(\mathop \textit{PP}\nolimits _{i2} \mathop 2\nolimits ^n )\bmod (\mathop 2\nolimits ^{2n-1} -\mathop 2\nolimits ^n )$. Note that for some partial products with length less than 3n-2 bits, PP $_{i2}$ = 0. Hence, the bits in the bit positions $(3n-3)$ to $(2n-1)$ shall be mapped as bit positions 2n-2 to n bit positions as additional words. Note that for partial products having more than (3$n-$2) bits, the bits in the bit positions 4n-4 to 3n-2 will also be mapped between 2n-2 to n bit positions. Since the partial products are of different lengths, some of the repositioned bits can be accommodated in vacant bit positions. Thus, the number of (2$n-$1)-bit words to be added is only n.

An example will illustrate this computation. Consider multiplication of $e\times$10753 mod 32512 for the moduli set {256,127,255,511} where e is$e_{14}e_{13}e_{12}e_{11}e_{10}e_{9}e_{8}e_{7}e_{6}e_{5}e_{4}e_{3}e_{2}e_{1}e_{0}$. (Note that $M_{12}$ = 32,512, $M_{34} = 130,305$ and f= 10,753 for n = 8). The modulo $(2^{2n-1}-2^{n})$ reduced partial products are as illustrated in Table 1. Note that only partial products corresponding to “1” in the multiplier 10,753 need to be considered. The partial product corresponding to the multiplier 2$^{9}$ can be seen to be folded two times in the second, third and fourth rows shown in bold in Table 1.

Table 1 Modulo $(2^{2n-1}-2^{n})$ reduced partial products for computing ($e\times$10753) mod (32512)

Table 2 Bit matrix for computing X following (13)

Fig. 3

Converter based on mixed radix conversion a algorithm and b architecture

It can be seen that only bits beyond nth bit position need to be added using a carry-save adder tree. The carry bits can be placed in the vacant bit in the n-bit carry vector due to the mod $(2^{2n-1}-2^{n})$ operation. The computation of T needs ($n-2)(n-1$) full-adders for the CSA tree (CSA5) and two (2$n-$1) bit CPAs cascaded for realizing addition mod $M_{12 }$(Mod $(2^{2n-1}-2^{n})$ Adder 2) thus needing (4n-2) full-adders.

The computation of (6) next can be carried out as follows:

$$\begin{aligned} \mathop {X=\mathop X\nolimits _{34} +\mathop M\nolimits _{34} }\nolimits T=\mathop X\nolimits _{34} +T(\mathop 2\nolimits ^{2n+1} -\mathop 2\nolimits ^{n+1} -\mathop 2\nolimits ^n +1). \end{aligned}$$

(13)

Denoting T as the $(2n-1)$-bit word $t_{2n-2}t_{2n-3}{\ldots }t_{1}t_{0}$, the bit matrix corresponding to (13) is presented in Table 2. In order to take care of the two’s complementing the two words $T\times 2^{n}, T\times 2^{n+1}$, a carry-in of 1 can be added to both the CSA stages. Note that the four 4n-bit words need to be added using two-level CSA (CSA6 and CSA7) followed by a 4n-bit CPA (Adder 4) to obtain the final decoded wordX as shown in Fig. 2d. The CSA needs (3n-3) full-adders and $(2n+2)$ EXNOR/OR pairs since many bits are “1,” and the CPA needs 4n full-adders and the computation time is (4n+2)$D_{FA}$. The conversion time is the sum of computation times of $X_{34}, T$ and X since the computation time is more for $X_{34 }$ than $X_{12}$.

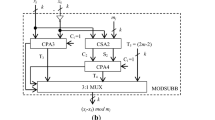
3.2 Mixed Radix Conversion-Based Converter

We consider next RNS to binary converter using mixed radix conversion for the same moduli set. The MRC technique and its implementation architecture are presented in Fig. 3a, b. This needs three steps. In the first step, three operations are performed in parallel each needing one modulo subtraction followed by one modulo multiplication with a multiplicative inverse following (1). In the second step, two such operations are performed in parallel, and in third step one such operation is needed. The final stage uses the mixed radix digits $d_{1}, d_{2}$ and $d_{3}$ obtained in these three steps to compute the most significant 3n bits of X denoted as $X_{H}$ as

$$\begin{aligned} \mathop X\nolimits _H =\mathop d\nolimits _1 +\mathop d\nolimits _2 (\mathop 2\nolimits ^{n-1} -1)+\mathop d\nolimits _3 (\mathop 2\nolimits ^n -1)(\mathop 2\nolimits ^{n-1} -1). \end{aligned}$$

(14)

The multiplicative inverses needed in the first step are

$$\begin{aligned}&{ {\left( {\frac{1}{ m_1 }} \right) }_{ m_2 } =\left( {\frac{1}{ 2^n }} \right) }_{ 2^{n-1} -1} \nonumber \\&= 2^{n-2} , { {\left( {\frac{1}{ m_1 }} \right) }_{ m_3 } =\left( {\frac{1}{ 2^n }} \right) }_{ 2^n -1} =1, { {\left( {\frac{1}{ m_1 }} \right) }_{ m_4 } =\left( {\frac{1}{ 2^n }} \right) }_{ 2^{n+1} -1} =2. \end{aligned}$$

(15a)

The multiplicative inverses needed in the second step are

$$\begin{aligned} \mathop {\left( {\frac{1}{\mathop m\nolimits _2 }} \right) }\nolimits _{\mathop m\nolimits _3 } =\mathop {\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^n -1} =-2,\mathop {\mathop {\left( {\frac{1}{\mathop m\nolimits _2 }} \right) }\nolimits _{\mathop m\nolimits _4 } =\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =\frac{\mathop 2\nolimits ^{n+1} -5}{3}=\gamma .\nonumber \\ \end{aligned}$$

(15b)

The last step needs the multiplicative inverse

$$\begin{aligned} \mathop {\left( {\frac{1}{\mathop m\nolimits _3 }} \right) }\nolimits _{\mathop m\nolimits _4 } =\mathop {\left( {\frac{1}{\mathop 2\nolimits ^n -1}} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =-2. \end{aligned}$$

(15c)

Thus, all the multiplicative inverses are simple except $\mathop {\gamma =\left( {\frac{1}{\mathop m\nolimits _2 }} \right) }\nolimits _{\mathop m\nolimits _4 } =\frac{\mathop 2\nolimits ^{n+1} -5}{3}$. Note that $\gamma$ can be derived as follows: We need to find $\gamma$ such that

$$\begin{aligned} \gamma \mathop {\times m}\nolimits _2 =1\bmod \mathop m\nolimits _4 \end{aligned}$$

or

$$\begin{aligned} \gamma \times (\mathop 2\nolimits ^{n-1} -1)=1\bmod (\mathop 2\nolimits ^{n+1} -1) \end{aligned}$$

(16a)

Multiplying both sides of (16a) with 4, we have

$$\begin{aligned} \gamma \times (\mathop 2\nolimits ^{n+1} -4)=4\bmod (\mathop 2\nolimits ^{n+1} -1) \end{aligned}$$

(16b)

or

$$\begin{aligned} \gamma \times (-3)=4\bmod (\mathop 2\nolimits ^{n+1} -1). \end{aligned}$$

(16c)

Thus, we have

$$\begin{aligned} \gamma =\left( {\frac{-4}{3}} \right) \bmod (\mathop 2\nolimits ^{n+1} -1)=\left( {\frac{\mathop 2\nolimits ^{n+1} -5}{3}} \right) \bmod (\mathop 2\nolimits ^{n+1} -1). \end{aligned}$$

(16d)

Note that$\mathop {\left( {\mathop {\left( {\mathop x\nolimits _2 -\mathop x\nolimits _1 } \right) }\nolimits _{\mathop 2\nolimits ^{n-1} -1} \mathop 2\nolimits ^{n-2} } \right) }\nolimits _{\mathop 2\nolimits ^{n-1} -1}$is realized by the MODSUB1 block followed by left circular shift of ($n-2$) bits (Fig. 3b) to obtain $d_{1}$. This block is same as that shown in Fig. 2a. The computation of $\mathop {\left( {\mathop x\nolimits _3 -\mathop x\nolimits _1 } \right) }\nolimits _{\mathop 2\nolimits ^n -1}$ needs addition of $x_{3 }$ with one’s complement of $x_{1 }$in a n-bit CPA with EAC (MODSUB2 in Fig. 3b) to yield directly $a_{1 }$ since multiplication by the multiplicative inverse 1 does need any additional computation. Next, $\mathop {\left( {\mathop x\nolimits _4 -\mathop x\nolimits _1 } \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1}$needs addition of, one’s complement of, $x_{1}$ prepended with one zero bit, with $x_{4 }$ in a $(n+1)$-bit CPA with EAC (MODSUB3). The multiplication of this result with the multiplicative inverse 2 mod ($2^{n+1} -1$) is realized by left circular shift (CLS) of the output of MODSUB3 by one bit to obtain $a_{2}$.

The computation of $\mathop {\left( {\mathop a\nolimits _1 -\mathop d\nolimits _1 } \right) }\nolimits _{\mathop 2\nolimits ^n -1}$ can be carried out by adding $a_{1}$ with one’s complement of $d_{1}$ prepended with a zero bit, in a n-bit CPA with EAC (MODSUB4). The multiplication with multiplicative inverse $-2 \hbox {mod} (2^{n}-1)$ is realized by one-bit left circular shift (CLS) followed by one’s complementing (inversion of all bits) for obtaining $d_{2}$. Similarly, $\mathop {\left( {\mathop a\nolimits _2 -\mathop d\nolimits _1 } \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1}$ needs addition of $a_{2}$ with one’s complement of $d_{1}$ prepended with two zero bits, in a $(n+1)$-bit CPA with EAC (MODSUB5). Note that the output of MODSUB5 block needs to be multiplied with $\gamma$ (see (15b)) and reduced mod $(2^{n+1}-1)$ in the block MODMUL.

Table 3 Bit matrix for computing (17)

The multiplicative inverse $\gamma$ can be expressed as

$$\begin{aligned}&\mathop {\gamma =\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =\frac{\mathop 2\nolimits ^{n+1} -5}{3}\nonumber \\&\quad =\frac{\mathop 2\nolimits ^{n+1} -5}{\mathop 2\nolimits ^2 -1}=\mathop 2\nolimits ^{n-1} +\mathop 2\nolimits ^{n-3} +\cdots +\mathop 2\nolimits ^3 +1\,\hbox {for}\, n \quad \ge 4. \end{aligned}$$

(17)

It can be seen for $n = 4, 6, 8, 10$ to be 9, 41, 169, 681. The multiplicative inverse $\gamma$ will have n / 2 bits which are 1 thus needing only n / 2 number of partial products. The multiplication with $2^{m}$ mod $(2^{n+1}-1)$ can be accomplished by left circular shift (CLS) of m bits. Thus, the number of partial products obtained are n/2 each having $(n+1)$ bits. The addition of these with EAC needs a CSA tree of (n / 2)-2 levels followed by a $(n+1)$-bit CPA with EAC. The hardware and time requirements for multiplication of $\mathop {\left( {\mathop a\nolimits _2 -\mathop d\nolimits _1 } \right) }\nolimits _{\mathop m\nolimits _4 }$with $\gamma$ in the MODMUL block in Fig. 3b are $(n+1)\left( {\frac{n}{2}-1} \right) FA$ and $(5n/2)\mathop \Delta \nolimits _{FA}$.

The computation of $\mathop {\left( {\mathop b\nolimits _1 -\mathop d\nolimits _2 } \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1}$ can be realized using the block shown in dotted lines in Fig. 2b (with $b_{1}$ in place of $x_{4}$ and $d_{2}$ in place of $x_{3}$ using MODSUB6). The multiplication with the multiplicative inverse -2 mod $(2^{n+1}-1)$ is carried out by left circular shift (CLS) by one bit followed by inversion of all the bits (one’s complementing) to obtain $d_{3}$.

Denoting $d_{1}, d_{2}$ and $d_{3}$ in (14) of bit lengths ($n-1$), n and $(n+1)$ bits, respectively, as $d_{1(n-2)}d_{1(n-3) } \ldots d_{11}d_{10}, d_{2(n-1)}d_{2(n-2)}\ldots d_{21}d_{20}$ and $d_{3n}d_{3(n-1)}\ldots d_{31}d_{30}$, the various words that need to be added for the computation of $X_{H}$ following (14) for n = 8 are presented in the bit matrix in Table 3. Note that all the 1 bits due to one’s complementing and addition of three “1”s for two’s complementing of three terms have been combined as a single word $h = 2^{3n}-3\times 2^{2n}+2^{n-1}+1$. The bit mapping block (Fig. 3b) obtains the various 3n-bit words from $d_{1}, d_{2}$ and $d_{3}$ which are added in a CSA (CSA8) needing $(4n+3)FA+(2n-1)$ HA followed by a CPA (Adder 5) needing 3nFA. The computation time is $(3n+3)\Delta _{FA}$. Next, $X_{H}$ is appended with $x_{1}$ as LSBs to yield the final decoded word.

Table 4 Hardware and conversion time evaluation of various reverse converters

4 Hardware and Conversion Time Evaluation of Proposed Converters

The hardware requirement and conversion time of the proposed converters for moduli set M1 (n even) using two-level MRC (Converter 1) and MRC (Converter 2) are presented as entries D1 and D2 in Table 4. The hardware requirements of the three converters described in [12] for Design I are presented as entries D3–D5 in Table 4 for comparison. Note that the design D5 uses a ROM, whereas the others use combinational logic. Three other converters described in [12] Design II need ($n^{2}$-15n)/2 less number of full-adders than those given in Table 4 in entries D3–D5 and their conversion time is also less by (2n-2+$p-q) \quad D_{FA}$. The two-stage converter D6 of Taheri et al. [33] uses first-stage converter of three-moduli set $M_{b}$ {$2^{n}-1, 2^{n+1}-1, 2^{n-1}-1$} using MRC and uses a second stage using MRC of the composite moduli set {$M_{b}$, $2^{n}$}. The design D7 for moduli set M2 [39] using modulus $2^{k}$ in place of $2^{n}$ in the moduli set M1 is based on MRC.

We also consider the five converters D8–D12 for the moduli set M3{$2^{n}, 2^{n}-1, 2^{n}+1, 2^{n+1}-1$). The two-stage designs D8 [4] and D9 [15] are based on MRC of the composite moduli set {$M_{c}, 2^{n+1}-1$} where $M_{c}$ is the popular three-moduli set {$2^{n}-1, 2^{n}+1, 2^{n}$} in the second stage and use the three-moduli RNS to binary converter of Piestrak and Dhurkadas [10, 23] in the first stage. The design D10 [35] has employed CRT. The designs D11 and D12 [6] also use MRC of the composite moduli set {$M_{c}, 2^{n+1}-1$}, but use the three-moduli RNS to binary converter Converter 1 due to Wang et al. [36]. The designs D13 and D14 [6] for the moduli set M4{$2^{n}, 2^{n}-1, 2^{n}+1, 2^{n-1}-1$} [6] (n even) also use Wang et al. Converter 1 [36] in the front end followed by MRC of the composite moduli set {$M_{c}, 2^{n-1}-1$}. The converter D15 for moduli set M5 {$2^{n}, 2^{n}-1, 2^{n}+1, 2^{n+1}+1$} (n odd) [4] uses MRC for the composite moduli set {$M_{c}, 2^{n+1}+1$} and uses the reverse converter of Piestrak [23] and Dhurkadas [10] in the front end for three-moduli RNS to binary converter. The design D16 [29] for moduli set M5 uses a two-level converter similar to the architecture in Fig. 1 and use MRC in both the levels. The design D17 [5] for moduli set M5 is based on CRT. The converter D18 for the moduli set M6{$2^{n}, 2^{n}-1, 2^{n}+1, 2^{n-1}+1$} (n odd) [19] uses MRC on the composite moduli set {$M_{c}, 2^{n-1}+1$} and has used the three-moduli RNS to binary converter of Wang, Jullien and Miller [37] in the first stage. The converters D19 and D20 for moduli set M6 use two-level reverse converter following Fig. 1. The two-stage converter D21 for the moduli set M7 {$2^{n}, 2^{n}-1, 2^{n}+1, 2^{n+1}-1, 2^{n-1}-1$} [8] uses MRC on the composite moduli set {$\hbox {M3}, 2^{n-1}-1$} and uses the four-moduli reverse converter of [6] for the moduli set M3 in the first stage. The converters D22 [30] and D23 [30] for moduli sets M8 {$2^{n}, 2^{n}-1, 2^{n}+1, 2^{2n+1}-1$} and M9 {$2^{2n}, 2^{n}-1, 2^{n}+1, 2^{2n+1}-1$}, respectively, also use same architecture as in Fig. 1 considering two pairs of moduli in first stage. The design D24 [7] for moduli set M10{$2^{n}, 2^{n}-1, 2^{n}+1, 2^{2n}+1$} is based on New CRT-I [38]. The converter D25 [17] for moduli set M8{$2^{n}, 2^{n}-1, 2^{n}+1, 2^{2n+1}-1$} is based on the architecture of Fig. 1, whereas the converter D26 [17] for moduli set M11{$2^{2n}, 2^{n}-1, 2^{n}+1, 2^{2n}+1$} uses New CRT-I [38]. The converter D27 [26] for moduli set M12 {$2^{n-5}-1, 2^{n-3}-1, 2^{n-3}+1, 2^{n-2}+1, 2^{n-1}-1, 2^{n-1}+1,2^{n}, 2^{n}+1$} considers four pairs of moduli in the first level and two pairs of composite moduli in second level and one pair of composite moduli in the third level. It uses MRC for each two-moduli reverse converter in first and second levels and uses CRT in the third level. The hardware requirements in terms of gates as well as conversion time for all the 27 converters are presented in Table 4. In Table 4, we denote the converters following the architecture of Fig. 1 as MRC(2-2) and converters using converters for three-moduli set $M_{{a}}$ or $M_{b}$ or $M_{c}$ in first stage and MRC in second stage as MRC (3-1) converter. Note that the three-moduli converters could have been designed by any technique—MRC, CRT or New CRT-I. The other converters presented in Table 4 have been described as using New CRT-I or MRC (4-1) or MRC or three-stage (MRC, MRC, CRT) types. The corresponding hardware requirements and conversion times using the unit-gate model [34] are presented in Table 5. We have considered the gates needed for full-adder, half-adder, 2:1 MUX, EXOR, AND, OR gates as 7, 4, 3, 2, 1 and 1 and the delays as 4, 2, 2,2,1,1 unit delays $\Delta _{g}$, respectively. Note that we have not considered the equivalent gates of the ROM for the converters D5 and D17, but only number of ROM bits needed are given in brackets.

Table 5 Hardware and conversion time evaluation of various reverse converters in terms of unit gates

Table 6 Gate requirement and conversion time of various reverse converters for various DR

If we consider converters D8, D9, D11–D15, D18 using $M_{c}$, D9 needs lowest $\hbox {AT}^{2}$. Among the converters D24 and D26 using New CRT-I, converter D26 has lowest $\hbox {AT}^{2}$. For the five-moduli converter D21, we note that $\hbox {AT}^{2}$ is lower than D1 and D15 for all dynamic ranges, whereas $\hbox {AT}^{2}$ is lower than that of converters D3 for DR 16, 48 and 64 bits and lower than that of converter D10 and D16 for DR of 48 bits. Among the converters D7, D22–D26, converter D26 exhibits lowest $\hbox {AT}^{2}$ for DR 16, 32 and 64 bits and D23 has lowest for 48-bit DR.

All the moduli sets M1–M12 have different dynamic ranges (DR) varying from about 4n-1 bits to (8n-15) bits for the chosen n(and k values). The moduli sets M5 and M6 are possible for only odd n, and the moduli sets M1-M4 and M7 are possible for even nonly. The other moduli sets are possible for even or odd n values. The gate requirement and conversion times estimated following Table 5 for realizing the four dynamic ranges 16 bits, 32 bits, 48 bits and 64 bits are presented together with the needed n and k values in Table 6. The plots showing area in unit gates, conversion time, AT (area$\times$ Time) and A$\times$T$^{2 }$(area $\times$ Time$^{2})$ for four dynamic ranges 16 bits, 32 bits, 48 bits and 64 bits are presented in Fig. 4a–d for appropriate choice of n (and k wherever applicable).

The converter designs D1, D16, D19, D20, D22, D23 and D25 use MRC (2-2) two-stage reverse converters following Fig. 1. The converter designs D2–D9, D11–D15, D18–D20 are also two-stage converters, but in the first stage they employ a three-moduli reverse converter for the moduli sets $M_{a}$ or $M_{b}$ or $M_{c}$. The two-stage reverse converter for five-moduli set M7 converter D21 uses MRC in second stage, and the converter for four-moduli set M3 is used in first stage. All these use mixed radix conversion in the second stage. The converter D2 uses conventional MRC needing three successive steps for finding mixed radix digits and finally computes the decoded word. The converters D24 and D26 uses New CRT-I, whereas converters D10 and D17 use CRT.

The following conclusions can be arrived at from Table 6 for the four DRs considered. Among all the reverse converters considered, D26 exhibits lowest area for 16-bit DR and D25 needs lowest resources for other dynamic ranges. Regarding conversion time, D23 needs least among all designs. For 64-bit DR, D26 is comparable with D23 regarding conversion time.

Among all the converters for the moduli set M1, converter D2 needs lowest hardware resources, whereas D6 needs the least conversion time. The converter D1 needs low area than D3, D4, D5 and D6 for all dynamic ranges. The converter D2 needs lower conversion time than converter D3. The converter D7 using modulus 2$^{k}$ needs lower area than all converters for the moduli set M1 and more conversion time than converter D6 for all DRs and more conversion time than D4 and D5 for DRs of 48 bits and 64 bits.

Fig. 4

a Area (unit gates) A and b conversion time T, c $A\times T$ and d $(A \times T^{2})$ of various reverse converters for dynamic ranges 16, 32, 48 and 64 bits

Among the MRC (2-2) converters following Fig. 1 (D1, D16, D19, D20, D22, D23, D25), the design D25 needs lowest area, whereas D23 needs least conversion time. Among all the four-moduli reverse converters using converter for moduli set $M_{c}$ in the front end (D8, D9, D11–D15, D18), the converter D8 needs lowest area and converter D9 has least conversion time. Among the two converters using New CRT-I, converter D26 needs less area and conversion time than that of converter D24.

The five-moduli reverse converter D21 needs lower area than converters D1, D3–D6, D10, D17 for all dynamic ranges and less area than converters D16 and D20 for dynamic ranges 32, 48 and 64 bits. It also needs less area than converters D15 for DR of 16, 48 and 64 bits. The converter D21 needs less conversion time than that of converters D1, D17 for all dynamic ranges and less than that of converter D3 for 16 bits, and converters D15 for DR of 16, 32 and 64 bits.

We also consider the moduli sets for comparison which have widely differing word lengths (n to $(2n+1)$ bits) for the moduli. These are D7, D22–D26. Among these, converter D25 needs lowest area, whereas converter D23 has lowest conversion time.

We next consider comparison using Table 6 and plots in Fig. 4c regarding AT. AT is lowest for converter D26 considering all converters. Among all the converters D1–D6 for moduli set M1, D6 needs lowest AT for 16-, 32- and 48-bit DR and for 64-bit DR D2 needs lowest AT. Considering D7 also, the converter D7 needs lowest AT. Among MRC (2-2) converters D1, D16, D19, D20, D22, D23 and D25, the converter D23 has lowest AT. If we consider converters D8, D9, D11–D15, D18 using $M_{c}$, for DR 16 bits and 32 bits, D8 needs lowest AT, whereas for 48-bit and 64-bit DR, D9 needs lowest AT. Among the converters D24 and D26 using New CRT-I, converter D26 has lowest AT. For the five-moduli converter D21, we note that AT is lower than D1, D3 and D4 for all dynamic ranges, whereas AT is lower than that of converters D10 and D15 for DRs of 16, 48 and 64 bits and lower than that of converter D16 for DRs of 48 and 64 bits. Among the converters D7, D22–D26, converter D26 exhibits lowest AT for DRs of 16, 32 and 64 bits and D23 has lowest AT for 48-bit DR.

Table 7 FPGA implementation results of converters D1 and D2

We next consider comparison of various converters regarding $\hbox {AT}^{2}$. AT is lowest for converter D26 considering all converters. Among all the converters D1–D6 for moduli set M1, D6 needs lowest $\hbox {AT}^{2}$ and considering D7 also, the converter D7 needs lowest $\hbox {AT}^{2}$ for DRs of 16, 32 and 48 bits. Among MRC (2-2) converters D1, D16, D19, D20, D22, D23 and D25, the converter D23 has lowest $\hbox {AT}^{2}$.

4.1 FPGA Implementation Results

The converters D1 and D2 have been realized for n = 4, 8 and 16 on Xilinx Device Virtex6—xc6vhx380t, Package: ff1923of Speed Grade 3 using Verilog HDL. These roughly correspond to dynamic ranges of 16, 32 and 64 bits, respectively. The post-placement and routing results of area requirement in slices and the conversion time are presented in Table 7. It can be seen that the converter D2 needs less area than converter D1 for n = 8 and n = 16, whereas the conversion times comprise of only combinational logic path delay.

5 Conclusion

In this paper, novel RNS to binary converters for the moduli set {$2^{n}, 2^{n}-1, 2^{n+1}-1, 2^{n-1}-1$} for n even using two-level MRC-based converter are presented. The proposed converters have been compared with converters proposed earlier for this moduli set as well as other moduli sets using four, five and eight moduli described in the literature for similar dynamic range. The proposed converters have been found to be having advantage ether in hardware requirement or conversion time over some of the previous reported converters. The advantage of this moduli set is the use of moduli which are convenient for fast arithmetic operations such as modulo addition, subtraction and multiplication and binary to RNS conversion.

The comparison among all the converters considered has shown that four-moduli RNS converters using vertical extension, i.e., one modulus $2^{x}$ with x larger than the word length of conjugate moduli {$2^{n}-1,2^{n}+1$} may lead to lower conversion time and/or lower hardware resource requirement (converters D22–D26). These can have the fourth modulus of word length n to $(2n+1)$ bits. However, it must be noted that the arithmetic components for the moduli channels like modulo adders, modulo multipliers in channels of bigger word length using moduli $(2^{2n+1}-1)$ or $(2^{2n}+1)$ may limit the overall performance of RNS arithmetic operations, whereas operations in the $2^{x}$ moduli channel can be area efficient and time efficient. The computation in case of moduli of type $(2^{\alpha }-1)$ and $2^{x}$ can be advantageous in situations like FIR filters where repeated MAC operations need to be carried out and in cryptography applications [13].

Appendix

In this Appendix, we consider the two different pairings of moduli in the two-level MRC. In the case of the pairing of Moduli $M_{13}, M_{24}$, the various multiplicative inverses are as follows:

In the first level we have $\mathop {\left( {\frac{1}{\mathop 2\nolimits ^n }} \right) }\nolimits _{\mathop 2\nolimits ^n -1} =1$ and $\mathop {\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =\frac{\mathop 2\nolimits ^{n+1} -5}{3}=\mathop 2\nolimits ^{n-1} +\mathop 2\nolimits ^{n-3} +\cdots +\mathop 2\nolimits ^3 +1$ and in the second level, we have $\mathop {\left( {\frac{1}{\mathop {(2}\nolimits ^{n-1} -1)(\mathop 2\nolimits ^{n+1} -1)}} \right) }\nolimits _{\mathop {\mathop 2\nolimits ^n (2}\nolimits ^n -1)} =\mathop 2\nolimits ^{2n-1} -7\times \mathop 2\nolimits ^{n-1} +1=\mathop 2\nolimits ^{n-1} (\mathop 2\nolimits ^n -7)+1$. This has been derived using extended Euclid algorithm. Thus, in the first level, multiplication with one of the multiplicative inverses takes more time than in the case of choice of $M_{12}$,$M_{34}$. In the second level, the multiplicative inverse has ($n-1$) number of bits which are “1” and hence ($n-1$) partial products are needed to be added. The modulo $M_{13 }$ reduction can follow a similar method as described in the case of mod $M_{12}$ reduction.

In the case of the pairing of Moduli $M_{14}, M_{23}$, the various multiplicative inverses are as follows:

In the first level, we have $\mathop {\left( {\frac{1}{\mathop 2\nolimits ^n }} \right) }\nolimits _{\mathop 2\nolimits ^{n+1} -1} =2$ and $\mathop {\left( {\frac{1}{\mathop 2\nolimits ^{n-1} -1}} \right) }\nolimits _{\mathop 2\nolimits ^n -1} =-2$. In the second level, we have $\mathop {\left( {\frac{1}{\mathop {(2}\nolimits ^{n-1} -1)(\mathop 2\nolimits ^n -1)}} \right) }\nolimits _{\mathop {\mathop 2\nolimits ^n (2}\nolimits ^{n+1} -1)} =\frac{\mathop 2\nolimits ^{2n} +19\times \mathop 2\nolimits ^{n-1} +3}{3}=\mathop 2\nolimits ^{n-1} (\mathop 2\nolimits ^{n-1} +\mathop 2\nolimits ^{n-3} +\cdots +\mathop 2\nolimits ^4 +1)+1$. This has been obtained using extended Euclid algorithm.

The multiplicative inverses in the first level are simple, whereas that in the second level has $(n/2)+1$ bits which are “1,” thus leading to $(n/2)+1$ partial products which need to be reduced mod $M_{14}$ following a similar method as described in the case of mod $M_{12}$ reduction.