Analytical treatments of time-fractional seventh-order nonlinear equations via Elzaki transform

Abstract

In this article, we’ll show how to solve the time-fractional seventh-order Lax’s Korteweg–de Vries and Kaup–Kupershmidt equations analytically using the homotopy perturbation approach, the Adomian decomposition method, and the Elzaki transformation. The KdV equation is a general integrable equation with an inverse scattering transform-based solution that arises in a variety of physical applications, including surface water waves, internal waves in a density stratified fluid, plasma waves, Rossby waves, and magma flow. Fractional derivative is described in the Caputo sense. The solutions to fractional partial differential equation is computed using convergent series. The numerical computations and graphical representations of the analytical results obtained using the homotopy perturbation and decomposition techniques. Moreover, plots that are simple to grasp are used to compare the integer order and fractional-order solutions. After only a few iterations, we may easily obtain numerical results that provide us better approximations. The exact solutions and the derived solutions were observed to be very similar. The suggested methods have also acquired the highest level of accuracy. The most prevalent and convergent techniques for resolving nonlinear fractional-order partial differential issues are the applied techniques.

1 Introduction

The derivative of a function can be extended in any order using the branch of calculus known as fractional calculus. The use of fractional calculus across numerous disciplines of applied science and engineering to describe the properties of various real physical phenomena has captured the attention of many scholars in particular fields of applied science and engineering in recent years. The concept of the fractional derivative has been established in response to the problems brought on by heterogeneity. The fast development of mathematical techniques with computer packages led to many researchers working on FC to illustrate their belvederes while studying complex models. Recently, senior scholars provided a number of novel ideas for the FC, and those provided the framework. FC is a commonly used idea and theory that is connected to real-world initiatives [1,2,3,4,5]. Integrals and derivatives are addressed by FC to an arbitrary real or complex order. Recently, a number of fractional operators, including Caputo, Caputo Fabrizio, Atangana–Baleanu, Katugampola, Hilfer, etc. have been proposed and implemented for dealing with real-world applications. The fractional calculus has demonstrated that it is the best tool for studying problems in the actual world. The Caputo fractional derivative is often used in practical applications, as it enables one to include the traditional initial and boundary conditions in formulating mathematical models. Moreover, as in the integer-order derivative, the Caputo fractional derivative of a constant is zero [6].

A detailed association among an unknown function and its partial derivatives is expressed using partial differential equations (PDEs). Nearly every area of engineering and study uses PDEs. PDEs are now being used more frequently in disciplines like biology, economics, image processing, graphics and social sciences. As a result, relevant functions in these variables can be formed when some independent variables relate with one another in every of the areas listed before. This enables the modeling of diverse processes through equations for the corresponding functions. There are many aspects to the study of PDEs. Developing techniques for identifying explicit solutions was the conventional approach that predominated the eighteenth century. It’s vital to note that certain highly complicated problems were not solved via computers. In most cases, it is also preferred for the solution to be distinct and robust to minor data interruptions. If these requirements are satisfied, the equation can be understood theoretically [7,8,9].

Modern calculus tools like fractional partial differential equations (FPDEs) can be used to model a number of events in the applied sciences and engineering. Researchers began to be interested in fractional calculus since it was difficult to treat nonlinear real-world processes in conventional calculus [10,11,12,13,14,15,16]. The proper description of the behavior of significant physical processes in this context depends on the approximation of FPDEs and analytical solutions. In light of the aforementioned assertion, mathematicians have developed and taken into practice a number of computations and analytical techniques to determine the solutions for a variety of significant mathematical models that represent challenges. Mathematicians continue to make the best efforts possible in this area despite the fact that computing the analytical and sometimes even approximative solutions of some nonlinear FPDEs and systems of FPDEs is very difficult. Several studies have been done throughout the years in the domains of science and engineering all across the world, and many approaches have been created to offer the best solutions attainable. The world is always being faced with new, tough, and complex difficulties and problems; examples include [17,18,19,20,21]. This is an unstoppable process, and new techniques are being established on a daily basis. The literature has suggested a variety of approaches to addressing FDEs, which include the Fractional complex transform [22], Finite difference methods [23], Adomian Decomposition method [24], Residual power series method [25], Homotopy Analysis method [26], Differential transform method [27], the Variational Iteration method [28], and the predictor-corrector approach [29].

This article develops the solution of time-fractional seventh-order Lax’s Korteweg–de Vries equation and Kaup–Kupershmidt equation using the Elzaki transform decomposition technique (ETDM) and the Homotopy Perturbation Transform Method (HPTM). The Elzaki transform was created by Tarig Elzaki to help resolving ordinary and PDEs in the time domain simpler. On the other hand, the Adomian decomposition approach [30, 31], which is well known, provides precise solutions in the form of a convergent series for the solution of linear and nonlinear, homogeneous and nonhomogeneous differential equations. In 1998, he introduced HPM [32, 33]. According to this method, the accuracy is assumed to be an in series solution with a large number of terms that quickly converges to the actual derived solution. Nonlinear PDEs can be successfully solved using this method. A higher degree of accuracy was demonstrated when the HPTM findings were contrasted with the actual solutions to the problems. The newly developed technique is a mix form of HPM and the Elzaki transform. The time-fractional seventh-order nonlinear equations are solved analytically using the existing methods, which are demonstrated to be highly efficient. The outcomes of the suggested techniques are reliable and offer precise solutions to the desired issues. Our methods produced infinite series as the results in the numerical examples. When we write the series in closed form, it gives precise solutions to the relevant equations. Researchers can use this study as a fundamental reference to examine these strategies and employ it in many applications to get accurate and approximative results in a few easy steps. The results of fractional problem analysis using the suggested methodologies are also used to examine the issues from a fractional aspect.

The Korteweg–de Vries (KdV) equation is an example of a partial differential equation. It has been used as a model for the evolution and interaction of nonlinear waves to describe a wide range of physical phenomena. This equation was derived as an evolution that controlled the propagation of long, low-amplitude, one-dimensional surface gravity waves in a shallow water channel [34]. Nowadays, the KdV equation is applied in many areas of physics, such as lattice dynamics, collision-free hydromagnetic waves, stratified internal waves, ion-acoustic waves, and plasma physics [35]. Some possible physical phenomena in the framework of quantum mechanics have been represented using a KdV model. It serves as a model for the propagation of shock wave, turbulence, solitons, mass transport in fluid dynamics, boundary layer behavior, continuum mechanics and aerodynamics [36]. In this study, we aim to solve a fractional-order nonlinear Lax’s Korteweg–de Vries equation using two analytical methods.

$$\begin{aligned} \begin{aligned} D_{\i }^\mu {{\mathcal {Y}}(\omega ,{\i })}=&-140{\mathcal {Y}}^{3}(\omega ,{\i }){\mathcal {Y}}_{\omega }(\omega ,{\i })-70{\mathcal {Y}}^{3}_{\omega }(\omega ,{\i })\\&-280{\mathcal {Y}}(\omega ,{\i }){\mathcal {Y}}_{\omega }(\omega ,{\i }){\mathcal {Y}}_{\omega \omega }(\omega ,{\i })-70{\mathcal {Y}}^{2}(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega }(\omega ,{\i })\\&-70{\mathcal {Y}}_{\omega \omega }(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega }(\omega ,{\i })-42{\mathcal {Y}}_{\omega }(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega \omega }(\omega ,{\i })\\&-14{\mathcal {Y}}(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega \omega \omega }(\omega ,{\i })-{\mathcal {Y}}_{\omega \omega \omega \omega \omega \omega \omega }(\omega ,{\i }),\\&\ \ \ \ \ 0<\mu \le 1,\\ \end{aligned} \end{aligned}$$

(1)

and Kaup–Kupershmidt equation

$$\begin{aligned} \begin{aligned} D_{\i }^\mu {{\mathcal {Y}}(\omega ,{\i })}=&-2016{\mathcal {Y}}^{3}(\omega ,{\i }){\mathcal {Y}}_{\omega }(\omega ,{\i })-630{\mathcal {Y}}^{3}_{\omega }(\omega ,{\i })\\&-2268{\mathcal {Y}}(\omega ,{\i }){\mathcal {Y}}_{\omega }(\omega ,{\i }){\mathcal {Y}}_{\omega \omega }(\omega ,{\i })-504{\mathcal {Y}}^{2}(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega }(\omega ,{\i })\\&-252{\mathcal {Y}}_{\omega \omega }(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega }(\omega ,{\i })-147{\mathcal {Y}}_{\omega }(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega \omega }(\omega ,{\i })\\&-42{\mathcal {Y}}(\omega ,{\i }){\mathcal {Y}}_{\omega \omega \omega \omega \omega }(\omega ,{\i })-{\mathcal {Y}}_{\omega \omega \omega \omega \omega \omega \omega }(\omega ,{\i }),\\&\ \ \ \ \ 0<\mu \le 1,\\ \end{aligned} \end{aligned}$$

(2)

The parameter $\mu$ here denotes the order of the fractional derivative. These equations serve as a mathematical representation of the complex physical processes that develop in biology, physics, chemistry and engineering. Examples include nonlinear optics, quantum mechanics, plasma physics, long wave propagation in shallow water under gravity, and fluid mechanics. Several researchers have used the modified Cole–Hopf transformation method [37], variational iteration method [38], and pseudospectral method [39] to solve the seventh-order Lax’s Korteweg–de Vries. In [40], time-fractional Rosenau–Hyman equation is solved numerically using the residual power series technique and perturbation-iteration algorithm which is a model that is comparable to KdV. Pomeau et al. [41] investigated the stability of the KdV equation in terms of singular perturbation and came up with the classical model of Eq. 2.

The format of the present article is as follows: In Sect. 2, we begin with the fundamental concept of fractional calculus. In Sects. 3 and 4, we go over the core ideas behind the suggested methods. In Sects. 5 we give the convergence analysis of the suggested techniques. These methods are used in Sect. 6 to solve the time-fractional Lax’s Korteweg–de Vries and Kaup–Kupershmidt (KK) issues with the given initial condition. The conclusion is presented in Sect. 6.

2 Preliminaries

We presented some fundamental concept of fractional calculus.

2.1 Definition

The fractional derivative in Abel–Riemann manner is taken as [42,43,44]

$$\begin{aligned} D^{\mu }{\mathcal {Y}}(\omega )= {\left\{ \begin{array}{ll} \frac{\mathrm{{d}}^\varsigma }{\mathrm{{d}}\omega ^\varsigma }{\mathcal {Y}}{(\omega )}, \ \ \mu = \varsigma ,\\ \frac{1}{\Gamma (\varsigma -\mu )}\frac{\mathrm{{d}}}{\mathrm{{d}}\omega ^\varsigma }\int _0^\omega \frac{{\mathcal {Y}}(\omega )}{(\omega -\phi )^{\mu -\varsigma +1}}\mathrm{{d}}\phi , \ \ \varsigma -1< \mu < \varsigma , \end{array}\right. } \end{aligned}$$

where $\varsigma \in Z^+$, $\mu \in R^+$ and

$$\begin{aligned} D^{-\mu }{\mathcal {Y}}(\omega )=\frac{1}{\Gamma (\mu )}\int _0^{\omega }(\omega -\phi )^{\mu -1}{\mathcal {Y}}(\phi )d\phi , \ \ 0<\mu \le 1. \end{aligned}$$

2.2 Definition

The fractional integral in Abel–Riemann manner is taken as [42,43,44]

$$\begin{aligned} J^{\mu }{\mathcal {Y}}(\omega )=\frac{1}{\Gamma (\mu )}\int _0^\omega (\omega -\phi )^{\mu -1}{\mathcal {Y}}(\omega )\mathrm{{d}}\omega , \ \ \omega>0, \ \ \mu >0. \end{aligned}$$

with below properties

$$\begin{aligned} \begin{aligned} J^{\mu }\omega ^\varsigma =\frac{\Gamma (\varsigma +1)}{\Gamma (\varsigma +\mu +1)}\omega ^{\varsigma +\phi },\\ D^{\mu }\omega ^\varsigma =\frac{\Gamma (\varsigma +1)}{\Gamma (\varsigma -\mu +1)}\omega ^{\varsigma -\phi }. \end{aligned} \end{aligned}$$

2.3 Definition

The fractional derivative in Caputo manner is taken as [42,43,44]

$$\begin{aligned} D^{\mu }{\mathcal {Y}}(\omega )= {\left\{ \begin{array}{ll} \frac{1}{\Gamma (\varsigma -\mu )}\int _0^\omega \frac{{\mathcal {Y}}^\varsigma (\phi )}{(\omega -\phi )^{\mu -\varsigma +1}}\mathrm{{d}}\phi ,\ \ \varsigma -1<\mu <\varsigma ,\\ \frac{\mathrm{{d}}^\varsigma }{\mathrm{{d}}\omega ^\varsigma }{\mathcal {Y}}(\omega ), \ \ \varsigma =\mu . \end{array}\right. } \end{aligned}$$

(3)

with below properties

$$\begin{aligned} \begin{aligned} J^\mu _\omega D^\mu _\omega {{\mathcal {Y}}}(\omega )&=g(\omega )-\sum _{k=0}^{m}g^{k}(0^{+})\frac{\omega ^k}{k!},\ \ \mathrm{{for}} \ \ \omega >0,\ \ \mathrm{{and}}\, \varsigma -1 < \mu \le \varsigma , \ \ \varsigma \in N.\\ D^\mu _{\omega } J^\mu _{\omega }{{\mathcal {Y}}}(\omega )&=g(\omega ).\\ \end{aligned} \end{aligned}$$

(4)

2.4 Definition

The ET of Caputo operator is taken as

$$\begin{aligned} \texttt {E}[D^{\mu }_\omega {{\mathcal {Y}}}(\omega )]=s^{-{\mu }}{} \texttt {E}[{{\mathcal {Y}}}(\omega )]-\sum _{k=0}^{\varsigma -1}s^{2-{\mu }+k}{{\mathcal {Y}}}^{(k)}(0), \ \ \mathrm{{where}} \ \ \varsigma -1<{\mu } <\varsigma . \end{aligned}$$

3 Analysis of the HPTM

To present the concept of HPTM, we examine the FPDE of the form

$$\begin{aligned} D_{{\i }}^{\mu }{\mathcal {Y}}(\omega ,{\i })={\mathcal {F}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })+{\mathcal {G}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i }), \ \ 0<\mu \le 1, \end{aligned}$$

(5)

with initial condition

$$\begin{aligned} {\mathcal {Y}}(\omega ,0)=\kappa (\omega ). \end{aligned}$$

Here, $D_{{\i }}^{\mu }=\frac{\partial ^{\mu }}{\partial {\i }^{\mu }}$ denotes the fractional Caputo operator of order $\mu$, and ${\mathcal {F}}_1[\omega ],$ ${\mathcal {G}}_1[\omega ]$ are linear and nonlinear functions.

Apply the ET, we get

$$\begin{aligned}{} & {} \texttt {E}[D_{{\i }}^{\mu }{\mathcal {Y}}(\omega ,{\i })]=\texttt {E}[{\mathcal {Y}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })+{\mathcal {R}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })], \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \frac{1}{u^{\mu }}\{M(u)- u^2 {\mathcal {Y}}(\omega ,0)\}=\texttt {E}[{\mathcal {F}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })+{\mathcal {G}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })]. \end{aligned}$$

(7)

On simplification we have

$$\begin{aligned} M(u)=u^2 {\mathcal {Y}}(\omega ,0)+u^{\mu }{} \texttt {E}[{\mathcal {F}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })+{\mathcal {G}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })]. \end{aligned}$$

(8)

Apply the inverse ET, we get

$$\begin{aligned} {\mathcal {Y}}(\omega ,{\i })={\mathcal {Y}}(\omega ,0)+\texttt {E}^{-1}[u^{\mu }{} \texttt {E}[{\mathcal {F}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })+{\mathcal {G}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })]]. \end{aligned}$$

(9)

By applying homotopy perturbation method (HPM) to (9), we have

$$\begin{aligned} {\mathcal {Y}}(\omega ,{\i })={\mathcal {Y}}(\omega ,0)+\epsilon [\texttt {E}^{-1}[u^{\mu }{} \texttt {E}[{\mathcal {F}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })+{\mathcal {G}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })]]]. \end{aligned}$$

(10)

The basic series form solution is as

$$\begin{aligned} {\mathcal {Y}}(\omega ,{\i })=\sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {Y}}_{k}(\omega ,{\i }), \end{aligned}$$

(11)

having homotopy parameter $\epsilon \in [0,1]$.

The nonlinear term is taken as

$$\begin{aligned} {\mathcal {G}}_1[\omega ]{\mathcal {Y}}(\omega ,{\i })=\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {Y}}). \end{aligned}$$

(12)

The homotopy polynomial $H_{k}$ is determined as

$$\begin{aligned} H_{k}({\mathcal {Y}}_{0},{\mathcal {Y}}_{1},...,{\mathcal {Y}}_{n})=\frac{1}{\Gamma (n+1)}D_{\epsilon }^{k}\left[ {\mathcal {G}}_1\left( \sum _{k=0}^{\infty }\epsilon ^{i}{\mathcal {Y}}_{i}\right) \right] _{\epsilon =0}, \end{aligned}$$

(13)

with $D_{\epsilon }^{k}=\frac{\partial ^{k}}{\partial \epsilon ^{k}}.$

By inserting (11) and (12) in (10), we have

$$\begin{aligned} \sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {Y}}_{k}(\omega ,{\i })={\mathcal {Y}}(\omega ,0)+\epsilon \times \left( \texttt {E}^{-1}\left[ u^{\mu }{} \texttt {E}\{{\mathcal {F}}_1\sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {Y}}_{k}(\omega ,{\i })+ \sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {Y}})\}\right] \right) .\nonumber \\ \end{aligned}$$

(14)

Equating the $\epsilon$ coefficient, we have

$$\begin{aligned} \begin{aligned} \epsilon ^{0}&:{\mathcal {Y}}_{0}(\omega ,{\i })={\mathcal {Y}}(\omega ,0),\\ \epsilon ^{1}&:{\mathcal {Y}}_{1}(\omega ,{\i })=\texttt {E}^{-1}\left[ u^{\mu }{} \texttt {E}({\mathcal {F}}_1[\omega ]{\mathcal {Y}}_{0}(\omega ,{\i })+H_{0}({\mathcal {Y}}))\right] ,\\ \epsilon ^{2}&:{\mathcal {Y}}_{2}(\omega ,{\i })=\texttt {E}^{-1}\left[ u^{\mu }{} \texttt {E}({\mathcal {F}}_1[\omega ]{\mathcal {Y}}_{1}(\omega ,{\i })+H_{1}({\mathcal {Y}}))\right] ,\\&.\\&.\\&.\\ \epsilon ^{k}&:{\mathcal {Y}}_{k}(\omega ,{\i })=\texttt {E}^{-1}\left[ u^{\mu }{} \texttt {E}({\mathcal {F}}_1[\omega ]{\mathcal {Y}}_{k-1}(\omega ,{\i })+H_{k-1}({\mathcal {Y}}))\right] ,\ \ k>0,\,k\in N. \end{aligned} \end{aligned}$$

(15)

Hence, the series form solution of the proposed method is as

$$\begin{aligned} {\mathcal {Y}}(\omega ,{\i })=\lim _{M\rightarrow \infty }\sum _{k=1}^{M}{\mathcal {Y}}_{k}(\omega ,{\i }). \end{aligned}$$

(16)

4 Analysis of the ETDM

To present the concept of ETDM, we examine the FPDE of the form

$$\begin{aligned} D_{\i }^\mu {{\mathcal {Y}}(\omega ,{\i })}={\mathcal {F}}_1(\omega ,{\i })+{\mathcal {G}}_1(\omega ,{\i }), \quad 0< \mu \le 1, \end{aligned}$$

(17)

with initial condition

$$\begin{aligned} {\mathcal {Y}}(\omega ,0)=\kappa (\omega ). \end{aligned}$$

Here, $D_{\i }^\mu =\frac{\partial ^\mu }{\partial {\i }^\mu }$ denotes the fractional Caputo operator of order $\mu$, and ${\mathcal {F}}_1$ and ${\mathcal {G}}_1$ are linear and non-linear functions.

Apply the ET, we get

$$\begin{aligned} \begin{aligned}&\texttt {E}[D_{\i }^\mu {{\mathcal {Y}}(\omega ,{\i })}]=\texttt {E}[{\mathcal {F}}_1(\omega ,{\i })+{\mathcal {G}}_1(\omega ,{\i })],\\&\frac{1}{u^{\mu }}\{M(u)- u^2 {\mathcal {Y}}(\omega ,0)\}=\texttt {E}[{\mathcal {F}}_1(\omega ,{\i })+{\mathcal {G}}_1(\omega ,{\i })].\\ \end{aligned} \end{aligned}$$

(18)

On simplification we have

$$\begin{aligned} M(u)=u {\mathcal {Y}}(\omega ,0)+u^{\mu }{} \texttt {E}[{\mathcal {F}}_1(\omega ,{\i })+{\mathcal {G}}_1(\omega ,{\i })]. \end{aligned}$$

(19)

Apply the inverse ET, we get

$$\begin{aligned} {\mathcal {Y}}(\omega ,{\i })={\mathcal {Y}}(\omega ,0)+\texttt {E}^{-1}[u^{\mu }{} \texttt {E}[{\mathcal {F}}_1(\omega ,{\i })+{\mathcal {G}}_1(\omega ,{\i })]. \end{aligned}$$

(20)

In terms of ADM, the basic series form solution is as

$$\begin{aligned} {\mathcal {Y}}(\omega ,{\i })=\sum _{m=0}^{\infty }{\mathcal {Y}}_m(\omega ,{\i }). \end{aligned}$$

(21)

The nonlinear term is taken as

$$\begin{aligned} {\mathcal {G}}_1(\omega ,{\i })=\sum _{m=0}^{\infty }{\mathbb {A}}_m({\mathcal {Y}}), \end{aligned}$$

(22)

with

$$\begin{aligned} {\mathbb {A}}_m\Bigg ({\mathcal {Y}}_{0},{\mathcal {Y}}_{1},{\mathcal {Y}}_{2},\cdots ,{\mathcal {Y}}_{m}\Bigg )\!=\!\frac{1}{m!}\left[ \frac{\partial ^m}{\partial \ell ^m}\left\{ {\mathcal {G}}_1\left( \sum _{m=0}^{\infty }\ell ^m{\mathcal {Y}}_m\right) \right\} \right] _{\ell =0},\ \ m=0,1,2,\cdots .\nonumber \\ \end{aligned}$$

(23)

By inserting (21) and (22) in (20), we have

$$\begin{aligned} \sum _{m=0}^{\infty }{\mathcal {Y}}_m(\omega ,{\i })={\mathcal {Y}}(\omega ,0)+\texttt {E}^{-1} u^\mu \left[ \texttt {E}\left\{ {\mathcal {F}}_1\Bigg (\sum _{m=0}^{\infty }{\mathcal {Y}}_m(\omega ,{\i })\Bigg )+\sum _{m=0}^{\infty }{\mathbb {A}}_m({\mathcal {Y}})\right\} \right] .\nonumber \\ \end{aligned}$$

(24)

By equating both sides, we have

$$\begin{aligned} {\mathcal {Y}}_0(\omega ,{\i })= & {} {\mathcal {Y}}(\omega ,0),\nonumber \\ {\mathcal {Y}}_1(\omega ,{\i })= & {} \texttt {E}^{-1}\left[ u^\mu \texttt {E}\{{\mathcal {F}}_1({\mathcal {Y}}_0)+{\mathbb {A}}_0\}\right] . \end{aligned}$$

(25)

Hence, the general solution of the proposed method for $m\ge 1$ is as

$$\begin{aligned} {\mathcal {Y}}_{m+1}(\omega ,{\i })=\texttt {E}^{-1}\left[ u^\mu \texttt {E}\{{\mathcal {F}}_1({\mathcal {Y}}_m)+{\mathbb {A}}_m\}\right] .\\ \end{aligned}$$

5 Convergence analysis

In this section, the proposed approaches convergence are illustrated.

Theorem 5.1

Assume that the accurate solution of (5) is $\Psi (\theta ,{\i })$ and let $\Psi (\theta ,{\i })$, $\Psi _{n}(\theta ,{\i })\in H$ and $\wp \in (0,1)$, where H illustrates the Hilbert space. The obtained solution $\sum _{q=0}^{\infty }\Psi _{q}(\theta ,{\i })$ converge to $\Psi (\theta ,{\i })$ if $\Psi _{q}(\theta ,{\i })\le \Psi _{q-1}(\theta ,{\i }) \ \ \forall q>A$, i.e., for any $\theta>0\exists A>0$, such that $||\Psi _{q+n}(\theta ,{\i })||\le \beta ,\forall m,n\in N.$

Proof

Consider a sequence of $\sum _{q=0}^{\infty }\Psi _{q}(\theta ,{\i }).$

$$\begin{aligned} \begin{aligned} {\mathcal {J}}_{0}(\theta ,{\i })&=\Psi _{0}(\theta ,{\i }),\\ {\mathcal {J}}_{1}(\theta ,{\i })&=\Psi _{0}(\theta ,{\i })+\Psi _{1}(\theta ,{\i }),\\ {\mathcal {J}}_{2}(\theta ,{\i })&=\Psi _{0}(\theta ,{\i })+\Psi _{1}(\theta ,{\i })+\Psi _{2}(\theta ,{\i }),\\ {\mathcal {J}}_{3}(\theta ,{\i })&=\Psi _{0}(\theta ,{\i })+\Psi _{1}(\theta ,{\i })+\Psi _{2}(\theta ,{\i })+\Psi _{3}(\theta ,{\i }),\\&\vdots \\ {\mathcal {J}}_{q}(\theta ,{\i })&=\Psi _{0}(\theta ,{\i })+\Psi _{1}(\theta ,{\i })+\Psi _{2}(\theta ,{\i })+\cdots +\Psi _{q}(\theta ,{\i }).\\ \end{aligned} \end{aligned}$$

(26)

We must illustrate that ${\mathcal {J}}_{q}(\theta ,{\i })$ forms a "Cauchy sequence" in order to attain the chosen result. Also, let’s take

$$\begin{aligned} \begin{aligned} ||{\mathcal {J}}_{{q}+1}(\theta ,{\i })-{\mathcal {J}}_{q}(\theta ,{\i })||&=||\Psi _{{q}+1}(\theta ,{\i })||\le \wp ||\Psi _{q}(\theta ,{\i })||\\&\le \wp ^{2}||\Psi _{q-1}(\theta ,{\i })||\le \wp ^{3}||\Psi _{q-2}(\theta ,{\i })||\cdots \\&\le \wp _{q+1}||\Psi _{0}(\theta ,{\i })||. \end{aligned} \end{aligned}$$

(27)

For $q,n\in N$, we have

$$\begin{aligned} \begin{aligned}&||{\mathcal {J}}_{q}(\theta ,{\i })-{\mathcal {J}}_{n}(\theta ,{\i })||\\&\quad =||\Psi _{{q}+n}(\theta ,{\i })||=||{\mathcal {J}}_{q}(\theta ,{\i })-{\mathcal {J}}_{q-1}(\theta ,{\i })+({\mathcal {J}}_{q-1}(\theta ,{\i })-{\mathcal {J}}_{q-2}(\theta ,{\i }))\\&\qquad +({\mathcal {J}}_{q-2}(\theta ,{\i })-{\mathcal {J}}_{q-3}(\theta ,{\i }))+\cdots +({\mathcal {J}}_{n+1}(\theta ,{\i })-{\mathcal {J}}_{n}(\theta ,{\i }))||\\&\quad \le ||{\mathcal {J}}_{q}(\theta ,{\i })-{\mathcal {J}}_{q-1}(\theta ,{\i })||+||({\mathcal {J}}_{q-1}(\theta ,{\i })-{\mathcal {J}}_{q-2}(\theta ,{\i }))||\\&\qquad +||({\mathcal {J}}_{q-2}(\theta ,{\i })-{\mathcal {J}}_{q-3}(\theta ,{\i }))||+\cdots +||({\mathcal {J}}_{n+1}(\theta ,{\i })-{\mathcal {J}}_{n}(\theta ,{\i }))||\\&\quad \le \wp ^{q}||\Psi _{0}(\theta ,{\i })||+\wp ^{q-1}||\Psi _{0}(\theta ,{\i })||+\cdots +\wp ^{q+1}||\Psi _{0}(\theta ,{\i })||\\&\quad =||\Psi _{0}(\theta ,{\i })||(\wp ^{q}+\wp ^{q-1}+\wp ^{q+1})\\&\quad =||\Psi _{0}(\theta ,{\i })||\frac{1-\wp ^{q-n}}{1-\wp ^{q+1}}\wp ^{n+1}. \end{aligned} \end{aligned}$$

(28)

As $0<\wp <1$, and $\Psi _{0}(\theta ,{\i })$ are bound, so take $\beta =1-\wp /(1-\wp _{q-n})\wp ^{n+1}||\Psi _{0}(\theta ,{\i })||$, and we get

$$\begin{aligned} ||\Psi _{q+n}(\theta ,{\i })||\le \beta ,\quad \forall q,n\in N. \end{aligned}$$

(29)

Hence, $\{\Psi _{q}(\theta ,{\i })\}_{q=0}^{\infty }$ makes a "Cauchy sequence" in H. It proves that the sequence $\{\Psi _{q}(\theta ,{\i })\}_{q=0}^{\infty }$ is a convergent sequence with the limit $\lim _{q\rightarrow \infty }\Psi _{q}(\theta ,{\i })=\Psi (\theta ,{\i })$ for $\exists \Psi (\theta ,{\i })\in {\mathcal {H}}$ which complete the proof. $\square$

Theorem 5.2

Assume that $\sum _{h=0}^{k}\Psi _{h}({\theta },{\i })$ is finite and $\Psi (\theta ,{\i })$ reflect the series solution. Considering $\wp >0$ with $||\Psi _{h+1}(\theta ,{\i })||\le ||\Psi _{h}(\theta ,{\i })||$, the maximum absolute error is determined as

$$\begin{aligned} ||\Psi (\theta ,{\i })-\sum _{h=0}^{k}\Psi _{h}(\theta ,{\i })||<\frac{\wp ^{k+1}}{1-\wp }||\Psi _{0}(\theta ,{\i })||. \end{aligned}$$

(30)

Proof

Suppose $\sum _{h=0}^{k}\Psi _{h}(\theta ,{\i })$ is finite which implies that $\sum _{h=0}^{k}\Psi _{h}(\theta ,{\i })<\infty$.

Let us consider

$$\begin{aligned} \begin{aligned} ||\Psi (\theta ,{\i })-\sum _{h=0}^{k}\Psi _{h}(\theta ,{\i })||=&||\sum _{h=k+1}^{\infty }\Psi _{h}(\theta ,{\i })||\\ \le&\sum _{h=k+1}^{\infty }||\Psi _{h}(\theta ,{\i })||\\ \le&\sum _{h=k+1}^{\infty }\wp ^{h}||\Psi _{0}(\theta ,{\i })||\\ \le&\wp ^{k+1}(1+\wp +\wp ^{2}+\cdots )||\Psi _{0}(\theta ,{\i })||\\ \le&\frac{\wp ^{k+1}}{1-\wp }||\Psi _{0}(\theta ,{\i })||. \end{aligned} \end{aligned}$$

(31)

which complete the proof of theorem. $\square$

Theorem 5.3

The result of (17) is unique when $0<(\varphi _{1}+\varphi _{2})(\frac{{{{{\i }}}}^{{\wp }}}{\Gamma ({\wp }+1)})<1.$

Proof

Let $H=(C[J],||.||)$ with the norm $||\phi ({\i })||={max}_{{\i }\in J}|\phi ({\i })|$ is Banach space, $\forall$ continuous function on J. Let $I:H\rightarrow H$ is a non-linear mapping, where

$$\begin{aligned} {\mathcal {M}}^{C}_{l+1}={\mathcal {M}}^{C}_{0}+\texttt {E}^{-1}[u^{\wp }{} \texttt {E}[{\mathcal {F}}_1({\mathcal {M}}_{l}(\theta ,{\i }))+{\mathcal {G}}_1({\mathcal {M}}_{l}(\theta ,{\i }))]], \ \ l\ge 0. \end{aligned}$$

Suppose that $|{\mathcal {F}}_1({\mathcal {M}})-{\mathcal {F}}_1({\mathcal {M}}^{*})|<\varphi _{1}|{\mathcal {M}}-{\mathcal {M}}^{*}|$ and $|{\mathcal {G}}_1({\mathcal {M}})-{\mathcal {G}}_1({\mathcal {M}}^{*})|<\varphi _{2}|{\mathcal {M}}-{\mathcal {M}}^{*}|$, where ${\mathcal {M}}:={\mathcal {M}}(\theta ,{\i })$ and ${\mathcal {M}}^{*}:={\mathcal {M}}^{*}(\theta ,{\i })$ are two separate function values and $\varphi _{1}$,$\varphi _{2}$ are Lipschitz constants.

$$\begin{aligned} \begin{aligned} ||I{\mathcal {M}}-I{\mathcal {M}}^{*}||&\le max_{t\in J}|\texttt {E}^{-1}\Big [u^{\wp }{} \texttt {E}[{\mathcal {F}}_1({\mathcal {M}})-{\mathcal {F}}_1({\mathcal {M}}^{*})]\\&\quad +u^{\wp }{} \texttt {E}[{\mathcal {G}}_1({\mathcal {M}})-{\mathcal {G}}_1({\mathcal {M}}^{*})]|\Big ]\\&\le max_{{\i }\in J}\Big [\varphi _{1}{} \texttt {E}^{-1}[u^{\wp }{} \texttt {E}[|{\mathcal {M}}-{\mathcal {M}}^{*}|]]\\&\quad +\varphi _{2}{} \texttt {E}^{-1}[u^{\wp }{} \texttt {E}[|{\mathcal {M}}-{\mathcal {M}}^{*}|]]\Big ]\\&\le max_{t\in J}(\varphi _{1}+\varphi _{2})\left[ \texttt {E}^{-1}[u^{\wp }{} \texttt {E}|{\mathcal {M}}-{\mathcal {M}}^{*}|]\right] \\&\le (\varphi _{1}+\varphi _{2})\left[ \texttt {E}^{-1}[u^{\wp }{} \texttt {E}||{\mathcal {M}}-{\mathcal {M}}^{*}||]\right] \\&=(\varphi _{1}+\varphi _{2})(\frac{{{{{\i }}}}^{{\wp }}}{\Gamma ({\wp }+1)})||{\mathcal {M}}-{\mathcal {M}}^{*}|| \end{aligned} \end{aligned}$$

(32)

I is contraction as $0<(\varphi _{1}+\varphi _{2})(\frac{{{{{\i }}}}^{{\wp }}}{\Gamma ({\wp }+1)})<1$. The result of (17) is unique by means of Banach fixed point theorem. $\square$

Theorem 5.4

The result of (17) is convergent.

Proof

Let ${\mathcal {M}}_{m}=\sum _{r=0}^{m}{\mathcal {M}}_{r}(\theta ,{\i })$. To show that ${\mathcal {M}}_{m}$ is a Cauchy sequence in H. Let

$$\begin{aligned} \begin{aligned}&||{\mathcal {M}}_{m}-{\mathcal {M}}_{n}||=max_{{\i }\in J}|\sum _{r=n+1}^{m}{\mathcal {M}}_{r}|, \ \ n=1,2,3,\cdots \\&\le max_{{\i }\in J} \left| \texttt {E}^{-1}\left[ u^{\wp }{} \texttt {E}\left[ \sum _{r=n+1}^{m}({\mathcal {F}}_1({\mathcal {M}}_{r-1})+{\mathcal {G}}_1({\mathcal {M}}_{r-1}))\right] \right] \right| \\&=max_{{\i }\in J} \left| \texttt {E}^{-1}\left[ u^{\wp }{} \texttt {E}\left[ \sum _{r=n+1}^{m-1}({\mathcal {F}}_1({\mathcal {M}}_{r})+{\mathcal {G}}_1({\mathcal {M}}_{r}))\right] \right] \right| \\&\le max_{{\i }\in J}|\texttt {E}^{-1}[u^{\wp }{} \texttt {E}[({\mathcal {F}}_1({\mathcal {M}}_{m-1})-{\mathcal {F}}_1({\mathcal {M}}_{n-1})+{\mathcal {G}}_1({\mathcal {M}}_{m-1})-{\mathcal {G}}_1({\mathcal {M}}_{n-1}))]]|\\&\le \varphi _{1}max_{{\i }\in J}|\texttt {E}^{-1}[u^{\wp }{} \texttt {E}[({\mathcal {F}}_1({\mathcal {M}}_{m-1})-{\mathcal {F}}_1({\mathcal {M}}_{n-1}))]]|\\&\quad +\varphi _{2}max_{{\i }\in J}|\texttt {E}^{-1}[u^{\wp }{} \texttt {E}[({\mathcal {G}}_1({\mathcal {M}}_{m-1})-{\mathcal {G}}_1({\mathcal {M}}_{n-1}))]]|\\&=(\varphi _{1}+\varphi _{2})(\frac{{{{{\i }}}}^{{\wp }}}{\Gamma ({\wp }+1)})||{\mathcal {M}}_{m-1}-{\mathcal {M}}_{n-1}|| \end{aligned} \end{aligned}$$

(33)

Let $m=n+1$, then

$$\begin{aligned} \begin{aligned}&||{\mathcal {M}}_{n+1}-{\mathcal {M}}_{n}||\\&\quad \le \varphi ||{\mathcal {M}}_{n}-{\mathcal {M}}_{n-1}||\le \varphi ^{2}||{\mathcal {M}}_{n-1}{\mathcal {M}}_{n-2}||\le \cdots \le \varphi ^{n}||{\mathcal {M}}_{1}-{\mathcal {M}}_{0}||, \end{aligned} \end{aligned}$$

(34)

where $\varphi =(\varphi _{1}+\varphi _{2})(\frac{{{{{\i }}}}^{{\wp }}}{\Gamma ({\wp }+1)})$. Similarly, we have

$$\begin{aligned} \begin{aligned} ||{\mathcal {M}}_{m}-{\mathcal {M}}_{n}||&\le ||{\mathcal {M}}_{n+1}-{\mathcal {M}}_{n}||+||{\mathcal {M}}_{n+2}{\mathcal {M}}_{n+1}||+\cdots +||{\mathcal {M}}_{m}-{\mathcal {M}}_{m-1}||,\\&(\varphi ^{n}+\varphi ^{n+1}+\cdots +\varphi ^{m-1})||{\mathcal {M}}_{1}-{\mathcal {M}}_{0}||\le \varphi ^{n}\left( \frac{1-\varphi ^{m-n}}{1-\varphi }\right) ||{\mathcal {M}}_{1}||, \end{aligned}\nonumber \\ \end{aligned}$$

(35)

As $0<\varphi <1$, we get $1-\varphi ^{m-n}<1$. Hence,

$$\begin{aligned} \begin{aligned} ||{\mathcal {M}}_{m}-{\mathcal {M}}_{n}||\le \frac{\varphi ^{n}}{1-\varphi }max_{{\i }\in J}||{\mathcal {M}}_{1}||. \end{aligned} \end{aligned}$$

(36)

Since $||{\mathcal {M}}_{1}||<\infty ,\ \ ||{\mathcal {M}}_{m}-{\mathcal {M}}_{n}||\rightarrow 0$ when $n \rightarrow \infty$. Hence, ${\mathcal {M}}_m$ is a Cauchy sequence in H, illustrating that the series ${\mathcal {M}}_m$ is convergent.$\square$

6 Applications

Example 6.1

Assume the seventh-order TFLK-dV equation:

$$\begin{aligned} \begin{aligned} D_{\i }^\wp {{\mathcal {M}}(\theta ,{\i })}&=-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\qquad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\qquad -70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\qquad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i }),\\&\quad \ \ \ \ \ 0<\wp \le 1,\\ \end{aligned} \end{aligned}$$

(37)

with initial condition

$$\begin{aligned} {\mathcal {M}}(\theta ,0)=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta )). \end{aligned}$$

Apply the ET, we get

$$\begin{aligned} \begin{aligned} \texttt {E}\left( \frac{\partial ^{\wp }{\mathcal {M}}}{\partial {\i }^{\wp }}\right)&=\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]. \end{aligned} \end{aligned}$$

(38)

After, we get

$$\begin{aligned} \frac{1}{u^{\wp }}\{M(u)- u^2 {\mathcal {M}}(\theta ,0)\}&=\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -70 {\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ],\end{aligned}$$

(39)

$$\begin{aligned} M(u)&=u{\mathcal {M}}(\theta ,0)+u^{\wp }{} \texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-70 {\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]. \end{aligned}$$

(40)

Apply the inverse ET, we get

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })&={\mathcal {M}}(\theta ,0)+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&-\quad {\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ],\nonumber \\ {\mathcal {M}}(\theta ,{\i })&=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta ))+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ]. \end{aligned}$$

(41)

In HPM manner, the basic series form solution is as:

$$\begin{aligned} \begin{aligned} \sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {M}}_{k}(\theta ,{\i })&=\Bigg (2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta ))\Bigg )+\Bigg (\texttt {E}^{-1}\Bigg [u^{\wp }{} \texttt {E}\Bigg [-140\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\\&\quad -70\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg ) -280\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\\&\quad -70\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )-70\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\\&\quad -42\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )-14\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\\&\quad -\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {M}}_{k}(\theta ,{\i })\Bigg )_{\theta \theta \theta \theta \theta \theta \theta }\Bigg ]\Bigg ]\Bigg ).\\ \end{aligned} \end{aligned}$$

(42)

Equating the $\epsilon$ coefficient, we have

$$\begin{aligned} \epsilon ^{0}&:{\mathcal {M}}_{0}(\theta ,{\i })=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta )),\\ \epsilon ^{1}&:{\mathcal {M}}_{1}(\theta ,{\i })=\frac{256\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{\Gamma (\wp +1)},\\ \epsilon ^{2}&:{\mathcal {M}}_{2}(\theta ,{\i })=\frac{16384{\i }^{2\wp }\rho ^{16}(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{\Gamma (2\wp +1)},\\&\vdots \end{aligned}$$

Hence, the series form solution of the proposed method is as

$$\begin{aligned} \begin{aligned} {\mathcal {M}}({\theta },{{\i }})&={{\mathcal {M}}}_{0}({\theta },{{\i }})+{{\mathcal {M}}}_{1}({\theta },{{\i }})+{{\mathcal {M}}}_{2}({\theta },{{\i }})+\cdots \\ {\mathcal {M}}({\theta },{{\i }})&=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta ))+\frac{256\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{\Gamma (\wp +1)}\\&\quad +\frac{16384{\i }^{2\wp }\rho ^{16}(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{\Gamma (2\wp +1)}+\cdots \\ \end{aligned} \end{aligned}$$

Solution by means of ETDM

Apply the ET, we get

$$\begin{aligned} \begin{aligned} \texttt {E}\left\{ \frac{\partial ^{\wp }{\mathcal {M}}}{\partial {\i }^{\wp }}\right\}&=\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ].\\ \end{aligned} \end{aligned}$$

(43)

After, we get

$$\begin{aligned} \frac{1}{u^{\wp }}\{M(u)- u^2 {\mathcal {M}}(\theta ,0)\}&=\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ],\end{aligned}$$

(44)

$$\begin{aligned} M(u)&= u^2 {\mathcal {M}}(\theta ,0)+u^{\wp }{} \texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })-280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })-14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]. \end{aligned}$$

(45)

Apply the inverse ET, we get

$$\begin{aligned} \begin{aligned} {\mathcal {M}}(\theta ,{\i })&={\mathcal {M}}(\theta ,0)+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\\&\quad -70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ],\\ {\mathcal {M}}(\theta ,{\i })&=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta ))+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-140{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })\\&\quad -70{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })-280{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\\&\quad -70{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-70{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -14{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ].\\ \end{aligned} \end{aligned}$$

(46)

In ADM manner, the basic series form solution is as:

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i }). \end{aligned}$$

(47)

The nonlinear terms are taken as ${\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }) =\sum _{m=0}^{\infty }{\mathbb {A}}_m, {\mathcal {M}}^{3}_{\theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {B}}_m,{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {C}}_m, {\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {D}}_m, {\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {E}}_m, {\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {F}}_m, {\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {G}}_m.$ Thus, we get

$$\begin{aligned} \sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i })&={\mathcal {M}}(\theta ,0) -\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-140\sum _{m=0}^{\infty }{\mathbb {A}}_m-70\sum _{m=0}^{\infty }{\mathbb {B}}_m\nonumber \\&\quad -280\sum _{m=0}^{\infty }{\mathbb {C}}_m-70\sum _{m=0}^{\infty }{\mathbb {D}}_m-70\sum _{m=0}^{\infty }{\mathbb {E}}_m-42\sum _{m=0}^{\infty }{\mathbb {F}}_m\nonumber \\&\quad -14\sum _{m=0}^{\infty }{\mathbb {G}}_m-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ],\nonumber \\ \sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i })&=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta )) -\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-140\sum _{m=0}^{\infty }{\mathbb {A}}_m\nonumber \\&-70\sum _{m=0}^{\infty }{\mathbb {B}}_m-280\sum _{m=0}^{\infty }{\mathbb {C}}_m\nonumber \\&\quad -70\sum _{m=0}^{\infty }{\mathbb {D}}_m-70\sum _{m=0}^{\infty }{\mathbb {E}}_m-42\sum _{m=0}^{\infty }{\mathbb {F}}_m\nonumber \\&-14\sum _{m=0}^{\infty }{\mathbb {G}}_m-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ]. \end{aligned}$$

(48)

By equating both sides, we have

$$\begin{aligned} {\mathcal {M}}_0(\theta ,{\i })=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta )). \end{aligned}$$

On $m=0$,

$$\begin{aligned} {\mathcal {M}}_1(\theta ,{\i })=\frac{256\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{\Gamma (\wp +1)}. \end{aligned}$$

On $m=1$,

$$\begin{aligned} {\mathcal {M}}_2(\theta ,{\i })=\frac{16384{\i }^{2\wp }\rho ^{16}(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{\Gamma (2\wp +1)}. \end{aligned}$$

Hence, the series form solution of the proposed method is as

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i }) ={\mathcal {M}}_0(\theta ,{\i })+{\mathcal {M}}_1(\theta ,{\i })+{\mathcal {M}}_2(\theta ,{\i })+\cdots \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathcal {M}}(\theta ,{\i })&=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho \theta ))+\frac{256\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{\Gamma (\wp +1)}\\&\quad +\frac{16384{\i }^{2\wp }\rho ^{16}(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{\Gamma (2\wp +1)}+\cdots \\ \end{aligned} \end{aligned}$$

By choosing $\wp =1$ we get

$$\begin{aligned} {\mathcal {M}}({\theta },{{\i }})=2\rho ^{2}{{\,\textrm{sech}\,}}^{2}(\rho (\theta -64\rho ^{6}{\i })). \end{aligned}$$

(49)

Example 6.2

Let’s suppose the seventh-order TK-K equation:

$$\begin{aligned} \begin{aligned} D_{\i }^\wp {{\mathcal {M}}(\theta ,{\i })}&=-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&-2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&-252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&-42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i }), \ \ \ \ \ 0<\wp \le 1,\\ \end{aligned} \end{aligned}$$

(50)

having initial source

$$\begin{aligned} {\mathcal {M}}(\theta ,0)=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta )). \end{aligned}$$

After, we have

$$\begin{aligned} \begin{aligned} \texttt {E}\left( \frac{\partial ^{\wp }{\mathcal {M}}}{\partial {\i }^{\wp }}\right)&=\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }) {\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]. \end{aligned} \end{aligned}$$

(51)

After, we obtain

$$\begin{aligned} \frac{1}{u^{\wp }}\{M(u)- u^2 {\mathcal {M}}(\theta ,0)\}&=\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ], \end{aligned}$$

(52)

$$\begin{aligned} \begin{aligned} M(u)&=u{\mathcal {M}}(\theta ,0)+u^{\wp }{} \texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ].\\ \end{aligned} \end{aligned}$$

(53)

Apply the inverse ET, we get

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })&={\mathcal {M}}(\theta ,0)+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\nonumber \\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ],\nonumber \\ {\mathcal {M}}(\theta ,{\i })&=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta ))+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })\nonumber \\&\quad -630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })-2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}(\theta ,{\i })\nonumber \\&\quad {\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ]. \end{aligned}$$

(54)

In terms of HPM, the basic series form solution is as:

$$\begin{aligned} \sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {M}}_{k}(\theta ,{\i })&=\Bigg (\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta ))\Bigg )\nonumber \\&\quad +\Bigg (\texttt {E}^{-1}\Bigg [u^{\wp }{} \texttt {E}\Bigg [-2016\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )-630\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\nonumber \\&\quad -2268\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )-504\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\nonumber \\&\quad -252\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )-147\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )\nonumber \\&\quad -42\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}H_{k}({\mathcal {M}})\Bigg )-\Bigg (\sum _{k=0}^{\infty }\epsilon ^{k}{\mathcal {M}}_{k}(\theta ,{\i })\Bigg )_{\theta \theta \theta \theta \theta \theta \theta }\Bigg ]\Bigg ]\Bigg ). \end{aligned}$$

(55)

Equating the $\epsilon$ coefficient, we have

$$\begin{aligned} \begin{aligned} \epsilon ^{0}&:{\mathcal {M}}_{0}(\theta ,{\i })=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta )),\\ \epsilon ^{1}&:{\mathcal {M}}_{1}(\theta ,{\i })=-\frac{4\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{3\Gamma (\wp +1)},\\ \epsilon ^{2}&:{\mathcal {M}}_{2}(\theta ,{\i })=\frac{16\rho ^{16}{\i }^{2\wp }(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{9\Gamma (2\wp +1)},\\&\vdots \end{aligned} \end{aligned}$$

Hence, the series form solution of the proposed method is as

$$\begin{aligned} \begin{aligned} {\mathcal {M}}({\theta },{{\i }})&={{\mathcal {M}}}_{0}({\theta },{{\i }})+{{\mathcal {M}}}_{1}({\theta },{{\i }})+{{\mathcal {M}}}_{2}({\theta },{{\i }})+\cdots \\ {\mathcal {M}}({\theta },{{\i }})&=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta ))-\frac{4\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{3\Gamma (\wp +1)}\\&\quad +\frac{16\rho ^{16}{\i }^{2\wp }(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{9\Gamma (2\wp +1)}+\cdots \\ \end{aligned} \end{aligned}$$

Solution by means of ETDM

Apply the ET, we get

$$\begin{aligned} \begin{aligned} \texttt {E}\left\{ \frac{\partial ^{\wp }{\mathcal {M}}}{\partial {\i }^{\wp }}\right\}&=\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }) {\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ].\\ \end{aligned} \end{aligned}$$

(56)

After, we obtain

$$\begin{aligned} \begin{aligned} \frac{1}{u^{\wp }}\{M(u)- u^2 {\mathcal {M}}(\theta ,0)\}&=\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\\&\quad -504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ],\\ \end{aligned} \end{aligned}$$

(57)

$$\begin{aligned} \begin{aligned} M(u)&= u^2 {\mathcal {M}}(\theta ,0)+u^{\wp }{} \texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })-630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })\\&\quad -2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\\&\quad -252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })\\&\quad -42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ].\\ \end{aligned} \end{aligned}$$

(58)

Apply the inverse ET, we get

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })&={\mathcal {M}}(\theta ,0)+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })\nonumber \\&\quad -630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })-2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })\nonumber \\&\quad -504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ],\nonumber \\ {\mathcal {M}}(\theta ,{\i })&=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta ))+\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-2016{\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })\nonumber \\&\quad -630{\mathcal {M}}^{3}_{\theta }(\theta ,{\i })-2268{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i })\nonumber \\&\quad {\mathcal {M}}_{\theta \theta }(\theta ,{\i })-504{\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })-252{\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -147{\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })-42{\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })\nonumber \\&\quad -{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ]. \end{aligned}$$

(59)

In terms of ADM, the basic series form solution is as:

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i }). \end{aligned}$$

(60)

Let us assume nonlinear terms by adomian polynomial as ${\mathcal {M}}^{3}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }) =\sum _{m=0}^{\infty }{\mathbb {A}}_m, {\mathcal {M}}^{3}_{\theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {B}}_m, {\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {C}}_m, {\mathcal {M}}^{2}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {D}}_m, {\mathcal {M}}_{\theta \theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {E}}_m, {\mathcal {M}}_{\theta }(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {F}}_m, {\mathcal {M}}(\theta ,{\i }){\mathcal {M}}_{\theta \theta \theta \theta \theta }(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathbb {F}}_m.$ So, we get

$$\begin{aligned} \begin{aligned} \sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i })&={\mathcal {M}}(\theta ,0) -\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-2016\sum _{m=0}^{\infty }{\mathbb {A}}_m-630\sum _{m=0}^{\infty }{\mathbb {B}}_m\\&\quad -2268\sum _{m=0}^{\infty }{\mathbb {C}}_m-504\sum _{m=0}^{\infty }{\mathbb {D}}_m-252\sum _{m=0}^{\infty }{\mathbb {E}}_m\\&\quad -147\sum _{m=0}^{\infty }{\mathbb {F}}_m-42\sum _{m=0}^{\infty }{\mathbb {G}}_m-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ],\\ \sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i })&=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta )) -\texttt {E}^{-1}\Bigg [u^\wp \Bigg \{\texttt {E}\Bigg [-2016\sum _{m=0}^{\infty }{\mathbb {A}}_m\\&\quad -630\sum _{m=0}^{\infty }{\mathbb {B}}_m-2268\sum _{m=0}^{\infty }{\mathbb {C}}_m-504\sum _{m=0}^{\infty }{\mathbb {D}}_m-252\sum _{m=0}^{\infty }{\mathbb {E}}_m\\&\quad -147\sum _{m=0}^{\infty }{\mathbb {F}}_m-42\sum _{m=0}^{\infty }{\mathbb {G}}_m-{\mathcal {M}}_{\theta \theta \theta \theta \theta \theta \theta }(\theta ,{\i })\Bigg ]\Bigg \}\Bigg ].\\ \end{aligned} \end{aligned}$$

(61)

By equating both sides, we have

$$\begin{aligned} {\mathcal {M}}_0(\theta ,{\i })=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta )). \end{aligned}$$

Fig. 1

The graphical view of accurate and our approaches solution

Fig. 2

The graphical view of our approaches solution at $\wp =0.8,0.6$

Fig. 3

The graphical view of our approaches solution at different orders of $\wp$

Fig. 4

The graphical view of our approaches solution by means of absolute error

Table 1 Nature of accurate and our approaches solution for TFLK-dV equation at various orders of $\wp$

Table 2 Comparison of our approaches solution by means of absolute error at different orders of $\wp$

On $m=0$,

$$\begin{aligned} {\mathcal {M}}_1(\theta ,{\i })=-\frac{4\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{3\Gamma (\wp +1)}. \end{aligned}$$

On $m=1$,

$$\begin{aligned} {\mathcal {M}}_2(\theta ,{\i })=\frac{16\rho ^{16}{\i }^{2\wp }(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{9\Gamma (2\wp +1)}. \end{aligned}$$

Hence, the series form solution of the proposed method is as

$$\begin{aligned} {\mathcal {M}}(\theta ,{\i })=\sum _{m=0}^{\infty }{\mathcal {M}}_m(\theta ,{\i }) ={\mathcal {M}}_0(\theta ,{\i })+{\mathcal {M}}_1(\theta ,{\i })+{\mathcal {M}}_2(\theta ,{\i })+\cdots \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathcal {M}}(\theta ,{\i })&=\frac{\rho ^{2}}{3}(1-\frac{3}{2}\tanh ^{2}(\rho \theta ))-\frac{4\rho ^{9}{\i }^{\wp }\tanh (\rho \theta ){{\,\textrm{sech}\,}}^{2}(\rho \theta )}{3\Gamma (\wp +1)}\\&\quad +\frac{16\rho ^{16}{\i }^{2\wp }(\cosh (2\rho \theta )-2){{\,\textrm{sech}\,}}^{4}(\rho \theta )}{9\Gamma (2\wp +1)}+\cdots \\ \end{aligned} \end{aligned}$$

By choosing $\wp =1$ we get

$$\begin{aligned} {\mathcal {M}}({\theta },{{\i }})=\frac{\rho ^{2}}{3}\Bigg (1-\frac{3}{2}\tanh ^{2}\Bigg (\rho \Bigg [\theta +\frac{4\rho ^{6}}{3}{\i }\Bigg ]\Bigg )\Bigg ). \end{aligned}$$

(62)

Fig. 5

The graphical view of accurate and our approaches solution

Fig. 6

The graphical view of our approaches solution at $\wp =0.8,0.6$

Fig. 7

The graphical view of our approaches solution at different orders of $\wp$

Fig. 8

The graphical view of our approaches solution by means of absolute error

Table 3 Nature of the accurate and proposed approaches solution at various orders of $\wp$

Table 4 Numerical simulation in sense of absolute error at numerous values of $\wp$

7 Numerical simulation studies

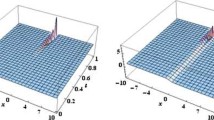
In this study, the exact approximate solution of time-fractional seventh-order nonlinear equations has been studied using two novel approaches. The Caputo fractional derivative operator at any order for variable values of space and time is presented as exact analytical solutions for the time-fractional seventh-order nonlinear equations via Maple. The numerical results demonstrate the technique’s applicability, and the precision of the approach is assessed in light of the precise results. The suggested approaches solution plot of ${\mathcal {M}}({\theta },{{\i }})$ is shown in Fig. 1a, while Fig. 1b shows the actual solution plot. Figure 2a,b display the fractional-order behavior of ${\mathcal {M}}({\theta },{{\i }})$ for $\wp =0.8$ and 0.6. Figure 3a, b show the plots of ${\mathcal {M}}({\theta },{{\i }})$ for the range of $\wp =0.25, 0.50, 0.75,$ and 1, whereas Fig. 4 displays the error evaluation for the same equation generated by both methods. For various values of $\theta$ and ${\i }$, the analytical solution to the equation ${\mathcal {M}}({\theta },{{\i }})$ is displayed in Table 1 while the error evaluation has been evaluated in Table 2 for various values of $\theta$ and ${\i }$. The proposed techniques solution plot of ${\mathcal {M}}({\theta },{{\i }})$ is shown in Fig. 5a, while Fig. 5b shows the actual solution plot. Figure 6a, b display the graphical representations of ${\mathcal {M}}({\theta },{{\i }})$ for $\wp =0.8$ and 0.6. Figure 7a, b show the plots of ${\mathcal {M}}({\theta },{{\i }})$ for the range of $\wp =0.25, 0.50, 0.75,$ and 1, whereas Fig. 8 displays the error evaluation for the same equation generated by both methods. For various values of $\theta$ and ${\i }$, the analytical solution to the equation ${\mathcal {M}}({\theta },{{\i }})$ is displayed in Table 3 while the error evaluation has been evaluated in Table 4 for various values of $\theta$ and ${\i }$. It need to be noted that throughout the calculations, we used second-order approximations and that using accurate results to the problem gave us a better estimate. We could have obtained more accurate approximation solutions by increasing the order of the approximation, which results in more terms in the solution.

8 Conclusion

The ETDM and the HPTM are two unique methodologies that have been thoroughly examined in this work for solving non-linear fractional seventh-order Lax’s Korteweg–de Vries and Kaup–Kupershmidt equations. The methods that are proposed are the combined form of the Elzaki transformation with the homotopy perturbation method and the Adomian decomposition approach. The fractional-order solutions give different dynamics for different fractional orders of the derivative. In comparison to numerical studies, which require more complex computations, the task can be completed quite simply and effectively using analytical solutions. After all, the researchers can now choose the fractional-order issue whose solution is comparable and extremely close to the experimental results of any physical problem. The graphical analysis of the revealed solutions was executed. The study’s findings showed that the precise solutions offered and those actually found were very congruent. As the problems fractional orders change, different dynamical patterns emerge in the solutions, which are generated for various fractional orders. The tables show the applicability of the suggested methods by offering a variety of fractional-order results. The existing approaches have shown to be an efficient and straightforward process when compared to the precise solution. Finally, this research leads us to the conclusion that the suggested approaches are strong and useful mathematical tool for examining a variety of real problems that arise in the natural sciences and engineering and that may be represented by fractional differential equations.