1 Introduction

The fractional calculus (FC) is the generic generalization of integer-order calculus to licentious order integration and differentiation with non integer order. The FC dates back to 1695, when l’Hôpital addressed Leibniz regarding the probable meaning of \(\frac{d^{1/2} x(t)}{dt^{1/2}}\), which represents the semi derivative of x(t) with respect to t. Due to its advantageous qualities such as analyticity, linearity and non locality, fractional calculus has recently become a powerful tool. Furthermore, there are numerous pioneering references accessible for various definitions of FC, which lay the foundation for FC [1,2,3,4]. With the rapid advancement of digital computer technology, many researchers are turning their attention to the theory and applications of fractional calculus, for example, Jacob Robert Emden (1862–1940), a Swiss astrophysicist and Sir Ralph Howard Fowler (1889–1944), an English astronomer are the namesakes of the famous Emden–Fowler (EF) equation [5, 6], the generalized derivative operator [7], the HAM [8, 9], the Caputo–Fabrizio fractional derivative [10], the asymptotic behavior [11], the adomian decomposition method [12], the conformable derivative [13], the q-homotopy analysis transform method [14], the homotopy perturbation transform method [15], the modified \((G'/G)\)-expansion method [16, 17], the modified invariant subspace method [18], the finite difference method [19], the multi-variable Aleph-function [20], the Aboodh adomian decomposition method (a powerful research tool, used to successfully develop the solution of ZKEs) [21], the capacity and applicable of the projected scheme [22, 23], the Banach’s fixed point speculation (which is investigated for the controlling fractional-order model in order to determine the existence and uniqueness of the achieved solution) [24, 25], some new voltage behavior such as dark–bright soliton solution, trigonometric and complex function solutions [26,27,28,29,30], magnetohydrodynamic [31], the uniform Haar wavelet resolution technique [32], the singular boundary value problems [33], the analytical solutions [34], the \(\exp (-k(p))\)-expansion technique [35], the Caputo fractional derivatives [36], the generalized Adams–Bashforth–Moulton method [37, 38], some standard fixed point theorems and fractional calculus theories [39], the pseudo-spectral collocation method [40], Caputo–Fabrizio fractional derivative [41], the Mittag–Leffler rule with fractal derivative generalized [42], and so on.

To investigate these equations, mathematicians developed some of the most extensively used statistics. Emden–Fowler’s differential equation is one of these equations. It has numerous applications in various scientific fields. This equation is expressed in its general form as

$$\begin{aligned} x^{-\kappa }\frac{d^m}{dx^m}\left( x^{\kappa }\frac{d^n}{dx^n}\right) y + h(x)j(x)=0,\quad \kappa >0. \end{aligned}$$
(1)

Wazwaz [12] proposed this equation and it explains a lot of remarkable facts. The Emden–Fowler equations were first proposed by Fowler as a solution to an astronomical problem [5], Berkovich [6], followed up with a consideration of its particular situations and changed into simpler forms. Other properties of the above equation, such as fastness, asymptotic evolution, continuity, boundary value problem, oscillations, and boundedness were discussed by Wong [5] in 1975.

The homotopy perturbation transform method (HPTM) is described, in which continuous mapping is produced from the initial obligation to the exact solutions. The subsidiary parameter confirms solutions convergence. HPTM is recognized even if a given non-linear problem does not restrain any small/large parameters. The convergence zone and rate of approximation category can be adjusted and controlled. It can also be used to approximate a nonlinear issue by varying the base functions. The connection of semi-analytical approaches with the Laplace transform is well-known for avoiding time-consuming repercussions and requiring less CPU time to examine numerical solutions to nonlinear problems described in real-life applications. By selecting a suitable value for the auxiliary parameter alpha, we may easily alter and regulate the convergence zone of solution series in a vast allowed realm. Also, with the same grade point and order of solution range, it can yield many more acceptable solutions than all other analytical techniques. The development in HPTM is the creation of a novel correction function using homotopy polynomials. Five test issues confirm the accuracy of this strategy. This method can be used to solve multi-dimensional fractional physical problems with ease. The motion of a drop with memory in time is described by time-fractional differential equations. When variations are heavy-tailed, space fractional derivatives emerge to depict drop motion that accounts for a transform in the flow field over the exhaustive system. In addition, the fractional derivatives show that the system memory is modulated or weighted. Electrical signal publicity in a transmission line, wave propagation, signal dissection, and other applications use the Emden–Fowler equation. Because of this, fractional modelling is appropriate for such systems. As a result, understanding the multi-dimensional fractional order Emden–Fowler equation is crucial. It appears to be intriguing to discover a numerical solution of the fractional order Emden–Fowler equation using HPTM because of its ability to provide a parameter that allows us to regulate and change the series solution’s convergence zone. HPTM also eliminates the need for linearization, discretized, small dislocation, or any restricted assumptions, significantly reduces mathematical computational, provides nonlocal effect, promises a big convergence zone, and eliminates the need to calculate complicated polynomials, integrations, or small/large physical parameters. Conformable derivatives yield Caputo type fractional operators [43, 44], the Mittag–Leffler power law [45], the application of the improved q-HAM and the optimal perturbation iteration process yield semi-analytical solutions to the Emden–Fowler problem [46] modified iterative method [47] and cylindrical coordinate system [48]. For temporal and spatial discretization, a modified leap-frog finite difference scheme with stabilized term and a central finite difference scheme are used [49]. On the basis of strength and stiffness theory and calculation, applied materials were determined, and applied physics calculations were carried out [50], criteria for oscillation in second-order Emden–Fowler delay differential equations with a sub-linear neutral term [51], the extended sinh-Gordon equation expansion method [52], and the incomplete global GMERR algorithm and the global GMERR algorithm [53]. The various simulations are used to demonstrate the physical behaviors of the acquired solution with respect to the fractional integer order [54,55,56,57,58,59,60,61,62], the Laplace transform [63, 64] and the second-order Emden–Fowler neutral delay DEs as an application of oscillation criteria [65, 66]. The EFEs under the Dirichlet boundary value problem are the application of the variational method [67], the q-homotopy analysis transform method [68], and the statistical analysis [69]. The development, analysis, and application of a free coefficient algorithm can also reveal a desirable or undesirable property/behavior [70,71,72], to the best of our knowledge. This is the first time the Caputo–Fabrizio derivative has been applied to a singular differential equation problem.

Some basic definitions of fractional calculus are presented in § 2 and the HPTM is discussed in § 3. The solution of the Emden–Fowler equation using the Caputo–Fabrizio type fractional operator by HPTM is given in § 4. The results and discussion are given in § 5 and finally, the conclusion is presented in § 6.

2 Preliminaries

Here we present some fundamental definitions of the Riemann–Liouville (R–L) fractional differentiation, Laplace transform (LT) and FCD [15, 35].

Definition 1

The Caputo derivative is defined for \(\alpha \ge 0\) and \(n\in N\cup {0}\) is defined as follows (see ref. [15]):

$$\begin{aligned} ^{\textrm{CF}}_0\;D_t^\alpha \;u(t)= \frac{1}{\Gamma (n-\alpha )}\int _{0}^{t}(t-\xi )\frac{d^n}{dt^n} u(\xi ) d\xi , \end{aligned}$$
(2)

where \(^{\textrm{CF}}_0\;D_t^\alpha \;\) is the Caputo–Fabrizio derivative.

Definition 2

Assume u be a function \(u \in H^1(a_1,b_1),~ b_1>0,~ 0<\alpha <1.\) Then, the fractional Caputo–Fabrizio fractional operator is defined as (see [15]):

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0\;D_t^\alpha \;u(t)= \frac{M(\alpha )}{1-\alpha )}\int _{0}^{t}\exp \left[ -\frac{\alpha (1-\xi )}{1-\alpha }\right] u'(\xi )d\xi ,\nonumber \\{} & {} \quad t\ge 0,\ 0<\alpha <1, \end{aligned}$$
(3)

with normalized functions \(M(\alpha )\) which depends on \(\alpha \in M(0)= M(1)=1.\)

Definition 3

The CFD of order \( 0<\alpha <1\) is given by (see [15])

$$\begin{aligned} {}^{\textrm{CF}}_0\;D_t^\alpha \; u(t)= & {} \frac{2(1-\alpha )}{M(\alpha )(2-\alpha )}u(t)+ \frac{2\alpha }{M(\alpha )(2-\alpha )} \nonumber \\{} & {} \quad \int _{0}^{t} u(\xi )d\xi ,\quad t\ge 0, \end{aligned}$$
(4)

where \(^{\textrm{CF}}_0\;D_t^\alpha \;u(t)=0,\) if u is a constant function.

Definition 4

The Laplace transform (LT) for the CFD of order \( 0<\alpha <1\) and \(m\in N\) is given by (see [15])

$$\begin{aligned}{} & {} {\mathcal {L}}\left[ ^{\textrm{CF}}_0\;D_t^{(m+\alpha )}\; u(t)\right] (s) \nonumber \\{} & {} \quad = \frac{1}{1-\alpha } {\mathcal {L}}[u^{m+1}(t)] {\mathcal {L}}\left[ \exp \left( \frac{-\alpha }{(1-\alpha )}t\right) \right] \nonumber \\{} & {} \quad = \frac{s^{m+1} {\mathcal {L}}[u(t)]- s^m u(0)-s^{m-1}u'(0) \cdots - u^m (0) }{s+\alpha (1-s)}. \nonumber \\ \end{aligned}$$
(5)

In particular, we have

$$\begin{aligned}{} & {} {\mathcal {L}} \left[ ^{\textrm{CF}}_0\;D_t^{(m+\alpha )}\;u(t)\right] (s) = \frac{s {\mathcal {L}}(u(t))}{s+ \alpha (1-s)},~~~~ m=0, \\{} & {} {\mathcal {L}}\left[ ^{\textrm{CF}}_0\;D_t^{(m+\alpha )}\;u(t)\right] (s) = \frac{s^2 {\mathcal {L}}(u(t))- su(o)-u'(0)}{s+ \alpha (1-s)},\\{} & {} m =1. \end{aligned}$$

3 General description of homotopy perturbation transform method via Caputo–Fabrizio type operator

This section presents a powerful scheme called the homotopy perturbation transform method [15]. We look at the following equation of nonlinear partial differential equation along with the Caputo–Fabrizio derivative:

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0\;D^{m+\alpha }_t u(x,t) + \beta u(x,t) + \varphi u(x,t)\nonumber \\{} & {} = k(x,t),\quad n-1< \alpha +m \le n, \end{aligned}$$
(6)

such that

$$\begin{aligned} \frac{\partial ^l u(x,0)}{\partial t^l} = f_l(x), \quad l= 0,1,2, \ldots , n-1. \end{aligned}$$
(7)

Now, by applying the LT on eq. (6) and eq. (7), we get

$$\begin{aligned}{} & {} {\mathcal {L}}[u(x,t)]= \Theta (x,s) \nonumber \\{} & {} - \left( \frac{s+ \alpha (1- s)}{s^{n+1}} \right) {\mathcal {L}} [\beta u(x,t) + \varphi u(x,t)], \end{aligned}$$
(8)

where

$$\begin{aligned}{} & {} \Theta (x,s) = \frac{1}{s^{m+1}}[s^m f_0(x)+ s^{m-1}f_1(x)\nonumber \\{} & {} + \cdots + f_m(x)]+ \frac{s+ \alpha (1-s)}{s^{n+1}} {\tilde{k}}(x,s). \end{aligned}$$
(9)

Taking the inverse Laplace transformation (eq. (8)), we have

$$\begin{aligned}{} & {} u(x,t)= \Theta (x,s) - {\mathcal {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{n+1}} \right) \right. \nonumber \\{} & {} \quad \left. {\mathcal {L}}[\beta u(x,t) + \varphi u(x,t)] \right] , \end{aligned}$$
(10)

where \(\Theta (x,s)\) is the term that arises from the source term, and it specifies the initial conditions. The solution u(x, t) can be extended into an infinite sequence using the regular homotopy perturbation method as follows:

$$\begin{aligned} u(x,t) = \sum _{n=0}^{\infty } p^n u_n(x,t). \end{aligned}$$
(11)

where \(u_m(x,t)\) are known functions and is given by

$$\begin{aligned} \varphi u(x,t) = \sum _{n=0}^{\infty } p^n H_n(x,t). \end{aligned}$$
(12)

The polynomial \(H_n(x,t)\) are defined as [8, 9]

$$\begin{aligned} H_m(u_0, u_1, u_2, \ldots ,u_n)= & {} \frac{1}{n!}\frac{\partial ^m}{\partial p^m}\left[ \left( \sum _{m=0}^{\infty } p^i u_i \right) \right] _{p=0}, \nonumber \\ m= & {} 0,1,2, \ldots . \end{aligned}$$
(13)

Substituting eq. (11) and eq. (12) into eq. (10), we get

$$\begin{aligned} \sum _{m=0}^{\infty } u_m(x,t){} & {} = \Theta (x,s) - p {\mathcal {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \right. \nonumber \\{} & {} \quad \left. {\mathcal {L}} \left[ \!\beta \sum _{m=0}^{\infty }p^m u_m(x,t) + \sum _{n=0}^{\infty }p^m H_m \!\right] \!\right] . \nonumber \\ \end{aligned}$$
(14)

Comparing the coefficients of \(p^0\), \(p^1\), \(p^2\), \(p^3\) and \(p^4\), we get

$$\begin{aligned}{} & {} p^0 : u_0(x,t) = \Theta (x,s),\\{} & {} p^1 : u_1(x,t) \\{} & {} \quad = - {\mathcal {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathcal {L}} [\beta u_0(x,t) + H_0 (u) ] \right] , \\{} & {} p^2 : u_2(x,t) \\{} & {} \quad = -{\mathcal {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathcal {L}} [\beta u_1(x,t) + H_1 (u) ] \right] ,\\{} & {} p^3 : u_3(x,t) \\{} & {} \quad = -{\mathcal {L}}^{-1} \left[ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) {\mathcal {L}} [\beta u_2(x,t) + H_2 (u) ] \right] ,\\ \vdots \\{} & {} p^{m+1} : u_{m+1}(x,t)= -{\mathcal {L}}^{-1} \Bigg [ \left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \\{} & {} \quad {\mathcal {L}}[\beta u_{m+1}(x,t) + H_{m+1} (u) ] \Bigg ]. \end{aligned}$$

With the help of HPTM, the series solutions are

$$\begin{aligned} u(x,t) = \sum _{m=0}^{\infty } u_m(x,t). \end{aligned}$$
(15)

This approach avoids linearization and weak nonlinearity assumptions, and the solution is created in the form of a general solution, making it more practical than the method of simplifying physical problems.

4 Semi-analytical experiments

In this section, we will solve various types of Emden–Fowler equations using the homotopy perturbation transform method (see [46]).

Example 1

Contemplate the Emden–Fowler equation

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0\;D_t^\alpha \;u(x,t)= \frac{\partial ^2 u}{\partial x^2}+ \frac{5}{x}\frac{\partial u}{\partial x}\nonumber \\{} & {} \quad - (12t^2-2tx^2 + 4t^4x^2)u(x,t), \end{aligned}$$
(16)

with the IC

$$\begin{aligned} u(x,0)= 1. \end{aligned}$$
(17)

Using the Laplace transformation on both sides of equations(16) and (17), we get

$$\begin{aligned}{} & {} L [u(x,t)]= \frac{1}{s} + \left( \frac{s+ \alpha (1-s)}{s} \right) \nonumber \\{} & {} \quad {\mathcal {L}}\left[ \frac{\partial ^2 u}{\partial x^2}+\frac{5}{x}\frac{\partial u}{\partial x}- (12t^2-2tx^2 + 4t^4x^2)u(x,t) \right] .\nonumber \\ \end{aligned}$$
(18)

Applying the inverse of the LT to eq.(18), we get

$$\begin{aligned}{} & {} u(x,t)= 1 + {\mathcal {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \nonumber \\{} & {} \left. {\mathcal {L}}\left[ \frac{\partial ^2 u}{\partial x^2} + \frac{5}{x}\frac{\partial u}{\partial x}- (12t^2-2tx^2 + 4t^4x^2)u(x,t) \right] \right] . \nonumber \\ \end{aligned}$$
(19)

Now, applying the HPTM, we get

$$\begin{aligned} \begin{aligned}&\sum _{m=0}^{\infty } u_m = + p{\mathcal {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \\&\quad \left. {\mathcal {L}}\left[ \sum _{m=0}^{\infty }p^m u_m+ \frac{5}{x} \sum _{m=0}^{\infty }p^m u_m\right. \right. \\&\quad \left. \left. - (12t^2-2tx^2 + 4t^4x^2) \sum _{m=0}^{\infty }p^m u_m \right] \right] . \end{aligned} \end{aligned}$$
(20)

Using the above conditions, we get

$$\begin{aligned}&p^0 : u_0(x,t)= 1,\\&p^1 : u_1(x,t)= -\frac{4}{3} t^3 (3 \alpha +x^2 \alpha )\\&\quad -2 t (-x^4+x^4 \alpha )\\&\quad +t^2 (-12-4 x^2+12 \alpha +4 x^2 \alpha +x^4\alpha ),\\&p^2: u_2(x,t) = \frac{8}{9} t^6 (9 \alpha ^2+6 x^2 \alpha ^2+x^4 \alpha ^2)\\&\quad +2 t (32 x^2+x^4-64 x^2 \alpha -2 x^4 \alpha \\&\quad +32 x^2 \alpha ^2+x^4 \alpha ^2)\\&\quad - 2 t^2 (30+2 x^2-60 \alpha -36 x^2 \alpha -x^4 \alpha \\&\quad +30 \alpha ^2+34 x^2 \alpha ^2+x^4 \alpha ^2)\\&\quad + \frac{1}{3} t^3 (-108 \alpha -4 x^2 \alpha +108 \alpha ^2\\&\quad +36 x^2 \alpha ^2+x^4 \alpha ^2)\\&\quad -\frac{8}{15} t^5 (-90 \alpha -60 x^2 \alpha -10 x^4 \alpha \\&\quad +90 \alpha ^2+60 x^2 \alpha ^2+13 x^4 \alpha ^2+x^6 \alpha ^2)\\&\quad + \frac{4}{3} t^4 (-6 x^4 \alpha -2 x^6 \alpha -3 \alpha ^{2}\\&\quad +6 x^4 \alpha ^2+2 x^6 \alpha ^2), \end{aligned}$$
$$\begin{aligned}&p^3: u_3(x,t) = -2 t (-384-64 x^2-x^4\\&\quad +1152 \alpha +192 x^2 \alpha +3 x^4 \alpha -1152 \alpha ^2\\&\quad -192 x^2 \alpha ^2-3 x^4 \alpha ^2+384 \alpha ^3+ \cdots )\\&\quad + t^2 (-108-4 x^2+1476 \alpha +204 x^2 \alpha +3 x^4 \alpha \\&\quad -2628 \alpha ^2-396 x^2 \alpha ^2-6 x^4 \alpha ^2\\&\quad +1260 \alpha ^3+196 x^2 \alpha ^3+ \cdots )\\&\quad -\frac{1}{3} t^3 (264 \alpha +8 x^2 \alpha -1680 \alpha ^2-208 x^2 \alpha ^2\\&\quad -3 x^4 \alpha ^2+1416 \alpha ^3+200 x^2 \alpha ^3+3 x^4 \alpha ^3)\\&\quad +\frac{32}{81} t^9 (27 \alpha ^3+27 x^2 \alpha ^3+9 x^4 \alpha ^3+x^6 \alpha ^3)\\&\quad -\frac{4}{45} t^6 (-1530 \alpha ^2-700 x^2 \alpha ^2-10 x^4 \alpha ^2\\&\quad +1530 \alpha ^3+796 x^2 \alpha ^3+73 x^4 \alpha ^3+x^6 \alpha ^3)\\&\quad + \frac{4}{15} t^5 (1620 \alpha +760 x^2 \alpha +20 x^4 \alpha -3240 \alpha ^2\\&\quad -1904 x^2 \alpha ^2-292 x^4 \alpha ^2-4 x^6 \alpha ^2+ 1617 \alpha ^3+ \cdots )\\&\quad -\frac{1}{12} t^4 (3072 x^2 \alpha +2016 x^4 \alpha +32 x^6 \alpha \\&\quad +204 \alpha ^2-6140 x^2 \alpha ^2{-}4032 x^4 \alpha ^2-64 x^6 \alpha ^2{-}\cdots )\\&\quad - \frac{2}{9} t^8 (-432 \alpha ^2-432 x^2 \alpha ^2-144 x^4 \alpha ^2\\&\quad -16 x^6 \alpha ^2+432 \alpha ^3+432 x^2 \alpha ^3+153 x^4 \alpha ^3+ \cdots )\\&\quad + \frac{16}{63} t^7 (-63 x^4 \alpha ^2-42 x^6 \alpha ^2-7 x^8 \alpha ^2\\&\quad +36 \alpha ^3+16 x^2 \alpha ^3+63 x^4 \alpha ^3+42 x^6 \alpha ^3+7x^8 \alpha ^3)\\ \vdots \end{aligned}$$

Hence the series solution is given by

$$\begin{aligned} u(x,t) = \sum _{m=0}^{\infty } u_m(x,t)= u_0+ u_1+ u_2+ u_3+\cdots . \nonumber \\ \end{aligned}$$
(21)

Therefore, it converges to exact solution of the integer-order EFEs as \(u(x,t)= e^{x^2 t^2}\).

Example 2

Contemplate the Emden–Fowler equation

$$\begin{aligned}{} & {} {}^{\textrm{CF}}_0\;D_t^\alpha \;u(x,t)= \frac{\partial ^2 u}{\partial x^2}+ \frac{2}{x}\frac{\partial u}{\partial x}\nonumber \\{} & {} \quad - (5+4x^2)u(x,t)-(6-5x^2-4x^4), \end{aligned}$$
(22)

with the IC

$$\begin{aligned} u(x,0)= x^2 + e^{x^2}. \end{aligned}$$
(23)

Using the Laplace transformation on both sides of equations (22) and (23), we get

$$\begin{aligned}{} & {} {\mathcal {L}}[u(x,t)]= \frac{1}{s}(x^2 + e^{x^2})-\left( \frac{s+ \alpha (1-s)}{s} \right) \nonumber \\{} & {} \quad {\mathcal {L}}(6+5x^2-4x^2) + \left( \frac{s + \alpha (1-s)}{s} \right) \nonumber \\{} & {} \qquad {\mathcal {L}}\left[ \!\frac{\partial ^2 u}{\partial x^2}+ \frac{2}{x}\frac{\partial u}{\partial x}- (5+4x^2)u\! \right] . \end{aligned}$$
(24)

Applying the inverse of the LT to eq. (24), we get

$$\begin{aligned}{} & {} u(x,t)= x^2 + e^{x^2}\nonumber \\{} & {} \quad +(-6+5 x^2-4 x^2)(1-\alpha + \alpha t) + {\mathcal {L}}^{-1}\nonumber \\{} & {} \quad \left[ \left( \frac{s+ \alpha (1-s)}{s} \right) {\mathcal {L}}\left[ \frac{\partial ^2 u}{\partial x^2}+ \frac{2}{x}\frac{\partial u}{\partial x}- (5+4x^2)\! \right] \right] .\nonumber \\ \end{aligned}$$
(25)

Applying the HPTM, we get

$$\begin{aligned} \begin{aligned}&\sum _{m=0}^{\infty } u_m= x^2 + e^{x^2}-(6+5x^2-4x^2)(1-\alpha + \alpha t)\\&+ p{\mathcal {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \\&\left. {\mathcal {L}}\left[ \!\sum _{m=0}^{\infty }p^m u_m{+}\frac{2}{x} \sum _{m=0}^{\infty }\!p^m u_m{-}(5{+}4x^2)\sum _{m=0}^{\infty }p^m u_m\! \right] \right] , \end{aligned} \nonumber \\ \end{aligned}$$
(26)

Using the above conditions, we get

$$\begin{aligned}&p^0 : u_0(x,t)~=~~ x^2+ e^{x^2}\\&+ (-6+5 x^2-4 x^4) (1-\alpha +t \alpha ),\\&p^1 : u_1(x,t)~=~~ 30+7 e^{x^2}-80 x^2+4 e^{x^2} x^2\\&-8 x^4-54 \alpha -7 e^{x^2} \alpha +54 t \alpha +7 e^{x^2} t \alpha \\&+155 x^2 \alpha -4 e^{x^2} x^2 \alpha \\&-155 t x^2 \alpha +4 e^{x^2} t x^2 \alpha +12 x^4 \alpha \\&-12 t x^4 \alpha +24 \alpha ^2-48 t \alpha ^2+12 t^2 \alpha ^2\\&- 75 x^2 \alpha ^2+150 t x^2 \alpha ^2-\frac{75}{2} t^2 x^2 \alpha ^2\\&-4 x^4 \alpha ^2+8 t x^4 \alpha ^2-2 t^2 x^4 \alpha ^2\\&p^2 : u_2(x,t)~=~~ \frac{1}{2} t^2 \alpha ^2 \\&(-1302+73 e^{x^2}-550 x^2+88 e^{x^2} x^2-16 x^4\\&+16 e^{x^2} x^4+1278 \alpha +465 x^2 \alpha +12 x^4 \alpha )\\&+ (-1+\alpha ) (630-73 e^{x^2}+360 x^2\\&-88 e^{x^2} x^2+8 x^4-16 e^{x^2} x^4-876 \alpha \\&+73 e^{x^2} \alpha -395 x^2 \alpha \ldots ),\\&-t \alpha (1506-146 e^{x^2}+755 x^2-176 e^{x^2} x^2\\&+20 x^4-32 e^{x^2} x^4-2604 \alpha +146 e^{x^2} \alpha \\&-1100 x^2 \alpha \ldots )\\&+ \frac{1}{6} t^3 (-426 \alpha ^3\\&-155 x^2 \alpha ^3-4 x^4 \alpha ^3), \end{aligned}$$
$$\begin{aligned}&p^3: u_3(x,t) = -2790+1039 e^{x^2}\\&-520 x^2+1932 e^{x^2} x^2-8 x^4+720 e^{x^2} x^4+64 e^{x^2} x^6\\&+8826 \alpha -3117 e^{x^2} \alpha + \cdots \\&-\frac{1}{6}t^3 \alpha ^3 (-1854-601e^{x^2}\\&-7403 x^2-1112 e^{x^2} x^2-2276 x^4-272 e^{x^2} x^4\\&-64 x^6+2244 \alpha + \cdots )\\&+ t (-1+\alpha ) \alpha (8826-3117 e^{x^2}\\&+1675 x^2-5796 e^{x^2} x^2+28 x^4-2160 e^{x^2} x^4\\&-192 e^{x^2} x^6- \cdots )\\&+ \frac{1}{2} t^2 \alpha ^2 (-2826+2679 e^{x^2}\\&+6483 x^2+4976 e^{x^2} x^2+2260 x^4+1712 e^{x^2} x^4\\&+64 x^6+128 e^{x^2} x^6+ \cdots )\\&+ \frac{1}{24}t^4 (-1356 \alpha ^4 -235 x^2 \alpha ^4-4 x^4 \alpha ^4). \end{aligned}$$

Hence the series solution is given by

$$\begin{aligned} u(x,t) = \sum _{m=0}^{\infty } u_m(x,t)= u_0+ u_1+ u_2+ u_3+\cdots .\nonumber \\ \end{aligned}$$
(27)

Therefore, it converges to exact solution of the integer-order EFEs as \(u(x,t)= e^{t+x^2}+x^2\).

Example 3

Contemplate the Emden–Fowler equation

$$\begin{aligned}{} & {} {}^{\textrm{CF}}_0\;D_t^\alpha \;u(x,t)= \frac{\partial ^2 u}{\partial x^2}+ \frac{4}{x}\frac{\partial u}{\partial x}\nonumber \\{} & {} \quad - (18x+9x^4)u(x,t)+2+(18x+9x^4)t^2, \end{aligned}$$
(28)

with the IC

$$\begin{aligned} u(x,0)= e^{x^3}. \end{aligned}$$
(29)

Using the Laplace transformation on both sides of equations (28) and (29), we get

$$\begin{aligned}{} & {} {\mathcal {L}}[u(x,t)]= \frac{1}{s}e^{x^3}\nonumber \\{} & {} \quad +\left( \frac{s+ \alpha (1-s)}{s} \right) {\mathcal {L}}(18x+9x^4)t^2 \nonumber \\{} & {} \quad + \left( \frac{s + \alpha (1-s)}{s} \right) \nonumber \\{} & {} \quad {\mathcal {L}}\left[ \frac{\partial ^2 u}{\partial x^2}+ \frac{4}{x}\frac{\partial u}{\partial x}- (18x+9x^4)u \right] . \end{aligned}$$
(30)

Applying the inverse of the LT to eq. (30), we get

$$\begin{aligned} \begin{aligned} u(x,t)&= e^{x^3}+\text { }2+18 t^2 x+9 t^2 x^4-2 \alpha +2 t \alpha \\&\quad -18 t^2 x \alpha +6 t^3 x \alpha -9 t^2 x^4 \alpha +3 t^3 x^4\\&\quad + {\mathcal {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \\&\left. \qquad {\mathcal {L}}\left[ \frac{\partial ^2 u}{\partial x^2}+ \frac{4}{x}\frac{\partial u}{\partial x}- (18x+9x^4) \right] \right] . \end{aligned} \end{aligned}$$
(31)
Fig. 1
figure 1

Comparison of our approximate solution u(x, t) for different values of \(\alpha = 1.25\), \(\alpha = 1.50\), \(\alpha = 1.75\) and \(\alpha =2\) for Example 4.1.

Full size image
Fig. 2
figure 2

Surface show the 3D wave function u(x, t) at (a) \(\alpha = 1.25\), (b) \(\alpha = 1.50\), (c) \(\alpha = 1.75\) and (d) \(\alpha = 2\).

Full size image

Now applying the HPTM, we get

$$\begin{aligned}{} & {} \sum _{m=0}^{\infty } u_m= e^{x^3}+\text { }2+18 t^2 x+9 t^2 x^4-2 \alpha +2 t \alpha \nonumber \\{} & {} \quad -18 t^2 x \alpha +6 t^3 x \alpha -9 t^2 x^4 \alpha +3 t^3 x^4 \nonumber \\{} & {} + p{\mathcal {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s}\right) {\mathcal {L}}\left[ \sum _{m=0}^{\infty }p^m u_m\right. \right. \nonumber \\{} & {} \left. \left. \quad + \frac{4}{x}\sum _{m=0}^{\infty }p^m u_m- (18x+9x^4)\sum _{m=0}^{\infty }p^m u_m \right] \right] . \end{aligned}$$
(32)
Fig. 3
figure 3

Comparison of approximate solution u(x, t) for different values of \(\alpha = 1.25\), \(\alpha = 1.50\), \(\alpha = 1.75\) and \(\alpha =2\) for Example 4.2.

Full size image
Fig. 4
figure 4

Surface show the 3D wave function u(x, t) at (a) \(\alpha = 1.25\), (b) \(\alpha = 1.50\), (c) \(\alpha = 1.75\) and (d) \(\alpha = 2\).

Full size image

Using the above conditions, we get

$$\begin{aligned}&p^0 : u_0(x,t)~=~~ e^{x^3}+\text { }2+18 t^2 x+9 t^2 x^4\\&\quad -2 \alpha +2 t \alpha -18 t^2 x \alpha +6 t^3 x \alpha -9 t^2 x^4 \alpha +3 t^3 x^4\\&p^1 : u_1(x,t)~=~ 2+\frac{72 t^2}{x}+18 t^2 x\\&\quad +252 t^2 x^2+9 t^2 x^4-4 \alpha +4 t \alpha -\frac{144 t^2 \alpha }{x}\\&\quad +\frac{48 t^3 \alpha }{x}-36 t^2 x \alpha +12 t^3 x \alpha \\&\quad -504 t^2 x^2 \alpha +168 t^3 x^2 \alpha -18 t^2 x^4 \alpha \\&\quad +6 t^3 x^4 \alpha +2 \alpha ^2-4 t \alpha ^2+ t^2 \alpha ^2\\&\quad +\frac{72 t^2 \alpha ^2}{x}-\frac{48 t^3 \alpha ^2}{x} +\frac{6 t^4 \alpha ^2}{x} +18 t^2 x \alpha ^2 \end{aligned}$$
Fig. 5
figure 5

Comparison of approximate solution u(x, t) for different values of \(\alpha {=} 1.25\), \(\alpha {=} 1.50\), \(\alpha {=} 1.75\) and \(\alpha {=}2\) for Example 4.2.

Full size image
Fig. 6
figure 6

Surface show the 3D wave function u(x, t) at (a) \(\alpha = 1.25\), (b) \(\alpha = 1.50\), (c) \(\alpha = 1.75\) and (d) \(\alpha = 2\).

Full size image
$$\begin{aligned}&\quad -12 t^3 x \alpha ^2+\frac{3}{2}t^4 x \alpha ^2 +252 t^2 x^2 \alpha ^2-168 t^3 x^2 \alpha ^2\\&\quad +21 t^4 x^2 \alpha ^2+9 t^2 x^4 \alpha ^2 -6 t^3 x^4 \alpha ^2+ \alpha ^2\\&\ldots p^2 : u_2(x,t)~=~~ -2 t \\&\quad \left( -2 \alpha +18 x \alpha +9 x^4 \alpha +6 \alpha ^2-3 \alpha ^3\right) +2\\&\quad ({-}18 x{-}9 x^4{-}2 \alpha {+}18 x \alpha {+}9 x^4 \alpha {+}3 \alpha ^2- \cdots )\\&\quad +\frac{\begin{array}{c}3 t^5 (-16 \alpha ^3+16 x^2 \alpha ^3+280 x^3 \alpha ^3\\ +2 x^4 \alpha ^3+56 x^5 \alpha ^3+x^7 \alpha ^3)\end{array}}{20x^3} \end{aligned}$$
$$\begin{aligned}&\quad -\frac{\begin{array}{c}9 t^4 (16 \alpha ^2-16 x^2 \alpha ^2-280 x^3 \alpha ^2-2 x^4 \alpha ^2\\ -56 x^5 \alpha ^2 -x^7 \alpha ^2-16 \alpha ^3+16 x^2 \alpha ^3 \cdots )\end{array}}{4 x^3}\\&\quad - \frac{1}{x^3}3 t^2 \\&\quad (48-48 x^2-840 x^3-6 x^4-168 x^5-3 x^7-144 \alpha \\&\quad +144 x^2 \alpha +2520 x^3 \alpha +18 x^4 \alpha + \cdots )\\&\quad \frac{1}{3 x^3}t^3 \left( -432 \alpha +432 x^2 \alpha \right. \\&\quad \left. +7560 x^3 \alpha +54 x^4 \alpha +1512 x^5 \alpha +27 x^7 \alpha \right. \\&\quad \left. +864 \alpha ^2-864 x^2\alpha ^2- \cdots \right) .\\&\vdots \end{aligned}$$

Hence series solution is given by

$$\begin{aligned} u(x,t) = \sum _{m=0}^{\infty } u_m(x,t)= u_0+ u_1+ u_2+ u_3+ \cdots \nonumber \\ \end{aligned}$$
(33)

Therefore, it converges to the exact solution \(u(x,t)= e^{x^3} +t^2\) of the integer-order EFEs.

5 Results and discussion

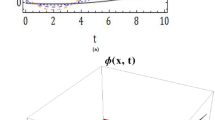
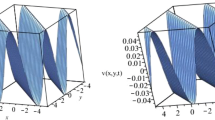
In this section, we show the 2-dimensional and 3-dimensional graphs for some of the reported solutions with a suitable parameter choice. Figure 1 shows the comparison of approximate solution for eq. (16) attained by HPTM versus t for different values of \(\alpha \). Figure 2(a)–(d) shows the profile of the third-order approximation solution for 3D wave function for second-order fractional nonlinear EFEs for \(-1\le x \le 1\) and \(0\le t \le 1\) at \(\alpha = 1.25\), 1.50, 1.75 and \(\alpha = 2\), for eq.(16) by the application of initial condition represented by eq.(17) of u(x, t). Figure 2 depicts the solitary wave nature of the approximate solution produced by HPTM for the second-order fractional nonlinear EFEs. Figure 3 shows the comparison of approximate solution for eq. (22) attained by HPTM versus t for different values of \(\alpha \). Figures 3(a)–(d) shows the profile of the third-order approximation solution for 3D wave function for second-order fractional nonlinear EFEs for \(-1\le x \le 1\) and \(0\le t \le 1\) at \(\alpha = 1.25\), 1.50, 1.75 and \(\alpha = 2\) for eq. (22) by the application of initial condition represented by eq. (23) of u(x, t). Figure 3 depicts the solitary wave nature of the approximate solution produced by HPTM for the second order fractional nonlinear EFEs. Figure 4 shows the comparison of approximate solution for eq. (28) attained by HPTM versus t for different values of \(\alpha \). Figure 4(a)–(d) shows the profile of the third-order approximation solution for 3D wave function for second-order fractional nonlinear EFEs for \(-1\le x \le 1\) and \(0\le t \le 1\) at \(\alpha = 1.25\), 1.50, 1.75 and \(\alpha = 2\), for eq. (28) by the application of initial condition represented by eq. (29) of u(x, t). Figure 4 depicts the solitary wave nature of the approximate solutions produced by HPTM for the second-order fractional nonlinear EFEs.

6 Conclusion

In this present work, the homotopy perturbation transform method has been used to obtain semi-analytical solutions to the nonlinear time fractional nonlinear EFEs with great precision and accuracy. The collected findings reveal that up to third-order approximation the accuracy is very high. By setting \(1< \alpha \le 2\), we can discover the classical solution to these model. The results show that the HPTM is a very effective and powerful approach for studying various quantum nonlinear model. This approach can also be used to investigate more complex phenomena in science and engineering. This technique is also ideal for studying higher-order nonlinear model, which can be found in a wide range of physical sciences fields. To demonstrate the relevance and efficacy of the considered strategy, we looked at three different examples of the projected model. The secure outputs show that a basic HPTM algorithm was used to generate standardized semi-analytical solutions. The suggested approach is unique in that it provides a simple solution, a critical convergence zone, and a non-local influence. Finally, the proposed scheme can be used to examine the behavior of nonlinear systems that exist in quantum mechanics as a novel tool over previous available analytical techniques.