1 Introduction

In 1971, Chua postulated the concept of memristor, which is characterised by the relationship between the flux and the charge [1]. A memristor is a nonlinear resistor with memory, whose resistances are dependent on the state and history of the memristor. Ever since the \(\hbox {TiO}_{2}\) memristor was reported in 2008 by the HP Labs [2], there has been a torrent of memristor researches from both industry and academia to uncover the characteristics of the memristor for building new generation of computers, brain-like machines and nonlinear circuits [3,4,5].

It has been proved that a fractional-order model of an actual circuit element is more consistent with the characteristics of the element. The main advantages of a fractional-order model of a circuit element are its long-memory dependency and the ability to increase the degree of freedom for the model through the fractional-order parameters [6]. So the fractional-order models are more suitable for describing the devices with historical memory such as memristors [7]. Therefore, fractional-order calculus-based memristor modelling has attracted great attention from academia.

In 2012, Petrás̆ and Chen [8] introduced the fractional-order models of memristor, memcapacitor and meminductor. Then a fractional-order memristor model was constructed in ref. [9], and the relation of the excitation voltage, the fractional-order memristance and the fractional order was discussed in detail. Based on [8], Fouda and Radwan [10] further studied the responses of the fractional-order memristor under the DC and periodic signals. Based on the memory fading of titanium dioxide memristors, Yu and Wang [7] studied the series and parallel circuits of the fractional-order memristors and capacitors or inductors, and indicated that fractional-order state equations are the most effective method to describe the state between memory-less and ideal memory. Furthermore, Hamed et al [11] and Elsafty et al [12] used a fractional-order capacitor to design fractional-order memristor emulators, and analysed the pinched hysteresis behaviour and double pinch-off points of the fractional-order memristor emulators. Very recently, a non-volatile fractional-order memristor model is proposed in ref. [13]. Chaotic behaviour has been found in many fractional-order systems [14,15,16], and the engineering applications of the fractional-order chaotic systems have also been developed [17, 18].

In recent years, researchers have tried to use fractional-order memristors to construct chaotic circuits, and proposed some different fractional-order memristor-based chaotic systems, such as the simplest fractional-order memristor-based chaotic systems [19], fractional-order memristor-based Chua’s circuits [20], fractional-order memristive circuits [3], fractional-order generalised memristor-based chaotic systems [21] and active non-volatile fractional-order memristor-based Chua’s circuits by using fractional-order memristors, capacitors and inductors [13].

Chua found that local activity is the origin of complexity [22], and proposed the concept of locally active memristor, which is defined to be any memristor showing a negative differential resistance (NDR) in its DC V–I plot [23]. Locally active memristors are necessary conditions of oscillating systems [24], and can amplify infinitesimal fluctuations in energy for generating and maintaining complex oscillations. Fortunately, Williams et al manufactured actual locally active memristors, which can exhibit both temperature- and current-controlled NDRs and can be applied to chaotic neural networks as an essential device for both chaotic oscillation module and synapses of the neural networks [25, 26].

It has been found that locally active memristors have important applications in complex systems, neural networks and so on. However, fractional-order modelling of locally active memristors has not been found. Therefore, this paper introduces a fractional-order voltage-controlled locally active memristor model, from which many complex dynamics such as non-volatility, chaos and coexisting attractors are found [27].

2 Fractional-order memristor modelling

The voltage-controlled generic memristor is defined as

$$\begin{aligned} \left\{ \begin{array}{l} i\left( t \right) = G\left( x \right) v\left( t \right) ,\\ \dot{x} = f\left( x \right) v, \end{array} \right. \end{aligned}$$
(1)

where v(t), i(t) and x are the voltage, current and the state variable of the memristor, respectively.

A fractional-order voltage-controlled memristor can be defined as

$$\begin{aligned} \left\{ \begin{array}{l} i\left( t \right) = G\left( x \right) v\left( t \right) ,\\ \displaystyle {}_0D_t^\alpha x\left( t \right) = f\left( x \right) v, \end{array} \right. \end{aligned}$$
(2)

where \(_{0}D^{\alpha }_{t}\) is the fractional-order arithmetic operator, \(\alpha \) is the order of fractional calculus and 0 and t represent integral range. The fractional-order arithmetic operator is defined as

$$\begin{aligned} {}_0D_t^\alpha = f\left( {v\left( t \right) } \right) = \left\{ \begin{array}{lllll} \displaystyle \frac{{{\mathrm{d}^\alpha }}}{{\mathrm{d}{t^\alpha }}},&{}\quad \alpha > 0,\\ 1, &{}\quad \alpha = 0,\\ \int _0^t {{\left( {\mathrm{d}\tau } \right) }^{ - \alpha }}, &{}\quad \alpha < 0 \end{array} \right. \end{aligned}$$
(3)

According to the theory of fractional-order arithmetic theory, the initial conditions expressed in terms of both Riemann–Liouville and Caputo fractional-order derivative have physical significances [28,29,30]. However, we focus on using the derivative of Caputo to describe the state equation of a fractional-order memristor, because the initial condition of fractional-order differential equation with Caputo derivative is the same as that of the integer differential equation [31]. The mathematical description of a fractional-order memristor is

$$\begin{aligned} {}_0^CD_t^\alpha x\left( t \right) = \frac{1}{{\Gamma \left( {q - \alpha }\right) }} \int _0^t {\frac{{{x^{\left( q \right) }}\left( \tau \right) }}{{{{\left( {t-\tau } \right) }^{\left( {1 + \alpha - q} \right) }}}}\mathrm{d}\tau } , \end{aligned}$$
(4)

where \(\Gamma ( \cdot )\) is a gamma function and \(q>\alpha \) and \(q\in N\) (integer).

Here, we proposed a new fractional-order voltage-controlled locally active memristor model based on the Caputo derivative:

$$\begin{aligned} \left\{ \begin{array}{l} i\left( t \right) = W\left( {x\left( t \right) } \right) v\left( t \right) = ( {x{{\left( t \right) }^2} - x\left( t \right) + m}) v\left( t \right) ,\\ \displaystyle {}_0^CD_t^\alpha x\left( t \right) = v\left( t \right) \left( {\alpha > 0} \right) , \end{array} \right. \end{aligned}$$
(5)

where m can be considered as the parasitic conductance or internal conductance of the fractional-order memristor. Under the \(v(t) =\sin (\omega t)\) excitation, the pinched hysteresis curve and the memductance vs. state x of the memristor are shown in figure 1. Observe that the memristor exhibits negative resistance over the range of \(-0.1< x < 1.15\), thereby showing local activity.

Fig. 1
figure 1

Characteristics of the fractional-order voltage-controlled locally active memristor model: (a) v–i pinched hysteresis curve under the excitation signal with the amplitude \(A = 1\ \hbox {V}\) and different frequencies \(\omega = 10\), 50 and \(300\ \hbox {rad}/\hbox {s}\) and (b) memductance vs. the state variable x, where x \(\in \) [\(-1, 2\)].

Full size image

Under the definition of the derivative of Caputo [7], \({}_0^CD_t^{1 - \alpha }({}_0^CD_t^\alpha x\left( t)\right) =\dot{x}\left( t\right) \). So \(\dot{x}\left( t\right) ={}_0^CD_t^{1-\alpha } v\left( t \right) \). We take the driving voltage as

$$\begin{aligned} {v\left( t \right) = A\sin \left( {\omega t} \right) ,} \end{aligned}$$
(6)

where A is the excitation amplitude and \(\omega \) is the excitation frequency. So we have

$$\begin{aligned} \dot{x}\left( t \right) = A{}_0^CD_t^{1 - \alpha }\sin \left( {\omega t} \right) . \end{aligned}$$
(7)

According to Euler’s formula and the principle of short time memory, eq. (7) can be simplified as

$$\begin{aligned} \dot{x}\left( t \right) \approx A{\omega ^{1 - \alpha }} \sin \left( {\omega t + \frac{{1 - \alpha }}{2}\pi } \right) . \end{aligned}$$
(8)

And we can integrate both sides of eq. (8):

$$\begin{aligned} x\left( t \right)&= x\left( 0 \right) + \frac{A}{{{\omega ^\alpha }}}\nonumber \\&\quad \times \left[ {\cos \left( {\frac{{1 - \alpha }}{2}\pi } \right) -\cos \left( {\omega t + \frac{{1 - \alpha }}{2}\pi } \right) } \right] . \end{aligned}$$
(9)

According to ref. [32], the area of hysteresis lobe can reflect the memory capacity of the memristor. The larger the lobe area, the stronger is the memristor memory. The formula for calculating the lobe area is given as [33]

$$\begin{aligned} S1 = \oint _{A1} {i\left( t \right) \mathrm{d}v\left( t \right) } , \end{aligned}$$
(10)

where S1 represents the area enclosed by the hysteresis loop in the fourth quadrant, as shown in figure 2.

Fig. 2
figure 2

Lobe area of the pinched hysteresis curve in the fourth quadrant when the excitation signal \(v\left( t \right) = A\sin \left( {\omega t} \right) \).

Full size image

According to eqs (5) and (6), eq. (10) can be simplified as

$$\begin{aligned} S1= & {} \int _0^{{\pi }/{\omega }} ( {{x^2} - x - 0.14} ) \cdot A \cdot \sin \left( {\omega t} \right) \mathrm{d}A \nonumber \\&\cdot \sin \left( {\omega t} \right) . \end{aligned}$$
(11)

Let \(x(0) = 0\), and then substituting eq. (9) into eq. (11) we get

$$\begin{aligned} S1&= \oint _{A1} {i\left( t \right) \mathrm{d}v\left( t \right) } \nonumber \\&= \int _0^{{\pi }/{\omega }} {( {{x^2} - x - 0.14} ) \cdot A \cdot \sin \left( {\omega t} \right) \mathrm{d}A \cdot } \sin \left( {\omega t} \right) \nonumber \\&=\displaystyle \frac{A^2\omega }{2}\left( -\frac{A^2}{\omega ^{2\alpha }} \frac{3\pi \sin \left( {\alpha \pi } \right) +32\sin {{\left( {\frac{{\alpha \pi }}{2}} \right) }^2}}{12\omega }\right. \nonumber \\&\qquad \qquad \qquad \quad \left. +\frac{A}{\omega ^\alpha } \frac{4\sin \left( \frac{\alpha \pi }{2}\right) }{3\omega }\right) . \end{aligned}$$
(12)

When \(A=1\), the calculated lobe areas are listed in table 1, where only the case \(\alpha > 0.5\) is discussed, since the hysteretic curve in the second quadrant will shift to the third quadrant when the order is less than 0.5.

Table 1 The relationship between orders and lobe areas.
Full size table

It is found from table 1 that when the order \(\alpha \) gradually decreases from 1 to 0.5, the area S1 first increases and then decreases, indicating that the memristor’s memory gradually became stronger and then weaker, as shown in figure 3.

Fig. 3
figure 3

The lobe areas of pinched hysteresis curves in the fourth quadrant vary with the order \(\alpha \) of the fractional-order memristor: (a) \(\alpha =0.8\), 0.9, 1 and (b) \(\alpha = 0.5\), 0.6, 0.7.

Full size image

When the hysteretic curve is in the second quadrant, as shown in figure 4, the side lobe area of the hysteresis curve is as follows:

$$\begin{aligned} S2&= - \oint _{A2} {i\left( t \right) \mathrm{d}v\left( t \right) } \nonumber \\&= \int _{{\pi }/{\omega }}^{{{2\pi }}/{\omega }} - ( {{x^2} - x - 0.14} )\nonumber \\&\qquad \cdot A \cdot \sin \left( {\omega t} \right) \mathrm{d}A \cdot \sin \left( {\omega t} \right) \nonumber \\&= \displaystyle \frac{{{A^2}w}}{2}\left( { - \frac{{{A^2}}}{{{\omega ^{2\alpha }}}} \frac{{3\pi \sin \left( {\alpha \pi } \right) - 32\sin {{\left( {\frac{{\alpha \pi }}{2}} \right) }^2}}}{{12\omega }}} \right) \nonumber \\&\quad - \displaystyle \frac{{{A^3}w}}{{2{\omega ^\alpha }}} \frac{{4\sin \left( {\frac{{\alpha \pi }}{2}} \right) }}{{3\omega }}. \end{aligned}$$
(13)
Fig. 4
figure 4

Side lobe area of pinched hysteresis curves in the second quadrant under the excitation signal \(v\left( t \right) = A\sin \left( {\omega t} \right) \).

Full size image
Fig. 5
figure 5

Side lobe area of pinched hysteresis curves in the second quadrant with different values of order \(\alpha \) of the fractional-order memristor, where yellow, green, red and blue curves represent \(\alpha =0.5\), 0.6, 0.8 and 1, respectively.

Full size image

When \(\alpha \in [0.5,1]\), the obtained data about the relation between order \(\alpha \) and area S are shown in table 2:

Table 2 The relationship between orders and lobe areas
Full size table

It is shown in table 2 that the area S2 increases as order \(\alpha \) decreases over the range of \(0.5 \le \alpha \le 1\), which indicates that the memristor memory gradually becomes stronger with the decrease of the order \(\alpha \) in the second quadrant.

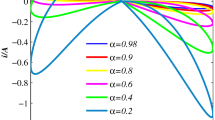
The area S of the whole hysteresis curve of the fractional-order memristor is: \(S = S1 + S2\), which is shown in figure 6.

Fig. 6
figure 6

The area S of pinched hysteresis curves vs. the order \(\alpha \) of the fractional-order memristor over the range of \(\alpha \in [0.5,1]\).

Full size image
Fig. 7
figure 7

DRM diagram of the fractional-order memristor.

Full size image

It follows from figure 6 that the area of the fractional-order pinched hysteresis curve decreases gradually with the increase in the order \(\alpha \in [0.5,1]\) and finally reaches the minimum value at \(\alpha = 1\). This indicates that the memory of fractional-order memristor is stronger than that of the integer-order memristor, and the lower the order of fractional-order memristor is, the better is the memory.

Fig. 8
figure 8

Influence of order (\(\alpha = 0.\)5, 0.6, 0.8, 1) on different characteristics of the fractional-order memristor: (a) pinched hysteresis curves, (b) memristance and (c) the instantaneous power.

Full size image
Fig. 9
figure 9

The schematic of the fractional-order chaotic system.

Full size image
Fig. 10
figure 10

Trajectories of the system attractor: (a) x–y–z space phase diagram, (b) x–y plane phase diagram, (c) x–z plane phase diagram and (d) y–w plane phase diagram.

Full size image

2.1 Non-volatility of the fractional-order memristor

The resistance of the fractional-order memristor is controlled by its voltage and can be memorised when its power is cut off, thereby making the memristor a non-volatile memory.

Here, two tools, the dynamic route map (DRM) and power-off plot (POP) are used to analyse the non-volatile memory of the memristor. DRM is a collection of the dynamic routes on \(\mathrm{d}^\alpha x/\mathrm{d}{t^\alpha }{-}x\) plane, each parametrised by a value of the memristor voltage v. In particular, POP is a special dynamic route with \(v = 0\) (i.e., the power is turned off). It says that if there are two or more stable intersections (equilibria) between POP and x-axis, the memristor exhibits non-volatility. Besides, any point on a dynamic route lying in the upper half plane (resp., lower half plane) must move to the right (resp., left), because \({\mathrm{d}^\alpha }x/\mathrm{d}{t^\alpha }> 0\) (resp., \({\mathrm{d}^\alpha }x/\mathrm{d}{t^\alpha } < 0\)).

Figure 7 shows the DRM of dynamic routes with \(v=\pm 2\ \mathrm{V}\), \(\pm 1\ \hbox {V}\), 0 V, corresponding to yellow, blue and red trajectories, respectively. It can be seen that the POP (red trajectory) and x-axis overlap with each other, indicating that the memristor has infinite number of stable equilibria and therefore is non-volatile.

Fig. 11
figure 11

Distribution of characteristic roots at the equilibrium point (0, 0, 0, 0) of the system.

Full size image
Table 3 Corresponding system state parameters at different equilibrium points.
Full size table
Fig. 12
figure 12

The system trajectories corresponding to the different equilibrium points (d, 0, 0, 0), where \(d = -0.4, -0.3, -0.2, -0.1, 0. 0.1, 0.2, 0.3\) and 0.4, \(\alpha =0.9\), (x(0), y(0), z(0), \(w(0)) = (0, 0.1, 0, 0)\).

Full size image

When a voltage pulse with a pulse magnitude of 1 V and pulse width of \(\Delta t\) is applied across the memristor, the dynamic route changes instantaneously from the red POP to the upper blue route where \({\mathrm{d}^\alpha }x/\mathrm{d}{t^\alpha } > 0\), i.e., the state variable x jumps from A to B. And then the state x must move to the right along the dynamic route parametrised by \(v=1\ \hbox {V}\) until \(t = \Delta t\), when the voltage pulse switches back to zero, and the dynamic route reverses back abruptly to the POP where \({\mathrm{d}^\alpha }x/\mathrm{d}{t^\alpha } = 0\) (i.e., state variable x jumps directly from point C on blue route to point D on red POP) and remains there until it is excited by another voltage pulse at a later time of \(t > \Delta t\). Thus, the memristor always remembers its state before the power is turned off, i.e., the state or the memductance is not changed before and after the power failure: \({x_{\mathrm{D}}} = {x_{\mathrm{C}}}\) or \(W\left( {{x_{\mathrm{D}}}} \right) =W\left( {{x_{\mathrm{C}}}} \right) \), showing the non-volatility of the fractional-order memristor, where \(x_{\mathrm{C}}\) and \(x_{\mathrm{D}}\) are the states before and after the power-off, corresponding to the state at points C (i.e., \(v=1\ \hbox {V}\)) and D (i.e., \(v= 0\ \hbox {V}\)) of figure 7, respectively.

Fig. 13
figure 13

(a) Bifurcation diagram varying with parameter \(c \in \) [13, 20] and (b) Lyapunov exponent spectrum varying with \(c\in \) [13, 20].

Full size image
Fig. 14
figure 14

The phase trajectories of the x–y plane for (a) \(c=13\) and (b) \(c=15\).

Full size image

2.2 Numerical simulation of the memristor

Figure 8a shows the pinched hysteresis curves of the memristor in the v–i plane vs. different fractional-order values. It can be seen that fractional-order memristors (\(0.5 \le \alpha \le 1\)) possess better memory than the integer-order memristors (\(\alpha =1\)).

The memristances with respect to the different order values are shown in figure 8b, from which we can see that the memristor always exhibits active characteristics over the range of \(0.5\le \alpha \le 1\).

Figure 8c shows that the instantaneous power changes with the order values of the memristor, showing that the instantaneous power is always non-positive when \(0.5\le \alpha \le 1\), i.e., \(p\left( t \right) \le 0\), which corresponds to the activity of the memristor.

3 Chaotic circuit based on fractional-order memristor

3.1 Fractional-order chaotic system

Compared with the integer-order models, the fractional-order models of the basic circuit elements are more accurate and agree with the electrical characteristics of the actual elements [34]. For example, fractional-order models of the capacitor and the inductor are as follows [35]:

$$\begin{aligned}&C\frac{{{\mathrm{d}^\alpha }v \left( t \right) }}{{\mathrm{d}{t^\alpha }}} = i(t), \end{aligned}$$
(14)
$$\begin{aligned}&L\frac{{{\mathrm{d}^\alpha }i\left( t \right) }}{{\mathrm{d}{t^\alpha }}} = v\left( t \right) . \end{aligned}$$
(15)

We know from the previous analysis that the proposed fractional-order memristor is an active device, which can amplify infinitesimal signals in its active region to generate complex phenomena [22]. Therefore, we can use the active fractional-order memristor to construct a chaotic circuit, which is shown in figure 9, where both the capacitor and the inductor are fractional-order devices.

According ref. [36], the negative-value elements are obtained by means of current inversion via amplifier A1 and resistors R1 and R2, as shown in Appendix A in ref. [36]. The parameter k is given by \(k=R1/R2\). Here, we take \(k=1\).

Fig. 15
figure 15

Bifurcation diagram of the system varying with order \(\alpha \in \) [0.7, 1] and initial condition (0, 0.1, 0, 0).

Full size image
Fig. 16
figure 16

Bifurcation diagram and Lyapunov exponent spectrum of the system varying with initial values x(0) \(\in \) [\(-0.8, -0.427\)]: (a) Bifurcation diagram and (b) Lyapunov exponent spectrum.

Full size image
Fig. 17
figure 17

The evolution of the system phase diagram varying with the initial value x(0) from \(-0.8\) to 0.9.

Full size image

According to Kirchhoff’s laws, the circuit equations are described by

$$\begin{aligned}&f\left( {x,{v_1},{i_L},{v_2}} \right) \nonumber \\&\quad = \left\{ \begin{array}{lllll} \displaystyle \frac{{{\mathrm{d}^\alpha }x}}{{\mathrm{d}{t^\alpha }}} = {v_1},\\ {C_1}\displaystyle \frac{{{\mathrm{d}^\alpha }{v_1}}}{{\mathrm{d}{t^\alpha }}} = {i_L} - ( {{x^2} - x + m} ){v_1},\\ L\displaystyle \frac{{{\mathrm{d}^\alpha }{i_L}}}{{\mathrm{d}{t^\alpha }}} = {v_1} - R{i_L} - {v_2},\\ {C_2}\displaystyle \frac{{{\mathrm{d}^\alpha }{v_2}}}{{\mathrm{d}{t^\alpha }}} = {i_L}, \end{array} \right. \end{aligned}$$
(16)

where the first equation of eq. (16) is the state equation of the fractional-order memristor defined by eq. (5). And the system is a commensurate system. By setting \(y={v_1}\), \(z={i_L}\), \( w = {v_2}\), \(a = 1/{C_1}\), \(b = 1/L\), \(c=1/{C_2}\), \(M = R\), eq. (16) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{lllll} \displaystyle \frac{{{\mathrm{d}^\alpha }x}}{{\mathrm{d}{t^\alpha }}} = y\left( {\alpha > 0} \right) ,\\ \displaystyle \frac{{{\mathrm{d}^\alpha }y}}{{\mathrm{d}{t^\alpha }}} = a\left( {z - \left( {{x^2} - x - \frac{1}{7}} \right) y} \right) ,\\ \displaystyle \frac{{{\mathrm{d}^\alpha }z}}{{\mathrm{d}{t^\alpha }}} = b\left( {y - Mz - w} \right) ,\\ \displaystyle \frac{{{\mathrm{d}^\alpha }w}}{{\mathrm{d}{t^\alpha }}} = cz, \end{array} \right. \end{aligned}$$
(17)
Fig. 18
figure 18

Time-domain diagrams and phase diagrams of different initial values of the system: (a) The time-domain diagrams of \(x(0) =-0.75\) and \(x(0) =\) 0, (b) the phase diagrams of \(x(0) =-0.75\) and \(x(0) = 0\), (c) the time-domain diagrams of \(x(0) = -0.3\) and \(x(0) = 1\) and (d) the phase diagrams of \(x(0) = -0.3\) and \(x(0) = 1\).

Full size image
Fig. 19
figure 19

Bifurcation diagrams varying with initial state \(x (0) \in [-1, 1]\) for \(\alpha = 0.99\) (red) and \(\alpha = 0.9\) (blue).

Full size image
Fig. 20
figure 20

Coexisting attractors with different initial conditions: (a) \(x(0) = -0.295, -0.291, -0.288, -0.284\), corresponding to the yellow, blue, purple and red trajectories, respectively and (b) \(x(0) = 1.13, 1.23, 1.27\), corresponding to the yellow, green and red trajectories, respectively.

Full size image
Fig. 21
figure 21

Entropy spectral complexity varying with the parameter \(c \in \) [13, 20] and (x(0), y(0), z(0), \(w(0)) = (0, 0.1, 0, 0)\): (a) SE complexity and (b) C0 complexity.

Full size image

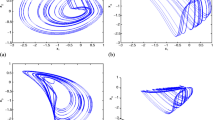
where \({x^2} - x - (1/7) = G(x)\). The values of circuit components and initial conditions are determined by a trial-and-error method so that the circuit can generate chaos. Here, we take parameters \(a=7.69\), \(b = 1\), \(c = 18\), \(M = 0.6\), \(\alpha = 0.9\), and the initial condition (x(0), y(0), z(0), \(w(0)) = (0, 0.1, 0, 0)\). The calculated Lyapunov exponents of eq. (17) are: \(\hbox {LE}1= 0.4396\), \(\hbox {LE}2=0\), \(\hbox {LE}3=-0.0559\), \(\hbox {LE}4=-7.6073\). This means that the circuit is in a chaotic state. The Adomian algorithm [13] (step size 0.01) was used to simulate the system, and the obtained chaotic attractors are shown in figure 10.

3.2 Characteristic analysis of the chaotic system

3.2.1 Basic dynamic properties of the circuit

Let the left side of eq. (17) be zero, i.e.,

$$\begin{aligned} \left\{ \begin{array}{lll} y=0,\\ a\left( {z - \left( {{x^2} - x - \dfrac{1}{7}} \right) y} \right) =0,\\ b\left( {y - Mz - w} \right) =0,\\ cz=0. \end{array} \right. \end{aligned}$$
(18)

By solving eq. (18), the equilibrium points of the system are (d, 0, 0, 0), where d is an arbitrary constant, that is, the system has an infinite number of equilibrium points (i.e., a line of equilibria). Linearising system (16) at the equilibrium points, the Jacobian matrix is obtained as follows:

$$\begin{aligned} J=\left[ {\begin{array}{cccc} 0&{}1&{}0&{}0\\ 0&{}{ - a\left( {{d^2} - d - \dfrac{1}{7}} \right) }&{}a&{}0\\ 0&{}b&{}{ - bM}&{}{ - b}\\ 0&{}0&{}c&{}0 \\ \end{array}} \right] . \end{aligned}$$
(19)

Let \(a=7.69\), \(b=1\), \(c=18\) and \(M=0.6\) at the equilibrium point (0, 0, 0, 0). The characteristic roots of the Jacobian matrix are

$$\begin{aligned} \left\{ \begin{array}{l} {\lambda _1} = 0,\\ {\lambda _2} = 1.6944,\\ {\lambda _3} = - 0.5977 + 3.3640i,\\ {\lambda _4} = - 0.5977 - 3.3640i. \end{array} \right. \end{aligned}$$
(20)

When all the eigenvalues of the Jacobian matrix satisfy the condition: \(| {\arg \left( \lambda \right) } | >{{\alpha \pi }/2}\), where \(\alpha \) is a fractional-order integral order, it can be said that the fractional-order system is asymptotically stable [37]. Therefore, the necessary condition for a system to be unstable is that there must be a characteristic root that satisfies the condition [13]

$$\begin{aligned} \alpha > {\alpha '} = \frac{2}{\pi }{\tan ^{ - 1}}\left( {\frac{{| \gamma |}}{{| \beta |}}} \right) , \end{aligned}$$
(21)

where \(\gamma \) is the imaginary part and \(\beta \) is the real part of a characteristic root. It can be seen from eq. (20) that the characteristic root \({\lambda _2}\) is already in the unstable region, as shown in figure 11. Therefore, we only need to ensure that \(\alpha > 0\) to make the system unstable at the equilibrium point (0, 0, 0, 0).

Table 3 lists the corresponding eigenvalues when taking different equilibrium points. When the fractional-order \(\alpha >\alpha '\), it indicates that the system is unstable, otherwise it is stable. It can be seen from figure 12 that the system shows chaos over the range of d \(\in \) [\(-0.1\), 0.4], where \(\alpha >\alpha '\), verifying the stability criterion of the system.

Fig. 22
figure 22

Entropy spectral complexity varying with the parameter c \(\in \) [13, 20] when \(\alpha = 0.95\) (blue), 0.9 (red) and 0.8 (green); (x(0), y(0), z(0), \(w(0)) = (0, 0.1, 0, 0)\): (a) SE complexity and (b) C0 complexity.

Full size image
Fig. 23
figure 23

Bifurcation space diagram of the system varying with different parameters and (x(0), y(0), z(0), \(w(0)) = (0, 0.1, 0, 0)\): (a) \(a\in \) [5, 10] and \(c\in \) [10, 20] and (b) \(\alpha \in \) [0.75, 1] and \(c\in \) [10, 20].

Full size image

3.2.2 Bifurcation with parameter c

With the changes of system parameters, the system will be in different states due to the stability changes of equilibria. In figure 16a, we explore the dynamics of the system under different initial conditions over the range of \(x\left( 0 \right) \in \left[ { - 0.8,1} \right] \), where \(y (0) = 0.1\), \(z (0) = 0\), \(w (0) = 0\). We can find evolution of dynamics via the bifurcation diagram, and then predict the dynamics under other initial conditions in all the cases. Under the initial conditions (0, 0.1, 0, 0) and \(\alpha = 0.9\) , \(a = 7.69\), \(b = 1\), \(M = 0.6\), the bifurcation diagram and the corresponding Lyapunov exponent spectrum of the system with respect to parameter c over the range of c \(\in \) [13, 20] are shown in figures 13a and 13b, respectively. In figure 13b, LE1, LE2 and LE3 represent three Lyapunov exponents, and the fourth Lyapunov exponent LE4 is deleted for clarity because its values are so small.

As shown in figure 13, when \(c \in [13,13.8]\), the system exhibits chaos and periodic behaviours intermittently. When the parameter c increases gradually, the system still shows an obvious periodic motion for a small interval of c, but this motion will be disturbed by a brief sudden chaotic motion, which is followed by periodic motion. This situation is repeated, resulting in intermittent chaos. Finally, the system shows quasiperiodic behaviours over the range of \(c \in \) [19, 20] [38]. The attractors of the system on the phase plane are shown in figure 14.

3.2.3 Bifurcation with the fractional-order \(\alpha \)

Figure 15 shows the bifurcation diagram of the system with fractional-order \(\alpha \). It can be seen that chaos is mainly concentrated in the region of \(\alpha \in \left[ {0.77,1} \right] \)

In the case of constant parameters, different initial values cause the system to generate different attractors called the coexisting attractors. For fixed values of \(\alpha =0.99\), \(a = 7.69\), \(b=1\), \(M = 0.6\), \(c = 18\), \(h = 0.01\) (fractional-order step size) and \(N = 40000\), the bifurcation diagram of the system with respect to parameter x(0) over the range of \([-0.8, 1]\) is shown in figure 16, where LE4 is too small to be displayed in the figure.

Fig. 24
figure 24

Circuit simulation diagram: (a) System circuit simulation and (b) system simulation phase diagram.

Full size image

It can be seen from figure 16 that there are many coexistence attractors in the system. The system exhibits chaotic behaviour in the parameter range of \(x(0) \in [ - 0.8, - 0.427]\). When \(x(0) \in [ - 0.8, - 0.7]\) and \(x(0) \in [ - 0.7, - 0.427]\), it generates a left scroll and a double scroll, respectively, as shown in figure 17. Furthermore, when \(x(0) \in [ - 0.427, - 0.27]\), it has a reverse periodic bifurcation state, and then goes into chaos again. Finally, the system enters a periodic orbit in the initial value range of \(x(0) \in [0.864,1]\) via a reverse periodic bifurcation. Various coexisting attractors are shown in figure 17.

In figures 18a and 18b, it can be seen that when \(x(0) = 0\) (red), the system rapidly enters into a chaotic state and generates a right scroll. However, when \(x(0) = -0.75\) (blue), the system oscillates slowly until \(N = 9500\), enters chaos and generates a left scroll, while in figures 18c and 18d, when \(x(0) =-0.3\) (blue) and \(x(0) = 1\) (red), the system exhibits periodic oscillation.

Figure 19 shows the bifurcation diagram with respect to initial value x(0), where red and blue bifurcations correspond to \(\alpha = 0.99\) and \(\alpha = 0.9\), respectively; and the parameters are: \(a = 7.69\), \(b = 1\), \(M = 0.6\) and \(c = 18\). It can be seen that the fractional-order system exhibits abundant coexisting dynamics, as shown in figure 20, where the trajectories starting at different initial points eventually tend to different limit cycles, showing the abundant coexisting dynamics and multistability.

3.3 Complexity analysis

In fact, the complexity of a chaotic system is also one of the methods to describe the dynamic characteristics of a chaotic system, which has the same effect as Lyapunov exponents, bifurcation diagram, dissipative property and phase diagrams [28]. Spectral entropy (SE) algorithm uses the energy distribution in the Fourier transform domain to obtain entropy spectrum values based on Shannon entropy algorithm. When the power spectrum of the sequence becomes more unstable, the structure composition becomes simpler. Therefore, the sequence amplitude will be less obvious, and the measured value will be smaller. The main idea of C0 algorithm is to divide the sequence into regular and irregular parts, and the proportion of irregular part can be calculated. The more is the irregular part in the whole sequence, the closer is the corresponding signal to the random signal, leading to better complexity and larger corresponding values. As shown in figure 21, the complexity varies with parameter c, where \(a = 7.69\), \(b = 1\) and \(M = 0.6\).

Figure 21 shows that the complexity of the fractional-order chaotic system is consistent with the Lyapunov exponent spectrum shown in figure 13b. The SE complexity and C0 complexity are also consistent, and the complexity of chaotic state is greater than that of the non-chaotic state in the same system.

When \(\alpha = 0.95\), \(\alpha = 0.9\) and \(\alpha = 0.8\), the resulting entropy spectrum complexity is shown in figure 22. As shown in figure 22, entropy spectrum complexity gradually increases with the decrease of fractional order, indicating that the lower the fractional-order of the system is, the more is the complexity of the system. It follows that a fractional-order chaotic system with lower order \(\alpha \) can generate more complex chaotic sequences.

We take the SE complexity as the standard quantity to describe the complexity change of the system under the changes of double parameters, where \(b = 1\) and \(M = 0.6\). The colour scale on the right of each plot represents the value of entropy spectrum of the system. The larger is the entropy scale, the larger is the colour scale and redder is the colour. It can be seen from figure 23a that parameters a and c are mutually restricted, and the influences of parameters a and c on the system are similar. The chaotic region of the system is mainly concentrated in the middle part that looks like a ‘path’. As can be seen from figure 23b, the influence of parameter c on the system in certain range is greater than that of parameter \(\alpha \), and the chaos of the system is mainly concentrated in the range of \(c \in [14,18]\) .

To verify the dynamic characteristics of the system, a circuit simulation experiment was performed by using Multisim. Figure 24a shows the simulation circuit built according to eq. (15), where \(\alpha = 0.9\), and the simulated results are shown in figures 24b and 24c.

4 Conclusion

This paper proposed a fractional-order locally active memristor model, whose dynamics has been analysed in detail, including continuous memory and switching, the effects of the fractional-order \(\alpha \) on memory, pinched hysteresis curve, memristance and power of the memristor. Based on the memristor we designed a chaotic circuit, and its dynamics have been analysed by using bifurcation, Lyapunov exponent spectrum, equilibria and complexity analysis.

It has been found that the fractional-order memristor has continuous memory which is better than the memristor with integer order. By applying an external voltage to the memristor, it can be quickly switched from one state to another, and therefore can be used to mimic synaptic characteristic of neurons and realise information storage. The proposed chaotic circuit can exhibit various coexisting attractors and continuous chaos in the range of \(0.75<\) fractional-order \(\alpha < 1\). It has also been shown that the lower the order of fraction is, the higher is the complexity of the chaotic system. The proposed memristor model can serve the roles of memristive memory and memristive synaptic plasticity for computing.