Fractional-order Memristor Response Under DC and Periodic Signals

Abstract

Recently, there is an essential demand to extend the fundamentals of the conventional circuit theory to include the new generalized elements, fractional-order elements, and mem-elements due to their unique properties. This paper presents the relationships between seven different elements based on the four physical quantities and the fractional-order derivatives. One of them is the Fractional-order memristor, where the memristor dynamic is expressed by fractional-order derivative. This element merge the memristive and fractional-order concepts together where the conventional modeling becomes a special case. Moreover, the mathematical modeling of the fractional-order memristor is introduced. In addition, the response of applying DC, sinusoidal, and nonsinusoidal periodic signals is discussed. Finally, different numerical simulations are presented.

1 Introduction

The Memristor is the newest electrical element whose existence was theoretically proven by Chua in a seminal paper in 1971 [4]. Chua postulated that element for the sake of completing the two-terminal electrical elements, where the memristor offers the missing link between flux $\varphi$ and charge $q$. Then in 1980, Chua generalized the axiomatic approach of two-terminal elements definition to define an infinite variety of higher order basic circuit elements [5]. Moreover, Chua defined a new general element and named it as $v^{(\alpha )}-i^{(\beta )} element$ which has a constitutive relation involving only the two variables $v^{(\alpha )}$ and $i^{(\beta )}$, where $\alpha$ and $\beta$ are integer numbers.

Although the theoretical concepts related to this fourth passive two-terminal element have been postulated more than 40 years ago, the first passive realization was introduced by HP-lab a few years ago [23]. Since the existence of the passive memristor device, huge research interests and projects have been directed toward the new applications related to this element [7, 13, 25]. For example, the memristor can be used as a nonvolatile memory instead of the capacitor and transistor circuits because it can memorize its previous state. Therefore, building the memristor-based logic and digital circuits instead of transistors draws great attention due to its nano-dimension size [2]. In addition, the time-varying property of the memristor resistance introduces many novel fundamentals in the analogy circuit design such as in the case of memristor-based oscillators [9, 10].

The fractional-order elements or constant phase elements (CFE) were introduced a long time ago (like fractional-order capacitor (FOC) and fractional-order inductor (FOI)) to model the practical elements (frequency dependent losses) [20]. In order to analyze these elements, the knowledge of fractional calculus is necessary where integer calculus is not applicable. Fractional calculus is very useful in modeling due to its privileges over integer calculus. The main advantages of fractional-order modeling are its long-memory dependency and also the ability to increase the degree of freedom for the system through the added fractional-order parameters. The basic and fundamental definitions in many applications have been generalized in the fractional-order sense such as in the control theory [3], circuit theory [6, 16, 18, 19, 22], waveguide modeling [8], and in the fractional-order Smith chart [17]. In the circuit theory, the fractional-order element (FOE) is considered as a generalized element that covers the conventional three passive elements which are inductor, resistor, and capacitor when the fractional-order parameter equals to $-1, 0$, and $1$, respectively. One of the realizations of the half-order capacitor can be obtained by dipping a capacitive type probe, coated with a porous film of polymer of particular thickness, into a polarizable medium [1, 21] or tree shape of equal values can be used to realize the half-order fractional element [12].

This paper is organized as follows. Section 2 discusses the relationships between the fractional-order elements. The mathematical analysis of the FOM is discussed in Sect. 3. Moreover, the response of the FOM under step, sinusoidal, and periodic excitation signals is introduced. As an example, the FOM response under a square wave signal is analyzed in Sect. 4. Finally, the conclusion is given.

2 Fractional-order Elements Relations

In the year 1980, Chua generalized the axiomatic approach of two-terminal elements definition to interpret an infinite variety of higher order basic circuit elements [5]. Moreover, Chua defined a new general element and named it as $v^{(\alpha )}-i^{(\beta )} element$ which has a constitutive relation involving only the two variables $v^{(\alpha )}$ and $i^{(\beta )}$, where $\alpha$ and $\beta$ are integer numbers representing the derivative order. For instance, if $(\alpha , \beta )$ equals $(0, 0)$, this element represents resistor; and $(-1, 0), (0, -1)$, and $(-1, -1)$ correspond to inductor, capacitor, and memristor, respectively. But later, this definition was generalized to the fractional-order domain [24].

The conventional elements are linked as shown in Fig. 1, where links (1), (2), and (3) represent $R, L$, and $C$, respectively, and link (4) represents the memristor. The fractional-order capacitor $(FOC)$ relates between the fractional derivative of the charge and the voltage which is represented in link (5) and link (8) with fractional-order $1-\alpha$ and $\alpha$, respectively. Also, the fractional-order inductor $(FOI)$ relates between the fractional derivative of the flux and the current which is represented in link (6) and link (8) with fractional order $1-\alpha$ and $\alpha$, respectively. So, the missing link is between the fractional-order derivative of charge and the fractional-order derivative of flux (link (9)) representing the fractional-order memristor$(FOM)$. All the links are linear elements except link (4) and link (9) which are nonlinear elements.

Fig. 1

Fractional-order elements relations

Generally, the relation between any fractional-order derivative of charge $D^{\alpha }q$ and any fractional-order derivative of flux $D^{\beta }\varphi$ represents one of elements $R, L, C,$ $M,$ $FoC,$ $FOI$, and $FOM$ depending on the resulting order and linearity between the elements. Also, this relation could be generalized to include memcapacitor and meminductor in addition to fractional-order memcapacitor (FOMC) and fractional-order meminductor (FOMI).

3 Mathematical Analysis on FOM Model

The memristance is described as follows:

$$\begin{aligned} R_m=xR_\mathrm{on}+(1-x)R_\mathrm{off}, \end{aligned}$$

(1)

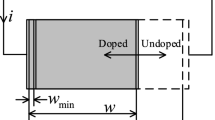
where $x$ represents the state variable of the memristor which physically represents the ratio between the length of doped region to the total length of the memristor $D$. Also, $R_\mathrm{on}$ and $R_\mathrm{off}$ represent the minimum and maximum resistances of the memristor, respectively. The fractional differential equation of memristor state, introduced in [11], is given by

$$\begin{aligned} \frac{d^\alpha x}{dt^\alpha }=\eta ki(t), \end{aligned}$$

(2)

where $\eta$ is the memristor polarity which is either 1 or $-$1, and $k$ is proportionality constant. By differentiating the memristance $R_m$, then

$$\begin{aligned} \frac{d^\alpha R_m}{dt^\alpha }= - R_d \frac{d^\alpha x}{dt^\alpha }. \end{aligned}$$

(3)

Substituting by (3) into (2) then

$$\begin{aligned} \frac{d^\alpha R_m}{dt^\alpha }= -\eta k R_d i(t), \end{aligned}$$

(4)

where $R_d$ is the difference between $R_\mathrm{off}$ and $R_\mathrm{on}$.

Using the basic definition of the fractional integral proposed by Riemann Liouville [14], and applying fractional integral of order $\alpha$ for both sides [11], then the memristance as a function of the input voltage and the time can be obtained as follows:

$$\begin{aligned} R_m=\left( R_\mathrm{in}^{\alpha +1}-\eta \alpha (\alpha +1)k R_d \int _0^t (t-\tau )^{\alpha -1}v(\tau )d\tau \right) ^{\frac{1}{\alpha +1}}. \end{aligned}$$

(5)

When $\alpha =1$, this equation tends to the known equation for HP memristor as follows:

$$\begin{aligned} R_m^2=R_\mathrm{in}^2-2\eta k R_d \int _0^t v(\tau )d\tau = R_\mathrm{in}^2-2\eta k R_d \varphi (t), \end{aligned}$$

(6)

which matches the published formula in [15], where $\varphi (t)$ represents the accumulated flux.

4 Excitation Signals Response

In this section, the response of FOM under different input voltage signals is discussed starting from step input signal and then sinusoidal waveforms which are the keys in the analysis of any periodic signal.

4.1 Step Input Response

In case of applying step input voltage across the memristor where the input signal is defined by

$$\begin{aligned} v(t)=V_\mathrm{DC} u(t), \end{aligned}$$

(7)

where $u(t)$ is the unit step function. Then by substituting from (7) into (6), the resistance of the memristor is given by

$$\begin{aligned} R_m=\left( R_\mathrm{in}^{\alpha +1}-\eta (\alpha +1)k R_d V_\mathrm{DC} t^\alpha \right) ^{\frac{1}{\alpha +1}}. \end{aligned}$$

(8)

It is clear from the previous equation that the memristance increases/decreases from the initial value until reaches its maximum resistance $R_\mathrm{off}$/ minimum resistance $R_\mathrm{on}$ in a certain time period which is called the saturation time $t_\mathrm{sat}$ for negative/positive sign of $(\eta V_\mathrm{DC})$, respectively.

Figure 2 shows the memristor behavior under step input voltage where the memristor parameters $k$, $V_\mathrm{DC}$, $R_\mathrm{off}$, and $R_\mathrm{on}$ are equal to $10^{4}$, 1 V, 38 k $\Omega$, 100 $\Omega$, respectively, for different values of $\alpha$. Therefore, the saturation time depends on the value of the fractional-order $\alpha$, where the saturation time increases as $\alpha$ increase for certain $V_\mathrm{DC}$.

Fig. 2

Memristance versus $\alpha$ and time for a negative $\eta V_\mathrm{DC}$ and b positive $\eta V_\mathrm{DC}$

The general formula of the saturation time $t_\mathrm{sat}$ in the fractional-order case at which the memristance increases or decreases from its initial value $R_\mathrm{in}$ to $R_\mathrm{off}$ or $R_\mathrm{on}$ is given by

$$\begin{aligned} t_\mathrm{sat}=\left( \frac{R_\mathrm{in}^{\alpha +1}-R_{bd}^{\alpha +1}}{(\alpha +1)\eta k R_d V_\mathrm{DC}} \right) ^{\!\!\frac{1}{\alpha }}, \end{aligned}$$

(9)

where $R_{bd}$ is the boundary memristance which is either $R_\mathrm{off}$ or $R_\mathrm{on}$. The maximum saturation time can be obtained when changing from minimum or maximum memristance to maximum or minimum memristance, respectively, as follows:

$$\begin{aligned} t_\mathrm{sat}|_\mathrm{max}=\left( \frac{R_\mathrm{off}^{\alpha +1}-R_\mathrm{on}^{\alpha +1}}{(\alpha +1)k R_d |V_\mathrm{DC}|} \right) ^{\!\!\frac{1}{\alpha }}. \end{aligned}$$

(10)

For the conventional model of the memristor $\alpha =1$, the saturation time will be reduced to the formula given in [15].

The saturation time surface as a function of the $\alpha -V_\mathrm{DC}$ plane and also versus three different cases of $\alpha =0.5, 1$ and $1.5$ are shown in Fig. 3a and b, respectively. It is clear from the above response that the saturation time can be controlled through the fractional order, where it can be less than 1 sec when $\alpha <0.5$ up to higher values when $\alpha >0.5$. It is worthy to note that the memristor will act as a linear resistor as $\alpha$ tends to $0$ with resistance $R_\mathrm{in}$.

Fig. 3

a Saturation time versus $\alpha$ and $V_\mathrm{DC}$, and b saturation time versus $V_\mathrm{DC}$ for different $\alpha$

4.2 Sinusoidal Input Response

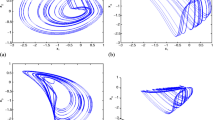
Conventionally, the sinusoidal response of circuit elements is extremely important in many applications and also in circuit theory especially in circuits which have lissajous curves. So in this section, a single tone is applied to the fractional-order memristor to study the effect of changing the fractional order and the frequency on the pinched hysteresis. Using MATHEMATICA, the fractional integral of sinusoidal is given by

$$\begin{aligned} J^{\alpha }\mathrm{sin}(2\pi f t)=\frac{2\pi f t^{\alpha +1} {}_1F_2 \Big [1;1+\frac{\alpha }{2},\frac{3+\alpha }{2};-\pi ^2 f^2 t^2\Big ]}{\Gamma (\alpha +2)}, \end{aligned}$$

(11a)

$$\begin{aligned} J^{\alpha }\mathrm{cos}(2\pi f t)=\frac{t^{\alpha } {}_1F_2 \Big [1;\frac{1+\alpha }{2},1+\frac{\alpha }{2};-\pi ^2 f^2 t^2\Big ]}{\Gamma (\alpha +1)}. \end{aligned}$$

(11b)

For single sinusoidal input which is given by $v(t)=V_o \,\mathrm{sin}\,(2\pi f t)$, the memristance is given by

$$\begin{aligned} R_m= {\left( R^{\alpha +1}_\mathrm{in}- 2\eta \pi kR_d {f t^{\alpha +1} {}_1F_2 \Big [1;1+\frac{\alpha }{2},\frac{3+\alpha }{2};-\pi ^2 f^2 t^2\Big ]}\right) }^{\frac{1}{\alpha +1}} \end{aligned}$$

(12)

Thus, the memristance is a function of some factors $\{\alpha , V_o, k, f \}$, but the most influential factor is $\alpha$ such that any small change leads to a new behavior and hysteresis as shown in Fig. 4a and c. Moreover, the hysteresis loops shape is changed due to changing frequency unlike HP memristor which has symmetric hysteresis and its size shrinks with increasing frequency preserving its shape (inclined 8) as shown in Fig. 4c. For the integer case at $\alpha =1$, the memristance tends to the same results published in [15] which is given by

$$\begin{aligned} R_m=\sqrt{R^2_\mathrm{in}\pm 4kR_d \frac{V_o}{{\omega }_o}{\mathrm{sin }^2 \left( \frac{{\omega }_ot}{2}\right) }}. \end{aligned}$$

(13)

Fig. 4

Numerical simulation of $I-V$ hysteresis for $(\alpha ,f)$ equals a (0.5,1), b (0.5,0.5) and c (0.55,1) at $R_\mathrm{in}$ = 20 k $\Omega , V_o$ = 10 mV, and $k=10^4$

4.3 Nonsinusoidal Periodic Signal Response

This subsection discusses the FOM response under any periodic input waveform by using the Fourier series expansion where any periodic signal can be expanded into

$$\begin{aligned} v\left( t\right) =a_o+\sum ^{\infty }_{n=1}{a_n{\sin \left( 2\pi ft\right) \ }+b_n{\cos \left( 2\pi ft\right) \ }}. \end{aligned}$$

(14)

In order to get a closed form expression for the instantaneous memristance, the fractional integral of the voltage $J^\alpha v(t)$ should be calculated. By integrating (14) using (11) so

$$\begin{aligned} J^{\alpha }v\left( t\right) =\frac{a_ot^{\alpha }}{\Gamma \left( \alpha +1\right) }+ \sum ^{\infty }_{n=1}{a_n J^\alpha {\sin \left( 2\pi ft\right) \ }+b_n J^\alpha {\cos \left( 2\pi ft\right) \ }}. \end{aligned}$$

(15)

By substituting (15) into (5), the complete expression of the instantaneous memristance is obtained. As an example for the periodic signal, a square wave signal is applied and which is defined as:

$$\begin{aligned} v(t)= \left\{ \begin{array}{l l} V_{o1} &{} \quad 0<\tau \le \beta T\\ V_{o2} &{} \quad \beta T<\tau \le T \end{array} \right. \quad 0\le \beta \le 1, \end{aligned}$$

(16)

where $\tau = mod(t,T)$. Since the applied signal alternates between positive and negative voltages with sharp transitions, then the step response can be used periodically using the last value as the initial value of the next step. So the FOM changes up and down as the voltage changes periodically. By applying Fourier series expansion to the input signal, the coefficients are given by $a_o=\beta V_{o1}+(1-\beta ) V_{o2}$, $a_n=((V_{o1}-V_{o2} )/n\pi ) \,\mathrm{sin} \,(2\beta n\pi )$, and $b_n= ((V_{o1}-V_{o2})/n\pi )(1-\mathrm{cos}\, (2\beta n\pi ))$. Therefore, the fractional integral of the voltage is given by

$$\begin{aligned} J^\alpha v(t)= \left\{ \begin{array}{l l} V_{o1}\tau ^\alpha &{} 0<\tau \le \beta T\\ V_{o1}(\beta T)^\alpha +V_{o2}\big (\tau ^\alpha -(\beta T)^\alpha \big ) &{} \beta T<\tau \le T \end{array} \right. . \end{aligned}$$

(17)

then, the instantaneous memristance is given as follows:

$$\begin{aligned} R_m^{\alpha +1}= R_\mathrm{in}^{\alpha +1}-\eta (\alpha +1)k R_d \left\{ \begin{array}{l l} V_{o1} \tau ^\alpha &{} 0<\tau \le \beta T\\ V_{o1}-V_{o2})(\beta T)^\alpha +V_{o2}\tau ^\alpha &{} \beta T<\tau \le T \end{array} \right. . \end{aligned}$$

(18)

Moreover, Fig. 5a shows the instantaneous memristance for $\alpha =0.5, \beta =0.5,$ and $V_{o2}=-V_{o1}=1$, but as is obvious the memristance decreases until it reaches the boundary due to the effect of the fractional-order unlike the conventional case where the memristance is completely periodic. As $\alpha$ increases, the average transient memristance slope increases and converges to conventional case ($\alpha =1$) where the memristance does not saturate [15]. However, a periodic memristance can be obtained by using a square wave with duty cycle given by

$$\begin{aligned} \beta =\Big (\frac{V_{o2}}{V_{o2}-V_{o1}}\Big )^{1/\alpha }. \end{aligned}$$

(19)

Figure 5(c) shows a periodic memristance at different applied frequencies for $\alpha =0.5, \beta =0.25,$ and $V_{o2}=-V_{o1}=1$.

Fig. 5

Transient memristance for a different applied frequencies, b different $\alpha$, and c different applied frequencies without average term at $R_\mathrm{on}, R_\mathrm{off}, k$ and $R_\mathrm{in}$ equal 100 $\Omega$, 38 k $\Omega , 10^4$, and 10 k $\Omega$, respectively

5 Conclusion

This paper introduced the analysis of the fractional-order memristor model and its relationship to other fractional-order elements. The proposed model has an extra degree of freedom that can be used for better interpolation of the practical memristor. Moreover, its response under sinusoidal and periodic signals using Fourier series expansion was derived and verified numerically via many simulation results.