1 Introduction

High-red-shift supernova, cosmic microwave background fluctuation, galaxy clustering and large-scale structures have confirmed cosmic acceleration [1,2,3,4,5,6,7,8,9,10]. Dark energy (DE) is assumed to be the best candidate to explain the present cosmic acceleration. It is also believed that 96% of the Universe consists of DE and dark matter (DM). The cosmological constant, quintessence, Phantom, K-essence, holographic dark energy (HDE) and modified holographic Ricci dark energy (MHRDE) are various candidates of DE [11, 12]. The modified gravity models are the natural gravitational alternatives for DE [13, 14]. Several relativists showed their interest in the modified gravitational theory, the f(T) gravity [15,16,17], to explain the acceleration of the cosmic expansion. Einstein [18] promulgated that in the linear model, the f(T) theory can be directly reduced to the teleparallel equivalent of general relativity (TEGR). Linder [19] proposed two new f(T) models to explain the accelerating expansion of the Universe. Karami and Abdolmaleki [20] achieved the polytropic gas, the standard Chaplygin gas, the generalised Chaplygin gas and the modified Chaplygin gas models of DE. Sharif and Rani [21] investigated anisotropic Universe in the context of f(T) gravity. The resolution of DM problem in the light of f(T) gravity is considered by Jamil et al [22, 23]. Setare and Darabi [24] obtained the phantom phase of the Universe using the power-law solution. Rodrigues et al [25] obtained Bianchi type-I, type-III and Kantowaski–Sachs anisotropic cosmological models. Jamil and Yussouf [26] studied f(T) models within the Kantowaski–Sachs Universe. Krššák and Saridakis [27] obtained the covariant formulation of f(T) gravity. Ferraro and Guzmán [28] examined the extra degree of freedom in f(T) gravity. Ferraro and Guzmán [29] formalised the Hamiltonian in the teleparallel gravity. Toporensk and Tretyakov [30] investigated cosmological perturbations in teleparallel gravity.

HDE models have received considerable attention in describing the accelerated expansion of the Universe. Depending on the entropy–area relation of black holes (Cohen et al [31], Hsu [32], Gao et al [33]) and in the light of holographic principle, the standard holographic dark energy (HDE) is defined and characterised by

$$\begin{aligned} \rho _{D} =3c^{2}M_{pl}^{2} L^{-2}, \end{aligned}$$

where c is a numerical constant. Granda and Oliveros [34] elaborated the concept of HDE. Setare [35] studied the HDE model with non-flat Friedmann–Robertson–Walker (FRW) metric in Brans–Dicke cosmology. Setare and Vanegas [36] investigated an interacting HDE model and discussed cosmological implications. Sarkar and Mahanta [37], Sarkar [38], Adhav et al [39], Kiran et al [40], Santhi et al [41], Das and Sultana [42, 43] and Santhi et al [44, 45] investigated HDE in general relativity and scalar–tensor theories of gravitation. Srivastava and Singh [46] conferred HDE model for the FRW Universe in Brans–Dicke theory. Felegary et al [47] considered the dynamics of an interacting HDE model in Brans–Dicke cosmology. Srivastava and Singh [48] studied the non-interacting HDE with infrared cut-off as the future event horizon. Varshney et al [49] explored the tsallis holographic dark energy (THDE) model admitting mutual interaction between DM and DE. The above discussion inspired us to study LRS Bianchi type-I space–time with DM and MHRDE in the framework of f(T) gravity.

2 f(T) Gravity formalism

The action of teleparallel gravity is given as

$$\begin{aligned} S=\int {\left[ {T+f(T)+L_{\mathrm{matter}} } \right] } e \text{ d}^{4}x. \end{aligned}$$
(2.1)

The field equations of f(T) gravity following Sharif and Rani [50] are as follows:

$$\begin{aligned}&S_{\mu }^{\nu \rho } \partial _{\rho } Tf_{TT} +\left[ e^{-1}e_{\mu }^{i} \partial _{\rho } \left( {ee_{i}^{\alpha } S_{\alpha }^{\nu \rho } } \right) +T^{\alpha }_{\lambda \mu } S_{\alpha }^{\nu \lambda } \right] \left( {1+f_{T} } \right) \nonumber \\&\quad +\frac{1}{4}\delta _{\mu }^{\nu } \left( {T+f} \right) =k^{2}(T_{\mu }^{\nu } +\bar{{T}}_{\mu }^{\nu }), \end{aligned}$$
(2.2)

where \(T_{\mu }^{\nu } \) is the energy–momentum tensor,

$$\begin{aligned} f_{T} =\frac{\hbox {d}f(T)}{\hbox {d}T}, \end{aligned}$$

and by setting \(f(T)=\hbox {constant}\) which is equivalent to the general relativity.

3 Metric space and field equations

Bianchi type-I (B-I) Universe is one of the simplest models of an anisotropic Universe that describes a homogeneous and spatially flat Universe. Hence, we consider LRS Bianchi type-I space–time which is the straightforward generalisation of the flat FRW Universe and is of the form

$$\begin{aligned} \hbox {d}s^{2}=\hbox {d}t^{2}-A^{2}(t)\hbox {d}x^{2}-B^{2}(t)\left[ {\hbox {d}y^{2}+\hbox {d}z^{2}} \right] , \end{aligned}$$
(3.1)

where A and B are functions of cosmic time t only. The corresponding torsion scalar is given by

$$\begin{aligned} T=-2\left( {2\frac{\dot{{A}}}{A}\frac{\dot{{B}}}{B}+\frac{\dot{{B}}^{2}}{B^{2}}} \right) . \end{aligned}$$
(3.2)

The energy–momentum tensor of matter coupled with HDE is defined as

$$\begin{aligned}T_{\nu \mu } =\rho _{m} u_{\nu } u_{\mu } \end{aligned}$$

and

$$\begin{aligned} \bar{{T}}_{\nu \mu } =\left( {\rho _{\lambda } +p_{\lambda } } \right) u_{\nu } u_{\mu } -g_{\nu \mu } p_{\lambda }, \end{aligned}$$
(3.3)

where \(\rho _{m},\rho _{\lambda } \) are the energy densities of matter and HDE and \(p_{\lambda }\) is the pressure of HDE. The energy–momentum tensor of DE can be parametrised as

$$\begin{aligned} \bar{{T}}_{\nu \mu } =\text{ diag }\left[ 1,-w_{\lambda } ,-w_{\lambda } ,-w_{\lambda } ) \right] \rho _{\lambda }, \end{aligned}$$
(3.4)

whereas \(w_{\lambda } ={p_{\lambda } }/{\rho _{\lambda } }\) is the equation of state (EoS) parameter of DE. The density of HDE

$$\begin{aligned} \rho _{\mathrm{DE}} \approx \;\left( {\alpha _{1} \,H^{2}+\beta _{1} \,\dot{{H}}} \right) , \end{aligned}$$

where H is the Hubble parameter and \(\alpha _{1} \,,\beta _{1} \,\)are constants. Chen and Jing [51] assumed the density of DE containing the Hubble parameter H, the first-order and the second-order derivatives. The new form of the energy density of DE is given by

$$\begin{aligned} \rho _{\lambda } =\;\left( {3\eta _{1} \,\ddot{{H}}H^{-1}+3\eta _{2} \,\dot{{H}}+3\eta _{3} H^{2}} \right) , \end{aligned}$$
(3.5)

where \(\eta _{1} ,\eta _{2} ,\eta _{3}\) are the arbitrary dimensionless parameters.

Using eqs (2.2), (3.1), (3.3) and (3.4), the field equations can be written as

$$\begin{aligned}&\left( {T+f} \right) +4\left( {1+f_{T} } \right) \left\{ {\frac{\ddot{{B}}}{B}+\frac{\dot{{B}}^{2}}{B^{2}}+\frac{\dot{{A}}}{A}\frac{\dot{{B}}}{B}} \right\} \nonumber \\&\quad +4\frac{\dot{{B}}}{B} \dot{{T}}f_{TT} =-k^{2}w_{\lambda } \rho _{\lambda }, \end{aligned}$$
(3.6)
$$\begin{aligned}&\left( {T+f} \right) +2\left( {1+f_{T} } \right) \left\{ {\frac{\ddot{{A}}}{A}+\frac{\ddot{{B}}}{B}+\frac{\dot{{B}}^{2}}{B^{2}}+3\frac{\dot{{A}}}{A}\frac{\dot{{B}}}{B}} \right\} \nonumber \\&\quad +2\left\{ {\frac{\dot{{A}}}{A}+\frac{\dot{{B}}}{B}} \right\} \dot{{T}} f_{TT} =-k^{2}w_{\lambda } \rho _{\lambda } , \end{aligned}$$
(3.7)
$$\begin{aligned}&\left( {T+f} \right) +4\left( {1+f_{T} } \right) \left\{ {\frac{\dot{{B}}^{2}}{B^{2}}+2\frac{\dot{{A}}}{A}\frac{\dot{{B}}}{B}} \right\} \nonumber \\&\quad =k^{2}(\rho _{m} +\rho _{\lambda } ), \end{aligned}$$
(3.8)

where the dot (\(\cdot )\) represents the differentiation with respect to time t.

Equations (3.6)–(3.8) are three differential equations with seven unknowns namely \(A, B, f, w_{\lambda } , \rho _{\lambda } ,\rho _{m} ,p_{\lambda } \). Additional constraints relating these parameters are required to obtain explicit solutions of the system. The spatial volume is given by

$$\begin{aligned} V=a^{3}=AB^{2}. \end{aligned}$$
(3.9)

The deceleration parameter is expressed as

$$\begin{aligned} q=\frac{\hbox {d}}{\hbox {d}t}\left( {\frac{1}{H}} \right) -1. \end{aligned}$$
(3.10)

The Universe exhibits decelerating expansion if \(q>0\). It expands with constant rate if \(q=0\), accelerating power law expansion if \(-1<q<0\) and exponential expansion if \(q=-1\). The mean Hubble parameter yields

$$\begin{aligned} H=\frac{1}{3}\left( {H_{1} +H_{2} +H_{3} } \right) , \end{aligned}$$
(3.11)

where

$$\begin{aligned} H_{1} =\frac{\dot{{A}}}{A}, H_{2} =H_{3} =\frac{\dot{{B}}}{B} \end{aligned}$$

are the directional Hubble parameters along x-, y- and z-axes respectively. The Hubble parameter, spatial volume and scale factor are correlated by

$$\begin{aligned} H=\frac{1}{3}\frac{\dot{{V}}}{V}=\frac{1}{3}\left( {H_{1} +H_{2} +H_{3} } \right) =\frac{\dot{{a}}}{a}. \end{aligned}$$
(3.12)

The mean anisotropic parameter is defined as

$$\begin{aligned} A_{m} =\frac{1}{3}\sum \limits _{i=1}^3 {\left( {\frac{H_{i} -H}{H}} \right) } ^{2}. \end{aligned}$$
(3.13)

The expressions for expansion scalar and shear scalar are as follows:

$$\begin{aligned}&\theta =u_{;\mu }^{\mu } =\frac{\dot{{A}}}{A}+2\frac{\dot{{B}}}{B}, \end{aligned}$$
(3.14)
$$\begin{aligned}&\sigma ^{2}=\frac{3}{2}H^{2}A_{m}. \end{aligned}$$
(3.15)

4 Solution of the field equations

The exact solution of the field equations is obtained by depicting f(T) model (Han Dong et al [52]) as

$$\begin{aligned} f(T)=T^{\eta }. \end{aligned}$$
(4.1)

Using eqs (3.6) and (3.7) yields

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\dot{{A}}}{A}-\frac{\dot{{B}}}{B}} \right) +\left( {\frac{\dot{{A}}}{A}-\frac{\dot{{B}}}{B}} \right) \frac{\dot{{V}}}{V}=0 \end{aligned}$$
(4.2)

which on integration gives

$$\begin{aligned} \frac{A}{B}=k_{2} \exp \left[ {k_{1} \int {\frac{\hbox {d}t}{V}} } \right] , \end{aligned}$$
(4.3)

where \(k_{1} \) and \(k_{2}\) are constants of integration.

Using eq. (3.9), the metric potentials can be expressed in explicit forms as

$$\begin{aligned} A=D_{1} V^{\frac{1}{3}}\exp \left( {\chi _{1} \int {\frac{1}{V}\hbox {d}t} } \right) , \end{aligned}$$
(4.4)
$$\begin{aligned} B=D_{2} V^{\frac{1}{3}}\exp \left( {\chi _{2} \int {\frac{1}{V}\hbox {d}t} } \right) , \end{aligned}$$
(4.5)

whereas \(D_{i} (i=1,\;2)\) and \(\chi _{i} (i=1,\;2)\) satisfy the relation \(D_{1} D_{2}^{2} =1\) and \(\chi _{1} +2\chi _{2} =0\). As the field equations are highly nonlinear, an extra condition is needed to solve the system completely. After thoroughly reviewing refs [53,54,55,56,57], two different volumetric expansion laws are considered:

$$\begin{aligned} V=at^{b} \end{aligned}$$
(4.6)

and

$$\begin{aligned} V=\alpha \mathrm{e}^{\beta t}, \end{aligned}$$
(4.7)

where \(a,b,\alpha ,\beta \) are constants. The power-law expansion is specified by eq. (4.6) and the exponential expansion is specified by eq. (4.7).

5 Model for the power law

Using eqs (4.4)–(4.6), the scale factors are obtained as

$$\begin{aligned} A=D_{1} a^{\tfrac{1}{3}}t^{\tfrac{b}{3}}\exp \left\{ {\frac{\chi _{1} }{a(1-b)}t^{1-b}} \right\} \end{aligned}$$
(5.1)

and

$$\begin{aligned} B=D_{2} a^{\frac{1}{3}}t^{\frac{b}{3}}\exp \left\{ {\frac{\chi _{2} }{a(1-b)}t^{1-b}} \right\} . \end{aligned}$$
(5.2)

At the initial epoch, the, metric potentials vanish. Thus, the model has an initial singularity. As \(t\rightarrow \infty \), the scale factors diverge to infinity. Hence, there will be big rip at least as far in the future since the metric potentials tend to infinity at \(t\rightarrow \infty \) [58, 59].

Using eqs (5.1) and (5.2), the LRS Bianchi type-I space–time filled with matter and MHRDE fluid becomes

$$\begin{aligned} \hbox {d}s^{2}= & {} \hbox {d}t^{2}-D_{1}^{2} a^{\frac{2}{3}}t^{\frac{2b}{3}}\exp \left\{ {\frac{2\chi _{1} }{a(1-b)}t^{1-b}} \right\} \hbox {d}x^{2}\nonumber \\&-D_{2}^{2} a^{\frac{2}{3}}t^{\frac{2b}{3}}\exp \left\{ {\frac{2\chi _{2} }{a(1-b)}t^{1-b}} \right\} \left( {\hbox {d}y^{2}+\hbox {d}z^{2}} \right) .\nonumber \\ \end{aligned}$$
(5.3)

The torsion scalar is found to be

$$\begin{aligned} T=\frac{-2b^{2}}{3t^{2}}-\frac{2\chi _{2} (2\chi _{1} +\chi _{2} )}{a^{2}t^{2b}}. \end{aligned}$$
(5.4)

The mean Hubble’s parameter is given by

$$\begin{aligned} H=\frac{b}{3t}. \end{aligned}$$
(5.5)
Fig. 1
figure 1

Hubble parameter vs. time.

Full size image

Expansion scalar is given by

$$\begin{aligned} \theta =\frac{b}{t}. \end{aligned}$$
(5.6)
Fig. 2
figure 2

Scalar expansion vs. time.

Full size image

Using the directional and mean Hubble’s parameter, anisotropy parameter is obtained as

$$\begin{aligned} \Delta =\frac{3\chi ^{2}}{a^{2}b^{2}t^{2\left( {b-1} \right) }}. \end{aligned}$$
(5.7)
Fig. 3
figure 3

Anisotropic parameter vs. time.

Full size image

Shear scalar is expressed as

$$\begin{aligned} \sigma ^{2}=\frac{\chi ^{2}}{2a^{2}t^{2b}}. \end{aligned}$$
(5.8)
Fig. 4
figure 4

Shear scalar vs. time.

Full size image

The deceleration parameter is derived as

$$\begin{aligned} q=\frac{3}{b}-1, \end{aligned}$$
(5.9)

where \(\chi ^{2}=2\chi _{1}^{2} +\chi _{2}^{2} =\) constant.

Fig. 5
figure 5

Deceleration parameter vs b.

Full size image

It is observed from eq. (5.4) that the torsion scalar is time-dependent. Figure 1 depicts the variation of the Hubble parameter concerning time. It shows that Hubble parameter is a decreasing function of time. As specified in figures 2 and 4, it is clear that at the initial epoch, the expansion and shear scalar diverge. Equation (5.6) shows that the expansion scalar is infinite at the beginning, i.e. \(t=0.\) It suggest that Universe starts evolving with zero volume and infinite expansion rate at \(t=0\), which is the Big-Bang scenario. The anisotropy parameter is very large initially but decreases with time and vanishes at \(t\rightarrow \infty \) as shown in figure 3. Thus, the model shows an isotropic state at the later time of its evolution. From figure 5, it is observed that the deceleration parameter is negative, i.e. the Universe is accelerating.

The energy density of MHRDE

$$\begin{aligned} \rho _{\lambda } =\frac{1}{t^{2}}\left\{ {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right\} . \end{aligned}$$
(5.10)
Fig. 6
figure 6

Energy density (MHRDE) vs. redshift z.

Full size image

Density of matter

$$\begin{aligned} \rho _{m}= & {} \frac{1}{k^{2}}\left\{ \frac{4b^{2}}{3t^{2}}+\frac{4\chi _{2} \left( {2\chi _{1} +\chi _{2} } \right) }{a^{2}t^{2b}}\right. \nonumber \\&\left. -\frac{1}{k^{2}t^{2}}\left( {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right) \right\} . \end{aligned}$$
(5.11)
Fig. 7
figure 7

Dark matter energy density vs. redshift z.

Full size image

With appropriate values of constant integration and other physical parameters, it is observed that density of MHRDE is a positive decreasing function of time and converges to zero as \(t\rightarrow \infty .\) After a critical review of eq. (5.11), it is observed that the energy density of matter is a positive decreasing function of time t. At the initial epoch (\(t=0)\), \(\rho _{m} \rightarrow \infty \), i.e., the Universe has infinitely large energy density and at large time (\(t\rightarrow \infty \)), the energy density is null (\(\rho _{m} \rightarrow 0\)). Energy density remains positive throughout the evolution of the Universe as depicted in figure 7.

Equation of state (EoS) parameter of MHRDE

$$\begin{aligned} \omega _{\lambda } =-\frac{1}{k^{2}\rho _{\lambda } }\left\{ {\frac{12b(b-2)}{9t^{2}}+\frac{12\chi _{2}^{2} }{a^{2}t^{2b}}} \right\} . \end{aligned}$$
(5.12)
Fig. 8
figure 8

EoS parameter vs. redshift z.

Full size image

It is depicted in figure 8 that the EoS parameter is negative throughout the cosmic evolution. With the growth of time, it asymptotically increases from a higher negative value to approach dust model at later times. From figure 8, one can see that the EoS parameter remains always in between \(-1<\omega <-\frac{1}{3}\) at present, as expected. However, it crosses the phantom line \(\omega <-1\) in the near future. Thus, the derived DE model is in good agreement with the well-established theoretical result as well as the recent observations.

HDE density parameter

$$\begin{aligned} \Omega _{\lambda } =\frac{3}{m^{2}}\left\{ {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right\} . \end{aligned}$$
(5.13)

Dark matter energy density parameter

$$\begin{aligned} \Omega _{m}= & {} \frac{1}{3}\left\{ \frac{12b^{2}}{k^{2}m^{2}}+\frac{36\chi _{2} \left( {2\chi _{1} +\chi _{2} } \right) }{a^{2}m^{2}t^{2b-2}}\right. \nonumber \\&\left. -\frac{9}{k^{2}m^{2}}\left( {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right) \right\} . \end{aligned}$$
(5.14)

The overall density parameter

$$\begin{aligned} \Omega= & {} \frac{3}{m^{2}}\left\{ {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right\} \nonumber \\&+\frac{1}{3}\left\{ \frac{12b^{2}}{k^{2}m^{2}}+\frac{36\chi _{2} \left( {2\chi _{1} +\chi _{2} } \right) }{a^{2}m^{2}t^{2b-2}}\right. \nonumber \\&\left. -\frac{9}{k^{2}m^{2}}\left( {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right) \right\} . \end{aligned}$$
(5.15)

Pressure of MHRDE yields

$$\begin{aligned} p_{\lambda } =-\frac{1}{k^{2}}\left\{ {\frac{12b(b-2)}{9t^{2}}+\frac{12\chi _{2}^{2} }{a^{2}t^{2b}}} \right\} . \end{aligned}$$
(5.16)
Fig. 9
figure 9

Overall density parameter vs. time.

Full size image
Fig. 10
figure 10

Pressure (MHRDE) vs. time.

Full size image

The coincidence parameter is given by

$$\begin{aligned} r{=}\frac{\frac{1}{k^{2}}\left\{ {\frac{4b^{2}}{3t^{2}}\,{+}\,\frac{4\chi _{2} \left( {2\chi _{1} +\chi _{2} } \right) }{a^{2}t^{2b}}\,{-}\,\frac{1}{k^{2}t^{2}}\left( {6\eta _{1} -m\eta _{2} \,{+}\,\frac{m^{2}\eta _{3} }{3}} \right) } \right\} }{\frac{1}{t^{2}}\left\{ {6\eta _{1} -m\eta _{2} +\frac{m^{2}\eta _{3} }{3}} \right\} }.\nonumber \\ \end{aligned}$$
(5.17)

Figure 9 depicts the variation of the overall density parameter of MHRDE vs. cosmic time during the evolution of the Universe. It can be seen that the overall density parameter tends to some constant value for sufficiently large time for suitable values of the constants. Thus, the Universe becomes spatially homogeneous, isotropic and flat at late times, which is supported by the current observations. It is clear from figure 10 that pressure of the MHRDE assumes negative values throughout the evolution of the cosmic time and vanishes as time increases indefinitely. For an accelerated expansion of the Universe under the observational data, a negative pressure is required to produce an antigravity effect. From eq. (5.17), it is observed that, r increases linearly throughout the evolution of the Universe.

6 Model for exponential law

Using eqs (4.4), (4.5) and (4.7), the scale factors can be expressed as

$$\begin{aligned} A=D_{1} \alpha ^{\frac{1}{3}}\text{ e}^{\frac{\beta t}{3}}\exp \left\{ {\frac{-\chi _{1} }{\alpha \beta }\text{ e}^{-\beta t}} \right\} \end{aligned}$$
(6.1)

and

$$\begin{aligned} B=D_{2} \alpha ^{\frac{1}{3}}\text{ e}^{\frac{\beta t}{3}}\exp \left\{ {\frac{-\chi _{2} }{\alpha \beta }\text{ e}^{-\beta t}} \right\} . \end{aligned}$$
(6.2)

At the initial epoch (\(t\rightarrow 0)\), the model has no singularity because the scale factors have constant values. With the increment in time, the scale factors tend to infinity for large time \(\left( {t\rightarrow \infty } \right) \). The spatial volume is finite at \(t=0\) and expands with an increase in time from a finite value to infinitely large value. This is consistent with the Big-Bang scenario [60, 61].

Using eqs (6.1) and (6.2), the LRS Bianchi type-I space–time filled with matter and MHRDE becomes

$$\begin{aligned} \hbox {d}s^{2}= & {} \hbox {d}t^{2}-D_{1}^{2} \alpha ^{\frac{2}{3}}\text{ e}^{\frac{\beta t}{3}}\nonumber \\&\times \exp \left\{ {-2\left[ {\frac{\chi _{1} }{\alpha \beta }\text{ e}^{-\beta t}} \right] } \right\} \left( {\mathrm{d}x^{2}} \right) -D_{2}^{2} \alpha ^{\frac{2}{3}}\text{ e}^{\frac{\beta t}{3}}\nonumber \\&\times \exp \left\{ {-2\left[ {\frac{\chi _{2} }{\alpha \beta }\text{ e}^{-\beta t}} \right] } \right\} \left( {\hbox {d}y^{2}+\hbox {d}z^{2}} \right) . \end{aligned}$$
(6.3)

The torsion scalar is derived as

$$\begin{aligned} T=-2\left\{ {\frac{\beta ^{2}}{3}+\frac{\chi _{2} (2\chi _{1} +\chi _{2} )\mathrm{e}^{-2\beta t}}{\alpha ^{2}}} \right\} . \end{aligned}$$
(6.4)

The mean Hubble’s parameter is given by

$$\begin{aligned} H=\frac{\beta }{3}. \end{aligned}$$
(6.5)

The anisotropy parameter of the expansion is

$$\begin{aligned} \Delta =\frac{3\chi ^{2}\text{ e }{ }^{-2\beta t}}{\alpha ^{2}\beta ^{2}}. \end{aligned}$$
(6.6)
Fig. 11
figure 11

Anisotropy parameter vs. time.

Full size image

The expansion scalar yields

$$\begin{aligned} \theta =\beta . \end{aligned}$$
(6.7)

The shear scalar is obtained as

$$\begin{aligned} \sigma ^{2}=\frac{\chi ^{2}\text{ e}^{-2\beta t}}{2\alpha ^{2}}. \end{aligned}$$
(6.8)
Fig. 12
figure 12

Shear scalar vs. time.

Full size image

The deceleration parameter

$$\begin{aligned} q=-1. \end{aligned}$$
(6.9)

It is observed that the torsion scalar is time-dependent. As \(t\rightarrow \infty \), the torsion tensor tends to a constant value, i.e. \(-2\beta ^{2}/{3}\). The mean Hubble parameter is constant. The mean anisotropic parameter decreases to null exponentially with an increase in time (figure 11). Thus, the space approaches isotropy in this model. The expansion of the scalar is constant throughout the evolution of the Universe. The shear scalar is also finite at the initial epoch and becomes zero as time increases as depicted in figure 12. The rate of expansion of the Universe is the fastest in this model as

$$\begin{aligned} \frac{\hbox {d}H}{\hbox {d}t}=0\Rightarrow q=-1. \end{aligned}$$

Hence, the derived model may represent the inflationary era in the early Universe and very late times of the Universe. The deceleration parameter is negative, i.e. the Universe is fast that is in agreement with the current observations of SNe Ia and CMB. Using eqs (6.7) and (6.8), it can be observed that \(\sigma ^{2}/{\theta ^{2}}\) tends to zero as \(t\rightarrow \infty \) which implies that the fluid behaves like isotropic DE.

The energy density of MHRDE is given by

$$\begin{aligned} \rho _{\lambda } =\frac{\beta ^{2}\eta _{3} }{3}. \end{aligned}$$
(6.10)

The energy density of matter is found to be

$$\begin{aligned} \rho _{m} =\frac{1}{k^{2}}\left\{ {\frac{4\beta ^{2}}{3}+\frac{4\chi _{2} \left( {2\chi _{1} +\chi _{2} } \right) \text{ e}^{-2\beta t}}{\alpha ^{2}}-\frac{k^{2}\beta ^{2}\eta _{3} }{3}} \right\} .\nonumber \\ \end{aligned}$$
(6.11)
Fig. 13
figure 13

Dark matter energy density vs. redshift z.

Full size image

The density of HDE is constant. The density of matter is constant at the early stage \(\left( {t=0} \right) \) of the Universe and show monotonic behaviour in the evolving cosmic time. With the increase in time indefinitely, the density of matter decreases and for \(k=\beta =\eta _{3} =1\), it tends to 1. Figure 13 shows that the energy density remains positive throughout the evolution of the Universe. It can be observed that the Universe is dominated by DE which may be the strongest evidence for the present cosmic expansion. All the solutions obtained are consistent with the observational results.

The EoS parameter of MHRDE is

$$\begin{aligned} \omega _{\lambda } =-\frac{1}{k^{2}\rho _{\lambda } }\left\{ {\frac{4\beta ^{2}}{3}-\frac{4\chi _{2} (2\chi _{1} +\chi _{2} )}{\alpha ^{2}\text{ e}^{2\beta t}}-\frac{k^{2}\beta ^{2}\eta _{3} }{3}} \right\} .\nonumber \\ \end{aligned}$$
(6.12)
Fig. 14
figure 14

EoS parameter vs. redshift z.

Full size image

HDE density parameter

$$\begin{aligned} \Omega _{\lambda } =\eta _{3}. \end{aligned}$$
(6.13)

DM energy density parameter

$$\begin{aligned} \Omega _{m} =\frac{4}{k^{2}}+\frac{12\chi _{2} \left( {\chi _{2} +2\chi _{1} } \right) }{\beta ^{2}k^{2}\alpha ^{2}\text{ e}^{2\beta t}}-\eta _{3}. \end{aligned}$$
(6.14)

The overall density parameter

$$\begin{aligned} \Omega =\frac{4}{k^{2}}+\frac{12\chi _{2} \left( {\chi _{2} +2\chi _{1} } \right) }{\beta ^{2}k^{2}\alpha ^{2}\text{ e}^{2\beta t}}. \end{aligned}$$
(6.15)

Pressure of MHRDE is given by

$$\begin{aligned} p_{\lambda } =-\frac{1}{k^{2}}\left\{ {\frac{4\beta ^{2}}{3}-\frac{4\chi _{2} (2\chi _{1} +\chi _{2} )}{\alpha ^{2}\text{ e}^{2\beta t}}-\frac{k^{2}\beta ^{2}\eta _{3} }{3}} \right\} .\nonumber \\ \end{aligned}$$
(6.16)

The coincidence parameter is given by

$$\begin{aligned} r=\frac{\frac{1}{k^{2}}\left\{ {\frac{4\beta ^{2}}{3}+\frac{4\chi _{2} \left( {2\chi _{1} +\chi _{2} } \right) \text{ e}^{-2\beta t}}{\alpha ^{2}}-\frac{k^{2}\beta ^{2}\eta _{3} }{3}} \right\} }{\frac{\beta ^{2}\eta _{3} }{3}}. \end{aligned}$$
(6.17)

In figure 14, the dynamical aspect of the model is assessed through the plot of the EoS parameter as a function of redshift. The EoS parameter decreases from an initial positive value to behave like DE at the late phase. The overall density parameter of the MHRDE approaches the constant value 4 as \(t\rightarrow \infty \) for \(k=1\) as shown in figure 15. The derived model predicts a flat Universe for large times and the present day Universe is very close to flat which is compatible with the observational results. It is observed that the pressure of HDE is always negative as depicted in figure 16. It can be seen that coincidence parameter at very early stage of evolution varies, but after some finite time t, it converges to a constant value and remains constant throughout the evolution.

7 Stability of the model

Using the function

$$\begin{aligned} c_{s}^{2} =\frac{\hbox {d}p}{\hbox {d}\rho }, \end{aligned}$$

the stability of the model can be discussed. The stability of the model occurs when the function \(c_{s}^{2} \) is positive. It is clear that the power-law model is initially stable but with expansion it becomes unstable whereas the exponential law model is unstable.

Fig. 15
figure 15

Overall density parameter vs. time.

Full size image
Fig. 16
figure 16

Pressure (HDE) vs. time.

Full size image

8 Statefinder diagnostic

Sahni et al [62] introduced a diagnostic proposal that makes use of the parameter pair \(\left\{ {r,s} \right\} \), the so-called ‘statefinder’. The statefinder pair \(\left\{ {r,s} \right\} \) is defined as

$$\begin{aligned} r=\frac{\dddot{a}}{aH^{3}},\quad s=\frac{r-1}{3\left( {q-\frac{1}{2}} \right) }. \end{aligned}$$
(8.1)

In power-law model, the statefinder parameters are found to be

$$\begin{aligned} r=\frac{b^{2}-9b+18}{b^{2}}\quad \hbox {and}\quad s=\frac{2}{b} \end{aligned}$$
(8.2)

The relation between the parameters is obtained as

$$\begin{aligned} r=\frac{9s^{2}-9s+2}{2}. \end{aligned}$$
(8.3)

In exponential expansion, the statefinder parameters are found to be

$$\begin{aligned} r=1\quad \hbox {and}\quad s=0. \end{aligned}$$
(8.4)

It can be observed from eqs (8.2) and (8.4) that the values of r and s ultimately correspond to the derived model to \(\Lambda \) CDM.

9 Jerk parameter

The dimensionless quantity containing the third-order derivative of the average scale factor concerning the cosmic time is termed as cosmic jerk parameter. The jerk parameter is defined as (Visser [63, 64])

$$\begin{aligned} j(t)=\frac{1}{H^{3}}\frac{\dddot{a}}{a}=q+2q^{2}-\frac{\dot{{q}}}{H}, \end{aligned}$$
(9.1)

where H is the Hubble parameter and the dot denotes differentiation with respect to the cosmic time. Flat \(\Lambda \) CDM models have a constant jerk

$$\begin{aligned} j(t)=1. \end{aligned}$$
(9.2)

In power-law model, the jerk parameter yields

$$\begin{aligned} j(t)=\frac{b^{2}-9b+18}{b^{2}}. \end{aligned}$$
(9.3)

In exponential expansion model, the jerk parameter is found to be

$$\begin{aligned} j(t)=1. \end{aligned}$$
(9.4)

10 Discussion and concluding remarks

In this article, spatially homogeneous and anisotropic LRS Bianchi type-I cosmological models are discussed in the presence of matter and MHRDE in the framework of a modified gravity theory known as f(T) gravity. Exponential and power-law volumetric expansion are assumed to obtain the solution of the field equations.

Power law expansion

  • At the initial epoch, the metric potentials vanish which is consistent with the Big-Bang model. The mean Hubble parameter is a decreasing function of time and is always positive from the beginning of the cosmic evolution to the end. This shows that we have only expanding Universe.

  • The observed isotropy of the Universe can be achieved in the derived model at the present epoch as the mean anisotropic parameter decreases with time and tends to zero at late times.

  • The matter–energy density and MHRDE density are decreasing functions of time and attain constant value at late times. Energy density is an increasing function of z and the effective pressure has a transition from negative to positive. The present study demonstrates the expanding behaviour of the Universe and on the other hand negative pressure indicates the cosmic accelerated expansion of the Universe.

  • The transitional behaviour of the EoS parameter of this model fits with SNIa data. The behaviour of EoS \(\omega \) in this model is consistent with quintom model which allows \(\omega \) crossing –1.

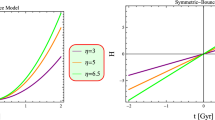
  • It can be observed that the Universe undergoes a smooth transition from early deceleration \(\left( {q>0} \right) \) to late time acceleration \(\left( {q<0} \right) \). The statefinder pair depends on the parameter b of the deceleration parameter.

  • Also, r and s are independent of cosmic time. Equation (9.3) gives a positive value for an appropriate choice of b. Thus, there is a smooth transition of the Universe from decelerating to accelerating phase of the Universe.

Exponential volumetric expansion

  • The Universe starts with zero volume at the initial epoch which is the Big-Bang scenario [65] and expands exponentially approaching infinite volume. The Universe expands homogeneously.

  • The deceleration parameter appears with negative sign implying accelerating expansion of the Universe.

  • The anisotropy parameter measures a constant value at the initial epoch while it vanishes at infinite time of the Universe. Hence, the present model is isotropic at late time which is consistent with the current observations.

  • The range is in good agreement with the recent astrophysical observations for the EoS parameter.

  • The model behaves like \(\Lambda \) CDM with the statefinder pair having values \(\left\{ {1,0} \right\} \) [66].

  • The energy density of matter deceases with the evolution of time in both power-law model and exponential law which resembles the investigations of Raushani et al [67]. The results obtained and the observed behaviour of the models agree with the recent observational facts of cosmology.