1 Introduction

Recently researches are going on for finding out the origin of accelerated expansion of the present universe. Observational evidences point towards an accelerated expansion of the universe. The astrophysical observations of the SNe Ia (Permutter et al. 1999), Cosmic Microwave Radiation (Bennett et al. 2003; Spergel et al. 2003), X-ray (Allen et al. 2004), are the main evidences for this cosmic acceleration. For this accelerating expansion of the universe a new energy with negative pressure is driven which is commonly known as dark energy (DE) (Peebles and Ratra 2003). Dark energy is a major component in energy field of the universe (Ade et al. 2013). The dark energy which is responsible for accelerated expansion of the universe has been captured a vast range of research in astrophysics. But till now the nature of dark energy is a challenging problem in theoretical physics. The earliest and simplest candidate of dark energy is the cosmological constant with time-independent equation of state \(\omega= - 1\). But from the theoretical point of view it faces the fine tuning and cosmic coincidence problem (Weinberg 1989; Overduin and Coperstock 1998). There are some other dynamical dark energy models which have time-dependent equation of state to explain the accelerated expansion of the universe such as quintessence (Wetterich 1988; Steinhardt et al. 1999), phantom (Caldwell 2002), quintom (Noijiri et al. 2005), tachyon (Padmanabhan 2002), dilation (Gasperini et al. 2002) with interacting dark energy models such as holographic (Setare 2007) and agegraphic (Cai 2007) models.

Holographic dark energy models provide a more simple and reasonable frame to investigate the problem of DE (Setare 2006; Sheykhi 2009). The energy density of holographic dark energy is \(\rho_{de} = 3c^{2}M^{2}_{pl}L^{ -2}\), where \(L\) is the infrared (IR) cutoff radius, \(M^{2}_{pl} = 1/8\pi G\) is the Planck mass and \(c\) is a constant (Li 2004). The IR cutoff has been considered as the Hubble radius (Cohen et al. 1999; Horava and Minic 2000; Thomas 2002), the particle horizon (Fischler and Susskind 1998; Bousso 1999), the future event horizon (Li 2004; Huang and Li 2004), the cosmological conformal time (Cai 2007; Wei and Cai 2008) or other generalized IR cutoff (Elizalde et al. 2005; Gao et al. 2009; Granda et al. 2008, 2009; Chen and Jing 2009; Cai et al. 2009; Xu et al. 2009; Duran and Pavon 2011; Chimento and Richarte 2011). Gao et al. (2009) have proposed a HDE model, where the future event horizon is replaced by the inverse of the Ricci scalar curvature, and this model is named as “Ricci dark energy model” (RDE), that is, a holographic Ricci DE model, whose length scale is the inverse of the Ricci curvature scalar, i.e. \(L \approx| R|^{ - 1/2}\). Granda and Oliveros (2008, 2009) suggested a new holographic Ricci DE model with the density of DE as \(\rho_{de} = 3M^{2}_{pl}( \eta H^{2} + \varsigma\dot{H} )\). In the same year, Chen and Jing (2009) modified this model as \(\rho _{de} = 3M^{2}_{pl}( \eta H^{2} + \varsigma\dot{H} + \xi\ddot{H}H^{ - 1})\).

Kumar and Yadav (2011) studied power-law and exponential-law cosmologies within the framework of Bianchi-V models with non-interacting matter fluid and DE components. Also Kumar (2013) investigated Bianchi-V space time by considering hybrid expansion law (HEL) for the average scale factor that yields power-law and exponential-law cosmologies. This motivates us in this paper to study the LRS Bianchi type II space time using hybrid expansion law (HEL) filled with dark matter and anisotropic modified holographic Ricci dark energy. Mishra and Tripathy (2015) have constructed an anisotropic dark energy cosmological model in the framework of General Relativity at the backdrop of spatially homogeneous and anisotropic Bianchi V metric by considering hybrid expansion law which establishes a cosmic transition from early deceleration to late time acceleration.

Also Misner (1968) has shown that CMBR is in favor of the existence of the anisotropic phase of the universe which becomes isotropic at late times. Thus models with anisotropic background which approach to isotropy at late times has given much importance for describing the evolution of the universe. Adhav et al. (2012), Katore et al. (2012), Kumar and Yadav (2011), and many researchers have studied cosmological models in presence of anisotropic dark energy. Das and Sultana (2015) have recently studied magnetized anisotropic ghost dark energy model. To investigate the problems like the formation of galaxies and the process of homogenization and isotropization of the universe, it becomes necessary to study the problems relating to inhomogeneous and anisotropic space-time (MacCallum et al. 1979). The above mentioned works has inspired us to study the anisotropic behavior of modified holographic Ricci dark energy in Bianchi type-II cosmological model. Bianchi type-II space-times play a fundamental role in constructing models both geometrically and physically for describing the early stages of evolution of the universe. Haji-Boutrons (1986) had derived exact solutions to Einstein’s field equations for LRS Bianchi type-II space-time. Asseo and Sol (1987) emphasized the cosmological importance of Bianchi type II models. Locally rotationally symmetric (LRS) Bianchi type-II spacetimes have already been considered by a number of authors. Lorenz (1980) has presented exact solutions for rotationally symmetric (LRS) Bianchi type II space-time with stiff-matter and an electromagnetic field. Singh and Kumar (2007) have formulated a special law of variation of Hubble’s parameter for anisotropic and homogeneous LRS Bianchi Type-II perfect fluid models in general relativity that yields a constant value of deceleration parameter. It is believed that the early universe may not have been exactly uniform. This motivates us to describe the early stages of the universe with the models having anisotropic background.

The paper is organized as follows: The metric and field equations are given in Sect. 2. The solution of the field equations and isotropization are described in Sect. 3. Also Sect. 4 deals with cosmic jerk parameter. The paper concludes with concluding remarks in Sect. 5.

2 The metric and field equations

Let us consider here the locally rotationally symmetric Bianchi type-II metric of the form

$$ ds^{2} = - dt^{2} + A^{2}\left( dx - zdy \right)^{2} + B^{2}\bigl(dy^{2} +dz^{2} \bigr), $$
(1)

where \(A(t)\) and \(B(t)\) are the scale factors in the directions of \(x\), \(y\) and \(z\) axes respectively and functions of cosmic time \(t\).

We assume that the universe is filled with matter and anisotropic modified holographic Ricci dark energy fluid. The Einstein field equations are represented by

$$ R_{\mu\nu} - \frac{1}{2}g_{\mu\nu} R = {-} ( T_{\mu\nu} +\overline{T}_{\mu\nu} ), $$
(2)

where \(R_{\mu\nu}\) is the Ricci tensor, \(R\) the Ricci scalar, \(T_{\mu \nu}\) and \(\overline{T}_{\mu\nu}\) are the energy momentum tensor for matter and anisotropic modified holographic Ricci dark energy. They have the following form

$$ \textstyle\begin{array}{l} T_{\mu\nu} = \operatorname {diag}[ \rho_{m}, 0, 0, 0 ], \\ \overline{T}_{\mu\nu} = \operatorname {diag}[ \rho_{\mathit{MH}}, {-}p_{\mathit{MH}_{x}}, {-}p_{\mathit{MH}_{y}}, {-}p_{\mathit{MH}_{z}}], \end{array} $$
(3)

where \(\rho_{m}\) is the energy density of matter and \(\rho_{\mathit{MH}}\) is the energy density for the modified holographic Ricci dark energy, \(p_{\mathit{MH}_{x}}\), \(p_{\mathit{MH}_{y}}\) and \(p_{\mathit{MH}_{z}}\) are the pressures in the directions of \(x\), \(y\) and \(z\) respectively.

By parametrising it, we get

$$\begin{aligned} \overline{T}_{\mu\nu} =& \operatorname {diag}[ 1, {-} \omega_{x}, {-} \omega_{y}, {-} \omega_{z}]\rho_{\mathit{MH}} \\ =& \operatorname {diag}\bigl[ 1, {-} \omega_{\mathit{MH}}, {-} ( \omega_{\mathit{MH}} + \delta), {-} ( \omega_{\mathit{MH}} + \delta) \bigr]\rho_{\mathit{MH}}, \end{aligned}$$
(4)

where \(\omega_{x} = \omega_{\mathit{MH}}\), \(\omega_{y} = \omega_{\mathit{MH}} + \delta\), \(\omega_{z} = \omega_{\mathit{MH}} + \delta\) are the directional EOS parameters of the modified holographic Ricci dark energy on \(x\), \(y\) and \(z\) axes respectively. The skewness parameter \(\delta\) is the deviations from \(\omega_{\mathit{MH}}\) in the directions of \(y\) and \(z\). Here \(\omega_{\mathit{MH}}\) and \(\delta\) need not be constants and can be functions of cosmic time \(t\).

The Einstein’s field equation (2), together with Eqs. (3) and (4) for the space time (1) leads to the following system of equations

$$ 2\frac{\dot{A}\dot{B}}{AB} + \frac{\dot{B}^{2}}{B^{2}} - \frac{1}{4}\frac{A^{2}}{B^{4}} = \rho_{m} + \rho_{\mathit{MH}}, $$
(5)
$$ 2\frac{\ddot{B}}{B} + \frac{\dot{B}^{2}}{B^{2}} - \frac{3}{4}\frac{A^{2}}{B^{4}} = - \omega_{\mathit{MH}}\rho_{\mathit{MH}}, $$
(6)
$$ \frac{\ddot{A}}{A} + \frac{\ddot{B}}{B} + \frac{\dot{A}\dot {B}}{AB} + \frac{1}{4}\frac{A^{2}}{B^{4}} = - \left( \omega_{\mathit{MH}} + \delta \right)\rho_{\mathit{MH}}, $$
(7)

where a overhead dot (⋅) denotes derivative with respect to the cosmic time \(t\).

3 Isotropization and cosmological solution

For LRS Bianchi type-II space time the expressions for the physical and geometrical properties such as the average scale factor \(a\) and the spatial volume \(V\) are defined as

$$ a = V^{1/3} = \bigl( AB^{2} \bigr)^{1/3}. $$
(8)

The directional Hubble parameters, expressing the volumetric expansion rates of the universe along the \(x\), \(y\) and \(z\) directions respectively are (Pradhan et al. 2011)

$$ H_{x} = \frac{\dot{A}}{A}, \qquad H_{y} = H_{z} = \frac{\dot{B}}{B}, $$
(9)

and the average Hubble parameter giving the volumetric expansion of the universe is defined as follows

$$ H = \frac{1}{3}\frac{\dot{V}}{V} = \frac{1}{3}(H_{x} + 2H_{y}). $$
(10)

The average anisotropy parameter \(\bar{A}_{m}\) of the expansion is crucial when deciding whether the model approaches isotropy or not and it is defined as follows (Kumar and Akarsu 2012)

$$ \bar{A}_{m} = \frac{1}{3}\sum_{i = 1}^{3} \left( \frac{H_{i} - H}{H} \right)^{2} = \frac{2}{9H^{2}}(H_{x} - H_{y})^{2}. $$
(11)

Here \(H_{i}\) \(( i = x, y, z )\), i.e. \(H_{x} = \frac{\dot{A}}{A}\), \(H_{y} = H_{z} = \frac{\dot{B}}{B}\) represents the directional Hubble parameters. \(\bar{A}_{m}\) is the measure of the deviation from isotropic expansion and the universe expands isotropically when \(\bar{A}_{m} = 0\).

Solving Eqs. (6) and (7), we get the relation

$$ \frac{\dot{A}}{A} - \frac{\dot{B}}{B} = \frac{c_{1}}{V} e^{-\int\frac{\delta\rho_{\mathit{MH}} +\frac{A^{2}}{B^{4}}}{\frac{\dot{A}}{A} -\frac{\dot{B}}{B}}dt}, $$
(12)

where \(c_{1}\) is the constant of integration.

Following Adhav (2011), in order to solve the above equation we assume

$$ \delta\rho_{\mathit{MH}} + \frac{A^{2}}{B^{4}} = \frac{\dot{A}}{A} - \frac{\dot{B}}{B}. $$
(13)

Using (13) on (12),

$$ \frac{\dot{A}}{A} - \frac{\dot{B}}{B} = \frac{c_{1}}{V}e^{ - t}. $$
(14)

Thus using (14), the expression for the anisotropic parameter \(\bar{A}_{m}\) reduces to

$$ \bar{A}_{m} = \frac{2}{9H^{2}}(H_{x} - H_{y})^{2} = \frac{2}{9H^{2}}\frac{c_{1}^{2}}{V^{2}}e^{ - 2t}. $$
(15)

Using (13), the Einstein’s field equations (5)–(7) reduce to

$$ 8\frac{\dot{A}\dot{B}}{AB} + 4\frac{\dot{B}^{2}}{B^{2}} - \frac {\dot{A}}{A} + \frac{\dot{B}}{B} = 4\rho_{m} + \left( 4 - \delta \right)\rho_{\mathit{MH}}, $$
(16)
$$ 8\frac{\ddot{B}}{B} + 4\frac{\dot{B}^{2}}{B^{2}} - 3\frac{\dot{A}}{A} +3\frac{\dot{B}}{B} = {-} ( 4\omega_{\mathit{MH}} + 3\delta)\rho_{\mathit{MH}}, $$
(17)
$$\begin{aligned} &{4\frac{\ddot{A}}{A} + 4\frac{\ddot{B}}{B} + 4\frac{\dot {A}\dot{B}}{AB} + \frac{\dot{A}}{A} - \frac{\dot{B}}{B}} \\ &{\quad = {-} ( 4\omega_{\mathit{MH}} + 3\delta)\rho_{\mathit{MH}}.} \end{aligned}$$
(18)

The continuity equation can be written as

$$\begin{aligned} &{\dot{\rho}_{m} + 3H\rho_{m} + \left( 1 - \delta\right )\dot{\rho}_{\mathit{MH}} - \dot{\delta} \rho_{\mathit{MH}}} \\ &{\quad {}+ 3H\left( 1 + \omega_{\mathit{MH}} \right)\rho_{\mathit{MH}} = 0.} \end{aligned}$$
(19)

Thus the continuity equation for matter is

$$ \dot{\rho}_{m} + 3H\rho_{m} = 0. $$
(20)

And the continuity equation for modified holographic Ricci dark energy is

$$ \left( 1 - \delta\right)\dot{\rho}_{\mathit{MH}} - \dot{\delta} \rho _{\mathit{MH}} + 3H\left( 1 + \omega_{\mathit{MH}} \right)\rho_{\mathit{MH}} = 0. $$
(21)

Here we have three field equations (16)–(18) with five unknowns \(A\), \(B\), \(\rho_{m}\), \(\omega_{\mathit{MH}}\) and \(\rho_{\mathit{MH}}\). In order to solve the system completely we need two extra relations.

For \(M^{2}_{pl} = 8\pi G = 1\), the modified holographic Ricci dark energy density proposed by Chen and Jing (2009) is given by

$$ \rho_{\mathit{MH}} = 3\bigl( \eta H^{2} + \zeta\dot{H} + \xi\ddot{H}H^{ - 1}\bigr), $$
(22)

where \(\eta\), \(\zeta\) and \(\xi\) are constants.

Following Akarsu et al. (2014), we consider the average scale factor ‘\(a\)’ as a combination of power law and exponential law

$$ a = a_{0}\left( \frac{t}{t_{0}} \right)^{\alpha} e^{\beta(\frac{t}{t_{0}} - 1 )}, $$
(23)

where \(\alpha\) and \(\beta\) are non-negative constants and \(a_{0}\) and \(t_{0}\) represents the present value of scale factor and age of the universe. The relation (23) gives the exponential law when \(\alpha= 0\) and the power law when \(\beta= 0\). This is a combination of exponential and power law, which is commonly known as Hybrid expansion law (HEL).

Using (23), Eq. (8) gives the spatial volume \(V\) of the model as

$$ V = a^{3} = a_{0}^{3}\left( \frac{t}{t_{0}} \right)^{3\alpha} e^{3\beta( \frac{t}{t_{0}} - 1 )}. $$
(24)

Again Eq. (14) gives

$$ \frac{A}{B} = c_{2}\exp\biggl[ c_{1}a_{0}^{ - 3} \int e^{ - t}\left(\frac{t}{t_{0}} \right)^{ - 3\alpha} e^{ -3\beta( \frac{t}{t_{0}} -1 )} dt \biggr]. $$
(25)

Equations (24) and (25) yield

$$\begin{aligned} A =& c_{2}^{2/3}a_{0}\left( \frac{t}{t_{0}} \right)^{\alpha} e^{\beta(\frac{t}{t_{0}} - 1 )} \\ &{}\times\exp\biggl[ \frac{2c_{1}a_{0}^{ - 3}}{3}\int \left( \frac{t}{t_{0}} \right)^{ - 3\alpha} e^{ - t}e^{-3\beta(\frac{t}{t_{0}} - 1 )} dt \biggr], \end{aligned}$$
(26)

and

$$\begin{aligned} B =& c_{2}^{ - 1/3}a_{0}\left( \frac{t}{t_{0}} \right)^{\alpha} e^{\beta( \frac{t}{t_{0}} - 1 )} \\ &{}\times \exp\biggl[ -\frac{c_{1}a_{0}^{ - 3}}{3}\int\left( \frac{t}{t_{0}} \right)^{ - 3\alpha} e^{-t}e^{-3\beta( \frac{t}{t_{0}} - 1 )} dt \biggr], \end{aligned}$$
(27)

where \(c_{2}\) is an integration constant.

The expressions for directional Hubble parameters, Hubble parameter, the deceleration parameter and the anisotropic parameter are

$$\begin{aligned} H_{x} =& \frac{\dot{A}}{A} = \frac{\alpha}{t} + \frac{\beta}{t_{0}} \\ &{}+\frac{2c_{1}a_{0}^{ - 3}}{3} \left( \frac{t}{t_{0}} \right)^{ -3\alpha} e^{- t} e^{ - 3\beta( \frac{t}{t_{0}} - 1 )}, \end{aligned}$$
(28)
$$\begin{aligned} H_{y} =& H_{z} = \frac{\dot{B}}{B} \\ =& \frac{\alpha}{t} + \frac{\beta}{t_{0}} - \frac{c_{1}a_{0}^{ - 3}}{3}\left( \frac{t}{t_{0}} \right)^{ -3\alpha} e^{ - t} e^{ - 3\beta( \frac{t}{t_{0}} - 1 )}, \end{aligned}$$
(29)
$$ H = \frac{\dot{a}}{a} = \frac{1}{3}(H_{x} + 2H_{y}) = \frac{\alpha}{t} + \frac{\beta}{t_{0}}, $$
(30)
$$ q = - \frac{a\ddot{a}}{\dot{a}^{2}} = - 1 + \alpha t_{0}^{2} \left( \alpha t_{0} + \beta t \right)^{ - 2}, $$
(31)
$$ \bar{A}_{m} = \frac{2c_{1}^{2}a_{0}^{ - 6}}{9}e^{ - 2t} \left(\frac{t}{t_{0}} \right)^{ - 6\alpha} e^{ - 6\beta( \frac{t}{t_{0}} -1 )} \left( \frac{\alpha}{t} + \frac{\beta}{t_{0}} \right)^{ - 2}\!\!. $$
(32)

Also from Eq. (21), we obtain

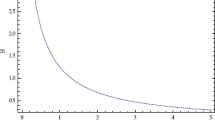
$$ \omega_{\mathit{MH}} = - 1 + \frac{\dot{\delta}}{3H} - \left( 1 - \delta \right)\frac{\dot{\rho}_{\mathit{MH}}}{3H\rho_{\mathit{MH}}}. $$
(33)

From Fig. 1 we see that the deceleration parameter (DP) is positive at early stage of the universe and also negative for late time universe. Thus it indicates that the universe exhibits transition from deceleration to acceleration. DP (\(q\)) is a decreasing function of cosmic time.

Fig. 1
figure 1

The variation of the deceleration parameter \(q\) is shown against cosmic time \(t\) with \(\alpha= 0.1\), \(\beta= 1.55\) and \(t_{0} = 13.7\)

Full size image

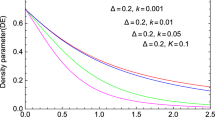
From Fig. 2, we observe that at early stage of the evolution of the universe the anisotropic parameter \(\bar{A}_{m}\) sharply increases and then decreases and at later times it ultimately tends to zero. Thus at late times the universe becomes isotropic.

Fig. 2
figure 2

The variation of anisotropic parameter \(\bar{A}_{m}\) is shown against cosmic time \(t\) with \(c_{1} = 0.12\), \(a_{0} = 1\), \(\alpha= 0.1\), \(\beta= 1.55\), \(t_{0} = 13.7\)

Full size image

The expressions for energy density of matter \(\rho_{m}\), energy density of modified holographic Ricci dark energy \(\rho_{\mathit{MH}}\), the skewness parameter \(\delta\) and EOS parameter of modified holographic Ricci dark energy \(\omega_{\mathit{MH}}\) are obtained using Eqs. (26), (27) and (30) in (20), (22), (13) and (33) respectively

$$ \rho_{m} = c_{3}a_{0}^{ - 3}\left( \frac{t}{t_{0}} \right)^{ - 3\alpha} e^{- 3\beta( \frac{t}{t_{0}} - 1 )}, $$
(34)

where \(c_{3}\) is the integration constant.

$$\begin{aligned} \rho_{\mathit{MH}} =& 3t^{ - 2} \bigl\lfloor \eta\left( \alpha t_{0} + \beta t \right)^{2}t_{0}^{ - 2} - \alpha\zeta \\ &{}+ 2\alpha\xi t_{0}\left( \alpha t_{0} + \beta t \right)^{ - 1} \bigr\rfloor , \end{aligned}$$
(35)
$$\begin{aligned} &{\delta= \frac{H_{x} - H_{y} - \frac{A^{2}}{B^{4}}}{3( \eta H^{2} +\zeta\dot{H} + \xi\ddot{H}H^{ - 1} )},} \end{aligned}$$
(36)
$$\begin{aligned} &{\omega_{\mathit{MH}} = - 1 + \frac{\dot{H}_{x} - \dot{H}_{y} - (2H_{x} -4H_{y} ) \frac{A^{2}}{B^{4}} - \dot{\rho}_{\mathit{MH}}}{3H( \eta H^{2} + \zeta\dot{H} + \xi\ddot{H}H^{ - 1} )}.} \end{aligned}$$
(37)

In Fig. 3, the black line represents matter energy density and red line indicates the modified holographic Ricci dark energy density.

Fig. 3
figure 3

The variation of the matter energy density \(\rho_{m}\), modified holographic Ricci dark energy density \(\rho_{\mathit{MH}}\) are shown against cosmic time \(t\), with \(c_{3} = 0.01\), \(a_{0} = 1\), \(\alpha= 0.1\), \(\beta= 1.55\), \(\eta=1\), \(\zeta= 0.5\), \(\xi= 0.4\), \(t_{0} = 13.7\)

Full size image

It is observed from Fig. 3, that both the dark matter and modified holographic Ricci dark energy densities decrease as the universe expands. At late times the matter energy density tends to zero and the modified holographic Ricci Dark energy density tends to a small value.

From Fig. 4, it is seen that the skewness parameter at early stage of the evolution of the universe increases sharply and then decreases and tends to zero at late times. Thus at later age of the universe the anisotropy of the modified holographic Ricci dark energy becomes isotropic.

Fig. 4
figure 4

The figure shows the skewness parameter \(\delta\) vs. cosmic time \(t\) with \(c_{1} = 0.12\), \(c_{2} = 0.05\), \(a_{0} = 1\), \(\alpha= 0.1\), \(\beta= 1.55\), \(\eta= 1\), \(\zeta= 0.5\), \(\xi= 0.4, t_{0} = 13.7\)

Full size image

Again Fig. 5 shows that the EOS parameter of modified holographic Ricci dark energy \(\omega_{\mathit{MH}}\) tends to −1 at late times. Thus at late times it behaves like cosmological constant.

Fig. 5
figure 5

The figure shows the EOS parameter \(\omega_{\mathit{MH}}\) vs. cosmic time \(t\) with \(c_{1} = 0.12\), \(c_{2} = 0.05\), \(a_{0} =0.001\), \(\alpha= 0.1\), \(\beta= 1.55\), \(\eta= 1\), \(\zeta= 0.5\), \(\xi= 0.4\), \(t_{0} = 13.7\)

Full size image

The matter energy density \(\varOmega _{m}\) and the modified holographic Ricci dark energy density parameter \(\varOmega _{\mathit{MH}}\) are defined as

$$ \varOmega _{m} = \frac{\rho_{m}}{3H^{2}} \quad\mbox{and} \quad \varOmega _{\mathit{MH}} = \frac{\rho_{\mathit{MH}}}{3H^{2}}. $$
(38)

And the total energy density parameter is

$$\begin{aligned} \varOmega =& \eta+ \frac{c_{3}a_{0}^{ - 3}}{3}\left( \frac{t}{t_{0}} \right)^{ - 3\alpha} e^{ - 3\beta( \frac{t}{t_{0}} - 1 )} \left(\frac{\alpha}{t} + \frac{\beta}{t_{0}} \right)^{ - 2} \\ &{}- \frac{\alpha \varsigma}{t^{2}}\left( \frac{\alpha}{t} + \frac{\beta}{t_{0}} \right)^{ - 2} + \frac{2\alpha\xi}{t^{3}}\left( \frac{\alpha}{t} + \frac {\beta}{t_{0}} \right)^{ - 3}. \end{aligned}$$
(39)

Figure 6 shows that as the universe expands, the total energy density \(\varOmega \) of the universe approaches to 1. Thus at late times the universe becomes spatially homogeneous, isotropic and flat.

Fig. 6
figure 6

The figure shows the plot of total energy density parameter \(\varOmega \) vs. cosmic time \(t\) with \(c_{3} = 0.01\), \(a_{0} = 1\), \(\alpha= 0.1\), \(\beta= 1.55\), \(\eta=1\), \(\zeta= 0.5\), \(\xi= 0.4\), \(t_{0} = 13.7\)

Full size image

4 Cosmic jerk parameter

It is thought that at the early universe, the dark energy would have been too small to counteract the gravity of the matter in the universe and thus the expansion was initially slow. But the dark energy dominated the matter as the universe began to expand and grew bigger in course of time and it had been started to accelerate from five to six billion years ago (Capozziello et al. 2006). It is believed that the transition from the decelerating to the accelerating phase of the universe is due to a cosmic jerk. This transition of the universe occurs for different models with a positive value of the jerk parameter and the negative value of the deceleration parameter (Blandford et al. 2004; Chiba and Nakamura 1998; Sahin 2002; Visser 2004, 2005). As an example, the \(\varLambda \)CDM models have a constant jerk \(j = 1\).

The cosmic jerk parameter is a dimensionless quantity containing the third order derivative of the average scale factor with respect to the cosmic time and it is defined as

$$ j\left( t \right) = \frac{1}{H^{3}}\frac{\dddot{a}}{a} = q + 2q^{2} - \frac{\dot{q}}{H}. $$
(40)

Using Eqs. (30) and (31) in (40), we get the expression for the jerk parameter as

$$\begin{aligned} j( t ) =& 1 - 3\alpha t_{0}^{2} \left( \alpha t_{0} + \beta t \right)^{ - 2} + 2\alpha^{2} t_{0}^{4} \left( \alpha t_{0} + \beta t\right)^{ - 4} \\ &{} + 2\alpha\beta t t_{0}^{3} \left( \alpha t_{0} +\beta t\right)^{ - 4}. \end{aligned}$$
(41)

Figure 7 shows that the cosmic jerk parameter is positive throughout the entire life of the universe and tends to 1 at late times.

Fig. 7
figure 7

The figure shows the cosmic jerk parameter \(j\) vs. cosmic time \(t\) with \(\alpha=0.1\), \(\beta= 1.55\), \(t_{0} = 13.7\)

Full size image

5 Concluding remarks

Here in this paper we have presented the LRS Bianchi type II space time filled with dark matter and anisotropic modified Ricci dark energy. We have found an exact solution of Einstein’s field equations by considering the hybrid expansion law. We have also studied the isotropy of the space and the expansion of the universe. It is seen that the anisotropy of the universe and the skewness parameter of the modified holographic Ricci dark energy tends to zero at later age of the universe. And hence our results are in favor of the recent observational data which suggested the present day isotropic behavior of the universe. From Fig. 5, it is observed that the value of the EOS parameter of modified Holographic Ricci dark energy is found to be negative and at later age of the universe it becomes equal to −1. Interestingly, at late times the modified holographic Ricci dark energy behaves like cosmological constant. It is also seen that the value of the cosmic jerk parameter is positive throughout the entire history of this model. This shows that our model strongly agrees the present day observations.