1 Introduction

Recent observational data indicate that our Universe is currently in accelerated phase (Riess et al., 1998, 1999; Perlmutter et al. 1998; Hicken et al. 2009; Dunkley et al. 2009; Percival et al. 2010). The accelerating expansion of the universe may be explained in context of the dark energy (Bamba et al. 2012). Moreover, the universe is filled about 70 percent by this unknown ingredient i.e. Dark energy and in addition that about 25 percent of this is composed by dark matter (DM). Dark energy with negative pressure and positive energy density depends on the equation of state (EoS), p=ωρ, where ω is the function of cosmic time called EoS parameter (Sharif and Zubair 2010). The present data seem to slightly favor an evolving Dark Energy with EoS ω<−1 around the present epoch and ω>−1 in the recent past. Obviously, ω cannot cross −1 for quintessence or phantoms alone. Ray et al. (2010), Akarsu and Kilinc (2010a, 2010b), Pradhan et al. (2010), Yadav et al. (2011), Yadav and Yadav (2011), Pradhan and Amirhashchi (2011), Pradhan et al. (2011), Yadav (2011), Kumar and Singh (2011), Singh (2011), Kumar and Yadav (2011), Kumar (2011), Chandel et al. (2012b, 2014), Adhav (2012), Adhav et al. (2013b), Pradhan (2013), Mishra and Biswal (2014) are some of the authors who have obtained dark energy models with variable EoS parameter.

Several theories of gravitation have been proposed as alternative to Einstein’s theory to incorporate certain desirable features in the original theory. Noteworthy among them are scalar-tensor theories of gravitation i.e. Sen (1957), Brans and Dicke (1961), Nordtvedt (1970), Sen and Dunn (1971), Ross (1972), Canuto et al. (1977), Schmidt et al. (1981), Saez and Ballester (1985). Saez and Ballester (1985) formulated a scalar-tensor theory of gravitation in which the metric is coupled with a dimensionless scalar field ϕ in a simple manner. The coupling gives a satisfactory description of the weak fields. In spite of the dimensionless character of the scalar field an antigravity regime appears. This theory also suggests a possible way to solve missing matter problem in non-flat FRW cosmologies. Singh and Agrawal (1991), Reddy and Venkateswara Rao (2001), Reddy et al. (2006, 2013a, 2013b) Mohanty and Sahu (2004a, 2004b), Adhav et al. (2007), Tripathy et al. (2008), Sahu (2010), Katore et. al (2010, 2012a), Samanta et al. (2013) are some of the authors who have studied several aspects of the Saez-Ballester scalar-tensor theory.

Bianchi type-I dark energy model with variable equation of state (EoS) parameter is presented by Rao et al. (2012b) in a scalar-tensor theory of gravitation proposed by Brans and Dicke theory. A locally rotationally symmetric Bianchi type-II (LRS B-II) space-time with variable equation of state (EoS) parameter and constant deceleration parameter have been investigated by Naidu et al. (2012c) in the scalar-tensor theory proposed by Saez and Ballester theory. An axially symmetric Bianchi type-I space time with variable equation of state (EoS) parameter and constant deceleration parameter has been investigated by Reddy et al. (2012a) in scale covariant theory of gravitation. A five dimensional Kaluza-Klein dark energy model with variable equation of state (EoS) parameter and a constant deceleration parameter is presented by Reddy et al. (2012a) in Saez and Ballester theory of gravitation. Bianchi type-III dark energy model in Saez-Ballester scalar-tensor theory have been investigated by Naidu et al. (2012a). Spatially homogeneous Bianchi type-II, VIII & IX dark energy anisotropic as well as isotropic cosmological models with variable equation of state (EoS) parameter are presented by Rao et al. (2012a) in a scalar tensor theory of gravitation proposed by Saez and Ballester. Bianchi type III dark energy cosmological model in scalar tensor theory of gravitation is investigated by Katore et al. (2012b). A spatially homogeneous and anisotropic Bianchi type-V universe with variable equation of state (EoS) parameter and constant deceleration parameter is obtained by Naidu et al. (2012b) in a scalar-tensor theory of gravitation. Locally rotationally symmetric (LRS) Bianchi type-I dark energy cosmological model with variable equation of state (EoS) parameter in general scalar tensor theory of gravitation is obtained by Rao and Neelima (2013). Mahanta and Biswal (2013) have constructed LRS Bianchi type I dark energy models with variable equation of state (EoS) parameter in Barber’s second self creation theory. Rao et al. (2013) have presented spatially homogeneous anisotropic Bianchi type II, VIII and IX as well as isotropic space times filled with perfect fluid and Dark Energy possessing dynamical energy density in Saez-Ballester scalar-tensor theory of gravitation. Anisotropic Bianchi Type-III dark energy model with time dependent deceleration parameter in Saez-Ballester theory have been investigated by Rahman and Ansari (2013). The Bianchi type-IX cosmological model with variable ω has been studied by Ghate and Sontakke (2014) in the scalar tensor theory of gravitation proposed by Saez and Ballester theory in the presence and absence of magnetic field of energy density ρ b .

Motivated with the above research work, in this paper, we have investigated Homogeneous-Hypersurface dark energy model with variable EoS parameter in Saez-Ballester scalar-tensor theory of gravitation.

2 The model and the field equations

General solutions of Einstein’s field equations for a perfect fluid distribution satisfying a barotropic equation of state for the Hypersurface-homogeneous space time have been obtained by Stewart and Ellis (1968). We consider metrics admitting a group of motions G 4 on V 3, which are Locally Rotationally Symmetric (LRS) in the form

$$\begin{aligned} ds^{2} =& - dt^{2} + A^{2}(t)dx^{2} + B^{2}(t)\bigl(dy^{2} \\ &{} + \varSigma^{2} (y,K)dz^{2}\bigr), \end{aligned}$$
(1)

where A and B are the cosmic scale functions and Σ(y,K)=siny,y,sinhy for K=1,0,−1 respectively. Hajj-Boutros (1985) developed a method to build exact solutions of field equations in case of the metric (1) in presence of perfect fluid and obtained exact solutions of the field equations which add to the rare solutions not satisfying the barotropic equation of state. Some hypersurface-homogeneous cosmological models with bulk viscous fluid and time-dependent cosmological term are investigated by Verma and Shri Ram (2010). Hypersurface-homogeneous cosmological models containing a bulk viscous fluid with time varying G and Λ have been presented by Shri Ram and Verma (2010). Chandel et al. (2012a) have investigated hypersurface-homogeneous bulk viscous fluid cosmological models with time-dependent cosmological term. Katore et al. (2012c) studied the inflationary hypersurface-homogeneous cosmological models with massless scalar field with a flat potential. Katore et al. (2012d) study the hypersurface-homogeneous cosmological model in presence of perfect fluid within the framework of Barber’s second self-creation theory of gravitation.

The field equations given by Saez and Ballester (1985) are

$$\begin{aligned} &{R_{ij} - \frac{1}{2}g_{ij}R - w\phi^{m}\biggl(\phi_{,i}\phi_{,j} - \frac{1}{2}g_{ij}\phi_{,k}\phi^{,k}\biggr) = - T_{ij}, } \end{aligned}$$
(2)
$$\begin{aligned} &{2\phi^{m}\phi_{;i}^{i} + m\phi^{m - 1}\phi_{,k}\phi^{,k} = 0. } \end{aligned}$$
(3)

Here w and m are constants, T ij is an energy momentum tensor of matter, comma and semicolon denote partial and covariant differentiation respectively with respect to time t.

The energy momentum tensor of a fluid can be written most generally in an anisotropic diagonal form:

$$ T_{j}^{i} = \operatorname {diag}\bigl[T_{1}^{1},T_{2}^{2},T_{3}^{3},T_{4}^{4}\bigr]. $$
(4)

The simplest generalization of the EoS parameter of a perfect fluid may be to determine the EoS parameter separately on each spatial axis while preserving the diagonal form of the energy-momentum tensor in a consistent way with the considered metric.

Thus we may parametrize the energy-momentum tensor (4) as follows:

$$\begin{aligned} T_{j}^{i} =& \operatorname {diag}[p_{x},p_{y},p_{z}, - \rho] \\ =& \operatorname {diag}[\omega,\omega+ \gamma,\omega+ \delta, - 1]\rho, \end{aligned}$$
(5)

where ρ is the energy density; p x ,p y ,p z are pressure on x,y,z axes respectively; ω x ,ω y ,ω z are the directional EoS parameter p=ωρ along x,y,z axes respectively. The deviation from isotropy is parameterized by setting ω x =ω,ω y =ω+γ,ω z =ω+δ. Here ω,δ,γ are not necessarily constants and can be functions of the cosmic time t.

Since \(G_{2}^{2} = G_{3}^{3}\), the energy-momentum tensor (5) can be customized to the metric (1) by

$$ T_{j}^{i} = \operatorname {diag}[\omega,\omega+ \gamma,\omega+ \gamma, - 1]\rho. $$
(6)

In co-moving coordinate system, the field equations (2) and (3) for the metric (1) with the help of (6) take the form

$$\begin{aligned} &{\frac{2\ddot{B}}{B} + \frac{\dot{B}^{2}}{B^{2}} + \frac{K}{B^{2}} - \frac{w}{2}\phi^{m}\dot{\phi}^{2} = - \omega\rho, } \end{aligned}$$
(7)
$$\begin{aligned} &{\frac{\ddot{A}}{A} + \frac{\ddot{B}}{B} + \frac{\dot{A}}{A}\frac{\dot{B}}{B} - \frac{w}{2}\phi^{m}\dot{\phi}^{2} = - (\omega+ \gamma )\rho, } \end{aligned}$$
(8)
$$\begin{aligned} &{2\frac{\dot{A}}{A}\frac{\dot{B}}{B} + \frac{\dot{B}^{2}}{B^{2}} + \frac{K}{B^{2}} + \frac{w}{2}\phi^{m}\dot{\phi}^{2} = \rho, } \end{aligned}$$
(9)
$$\begin{aligned} &{\ddot{\phi} + \dot{\phi} \biggl( \frac{\dot{A}}{A} + 2\frac{\dot{B}}{B} \biggr) + \frac{m}{2}\frac{\dot{\phi}^{2}}{\phi } = 0, } \end{aligned}$$
(10)

where a dot denotes a derivative with respect to the cosmic time t.

3 Some basic equations

The anisotropy of the expansion can be parameterized after defining the directional Hubble parameters and the mean Hubble parameter of the expansion. The directional Hubble parameters, which determine the universe expansion rates in the directions of the x,y,z axes, defined as

$$ H_{x} = \frac{\dot{A}}{A},\qquad H_{y} = H_{z} = \frac{\dot{B}}{B}. $$
(11)

The mean Hubble parameter is given as

$$ H = \frac{1}{3}\frac{\dot{V}}{V} = \frac{1}{3}\biggl( \frac{\dot{A}}{A} + 2\frac{\dot{B}}{B} \biggr), $$
(12)

where V=(AB 2) is the volume of the universe.

The physical quantities of observational interest are the expansion scalar θ, the average anisotropy parameter A m and the shear scalar σ 2. These are defined as

$$\begin{aligned} &{\theta= u_{:i}^{i} = \biggl( \frac{\dot{A}}{A} + 2\frac{\dot{B}}{B} \biggr), } \end{aligned}$$
(13)
$$\begin{aligned} &{A_{m} = \frac{1}{3}\sum_{i = 1}^{3} \biggl( \frac{H_{i} - H}{H} \biggr)^{2}, } \end{aligned}$$
(14)
$$\begin{aligned} &{\sigma^{2} = \frac{3}{2}A_{m}H^{2}. } \end{aligned}$$
(15)

Using Eqs. (11) and (12), the average anisotropy parameter can be reduced to

$$ A_{m} = \frac{2}{9H^{2}}\biggl( \frac{\dot{A}}{A} - \frac{\dot{B}}{B} \biggr)^{2}. $$
(16)

From Eqs. (7) and (8), we get

$$ \frac{\dot{A}}{A} - \frac{\dot{B}}{B} = \frac{1}{V}\biggl[ \lambda+ \int \biggl( \frac{K}{B^{2}} - \gamma\rho\biggr)Vdt \biggr], $$
(17)

where λ is a real integration constant.

Using Eqs. (16) and (17), we obtain the anisotropy parameter of the expansion

$$ A_{m} = \frac{2}{9H^{2}}\biggl[ \lambda+ \int\biggl( \frac{K}{B^{2}} - \gamma\rho\biggr)Vdt \biggr]^{2}V^{ - 2}. $$
(18)

The anisotropy parameter can be reduced to the hypersurface-homogenous models in the presence of a perfect fluid (isotropic) by choosing γ=0, i.e.

$$ A_{m} = \frac{2}{9H^{2}}\biggl[ \lambda+ K\int\frac{V}{B^{2}}dt \biggr]^{2}V^{ - 2}. $$
(19)

The integral term in (18) vanishes for

$$ \gamma= \frac{K}{\rho B^{2}}. $$
(20)

Hence, the energy-momentum tensor (6) reduces to

$$ T_{j}^{i} = \operatorname {diag}\biggl[\omega,\omega+ \frac{K}{\rho B^{2}},\omega+ \frac{K}{\rho B^{2}}, - 1\biggr]\rho, $$
(21)

whereas the anisotropy parameter (18) reduces to

$$ A_{m} = \frac{2\lambda^{2}}{9H^{2}}V^{ - 2}. $$
(22)

The anisotropy parameter is the measure of the deviation from isotropic expansion. The anisotropy parameter of the expansion is crucial to determine whether the models approach isotropy or not. It is observed that the value of anisotropy parameter A m given by (22) is similar to A m ’s obtained for Bianchi type-I, Bianchi type-III, Bianchi type-V, Bianchi type-VI0, Hypersurface-homogenous and Kantowaski-Sachs in General Relativity (Kumar and Singh, 2007; Singh and Baghel, 2009; Singh et al., 2008; Akarsu and Kilinc, 2010a, 2010b; Adhav et al., 2011a, 2011b; Singh and Beesham, 2011a).

Using the energy-momentum tensor (21), the field equations (7)–(10) now read

$$\begin{aligned} &{\frac{2\ddot{B}}{B} + \frac{\dot{B}^{2}}{B^{2}} - \frac{w}{2}\phi^{m}\dot{\phi}^{2} = - (\omega+ \gamma )\rho, } \end{aligned}$$
(23)
$$\begin{aligned} &{\frac{\ddot{A}}{A} + \frac{\ddot{B}}{B} + \frac{\dot{A}}{A}\frac{\dot{B}}{B} - \frac{w}{2}\phi^{m}\dot{\phi}^{2} = - (\omega+ \gamma )\rho, } \end{aligned}$$
(24)
$$\begin{aligned} &{2\frac{\dot{A}}{A}\frac{\dot{B}}{B} + \frac{\dot{B}^{2}}{B^{2}} + \frac{w}{2}\phi^{m}\dot{\phi}^{2} = (1 - \gamma)\rho, } \end{aligned}$$
(25)
$$\begin{aligned} &{\ddot{\phi} + \dot{\phi} \biggl( \frac{\dot{A}}{A} + 2\frac{\dot{B}}{B} \biggr) + \frac{m}{2}\frac{\dot{\phi}^{2}}{\phi } = 0. } \end{aligned}$$
(26)

Now we have a set of four equations with six unknown functions A, B, ϕ, ρ, ω, γ. To get a determinate solution of field equations, we need extra conditions. One can introduce more conditions either by an assumption corresponding to some physical situation of an arbitrary mathematical supposition. However, these procedures have some drawbacks. Physical situation may lead to differential equations which will be difficult to integrate and mathematical supposition may leads to non physical situation. Therefore, we assume two volumetric expansion laws

$$\begin{aligned} &{V = c_{1}e^{3k_{2}t}, } \end{aligned}$$
(27)
$$\begin{aligned} &{V = c_{2}t^{3n}, } \end{aligned}$$
(28)

where c 1,c 2,k and n are positive constant. The exponential law model exhibit acceleration volumetric expansion for n>1. In power law model, for 0<n<1 the universe decelerates and for n>1 the universe accelerates. On the other hand the anisotropic fluid we dealt here can be considered in the context of dark energy in the models with exponential expansion and the power law expansion for n>1.

4 Model for exponential expansion

Using Eqs. (23) and (24), we get

$$ \frac{\dot{A}}{A} - \frac{\dot{B}}{B} = \frac{\lambda}{V}. $$
(29)

For the exponential volumetric expansion, using Eqs. (27) and (29), we obtain

$$\begin{aligned} &{A = c_{4}\exp\biggl( k_{2}t - \frac{2\lambda}{9k_{2}c_{1}}e^{ - 3k_{2}t} \biggr), } \end{aligned}$$
(30)
$$\begin{aligned} &{B = c_{3}\exp\biggl( k_{2}t + \frac{\lambda}{9k_{2}c_{1}}e^{ - 3k_{2}t} \biggr), } \end{aligned}$$
(31)

where c 3, c 4 are integration constants.

It is clear that, the scale factor admit constant values at time t=0, afterwards they evolve with time without any type of singularity and finally diverge to infinity. This is consistent with big bang scenario.

The scalar field is given by

$$ \phi= \biggl\{ \biggl( \frac{m + 2}{2} \biggr)\frac{e^{ - 3k_{2}t}}{( - 3k_{2})} \biggr\} ^{\frac{2}{m + 2}}. $$
(32)

Classical scalar fields are essential in the study of the present day cosmological models. In view of the fact that there is an increasing interest, in recent years, in scalar fields in general relativity and alternative theories of gravitation in the context of inflationary Universe and they help us to describe the early stages of evolution of the Universe. From Fig. 1, it is clear that the nature of scalar field is increasing as redshift (z) increases which resembles with Naidu et al. (2012a).

Fig. 1
figure 1

Scalar field vs. redshift (z)

Full size image

Making use of Eqs. (30)–(31) in (9), we can obtain the energy density of the fluid as

$$\begin{aligned} \rho =& 3k_{2}^{2} - \frac{\lambda^{2}}{9c_{1}^{2}}e^{ - 6k_{2}t} + \frac{K}{c_{3}\exp( k_{2}t + \frac{2\lambda}{9c_{1}}e^{ - 3k_{2}t} )} \\ &{} + \frac{w}{2}e^{ - 6k_{2}t}. \end{aligned}$$
(33)

The graphical representation (Fig. 2) shows the increasing behaviour of energy density as z→∞ which resembles with the results of Sharif and Azeem (2012).

Fig. 2
figure 2

Energy density vs. red shift (z). (For K=1 (blue line), K=−1 (green line) and K=0 (red line))

Full size image

The skewness parameter is

$$ \gamma= \frac{1}{\rho} \frac{K}{c_{3}^{2}\exp\left( 2k_{2}t + \frac{2\lambda}{9c_{1}}e^{ - 3k_{2}t} \right)}. $$
(34)

The Skewness parameter decreases with redshift as shown in Fig. 3 and tends to zero as z→∞ which resembles with the results Singh and Beesham (2011b).

Fig. 3
figure 3

Skewness parameter vs. redshift (z). (For K=−1 (blue line), K=1 (green line))

Full size image

Using Eqs. (29)–(30) in Eq. (7), we obtain the EoS parameter as

$$\begin{aligned} \omega =& - \frac{1}{\rho} \biggl\{ 4k_{2}^{2} + \frac{4\lambda k_{2}t}{3c_{1}}e^{ - 3k_{2}t} - \frac{\lambda^{2}}{9c_{1}^{2}}e^{ - 6k_{2}t} \\ &{}+ \frac{K}{c_{3}^{2}\exp( 2k_{2}t + \frac{2\lambda}{9c_{1}}e^{ - 3k_{2}t} )} - \frac{w}{2}e^{ - 6k_{2}t} \biggr\} . \end{aligned}$$
(35)

Models with ω crossing −1 near the past have been mildly favored by the analysis on the nature of dark energy from recent observations (for example see Astier et al. 2006). SNeIa alone favors a ω larger than −1 in the recent past and less than −1 today, regardless of whether using the thesis of a flat universe (Astier et al. 2006; Nojiri and Odintsov 2006) or not (Dicus and Repko 2004). The SN Ia data suggests that −1.67<ω<−0.62 (Knop et al., 2003) while the range of w by a combination of SN Ia data, CMB anisotropy and galaxy clustering statistic is −1.33<ω<−0.79 (Tegmark et al., 2004). The limit −1.44<ω<−0.92 is the latest observational results with 68 % confidence level (Hinshaw et al., 2009; Komatsu et al., 2009). Evolution of equation of state with respect to red-shift is shown in Fig. 4. We can see for large enough red-shift it goes to a huge positive amount, which shows an inflationary behavior for vacuum universe which resembles with the investigations of Masoudi and Saffari (2013). In terms of redshift the average scale factor (Amirhashchi, 2013; Malekjani, 2013; Debnath and Chattopadhyay, 2013) is defined through the relation \(1 + z = \frac{1}{a}\), where we have considered the value of mean scale factor at the present epoch to be 1 for graphical representation. In the past, ω evolves from a negative value and increases gradually to a constant value in future which resembles with Sahoo et al. (2014). For K=−1, the behavior of the equation of state resembles with Adhav et al. (2013a) as it approaches to stiff fluid ω=1.

Fig. 4
figure 4

EoS parameter vs. redshift (z). (For K=1 (blue line), K=−1 (green line) and K=0 (red line))

Full size image

The Hubble parameter is obtained as

$$ H = k_{2}. $$
(36)

The deceleration parameter yields as

$$ q = \frac{d}{dt}\biggl( \frac{1}{H} \biggr) - 1 = - 1. $$
(37)

The sign of q indicate whether the universe accelerates or decelerates. A positive sign of q corresponds to the standard decelerating model and the negative sign of q indicate acceleration. Cosmological observations indicated that the expansion of the universe is accelerating at the present and it was decelerating in the past. Here from Eq. (37), it is observed that the deceleration parameter is negative i.e. the universe is accelerating. Observational data (Ade et al. 2013) shows that the present value of deceleration parameter lies somewhere in the range −1<q<0. Therefore in this case we can construct an accelerating model of the universe.

The mean anisotropic parameter becomes

$$ A_{m} = \frac{1}{3}\sum_{i = i}^{3} \biggl( \frac{H_{i} - H}{H} \biggr)^{2} = \frac{2\lambda^{2}}{9k_{2}^{2}c_{1}^{2}}e^{ - 6k_{2}t}. $$
(38)

One should note that the above anisotropy parameter of the expansion is equivalent to the ones obtained for exponential expansion in Bianchi type-I (Kumar and Singh 2007) and Bianchi type-V (Singh et al. 2008; Singh and Baghel 2009) cosmological models with isotropic fluid and is exactly same for exponential expansion in Bianchi type-III (Akarsu and Kilinc, 2010a, 2010b) for anisotropic fluid. We observe that at t=0,A m ≠0 that means fluid anisotropic at early epoch and at t→∞,A m =0 i.e. at large time fluid isotropization, i.e. from Eq. (38), we should note that the anisotropy of the expansion A m is not promoted by the anisotropy of the fluid and decreases to null exponentially as t increase.

The expansion scalar and shear scalar are found to be

$$\begin{aligned} &{\theta= 3H = 3k_{2}, } \end{aligned}$$
(39)
$$\begin{aligned} &{\sigma^{2} = \frac{3}{2}A_{m}H^{2} = \frac{\lambda^{2}}{3k_{2}^{2}c_{1}^{2}}e^{ - 6k_{2}t}. } \end{aligned}$$
(40)

The rate of expansion of the universe is constant for k 2>0 and the shear scalar σ→0, as t→∞. The shear scalar is finite at t=0. Since H=k 2, hence \(\frac{dH}{dt} = 0\), which implies the greatest value of Hubble’s parameter and the fastest rate of expansion of the universe. Therefore the solutions conferred during this model are in line with the observations and will notice applications within the analysis currently time evolution of the particular universe.

One will observe that the universe approaches to symmetry monotonically even within the presence of the anisotropic fluid, and also the anisotropic fluid isotropizes and evolves to the constant just in case of exponential volumetrically expansion.

5 Model for power law expansion

For the power law volumetric expansion, using Eq. (28) we obtain

$$\begin{aligned} &{A = c_{6}t^{n}\exp\biggl( \frac{ - 2\lambda}{3(3n - 1)c_{2}}t^{1 - 3n} \biggr), } \end{aligned}$$
(41)
$$\begin{aligned} &{B = c_{5}t^{n}\exp\biggl( \frac{\lambda}{3(3n - 1)c_{2}}t^{1 - 3n} \biggr). } \end{aligned}$$
(42)

At t=0 both the scale factors vanish, start evolving with time and finally as t→∞ they diverge to infinity. This is consistent with the big bang model. As scale factors diverge to infinity at large time there will be Big rip at least as far in the future.

The scalar field is given by

$$ \phi= \biggl\{ \biggl( \frac{m + 2}{2} \biggr)\frac{t^{ - 3n + 1}}{( - 3n + 1)} \biggr\} ^{\frac{2}{m + 2}}. $$
(43)

It is clear that the nature of scalar field is increasing as redshift (z) increases. The physical behaviour of Scalar field vs. redshift in Fig. 5, resembles with the investigations of Farajollahi et al. (2011).

Fig. 5
figure 5

Scalar field vs. redshift (z)

Full size image

Making use of Eqs. (41) and (42) in (9), we obtain

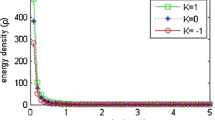
$$\begin{aligned} \rho =& \frac{6n^{2}}{t^{2}} - \frac{\lambda^{2}}{3c_{2}^{2}}t^{ - 6n} + \frac{K}{c_{5}^{2}}t^{ - 2n}\exp\biggl( \frac{2\lambda}{3(3n - 1)c_{2}}t^{1 - 3n} \biggr) \\ &{} - \frac{w}{2}t^{ - 6n}. \end{aligned}$$
(44)

It is observed in Fig. 6 that the behaviour of energy density is same for K=1,−1,0. At initial epoch, the energy density was positive and as redshift increases, it tends to be negative. The negative energy density does not violate any law of physics but this violates the weak energy condition. The negative energy density indicates that there is vacuum instability in the inertial frames at early stage of the evolution. The energy density decayed to be negative which resembles with Frampton (2004).

Fig. 6
figure 6

Energy density vs. redshift (z). (For K=1 (blue line), K=−1 (green line) and K=0 (red line))

Full size image

The skewness parameter is found as

$$ \gamma= \frac{1}{\rho} \frac{K}{c_{5}^{2}}t^{ - 2n}\exp\biggl( \frac{2\lambda}{3(3n - 1)c_{2}}t^{1 - 3n} \biggr). $$
(45)

It is clear from Eq. (45) that the skewness parameter tends to zero as t→∞. For K=1, the skewness parameter start with zero value, increases to maximum value and then approaches to zero i.e. the behavior of the fluid may be isotropic at early stage and may be isotropic in the future. This is in accordance with the results obtained by Akarsu and Kilinc (2010a, 2010b) and Katore et al. (2014) as shown in Fig. 7.

Fig. 7
figure 7

Skewness parameter vs. redshift (z). (For K=1 (red line), K=−1 (green line))

Full size image

The deviation free EoS parameter is obtained as

$$\begin{aligned} \omega =& \frac{ - 1}{\rho} \biggl\{ \frac{3n^{2}}{t^{2}} - \frac{2n}{t^{2}} + \frac{\lambda^{2}}{3c_{2}^{2}}t^{ - 6n} \\ &{} + \frac{K}{c_{5}^{2}}t^{ - 2n}\exp\biggl( \frac{2\lambda}{3(3n - 1)c_{2}}t^{1 - 3n} \biggr) - \frac{w}{2}t^{ - 6n} \biggr\} . \end{aligned}$$
(46)

In order to explain Dark Energy of the current universe, different kinds of fluids are characterized by the positive values of ω, with the help of Bianchi models. One can use ω with negative values. The universe passes through Λ CDM epoch, when ω=−1. We live in the phantom-dominated universe if ω<−1 and for ω>−1, the quintessence dark era occurs. It is worthwhile to mention here that observational analysis of a recent supernova strongly supports w<−1 being EoS parameter for phantom Dark Energy (Alam et al. 2004; Bertolami et al. 2004; Singh et al. 2003). Figure 8, clearly shows ω that evolves at intervals a spread, that is in nice agreement with SN Ia and cosmic radiation observations. We observe that in early stage of evolution of the universe, the EoS parameter ω was positive (i.e. the universe was matter dominated) and at late time it is evolving with negative value (i.e. at the present epoch) comes toward zero i.e. the universe may dominate by dust in the future. At z→∞, the value of ω turns out to be zero which indicate that the pressure of the universe vanishes at that epoch which resembles with Shamir and Bhatti (2012).

Fig. 8
figure 8

EoS parameter vs. redshift (z). (For K=1 (blue line), K=−1 (green line) and K=0 (red line))

Full size image

The Hubble parameter is obtained as

$$ H = \frac{n}{t}. $$
(47)

The deceleration parameter yields as

$$ q = \frac{d}{dt}\biggl( \frac{1}{H} \biggr) - 1 = \frac{1}{n} - 1. $$
(48)

For this model, we have noted that the volume of the universe expands indefinitely for all values of n. The deceleration parameter is always negative for n>1 indicating accelerating universe and attained its fastest rate of expansion q=−1 for large n.

The mean anisotropic parameter becomes

$$ A_{m} = \frac{2\lambda^{2}}{9n^{2}c_{2}^{2}}t^{2 - 6n}. $$
(49)

From the value of mean anisotropic parameter in Eq. (49), it is clear that the universe was anisotropic at early stage of evolution and approach to isotropy at large time. Mean anisotropic parameter behaves monotonically, decay to zero for \(n > \frac{1}{3}\) and diverge for \(n < \frac{1}{3}\) as t→∞, and is constant for \(n = \frac{1}{3}\) which resembles with (Akarsu and Kilinc, 2010a, 2010b; Adhav et al., 2011b).

The expansion scalar and shear scalar are found to be

$$\begin{aligned} &{\theta= \frac{3n}{t}, } \end{aligned}$$
(50)
$$\begin{aligned} &{\sigma^{2} = \frac{\lambda^{2}}{3c_{2}^{2}}t^{ - 6n}. } \end{aligned}$$
(51)

We observe that the Hubble parameter H, expansion scalar θ, shear scalar σ are very large near t∼0 and finally tends to zero as t→∞. The rate of expansion of the universe decreases with time.

6 Some observational parameters

In this section, we investigate the consistency of our models with the observational parameters. We measure the physical parameters such as redshift, look-back time, luminosity distance, distance modulus.

6.1 For exponential expansion model

6.1.1 Redshift

The average scale factor a and redshift z, are related by

$$ a = \frac{a_{0}}{1 + z}, $$
(52)

where a 0 is the present value of the scale factor. Hence

$$ a = c_{1}^{\frac{1}{3}}e^{kt}. $$
(53)

There follows that

$$ z = \biggl( \frac{e_{0}^{t}}{e^{t}} \biggr)^{k} - 1. $$
(54)

6.1.2 Look-back time

The look-back time, Δt=t 0−t(z), is the difference between the age of the universe at present time (z=0) and the age of the universe when a particular light ray at redshift z was emitted. The radial travel time (or look-back time) Δt for a photon emitted by a source at instant t and received at t 0 is given by

$$ t - t_{0} = \int_{a}^{a_{0}} \frac{da}{\dot{a}}. $$
(55)

From Eq. (54) we can get

$$ t = t_{0} - \frac{\ln(1 + z)}{H_{0}}. $$
(56)

This equation can be expressed as

$$ H_{0}(t_{0} - t) = z - \frac{z^{2}}{2} + \frac{z^{3}}{3} - \frac{z^{4}}{4} +\cdots, $$
(57)

where H 0 is the Hubble’s constant at present in km s−1⋅Mpc−1 and its value is believed to be somewhere between 50 and 100 km s−1 Mpc−1. For small z, we have

$$ H_{0}(t_{0} - t) \approx z. $$
(58)

6.1.3 Proper distance d(z)

The proper distance d(z) is defined as the distance between a cosmic source emitting light at any instant t=t 1 located at r−r 1 with redshift z and an observer at r=0 and t=t 0 receiving the light from the source emitted i.e.

$$ d(z) = r_{1}a_{0}, $$
(59)

where

$$ r_{1} = \int_{t_{1}}^{t_{0}} \frac{dt}{a} = H_{0}^{ - 1}a_{0}^{ - 1}z. $$
(60)

Hence

$$ d(z) = H_{0}^{ - 1}z. $$
(61)

The proper distance d(z) is linear with redshift z. From Eq. (60), we obtained d(z=∞) is always infinite.

6.1.4 Luminosity distance

Luminosity distance is another important concept of theoretical cosmology of a light source. The luminosity distance is a way of expanding the amount of light received from a distant object. In other words, it is defined in such a way as generalizes the inverse square law of the brightness in the static Euclidean space to an expanding curved space (Waga, 1993). The luminosity distance of a light source is derived as the ratio of the detected energy flux, L and the apparent luminosity l ∗, i.e.,

$$d_{L}^{2} = \frac{L}{4\pi l_{*}}. $$

It takes the form

$$ d_{L} = r_{1}(1 + z)a_{0} = (1 + z)d(z). $$
(62)

Using Eq. (60), Eq. (62) reduces to

$$ H_{0}d_{L} = (1 + z)z. $$
(63)

It is seen in Fig. 9, which the luminosity distance increases faster with red shift, exactly as required by the supernova data which resembles with the investigations of Singh et al. (2009). The physical behaviour of the luminosity distance vs redshift resembles with Singh and Beesham (2011a).

Fig. 9
figure 9

Luminosity distance vs. redshift (z)

Full size image

6.1.5 Distance modulus

It is necessary for the investigations of type Ia supernovae to explore dark energy and the constraint the models. Since SN Ia behave as excellent standard candles, they can be used to directly measure the expansion rate of the universe upto high redshift, comparing with the present rate. The distance modulus (μ(z)) is given by

$$ \mu(z) = 5\log d_{L} + 25. $$
(64)

Thus, the distance modulus (μ(z)) in terms of redshift parameter z is obtained as

$$ \mu(z) = 5\log\biggl[ \frac{z(1 + z)}{H_{0}} \biggr] + 25. $$
(65)

6.2 For power law model

To investigate the consistency of the power law model, we measure the physical parameters such as redshift, look-back time, luminosity distance etc. as we have obtained for the exponential expansion model.

6.2.1 Redshift

$$ z = \biggl( \frac{t_{0}}{t} \biggr)^{n} - 1. $$
(66)

6.2.2 Look-back time

$$ H_{0}(t_{0} - t) = n\biggl[ 1 - (1 + z)^{\frac{ - 1}{n}} \biggr]. $$
(67)

6.2.3 Luminosity distance

$$ d_{L} = \frac{(1 + z)H_{0}^{ - 1}}{1 - n}\biggl\{ 1 - (1 + z)^{1 - \frac{1}{n}} \biggr\} . $$
(68)

6.2.4 Distance modulus

The distance modulus (μ(z)) in terms of redshift parameter z is obtained as

$$ \mu(z) = 5\log\biggl[ \frac{(1 + z)H_{0}^{ - 1}}{1 - n}\biggl\{ 1 - (1 + z)^{1 - \frac{1}{n}} \biggr\} \biggr] + 25. $$
(69)

7 Conclusion

We have investigated anisotropic dark energy for Hypersurface-Homogeneous metric in the context of Saez-Ballester theory of gravitation. The two models of universe, i.e. exponential model and power law model are lead by the assumption of constant deceleration parameter. Some important cosmological physical parameters for the solutions such as expansion scalar θ, shear scalar σ 2, mean anisotropy parameter and average Hubble parameter are evaluated. The energy density ρ, the deviation—free EoS parameter ω and the skewness parameter δ are dynamics quantities (functions of time).

In the Exponential volumetric expansion, the scale factors attain constant values at initial time. With the increase in time, they start increasing without any type of initial singularity and finally diverge to infinity as t→∞. Thus the universe starts with zero volume at the initial epoch and expands exponentially approaching to infinite volume. At t=0, the anisotropy parameter A m is constant and decreases with time for k 2>0. It means that the universe was anisotropic at early stage and approaching to isotropy as time t increases i.e. the space approaches to isotropy in this model since A m →0 as t→∞. The expansion scalar is constant throughout the evolution of the universe and therefore the universe exhibits uniform exponential expansion in this model. The shear scalar is finite at t=0 and tends to \(\frac{\lambda^{2}}{3k_{2}^{2}c_{1}^{2}}\) as t increases. It has also been observed that \(\lim_{t \to0}\frac{\sigma^{2}}{\theta^{2}}\) turns out to be a constant. Thus homogeneity is approached by the model and the matter vanishes near the origin; this agrees with a result already given by Collins (1977). Also, the deceleration parameter appears with negative sign which implies accelerating expansion of the universe as one can expect for exponential volumetric expansion.

In the power law solutions, one gets q=−1 as n→∞, this implies an exponential evolution of the average scale factor. For this model, we have noted that the volume of the universe expands indefinitely for all values of n. The average scale factor has a linear growth with constant velocity and q=0 as n=1, which shows the marginal inflation (Singh and Beesham, 2011b). At t=0, the scale factor vanishes and hence the model has an initial point singularity. We observe that the Hubble parameter is infinite at t=0 and converges to zero as t→∞. The anisotropic parameter exhibits a non-trivial behaviour and tends to zero for late times for \(n > \frac{1}{3}\). The model is anisotropic, for all the values of 0<t<∞, as the shear scalar is non-zero. Dark Energy model presents the dynamics of EoS parameter provided by (46) whose range is in good agreement with the acceptable range by the recent observations (Knop et al., 2003; Tegmark et al., 2004; Komatsu et al., 2009; Hinshaw et al., 2009).

In both the models, the scalar field increases as redshift increases which resembles with the results of Naidu et al. (2012c). The astrophysical phenomena such as look-back time, luminosity distance are also discussed and show that the models are compatible with present observations. It is important to note that when ϕ→0, our results resembles to (Singh and Beesham, 2011b). Thus, even if we observe an isotropic expansion in the present universe we still cannot rule out possibility of Dark Energy with an anisotropic EoS within the framework of Saez-Ballester theory of gravitation in Homogeneous–Hypersurface space-time.