Estimation of Realistic Microtexture Region Orientation Distribution Functions Using Eddy Current Data

Abstract

Microtexture regions (MTRs) within titanium alloys are collections of grains with similar crystallographic orientation. The presence of MTRs can be detrimental to the life of an engine component; thus, a method for detecting and characterizing MTR is needed. Eddy current testing, a nondestructive evaluation method, is sensitive to changes in conductivity which are related to local changes in crystallographic orientation. Previous work has demonstrated the ability of eddy current testing to determine the orientation distribution function (ODF) of a simulated MTR within a simulated microstructure using approximate Bayesian computation techniques. This article will extend these methods to realistic MTR configurations. We review the ODF estimation technique, discuss modifications to the algorithm that are required to apply it to realistic microstructures and then demonstrate its use on simulated eddy current data of a real titanium specimen.

Introduction

Microtexture regions (MTR) within titanium alloys are collections of grains with similar crystallographic orientation. They have potential to have a significant impact on the component fatigue life due to their ability to drive early subsurface crack nucleation and accelerated crack growth.^1,2,3,4 Thus, a method of characterizing MTR is crucial for safe operation of components made from this material system.

Of primary interest is the size of the MTR as well as its primary orientation, described by a component orientation distribution function (cODF). Scanning electron microscopy (SEM) electron backscatter diffraction (EBSD) is capable of measuring the orientation of micron-scale surface grains and their aggregation in MTR. However, practical limitations prohibit the use of SEM EBSD for component-scale structures; in particular, the sample has to be relatively small, typically < $1'' \times 1''$ in area, with a flat, damage-free surface. One alternative to SEM EBSD is an electromagnetic inspection method called eddy current testing (ECT). While this method is sensitive to changes in local conductivity caused by spatially varying cODF, its spatial resolution is too low to resolve MTR. However, it was demonstrated in Ref. 5 that eddy current data can be used to recover the cODF of an MTR provided the boundaries of the MTR are known.

The methods developed in Ref. 5 utilized approximate Bayesian computational techniques along with simulated eddy current data to determine the cODFs of a simulated microstructure with known segmentation. The goal of this article is to extend those techniques to realistic microtexture configurations. As discussed in Ref. 5, the assumed grain size of the underlying specimen impacts the outcome of the inversion algorithm. While this is not an issue for simulated specimens, where the grain size is known, it does pose a challenge when applying the technique to realistic microstructures. In this article, we modify the inversion algorithm to accommodate the unknown grain size and develop a prior for the unknown cODFs that incorporates characteristics of realistic cODFs. The paper is organized as follows: "Definition of the Problem" section contains a detailed definition of the problem, "Methods" section describes the forward model, inversion technique and prior distribution, "Effects of Grain Size" section discusses the modification to the algorithm, "Numerical Examples" sectioin presents numerical results, and "Conclusion" section provides conclusions and future work.

Definition of the Problem

Microstructure of Titanium

Most titanium alloys of interest to us consist primarily of grains with hexagonal close-packed crystal structure, as shown in Fig. 1. The hexagonal prism shown in Fig. 1 represents the unit cell of crystal orientation for grains with hexagonal symmetry.

Crystallographic orientation is the set of rotations that generates the orientation of a grain with respect to the global frame of reference. In this work, it will be described in terms of three Euler angles: $(\psi _1, \theta , \psi _2)$. The first angle, $\psi _1$, describes the rotation about the original z-axis, $\theta$ describes the subsequent rotation about the new x-axis, and $\psi _2$ describes the final rotation about the new z-axis. The axis parallel to the z-axis is referred to as the c-axis of the crystal; the plane spanned by the x and y axes is referred to as the basal plane. The first and second Euler angles are referred to respectively as the heading and tilt of the c-axis.

In general, $\psi _1 \in [0, 2\pi ]$, $\theta \in [0, \pi ]$ and $\psi _2 \in [0, 2\pi ]$. However, due to the symmetry of the hexagonal crystal, all rotations can be expressed using Euler angles in the ranges of $\psi _1 \in [0, 2\pi ]$, $\theta \in [0, \pi /2]$ and $\psi _2 \in [0, \pi /3]$. In addition, the sensitivity of eddy current impacts the range of potential orientations. In $\alpha$-titanium, conductivity is isotropic in the basal plane but differs along the c-axis. Since eddy current is only sensitive to changes in conductivity, it is not sensitive to changes in the third Euler angle, which is simply a final rotation of the basal plane. For further background on microstructure, we refer to Ref. 6. For further information on the microstructure of titanium specifically, we refer to Ref. 7.

Definition of the ODF

Within this work, we will assume that the orientation of each grain is an independent realization of the random vector $(\Psi _1, \Theta , \Psi _2)$, whose joint probability distribution is given by the collection of cODFs that comprise the specimen ODF. In particular, if we assume that the underlying material V consists of p regions $V_1, V_2, \ldots and V_p$ such that

$$\begin{aligned} \bigcup _{h = 1}^p V_h = V, \quad V_i \cap V_j = \emptyset , i \ne j, \end{aligned}$$

(1)

and $f_h$ is the cODF for the region $V_h$; then, the ODF is given by

$$\begin{aligned} f(\psi _1, \theta , \psi _2 \mid x,y) = \left\{ \begin{array}{c} f_1(\psi _1, \theta , \psi _2), \quad (x,y) \in V_1 \\ f_2(\psi _1, \theta , \psi _2), \quad (x,y) \in V_2 \\ \vdots \\ f_p(\psi _1, \theta , \psi _2), \quad (x,y) \in V_p \end{array} \right. . \end{aligned}$$

(2)

Each cODF possesses the same properties as a probability density function, that is, it is strictly positive and integrates to 1.

Fig. 1

Unit cell of crystal orientation for grains with hexagonal symmetry. The three rotations represent the three Euler angles used to describe crystallographic orientation.

Methods

Eddy Current Forward Model

The forward model used to simulate data is the approximate impedance integral (AII) model, developed in Ref. 8. The starting point for the forward model is Maxwell’s equations; specifically, Ampere’s law and Faraday’s law in differential form are given by

$$\begin{aligned} \nabla \times \mathbf {H}&= j \omega \epsilon \mathbf {E}+ {\overline{\sigma }} \cdot \mathbf {E} \end{aligned}$$

(3)

$$\begin{aligned} \nabla \times \mathbf {E}&= -j \omega \mu \mathbf {H}, \end{aligned}$$

(4)

where $\omega$ is the angular frequency, $\mu$ is the permeability, $\epsilon$ is the scalar permitivitty, and ${\overline{\sigma }}$ is the anisotropic conductivity tensor. It is assumed there are no external fields; in addition, the only current sources are the induced currents in the conductive material and the displacement currents. As shown in Ref. 9, Eqs. 3 and 4 can be combined to yield the expression

$$\begin{aligned} \oint _S (\mathbf {E}\times \mathbf {H}) \cdot {\mathbf {n}} dS= & {} \int _V j \omega \mu \mathbf {H}\cdot \mathbf {H}+ j \omega \epsilon \mathbf {E}\cdot \mathbf {E} \\&+ \mathbf {E}\cdot ({\overline{\sigma }} \cdot \mathbf {E}) ] dV. \end{aligned}$$

(5)

where S is the surface enclosing a flaw in the conductive medium and V is the volume of the flaw. For our application, S is the entire surface of the sample. From Ref. 10, this expression can be related to the impedance of an eddy current coil to yield

$$\begin{aligned} \Delta Z&= \frac{1}{I^2} \oint _S (\mathbf {E}_b \times \mathbf {H}_a - \mathbf {E}_a \times \mathbf {H}_b) \cdot {\mathbf {n}} dS \\&= \frac{1}{I^2} \int _V \left[ j \omega \mu (\mathbf {H}_a \cdot \mathbf {H}_a - \mathbf {H}_b \cdot \mathbf {H}_b) \right. \\&\quad \left. + j \omega \epsilon (\mathbf {E}_a \cdot \mathbf {E}_a - \mathbf {E}_b \cdot \mathbf {E}_b) \right. \\&\quad \left. + \mathbf {E}_a \cdot (\sigma _a \mathbf {I}_{3 \times 3} \cdot \mathbf {E}_a) - \mathbf {E}_b \cdot (\overline{\sigma _b} \cdot \mathbf {E}_b) \right] dV, \end{aligned}$$

(6)

where all fields with the subscript a are the result of exciting the eddy current coil above an isotropic homogeneous material with conductivity $\sigma _a$, while all fields with the b subscript are the result of exciting the coil above an anisotropic, polycrystalline material. Due to the relatively low conductivity changes in a rotated grain, the Born approximation can be applied to Eq. 6. Under this approximation, we find that $\mathbf {H}_a \approx \mathbf {H}_b$ and $\mathbf {E}_a \approx \mathbf {E}_b$, in which case Eq. 6 becomes

$$\begin{aligned} \Delta Z = \frac{1}{I^2} \int _V {\mathbf {E}_a \cdot (\sigma _a \mathbf {I}_{3 \times 3} - {\overline{\sigma }}_b) \cdot \mathbf {E}_a} \; dV, \end{aligned}$$

(7)

The rotated, anisotropic conductivity tensor ${\overline{\sigma }}_b$ is a function of the local crystallographic orientation and is given by

$$\begin{aligned} {\overline{\sigma }}_b = \left[ \begin{array}{ccc} \sigma _{11} &{} \sigma _{12} &{} \sigma _{13}\\ \sigma _{12} &{} \sigma _{22} &{} \sigma _{23} \\ \sigma _{13} &{} \sigma _{23} &{} \sigma _{33} \end{array} \right] , \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{array}{cc} \sigma _{11} = \sigma _{xx} + (\sigma _{zz} - \sigma _{xx})s_1^2 s_2^2 &{} \sigma _{12} = s_1 c_1 s_2^2 (\sigma _{xx} - \sigma _{zz})/2 \\ \sigma _{13} = -s_1 c_2 s_2 (\sigma _{xx} - \sigma _{zz}) &{} \sigma _{22} = \sigma _{xx} + (\sigma _{zz} - \sigma _{xx})s_2^2 + (\sigma _{xx} - \sigma _{zz})s_1^2 s_2^2 \\ \sigma _{23} = c_1 c_2 s_2 (\sigma _{xx} - \sigma _{zz}) &{} \sigma _{33} = \sigma _{zz} +(\sigma _{xx} - \sigma _{zz} )s_2^2 \end{array} \end{aligned}$$

and $c_i$ and $s_i$ are the sine and cosine of the ith Euler angle, respectively. The fact that ${\overline{\sigma }}_b$ is dependent on only $\psi _1$ and $\theta$ is consistent with the fact that eddy current is not sensitive to changes in the third Euler angle within $\alpha$-titanium. For further details on this model, we refer to Ref. 8.

We note that the AII model produces the same response for orientations given by $(\psi _1, \theta )$ and $(\psi _1 + \pi , \theta )$. As a result, the solution to the inverse problem is non-unique. Thus, it is understood that for any solution we obtain, the same distribution with the first Euler angle rotated $\pi$ radians is also a solution.

In the numerical examples that follow, the data are simulated using a shielded elliptical absolute probe with axes equal to 750 µm and 250 µm. We note that for numerical computation of the model, the field $\mathbf {E}_a$ for this coil is pre-computed using COMSOL.

Approximate Bayesian Computation

As discussed in Ref. 5, one of the major challenges of the ODF estimation problem is the lack of a deterministic forward model that generates a set of simulated eddy current data given a fixed ODF. That is, even if we know the true ODF that generated a particular set of eddy current data, we are unable to recreate that data. As a result, traditional Bayesian inversion is not feasible since we cannot form a likelihood function. To resolve this issue, we instead make use of approximate Bayesian computation (see, for instance, Refs. 11,12,13,14). This method was first developed for problems where the likelihood function is either computationally expensive or does not exist. Recall that in traditional Bayesian computation, the solution to the inverse problem is the posterior distribution of the unknown $\xi$ conditioned on the measured data z, that is,

$$\begin{aligned} \pi _{\mathrm{post}}(\xi \mid z) \propto \pi (z \mid \xi ) \pi _{\mathrm{prior}}(\xi ), \end{aligned}$$

(9)

where $\pi (z \mid \xi )$ is the likelihood distribution and $\pi _{\mathrm{prior}}(\xi )$ is the prior distribution of the unknown. With approximate Bayesian computation, we consider a modified posterior distribution given by

$$\begin{aligned} \pi _{\mathrm{post}}(\xi , \rho \mid z) \propto \pi (z \mid \xi , \rho )\pi (\rho \mid \xi )\pi (\xi ), \end{aligned}$$

(10)

where $\rho$ is a simulated dataset drawn from $\pi (\rho \mid \xi )$. The function $\pi (z \mid \xi , \rho )$ is a weight function which attains high values when $\rho$ is close to z. This is essentially the analog to the likelihood function in traditional Bayesian computation. The weight function can either compare $\rho$ and z directly or it can compare summary statistics generated from each. Our approach is to compute summary statistics. To generate a sample from the modified posterior, we use a sequential Monte Carlo technique outlined in Ref. 15.

Summary Statistics for EC Data

Data Model

We begin by reviewing the data model for the inverse problem, originally developed in Ref. 5. The EC response due to the underlying cODFs is inherently random; that is, different draws from the cODFs will generate different EC responses even if the cODF within each region remains fixed. Thus, a fixed set of cODFs will produce a distribution of EC responses. Combined with the assumption that the individual grain orientations are independent realizations of the underlying cODFs, the averaging effect of the EC coil permits application of the Central Limit Theorem, implying that the EC measurements due to a fixed set of underlying cODFs follow a normal distribution.

Thus, the noiseless EC measurements ${\widetilde{z}} \in {\mathbb {C}}^m$ due to the set of underlying cODFs $f_1, f_2, \ldots , f_p$ can be written

$$\begin{aligned} {\widetilde{z}} = {\widetilde{z}}_{\mathrm{re}} + j {\widetilde{z}}_{\mathrm{im}}, \end{aligned}$$

(11)

where ${\widetilde{z}}_{\mathrm{re}}$ and ${\widetilde{z}}_{\mathrm{im}}$ are the real and imaginary portions of ${\widetilde{z}}$, respectively. Using the Central Limit Theorem, we can model ${\widetilde{z}}_{re}$ and ${\widetilde{z}}_{\mathrm{im}}$ as realizations of two standard normal random vectors $Z_{\mathrm{re}}$ and $Z_{\mathrm{im}}$,

$$\begin{aligned} Z_{\mathrm{re}} \sim N(\varvec{\mu }_{\mathrm{re}}, {\widetilde{\Gamma }}_{\mathrm{re}}), \quad Z_{\mathrm{im}} \sim N(\varvec{\mu }_{\mathrm{im}}, {\widetilde{\Gamma }}_{\mathrm{im}}), \end{aligned}$$

where

$$\begin{aligned} \varvec{\mu }_{\mathrm{re}}= & {} \mathbb {E}\left[ Z_{\mathrm{re}} \mid f(\psi _1, \theta ) \right] , \quad \\ {\widetilde{\Gamma }}_{\mathrm{re}}= & {} \mathbb {E}\left[ (Z_{\mathrm{re}} - \varvec{\mu }_{\mathrm{re}}) (Z_{\mathrm{re}} - \varvec{\mu }_{\mathrm{re}})^T \mid f(\psi _1, \theta ) \right] . \end{aligned}$$

The quantities $\varvec{\mu }_{\mathrm{im}}$ and ${\widetilde{\Gamma }}_{\mathrm{im}}$ are defined similarly. Then, for a set of measured EC data $z \in {\mathbb {C}}^m$, we may write

$$\begin{aligned} z_{\mathrm{re}}= & {} \varvec{\mu }_{\mathrm{re}} + \omega _{\mathrm{re}} + \epsilon _{\mathrm{re}}, \\&\omega _{\mathrm{re}} \sim N(0, {\widetilde{\Gamma }}_{\mathrm{re}}),\\&\epsilon _{\mathrm{re}} \sim N(0, \delta _{\mathrm{re}}^2 \mathbf {I}), \end{aligned}$$

where $\epsilon _{\mathrm{re}}$ represents iid measurement noise. Similarly,

$$\begin{aligned} z_{\mathrm{im}}= & {} \varvec{\mu }_{\mathrm{im}} + \omega _{\mathrm{im}} + \epsilon _{\mathrm{im}}, \\&\omega _{\mathrm{im}} \sim N(0, {\widetilde{\Gamma }}_{\mathrm{im}}), \\&\epsilon _{\mathrm{im}} \sim N(0, \delta _{\mathrm{im}}^2 \mathbf {I}), \end{aligned}$$

In the remaining calculations, define

$$\begin{aligned} \Gamma _{\mathrm{re}} = {\widetilde{\Gamma }}_{\mathrm{re}} + \delta _{\mathrm{re}}^2 \mathbf {I}, \quad \Gamma _{\mathrm{im}} = {\widetilde{\Gamma }}_{\mathrm{im}} + \delta _{\mathrm{im}}^2\mathbf {I}. \end{aligned}$$

Summary Statistics

Given a set of measured EC data $z \in {\mathbb {C}}^m$, we define the following quantities,

$$\begin{aligned} \zeta = \left[ \begin{array}{c} z_{\mathrm{re}} \\ z_{\mathrm{im}} \end{array} \right] \in {\mathbb {R}}^{2m}, \quad \mathbf {b}= \left[ \begin{array}{c} \varvec{\mu }_{\mathrm{re}} \\ \varvec{\mu }_{\mathrm{im}} \end{array} \right] \in {\mathbb {R}}^{2m}, \quad \Lambda = \left[ \begin{array}{cc} \Gamma _{\mathrm{re}} &{} {\widehat{\Gamma }} \\ {\widehat{\Gamma }}^T &{} \Gamma _{\mathrm{im}} \end{array} \right] , \end{aligned}$$

(12)

where ${\widehat{\Gamma }} \in {\mathbb {R}}^{m}$ is given by

$$\begin{aligned} {\widehat{\Gamma }} = \mathbb {E}\left[ (Z_{\mathrm{re}} - \varvec{\mu }_{\mathrm{re}} ) (Z_{\mathrm{im}} - \varvec{\mu }_{\mathrm{im}})^T \mid f(\psi _1, \theta ) \right] . \end{aligned}$$

Then, the model for the measured data is

$$\begin{aligned} \zeta = \mathbf {b}+ \mathbf {e}, \quad \mathbf {e}\sim N(0, \Lambda ), \end{aligned}$$

where $\mathbf {e}$ encompasses the variability due to both the underlying cODFs and the measurement noise.

The values needed to populate $\varvec{\mu }_{\mathrm{re}}$, $\varvec{\mu }_{\mathrm{im}}$ and ${\widetilde{\Gamma }}_{\mathrm{re}}$, ${\widetilde{\Gamma }}_{\mathrm{im}}$, ${\widehat{\Gamma }}$ can be computed numerically using the AII model. In particular, let

$$\begin{aligned} \mu _\ell ^{(h)} = \int _{V_h} \left( \mathbf {E}_a^\ell \right) ^T \left( \sigma _a \mathbf {I}_{3 \times 3} - \mathbb {E}_{f_h}\left[ \overline{\sigma _b}(\psi _1, \theta )\right] \right) \mathbf {E}_a^\ell \; dV, \end{aligned}$$

(13)

where the term $\mathbb {E}_{f_h}\left[ \overline{\sigma _b} (\psi _1, \theta ) \right]$ is computed by taking the expectation of each term in $\overline{\sigma _b}(\psi _1, \theta )$ with respect to $f_h$ and $\mathbf {E}_a^\ell$ is the incident electric field when the EC coil is centered at the $\ell$th measurement location. Then,

$$\begin{aligned} \mu _\ell = \sum _{h = 1}^p \int _{V_h} \mu _\ell ^{(h)}, \end{aligned}$$

(14)

and the $\ell$th entries of $\varvec{\mu }_{\mathrm{re}}$ and $\varvec{\mu }_{\mathrm{im}}$ are given by the real and imaginary portions of $\mu _\ell$, respectively. Similarly, define

$$\begin{aligned} \gamma _{\ell k}&= \sum _{h = 1}^p \int _{{\mathbb {R}}^2} \left( \int _{V_h} g(\mathbf {E}_a^\ell , \overline{\sigma _b}) dV \int _{V_h} g(\mathbf {E}^k_a, \overline{\sigma _b}) \; dV \right) \\&\quad f_h(\psi _1, \theta ) \; d\theta d\psi _1 - \mu _\ell ^{(h)} \mu _k^{(h)} \end{aligned}$$

(15)

where

$$\begin{aligned} g(\mathbf {E}_a^\ell , \overline{\sigma _b}) = (\mathbf {E}_a^\ell )^T (\sigma _a \mathbf {I}_{3 \times 3} - {\overline{\sigma }}_b(\psi _1, \theta ))\mathbf {E}_a^\ell . \end{aligned}$$

(16)

Then, the $(\ell ,k)$ and $(k,\ell )$ entries of ${\widetilde{\Gamma }}_{\mathrm{re}}$ and ${\widetilde{\Gamma }}_{\mathrm{im}}$ are given by the real and imaginary portions, respectively, of $\gamma _{\ell k}$. Lastly, the $(\ell , k)$ entry of ${\widehat{\Gamma }}$ is given by

$$\begin{aligned} {\widehat{\gamma }}_{\ell k}= & {} \sum _{h = 1}^p \int _{{\mathbb {R}}^2} \left( \int _{V_h} Re(g(\mathbf {E}_a^\ell , \overline{\sigma _b})) dV \int _{V_h} Im(g(\mathbf {E}^k_a, \overline{\sigma _b})) \; dV \right) \\&f_h(\psi _1, \theta ) \; d\theta d\psi _1 - Re \left( \mu _\ell ^{(h)} \right) Im\left( \mu _k^{(h)}\right) , \end{aligned}$$

(17)

where $Re(\cdot )$ and $Im(\cdot )$ denote the real and imaginary portions of a given quantity. Note that unlike $\Gamma _{re}$ and $\Gamma _{im}$, ${\widehat{\Gamma }}$ is not symmetric.

The summary statistics, defined in Ref. 5, are as follows. First, define

$$\begin{aligned} w = R^{-T}(\zeta - \mathbf {b}) \in {\mathbb {R}}^{2m}, \end{aligned}$$

(18)

where R is the Cholesky factor of $\Lambda$. Note that if $\Lambda$ and $\mathbf {b}$ are calculated using the set of cODFs that generated $\zeta$, then $w \sim N(0, \mathbf {I})$, that is, w is a standard normal random vector. In that case,

$$\begin{aligned} \mathbb {E}\left[ \Vert w \Vert \right] \approx \sqrt{2m}. \end{aligned}$$

(19)

Furthermore, due to the Central Limit Theorem,

$$\begin{aligned} {\overline{w}} \sim N \left( 0, \frac{1}{2m} \right) . \end{aligned}$$

(20)

where ${\overline{w}}$ denotes the mean of w. Our two summary statistics for the inverse problem are thus $\Vert w\Vert$ and ${\overline{w}}$.

For a candidate ODF ${\widehat{f}}$, we compute $\Lambda$ and $\mathbf {b}$ and then compute w as in Eq. 18. Denote the vector w computed using ${\widehat{f}}$ by $w_{{\widehat{f}}}$. If ${\widehat{f}}$ is close to the true value, then Eq. 19 and 20 should hold for $w_{{\widehat{f}}}$. The weight function used in the inversion, initially developed in Ref. 5, is Gaussian,

$$\begin{aligned} \pi (z \mid f, \Vert w_f\Vert , {\overline{w}}_f ) = \exp \left( -2m \left( {\overline{w}}_f \right) ^2 - \frac{( \Vert w_f \Vert - \sqrt{2m})^2}{\sigma _{\mathrm{norm}}^2} \right) , \end{aligned}$$

(21)

where $\sigma _{\mathrm{norm}}^2$ is the variance of the norm of a standard normal random vector of length 2m.

Parametric Distribution

Each unknown cODF is represented in the inverse problem using the Bingham distribution, which is a probability distribution on the hypersphere.¹⁶ It has been shown to represent different texture components well^17,18 and has been used to successfully model the ODF of a strongly textured specimen.¹⁹ The pdf for the Bingham distribution is expressed in terms of quaternions; in terms of Euler angles, the quaternion vector is given by

$$\begin{aligned} q= & {} \left[ \cos \left( \frac{\theta }{2} \right) \cos (\alpha ), -\sin \left( \frac{\theta }{2} \right) \cos (\beta ),\right. \\&\left. \sin \left( \frac{\theta }{2} \right) \sin (\beta ), -\cos \left( \frac{\theta }{2} \right) \sin (\alpha ) \right] , \end{aligned}$$

(22)

where $\alpha = \frac{1}{2}(\psi _1 + \psi _2)$ and $\beta = \frac{1}{2}(\psi _1 - \psi _2)$. The pdf is then given by

$$\begin{aligned} \pi (x) \propto \exp \left( -\sum _{j = 1}^4 \lambda _j v_j^T x \right) , \end{aligned}$$

where x is a unit quaternion, $v_j \in {\mathbb {R}}^4$, $1 \le i \le 4$ are orthonormal directions, and $\lambda _j < 0$, $1 \le i \le 4$.

In this work, we will apply the conventions defined in Ref. 19. In particular, $v_1 = q$ and $v_2$ and $v_3$ are the partial derivatives of $v_1$ with respect to $\psi _1$ and $\theta$, respectively. In addition, we set $\lambda _4 = 0$ and assume that $\lambda _1 \ge \lambda _2 \ge \lambda _3$. Due to the lack of sensitivity of EC in $\alpha$-titanium to the third Euler angle, we set $\psi _2 = 0$.

Prior Distribution

In the inverse problem, the Bingham distribution representing each unknown cODF is defined in terms of four parameters, as in Ref. 5. The first two, $\mu _\theta$ and $\mu _\psi$, are used to define the vectors $v_1$, $v_2$ and $v_3$. In particular,

$$\begin{aligned} q= & {} \left[ \cos \left( \frac{\mu _\theta }{2} \right) \cos (\frac{\mu _\psi }{2} ), -\sin \left( \frac{\mu _\theta }{2} \right) \cos (\frac{\mu _\psi }{2} ), \right. \\&\left. \sin \left( \frac{\mu _\theta }{2} \right) \sin (\frac{\mu _\psi }{2} ), -\cos \left( \frac{\mu _\theta }{2} \right) \sin (\frac{\mu _\psi }{2} ) \right] , \end{aligned}$$

and

$$\begin{aligned} v_2 = \frac{\partial v_1}{\partial \mu _\psi }, \quad v_3 = \frac{\partial v_1}{\partial \mu _\theta }. \end{aligned}$$

Furthermore, we fix $\lambda _1 = -0.5$ and define two auxiliary parameters,

$$\begin{aligned} \eta = \frac{\lambda _1}{\lambda _2}, \quad \kappa = \frac{\lambda _2}{\lambda _3}. \end{aligned}$$

Then, in the inverse problem we require $0 < \eta , \kappa \le 1$. Each cODF is thus defined by the four parameters: $\left( \mu _\psi , \mu _\theta , \eta , \kappa \right)$. The parameters $(\mu _\psi , \mu _\theta )$ indicate where most of the weight of the distribution lies, while $(\eta , \kappa )$ determine the shape of the distribution.

Assuming that the individual cODFs are independent, the prior distribution for the unknown f is given by

$$\begin{aligned} \pi _{\mathrm{prior}}(f) = \pi _{\mathrm{prior}}(f_1, f_2, \ldots , f_p) = \prod _{h = 1}^p \pi _{\mathrm{prior}}(f_h), \end{aligned}$$

which, in terms of parameters, is written

$$\begin{aligned} \pi _{\mathrm{prior}}(f) = \prod _{h = 1}^p \pi _{\mathrm{prior}}\left( \mu _\psi ^{(h)}, \mu _\theta ^{(h)}, \eta ^{(h)}, \kappa ^{(h)}\right) , \end{aligned}$$

where $\left( \mu _\psi ^{(h)}, \mu _\theta ^{(h)}, \eta ^{(h)}, \kappa ^{(h)}\right)$ is the set of parameters that defines $f_h$.

Fig. 2

(a) Inverse pole figure map of a set of EBSD data recorded from a Ti-6Al-4V specimen. (b) Segmentation of these EBSD data into regions defined by different cODFs using DREAM3D.

Figure 2 shows a set of EBSD data recorded from a specimen of Ti-6Al-4V along with the DREAM3D segmentation, which was run assuming a $20^\circ$ tolerance for misalignment in the c-axis between neighboring grains. We treat each region in the segmentation as being defined by its own cODF. To construct a prior for these parameters, we fit a single Bingham distribution to each of the cODFs in this specimen. Rather than estimate $\eta$ and $\kappa$ directly, we estimate the log of each of these parameters.

Fig. 3

Plots of the fitted parameters to each of the cODFs in Fig. 2 and the curves that define the bounds for the prior distribution. (a) The red and blue lines are the maximum and minimum allowable values for $\log (\eta )$ as a function of $\mu _\theta$. (b) The top and bottom surfaces are the maximum and minimum allowable values for $\log (\kappa )$ as a function of $(\mu _\theta , \log (\eta ))$ (Color figure online).

We found that the values of $\mu _\theta$, $\eta$ and $\kappa$ are highly correlated; however, none of the parameters exhibit any correlation with $\mu _\psi$.The prior for $(\mu _\psi , \mu _\theta , \eta , \kappa )$ is thus written

$$\begin{aligned} \pi _\mathrm{{prior}}(\mu _\psi , \mu _\theta , \eta , \kappa ) = \pi (\mu _\psi ) \pi (\kappa \mid \mu _\theta , \eta ) \pi (\eta \mid \mu _\theta ) \pi (\mu _\theta ). \end{aligned}$$

(23)

The prior for $\mu _\psi$ is a uniform distribution on the interval $(0, \pi )$; similarly, the prior for $\mu _\theta$ is a uniform distribution on the interval $(0, \pi /2)$.

To construct $\pi (\eta \mid \mu _\theta )$, we consider the plot in Fig. 3a, which shows the fitted values of $\mu _\theta$ versus the fitted values of $\log (\eta )$ for each of the cODFs in the specimen in Fig. 2. We desire a prior that for a fixed value of $\mu _\theta$ will allow for a range of values of $\eta$ without favoring any single value. To achieve this, we use a generalized Gaussian distribution,

$$\begin{aligned} \pi _{\mathrm{{prior}}}(\eta \mid \mu _\theta ) = \exp \left( - \left( \frac{\eta - \eta _{\mathrm{mid}}(\mu _\theta )}{\rho (\eta _{\mathrm{max}}(\mu _\theta ) - \eta _{\mathrm{min}}(\mu _\theta ))} \right) ^\nu \right) , \end{aligned}$$

(24)

where $\eta _{\mathrm{max}}(\mu _\theta )$ and $\eta _{\mathrm{min}}(\mu _\theta )$ are the maximum and minimum allowable values for $\eta$ as a function of $\mu _\theta$. In Fig. 3a, they are given by the red and blue curves, respectively. The function $\eta _{\mathrm{mid}}(\mu _\theta )$ is the midpoint of these two curves. Note that $\nu$ is a positive even integer and $\rho$ is a scalar chosen to ensure that for any value of $\eta$ that falls within the appropriate bounds, the value of the prior is approximately equal to 1.

Because we have only a few data points such that $\mu _\theta < 0.5$, we have limited information as to what the allowable values of $\eta$ should be for those values of $\mu _\theta$. As a result, the lower bound (blue curve) was chosen to allow for a larger range of potential vaues of $\eta$ for values of $\mu _\theta < 0.5$. Fitting the lower bound closer to the data points for $\mu _\theta < 0.5$ would import a higher degree of confidence in the range of allowable values for $\eta$ than we have based on these few data points. We ultimately found that the upper bound was more important as the ODF estimation algorithm tends towards flatter distributions represented by higher values of $\eta$.

The distribution $\pi (\kappa \mid \mu _\theta , \eta )$ is constructed in a similar fashion to restrict the value of $\kappa$ as a function of $\mu _\theta$ and $\eta$, that is,

$$\begin{aligned} \pi (\kappa \mid \mu _\theta , \eta ) = \exp \left( - \left( \frac{\kappa (\mu _\theta , \eta ) - \kappa _{\mathrm{mid}}(\mu _\theta , \eta )}{\rho (\kappa _{\mathrm{max}}(\mu _\theta , \eta ) - \kappa _{\mathrm{min}}(\mu _\theta , \eta ))} \right) ^\nu \right) . \end{aligned}$$

(25)

Figure 3b shows the surfaces which are the maximum and minimum allowable values for $\kappa$ for fixed values of $\eta$ and $\mu _\theta$.

Posterior Distribution

Combining the weight function (21) with the prior, we arrive at the following posterior distribution,

$$\begin{aligned} \pi _{\mathrm{{post}}}(f \mid z)= & {} \exp \left( -2m \left( {\overline{w}}_f \right) ^2 - \frac{( \Vert w_f \Vert - \sqrt{2m})^2}{\sigma _{\mathrm{norm}}^2} \right) \\&\pi _{\mathrm{{prior}}}(f), \end{aligned}$$

(26)

where $\pi _{\mathrm{{prior}}}(f)$ is as defined in the previous section.

Effects of Grain Size

One issue raised in Ref. 5 is the effect of the assumed grain size on the output of the algorithm. In this context, grain size refers to the size of a pixel (or group of neighboring pixels) defined by roughly the same orientation. As an example, the simulated specimen shown in Fig. 4 has a grain size of 12 $\mu$m. That is, each pixel represents a 12$\mu$m $\times 12\mu$m area and is defined by a different crystallographic orientation.

In the inversion, the assumed grain size is the discretization size used in the numerical integration to compute (15) and (17). Let $\gamma _{\ell k}(f, g)$ denote the expression from (15) computed for the ODF f and grain size g; then, as stated in Ref. 5,

$$\begin{aligned} \gamma _{\ell k}(f,g/s) = \frac{\gamma _{\ell k}(f, g)}{s^2}, \end{aligned}$$

where s is any real positive number. In the examples shown in Ref. 5, the true grain size was 12 $\mu$m, while the assumed grain size in the inversion was 24 $\mu$m. Thus, in these examples, we set $s = 2$. However, with realistic samples, the grain size is not constant and is likely not known. In fact, determining the grain size distribution in $\alpha$-titanium is a research question in its own right; see, for example.^20,21,22 As a result, s becomes an unknown in the inverse problem. In this work, we will demonstrate how to estimate s.

As an example, we consider the simulated microstructure and simulated eddy current signal shown in Fig. 4. We generated multiple samples from the posterior distribution (26) using the simulated data, assuming a different range for s each time. The discretization size was held fixed at 24 $\mu$m. Given that the true grain size is 12 $\mu$m, the correct value of s is roughly 2.

Fig. 4

Simulated data from a single elliptical MTR. (a) The inverse prole figure map of the simulated EBSD. The black outline indicates the region where eddy current measurements were simulated. (b) Imaginary portion of the simulated eddy current data. (c) Real portion of the simulated eddy current data.

Figure 5 shows the pole figure of the posterior mean for the cODF of the elliptical MTR generated when s was allowed to range from 0.3 to 0.4 as well as the pole figure of the posterior mean generated when s was allowed to range from 1.9 to 2. The pole figure for the true cODF is also shown. A similar set of results for the background region is also shown in Fig. 5.

Fig. 5

Posterior mean estimate of the cODF for the elliptical MTR with (a) $0.3 \le s \le 0.4$ and (b) $1.9 \le s \le 2$. The true pole figure for the region is shown in (c). The images in (d–f) are the corresponding results for the background region.

In both cases, the posterior mean that results when s is in the range of 0.3 to 0.4 is a poor estimate of the true cODF. Clearly, the sample generated with values close to $s = 2$ yields a much better set of approximations to the true cODF. However, since in reality we will not have access to the true pole figure, we require a method to determine which set of values of s is correct.

This can be achieved by comparing the value of $\mathbf {b}$, the mean EC response computed using this estimated cODF, to the measured data $\zeta$. Figure 6 shows the computed value of $\varvec{\mu }_{im}$ using the posterior means for $0.3 \le s \le 0.4$ and $1.9 \le s \le 2$ as well as the true value $z_{im}$ for our example. Clearly, the value of $\varvec{\mu }_{im}$ is much closer to the original data when assuming $1.9 \le s \le 2$ instead of $0.3 \le s \le 0.4$.

Fig. 6

Computed values of $\varvec{\mu }_{im}$ using the posterior means from the samples generated with (a) $0.3 \le s \le 0.4$ and (b) $1.9 \le s \le 2$. The simulated measured data $z_{im}$ are shown (c).

In addition, Fig. 7 shows a parametric plot of the value of the average negative log of the weight function as given in Eq. 21 versus the log of the average norm of the difference between the data vector $\zeta$ and the computed mean $\mathbf {b}$, that is, $\log \left( \left\| \zeta - \mathbf {b}\right\| ^2\right)$, for each of the generated samples. The different color points correspond to different ranges for the value of s, as indicated by the legend. We note that as the value of s increases, the average value of $\Vert \zeta - \mathbf {b}\Vert ^2$ decreases. Furthermore, the values of s that land in the range roughly around the correct value of $s = 2$ minimize both the negative log of the original weight function and the difference between $\zeta$ and $\mathbf {b}$. Thus, it appears that the statistic $\Vert \zeta - \mathbf {b}\Vert ^2$ contains information about the value of s.

Fig. 7

(a) Parametric plot showing the average value of the negative log of the weight function in Eq. 21 versus the average value of $\Vert \zeta - \mathbf {b}\Vert ^2$ for each of the samples generated using different values of s. Each point represents a different range for the value of s. The legend indicates the values of s that are included in each point. (b) Resulting marginal distribution of s computed using samples drawn from the posterior with and without the penalty term Eq. 28.

Fortunately, we do not need to regenerate the $\ell$-curve shown in Fig. 7 every time we run the algorithm to get the correct value of s. Rather, by adding a penalty term to the original cost function, and adding s as an unknown in the optimization, the correct value of s will emerge naturally. Specifically, we replace the original weight function in Eq. 21 with

$$\begin{aligned} \pi (z \mid f, \Vert w_f\Vert , {\overline{w}}_f, s )= & {} \exp \left( -2m \left( {\overline{w}}_f \right) ^2 \right. \\&\left. - \frac{( \Vert w_f \Vert - \sqrt{2m})^2}{\sigma _{\mathrm{norm}}^2} - \frac{\Vert \zeta - \mathbf {b}\Vert ^2}{\Vert \zeta - \mathbf {b}^* \Vert ^2}\right) , \end{aligned}$$

(27)

where $\mathbf {b}^*$ is the mean vector that yields the minimum of $\Vert \zeta - \mathbf {b}\Vert ^2$ only. Note that the term

$$\begin{aligned} \frac{\Vert \zeta - \mathbf {b}\Vert ^2}{\Vert \zeta - \mathbf {b}^* \Vert ^2} \end{aligned}$$

(28)

serves as a penalty to discourage solutions that maximize Eq. 21 but do not result in values of $\varvec{\mu }_{\mathrm{re}}$ and $\varvec{\mu }_{\mathrm{im}}$ that resemble the measured data.

With the addition of s as an unknown, the posterior distribution becomes

$$\begin{aligned} \pi ( f, s \mid z)= & {} \exp \left( -2m \left( {\overline{w}}_f \right) ^2 \right. \\&\left. - \frac{( \Vert w_f \Vert - \sqrt{2m})^2}{\sigma _{\mathrm{norm}}^2} - \frac{\Vert \zeta - \mathbf {b}\Vert ^2}{\Vert \zeta - \mathbf {b}^* \Vert ^2}\right) \\&\pi _{\mathrm{prior}}(f) \pi _{\mathrm{prior}}(s), \end{aligned}$$

(29)

where $\pi _{\mathrm{prior}}(f)$ is the same as given in Sect. 3.3.4. The prior for s is constructed to ensure that s is positive.

To demonstrate that this modified posterior does find the correct value of s, we generated a sample from Eq. 29. For comparison, we also generated a sample from Eq. 29 without the penalty term Eq. 28. In each case, the range of s was restricted so that $0.5 \le s \le 3$. Figure 7 shows the resulting marginal distribution of s with and without the penalty term. As is evident from the resulting histogram, with the penalty term, the marginal distribution of s is centered around the correct value of 2. Without the penalty, the possible values of s are more spread out, with values near 0.5 being the most likely choice for s. In general, we found that without the penalty term, smaller values of s will be favored by the posterior.

The penalty term relies on having access to the vector $\mathbf {b}^*$ that minimizes $\Vert \zeta - \mathbf {b}\Vert ^2$. Note that $\mathbf {b}^*$ is generally not associated with a single choice of ODF. To find it, we minimize the function

$$\begin{aligned} h(f) = \Vert \zeta - \mathbf {b}(f) \Vert ^2. \end{aligned}$$

(30)

In the examples that follow in "Numerical Examples" section, the set of ODFs that minimizes Eq. 30 is used as a starting point to maximize the posterior.

Numerical Examples

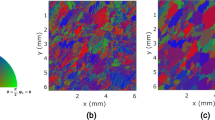
One of the main goals of this article is to apply the techniques developed in Ref. 5 to realistic MTR configurations; in Ref. 5, only simulated microstructures were used. Figure 8 shows a section of real EBSD data taken of a titanium alloy specimen along with the simulated eddy current data. The eddy current data were simulated using a shielded elliptical coil with axes equal to 250 µm and 750 µm at a frequency of 15 MHz with a measurement step size of 75 µm in both the x and y directions. Assuming that the long axis of the coil aligning with the y-axis corresponds to a coil rotation of $0^\circ$, the coil was rotated $30^\circ$ counterclockwise. We will apply the ODF estimation algorithm to this data.

Fig. 8

(a) EBSD data of a realistic titanium alloy specimen. Data are recorded in the box indicated by the black lines in the specimen. (b) DREAM3D segmentation with regions below the resolution of the coil consolidated into a single background region. (c) Imaginary portion of the simulated eddy current data. (d) Real portion of the simulated eddy current data.

To proceed, we need a segmentation of the material to feed in to the algorithm. The DREAM3D segmentation of this specimen into regions defined by different cODFs identified around 300 separate regions. However, many of these regions are too small to be independently resolved by the eddy current coil. As such, we will not attempt to estimate the cODF of each of these regions in the inverse problem. We consolidated all of the regions that fall below the resolution of the coil into a single background region; this reduced segmentation, shown in Fig. 8, will be used in the inversion of this data.

Figures 9 and 10 show the maximum a posteriori (MAP) estimates of the cODF for seven different regions. The algorithm performs well. With the exception of region 3, the algorithm successfully estimates the distribution of the second Euler angle for each region. We suspect that the results for region 3 are somewhat poor for two reasons: first, this region is relatively small; second, its true cODF may not be best described by a single Bingham distribution. Although slightly less accurate than the estimates of the second Euler angle, estimates of the first Euler angle are generally good.

Fig. 9

MAP estimates of several of the cODFs from the specimen in Fig. 8. Each row corresponds to a different region; the left column shows the segmentation with the appropriate region labeled. The middle column is the pole figure for the estimated cODF, and the right column shows the true cODF for each region.

Fig. 10

MAP estimates of several of the cODFs from the specimen in Fig. 8. Each row corresponds to a different region; the left column shows the segmentation with the appropriate region labeled. The middle column is the pole figure for the estimated cODF, and the right column shows the true cODF for each region.

Ideally, we would like to be able to predict the orientation of the c-axis with an error of no more than $5^\circ$. To determine how well we estimated the tilt of the c-axis in each region, we compared the MAP estimate of $\mu _\theta$ to the median of the true marginal distribution of the second Euler angle. (We observed that the median corresponds better to the peak of the marginal distribution than the mean.) With the exception of Region 3, the error in the estimate of the tilt of the c-axis was < $9^\circ$. Most encouragingly, the algorithm predicted the tilt of the c-axis for both Regions 1 and 2 within $2^\circ$.

We repeated this process for the heading of the c-axis by comparing the MAP estimate of $\mu _\psi$ to the median of the true marginal distribution of the first Euler angle. The error in the prediction for Region 1 was around $30^\circ$; in general, we found that the algorithm struggles to predict the heading of the c-axis when the tilt is close to $0^\circ$. The results are better when the tilt is closer to $\pi /2$, as in Regions 2, 4, 6 and 7. In each of these regions, the error in the prediction of the heading is < $10^\circ$. However, none are within the desired $5^\circ$ tolerance.

Another factor to consider beyond the accuracy of the MAP estimates is the uncertainty in these estimates. Thus, in addition to computing the MAP estimate for each cODF, we generated a sample from the posterior distribution and used it to generate 95% predictive envelopes (see Ref. 23). Each sample point was weighted based on its value of (29) and then sorted in order of descending weight. The first $n_{95}$ sample points in the sorted sample with weights summing to approximately 0.95 were included in the predictive envelope. To visualize the 95% predictive envelopes, we consider the marginal cumulative distribution functions (CDFs) for the first and second Euler angles, as in Ref. 5.

Figures 11 and 12 show the estimated marginal CDFs, along with the 95% predictive envelopes, for each of the regions shown in Figs. 9 and 10. We note that the MAP estimates of the marginal CDF for the second Euler angle are generally in good agreement, with the exception of Region 3. In addition, the true CDF is contained within the 95% predictive envelope. We note that for Region 1, a small portion of the true CDF falls outside the 95% predictive envelope. We attribute this to the fact that the true cODF cannot be described by a single Bingham distribution. However, our estimate does contain the salient features of the distribution. Not surprisingly, the largest regions, 1 and 2, have the smallest predictive envelopes. Furthermore, the width of the predictive envelope seems to increase when the size of the region decreases. Region 3, where the algorithm performs the worst, contains the largest predictive envelope and is also the smallest region.

As mentioned previously, the AII model has the same output for both $(\psi _1, \theta )$ and $(\psi _1 + \pi , \theta )$. Thus, to compare the estimated CDF to the true CDF for the first Euler angle, we subtracted $\pi$ from each of the true crystallographic orientations with a value of $\psi _1 > \pi$. This way, all of the true orientations can be described on the interval $\psi _1 \in [0, \pi ]$. Although in all cases the true CDF is contained in the 95% predictive envelope, there is a noticeably higher degree of uncertainty in the estimate of the first Euler angle. In the case of regions 6 and 7, the distribution of potential values for $\mu _\psi$ is bimodal. Note that the two modes of the distribution of $\mu _\psi$ share a reference angle. While the correct value of $\mu _\psi$ does produce a slightly closer match to the data, the difference is small. Thus, we do not have a means of eliminating the uncertainty between the two modes using a single eddy current dataset; however, it is possible that incorporating a second dataset recorded with a different orientation of the coil could help with this problem. This will be a topic of future work.

Fig. 11

Marginal cumulative distribution function (CDF) of the first and second Euler angles for each of the regions shown in Figs. 9 and 10. The blue line is the true CDF, the red line is the MAP estimate, and the gray region represents the 95% predictive envelope (Color figure online).

Fig. 12

Marginal cumulative distribution function (CDF) of the first and second Euler angles for each of the regions shown in Figs. 9 and 10. The blue line is the true CDF, the red line is the MAP estimate, and the gray region represents the 95% predictive envelope (Color figure online).

Conclusion

In this work, we successfully applied the algorithm developed in Ref. 5 to realistic MTR configurations. In particular, we modified the inversion method to account for unknown grain size and added a prior distribution based on realistic cODFS. The algorithm was then applied to eddy current data simulated using real EBSD data; our method was able to successfully recover the cODF of several different regions in this specimen.

Moving forward, the next step is to apply this method to real eddy current data. The AII model that was used to simulate eddy current data in this work assumes that any grain on the surface of the specimen extends as a pillar through the specimen. Thus, it does not consider any contributions from regions below the surface. This will need to be modified when applying the method to real data, where regions below the surface may impact the measurements. In addition, this method does require a segmentation of the underlying material into regions defined by different cODFs. Finding this segmentation using either eddy current data or another higher resolution NDE technique is a topic of future work.