Unsupervised Learning for Efficient Texture Estimation From Limited Discrete Orientation Data

Abstract

The estimation of orientation distribution functions (ODFs) from discrete orientation data, as produced by electron backscatter diffraction or crystal plasticity micromechanical simulations, is typically achieved via techniques such as the Williams–Imhof–Matthies–Vinel (WIMV) algorithm or generalized spherical harmonic expansions, which were originally developed for computing an ODF from pole figures measured by X-ray or neutron diffraction. These techniques rely on ad-hoc methods for choosing parameters, such as smoothing half-width and bandwidth, and for enforcing positivity constraints and appropriate normalization. In general, such approaches provide little or no information-theoretic guarantees as to their optimality in describing the given dataset. In the current study, an unsupervised learning algorithm is proposed which uses a finite mixture of Bingham distributions for the estimation of ODFs from discrete orientation data. The Bingham distribution is an antipodally-symmetric, max-entropy distribution on the unit quaternion hypersphere. The proposed algorithm also introduces a minimum message length criterion, a common tool in information theory for balancing data likelihood with model complexity, to determine the number of components in the Bingham mixture. This criterion leads to ODFs which are less likely to overfit (or underfit) the data, eliminating the need for a priori parameter choices.

1 Introduction

The connection between crystallographic preferred orientations (texture) in polycrystalline specimens and anisotropic material response/properties is widely recognized, and research into the quantitative analysis of texture has a long history in materials science and geology.[1,2,3,4,5,6,7] The relative frequency of crystal orientations within a sample is described mathematically via the orientation distribution function (ODF). Experimental techniques for the estimation of the ODF can be categorized as either macrotexture (or bulk/sample) texture techniques, such as X-ray or neutron diffraction,[8,9] where the relative frequency of orientations is averaged over hundreds of thousands of grains, or meso/microtexture techniques, such as electron backscatter diffraction (EBSD)[10,11] or high-energy X-ray diffraction microscopy (HEDM),[12] which provide spatially resolved 2D or 3D orientation maps of a much smaller number of grains (hundreds to tens of thousands).

Techniques for the estimation of orientation statistics from discrete orientation data grew organically out of the existing direct, such as the Williams–Imhof–Matthies–Vinel (WIMV) algorithm, and spherical harmonic techniques for macrotexture analysis, and rely on building up the ODF from the superposition of contributions from the individual orientations.[1,3,13,14,15,16] The most common method for ODF estimation from discrete measurements is based on the generalized spherical harmonics championed by Bunge.[1] In the harmonic method, the Fourier coefficients for the ODF are estimated from the superposition of the Fourier coefficients of the individual orientations convolved with a smoothing kernel. This procedure relies heavily on assumptions made a priori on the type and degree of smoothing. In addition, ad-hoc methods are required both for choosing the bandwidth of the spherical harmonics as well as to enforce positivity constraints (to make a proper ODF). The degree of smoothing and bandwidth as well as the number of discrete orientations required for accurate ODF estimation has a long history of debate in the literature.[17,18,19,20] A recent advance, on this front, is the development of automatic smoothing kernel optimization available in the MTEX Quantitative Texture Analysis Software,[21] which assists the user in determining the appropriate level of smoothing and issues a warning if too low a bandwidth is used. Despite this advance, neither the direct nor harmonic approaches provide information-theoretic guarantees as to their optimality in describing a given dataset. As will be shown in the case studies, even with optimized kernel selection, these methods can produce ODFs which are quite sensitive to the choice of initial parameters, and overfitting is a constant concern.

In the current study, we model the ODF as a finite mixture of Bingham distributions. The Bingham distribution is a very flexible distribution defined on the unit hypersphere.[22] It was first applied to texture modeling by Schaeben and Kunze,[23,24,25,26] who demonstrated that the Bingham distribution could accurately represent individual texture components including fibers, sheets, and anisotropic spreads around individual orientations. For unimodal ODFs, a single Bingham distribution will usually suffice to fit the observed data. For more realistic and complicated ODFs, we use a mixture of Bingham distributions. We solve the resulting ODF estimation problem with an unsupervised learning algorithm to estimate the parameters of a Bingham mixture, where the quality and quantity of the discrete orientation data are explicitly taken into account to greatly reduce the chance of under- or overfitting the data, while eliminating the need to make a priori decisions about smoothing. The “correct” number of mixture components in the Bingham mixture distribution is selected based on a minimum message length criterion which balances the goodness of fit to the data against the complexity of the resulting ODF.

Historically speaking, the main advantage of using spherical harmonics over analytic distributions (such as the Bingham) to model texture was computational simplicity and speed. The Bingham distribution was first described in 1974,[22] long after the theory of generalized spherical harmonics, and efficient computational schemes for Bingham parameter estimation were not available until recently. The prime computational difficulty in working with the Bingham distribution is that the normalization constant is complex and costly to compute in real time. To circumvent these problems, we make use of a new open-source software library called the Bingham Statistics Library which has recently been developed in the robotics community and provides efficient and accurate maximum-likelihood fitting and statistical inference tools for the Bingham distribution.[27]

With the current generation of EBSD cameras, capable of taking and indexing >100 diffraction patterns per second in ideal materials, the generation of detailed orientation maps that contain tens or hundreds of thousands of grains is now fairly routine. It is a fair question to ask why a radically different approach to ODF estimation is even required; as when the number of orientations are increased, the ODFs produced from EBSD via harmonic analysis converge to the macrotexture ODFs produced from diffraction experiments. However, there are many instances where we are interested in a true microtexture measurement, for example, when studying highly localized phenomena such as duplex microstructures and macrozone formation in α / β Ti alloys,[28,29] ridging and roping in rolled Al,[30] orientation clustering due to texture memory in HDDR-produced magnets,[31] localized plastic deformation at crack tips,[32] etc. The description of texture gradients[33,34] and other nonhomogeneous materials pose a challenge particularly if the gradients are steep and transitory regions are of interest. There is also a critical need for quantitative analysis of texture on mesoscale volumes resulting from crystal plasticity simulations. The comparison of macrotexture ODFs with those resulting from crystal plasticity (CP)-based micromechanical simulations is often a primary method of model validation and verification. Typically, these simulations are performed on statistical volume elements that contain a few hundred to a thousand grains for full field simulations, such as CP-FEM,[35] and a few thousand grains for homogenized or mean-field models, such as self-consistent models.[36] Quantitative comparison of the simulated textures with experimentally measured ODFs is difficult, as the intensity values are strongly dependent on the degree of smoothing and bandwidth selection as well as the resolution on which the ODFs are computed.

The main focus of this article is the introduction of the unsupervised learning algorithm, the discussion of its main features, and the demonstration of its effectiveness via some simple case studies. The selected case studies are all examples of ODF fitting in materials with triclinic crystal symmetry (C ₁ Point group). The scope of the article is restricted to the triclinic case to maintain focus on the unsupervised learning algorithm rather than on the substantive additional material that would be required for a meaningful extension of the Bingham distribution to arbitrary crystallographic and sample symmetries. The key difficulty extending the Bingham model to higher symmetry materials is in the development of computationally efficient tools for the estimation of the symmetrized distribution parameters. The description of a symmetrized Bingham distribution and its inclusion into the unsupervised learning framework will be presented in a future publication.

Three main ideas are presented in this article: (1) the Modeling of ODFs as a finite mixture of Bingham distributions, (2) an unsupervised learning algorithm for fitting ODFs given the mixture model that maximizes the probability of measuring the set of discrete orientations, and (3) a minimum message length (MML) criteria to determine the appropriate number of Bingham distributions or texture components necessary to represent an arbitrary ODF. The unsupervised learning algorithm combined with the MML represents a significant advance over traditional approaches to texture estimation from discrete orientations as it removes the need to make a priori decisions about the fitting procedure and gives a formal information theoretic guarantee of an optimal (in some sense) solution given the available data.

It should be noted that the model chosen to represent the ODF can be completely decoupled from the unsupervised learning algorithm and MML criteria for number of components. Any mixture model, such as the representation of textures via texture components,[37,38,39,40] can replace the Bingham distribution-based model presented here. The Bingham distribution was chosen as it is the maximum entropy distribution of unit quaternions thus minimizing the amount of prior information built into the distribution or the shape of the ODF.

2 Notation and Conventions

This section serves to set the notation, definitions, and conventions used throughout the rest of this article and is by necessity very brief. For a comprehensive review of crystallographic orientations, texture, and the orientation distribution function, the reader is referred to the following standard references.[1,4,3,41] A crystallographic orientation, $\mathbf{g}\,\in\, SO(3)$ is defined as a proper rotation which maps the macroscale sample or laboratory basis vectors onto the local crystal lattice basis. SO(3) denotes the special orthogonal matrix group of proper rotations in three dimensions members of which are the 3 × 3 orthogonal matrices with determinant +1. $\mathbf{g}$ accepts multiple equivalent parameterizations including Euler angles, unit quaternions, Rodriguez vectors, and angle–axis pairs (for a review of the different parameterizations, see[42] and the references contained within).

Parameterization of SO(3) by unit quaternions was found to be particularly convenient for the current study. Working with the quaternion parameterization offers significant advantages over other orientation representations, such as Euler angles, including a simple and computationally efficient multiplication rule for the composition of rotations, a continuous group space with nondegenerate representation of all rotations, and a simple and intuitive physical interpretation.[42,43] A unit quaternion can be thought of as representing a point on the surface of the unit sphere in four dimensions, $\mathbb{S}^3 \subset \mathbb{R}^4.$ Visualizing quaternions and equivalently orientations as points on $\mathbb{S}^3$ allows for a straightforward extension of directional statistics on the unit circle and sphere to the more abstract notion of statistics on rotations. The mapping from quaternions to orientations is two to one in that each orientation has an equivalent representation by antipodal quaternions. This antipodal symmetry allows any hemisphere of $\mathbb{S}^3$ to be considered as a fundamental zone or fundamental region of orientations. However, when considering directional statistics on the hypersphere, it is convenient to consider the whole space and work with a distribution that is also antipodally symmetric, such as the Bingham, to avoid introducing jumps or discontinuities at the equator.

The Haar measure, or invariant measure, is required to ensure invariant integration over the rotation group. If we denote the uniform random ODF as $f_{UR}(\mathbf{g})$ , then it is customary to normalize the ODF by choosing the invariant measure $d \mathbf{g}$ such that $\int_{SO(3)}d\mathbf{g}=1.$ This normalization implies that $f_{UR}(\mathbf{g})=1 \forall \mathbf{g},$ which is consistent with the custom of expressing $f(\mathbf{g})$ in terms of multiples of the uniform random ODF (MRD). In order to avoid confusion with normalization, $f(\mathbf{g})$ will be used to denote an ODF in units of times random with measure $d\mathbf{g}$ and $p(\mathbf{g})$ will be used to denote a “proper” probability distribution (p.d.f).

For convenience, the freely available MTEX Matlab Toolbox for Quantitative Texture Analysis[21] will be utilized to make all plots in orientation space. The ODFs will be plotted as σ-sections which are derived from Matthies–Euler angles denoted [α, β, γ] as [α, β, σ = α + γ]. σ-section plots eliminate many of the distortions present in more commonly used plain sections through the Bunge–Euler orientation space, which facilitates the visual comparison between scatter plots of discrete points in the orientation space and continuous ODFs fit to those points. The MTEX toolbox will also be used to produce comparison ODFs fit by spherical harmonic analysis. In order to make comparisons to be as objective as possible, comparison ODFs will be produced using the MTEX automatic half-width selection with a bandwidth of l = 32 unless specifically noted otherwise.

Finally, information entropy, or texture entropy, will be employed as a scalar description of the sharpness or peak intensity of a given ODF. Texture entropy was chosen over the more well-known texture index[1] as it has a more rigorous connection to information and estimation theory.[44,45,46] The entropy of an ODF is defined as

$$ H\left(f({\mathbf{g}})\right)=E \left[ -\log{f({\mathbf{g}})} \right] = -\int\limits_{SO(3)}f({\mathbf{g}}) \log{f({\mathbf{g}})} d{\mathbf{g}} $$

(1)

The information entropy can be understood as a measure of the unpredictability of a random variable, in the same way that thermodynamic entropy is a measure of disorder.

The information entropy has important theoretical connections to probability theory that are relevant to the discussion of texture estimation. In particular, the principle of maximum entropy states that given some set of testable data about a system, the probability distribution that best represents the current state of the system will be the one that maximizes the information entropy. The principle of maximum entropy is also useful in developing prior distributions for Bayesian inference and in choosing candidate distributions for modeling purposes. Applying the principle of maximum entropy to model selection suggests that if nothing is known about the true distribution that generated some testable information, except that it belongs to a certain class of distributions, the distribution with the largest entropy should be chosen as the prior or candidate distribution. The reasoning is that by maximizing the entropy of the candidate distribution, we are maximizing the unpredictability of $\mathbf{g},$ thus minimizing the amount of prior information or equivalently minimizing the assumptions about the data built into the candidate distributions. In the case of our proposed model, the testable information is the set of statistics sufficient to estimate distribution parameters from a measured set of orientations $\mathcal{G}$. Given the second-order statistics computable from a discrete list of unit quaternions, the Bingham distribution (defined below) is the maximum entropy distribution on the unit hypersphere.

3 The Bingham Distribution

The Bingham distribution is an antipodally symmetric distribution on the unit hypersphere $\mathbb{S}^d \subset \mathbb{R}^{d+1}$. For orientations parameterized by unit quaternions d = 3, and the p.d.f. is given by

$$ p({\mathbf{g}};\Lambda,V)=\frac{1}{F(\Lambda)}\exp{\left\lbrace \sum_{i=1}^{4} \lambda_i \left( {\mathbf{v}}_i^T {\mathbf{g}}\right)^2\right\rbrace} $$

(2)

where $\mathbf{g}$ is a unit quaternion representing a rotation, $\Lambda$ is a vector of concentration parameters λ _i , V is a matrix, the columns of which, $\mathbf{v}_i,$ are orthogonal unit quaternions representing the principal directions of the distribution, and F is a normalization constant. Normalization of $p(\mathbf{g};\Lambda,V)$ to multiples of uniform random is trivially achieved by $p(\mathbf{g};\Lambda,V)F(\Lambda=[0,0,0])=f(\mathbf{g},\Lambda,V)$. The terms Bingham distribution and Bingham ODF will be used interchangeably to denote $f(g;\Lambda,V),$ while Bingham p.d.f will refer to $p(\mathbf{g};\Lambda,V).$

The concentration parameters, $\Lambda$ are unique only up to an additive constant, and for the current study, the convention λ₁ ≤ λ₂ ≤ λ₃ ≤ λ₄ = 0 is chosen to resolve the ambiguity.¹ We will denote $\Lambda$ as a 3-vector and ignore the implied λ₄ = 0. The Bingham distribution is a very flexible distribution on the hypersphere and was first used to model ODFs by Kunze and Schaeben, where they demonstrated that the Bingham distribution could be used to model single component, fiber, or surface textures in the case of triclinic crystal symmetry depending on the concentration parameters.[23,24,25 26] The sharpness of the texture is determined by the magnitude of the concentration parameters.

A key difficulty in working with the Bingham distribution is computation of the normalization constant $F(\Lambda)$. Following Bingham,[22] it can be seen that the normalization constant is proportional to a hyper-geometric function of matrix argument (a multivariable generalization of the confluent hyper-geometric function ₁ F ₁) with a series expansion

$$ \begin{aligned} F(\Lambda)&=2\cdot{}_1 F_1(\frac{1}{2};\frac{d+1}{2};\Lambda)=\\ & 2\sqrt{\pi}\sum_{\alpha_1,\dots,\alpha_d=0}^{\infty} \frac{\Gamma(\alpha_1+\frac{1}{2})\cdots \Gamma(\alpha_d+\frac{1}{2})}{\Gamma(\alpha_1+\cdots+\alpha_d+\frac{d+1}{2})} \frac{\lambda_1^{\alpha_1}\cdots\lambda_d^{\alpha_d}}{\alpha_1!\cdots \alpha_d!} \end{aligned} $$

(3)

The series expansion in Eq. [3] can be approximated by a recursive relation and precomputed to a lookup table for a discrete grid of $\Lambda$ values. Interpolation is then used to quickly estimate normalization constants on the fly for arbitrary $\Lambda$ values.[47]

The parameters $\Lambda$ and V can be estimated by a maximum likelihood approach. Given a set of N discrete orientations, $\mathcal{G}=\lbrace\mathbf{g}^{(1)},\ldots,\mathbf{g}^{(N)}\rbrace,$ finding the maximum likelihood estimate (MLE) $\hat{V}$ can be formulated in terms of the eigenvalues of the scatter matrix, $S=1/N\sum_i\mathbf{g}^{(i)}{\mathbf{g}^{(i)}}^T=E[\mathbf{g}\mathbf{g}^T].$ Notice that the scatter matrix is equivalent to the covariance of mean-centered data in $\mathbb{R}^n,$ and can be understood as a measure of dispersion of the measured orientations. The MLE mode of the distribution is the eigenvector of S corresponding to the largest eigenvalue, while the columns of $\hat{V}$ are the eigenvectors corresponding to the 2nd, 3rd, and 4th eigenvalues.

The MLE $\hat{\Lambda}$ is found by setting the partial derivatives of the data log-likelihood function, $\log{f(\mathcal{G} \vert \Lambda,V)}=\sum_{i=1}^N \log{f(\mathbf{g}_i \vert \Lambda,V)},$ with respect to $\Lambda$ to zero yielding

$$ \frac{1}{F(\Lambda)} \frac{\partial F(\Lambda)}{\partial \lambda_j}={\mathbf{v}}_j^TS{\mathbf{v}}_j $$

(4)

The values of the derivatives of F with respect to $\Lambda$ are precomputed and stored in a lookup table in the same manner as was done for F. Since the lookup tables for F and ∇ F are indexed by $\Lambda,$ a kD-tree can be used to find the nearest neighbors for a computed ∇ F /F to compute $\hat{\Lambda}$ by interpolation.[47]

Notice that S is a sufficient statistic for the Bingham distribution, in the sense that both $\hat{\Lambda}$ and $\hat{V}$ can be estimated from only the scatter matrix. While a proof is beyond the scope of this article, it can be shown that the Bingham distribution is the maximum entropy distribution on the unit hypersphere of all possible distributions which match the scatter matrix (second-order statistics of orientations).[48] As discussed previously, this max entropy property gives us an important theoretical justification for choosing the Bingham distribution to model texture.

4 Unsupervised Learning Framework

4.1 Mixture Model and Expectation Maximization Algorithm

Being a maximum entropy distribution on SO(3) makes the Bingham distribution a logical choice to model texture. However, in practice, many important textures contain multiple components and cannot be accurately described by a single unimodal distribution, and so a more complex model is required. For this purpose, we propose a finite Bingham mixture model. Finite mixture models are commonly utilized in many areas such as pattern recognition, computer vision, signal and image analysis and machine learning.[49] In the field of statistical pattern recognition, finite mixture models provide a formal (i.e. probabilistic) approach to unsupervised learning problems, such as clustering. Here, we visualize the existence of preferred crystallographic orientations as clustering on the unit hypersphere and frame the fitting of the finite Bingham mixture model as an unsupervised learning problem.

Mathematically, the Bingham mixture model can be expressed as

$$ f({\mathbf{g}}\vert \Theta)=\sum_{m=1}^k \alpha_m f({\mathbf{g}} \vert \boldsymbol{\theta}_m) $$

(5)

where k is the number of components in the mixture, α _m represents the mixing probabilities, $\boldsymbol{\theta}_m=\lbrace \Lambda_m,V_m \rbrace$ is the set of parameters for the mth Bingham component, and $\Theta=\lbrace{\varvec{\theta}}_{1};\ldots;{\varvec{\theta}}_{k};{\varvec{\alpha}}_{1};\ldots;{\varvec{\alpha}}_{k}\rbrace$ is the complete set of parameters necessary to specify the mixture model. As the α _m are probabilities, they must satisfy

$$ \begin{aligned} \alpha_m &\geq 0 \hbox { for all } m\\ \sum_{m=1}^k &\alpha_m =1 \end{aligned} $$

(6)

Given a set of n independent and identically distributed orientations, $\mathcal{G}=\lbrace \mathbf{g}^{(1)},\ldots,\mathbf{g}^{(n)}\rbrace$ and a potential set of parameters $\Theta,$ the likelihood function $f(\mathcal{G} \vert \Theta)$ gives the probability of measuring $\mathcal{G}$ given $\Theta,$ and is used as a measure of how well the mixture model parameters fit the measured data. As the Bingham p.d.f Eq. [2] contains an exponential, it is convenient to replace the likelihood with the log likelihood given by

$$ \begin{aligned} \log{f({\mathcal{G}}\vert \Theta)} &= \log{\prod_{i=1}^n f(g^{(i)}\vert \Theta)}\\ &=\sum_{i=1}^n \log{\sum_{m=1}^k \alpha_m f(g^{(i)}\vert\boldsymbol{\theta}_m)} \end{aligned} $$

(7)

While the log likelihood is no longer a true probability, it is still a valid measure of how well the parameters fit the data; as the natural logarithm is a monotonically increasing function and $\log{f(x)}$ and f(x) achieve maxima at the same value. The common approach to fitting a mixture model is to seek an estimate of $\Theta$ (in this case the ML estimate) which maximizes the likelihood of measuring the data:

$$\hat{\Theta }_{{ML}} = \mathop {\arg\max}\limits_{\Theta } \{ \log f(\mathcal{G}|\Theta )\}$$

(8)

Unfortunately, an analytic solution to Eq. [8] does not exist and a numerical algorithm must be employed to solve the optimization, given the constraints imposed by Eq. [6].[50] The expectation maximization (EM) algorithm is the usual choice for obtaining ML estimates of mixture parameters. The EM algorithm is an iterative procedure to find maxima of $f(\mathcal{G}\vert \Theta)$. For this study, we adopt a modified EM-type algorithm first proposed by Figueiredo and Jain which provides a selection criteria to determine the number of components in the mixture model, avoids some convergence problems associated with boundaries of the parameter space and is less sensitive to initial values.[51] The mechanism for estimating the number of components will be discussed in Section IV–B, and while discussing the basics of EM-type algorithms, we will assume the number of components is known and fixed at some value k.

For fitting mixture models, EM-type algorithms are predicated on interpreting the measured data, $\mathcal{G},$ as incomplete. The missing component is a k × n binary label matrix $\mathcal{Z}=\lbrace\mathbf{z}^{(1)},\ldots,\mathbf{z}^{(n)}\rbrace$ where the mth element of vector $\mathbf{z}^{(i)}, z^{(i)}_m,$ takes the value 1 if mixture m produced sample i and 0 otherwise. If $\mathcal{Z}$ could somehow be measured, then finding $\hat{\Theta}_{ML}$ would be reduced to the trivial estimation of the Bingham parameters for each component. The complete data log likelihood is then given by

$$ \log{f({\mathcal{G}},{\mathcal{Z}} \vert \Theta)}=\sum_{i=1}^n\sum_{m=1}^k z^{(i)}_m \log{\left[ \alpha_m f({\mathbf{g}}^{(i)}\vert \boldsymbol{\theta}_m ) \right]} $$

(9)

and is understood as the function from which $\hat{\Theta}_{ML}$ could be computed, if the complete data were known. The EM algorithm maximizes Eq. [9] by alternately estimating $\hat{\mathcal{Z}}$ given the current guess at $\hat{\Theta}$ (The E-step of the algorithm), then using the result to produce an updated guess of $\hat{\Theta}$ (the M-step of the algorithm), proceeding until a convergence criterion is met.

In the E-step, at the jth iteration, the conditional expectation of the complete log likelihood Eq. [9] is computed, given $\mathcal{G}$ and the current estimate $\hat{\Theta}(j)$. As Eq. [9] is linear with respect to $\mathcal{Z},$ this is accomplished by computing the conditional expectation $\mathcal{W}= E\left[\mathcal{Z}\vert \mathcal{G}, \hat{\Theta}(j)\right],$ and plugging it into $f(\mathcal{G},\mathcal{Z} \vert \mathbf{\Theta})$. In the EM literature, this is termed the Q function

$$ \begin{aligned} Q\left(\Theta,\hat{\Theta}\right) &= E\left[ \log{f({\mathcal{G}},{\mathcal{Z}} \vert \Theta) \big\vert {\mathcal{G}},\hat{\Theta}}\right]\\ &=\log{f({\mathcal{G}},{\mathcal{W}}\vert \Theta)} \end{aligned} $$

(10)

Bayes Law is then used to update the values of z ⁽ⁱ⁾ _m .

As the elements of $\mathcal{Z}$ are binary, $\mathcal{W}$ can be computed via

$$ \begin{aligned} w^{(i)}_m&=E\left[ z^{(i)}_m \vert {\mathcal{G}},\hat{\Theta}(j)\right]={\mathcal{P}}\left[z^{(i)}_m=1 \vert {\mathbf{g}}^{(i)},\hat{\Theta}(j) \right]\\ &=\frac{\hat{\alpha}_m(j) f\left({\mathbf{g}}^{(i)}\vert \hat{\boldsymbol{\theta}}_m(j)\right)} {\sum_{l=1}^k \hat{\alpha}_l(j) f\left({\mathbf{g}}^{(i)}\vert \hat{\boldsymbol{\theta}}_l(j)\right)} \end{aligned} $$

(11)

where $\mathcal{P}$ indicates probability, and α _m is interpreted as the prior probability that z ⁽ⁱ⁾ _m  = 1. w ⁽ⁱ⁾ _m is then understood as the posterior probability after observing $\mathbf{g}^{(i)}.$

In the M-step, the parameter estimates are updated via

$$ \hat{\Theta }(j + 1) = \mathop {\arg \max }\limits_{\Theta } \,Q(\Theta ,\hat{\Theta }) $$

(12)

under the constraints given by Eq. [6]. As we will see in the next section, this step will involve fitting a set of k Bingham distributions to k weighted datasets, with dataset weights for the mth Bingham being given by w ⁽ⁱ⁾ _m .

4.2 Determining the Number of Components

In the above discussion, it was assumed that the number of components was known when applying the EM algorithm to estimate $\hat{\Theta}_{ML}$. In practice, the number of mixture components is not known a priori and must be found as part of the fitting procedure. Determining the number of components requires managing a trade-off between a more complex model, which may overfit the data, and a more simplistic model with too few components to accurately represent the true texture. Figueiredo and Jain[51] proposed an EM-like algorithm, where $\hat{\Theta}$ is chosen in such a manner as to maximize the efficiency of the mixture model representation by employing a minimum message length criteria (MML). MML is a powerful tool for model comparison in information and communications theory, and was first explored by Wallace in 1968.[52] If one wishes to send compressed or encoded data over a communication channel, and the recipient does not a priori know the code, the message sent must consist of two parts: (1) the encoding or compression key followed by (2) an efficient compressed representation of the data. MML asserts that the “best” compression scheme minimizes the total message length (the code length plus the length of the encoded data), rather than only the length of the compressed data. Here, $\mathcal{G}$ are the data to be encoded as a Bingham mixture ODF with parameter $\Theta$. Let $\mathcal{L}(\mathcal{X})$ denote the length of $\mathcal{X}$. Then according to Shannon’s coding theorem, the shortest possible length for $\mathcal{G},$ encoded as a Bingham mixture with given parameters $\Theta,$ is $\mathcal{L}(\mathcal{G} \vert \Theta) = { -\log{f(\mathcal{G} \vert \Theta)}}.$ The total length of the data and Bingham mixture model is then $\mathcal{L}(\Theta,\mathcal{G})=\mathcal{L}(\Theta) + \mathcal{L}(\mathcal{G} \vert \Theta)$

The functional form for the code length, or equivalently the length of the Bingham mixture model, $\mathcal{L}(\Theta)$ is derived by Figueiredo and Jain, and the interested reader is referred to.[51] For a mixture with k components, the total message length is explicitly given by

$$ \begin{aligned} {\mathcal{L}}(\Theta,{\mathcal{G}}) &= \frac{N}{2}\left(\sum_{m=1}^k \log{\frac{n \alpha_m}{12}}\right)+ \frac{k}{2}\log{\frac{n}{12}}\\ &\quad+ \frac{k(N+1)}{2}-\log{f({\mathcal{G}}\vert \Theta)} \end{aligned} $$

(13)

where n is the number of discrete orientation measurements, and N is the number of independent scalar parameters necessary to specify each Bingham component.

Eq. [13] represents a balance between the number of mixture components and the accuracy of the texture fit. A poorly fitting model, i.e., small $f(\mathcal{G},\vert \Theta),$ will never be chosen, but a high likelihood is not sufficient to be the optimum either. The likelihood function is a measure of the probability of generating the data from the model, and not strictly a measure of the quality of the model itself. Consider that for a dataset of 500 orientations, the mixture model that maximizes the likelihood is an equal weighting of 500 delta distributions, which is obviously a very poor model. The MML criterion is a formal information theoretic invocation of Occam’s Razor, in that it asserts that the simplest/shortest explanation of the data is usually the best. The estimate of the optimal mixture parameters is then

$$ \hat{\Theta } = \mathop {\arg \min }\limits_{\Theta } \,\mathcal{L}(\Theta ,\mathcal{G}) $$

(14)

Implementing the MML criterion into the EM algorithm is accomplished through a modification of the M-step, Eq. [12]. First the mixing probabilities are estimated for the (j + 1)th iteration via

$$ \hat{\alpha}_m(j+1)= \frac{ \max{\left\lbrace 0, \left( \sum_{i=1}^n w_m^{(i)}\right)-\frac{N}{2}\right\rbrace} } { \sum_{l=1}^k \max{\left\lbrace 0, \left( \sum_{i=1}^n w_l^{(i)}\right)-\frac{N}{2}\right\rbrace} } $$

(15)

for $m=1,2,\ldots,k.$ Followed by

$$ \widehat{\theta }_{m} = \mathop {\arg \max }\limits_{{\theta _{m} }} \,Q(\Theta ,\hat{\Theta }(j))\quad {\text{for }}m:\hat{\alpha }_{m} (j + 1)>0 $$

(16)

The Q function is understood as the conditional expectation of the complete log likelihood, evaluated for the data $\mathcal{G}$ and the updated label matrix $\mathcal{W},$ given the current guess of the parameters. Thus, the optimization in Eq. [16] is accomplished by simply performing a weighted ML fit of the Bingham parameters for each component, where the weight of the ith orientation for the mth component is given by w ⁽ⁱ⁾ _m .

Notice that the Bingham parameters are only estimated for the components with nonzero mixing probabilities. Thus, the M-step, as described by Eq. [15], serves as an explicit rule for component annihilation. As the support of a component becomes too weak, meaning that its continued inclusion is not supported by the data, it is removed from the mixture and k(j + 1) = k(j) − 1. Direct implementation of Eq. [15] does have one potential failure mode, namely, if the initial number of components is large enough that no individual component has enough initial support (i.e. $\sum_{i=1}^n w_m^{(i)} < N/2 \forall m$), then all the components could be annihilated at the first iteration. This has been prevented by implementing the algorithm in a component-wise manner. Rather than simultaneously updating all α _m and $\boldsymbol{\theta}_m,$ they are updated in a sequential manner; i.e., compute $\mathcal{W}$ update α₁ and $\boldsymbol{\theta}_1,$ recompute $\mathcal{W}$ update α₂, and $\boldsymbol{\theta}_2,$ and so on. When a component is killed in this manner, the mixing probabilities of the remaining components are immediately renormalized increasing their chance of survival. This allows for the initialization of the algorithm with an arbitrarily large number of components and removes much of the sensitivity of traditional EM algorithms to starting conditions.

4.3 Algorithm Completion and Implementation

At each iteration, the E-step and M-step are performed until the relative decrease in $\mathcal{L}(\hat{\Theta},\mathcal{G})$ falls below a threshold value, ε. However, convergence of $\mathcal{L}(\hat{\Theta},\mathcal{G})$ for a k component mixture does not guarantee that the minimum has been reached. It is possible that a smaller values of $\mathcal{L}(\hat{\Theta},\mathcal{G})$ could be obtained with a k − 1 or smaller component mixture. This must be checked by sequentially removing components that were not killed by Eq. [15]. This is achieved by annihilating the component with smallest α _m , re-normalizing the remainder and re-starting the EM algorithm and running until convergence is again achieved. This is repeated until only one component remains when the algorithm is terminated. The mixture from the iteration that produced the minimum $\mathcal{L}(\hat{\Theta},\mathcal{G})$ is selected as the best possible representation of the ODF.

Pseudo-code showing the implementation of the algorithm is given in Appendix A. Demonstration Matlab[53] code reproducing the case studies presented in the following sections has been made available from the authors as part of the Bingham Statistics Library.[27] The Bingham Statistics Library contains an implementation of the Bingham distribution written in C and Matlab for directional statistics on $\mathbb{S}^1, \mathbb{S}^2,$ and $\mathbb{S}^3$. Optimized library functions for the EM Bingham mixture model described above will also shortly be included into the Bingham Statistics Library for use and testing by the larger texture community.

5 Case Studies

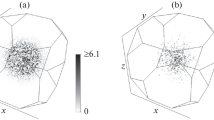
In this section, case studies demonstrating several ODF fits for triclinic crystal systems (triclinic crystal and triclinic sample symmetries) are presented to demonstrate key features and operation of the above unsupervised learning approach. As a first example, a relatively strong texture (maximum 14 times random, H =  − 0.6282) was generated as an equal-weighted four-component Bingham mixture with uniform, sheet, fiber, and unimodal components. The concentration parameters and texture entropy of the individual components are given in Table I. This mixture served as a ground truth from which the fit textures were compared and is shown in Figure 1(a). A discrete set of orientations $\mathcal{G}$ was generated by sampling 1000 orientations from the ground truth ODF. It should be kept in mind that 1000 points in the triclinic fundamental zone represents a fairly sparse sampling. For 1000 orientations sampled from a perfectly uniform random triclinic texture, the expected angle between a sampled orientation and its closest orientation is $\approx 15\,{\text{deg}},$ for this texture the average angular separation between orientations was $12\,{\text{deg}}$. For contrast, if one were to sample 1000 orientations from a uniform cubic-triclinic ODF, then the expected angular separation would be $<5\,{\text{deg}}$. Figure 1(b) shows the sampled orientations projected onto the ODF sections shown in Figure 1(a) and highlights this sparseness.

Table I Comparison of Ground Truth vs Fit Mixture Components

Fig. 1

Ground truth ODF, discrete sampled orientations, and fit ODFs for strongly textured triclinic symmetry case study. All ODFs are normalized to multiples of the uniform random distribution and colored to a linear color scale shown in (f). Contour lines indicate integer multiples of uniform random $0,1,\ldots,14.$ ODFs are shown as spherical projection of σ-sections produced by the MTEX texture software (Color figure online)

The texture was then fit from the sampled orientations by the unsupervised learning algorithm and via a generalized spherical harmonic expansion up to l = 32 allowing MTEX to optimize the smoothing kernel. For this case, the chosen kernel was a de la Vallée Poussin kernel with a half-width of $24\,{\text{deg}}$. The large degree of smoothing required in the harmonic ODF is a direct consequence of the sparseness of sampled orientations. The unsupervised learning algorithm was initialized with 20 randomly generated Bingham mixture components. The convergence tolerance for the change in $\mathcal{L}(\hat{\Theta},\mathcal{G}), \epsilon,$ was taken as 0.001 (See Section IV–C).

For this example, the algorithm completed in 116 EM iterations. Key details of the progression of the unsupervised learning algorithm are shown in Figure 2. Figure 2(a) is a scatterplot showing the combination of description length as a function of number of component k; each iteration is represented by a data point. As can be seen, a distinct minima in description length occurs with a four-component mixture. The concentration parameters and weights of the fit mixture agree reasonably well with the ground truth mixture as is shown in Table I. The evolution of the description length is shown in Figure 2(b) along with the iterations at which a mixture component was killed. The vertical lines in Figure 2(b) show where components were killed either by loss of support (solid lines) or by intentional removal of the weakest component after the convergence of the component-wise EM steps (dashed lines). In this case, the number of components was reduced down from 20 to 15 by loss of support before EM convergence was reached. Typically, when a component loses support and is removed, the description length will continue to decrease; however, when a component is killed after convergence of the component-wise EM, the description length will sharply jump as the orientations assigned to the killed components are reassigned.

Fig. 2

(a) Message length as a function of number of componets, k. Each iteration is represented by a data point. (b) Evolution of message length with increasing iterations. Iterations where a component was killed are indicated by vertical lines. Solid lines indicate that a component was killed by loss of support. Dashed lines indicate where the EM steps converged and a component was forcibly removed. (c) Log likelihood as a function of mixture components. It can be seen that the highest likelihood occurred at a 15-component. However, the four-component mixture had a shorter message length and was chosen as the best ODF (Color figure online)

The resulting ODFs are shown in Figures 1(c) and (d). As can be seen in Figure 1(c), the unsupervised learning algorithm does an excellent job of capturing the features of the texture as well as the minimum and maximum ODF values. The texture entropy for the fit texture was H =  − 0.6264 which compared excellently with H =  − 0.6282 for the ground truth ODF. The MTEX spherical harmonic ODF also does an excellent job of capturing the main features of the ODF but owing to the high degree of smoothing, the maximum intensity of the fit texture is roughly 1/2 of the ground truth maxima. The texture entropy for the harmonic fit with automatic kernel selection is accordingly higher at H =  − 0.4331.

As another point of comparison, a second spherical harmonic texture fit was performed (also taking l = 32), this time narrowing the smoothing kernel half-width to $10\,{\text{deg}}$ so that the resulting texture had the same maximum intensity as the ground truth ODF and unsupervised learning ODF. This example is not a true performance comparison as typically neither the texture intensity nor the optimum smoothing is known a priori. However, this example serves to highlight some of the difficulties associated with fitting ODFs from limited discrete orientation data. While the maximum intensities are the same the $10\,{\text{deg}}$ half-width ODF had a texture entropy of H =  − 0.8022 which was ≈ 30 pct lower than the ground truth value indicating the harmonic texture had sharper peaks. The resulting ODF is shown in Figure 1(e). As can be seen from the figure, the fit ODF also shows significant Gibbs oscillations with regions of nonphysical negative intensity (minimum values −0.2 time random). The fit ODF is also “spotty” in the sense that local peaks can be seen that correspond to individual sampled orientations. A comparison between 24-deg half-width ODF (Figure 1(d)) and the 10-deg half-width ODF (Figure 1(e)) highlights the difficulty in choosing appropriate smoothing parameters when fitting ODFs from discrete data using the common harmonic or direct methods. If the smoothing is too high, then the texture intensity is washed out as tight peaks are spread out into neighboring regions. If the smoothing is too low, then the resulting ODF is over-fit and spotty and for harmonic expansions, nonphysical negative intensities can be obtained. Eliminating the need to a priori choose the degree of smoothing while simultaneously avoiding nonphysical features when fitting ODFs from sparse orientation data is a prime gain of the proposed unsupervised learning algorithm.

Examining the evolution of the data log likelihood provides some insight into why an EM-type algorithm with minimum message length criteria was selected for the texture algorithm. As stated before, selecting the number of mixture components based on minimum description length allows for a trade off between how well the model matches the measured data (maximizing the data log likelihood Eq. [7]) and model complexity (minimizing the number of components). Figure 4(c) shows the evolution of the data log likelihood, and shows that the best fit (highest likelihood) to the discrete orientation data occurs at much higher number of components than are actually present in the ground truth texture. Typically, the log likelihood actually reaches its maximum value when initial EM convergence is reached, in this case with a 15-component mixture, and decrease with the removal of each subsequent component. Remember the likelihood is a probability measure on the model producing the data, not a direct description of the quality of the model, and an overfit model will often have a higher likelihood than the correct model. This is shown in Table II, which compares the log likelihood, message length (where applicable), and texture entropy for the ground truth texture and all of the various fits described above. Despite being a poor approximation of the ground truth texture, the harmonic ODF with $10\,{\text{deg}}$ smoothing has a log likelihood of 2 × the minimum message length fit and the ground truth texture. In a similar manner, the 15-component mixture has a high likelihood, as it has more degrees of freedom to more closely fit the data points. However, the larger message length tells us that the model is overly complex and that “better” models can be developed by reducing this complexity.

Table II Comparison of the Various ODF Estimates for the Strongly Textured Case Study

Two final notes before moving onto the next example: (1) It is interesting that the ground truth ODF had a slightly lower likelihood and longer message length than the fit four-component mixture, implying the minimum message length ODF is in some way “better” than the true ODF. It is important to remember that the fit ODF represents a point estimate of the mixture parameters, given the sampled orientations $\mathcal{G}$. If a different set of orientations were sampled and then fit, a second point estimate ODF would be obtained. If repeated point estimates were obtained from independent trials, then we would expect that, when averaged over all trials, the ground truth ODF would be a better fit than any single ODF fit to an independent trial. 2) The fact that the texture entropy is virtually identical for the ground truth and minimum message length ODFs provides anecdotal confirmation of its value as a scalar measure for texture comparison.

Accurate ODF estimation for weakly textured materials is generally more difficult than for strong textures. As a second case study, an ODF for a weakly textured material was generated by dividing the concentration parameters of the four components from the strongly textured example by 5 (see Table I). The resulting ODF is shown in Figure 3(a). While the peaks of this weaker ODF appear in the same place, they are much more diffuse and exhibit a much weaker maximum intensity of 2.4 times random. As in the first example, 1000 orientations were sampled from the mixture (Figure 3(b)) and fit using the unsupervised learning algorithm and as a harmonic series, again allowing MTEX to select the smoothing kernel half-width. In addition, the convergence criterion was maintained at 0.001, and k _max = 20 arbitrary components were used as the initial configuration. The resulting fits are shown in Figure 3(c), unsupervised learning, and 3(d), harmonic. As can be seen in the figure, an excellent match with the ground truth ODF is achieved with the unsupervised learning algorithm, both in terms of peak location and intensity. In contrast, while the maximum intensity values are well captured by the harmonic fit, the peak locations are visibly shifted relative to their ground truth locations. This is likely due to an artificial overlap of peaks due to the high smoothing, as when the extent of the smoothing kernel is reduced in extent, the peaks rotate back to their correct location, but with very high intensities (>5 times random), and significant oscillation is evident (resulting ODF not shown).

Fig. 3

Ground truth ODF, discrete sampled orientations, and fit ODFs for weakly textured triclinic symmetry case study. All ODFs are normalized to multiples of the uniform random distribution and colored to a linear color scale shown in (f). Color scale and contour lines are shown in (e). ODFs are shown as spherical projection of σ-sections produced by the MTEX texture software (Color figure online)

As can be seen in Figures 4(a) and (b), the unsupervised learning algorithm progressed quite differently than in the previous strongly textured example. Most striking is that the single component solution had much shorter message length than either: (1) any potential four-component solutions found by the algorithm or (2) the ground truth mixture. The evolution of the message length and transitions are shown in Figure 4(b). In contrast to the strongly textured example (see Figure 2(b)), most of the transitions for this case study are due to loss of support rather than being forcibly killed after convergence of the EM steps. There is also an interesting, and unexpected, large jump in message length at the transition from three to two components. Since it is caused by lack of support, one would expect a relatively smooth transition due to the dependence of code length on volume fraction (see Eq. [13]). This spike was cause by an interesting rearrangement of the mixture as the third component lost support. The first two (surviving components) were very similar (in terms of weights and parameters) and heavily overlapped. As support was removed from the third component, and added to the other two, the surviving components suddenly diverged, completely changing the character of the mixture. This rearrangement caused the temporary drop in likelihood as the remaining two components were in flux.

The message length, log likelihood, and texture entropy for the ground truth mixture, the best fit, the best four-component mixture, and the MTEX fit are shown in Table III. Quite surprisingly the message length for the ground truth mixture is much greater than the best fit, while the log likelihood values are almost identical. In fact, the message length for the ground truth is positive, indicating that the positive code length contribution to the message length overwhelms the negative encoded data length. This implies that there is a redundancy in the original description and not all the four components were required to express the ground truth texture accurately.

Table III Comparison of the Various ODF Estimates for the Weakly Textured Case Study

Whether a material is truly random or weakly textured is difficult to determine from limited discrete points by either direct methods or harmonic analysis. In both approaches, the ODF is represented as the superposition of the individual orientations convoluted with a smoothing kernel. Under such conditions, particularly when the number of orientations is limited, it is difficult to resolve statistically expected clustering in the samples from actual weak peaks in the ODF. As a final example, the ability of the unsupervised learning approach to fit uniform random textures is examined. Sets of orientations were sampled from uniform random ODFs, and fit by both the unsupervised learning approach and by harmonic analysis via MTEX with automated kernel selection. 100 independent trials were completed for ensembles of 100, 500, 1000, 2000, 5000, and 10000 orientations. It can be seen in Figure 5 that the entropy of unsupervised learning ODFs were significantly closer to zero than the harmonic textures for all ensemble sizes indicating that the fit textures were closer to uniform. Example fits for 1000 orientation are shown in Figure 6.

Fig. 4

(a) Message length as a function of number of componets, k. Each iteration is represented by a data point. (b) Evolution of message length with increasing iterations. Iterations where a component was killed are indicated by vertical lines. Solid lines indicate that a component was killed by loss of support. Dashed lines indicate where the EM steps converged and a component was forcibly removed (Color figure online)

Fig. 5

Comparison of average texture entropy (over 100 independent trials) for unsupervised learning ODFs vs spherical harmonic ODFs. Error bars indicate standard error. The unsupervised learning ODFs are significantly closer to uniform for all sample sizes

Fig. 6

Example of ODF estimates for a uniform random ODF from 1000 discrete orientations for (a) the unsupervised learning algorithm and (b) spherical harmonic expansion (Color figure online)

6 Discussion and Concluding Remarks

While significant effort and space has necessarily been spent on the details and implementation of the unsupervised learning algorithm and the underlying Bingham mixture model, the central message of the current study is that there is a fundamental difference between the traditional problem of estimating an ODF from a series of incompletely measured pole figures, obtained from X-ray or neutron diffraction, and the estimation of ODFs from individual orientation measurements from EBSD or as the output from micromechanics simulations. The primary goal of the current study was to develop a completely new approach to texture analysis, specifically for discrete orientation data, that minimizes the number of assumptions or a priori decisions that must be made in ODF estimation, while at the same time eliminating the possibility of nonphysical artifacts in the resulting ODF. In the development of the unsupervised learning approach only two assumption have been made, (1) that an arbitrary ODF can be accurately represented as a finite Bingham mixture and (2) that the individual orientation measurements are independent and identically distributed (i.i.d.). Some consequences of these assumptions are discussed hereafter.

The starting point for the development of the unsupervised learning algorithm was the hypothesis that the “best” ODF was the one that (1) maximized, in some sense, the probability of generating the discrete orientation data; and (2) where the level of detail (fluctuations) was a reflection of the uncertainty due to the quality/quantity of the measured orientations. These requirements naturally lead to the minimum message length criterion presented here. The end product is a data-driven approach to ODF estimation, based on well-developed concepts from information theory, that requires no a priori decisions on the part of the user. Another key advantage of this approach is the ability to produce reasonable ODF estimates from limited data on the scale of the statistical volumes commonly used in crystal plasticity finite elements or other full field micromechanics simulations (a few hundred grains).

The assumption that an arbitrary ODF can be represented by as a finite Bingham mixture is expected to hold for most textures of interest. There are some uncommon ODFs for which this assumption is clearly violated. These include the “cone fiber” texture as explored by Grewen and Wasserman and Matthies et al.[54,55] In order to capture these textures with a Bingham mixture model, a very large number of radially symmetric unimodal components would need to used. However, as mentioned in the introduction, the ODF model and the unsupervised learning approach are fairly decoupled. In this case, another mixture model such as a texture component basis could be substituted for the Bingham model,[37,38,39,40] and the minimum message length unsupervised learning approach can be applied without change.

The more restrictive assumption is that the discrete orientation measurements are i.i.d.. This assumption is likely to hold true when analyzing the output from homogenized or effective medium crystal plasticity simulations such as the well-known visco-plastic self-consistent model. The output of such simulations is an effective orientation for each grain and a weighting factor to account for the size of a particular grain. Each data point can be thought of as independently sampling a grain from a large polycrystal. In contrast, the individual orientations from an EBSD map exhibit a high degree of spatial correlation (e.g. within the spatial extent of a grain all sampled orientations will be clustered in some region of orientation space), this assumption clearly breaks down. For discussion purposes, one can imagine two extreme cases: (1) where a statistically significant number of grains are mapped, and (2) where a limited number of grains are mapped but each grain contains a large number of measurement points.

In the case of mapping a large number of grains, an approximate correction can be made by randomly sub-sampling points from the EBSD map. By sub-sampling uniformly over the EBSD map, the effects of local spatial correlations within grains can largely be removed. An ideal sampling density will be dependent on the grain size and spatial resolution of the original map. This is roughly equivalent to the common practice of measuring a “texture scan” via EBSD where the spatial step size is increased to roughly the grain size, so that a large number of grains are sampled with one or two measurement points per grain.

The second case, where an EBSD map contains a very limited number of grains, represents a very local microtexture measurement. In this case, one is often interested in the orientation spread within a single grain or in the understanding of highly localized orientation gradients and sub-structure formation rather than an estimate of the macrotexture ODF. In studying intragranular orientations, the unsupervised learning approach can potentially offer significant benefits over harmonic analysis as the resulting measured orientation spread is going to be highly dependent on the degree of smoothing and bandwidth selected. The advantage of the Bingham mixture model presented is two-fold: (1) no a priori information on the orientation spread is needed to properly estimate the peak widths, and (2) the minimum message length criteria gives an objective data-driven criteria for determining if the orientation spread within a grain is unimodal (single Bingham component) or multimodal (Bingham mixture) which could potentially be useful in studying active deformation modes or substructure development within a grain.

It is also important to note i.i.d. orientation measurements is also a central, but often neglected, assumption made in the application of direct methods (such as WIMV) and spherical harmonic techniques. The automatic kernel selection algorithm within MTEX can serve as a highlighting example. It has been documented that when performing half-width estimation from spatially correlated orientations (such as a list of orientations from an EBSD map) the recommended kernel will be overly sharp. The recommended approach is to remove the spatial correlation by estimating the kernel half-width from a weighted mean or effective orientation for each grain (See MTEX documentation and[21]). The degree to which the proposed unsupervised learning algorithm is affected by spatially correlated data is being investigated and will presented in a future publication.

In conclusion, this study represents a proof-of-concept application of the unsupervised learning algorithm. The main focus of this article was to lay out the details of the Bingham mixture model, the unsupervised learning approach, and the minimum message length criteria in a self-contained manner, and perform some simple demonstrations on “toy” texture estimation problems. Another study is ongoing on the development of efficient parameter estimation approaches for the Bingham distribution in the presence of arbitrary crystallographic and sample symmetry The application of these concepts to actual experimentally measured textures and predicted texture from crystal plasticity simulations is reserved for a future publication.

Appendix A: Implementation of the Expectation Maximization Algorithm

Pseudo-code detailing implementation of the complete EM-type algorithm for the fitting of finite Bingham mixtures is shown in Algorithm 1.