Static Modal Analysis: A Review of Static Structural Analysis Methods Through a New Modal Paradigm

Abstract

This article is a state-of-art review on static structural computations for pin-jointed structures, revising the last forty years of scientific research on the subject matter through the introduction of static modal analysis. This novel paradigm is inspired by the so-called singular value decomposition (SVD) of the equilibrium matrix and by dynamic modal analysis. In dynamics, modal analysis requires the solution of an eigenvalue problem, which returns the natural frequencies of the structure and the corresponding mode shapes of vibration, the eigenvectors. The application of the static modal analysis to the four types of linear trusses—determinate or indeterminate from the static and kinematic viewpoints—allows re-interpreting the well-known force method and displacement method of structural analysis. Central to this proposal is the solution of static equilibrium and compatibility equations in a modal space where the relations between the extensional, inextensional, and self-stress modes are unequivocally identified. Their physical interpretation, also at the equilibrium and compatibility levels, is discussed and illustrated by key accompanying examples of structures subjected to external loads. Several original diagrammatic representations of the static modal analysis contribute to the overall understanding and implementation of the mathematical relations. This approach brings out new aspects of the interrelationship between the force and displacement methods, which strengthen their complementarity.

1 Introduction

Tensegrity structures are a special type of pin-jointed assemblies where the struts in compression visually appear to “float inside an ocean” of cables in tension [1,2,3]. Their aesthetic appeal has inspired artists and architects for several decades [4, 5], while their complex structural behavior [6,7,8,9,10] has challenged many engineers and scientists for more than forty years of intensive research [11,12,13,14,15,16,17]. This is justified by the fact that fundamental laws of physics and structural engineering principles (e.g. the Hooke’s Law of linear elasticity [18, 19] and the degree of static indeterminacy of trusses [20]) must be employed and revised carefully to take into account phenomena arising from the existence of prestressing forces [21,22,23,24,25,26,27] and mechanisms [28,29,30,31,32,33,34,35,36,37].

Pellegrino [28] proposed in 1990 to classify pin-jointed structures into four types¹ of trusses depending on the number “s” of self-stress modes and number “m” of mechanisms that they possess intrinsically (Fig. 1). A self-stress mode is a particular pattern of internal forces that can exist without external loads (Fig. 1b and b′). The associated prestress level (i.e. a scalar that multiplies the self-stress mode in Fig. 1b) can be increased by shortening the cables or lengthening the struts through mechanical devices such as turnbuckles, hydraulic jacks, etc. [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Trusses possessing one or more self-stress modes are said to be statically indeterminate of degree “s” [11, 14, 20].

Fig. 1

Simple 2D (or 3D if specified) examples of the four types of trusses. In these simple examples, the degrees of static indeterminacy “s” are either equal to 0 or 1 (but not higher). Similarly, the degrees of kinematic indeterminacy “m” are either equal to 0 or 1 (but not higher)

A mechanism is defined as a particular pattern of incremental displacements which generates no elongations of the elements (Fig. 1c and c′). The mechanism is said infinitesimal if the condition of no elongation is limited to the occurrence of infinitesimal displacements (Fig. 1d and d′). Trusses with one or more mechanisms are said to be kinematically indeterminate of degree “m” [14].

Tensegrity structures belong to the type IV (Fig. 1d′) or to type II [47, 60, 61] because the presence of cables requires the introduction of self-stress forces.² The latter can only be introduced into statically indeterminate structures. For instance, shortening both legs of the truss in Fig. 1a will not generate any force, but only displacements. The shortening of both legs can be continued until the geometry reaches Fig. 1d. At this point, a geometrical degeneracy appears in the equilibrium conditions [10, 63] and the two-legs truss (type I) becomes a tightrope (type IV), i.e. the structure now possesses a mechanism and it can be self-stressed. In a similar manner, lengthening the three diagonals in Fig. 1a′ will displace the upper nodes and increase the angle of rotation between the two triangles in the bottom and top horizontal planes. The lengthening of the three diagonals can be continued until the angle reaches 30$^{\circ }$ (Fig. 1d′) [64]. Any further lengthening will induce self-stress forces in the system [56, 57], which then allows to replace the tensioned elements by cables (Fig. 1d′). This search of geometry in equilibrium with self-stress forces is generally called form-finding [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95]. The large imposed variations of the elements’ manufacturing lengths (from Fig. 1a′ to d′) require thus to revise Hooke’s Law [26, 27] because the elements’ stiffness cannot be assumed constant through the form-finding process. Large lengths variations also allow the deployment [96,96,97,98,99,100,101,102,103,104,105,106,107,108,109] and the control [41, 42, 45, 110,111,112,113,114,115,116,117,118,119,120,121,122] of tensegrity structures, which are of interest in many different applications. One concludes that the above-mentioned form-finding problems, nonlinear prestressing problems, deployment problems and control problems are different perspective viewpoints on the same reality, i.e. the computation of the final nodal coordinates and the internal forces of the elements for a given topology (i.e. fixed connectivities between elements and nodes).

One may note that (1) form-finding with given nodal coordinates may be called force-finding problems [123] or linear prestressing problems [124]; (2) topology-finding problems [94, 125,126,127,128,129,130] start from a ground-structure with an extremely high number of elements, and search for a topology by identifying each element as a cable, a strut, or inexistent while ensuring the stable equilibrium of the self-stress forces. Topology-finding refers thus to the inverse problem than form-finding, i.e. the computation of the topology for a given set of nodal coordinates. It is noted finally that (3) shape optimization [131, 132] and topology optimization [133,134,135,136,137,138,139,140,141,142,143,144,145] are special cases of form-finding and topology-finding respectively, where the nodal coordinates or the topology are searched, as well as the internal forces and the elements cross-sections (sizes), to best minimize the optimization objective (e.g. the mass, the embodied carbon, etc), and (4) the literature investigation led by the authors found very few references dealing with simultaneous shape and topology optimization problems [146,147,148]. For a larger discussion on structural optimization problems, the reader is referred to [141].

The present investigation considers that the form-finding and topology-finding of the tensegrity structures has already been performed and that prestress forces have already been implemented, i.e. the topology, the nodal coordinates and the manufacturing lengths are fixed. The focus of the current work is hence on the application of external loads to the structural nodes assuming small elastic strains in the elements. The limitations of the basic linear equations of equilibrium and compatibility when loads are added to trusses of type III and IV will be highlighted.

For structural engineering practitioners, it is well known that commercial software based on the Displacement Method fail to analyze structures that possess mechanisms, due to the singularity of the linear structural stiffness matrix. Scholars also recognize that this singularity is due to the inextensional modes that can be computed by singular value decomposition (SVD) of the equilibrium matrix [14, 15]. The SVD is thus established in the scientific literature because it provides fundamental insights into the behavior of any type of trusses, namely their self-stress modes, their extensional modes, and their inextensional modes. The introduction of the SVD in structural analysis [15] was thus a major breakthrough that greatly enhanced, among other aspects, the use of the computational version of the Force Method [36, 48, 149,150,151,152]. It is noted that (1) the mechanism pattern in Fig. 1c′ is valid for small displacements only, and (2) if the vertically-aligned element in Fig. 1b′ is a cable (i.e., withstanding only tension), then there exists a unilateral mechanism [153, 154], i.e. the center node can move upwards but not downwards. Therefore, the SVD has two known limitations, namely: (1) its results are valid at first order, and (2) it does not recognize the unilateral material properties of the elements. These limitations will not be further detailed.

Today, tensegrity structures are becoming increasingly popular for their various applications in different fields of engineering practice [9, 155, 156]. There is a crucial need for a state-of-the-art review that assembles and structures scientific advances spread among a multitude of investigation works, proposing an accessible entry point to new researchers. Furthermore, different experienced authors are still investing considerable efforts on the fundamental understanding of the behavior of tensegrity structures [36, 49, 50]. The latter have developed a purely mathematical approach to the structural analysis problem, often overlooking its physical interpretation. Recent findings conclude for instance that the mathematical expressions obtained using the Force Method are redundant with the ones obtained using the Displacement Method [50]. Such fundamental aspects of the interrelationship between both methods, which still seem to elude the bulk of the engineering and scientific communities, led the authors to undertake the current investigation. In addition to the state-of-the-art, this article also proposes novel mathematical relations, as well as physical and diagrammatic interpretations. A systematic and formal approach to the analysis of the four types of trusses is performed, enabled by the application of the principle of static modal analysis. This novel concept is applied to the four truss types (Fig. 1) in a growing order of complexity. Importantly, it is accompanied by physical explanations associated to a graphical illustration of the mathematical developments, leading to the emergence of new links between the Force Method and Displacement Method of linear analysis. Since it corresponds to a first application of the static modal analysis, no geometric or material non-linearities are considered here.

The present article is structured as follows. Section 2, Background and Objectives, starts by introducing the basic equations of linear analysis and the proposed graphical interpretation of the Force and Displacement Methods in Sect. 2.1. Section 2.2 details the Singular Value Decomposition of the equilibrium matrix and summarizes its known physical interpretations. The novel concept of static modal analysis is introduced at the end of Sect. 2, which also specifies in more detail the objectives. In Sect. 3, the linear Force and Displacement Methods are rigorously detailed for the four types of trusses using the static modal analysis, unveiling novel interrelationships between both methods. These mathematical demonstrations are graphically summarized in explicit roadmaps, and then physically interpreted through straightforward examples. Finally, some assumptions and perspectives are discussed in Sect. 4, Discussion.

2 Background and Objectives

2.1 Basic Equations of the Linear Displacement and Force Methods

2.1.1 Basic Equations

Consider a general three-dimensional (3D) pin-jointed structure with “n” nodes, “b” elements, connected to the exterior by “c” reactions, and having $n_{dof} = 3\cdot n-c$ degrees of freedom (DoF). Assuming small displacements, the linearized equations of static equilibrium, elastic constitutive relations (Hooke), and linearized compatibility, can be respectively written in the next matrix forms [14, 28]:

$$\begin{aligned} \left\{ {\varvec{f}}\right\}&=\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\} \end{aligned}$$

(1)

$$\begin{aligned} \left\{ {\varvec{t}}\right\}&= [{\varvec{K}}^{e}]\left\{ {\varvec{e}}\right\} \end{aligned}$$

(2)

$$\begin{aligned} \left\{ {\varvec{e}}\right\}&= [{\varvec{B}}]\left\{ {\varvec{d}}\right\} \end{aligned}$$

(3)

where the vectors are as follows: $\{{\varvec{f}}\}$ (size $n_{dof}\times 1$) are the resisting or internal forces, $\left\{ {\varvec{t}}\right\}$ (size $b\times 1$) are the axial internal forces in the elements (considered positive in tension), $\left\{ {\varvec{e}}\right\}$ (size $b\times 1$) are the element axial elongations, and $\left\{ {\varvec{d}}\right\}$ (size $n_{dof}\times 1$) are the nodal displacements. The equilibrium matrix $\left[ {\varvec{A}}\right]$ (size $n_{dof}\times b$) and the compatibility matrix $\left[ {\varvec{B}}\right]$ (size $b\times n_{dof}$) contain the direction cosines of the elements, and $[{\varvec{K}}^{e}]$ (size $b\times b$) is the elements’ stiffness matrix, which is diagonal (each $K_{kk}^{e}$ contains the stiffness $E_{k}A_{k}/l_{k}^{0}$ of the element k, where $E_{k}$, $A_{k}$, and $l_{k}^{0}$ stand for the Young’s modulus, the element’s cross-sectional area, and the elements’ manufacturing length, respectively). Note that:

• Equation (1) is physically interpreted in Appendix A and a systematic way to compute the equilibrium matrix $\left[ {\varvec{A}}\right]$ is presented in “Appendix A.4”.

• The equilibrium matrix presented in ref. [14] differs from the one in Eq. (1). It contained the differences of nodal coordinates between both element’s ends rather than the direction cosines. The differences between both equilibrium matrix formulations is detailed in “Appendix A.3” and our choice for Eq. (1) is justified in the first subsection of the Discussion.

• The principle of virtual work [157, 158] shows that the compatibility matrix $\left[ {\varvec{B}}\right]$ is the transpose of the equilibrium matrix $\left[ {\varvec{A}}\right]$:

  $$\begin{aligned} \left[ {\varvec{B}}\right] =\left[ {\varvec{A}}\right] ^{T} \end{aligned}$$

  (4)

• The flexibility matrix $\left[ {\varvec{F}}\right]$ is usually preferred in the Force Method. It is a diagonal matrix where each component $F_{kk}$ contains the flexibility $l_{k}^{0}/E_{k}A_{k}$ of the element k such that:

  $$\begin{aligned} \left[ {\varvec{F}}\right] =\left[ {\varvec{K}}^{e}\right] ^{-1} \end{aligned}$$

  (5)

The above equations assume small displacements $\left\{ {\varvec{d}}\right\}$, small elastic length variations $\left\{ {\varvec{e}}\right\}$, and constant direction cosines of the elements (i.e. constant equilibrium matrix $\left[ {\varvec{A}}\right]$, or small reorientations of the elements’ axes).

This article concerns one of the most common structural analysis problems, which consists in finding the axial forces $\left\{ {\varvec{t}}\right\}$, and possibly the elongations $\left\{ {\varvec{e}}\right\}$ and displacements $\left\{ {\varvec{d}}\right\}$, given a set of external loads $\left\{ {\varvec{f}}^{ext}\right\}$ applied to the structural nodes.

In a static problem, the resisting forces $\{{\varvec{f}}\}$ must equilibrate the external loads $\left\{ {\varvec{f}}^{ext}\right\}$ that act on the DoF of the structure, i.e. $\left\{ {\varvec{f}}\right\} =\left\{ {\varvec{f}}^{ext}\right\}$. In nonlinear problems, this is often expressed in terms of a residual, $\left\{ {\varvec{f}}^{res}\right\} =\left\{ {\varvec{f}}^{ext}\right\} -\left\{ {\varvec{f}}\right\}$, which is minimized iteratively until it falls below a specified tolerance, when convergence is accepted. Since in the literature it can be found that the vector $\{{\varvec{f}}\}$ in equation (1) corresponds to the applied loads, the nuance between loads and resisting forces is further illustrated in “Appendix A.1”. In the following of this article, it is assumed that the structure is in equilibrium with the external loads, i.e. $\left\{ {\varvec{f}}\right\} =\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\} =\left\{ {\varvec{f}}^{ext}\right\}$, and therefore the vector $\left\{ {\varvec{f}}\right\}$ is referred to as “loads”, although rigorously it corresponds to the internal or resisting forces; the objective of using the term “loads” is to avoid confusion with the vector of axial internal forces $\left\{ {\varvec{t}}\right\}$.

In the context of linear behavior, assumed in this work, the principle of superposition applies. In other words, the effect ($\left\{ {\varvec{t}}\right\}$, $\left\{ {\varvec{e}}\right\}$, $\left\{ {\varvec{d}}\right\}$) of a combination of sets of applied loads $\left\{ {\varvec{f}}\right\}$ is the sum of the individual effect of each set of loads taken separately³ (without change in the equilibrium matrix).

In all generality, trusses may thus be initially self-stressed. In other words, there may exist initial elongations $\left\{ {\varvec{e}}^{ini}\right\}$ and axial forces $\left\{ {\varvec{t}}^{ini}\right\}$ in self-equilibrium, i.e. without initial external loads $\left\{ {\varvec{f}}^{ini}\right\} =\left\{ \textbf{0}\right\}$. In this case, the forces $\left\{ {\varvec{t}}^{ini}\right\}$ lie in the null-space [14] of the equilibrium matrix $\left[ {\varvec{A}}\right]$ in such way that $\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}^{ini}\right\} =\left\{ \textbf{0}\right\}$. In their initial configuration, trusses may hence be self-stressed, pre-loaded, or both. In the following, we will refer without distinction to pre-stressed trusses [28]. The structural behavior of type III and type IV trusses (Fig. 1) depends on these pre-stress forces $\left\{ {\varvec{t}}^{ini}\right\}$, which will be discussed later.

This work does not address the self-stressing phase [38,39,40, 45, 47, 48, 51,52,53,54,55,56,58], i.e. it considers no variation ($\left\{ \delta {\varvec{l}}^{0}\right\} =\left\{ \textbf{0}\right\}$) of the manufacturing lengths $\left\{ {\varvec{l}}^{0}\right\}$ imposed by mechanical devices, which will be addressed in a future work. As mentioned, it instead focus on the linear superposition of external loads on pin-jointed structures using Eqs. (1)–(3).

2.1.2 Linear Mappings Viewpoint and Proposed Graphical Interpretation

The Eqs. (1)–(3) can be seen from the mathematic linear mappings viewpoint, where the matrices are employed as transformation operators from one vector space to another. For instance, in Eq. (1), the axial forces $\left\{ {\varvec{t}}\right\}$ in the elements can be easily transformed into the resisting forces $\left\{ {\varvec{f}}\right\} {\varvec{ }}$ through the equilibrium matrix $\left[ {\varvec{A}}\right]$. However, the reverse operation, i.e. finding the forces $\left\{ {\varvec{t}}\right\}$ given the external loads $\left\{ {\varvec{f}}\right\}$, is often more cumbersome since the rectangular matrix $\left[ {\varvec{A}}\right]$ (size $n_{dof}\times b$) cannot be inverted. This common structural analysis problem is generally solved through the Force Method (FM) or the Displacement Method (DM) as detailed in the next paragraphs.

In order to clarify and support the mathematical operations, graphical interpretations will be proposed throughout this paper. For instance, Fig. 2 provides a first graphical interpretation of the DM (Fig. 2a) and of the FM (Fig. 2b). The arrows illustrate the transformation of one vector space into another, expressed by a matrix premultiplication.

Fig. 2

Graphical interpretations of, a the Displacement Method, b the Force Method. Linear mappings are represented as arrows. Blue arrows stand for premultiplications (e.g. $\left\{ {\varvec{f}}\right\} =\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\}$ or $\left\{ {\varvec{f}}\right\} =\left[ {\varvec{K}}^{L}\right] \left\{ {\varvec{d}}\right\}$), while the dashed black arrows correspond to mathematically more complex operations

2.1.3 The Displacement Method (DM)

The displacement method (Fig. 2a) is widely used in engineering practice and can be summarized as follows. Given the loads $\left\{ {\varvec{f}}\right\}$, the DM finds first the displacements $\left\{ {\varvec{d}}\right\}$ by solving:

$$\begin{aligned} \left\{ {\varvec{f}}\right\} =\left[ {\varvec{K}}^{L}\right] \left\{ {\varvec{d}}\right\} \end{aligned}$$

(6)

where $\left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{A}}\right] [{\varvec{K}}^{e}]\left[ {\varvec{A}}\right] ^{T}$ (size $n_{dof}\times n_{dof}$) is the stiffness matrix of the structure obtained from assembling Eqs. (1)–(3). In traditional pin-jointed structures (i.e. trusses of type I and type II in Fig. 1), the system of Eq. (6) can be solved to find the $n_{dof}$ unknown displacements $\left\{ {\varvec{d}}\right\}$ because matrix $\left[ {\varvec{K}}^{L}\right]$ is square (size $n_{dof}\times n_{dof}$) and can be inverted.⁴ The elastic elongations $\left\{ {\varvec{e}}\right\}$ and corresponding forces $\left\{ {\varvec{t}}\right\}$ can then be obtained by post-processing through, respectively, the compatibility equation (3) and Hooke’s law (2).

However, in pin-jointed structures of type III and type IV, the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$ is singular (i.e. not invertible) for reasons that will be later clarified. To face these limitations of the well-known Displacement Method, the Force Method started arousing again the interest of the scientific community, as described next. Novel interrelationships with the DM will follow.

2.1.4 The Force Method (FM)

The Force Method exists in two versions. The “manual” one is shown in Fig. 3, briefly reminding how scholars usually teach it. The forces in the three-legs truss (Fig. 3, left) depend on (1) the forces due to the loads in a statically determinate truss resulting from the removal of the redundant leg (Fig. 3, center), (2) an hyperstatic unknown $\alpha$ determined by restoring the compatibility associated to the removed leg, and (3) self-stress forces, not considered in Fig. 3, but that could be added by arbitrarily choosing a prestress level $\alpha ^{ini}$ multiplying the self-stress mode $(\frac{\sqrt{2}}{2}, -1,\frac{\sqrt{2}}{2}$). In practice, self-stress forces can thus only be introduced into statically indeterminate trusses and the level $\alpha ^{ini}$ can be practically increased by arbitrarily shortening the cables or lengthening the bars through mechanical devices. It is again recalled that such self-stressing phase is not detailed in this article, apart from some considerations in the discussion section. The focus is thus limited to the application of external loads as shown in Fig. 3.

Fig. 3

Reminder of the force method used by scholars for teaching purposes applied to a simple type II truss with $s = 1$

The second version of the Force Method, aiming at computational implementation, is summarized as follows (Fig. 2b). Given the loads $\left\{ {\varvec{f}}\right\}$, the FM finds first the forces $\left\{ {\varvec{t}}\right\}$ by solving equation $\left\{ {\varvec{f}}\right\} {\varvec{ = }}\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\}$ as detailed later. Then, once the forces $\left\{ {\varvec{t}}\right\}$ are determined, the elastic elongations $\left\{ {\varvec{e}}\right\}$ and corresponding displacements $\left\{ {\varvec{d}}\right\}$ are found, respectively, by solving Eqs. (2) and (3) as shown in Fig. 2b. Solving Eq. (3) (i.e. $\left\{ {\varvec{e}}\right\} {\varvec{ = }}\left[ {\varvec{A}}\right] ^{T}\left\{ {\varvec{d}}\right\}$) to find the displacements from the elongations is also not straightforward, as discussed later.

The challenge of the Force Method lies thus in solving the equilibrium equations $\left\{ {\varvec{f}}\right\} {\varvec{ = }}\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\}$ and the compatibility equations $\left\{ {\varvec{e}}\right\} {\varvec{ = }}\left[ {\varvec{A}}\right] ^{T}\left\{ {\varvec{d}}\right\}$. The solutions depend on the degree “s” of static indeterminacy and on the degree “m” of kinematic indeterminacy⁵ [14].

In typical kinematically-determinate 3D structures (type I and type II), there are b unknown axial forces $\left\{ {\varvec{t}}\right\}$ in the elements for only $n_{dof}$ equilibrium equations (one for each row of the equilibrium matrix $\left[ {\varvec{A}}\right]$ of size $n_{dof}\times b$ with $n_{dof}\le b$) as further detailed in “Appendix A.2”. From Maxwell [20], the degree of static indeterminacy “s” can be defined as the number of missing equilibrium equations to uniquely determine the unknown axial forces:

$$\begin{aligned} s = b-\underbrace{\left( 3\cdot n-c\right) }_{n_{dof}} \end{aligned}$$

(7)

In the case of a planar (2D) structure, Eq. (7) still holds by considering that all nodes are fixed in one direction of the 3D system i.e. the number “c” of reactions is larger than the number “n” of nodes.

For statically determinate trusses (type I) with $s = 0$ and as many elements as degrees of freedom ($b = n_{dof}$), the equilibrium matrix $\left[ {\varvec{A}}\right]$ (size $n_{dof}\times b$) and the compatibility matrix $\left[ {\varvec{A}}\right] ^{T}$ are square. For these trusses, the inverse of matrix $\left[ {\varvec{A}}\right]$ exists and the FM can be summarized (Fig. 2b):

$$\begin{aligned} \left\{ {\varvec{t}}\right\}&= \left[ {\varvec{A}}\right] ^{-1}\left\{ {\varvec{f}}\right\} \end{aligned}$$

(8)

$$\begin{aligned} \left\{ {\varvec{e}}\right\}&= \left[ {\varvec{F}}\right] \left\{ {\varvec{t}}\right\} \end{aligned}$$

(9)

$$\begin{aligned} \left\{ {\varvec{d}}\right\}&={\left[ {\varvec{A}}\right] ^{T}}^{-1}\left\{ {\varvec{e}}\right\} \end{aligned}$$

(10)

Assembling Eqs. (8)–(10) brings out the first straightforward interrelation between the FM and the DM. Given that ${\left[ {\varvec{A}}\right] ^{T}}^{-1} ={\left[ {\varvec{A}}\right] ^{-1}}^{T}$, one obtains:

$$\begin{aligned} \left\{ {\varvec{d}}\right\} =\underbrace{{\left[ {\varvec{A}}\right] ^{-1}}^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{A}}\right] ^{-1}}_{\left[ {\varvec{K}}^{L}\right] ^{-1}}\left\{ {\varvec{f}}\right\} \end{aligned}$$

(11)

that the relation $\left[ {\varvec{K}}^{L}\right] ^{-1} ={\left[ {\varvec{A}}\right] ^{-1}}^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{A}}\right] ^{-1}$ is only valid for type I trusses. For the other types of trusses the interrelationships between the FM and the DM will take different forms, as obtained throughout this paper.

In statically indeterminate structures with $s>0$ (i.e. $b>n_{dof}$), the matrix $\left[ {\varvec{A}}\right]$ is rectangular and cannot be inverted, i.e. there are more unknown forces $\left\{ {\varvec{t}}\right\}$ than equilibrium equations. The forces $\left\{ {\varvec{t}}\right\}$ depend thus on s hyperstatic unknowns $\left\{ \varvec{\alpha }\right\}$ that must be determined through compatibility equations.

In the computational FM, the problem of inverting the equilibrium matrix was originally solved by Gaussian elimination [14, 28, 149, 150], which is the way to “remove any redundant bar” and obtain the self-stress modes (Fig. 3). Another invaluable tool to deal with rectangular or singular square matrices is the Moore-Penrose pseudo-inverse or generalized inverse [160]. It can be computed using the singular value decomposition (SVD), whose application to the equilibrium matrix was introduced in structural analysis in 1993 by Pellegrino [15]. The current article makes an extensive use of the SVD of matrix $\left[ {\varvec{A}}\right]$ and formulates the computational Force Method to deal with the four types of pin-jointed structures (see Fig. 1).

2.2 Singular Value Decomposition (SVD) of the Equilibrium and Compatibility Matrices

2.2.1 Mathematical SVD of Any Matrix [A]

The SVD of any matrix [A] allows to decompose it into three matrices $\left[ {\varvec{U}}\right]$, $\left[ \varvec{\varLambda }\right]$, and $\left[ {\varvec{V}}\right]$, as follows:

$$\begin{aligned} \left[ {\varvec{A}}\right] =\left[ {\varvec{U}}\right] \left[ \varvec{\varLambda }\right] \left[ {\varvec{V}}\right] ^{T} \end{aligned}$$

(12)

Pellegrino introduced the SVD in structural analysis [15] by applying Eq. (12) to the equilibrium matrix $\left[ {\varvec{A}}\right]$ as illustrated in Fig. 4. It can be observed that:

• The square matrix $\left[ {\varvec{U}}\right]$ contains $n_{dof}$ singular vectors $\left\{ {\varvec{U}}_{i}\right\}$ (size $n_{dof}\times 1$) which are orthonormal (i.e. $\left[ {\varvec{U}}\right] ^{T}\left[ {\varvec{U}}\right] =\left[ {\varvec{I}}\right]$).

• The square matrix $\left[ {\varvec{V}}\right]$ contains b singular vectors $\left\{ {\varvec{V}}_{i}\right\}$ (size $b\times 1$) which are orthonormal (i.e. $\left[ {\varvec{V}}\right] ^{T}\left[ {\varvec{V}}\right] =\left[ {\varvec{I}}\right]$).

• The rectangular matrix $\left[ \varvec{\varLambda }\right]$ (size $n_{dof}\times b$, similar to matrix $[{\varvec{A}}]$) contains $n_{dof}$ singular values $\varLambda _{ii}$ on its diagonal and zeros elsewhere.

• The mathematical rank r of the equilibrium matrix $[{\varvec{A}}]$ corresponds to the number of non-null singular values $\varLambda _{ii}$ within a certain zero threshold.⁶ Note that Quirant [160, Appendix B] proposed an interpretation concerning singular values close to zero and that before 1993, the mathematical rank r of the equilibrium matrix $\left[ {\varvec{A}}\right]$ was obtained as the number of nonzero rows after performing a gaussian elimination [14].

Fig. 4

Graphical illustration of the SVD of the equilibrium matrix $[{\varvec{A}}] =\left[ {\varvec{U}}\right] \left[ \varvec{\varLambda }\right] \left[ {\varvec{V}}\right] ^{T}$. Note that the number of mechanisms is $m = n_{dof}-r$, the number of self-stress modes is $s = b-r$ given the rank r of the equilibrium matrix. Figure adapted from Fig. 1 of ref. [15]

2.2.2 Definitions of the Degrees of Static and Kinematic Indeterminacy

Given the rank r of the equilibrium matrix $[{\varvec{A}}]$, Pellegrino and Calladine stated [14] that the degree of static indeterminacy “s” and the degree of kinematic indeterminacy “m” are defined as:

$$\begin{aligned} s&= b-r \end{aligned}$$

(13)

$$\begin{aligned} m&= n_{dof}-r \end{aligned}$$

(14)

For type I and type II trusses, the equilibrium matrix is full rank (i.e. $r = n_{dof}$), the degree of kinematic indeterminacy is null (i.e. $m = 0$ in Eq. (14)) and Eq. (7) is equivalent to Eq. (13). For type III and type IV trusses however, the equilibrium matrix is not full rank (i.e. $r<n_{dof}$) and the degree of kinematic indeterminacy is non-null (i.e. $m\ne 0$ in Eq. (14)). Therefore, two definitions of the degree of static indeterminacy “s” exist. The first (i.e. $s = b-n_{dof}$) in Eq. (7) is derived from the well-known Maxwell’s rules [20] whereas the second in Eq. (13) was introduced by Pellegrino and Calladine in 1986 [14] to face the limitations of Maxwell’s rules noticed by Calladine in 1978 [11].

For instance, the two-legs truss in Fig. 1a and the tightrope in Fig. 1d both have $b = 2$ elements and $n_{dof} = 2$ free DoF. According to Eq. (7), both trusses are thus statically determinate with $s = 0$. However, the tightrope is actually statically indeterminate with $s = 1$, because self-stress forces $\left\{ {\varvec{t}}\right\} =\left\{ 1,1\right\} ^{T}\cdot \alpha$ can be introduced by choosing arbitrarily a single ($s = 1$) parameter $\alpha$. Therefore, the forces cannot be directly computed via equilibrium alone, i.e. the tightrope is statically indeterminate and Eq. (7) does not hold. Similar conclusions can be obtained for the 3D truss in Fig. 1a′ and the tensegrity simplex in Fig. 1d′, both having $b = 12$ elements and $n_{dof} = 12$ free DoF.

Therefore, for type III and type IV trusses, Eq. (7) does not hold and Eq. (13) must be used instead.

2.2.3 The Four Fundamental Bases $\left[ {\varvec{U}}^{r}\right] ,\left[ {\varvec{U}}^{m}\right] ,\left[ {\varvec{V}}^{r}\right] ,\left[ {\varvec{V}}^{s}\right]$

In the general case of statically and kinematically indeterminate structures ($s>0, m>0$), the singular vectors can be sorted in two categories with $\left[ {\varvec{U}}\right] =\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] &{}\left[ {\varvec{U}}^{m}\right] \\ \end{bmatrix}$ and $\left[ {\varvec{V}}\right] =\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] &{}\left[ {\varvec{V}}^{s}\right] \\ \end{bmatrix}$ as shown in Fig. 4. The SVD of $[{\varvec{A}}]( =\left[ {\varvec{U}}\right] \left[ \varvec{\varLambda }\right] \left[ {\varvec{V}}\right] ^{T})$ can thus be rewritten:

$$\begin{aligned} \left[ {\varvec{A}}\right] = \begin{array}{l} \begin{bmatrix} \left[ {\varvec{U}}^{r}\right] &{}\left[ {\varvec{U}}^{m}\right] \\ \end{bmatrix} \\ \\ \end{array}\begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T} \\ \left[ {\varvec{V}}^{s}\right] ^{T} \\ \end{bmatrix} \end{aligned}$$

(15)

The SVD of the compatibility matrix $\left[ {\varvec{B}}\right]$ can also be obtained recalling that $\left[ {\varvec{B}}\right] =\left[ {\varvec{A}}\right] ^{T}$:

$$\begin{aligned} \left[ {\varvec{B}}\right] =\left[ {\varvec{V}}\right] \left[ \varvec{\varLambda }\right] ^{T}\left[ {\varvec{U}}\right] ^{T} \end{aligned}$$

(16)

Both the equilibrium and the compatibility matrices can thus be divided in four fundamental bases ($\left[ {\varvec{U}}^{r}\right] ,\left[ {\varvec{U}}^{m}\right] ,\left[ {\varvec{V}}^{r}\right] ,\left[ {\varvec{V}}^{s}\right]$) as introduced by Pellegrino and Calladine in 1986 [14], who obtained them by Gaussian elimination before the introduction of the SVD in structural analysis in 1993 [15]. These bases will be interpreted in the next subsection.

Several research studies have used the SVD of the equilibrium and compatibility matrices for structural analysis methods. The introduction of SVD was thus a major breakthrough, which greatly enhanced in particular the use of the FM [36, 48, 122, 149,150,151,152]. Some of these recent contributions developed a purely mathematical approach to the structural analysis problem [36] but overlooked the physical interpretation of the expressions developed. Moreover, a complete graphical roadmap on how they associate in a holistic manner has not yet been proposed. The literature review performed by the authors also did not find a physical interpretations of the SVD other than the ones described in the following paragraph. The present investigation will try to address the above shortcomings, and present additionally a new physical interpretation of the SVD.

2.2.4 Existing Interpretations of the SVD Results

According to Pellegrino [15], “the rather abstract physical meaning of the reduced variables produced by a full use of SVD was thought to be a drawback of the method...”. Therefore, he proposed a physical interpretation of the SVD results at the equilibrium and compatibility levels (Fig. 5a and b) using Eqs. (17) and (18):

(17)

(18)

The above equations were obtained from Eqs. (12) and (16) by using the orthonormality properties of the singular vectors ($\left[ {\varvec{U}}\right] ^{T}\left[ {\varvec{U}}\right] =\left[ {\varvec{I}}\right]$ and $\left[ {\varvec{V}}\right] ^{T}\left[ {\varvec{V}}\right] =\left[ {\varvec{I}}\right]$) and the fact that $\varLambda _{ii} = 0$ for $i>r$. Their comparison with Eqs. (1) and (3) allowed to draw the physical interpretation of the SVD represented in Fig. 5. A few remarks can be made with respect to this latter figure:

• The last s singular vectors $\left\{ {\varvec{V}}_{i}^{s}\right\}$ can be interpreted as a pattern of forces in self-equilibrium, i.e. without external loads (see Eq. (17)), the so-called self-stress modes.

• The last m singular vectors $\left\{ {\varvec{U}}_{i}^{m}\right\}$ can be interpreted as a pattern⁷ of displacements that generate no elongations. These inextensional modes of displacements are “strain free, or zero energy” [15], and can be called mechanisms [28,29,30,31,32,33,34,35,36,37].

Fig. 5

Physical interpretation of the SVD results, a at the equilibrium level, b at the compatibility level. Figure adapted from Fig. 2 of ref. [15]

Despite the pioneering contributions of Pellegrino in 1993 [15], the following points remain to be clarified in Fig. 5:

• The main issue is the lack of an apparent relation between Fig. 5a, b. The link, if any, between the modes $\left\{ {\varvec{V}}_{i}^{s}\right\}$ in Fig. 5a, b is unclear.

• Pellegrino [15] stated correctly that the last m singular vector $\left\{ {\varvec{U}}_{i}^{m}\right\}$ in Fig. 5a can be interpreted as a pattern of loads “which the assembly cannot equilibrate in its current configuration”. However, Eq. (17) does not allow to confirm this intuitive assertion.

• The last s singular vectors $\left\{ {\varvec{V}}_{i}^{s}\right\}$ in Fig. 5b have been interpreted as a pattern of “incompatible strains” in [15]. However, Eq. (18) does not allow to confirm this assertion. Incompatible strains are translated here as elongations that may exist requiring no displacements (together with the development of internal self-equilibrated forces in the truss elements).

• Each mode $\left\{ {\varvec{U}}_{i}\right\}$ was referred to as a set of displacements and a set of loads which are usually length-dimensional (e.g. in millimeters, inches, etc) and force-dimensional (e.g. in Newton, pound-force, etc), respectively. Hence the dimension of the modes was ambiguous. It is clarified later that the modes $\left\{ {\varvec{U}}_{i}\right\}$ are a dimensionless pattern.

• Each mode $\left\{ {\varvec{V}}_{i}\right\}$ was referred to as a set of (length-dimensional) elongations and a set of (force-dimensional) forces. It is clarified later that the modes $\left\{ {\varvec{V}}_{i}\right\}$ are a dimensionless pattern.

In response to the first main limitation above, different authors have proposed simple tentative graphical illustrations [14, 22, 28], which are not described here, to represent the links between the four fundamental bases ($\left[ {\varvec{U}}^{r}\right] ,\left[ {\varvec{U}}^{m}\right] ,\left[ {\varvec{V}}^{r}\right] ,\left[ {\varvec{V}}^{s}\right]$) both at equilibrium and compatibility levels. This article proposes novel physical and graphical interpretations of the SVD.

2.2.5 Existing Structural Computations Using the SVD

After a brief description of the use of the SVD for the Force Method in ref. [15], the next evidence of its application can be found in [151]; however, the latter is included in the scope of a geometrically nonlinear procedure. Therefore, both the linear Force Method [149, 150] and the linear Displacement Method have never been fully detailed using the SVD. Simultaneously, major references older than the introduction of the SVD in structural analysis, such as [12, 28], have never been reviewed using the SVD. The current work addresses this gap.

The main existing structural computations using the SVD are described next. Luo and Lu [151] proposed a review of Pellegrino’s structural computations [15] and stated, without derivation—which will be included later, that the SVD allows to write:

$$\begin{aligned} \left\{ {\varvec{t}}\right\}&=\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{U}}^{r}\right] ^{T}\left\{ {\varvec{f}}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ \varvec{\alpha }\right\} \end{aligned}$$

(19)

$$\begin{aligned} \left\{ {\varvec{d}}\right\}&=\left[ {\varvec{U}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{V}}^{r}\right] ^{T}\left\{ {\varvec{e}}\right\} +\left[ {\varvec{U}}^{m}\right] \left\{ \varvec{\beta }\right\} \end{aligned}$$

(20)

According to ref. [28, 15], the “s” hyperstatic unknowns $\left\{ \varvec{\alpha }\right\} =\left\{ \alpha _{1},\ldots ,\alpha _{s}\right\} ^{T}$ are determined using “s” exceeding compatibility equations, namely $\left[ {\varvec{V}}^{s}\right] ^{T}\left\{ {\varvec{e}}\right\} =\left\{ \textbf{0}\right\}$. On the other hand, the vector $\left\{ \varvec{\beta }\right\} =\left\{ \beta _{1},\ldots ,\beta _{m}\right\} ^{T}$ corresponds to the “m” kinematic unknowns, which will be discussed later.

Note that more recent references, including [54], rewrite Eqs. (19) and (20) as:

$$\begin{aligned} (\left\{ {\varvec{t}}\right\}&=\left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ \varvec{\alpha }\right\} \end{aligned}$$

(19')

$$\begin{aligned} \left\{ {\varvec{d}}\right\}&=\left[ {\varvec{B}}\right] ^{+}\left\{ {\varvec{e}}\right\} +\left[ {\varvec{U}}^{m}\right] \left\{ \varvec{\beta }\right\} \end{aligned}$$

(20')

where the generalized inverse of the equilibrium matrix $\left[ {\varvec{A}}\right] ^{+}$ is equal to $\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{U}}^{r}\right] ^{T}$ and the generalized inverse of the compatibility matrix $\left[ {\varvec{B}}\right] ^{+} ={\left[ {\varvec{A}}\right] ^{T}}^{+}$ is equal to $\left[ {\varvec{U}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{V}}^{r}\right] ^{T}$. Such equalities are confirmed by NumPy Developers [162]. In other words, the generalized inverse of a singular square or rectangular matrix is computed by SVD, then the zero singular values are removed and, finally, the nonzero singular values $\left[ \varvec{\varLambda }^{r}\right]$ are inverted and reassembled with their associated singular vectors $\left[ {\varvec{U}}^{r}\right]$ and $\left[ {\varvec{V}}^{r}\right]$. However, our literature review did not reveal a physical interpretation for the generalized inverses $\left[ {\varvec{A}}\right] ^{+}$ and $\left[ {\varvec{B}}\right] ^{+}$.

Finally, although the linear force method (Fig. 2b) may be completely solved today for the four types of pin-jointed structures (Fig. 1), the solution is spread among many references, which is a challenge for researchers. This article proposes a unified solution of the linear Force Method and Displacement Method by fully detailing the procedure and its physical interpretation.

2.3 Proposed Approach

2.3.1 Static Modal Analysis

The previous section concludes the state-of-the-art on static structural computations of pin-jointed structures. In the following, a review of the computational aspects under a new paradigm called Static modal analysis is performed.

In dynamics, modal analysis consists in determining the natural frequencies and mode shapes of vibration of the structure by solving the eigenvalue problem with the mass and stiffness matrices [163]. The eigenvalues correspond to the natural frequencies and the eigenvectors correspond to the mode shapes. This article introduces the concept of static modal analysis by taking inspiration from dynamic modal analysis and the singular value decomposition of the equilibrium matrix as discussed above [15].

In dynamic modal analysis, the displacements of the structure can be expressed as a linear combination of the mode shapes multiplied by their respective modal coordinates. Conversely, the modal coordinates can be found by orthogonal projection of the displacements on the mode shapes. The same principle is herein proposed for static modal analysis. As shown in Fig. 6 and detailed below, there are four spaces to be considered: (1) the structural or the Degrees of Freedom’s (DoF) space; (2) the static modal structural space; (3) the static modal elemental space, and (4) the local or elemental space.

Fig. 6

Proposed concept of static modal analysis: formal passage from the structural and elemental spaces to the associated static modal spaces, and conversely. Each arrow corresponds to a premultiplication by the neighbouring matrix

Loads and displacements expressed in the DoF space can be transformed into modal coordinates through the singular vector matrix $\left[ {\varvec{U}}\right]$, and conversely through its transpose $\left[ {\varvec{U}}\right] ^{T}$. From the structural (DoF) space to the modal structural space, one defines the static modal coordinates as follows:

$$\begin{aligned} \begin{aligned} \begin{Bmatrix} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{Bmatrix}&=\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] ^{T} \\ \left[ {\varvec{U}}^{m}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{f}}\right\} \\ \begin{Bmatrix} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{Bmatrix}&=\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] ^{T} \\ \left[ {\varvec{U}}^{m}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{d}}\right\} \end{aligned} \end{aligned}$$

(21)

where $\left\{ {\varvec{f}}^{r}\right\}$ and $\left\{ {\varvec{d}}^{r}\right\}$ are subvectors with size $(r\times 1$) and $\left\{ {\varvec{f}}^{m}\right\}$ and $\left\{ {\varvec{d}}^{m}\right\}$ are subvectors with size $(m\times 1$). Conversely, loads and displacements in modal coordinates can be expressed in the structural (DoF) space coordinates:

$$\begin{aligned} \begin{aligned} \left\{ {\varvec{f}}\right\} =\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] &{}\left[ {\varvec{U}}^{m}\right] \\ \end{bmatrix}\begin{Bmatrix} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{Bmatrix}&\Leftrightarrow \left\{ {\varvec{f}}\right\} =\left[ {\varvec{U}}^{r}\right] \left\{ {\varvec{f}}^{r}\right\} +\left[ {\varvec{U}}^{m}\right] \left\{ {\varvec{f}}^{m}\right\} \\ \left\{ {\varvec{d}}\right\} =\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] &{}\left[ {\varvec{U}}^{m}\right] \\ \end{bmatrix}\begin{Bmatrix} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{Bmatrix}&\Leftrightarrow \left\{ {\varvec{d}}\right\} =\left[ {\varvec{U}}^{r}\right] \left\{ {\varvec{d}}^{r}\right\} +\left[ {\varvec{U}}^{m}\right] \left\{ {\varvec{d}}^{m}\right\} \end{aligned} \end{aligned}$$

(22)

Similarly, forces and elongations can be alternatively expressed in the elemental space and in the static modal elemental space through the singular vector matrix $\left[ {\varvec{V}}\right]$ and its transpose $\left[ {\varvec{V}}\right] ^{T}$. From the elemental space to the modal space, one defines:

$$\begin{aligned} \begin{aligned} \begin{Bmatrix} {\varvec{t}}^{r} \\ {\varvec{t}}^{s} \\ \end{Bmatrix}&=\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T} \\ \left[ {\varvec{V}}^{s}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{t}}\right\} \\ \begin{Bmatrix} {\varvec{e}}^{r} \\ {\varvec{e}}^{s} \\ \end{Bmatrix}&=\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T} \\ \left[ {\varvec{V}}^{s}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{e}}\right\} \end{aligned} \end{aligned}$$

(23)

Conversely, the passages to the elemental space are expressed as:

$$\begin{aligned} \begin{aligned} \left\{ {\varvec{t}}\right\} =\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] &{}\left[ {\varvec{V}}^{s}\right] \\ \end{bmatrix}\begin{Bmatrix} {\varvec{t}}^{r} \\ {\varvec{t}}^{s} \\ \end{Bmatrix}&\Leftrightarrow \left\{ {\varvec{t}}\right\} =\left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\} \\ \left\{ {\varvec{e}}\right\} =\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] &{}\left[ {\varvec{V}}^{s}\right] \\ \end{bmatrix}\begin{Bmatrix} {\varvec{e}}^{r} \\ {\varvec{e}}^{s} \\ \end{Bmatrix}&\Leftrightarrow \left\{ {\varvec{e}}\right\} =\left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{e}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{e}}^{s}\right\} \end{aligned} \end{aligned}$$

(24)

In summary:

• Equations (21)–(24) describe the passage between the DoF or elemental spaces to the corresponding modal spaces through a novel mathematical change of variables. This mathematic formalization, the subsequent revised developments, and the physical interpretations, which were inspired by dynamic modal analysis, represent some contributions of this study.

• Since $\left[ {\varvec{U}}\right]$ and $\left[ {\varvec{V}}\right]$ appear both in Eqs. (12) and (16), the modal spaces can be physically interpreted both at the equilibrium or at the compatibility levels (Fig. 6).

• The orthonormality properties ($\left[ {\varvec{U}}\right] ^{T}\left[ {\varvec{U}}\right] = [{\varvec{I}}]$ and $\left[ {\varvec{V}}\right] ^{T}\left[ {\varvec{V}}\right] = [{\varvec{I}}]$) of the singular vectors allow straightforward back-and-forth passages between spaces through simple transpositions instead of inversions.

• The modal spaces can be arranged in three categories [28]: the (structural and elemental) extensional modes of bases $\left[ {\varvec{U}}^{r}\right]$ and $\left[ {\varvec{V}}^{r}\right]$, the self-stress modes of basis $\left[ {\varvec{V}}^{s}\right]$, and the inextensional modes of basis $\left[ {\varvec{U}}^{m}\right]$.

• The above equations clarify that the four fundamental bases are dimensionless patterns whereas their modal coordinates are not.

• In this article, the symbol $\left\{ {\varvec{d}}^{m}\right\}$ is equivalent to the symbol $\left\{ \varvec{\beta }\right\}$ generaly used in the literature (see Eq. (20)). However, the symbol $\left\{ {\varvec{d}}^{m}\right\}$ is prefered here because this physical quantity corresponds to (length-dimensional) modal displacements, and in order to differentiate it from the physical quantity $\left\{ {\varvec{f}}^{m}\right\}$ corresponding to (force-dimensional) modal loads.

• Similarly, the symbol $\left\{ {\varvec{t}}^{s}\right\}$ is equivalent to the symbol $\left\{ \varvec{\alpha }\right\}$ generaly used in the literature (see Eq. (19) and Fig. 3). However, the symbol $\left\{ {\varvec{t}}^{s}\right\}$ is prefered here because this physical quantity corresponds to (force-dimensional) modal forces.

• The term $\left[ {\varvec{V}}^{s}\right] \left\{ \varvec{\alpha }\right\}$ seemed to appear without explanation in Eq. (19). Equation (24) explains its origin.

All the points above will be further clarified throughout the paper.

2.3.2 Summary of the Objectives

The second goal of this article, in addition to the previous state-of-the-art, is to review the existing literature on the Force Method and Displacement Method from the viewpoint of static modal analysis, making extensive use of the singular value decomposition, in order to unify both methods of linear analysis for the four types of pin-jointed structures (Fig. 1). This is attained through the following objectives:

• Perform the mathematical derivation of the solution procedure for the four types of structures with the linear FM and DM, together with explicit physical explanations.

• Clarify the derivations through a novel graphical interpretation, with explicit indication of the links between the four fundamental bases, through simple diagrams that use arrows as visualization of the linear mappings; Fig. 7 corresponds to the general graphical roadmap of the linear DM (Fig. 7a) and FM (Fig. 7b) that will be built and referred to throughout the current article.

• Illustrate the solution procedure for each structural type with straightforward examples.

Fig. 7

New graphical roadmaps for the computation of statically/kinematically determinate/indeterminate trusses by the linear: a DM, b FM

3 The Linear Force and Displacement Methods by Static Modal Analysis

This chapter describes the linear force and displacement method (Fig. 2) for the four types of pin-jointed structures. The static modal analysis, i.e. the passages through the modal spaces, will be used extensively in order to solve the basic Eqs. (1), (2) and (3). In other words, this chapter explains the transformation of Fig. 6 into Fig. 7. Finally, note that the Force Method will always be detailed before the Displacement Method since the SVD was originally intended for the FM in order to invert Eq. (1).

Using the SVD of the equilibrium matrix $[{\varvec{A}}]$, expressed in Eq. (15), and the orthonormality of the singulars vectors, the basic Eqs. (1), (2) and (3) are rewritten:

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T} \\ \left[ {\varvec{V}}^{s}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{t}}\right\}&=\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] ^{T} \\ \left[ {\varvec{U}}^{m}\right] ^{T} \\ \end{bmatrix} \left\{ {\varvec{f}}\right\} \end{aligned}$$

(25)

$$\begin{aligned} \left\{ {\varvec{e}}\right\}&= [{\varvec{F}}]\left\{ {\varvec{t}}\right\} \end{aligned}$$

(9)

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\begin{bmatrix} \left[ {\varvec{U}}^{r}\right] ^{T} \\ \left[ {\varvec{U}}^{m}\right] ^{T} \\ \end{bmatrix} \left\{ {\varvec{d}}\right\}&=\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T} \\ \left[ {\varvec{V}}^{s}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{e}}\right\} \end{aligned}$$

(26)

In the modal spaces, using Eqs. (21) to (24) one finds for the first time that:

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ \begin{array}{c} {\varvec{t}}^{r} \\ {\varvec{t}}^{s} \\ \end{array}\right\}&=\left\{ \begin{array}{c} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{array}\right\} \end{aligned}$$

(27)

$$\begin{aligned} \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{e}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{e}}^{s}\right\}&=\left[ {\varvec{F}}\right] \left( \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\} \right) \end{aligned}$$

(28)

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ \begin{array}{c} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{array}\right\}&=\left\{ \begin{array}{c} {\varvec{e}}^{r} \\ {\varvec{e}}^{s} \\ \end{array}\right\} \end{aligned}$$

(29)

In the two (structural and elemental) static modal spaces, the linear FM intends to address the structural problem as: from known modal loads $\left\{ {\varvec{f}}^{r}\right\} ,\left\{ {\varvec{f}}^{m}\right\}$, determine the modal forces $\left\{ {\varvec{t}}^{r}\right\} ,\left\{ {\varvec{t}}^{s}\right\}$, followed by the associated modal elongations $\left\{ {\varvec{e}}^{r}\right\} ,\left\{ {\varvec{e}}^{s}\right\}$ and finally the modal displacements $\left\{ {\varvec{d}}^{r}\right\} ,\left\{ {\varvec{d}}^{m}\right\}$. After solving the structural problem through the FM, the interrelationship existing between the FM and the DM will be unveiled. Subsequently, the solution procedure will be physically interpreted for each structural type with simple examples.

This chapter is structured as follows:

• Section 3.1 details type I trusses, which are statically determinate ($s = 0$) and kinematically determinate ($m = 0$)

• Section 3.2 details type II trusses, which are statically indeterminate ($s>0$) and kinematically determinate ($m = 0$)

• Section 3.3 details types III and IV trusses, which are respectively statically determinate and indeterminate ($s\ge 0$), and both kinematically indeterminate ($m>0$)

3.1 Type I: Statically Determinate ($s = 0$) and Kinematically Determinate ($m = 0$)

3.1.1 Force Method

Figure 8 summarizes graphically the linear force method for type I trusses. The relations expressed in this figure, which corresponds to a particular version of Fig. 7b, are derived mathematically below.

Fig. 8

Graphical roadmap for the computation of type I trusses by the linear force method

Since the structure is statically and kinematically determinate, i.e. $s = 0$ and $m = 0$, from Fig. 4 one finds that the equilibrium matrix $[{\varvec{A}}]$ is square and full rank ($r = b = n_{dof}$) and that the SVD of $[{\varvec{A}}]$ gives $\left[ {\varvec{V}}^{s}\right] = \varnothing$, $\left[ {\varvec{V}}\right] =\left[ {\varvec{V}}^{r}\right]$, $\left[ {\varvec{U}}^{m}\right] = \varnothing ,$ $\left[ {\varvec{U}}\right] =\left[ {\varvec{U}}^{r}\right]$ and $\left[ \varvec{\varLambda }\right] =\left[ \varvec{\varLambda }^{r}\right]$. Equations (27)–(29) are thus rewritten:

$$\begin{aligned} \left[ \varvec{\varLambda }^{r}\right] \left\{ {\varvec{t}}^{r}\right\}&= \left\{ {\varvec{f}}^{r}\right\} \end{aligned}$$

(30)

$$\begin{aligned} \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{e}}^{r}\right\}&=\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} \end{aligned}$$

(31)

$$\begin{aligned} \left[ \varvec{\varLambda }^{r}\right] \left\{ {\varvec{d}}^{r}\right\}&= \left\{ {\varvec{e}}^{r}\right\} \end{aligned}$$

(32)

Since matrix $\left[ \varvec{\varLambda }^{r}\right]$ is square and diagonal with all $\varLambda _{ii}$ non null, it can be easily inverted under the diagonal form $\left[ \varvec{\varLambda }^{r}\right] ^{-1}$ (containing the values $1/\varLambda _{ii}$). Therefore, one finds for the first time the solution in the modal spaces:

$$\begin{aligned} \left\{ {\varvec{t}}^{r}\right\}&= \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left\{ {\varvec{f}}^{r}\right\} \end{aligned}$$

(33)

$$\begin{aligned} \left\{ {\varvec{e}}^{r}\right\}&=\left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} \end{aligned}$$

(34)

$$\begin{aligned} \left\{ {\varvec{d}}^{r}\right\}&= \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left\{ {\varvec{e}}^{r}\right\} \end{aligned}$$

(35)

Or, by back substitution into $\left\{ {\varvec{d}}\right\} =\left[ {\varvec{U}}^{r}\right] \left\{ {\varvec{d}}^{r}\right\}$ (i.e. Eq. (22)) of equations (35) (34), (33), and $\left\{ {\varvec{f}}^{r}\right\} =\left[ {\varvec{U}}^{r}\right] ^{T}\left\{ {\varvec{f}}\right\}$ (i.e. Eq (21)), one finds the relation between loads and displacements in the DoF space:

$$\begin{aligned} \left\{ {\varvec{d}}\right\} = \underbrace{\left[ {\varvec{U}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{V}}^{r}\right] ^{T}}_{{\left[ {\varvec{A}}\right] ^{+}}^{T}}\left[ {\varvec{F}}\right] \underbrace{\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{U}}^{r}\right] ^{T}}_{\left[ {\varvec{A}}\right] ^{+}}\left\{ {\varvec{f}}\right\} \end{aligned}$$

(36)

where the definitions [164] of generalized inverses of the equilibrium matrix $\left[ {\varvec{A}}\right] ^{+} =\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{U}}^{r}\right] ^{T}$ and of the compatibility matrix $\left[ {\varvec{B}}\right] ^{+} ={\left[ {\varvec{A}}\right] ^{T}}^{+} ={\left[ {\varvec{A}}\right] ^{+}}^{T} =\left[ {\varvec{U}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{V}}^{r}\right] ^{T}$ have been used. This ends the explanation of the passages indicated in Fig. 8, which the reader is invited to follow.

It is noted that, by comparison of Eq. (36) with Eq. (11), and in the particular case of type I trusses, one finds $\left[ {\varvec{A}}\right] ^{-1} =\left[ {\varvec{A}}\right] ^{+}$ and $\left[ {\varvec{B}}\right] ^{-1} =\left[ {\varvec{B}}\right] ^{+}$.

3.1.2 Interrelationship with the Displacement Method

The interrelationship between the FM and the DM methods for type I trusses was obtained in Eq. (11), to which the reader is invited to refer to.

3.1.3 Physical Interpretation

Figure 9 provides a physical interpretation of the extensional modes of equilibrium and compatibility of a simple truss with $b = 2$ elements and $n_{dof} = 2$ free degrees of freedom. First the equilibrium matrix $[{\varvec{A}}]$ is computed according to “Appendix A.4” from the nodal coordinates. It is noted that matrix $[{\varvec{A}}]$ has no unit and does not depend on the dimension L of the structure, i.e. it is dimensionless. The SVD of $\left[ {\varvec{A}}\right]$ is then computed, leading to the matrices of singular vectors $\left[ {\varvec{U}}\right]$ and $\left[ {\varvec{V}}\right]$, and the singular values $\varLambda _{ii}$. There are two non-null singular values. Hence the rank of the equilibrium matrix is $r = 2$. The degree of static indeterminacy is thus obviously $s = 0$, i.e. there are no self-stress modes $[{\varvec{V}}^{s}]$. Similarly, since the degree of kinematic indeterminacy is $m = 0$, there are also no mechanisms $\left[ {\varvec{U}}^{m}\right]$.

Finally, the two extensional modes are illustrated:

• At the equilibrium level, any (force-dimensional) load $\left\{ {\varvec{f}}\right\}$ can be expressed in terms of (force-dimensional) modal coordinates $\left\{ {\varvec{f}}^{r}\right\}$ through $\left\{ {\varvec{f}}^{r}\right\} =\left[ {\varvec{U}}^{r}\right] ^{T}\left\{ {\varvec{f}}\right\}$—see Eq. (21). The loads are thus expressed in the modal space of basis $\left[ {\varvec{U}}^{r}\right]$ (dimensionless). Similarly, any (force-dimensional) force $\left\{ {\varvec{t}}\right\}$ can be expressed in terms of (force-dimensional) modal coordinates $\left\{ {\varvec{t}}^{r}\right\}$ through $\left\{ {\varvec{t}}^{r}\right\} =\left[ {\varvec{V}}^{r}\right] ^{T}\left\{ {\varvec{t}}\right\}$—see Eq. (23). The forces are thus expressed in the modal space of basis $\left[ {\varvec{V}}^{r}\right]$ (dimensionless). In the modal spaces, the loads $f_{1}^{r}$ and $f_{2}^{r}$ are respectively in equilibrium with the forces $t_{1}^{r} = f_{1}^{r}/\varLambda _{11}$ and $t_{2}^{r} = f_{2}^{r}/\varLambda _{22}$—see Eq. (33). Finally, since the structure is statically determinate, the forces $\left\{ {\varvec{t}}\right\}$ are easily determined given any load $\left\{ {\varvec{f}}\right\}$ through a simple inversion of the equilibrium matrix $\left[ {\varvec{A}}\right] ^{-1} =\left[ {\varvec{A}}\right] ^{+}$, i.e. $\left\{ {\varvec{t}}\right\} =\left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\}$.

• At the compatibility level, any (length-dimensional) displacement $\left\{ {\varvec{d}}\right\}$ can be expressed in terms of (length-dimensional) modal coordinates $\left\{ {\varvec{d}}^{r}\right\}$ through $\left\{ {\varvec{d}}^{r}\right\} =\left[ {\varvec{U}}^{r}\right] ^{T}\left\{ {\varvec{d}}\right\}$—see Eq. (21). The displacements are thus expressed in the modal space of basis $\left[ {\varvec{U}}^{r}\right]$ (dimensionless). Similarly, any (length-dimensional) elongation $\left\{ {\varvec{e}}\right\}$ can be expressed in terms of (length-dimensional) modal coordinates $\left\{ {\varvec{e}}^{r}\right\}$ through $\left\{ {\varvec{e}}^{r}\right\} =\left[ {\varvec{V}}^{r}\right] ^{T}\left\{ {\varvec{e}}\right\}$—see Eq. (23). The elongations are thus expressed in the modal space of basis $\left[ {\varvec{V}}^{r}\right]$ (dimensionless). In the modal spaces, the elongations $e_{1}^{r}$ and $e_{2}^{r}$ are respectively compatible with the displacements $d_{1}^{r} = e_{1}^{r}/\varLambda _{11}$ and $d_{2}^{r} = e_{2}^{r}/\varLambda _{22}$—see Eq. (35). Finally, since the structure is kinematically determinate, the displacements $\left\{ {\varvec{d}}\right\}$ are easily determined given any elongation $\left\{ {\varvec{e}}\right\}$ through a simple inversion of the compatiblity matrix $\left[ {\varvec{B}}\right] ^{-1} =\left[ {\varvec{B}}\right] ^{+} ={\left[ {\varvec{A}}\right] ^{+}}^{T}$.

Fig. 9

Physical interpretation at the equilibrium and compatibility levels of the static modal analysis of a Type I truss

3.2 Type II: Statically Indeterminate ($s > 0$) and Kinematically Determinate ($m = 0$)

3.2.1 Force Method

Figure 10 summarizes graphically the linear force method for type II trusses. The relations expressed in this figure, which corresponds to another particular version of Fig. 7b, are derived below.

Fig. 10

Graphical roadmap for the computation of type II trusses by the linear force method

Assuming that the structure is statically indeterminate, i.e. $s>0$, and kinematically determinate, i.e. $m = 0$, from Fig. 4 one finds that the equilibrium matrix $[{\varvec{A}}]$ is rectangular and full rank (i.e. $r = n_{dof}$) and that the SVD of $[{\varvec{A}}]$ gives $\left[ {\varvec{V}}\right] =\left[ \left[ {\varvec{V}}^{r}\right] ,\left[ {\varvec{V}}^{s}\right] \right]$, $\left[ {\varvec{U}}^{m}\right] = \varnothing ,$ $\left[ {\varvec{U}}\right] =\left[ {\varvec{U}}^{r}\right]$ and $\left[ \varvec{\varLambda }\right] =\left[ \left[ \varvec{\varLambda }^{r}\right] ,\left[ \textbf{0}\right] \right]$. Equations (27)–(29) thus become:

$$\begin{aligned} \begin{array}{l} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix} \\ \\ \end{array}\left\{ \begin{array}{c} {\varvec{t}}^{r} \\ {\varvec{t}}^{s} \\ \end{array}\right\}&=\left\{ {\varvec{f}}^{r}\right\} \ \end{aligned}$$

(37)

$$\begin{aligned} \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{e}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{e}}^{s}\right\}&=\left[ {\varvec{F}}\right] \left( \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\} \right) \end{aligned}$$

(38)

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] \\ \left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ {\varvec{d}}^{r}\right\}&=\left\{ \begin{array}{c} {\varvec{e}}^{r} \\ {\varvec{e}}^{s} \\ \end{array}\right\} \end{aligned}$$

(39)

Equation (37) can be rewritten:

$$\begin{aligned} \left[ \varvec{\varLambda }^{r}\right] \left\{ {\varvec{t}}^{r}\right\} = \left\{ {\varvec{f}}^{r}\right\} \Leftrightarrow \left\{ {\varvec{t}}^{r}\right\} = \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left\{ {\varvec{f}}^{r}\right\} \end{aligned}$$

(40)

which illustrates that statically indeterminate trusses have more unknowns ($\left\{ {\varvec{t}}^{r}\right\}$,$\left\{ {\varvec{t}}^{s}\right\} )$ than equilibrium equations. Hence, there are still s hyperstatic unknowns $\left\{ {\varvec{t}}^{s}\right\}$ (often called $\left\{ \varvec{\alpha }\right\}$ in the literature, as mentioned before) that need to be determined. This will be accomplished by using the s exceeding compatibility equations of statically indeterminate trusses, expressed at the bottom of Eq. (39). In fact, Eq. (39) can be split into $r+s$ equations:

$$\begin{aligned} \left[ \varvec{\varLambda }^{r}\right] \left\{ {\varvec{d}}^{r}\right\}&= \left\{ {\varvec{e}}^{r}\right\} \Leftrightarrow \left\{ {\varvec{d}}^{r}\right\} = \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left\{ {\varvec{e}}^{r}\right\} \end{aligned}$$

(41)

$$\begin{aligned} \left\{ {\varvec{e}}^{s}\right\}&=\left\{ \textbf{0}\right\} \end{aligned}$$

(42)

Substituting Eq. (42) into the material law (38) leads to the modal elongations $\left\{ {\varvec{e}}^{r}\right\}$:

$$\begin{aligned} \left\{ {\varvec{e}}^{r}\right\} =\left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\} \end{aligned}$$

(43)

To determine $\left\{ {\varvec{t}}^{s}\right\}$ in equation (43), the s exceeding compatibility equations $\left\{ {\varvec{e}}^{s}\right\} =\left\{ \textbf{0}\right\}$ are re-expressed in the elements’ space according to Eq. (23):

$$\begin{aligned} \left[ {\varvec{V}}^{s}\right] ^{T}\left\{ {\varvec{e}}\right\} =\left\{ \textbf{0}\right\} \end{aligned}$$

(44)

Given Eqs. (9) and (24), one obtains $\left\{ {\varvec{e}}\right\} =\left[ {\varvec{F}}\right] \left\{ {\varvec{t}}\right\} =\left[ {\varvec{F}}\right] \left( \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\} \right)$. The hyperstatic unknowns $\left\{ {\varvec{t}}^{s}\right\}$ can be obtained by substituting the latter expression in Eq. (44) and solving it with respect to $\left\{ {\varvec{t}}^{s}\right\}$, which gives rise to:

$$\begin{aligned} \left\{ {\varvec{t}}^{s}\right\} =\underbrace{-\left( \left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{s}\right] \right) ^{-1}\left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] }_{\left[ {\varvec{R}}\right] }\left\{ {\varvec{t}}^{r}\right\} \end{aligned}$$

(45)

The linear mapping $\left[ {\varvec{R}}\right]$ describes for the first time the redistribution due to the static indeterminacy of the forces $\left\{ {\varvec{t}}^{r}\right\}$ (in equilibrium with the extensional loads $\left\{ {\varvec{f}}^{r}\right\}$) into the coordinates $\left\{ {\varvec{t}}^{s}\right\}$ activating the self-stress modes⁸.

Finally, given the coordinates $\left\{ {\varvec{t}}^{s}\right\}$, the modal elongations $\left\{ {\varvec{e}}^{r}\right\}$ are obtained with Eq. (43) and the extensional displacements $\left\{ {\varvec{d}}^{r}\right\}$ are found with equation (41). This ends the computation of the linear force method by static modal analysis for statically indeterminate and kinematically determinate trusses. The reader is invited to follow graphically all the above operations in Fig. 10.

Remark 1

This paragraph shows for the first time that, instead of Eqs. (40) and (45), it is possible to obtain the modal forces $\left\{ {\varvec{t}}^{r}\right\}$ and $\left\{ {\varvec{t}}^{s}\right\}$ simultaneously from the extensional loads $\left\{ {\varvec{f}}^{r}\right\}$ by completing the equilibrium Eq. (37) with the s compatibility equations (42), as follows:

$$\begin{aligned} \begin{bmatrix} {[}\varvec{\varLambda }^{r}] &{} [\textbf{0}] \\ \left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] &{}\left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{s}\right] \\ \end{bmatrix}\begin{Bmatrix} {\varvec{t}}^{r} \\ {\varvec{t}}^{s} \\ \end{Bmatrix} =\begin{Bmatrix} {\varvec{f}}^{r} \\ \textbf{0} \\ \end{Bmatrix} \end{aligned}$$

(46)

Solving this system of $r+s$ equations allows to determine uniquely the forces $\{{\varvec{t}}^{r}\}$ and $\{{\varvec{t}}^{s}\}$. The forces $\left\{ {\varvec{t}}\right\} =\left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\}$ in the elements can thus be expressed as a function of the loads $\left\{ {\varvec{f}}\right\}$ according to:

$$\begin{aligned} \begin{aligned} \left\{ {\varvec{t}}\right\} =&\underbrace{\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{U}}^{r}\right] ^{T}}_{\left[ {\varvec{A}}\right] ^{+}}\left\{ {\varvec{f}}\right\}+ \\&\quad \underbrace{-\left[ {\varvec{V}}^{s}\right] \left( \left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{s}\right] \right) ^{-1}\left[ {\varvec{V}}^{s}\right] ^{T}}_{\left[ {\varvec{SM}}^{t}\right] }\left[ {\varvec{F}}\right] \\&\quad \underbrace{\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left[ {\varvec{U}}^{r}\right] ^{T}}_{\left[ {\varvec{A}}\right] ^{+}}\left\{ {\varvec{f}}\right\} \end{aligned} \end{aligned}$$

(47)

A more compact notation can be obtained using the definition of the force sensitivity matrix $\left[ {\varvec{SM}}^{t}\right]$ [40, 50, 56, 58]. The latter is usually associated to the linear mappings $\left\{ {\varvec{t}}\right\} =\left[ {\varvec{SM}}^{t}\right] \left\{ \delta {\varvec{l}}^{0}\right\}$ (see Eq. (67) in discussion) which describes the increase of self-stress forces for arbitrarily chosen variations of the manufacturing lengths $\left\{ \delta {\varvec{l}}^{0}\right\}$ through mechanical devices. In the current context without self-stressing phase (i.e. $\left\{ \delta {\varvec{l}}^{0}\right\} =\left\{ \textbf{0}\right\}$), the presence of $\left[ {\varvec{SM}}^{t}\right]$ is justified with similar arguments to the redistribution matrix $[{\varvec{R}}]$ (detailed in footnote$^{8}$). The interested reader is invited to follow the full chain (i.e. Eq. (47)) of linear mappings on Fig. 10. Using the force sensitivity matrix, the previous expression can be recast as:

$$\begin{aligned} \left\{ {\varvec{t}}\right\} =\left( \left[ {\varvec{I}}\right] +\left[ {\varvec{SM}}^{t}\right] \left[ {\varvec{F}}\right] \right) \left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\} \end{aligned}$$

(48)

$\left[ {\varvec{A}}\right] ^{+}$ is the linear mapping turning the loads into a set of forces in equilibrium without considering the static indeterminacy, whereas $\left[ {\varvec{I}}\right] +\left[ {\varvec{SM}}^{t}\right] \left[ {\varvec{F}}\right]$ is the linear mapping redistributing the forces accounting additionally for the static indeterminacy and the compatibility of elongations. Finally, Eq. (48) provides a direct link from the loads to the forces which fill the gap in Fig. 2b for type II trusses.

Remark 2

This paragraph demonstrates for the first time that if all elements have the same stiffness $K_{kk}^{e}$, then the hyperstatic unknowns are null, i.e. $\left\{ {\varvec{t}}^{s}\right\} =\left\{ \textbf{0}\right\}$. One should start by noting that if $\left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] =\left[ \textbf{0}\right]$ in Eq. (46), it is obtained $\left\{ {\varvec{t}}^{s}\right\} =\left\{ \textbf{0}\right\}$. This happens when the flexibility matrix takes the form $\left[ {\varvec{F}}\right] =\frac{1}{K_{kk}^{e}}\cdot \left[ {\varvec{I}}\right]$, because in such case one obtains $\left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] =\frac{1}{K_{kk}^{e}}\cdot \left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{V}}^{r}\right]$, which is equal to zero by the orthonormality property ($\left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{V}}^{r}\right] =\left[ \textbf{0}\right]$) of the singular vectors. Therefore one concludes that when all elements have the same stiffness, the forces can be readily expressed $\left\{ {\varvec{t}}\right\} =\left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\}$, similarly to Type I trusses. This leads to the following alternative physical meaning of $\left[ {\varvec{A}}\right] ^{+}$: in a statically indeterminate truss, the linear mapping $\left[ {\varvec{A}}\right] ^{+}$ provides the internal forces $\left\{ {\varvec{t}}\right\}$ in equilibrium with the loads $\left\{ {\varvec{f}}\right\}$ under the assumption that all elements have the same stiffness.

3.2.2 Interrelationship with the Displacement Method

This subsection establishes for the first time a direct interrelationship between the displacement method and the force method for statically indeterminate trusses (type II). From $\left\{ {\varvec{d}}\right\} ={\left[ {\varvec{A}}\right] ^{+}}^{T}\left\{ {\varvec{e}}\right\}$, $\left\{ {\varvec{e}}\right\} =\left[ {\varvec{F}}\right] \left\{ {\varvec{t}}\right\}$ and equation (48), one obtains:

$$\begin{aligned} \left\{ {\varvec{d}}\right\} = {\left[ {\varvec{A}}\right] ^{+}}^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\} +{\left[ {\varvec{A}}\right] ^{+}}^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{SM}}^{t}\right] \left[ {\varvec{F}}\right] \left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\} \end{aligned}$$

(49)

which expresses the displacements as a function of the loads following the force method in Fig. 10. By comparison with the displacement method, $\left\{ {\varvec{d}}\right\} = \left[ {\varvec{K}}^{L}\right] ^{-1}\left\{ {\varvec{f}}\right\}$ (Fig. 2a), which uses the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{A}}\right] \left[ {\varvec{F}}\right] ^{-1}\left[ {\varvec{A}}\right] ^{T}$, one arrives to the equality:

$$\begin{aligned} \left[ {\varvec{K}}^{L}\right] ^{-1} = {\left[ {\varvec{A}}\right] ^{+}}^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{A}}\right] ^{+}+{\left[ {\varvec{A}}\right] ^{+}}^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{SM}}^{t}\right] \left[ {\varvec{F}}\right] \left[ {\varvec{A}}\right] ^{+} \end{aligned}$$

(50)

3.2.3 Physical Interpretation

Figure 11 provides a physical interpretation of the self-stress mode and of the extensional modes at the equilibrium and compatibility levels of a simple truss with $b = 3$ elements and $n_{dof} = 2$ free degrees of freedom. Similarly to type I trusses, the equilibrium matrix $[{\varvec{A}}]$ and its SVD are computed first. The degree of static indeterminacy is seen to be $s = 1$, i.e. there is one self-stress mode $\left\{ {\varvec{V}}_{1}^{s}\right\}$. The degree of kinematic indeterminacy is $m = 0$, i.e. there is no mechanism $\left[ {\varvec{U}}^{m}\right]$. The two extensional modes can be interpretated in a similar way to the statically determinate case, with the adjustment that $\varLambda _{11} =\sqrt{2}$ in this example.

Fig. 11

Physical interpretation at the equilibrium and compatibility levels of the static modal analysis of a type II truss

Finally, the self-stress mode $\left\{ {\varvec{V}}_{1}^{s}\right\}$ can be interpreted⁹:

• At the equilibrium level, if the elements have different stiffnesses, the internal forces $\left\{ {\varvec{t}}\right\} =\left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\} +\left\{ {\varvec{V}}_{1}^{s}\right\} \cdot t_{1}^{s}$ in equilibrium with the loads $\left\{ {\varvec{f}}\right\}$ will depend on an hyperstatic unknown $t_{1}^{s}$ to be determined through Eq. (45) or (46). The value of $t_{1}^{s}$ is thus not arbitrary and relies on the resolution of a system of equilibrium and compatibility equations. If all the elements have the same stiffness, however, the hyperstatic unknown is null and the internal forces are simply given by $\left\{ {\varvec{t}}\right\} =\left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}\right\}$.

• At the compatibility level, the modal elongation $e_{1}^{s}$ must be equal to 0 according to Eq. (42). One must however be aware that there exist situations wherein the modal elongation $e_{1}^{s}$ is different than zero. This happens when the structure is self-stressed through mechanical devices that shorten the cables or lengthen the struts as shortly addressed in the discussion section. The self-stress mode $\left\{ {\varvec{V}}_{1}^{s}\right\}$ is thus interpreted for the first time at the compatibility level as elongations that may exist and generate no displacements.

3.3 Types III and IV with Kinematic Indeterminacy ($m > 0$): Limitations of the linear equations (1)–(3)

3.3.1 Force Method

Figure 7b summarizes graphically the linear force method for type III and type IV trusses, which are kinematically indeterminate ($m>0$). The relations expressed in that figure are derived mathematically below. It is also formalized below for the first time that there exists no relations between the modal coordinates $\left\{ {\varvec{d}}^{m}\right\}$ and $\left\{ {\varvec{f}}^{m}\right\}$. A solution to this issue will also be discussed later.

Consider again the basic equations (1)–(3), the SVD of the equilibrium matrix $[{\varvec{A}}]$ in Eq. (15), and the definitions (21)–(24) of the modal coordinates. In the most general case of a structure which is statically indeterminate, i.e. $s>0$, and kinematically indeterminate, i.e. $m>0$, from Fig. 4 one finds that the equilibrium matrix $[{\varvec{A}}]$ is not full rank ($r = n_{dof}-m$) and that the SVD of $[{\varvec{A}}]$ gives $\left[ {\varvec{V}}\right] =\left[ \left[ {\varvec{V}}^{r}\right] ,\left[ {\varvec{V}}^{s}\right] \right]$, $\left[ {\varvec{U}}\right] =\left[ \left[ {\varvec{U}}^{r}\right] ,\left[ {\varvec{U}}^{m}\right] \right]$ and $\left[ \varvec{\varLambda }\right] =\begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}$ as shown in Eqs. (27)–(29). The latter equations can be respectively rewritten:

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] \\ \left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ {\varvec{t}}^{r}\right\} +\begin{bmatrix} \left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ {\varvec{t}}^{s}\right\}&=\left\{ \begin{array}{c} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{array}\right\} \end{aligned}$$

(51)

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] \\ \left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ {\varvec{d}}^{r}\right\} +\begin{bmatrix} \left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ {\varvec{d}}^{m}\right\}&=\left\{ \begin{array}{c} {\varvec{e}}^{r} \\ {\varvec{e}}^{s} \\ \end{array}\right\} \end{aligned}$$

(52)

The modal loads $\left\{ {\varvec{f}}^{r}\right\}$ and $\left\{ {\varvec{f}}^{m}\right\}$ can be directly obtained from $\left\{ {\varvec{f}}\right\}$ and are considered as the only known parameters, whereas all the other (sub)vectors are unknown. Firstly, the modal axial forces $\left\{ {\varvec{t}}^{r}\right\}$ are obtained from the upper part of Eq. (51), which leads to $\left\{ {\varvec{t}}^{r}\right\} =\left[ \varvec{\varLambda }^{r}\right] ^{-1}\left\{ {\varvec{f}}^{r}\right\}$. Then, the lower part of Eq. (52) leads to $\left\{ {\varvec{e}}^{s}\right\} =\left\{ \textbf{0}\right\}$, which can be solved similarly to Sect. 3.2 for type II trusses. This leads to the modal elongation $\left\{ {\varvec{e}}^{r}\right\} =\left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{r}\right] \left\{ {\varvec{t}}^{r}\right\} +\left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{F}}\right] \left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s}\right\}$ in Eq. (43) and to the determination of the hyperstatic unknowns $\left\{ {\varvec{t}}^{s}\right\} =\left[ {\varvec{R}}\right] \left\{ {\varvec{t}}^{r}\right\}$ in Eq. (45). In the case of type III trusses with $s = 0$, consider that the lower part of Eq. (52) does not exist, and $\left\{ {\varvec{t}}^{s}\right\}$ vanishes from Eq. (51). Whether the truss is statically determinate, i.e. $s = 0$ (type III), or indeterminate, i.e. $s>0$ (type IV), the equations above can be rewritten:

$$\begin{aligned} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] \\ \left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ {\varvec{t}}^{r}\right\}&=\left\{ \begin{array}{c} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{array}\right\} \end{aligned}$$

(51')

$$\begin{aligned} \begin{array}{l} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix} \\ \\ \end{array}\left\{ \begin{array}{c} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{array}\right\}&=\begin{array}{l} \left\{ {\varvec{e}}^{r}\right\} \\ \\ \end{array} \end{aligned}$$

(52')

The form above shows that the problem of kinematic indeterminacy can be solved independently of the degree of static indeterminacy because the modal coordinates $\left\{ {\varvec{t}}^{s}\right\}$ and $\left\{ {\varvec{e}}^{s}\right\}$ do not appear. The solution of kinematically indeterminate trusses is detailed as follows.

Equation (52)’ can be rewritten:

$$\begin{aligned} \left[ \varvec{\varLambda }^{r}\right] \left\{ {\varvec{d}}^{r}\right\} = \left\{ {\varvec{e}}^{r}\right\} \Leftrightarrow \left\{ {\varvec{d}}^{r}\right\} = \left[ \varvec{\varLambda }^{r}\right] ^{-1}\left\{ {\varvec{e}}^{r}\right\} \end{aligned}$$

(53)

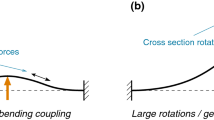
which illustrates that kinematically indeterminate trusses have more unknowns ($\left\{ {\varvec{d}}^{r}\right\}$, $\left\{ {\varvec{d}}^{m}\right\} )$ than compatibility equations, in Eq. (52)’. Therefore, there are still m kinematic unknowns $\left\{ {\varvec{d}}^{m}\right\}$ (often called $\left\{ \varvec{\beta }\right\}$ in the literature, as mentioned in a previous section) to be determined. The difficulty is that the m exceeding equilibrium equations ($\left[ \textbf{0}\right] \left\{ {\varvec{t}}^{r}\right\} =\left\{ {\varvec{f}}^{m}\right\}$) are useless. They only show that the inextensional loads $\left\{ {\varvec{f}}^{m}\right\}$ cannot be equilibrated by the truss in the initial geometry (as already intuitively stated in Fig. 5). In summary, m equations are missing to determine the m unknowns $\left\{ {\varvec{d}}^{m}\right\}$. The solution to this lack will be presented in the last sub-section of the Discussion.

3.3.2 Displacement Method: Proof of the Singularity of the Linear Stiffness Matrix

Similarly, the displacement method also fails to analyze kinematically indeterminate trusses because the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{A}}\right] \left[ {\varvec{K}}^{e}\right] \left[ {\varvec{A}}\right] ^{T}$ is singular. This fact is well known in engineering practice, where structural analysis software fail at solving trusses of type III and IV. However, since our literature review did not find the mathematical proof of this fact, the demonstration of the singularity of matrix $\left[ {\varvec{K}}^{L}\right]$ for these cases is presented. Starting from $\left\{ {\varvec{f}}\right\} =\left[ {\varvec{K}}^{L}\right] \left\{ {\varvec{d}}\right\}$, see Eq. (6), and using the SVD of the equilibrium matrix $\left[ {\varvec{A}}\right]$, one obtains:

$$\begin{aligned} \left\{ {\varvec{f}}\right\} =\underbrace{\left[ {\varvec{U}}\right] \left[ \varvec{\varLambda }\right] \left[ {\varvec{V}}\right] ^{T}}_{\left[ {\varvec{A}}\right] }\left[ {\varvec{K}}^{e}\right] \underbrace{\left[ {\varvec{V}}\right] \left[ \varvec{\varLambda }\right] ^{T}\left[ {\varvec{U}}\right] ^{T}}_{\left[ {\varvec{A}}\right] ^{T}}\left\{ {\varvec{d}}\right\} \end{aligned}$$

(54)

Then, using the definitions (21) of static modal analysis, one gets:

$$\begin{aligned} \left\{ \begin{array}{c} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{array}\right\} =\begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T} \\ \left[ {\varvec{V}}^{s}\right] ^{T} \\ \end{bmatrix} \begin{array}{l} \left[ {\varvec{K}}^{e}\right] \\ \\ \end{array} \begin{array}{l} \left[ \left[ {\varvec{V}}^{r}\right] ,\left[ {\varvec{V}}^{s}\right] \right] \\ \\ \end{array}\begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ \begin{array}{c} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{array}\right\} \end{aligned}$$

(55)

The latter equation is equivalent to:

$$\begin{aligned} \left\{ \begin{array}{c} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{array}\right\}= & {} \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix} \cdot \begin{bmatrix} \left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{K}}^{e}\right] \left[ {\varvec{V}}^{r}\right] &{}\left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{K}}^{e}\right] \left[ {\varvec{V}}^{s}\right] \\ \left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{K}}^{e}\right] \left[ {\varvec{V}}^{r}\right] &{}\left[ {\varvec{V}}^{s}\right] ^{T}\left[ {\varvec{K}}^{e}\right] \left[ {\varvec{V}}^{s}\right] \\ \end{bmatrix} \nonumber \\{} & {} \cdot \begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}\left\{ \begin{array}{c} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{array}\right\} \end{aligned}$$

(56)

Or to:

$$\begin{aligned} \left\{ \begin{array}{c} {\varvec{f}}^{r} \\ {\varvec{f}}^{m} \\ \end{array}\right\} =\underbrace{\begin{bmatrix} \left[ {\varvec{K}}^{L,r}\right] &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}}_{\left[ {\varvec{K}}^{L,mod}\right] }\left\{ \begin{array}{c} {\varvec{d}}^{r} \\ {\varvec{d}}^{m} \\ \end{array}\right\} \end{aligned}$$

(57)

where the matrix $\left[ {\varvec{K}}^{L,r}\right] =\left[ \varvec{\varLambda }^{r}\right] \begin{array}{l} \left[ {\varvec{V}}^{r}\right] ^{T}\left[ {\varvec{K}}^{e}\right] \\ \end{array}\left[ {\varvec{V}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right]$ corresponds to the stiffness of the extensional displacements such that $\left\{ {\varvec{f}}^{r}\right\} =\left[ {\varvec{K}}^{L,r}\right] \left\{ {\varvec{d}}^{r}\right\}$. Once again, Eq. (57) shows that m equations are missing to determine the m unknowns $\left\{ {\varvec{d}}^{m}\right\}$ because m rows of the matrix $\left[ {\varvec{K}}^{L,mod}\right]$ are null, i.e. $\left[ {\varvec{K}}^{L,mod}\right]$ is singular, i.e. it cannot be inverted. Back in the DoF space, one has finally:

$$\begin{aligned} \left\{ {\varvec{f}}\right\} =\underbrace{\left[ {\varvec{U}}\right] \left[ {\varvec{K}}^{L,mod}\right] \left[ {\varvec{U}}\right] ^{T}}_{\left[ {\varvec{K}}^{L}\right] }\left\{ {\varvec{d}}\right\} \end{aligned}$$

(58)

Equation (58) demonstrates that the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$ of type III and IV trusses is singular because it is built upon the modal linear stiffness matrix $\left[ {\varvec{K}}^{L,mod}\right]$ which in turn is also singular. One may note that:

• The form $\left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{U}}\right] \left[ {\varvec{K}}^{L,mod}\right] \left[ {\varvec{U}}\right] ^{T}$ in Eq. (58) appears to suggest that it corresponds to the SVD of $\left[ {\varvec{K}}^{L}\right]$. However, this is not true as demonstrated in the Discussion. In fact, the SVD of $\left[ {\varvec{K}}^{L}\right]$ does not produce the same extensional modes $\left[ {\varvec{U}}^{r}\right]$ and the same inextensional modes $\left[ {\varvec{U}}^{m}\right]$ as the SVD of the equilibrium matrix $\left[ {\varvec{A}}\right]$. The reason is that $\left[ {\varvec{K}}^{L,r}\right]$ may not be diagonal, and hence Eq. (58) does not correspond to the results of the SVD of matrix $\left[ {\varvec{K}}^{L}\right]$.

• To avert the singularity of the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$, the so-called geometric stiffness matrix $\left[ {\varvec{K}}^{G}\right]$ must be included, which shows up when nonlinear equilibrium is considered. This aspect is also addressed in the Discussion.

• For type I and II trusses (with $m = 0$), one obtains $\left[ {\varvec{K}}^{L,mod}\right] =\left[ {\varvec{K}}^{L,r}\right]$ in Eq. (57) because there are no inextensional modes (i.e. $\left\{ {\varvec{d}}^{m}\right\} = \varnothing$, $\left\{ {\varvec{f}}^{m}\right\} = \varnothing$). Therefore, the linear stiffness matrix can be inverted in type I and II trusses.

In short, it is concluded that the linear Displacement Method works only for types I and II trusses but not for types III and IV. This consideration and Eq. (57) allowed to sketch Fig. 7a which summarizes the procedure of the linear Displacement Method using static modal analysis.

3.3.3 Physical Interpretation

Consider the type III truss of Fig. 12a, which has been studied extensively in the literature [28, 36]. After computing the equilibrium matrix, its SVD is performed and the results are shown in Fig. 12b. Note that the extensional modes are not provided nor illustrated for conciseness. Only the inextensional mode $\left\{ {\varvec{U}}_{1}^{m}\right\}$ shown in Fig. 12c is here of interest.

Fig. 12

a Type III truss, a Geometry and characterization, b SVD results, c Physical interpretation of the SVD results, d Initial loads stiffening the mechanism, e Additional loads activating the mechanism

The meaning of the single inextensional mode is the following. Its basis is $\left\{ {\varvec{U}}_{1}^{m}\right\} =\frac{\left\{ -0.5, -1,-0.5, 1\right\} ^{T}}{\sqrt{2.5}}$ (dimensionless), where the factor $\frac{1}{\sqrt{2.5}}$ is justified by the orthonormality ($\left\{ {\varvec{U}}_{1}^{m}\right\} ^{T}\left\{ {\varvec{U}}_{1}^{m}\right\} = 1$). According to Fig. 5c, the inextensional mode $\left\{ {\varvec{U}}_{1}^{m}\right\}$ can be interpreted both:

• At the equilibrium level, as loads $\left\{ {\varvec{f}}\right\} =\left\{ {\varvec{U}}_{1}^{m}\right\} \cdot f_{1}^{m}$ which cannot be carried by the structure in its initial geometry, no matter the value of the (force-dimensional) modal coordinate $f_{1}^{m}$.

• At the compatibility level, as displacements $\left\{ {\varvec{d}}\right\} =\left\{ {\varvec{U}}_{1}^{m}\right\} \cdot d_{1}^{m}$ that generate no elongation (i.e. a mechanism). Note that such interpretation is only valid at first order, i.e. if the modal coordinate $d_{1}^{m}$ remains small, because the SVD is computed in the initial geometry. Therefore, a mechanism may be called infinitesimal.

The approach of static modal analysis allows adding, through Eq. (21), that:

• The orthogonal projection of any load $\left\{ {\varvec{f}}\right\}$ on an inextensional mode gives a (force-dimensional) modal coordinate $f_{1}^{m} =\left\{ {\varvec{U}}_{1}^{m}\right\} ^{T}\left\{ {\varvec{f}}\right\}$ that illustrates the loads’ ability to activate the mechanism, which is suggested without formalization in ref. [28] and which is fully detailed for the first time in ref. [56]. For instance, the initial loads $\left\{ {\varvec{f}}^{ini}\right\}$ in Fig. 12d do not activate the mechanism because $f_{1}^{m} =\left\{ {\varvec{U}}_{1}^{m}\right\} ^{T}\left\{ {\varvec{f}}^{ini}\right\} = 0$, whereas the additional load $\left\{ {\varvec{f}}\right\}$ in Fig. 12e does because $f_{1}^{m} =\left\{ {\varvec{U}}_{1}^{m}\right\} ^{T}\left\{ {\varvec{f}}\right\} =\frac{p}{\sqrt{2.5}}$.

As aforementioned, inextensional loads $\left\{ {\varvec{f}}^{m}\right\}$ cannot be equilibrated in this initial geometry. Therefore, the additional load $\left\{ {\varvec{f}}\right\}$ of Fig. 12e can only be equilibrated in a deformed geometry after large displacements.

4 Discussion

This section addresses four aspects that are judged relevant to be clarified, either with respect to other past works, the current one, or future endeavors. The first addresses the fact that Pellegrino and Calladine [14] used an alternative formulation for the equilibrium matrix, rather than the one presented in Eq. (1) adopted in the current work. The second compares the results of the SVD performed on the equilibrium matrix and on the linear stiffness matrix, which was discussed earlier in this document. Finally, with a view to future research developments, the third and fourth discussions briefly introduce other structural analysis problems, respectively related with the introduction of self-stress forces and the consideration of geometric stiffness, for which static modal analysis could be applied to provide new physical interpretations and fundamental insights.

4.1 About the Force Density Method Formulation $\left\{ {\varvec{f}}\right\} {\varvec{ = }}\left[ {\varvec{A}}^{FDM}\right] \left\{ {\varvec{q}}\right\}$

Many different authors [14, 94] prefer to state the basic equations (1) and (3) in the following alternative form:

$$\begin{aligned} \left\{ {\varvec{f}}\right\} =\left[ {\varvec{A}}^{FDM}\right] \left\{ {\varvec{q}}\right\} \end{aligned}$$

(59)

$$\begin{aligned} \left[ {\varvec{l}}\right] \left\{ {\varvec{e}}\right\} =\left[ {\varvec{A}}^{FDM}\right] ^{T}\left\{ {\varvec{d}}\right\} \end{aligned}$$

(60)

where $\left[ {\varvec{A}}^{FDM}\right]$ is a distinct formulation of the equilibrium matrix with respect to the equilibrium matrix $[{\varvec{A}}]$ used in this article. This section justifies the assumed authors’ choice for the latter. The equilibrium matrix $\left[ {\varvec{A}}^{FDM}\right]$ is described in detail in “Appendix A.3”. It contains the differences of nodal coordinates between each element’s ends (rather than the direction cosines in matrix $[{\varvec{A}}]$). The equilibrium matrix $\left[ {\varvec{A}}^{FDM}\right]$ provides a linear mapping between the Force Densities $\left\{ {\varvec{q}}\right\}$ [65] and the external loads $\left\{ {\varvec{f}}\right\}$. A force density in one element k is defined as the ratio between the axial force and the current length, i.e. $q_{k} =\frac{t_{k}}{l_{k}}$ for element k, or $\left\{ {\varvec{q}}\right\} =\left[ {\varvec{l}}\right] ^{-1}\left\{ {\varvec{t}}\right\}$ for all the elements (where the diagonal matrix $\left[ {\varvec{l}}\right]$ contains the current lengths $l_{k}$ of each element k). The Force Density Method (FDM) has demonstrated its very interesting mathematical properties by linearizing the form-finding problems [65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,95].

It is important to clarify that:

• The equilibrium matrix $\left[ {{\varvec{A}}}^{FDM}\right]$ was introduced by Pellegrino and Calladine [14]. In the compatibility equation (60), the displacements are thus compatible with an “elongation coefficient defined as elongation $\times$ length” [14].

• In 1993, Pellegrino [15] discussed the relations between “generalized strains and stresses” when he introduced the SVD method in structural analysis for the sake of generality. This raises some potential for confusion because, in engineering, strains refer to elongation / length.

• It is here made clear that in ref. [15], the SVD was introduced using the equilibrium matrix $\left[ {\varvec{A}}\right]$ (dimensionless) and not its reformulation $\left[ {\varvec{A}}^{FDM}\right]$ (length-dimensional) as illustrated by the example in Pellegrino [15] where the generalized stresses correspond in this case to force-dimensional forces and the generalized strains correspond to length-dimensional elongations.

In 1993, Pellegrino [15] used the same unit than in the present article but not in ref. [14]. The units and interpretations of the SVD of $\left[ {\varvec{A}}^{FDM}\right]$ (length-dimensional) are hence a somewhat unclear aspect:

$$\begin{aligned} \left[ {\varvec{A}}^{FDM}\right] =\left[ {\varvec{U}}^{FDM}\right] \left[ \varvec{\varLambda }^{FDM}\right] \left[ {\varvec{V}}^{FDM}\right] ^{T} \end{aligned}$$

(61)

Given Eqs. (59) and (60), the only possible explanation for the units is that the singular values $\left[ \varvec{\varLambda }^{FDM}\right]$ are now length-dimensional (i.e. no more dimensionless) whereas the singulars vectors $\left[ {\varvec{U}}^{FDM}\right]$ and $\left[ {\varvec{V}}^{FDM}\right]$ remain dimensionless. The definitions of modal coordinates in Eq. (23) become:

$$\begin{aligned} \begin{aligned} \begin{Bmatrix} {\varvec{q}}^{r} \\ {\varvec{q}}^{s} \\ \end{Bmatrix}&=\begin{bmatrix} \left[ {\varvec{V}}^{r,FDM}\right] ^{T} \\ \left[ {\varvec{V}}^{s,FDM}\right] ^{T} \\ \end{bmatrix}\left\{ {\varvec{q}}\right\} \\ \begin{Bmatrix} {\varvec{e}}^{r,FDM} \\ {\varvec{e}}^{s,FDM} \\ \end{Bmatrix}&=\begin{bmatrix} \left[ {\varvec{V}}^{r,FDM}\right] ^{T} \\ \left[ {\varvec{V}}^{s,FDM}\right] ^{T} \\ \end{bmatrix}\left[ {\varvec{l}}\right] \left\{ {\varvec{e}}\right\} \end{aligned} \end{aligned}$$

(62)

where the modal elongation coefficients $\left[ {\varvec{V}}^{FDM}\right] ^{T}\left[ {\varvec{l}}\right] \left\{ {\varvec{e}}\right\}$ (of dimension length squared) have a rather poor physical meaning and definitely do not correspond to strains (as it may be believed from the fact that $\left[ {\varvec{V}}^{FDM}\right]$ is dimensionless). This reason justifies our choice of basic equations (1)–(3) in this article.

4.2 About the Eigen Value Decomposition of the Linear Stiffness Matrix $\left[ {\varvec{K}}^{L}\right]$

The Singular Value Decomposition can be applied to any rectangular matrix $\left[ {\varvec{A}}\right]$ and leads to $\left[ {\varvec{A}}\right] =\left[ {\varvec{U}}\right] \left[ \varvec{\varLambda }\right] \left[ {\varvec{V}}\right] ^{T}$, see Eq. (12). This section discusses the case where the SVD is applied to the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$, which is square (size $n_{dof}\times n_{dof}$). In particular, it demonstrates that the equilibrium matrix and the linear stiffness matrix do not have the same fundamental bases $\left[ {\varvec{U}}\right] =\left[ \left[ {\varvec{U}}^{r}\right] ,\left[ {\varvec{U}}^{m}\right] \right]$, as it may be suggested by Eq. (58).

For square matrices $\left[ {\varvec{K}}^{L}\right]$, the Eigenvalue Decomposition (EVD) is more widely employed in structural engineering. The difference between the SVD and the EVD is first clarified. The latter allows to write¹⁰:

$$\begin{aligned} \begin{aligned} \left[ {\varvec{K}}^{L}\right] \left\{ {\varvec{W}}_{i}\right\}&=\left\{ {\varvec{W}}_{i}\right\} \cdot \varGamma _{ii} \\ \Leftrightarrow \left[ {\varvec{K}}^{L}\right]&=\left[ {\varvec{W}}\right] \left[ \varvec{\varGamma }\right] \left[ {\varvec{W}}\right] ^{-1} \end{aligned} \end{aligned}$$

(63)

where matrix $\left[ \varvec{\varGamma }\right]$ is diagonal and contains the eigenvalues $\varGamma _{ii}$ of matrix $\left[ {\varvec{K}}^{L}\right]$ and matrix $\left[ {\varvec{W}}\right]$ contains the eigenvectors $\left\{ {\varvec{W}}_{i}\right\}$. If furthermore the matrix $\left[ {\varvec{K}}^{L}\right]$ is normal, i.e. $\left[ {\varvec{K}}^{L}\right] ^{T}\left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{K}}^{L}\right] \left[ {\varvec{K}}^{L}\right] ^{T}$, then its EVD can be rewritten:

$$\begin{aligned} \left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{W}}\right] \left[ \varvec{\varGamma }\right] \left[ {\varvec{W}}\right] ^{T} \end{aligned}$$

(64)

which is called the spectral theorem in linear algebra. In this case, the eigenvectors are orthonormal $\left[ {\varvec{W}}\right] ^{T}\left[ {\varvec{W}}\right] =\left[ {\varvec{I}}\right]$. In engineering practice, it is well known that the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$ is symmetric, i.e. $\left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{K}}^{L}\right] ^{T}$, therefore it is also a normal matrix¹¹. To sum up, performing the EVD on the linear stiffness matrix leads to Eq. (64). Furthermore, performing the SVD on the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$ also leads to Eq. (64) where the left singular vectors are the same than the right singular vectors. In other words, the EVD is a special case of the SVD.

Based on the fact that the SVD and EVD of the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$ both leads to Eq. (64), the following development demonstrates that Eqs. (58) and (64) differ, except in a particular case. Wherein fact, when all the elements have the same stiffness $\left[ {\varvec{K}}^{e}\right] =\left[ {\varvec{I}}\right] \cdot K_{kk}^{e}$, Eq. (58) becomes:

$$\begin{aligned} \left[ {\varvec{K}}^{L}\right] =\left[ {\varvec{U}}\right] \underbrace{\begin{bmatrix} \left[ \varvec{\varLambda }^{r}\right] \left[ \varvec{\varLambda }^{r}\right] \cdot K_{kk}^{e} &{}\left[ \textbf{0}\right] \\ \left[ \textbf{0}\right] &{}\left[ \textbf{0}\right] \\ \end{bmatrix}}_{\left[ {\varvec{K}}^{L,mod}\right] }\left[ {\varvec{U}}\right] ^{T} \end{aligned}$$

(65)

In this particular case, the eigenvalues $\left[ \varvec{\varGamma }\right]$ are equal to $\left[ {\varvec{K}}^{L,mod}\right]$, which is diagonal, and the eigenvectors $\left[ {\varvec{W}}\right]$ of the linear stiffness matrix are equal to the singular vectors $\left[ {\varvec{U}}\right]$ of the equilibrium matrix. However, for the majority of structures, Eqs. (58) and (64) are different because the matrix $\left[ {\varvec{K}}^{L,r}\right]$ may not be diagonal¹². Therefore, one concludes that the eigenvectors $\left[ {\varvec{W}}\right]$ of the linear stiffness matrix are not equal to the singular vectors $\left[ {\varvec{U}}\right]$ of the equilibrium matrix. The implications include:

• In Eq. (58), since $\left[ {\varvec{K}}^{L,r}\right]$ may not be diagonal, one single extensional load ($\left\{ {\varvec{f}}^{r}\right\} =\left\{ 0, \ldots ,0, f_{i}^{r},0, \ldots ,0\right\} ^{T}$) may generate extensional displacements $\left\{ {\varvec{d}}^{r}\right\} =\left[ {\varvec{K}}^{L,r}\right] ^{-1}\left\{ {\varvec{f}}^{r}\right\}$ not only in the associated mode i but also in other modes.

• In Eq. (64), the eigenvectors $\left[ {\varvec{W}}\right]$ can be split into $\begin{bmatrix} \left[ {\varvec{W}}^{r}\right] &{}\left[ {\varvec{W}}^{m}\right] \\ \end{bmatrix}$. The eigenvectors $\left[ {\varvec{W}}^{r}\right]$ are associated to nonzero eigenvalues $\left[ \varvec{\varGamma }^{r}\right]$ while $\left[ {\varvec{W}}^{m}\right]$ are associated with zero eigenvalues.

• New modal coordinates (e.g. $\left\{ {\varvec{f}}^{r'}\right\} =$ $\left[ {\varvec{W}}^{r}\right] ^{T}\left\{ {\varvec{f}}\right\}$) could be defined in a similar manner than in Eq. (21). This would allow to establish a one-to-one relation between the new extensional load $f_{i}^{r'}$ and displacement $d_{i}^{r'}$ because $\left[ \varvec{\varGamma }^{r}\right]$ is always diagonal.

• The fact that the vectors $\left[ {\varvec{W}}^{m}\right]$ of the linear stiffness matrix and the vectors $\left[ {\varvec{U}}^{m}\right]$ of the equilibrium matrix are both associated to null eigen/singular values suggests that the vectors $\left[ {\varvec{W}}^{m}\right]$ and $\left[ {\varvec{U}}^{m}\right]$ are, if not equal, at least a linear combination of each others. This means that the mechanisms computed from matrix $\left[ {\varvec{K}}^{L}\right]$ and matrix $\left[ {\varvec{A}}\right]$ may not the same but they are related.

• Equation (58) demonstrated the singularity of the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right]$, i.e. the fact that it cannot be inverted for type III and IV trusses. The same conclusion can of course be drawn from Eq. (64) by counting the number of non-null eigen values $\varGamma _{ii}$. However, the unclear relationships between the (eigen and singular) values $\varGamma _{ii}$ and $\varLambda _{ii}$ (respectively computed from matrix $\left[ {\varvec{K}}^{L}\right]$ and matrix $\left[ {\varvec{A}}\right]$), as well as the fact that $\left[ {\varvec{W}}^{r}\right] \ne \left[ {\varvec{U}}^{r}\right]$ was observed in the example of Fig. 12, led the authors to try to shed some light on this issue.

• The pseudo-inverse of the linear stiffness matrix $\left[ {\varvec{K}}^{L}\right] ^{+}$corresponds to $\left[ {\varvec{W}}^{r}\right] \left[ \varvec{\varGamma }^{r}\right] ^{-1}\left[ {\varvec{W}}^{r}\right] ^{T}$ which will be used in Eq. (68) in another discussion.

4.3 About the Self-Stressing Phase

Although this article considered only the application of external loads, one may also consider the introduction of self-stress forces $\left\{ {\varvec{t}}^{ini}\right\}$ through imposed variations $\left\{ \delta {\varvec{l}}^{0}\right\}$ of the manufacturing lengths $\left\{ {\varvec{l}}^{0}\right\}$. The latter can be implemented using mechanical devices that shorten the cables or lengthen the struts. The analysis of this self-stressing phase provides another application where static modal analysis could be used. This is briefly introduced in the following.

According to Pellegrino (1990) [28], the material constitutive relation (9) can be rewritten:

$$\begin{aligned} \left\{ \delta {\varvec{l}}^{tot}\right\} {\varvec{ = }}\left\{ \delta {\varvec{l}}^{0}\right\} {\varvec{+}}\underbrace{\left[ {\varvec{F}}\right] \left\{ {\varvec{t}}\right\} }_{\left\{ {\varvec{e}}\right\} } \end{aligned}$$

(66)

where the vector $\left\{ \delta {\varvec{l}}^{tot}\right\}$ contains the total length variations of the elements which add up the imposed length variations $\left\{ \delta {\varvec{l}}^{0}\right\}$ and the elastic elongations $\left\{ {\varvec{e}}\right\}$ as illustrated in Fig. 13 for a single element.

Fig. 13

A single element equipped with a mechanical device. Both are assumed to have the same rigidity EA. The flexibility $F =\frac{l^{0}}{EA}$is considered constant since both the imposed and elastic length variations are assumed small

When several elements are assembled and form a statically indeterminate truss, imposing a length variation in a single element generates self-stress forces $\left\{ {\varvec{t}}\right\}$ not only in the element itself but also in the others. In other words, self-stress forces propagate among the truss elements [56, 58]. Analyzing the effects of imposed length variations on the structure may be performed either with the Force Method or with the Displacement Method. The application of the former [38,39,42, 45, 48, 50,51,52,53,54,58] resorts to the force sensitivity matrix $\left[ {\varvec{SM}}^{t}\right]$ as briefly introduced in Eq (47):

$$\begin{aligned} \left\{ {\varvec{t}}\right\} =\left[ {\varvec{SM}}^{t}\right] \left\{ \delta {\varvec{l}}^{0}\right\} \end{aligned}$$

(67)

The Displacement Method [47], on the other hand, makes use of external loads equivalent to the imposed lengths’ variations:

$$\begin{aligned} \left\{ {\varvec{d}}\right\} =\left[ {\varvec{K}}^{L}\right] ^{+}\underbrace{\left[ {\varvec{A}}\right] \left[ {\varvec{K}}^{e}\right] \left\{ \delta {\varvec{l}}^{0}\right\} }_{\left\{ {\varvec{f}}\right\} } \end{aligned}$$

(68)

Where $\left[ {\varvec{K}}^{L}\right] ^{+}$ is the pseudo-inverse of the linear stiffness matrix introduced in the precedent subsection. For more details on Eqs. (67) and (68), the reader is invited to refer to the concerned references. The following remarks complete this brief review:

• Equation (66) assumes that the variations of the manufacturing lengths $\left\{ \delta {\varvec{l}}^{0}\right\}$ are small and do not affect the stiffness $\left[ {\varvec{K}}^{e}\right]$(or flexibility $\left[ {\varvec{F}}\right]$) of the elements. Refer to [26, 27] for a reformulation of Eq. (66) which considers this effect, called modified axial stiffness.

• In statically indeterminate trusses, the modal elastic elongation $e_{1}^{s}$ may be different than zero in Fig. 11 due to the variations of the manufacturing lengths $\left\{ \delta {\varvec{l}}^{0}\right\}$ which is a way to increase the self-stress level $t_{1}^{s}$. However, the s exceeding compatibility conditions remain that the total modal elongations must be null $\left[ {\varvec{V}}^{s}\right] ^{T}\left\{ \delta {\varvec{l}}^{tot}\right\} {\varvec{ = }}\left\{ \textbf{0}\right\}$ [40].

• In kinematically indeterminate trusses (type III and IV), variations of the manufacturing lengths {$\delta \varvec{l}^{0}$ } can activate the mechanisms, i.e. produce inextensional displacements {d^m}. For instance, shortening one cable in the type III truss of Fig. 12 produces an inextensional displacement d₁^m, as measured by Pellegrino in 1990 [28]. One notes that this type III example is often used as a benchmark for numerical comparison [36]. In type IV trusses however, manufacturing lengths variations may both activate the mechanisms and increase the self-stress-levels. This phenomenon was recently measured [56, 57] on the type IV structure of Fig. 1d’, which may serve as another benchmark for numerical comparison.

One concludes that both the Force Method and the Displacement Method could be reviewed and interpreted from the static modal analysis viewpoint for the incorporation of the self-stressing phase. This is an outlook for future investigation.

4.4 About Existing Structural Computations to Determine the Kinematic Unknowns $\left\{ {\varvec{d}}^{m}\right\}$

It has been showed that additional loads $\left\{ \delta {\varvec{f}}\right\}$ activating the mechanisms $\left[ {\varvec{U}}^{m}\right]$ by the non-null factors $\left\{ {\varvec{f}}^{m}\right\} =\left[ {\varvec{U}}^{m}\right] ^{T}\left\{ \delta {\varvec{f}}\right\}$ cannot be equilibrated in the initial geometry, but only in a deformed geometry after large displacements. It may be assumed that these large displacements follow the mechanisms directions, i.e. $\left\{ {\varvec{d}}\right\} =\left[ {\varvec{U}}^{m}\right] \left\{ {\varvec{d}}^{m}\right\}$ where the “m” kinematic unknowns $\left\{ {\varvec{d}}^{m}\right\} =\left\{ d_{1}^{m},\ldots ,d_{m}^{m}\right\} ^{T}$ need to be determined. This consideration led Pellegrino [28] to rewrite in 1990 Eq. (1) as:

$$\begin{aligned} \left\{ \delta {\varvec{f}}\right\} {\varvec{ = }}\underbrace{\left[ {\varvec{U}}^{r}\right] \left[ \varvec{\varLambda }^{r}\right] }_{\left[ {\varvec{A}}^{r}\right] }\underbrace{\left[ {\varvec{V}}^{r}\right] ^{T}\left\{ \delta {\varvec{t}}\right\} }_{\left\{ \delta {\varvec{t}}^{r}\right\} }{\varvec{ +}}\left[ {\varvec{G}}\right] \left\{ {\varvec{d}}^{m}\right\} \end{aligned}$$

(69)

where $\left[ {\varvec{G}}\right]$ is the so-called geometric loads (also called product forces) matrix (size $n_{dof}\times m$) defined in ref. [13]. Note that, $\left[ {\varvec{A}}^{r}\right]$ (size $n_{dof}\times r$) and $\left\{ \delta {\varvec{t}}^{r}\right\}$ were originally computed in 1990 [28] through Gaussian elimination whereas, in Eq. (69) presented here, they are reviewed according to the SVD results of 1993 [15]. Equation (69) expresses thus $n_{dof}$ equilibrium equations as a function of the “m” kinematic unknowns $\left\{ {\varvec{d}}^{m}\right\} =\left\{ d_{1}^{m},\ldots ,d_{m}^{m}\right\} ^{T}$. Eq. (69) can be rewritten (see Eq. (16) in [28]):

$$\begin{aligned} \left\{ \delta {\varvec{f}}\right\} {\varvec{ = }}\begin{bmatrix} \left[ {\varvec{A}}^{r}\right] &{}\left[ {\varvec{G}}\right] \\ \end{bmatrix}\begin{Bmatrix} \delta {\varvec{t}}^{r} \\ {\varvec{d}}^{m} \\ \end{Bmatrix}{\varvec{ }} \end{aligned}$$

(70)

This equation can be solved by inversion of the square matrix $\begin{bmatrix} \left[ {\varvec{A}}^{r}\right] &{}\left[ {\varvec{G}}\right] \\ \end{bmatrix}$ to determine the “m” kinematic unknowns $\left\{ {\varvec{d}}^{m}\right\}$, as required. However, some clarifications are needed about the origin and the derivation of Eq. (69). For instance, the correlation between inextensional loads $\left\{ {\varvec{f}}^{m}\right\}$ and displacements $\left\{ {\varvec{d}}^{m}\right\}$ is not explicit in Eq. (70). In response to the unclear origin of Eq. (69), other authors [36, 47, 50] have preferred to restart from the variational form of Eq. (1), written as:

$$\begin{aligned} \left\{ \delta {\varvec{f}}\right\} {\varvec{ = }}\left[ {\varvec{A}}\right] \left\{ \delta {\varvec{t}}\right\} {\varvec{ +}}\left[ \delta {\varvec{A}}\right] \left\{ {\varvec{t}}^{ini}\right\} \end{aligned}$$

(71)

This expression deserves a short explanation. If large displacements occur, the equilibrium matrix in the deformed geometry $\left[ {\varvec{A}}^{def}\right]$ may be different than in the initial geometry $\left[ {\varvec{A}}\right]$. Geometric nonlinear effects occur and the equilibrium matrix must be recomputed several times during an iterative nonlinear procedure. Consider in Eq. (71) only an infinitesimal displacement $\left\{ \delta {\varvec{d}}\right\}$ and an infinitesimal variation $\left[ \delta {\varvec{A}}\right]$ of the equilibrium matrix $\left[ {\varvec{A}}\right]$ which correspond to the first infinitesimal linear step of this full nonlinear procedure. In Eq. (71) the increase in resisting forces $\left\{ \delta {\varvec{f}}\right\}$ now depends on the axial forces $\left\{ {\varvec{t}}^{ini}\right\}$ (already existing in the initial configuration, see Fig. 12d) and it takes into account their reorientations (i.e. the variation $\left[ \delta {\varvec{A}}\right]$ of the direction cosines).

In the Displacement Method, this phenomenon is often expressed [165, 166] via the so-called geometric stiffness matrix $\left[ {\varvec{K}}^{G}\right]$. Equations (71), (2) and (3) can be assembled into:

$$\begin{aligned} \left\{ \delta {\varvec{f}}\right\} =\left[ {\varvec{K}}^{L}\right] \left\{ \delta {\varvec{d}}\right\} +\underbrace{\left[ {\varvec{K}}^{G}\right] \left\{ \delta {\varvec{d}}\right\} }_{\left[ \delta {\varvec{A}}\right] \left\{ {\varvec{t}}^{ini}\right\} } \end{aligned}$$

(72)

Ref. [36] stated that the terms $\left[ {\varvec{K}}^{G}\right] \left\{ {\varvec{d}}\right\}$ and $\left[ \delta {\varvec{A}}\right] \left\{ {\varvec{t}}^{ini}\right\}$ are equivalent. Furthermore, it is clear that there is also a strong link between the geometric loads matrix $\left[ {\varvec{G}}\right]$ and the geometric stiffness matrix $\left[ {\varvec{K}}^{G}\right]$. Ref. [36] stated this link as $\left[ {\varvec{G}}\right] {\varvec{ = }}\left[ {\varvec{K}}^{G}\right] \left[ {\varvec{U}}^{m}\right]$. Finally, it may be pointed out that structures possessing inextensional modes, i.e. types III and IV trusses, are still difficult to analyze using the DM and Eq. (72). In fact, at the very beginning of the analysis, trusses of types III and IV are never pre-stressed ($\left\{ {\varvec{t}}^{ini}\right\} =\left\{ \textbf{0}\right\}$). Hence, the geometric stiffness matrix is also singular and Eq. (72) cannot be inverted to find the displacements. This important note justifies why structural analysis software using the DM will fail at analyzing tensegrity structures (such as in Fig. 1d’), even when geometric nonlinearity is taken into account. Fortunately, numerical artifices exist to overcome this phenomenon and launch the first calculation step, but they require to proceed to the SVD of the equilibrium matrix in an effort to eliminate the singularity (of at least one of both matrices $\left[ {\varvec{K}}^{L}\right]$ or $\left[ {\varvec{K}}^{G}\right]$) through imposed arbitrary incremental displacement ($\left\{ \varDelta {\varvec{d}}\right\} =\left[ {\varvec{U}}^{m}\right] \left\{ {\varvec{d}}^{m}\right\} \ne \left\{ \textbf{0}\right\}$) or imposed pre-stress forces ($\left\{ {\varvec{t}}^{ini}\right\} =\left[ {\varvec{A}}\right] ^{+}\left\{ {\varvec{f}}^{ini}\right\} +\left[ {\varvec{V}}^{s}\right] \left\{ {\varvec{t}}^{s,ini}\right\} \ne \left\{ \textbf{0}\right\}$). After this cumbersome very first calculation step, the nonlinear procedure of the DM with iterative updates of matrices $\left[ {\varvec{K}}^{L}\right]$ and $\left[ {\varvec{K}}^{G}\right]$ can be continued without further inconvenience.

This discussion is concluded by the well-known fact that the geometric stiffness must be considered to solve type III and type IV trusses. However, as shown in this subsection, the geometric stiffness exists under different formulations in the literature: reviewing, unifying, and interpreting them from the static modal analysis viewpoint may be addressed in a future work.

5 Conclusion

This article established the first of its kind state-of-the-art on static structural computations for all types of pin-jointed structures. It was followed by the introduction of the principle of static modal analysis by taking inspiration from the dynamic modal analysis and the singular value decomposition (SVD) of the equilibrium matrix. It allowed to review the Force Method (FM) and Displacement Method (DM), which are commonly used for the analysis of linear trusses subjected to external loading. Both methods of linear analysis were derived for the four types of trusses together with explicit graphical and physical explanations of the SVD results. The latter provides valuable insights into the structural behavior of self-stressed mechanisms such as the self-stress mode distributions and the mechanisms’ coordinates. The static modal analysis allows, through a mathematical change of variables and subsequent paradigm shift, an easy back-and-forth passage from the structural and elemental spaces to the associated static modal spaces, which are composed of extensional, self-stress, and inextensional modes. Their interpretation at the equilibrium and compatibility levels was performed, together with novel graphical interpretations using arrows as visualization of linear mappings. These graphical roadmaps of the linear FM and DM bring out new links between the fundamental static modes. The solution procedure for the four types of pin-jointed structures were illustrated with straightforward examples. Eventually, it has been rigorously formalized that the basic equations of linear analysis fail at solving kinematically indeterminate trusses (type III or IV). The approach presented herein enabled a comprehensive review of the existing literature on the Force Method and Displacement Method, highlighting novel unifying and complementary principles for both approaches. The introduction of self-stress forces and the consideration of geometric nonlinearities will be addressed in a future work.

Appendix A: Physical Interpretation of Basic Equation \(\left\{ {\varvec{f}}\right\} =\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\}\)

1.1 Appendix A.1: Nuance Between Resisting Forces $\left\{ {\varvec{f}}\right\}$ and External Loads $\left\{ {\varvec{f}}^{ext}\right\}$

Consider an element $k$ connecting node (1) to node (j) in Fig. 14. The element is subjected to an internal axial force $t_{k}$ whereas bending moments and shear forces are neglected. It has a current length $l_{k}$ (which is different than the manufacturing length $l_{k}^{0}$), a cross-sectional area $A_{k}$ and a Young’s modulus $E_{k}$. The axial force $t_{k}$ (positive in tension) can be decomposed into its components $\left\{ {\varvec{f}}\right\}$ at each element end in the three directions $X, Y, Z$ as follow:

Fig. 14

Plane view in a 3D reference system of element k connected to nodes (1) and (j). a: axial force $t_{k}$ in the element and its decomposition $\left\{ {\varvec{f}}\right\}$ on the end nodes, b: the direction cosines $c_{x,k}$ and $c_{z,k}$ in the X and Z directions for element $k$

$$\begin{aligned} \left\{ \begin{array}{c} f_{1x} \\ f_{1y} \\ f_{1z} \\ f_{jx} \\ f_{jy} \\ f_{jz} \\ \end{array}\right\} =\left\{ \begin{array}{c} -c_{x,k} \\ -c_{y,k} \\ -c_{z,k} \\ c_{x,k} \\ c_{y,k} \\ c_{z,k} \\ \end{array}\right\} \cdot t_{k} \end{aligned}$$

(73)

With the notations $c_{x,k} =\frac{\left( x_{j}-x_{1}\right) }{l_{k}}$, $c_{y,k} =\frac{\left( y_{j}-y_{1}\right) }{l_{k}}$ and $c_{z,k} =\frac{\left( z_{j}-z_{1}\right) }{l_{k}}$ expressing the direction cosines of element $k$ as shown in Fig. 14b where a direction has been defined for the element $k$ in a similar manner to vectors. Defining a direction to each element will reveal useful in Appendix A.4. Whether element $k$ is defined from node (1) to node (j), or from node (j) to node (1), has no influence since in both cases one obtains for instance $f_{jx} =\frac{\left( x_{j}-x_{1}\right) \cdot t_{k}}{l_{k}}$. Note in Fig. 14a that:

• The forces $\left\{ {\varvec{f}}\right\}$ are drawn in their physical directions (i.e. $f_{1x}$ is drawn to the left because it is negative).

• The resisting forces $\left\{ {\varvec{f}}\right\}$ are historically defined in the same direction as external loads $\left\{ {\varvec{f}}^{ext}\right\}$. Therefore, the Newton’s first law of motion (i.e. $\left\{ {\varvec{f}}^{ext}\right\} +\left\{ {\varvec{f}}\right\} =\left\{ \textbf{0}\right\} )$ becomes here the condition for static equilibrium $\left\{ {\varvec{f}}^{ext}\right\} =\left\{ {\varvec{f}}\right\}$.

The nuance between resisting forces $\left\{ {\varvec{f}}\right\}$ and external loads $\left\{ {\varvec{f}}^{ext}\right\}$ is that all the entries in the external loads vector $\left\{ {\varvec{f}}^{ext}\right\}$ are arbitrary whereas the resisting forces $\left\{ {\varvec{f}}\right\}$ follow Eq. (73), i.e. they are a multiple of the direction cosines.

1.2 Appendix A.2: Equilibrium of a General Pin-Jointed Structure

Consider a pin-jointed structure composed of $b$ elements, $n$ nodes and connected to exterior by $c$ reactions as shown in Fig. 15a. For conciseness and without loss of generality, consider that the 3D structure in Fig. 15a is fixed in the Y direction at all nodes. The vector $\left\{ {\varvec{f}}^{fix}\right\}$ of $c$ reactions also includes, for instance, a fixation on node (1) in the X direction as well as some other reactions elsewhere. External loads $\left\{ {\varvec{f}}^{ext}\right\}$ may be applied on the three directions of all nodes. There are thus $n_{dof} = 3\cdot n-c$ free Degree of Freedom and $c$ fixed DoF.

Fig. 15

a A general pin-jointed structure with $b$ elements, $n$ nodes and $c$ reactions $\left\{ {\varvec{f}}^{fix}\right\}$. All nodes are fixed by supports in the Y direction and are subjected to external loads $\left\{ {\varvec{f}}^{ext}\right\}$ in the three directions. The axial forces $\left\{ {\varvec{t}}\right\}$ in the elements are responsible for the resisting forces $\left\{ {\varvec{f}}\right\}$ on their end nodes. b the equilibrium matrix $\left[ {\varvec{A}}\right]$ of this structure. Figure adapted from [14]

One static equilibrium equation can be written for each node and direction (i.e. for each DoF). Using Eq. (73), one obtains $3\cdot n$ static equilibrium equations as follow:

(74)

(75)

The $n_{dof}$ Eq. (75) contain $b$ unknown axial forces $\left\{ {\varvec{t}}\right\}$ whereas the $c$ Eq. (74) contain moreover $c$ unknown reaction forces $\left\{ {\varvec{f}}^{fix}\right\}$. Eq. (74) can only be solved once the $b$ axial forces $\left\{ {\varvec{t}}\right\}$ have been determined. Hence Eq. (74) are disregarded for the moment and one focuses on Eq. (75). According to ref. [14], the equilibrium matrix $\left[ {\varvec{A}}\right]$ is defined in such a way that:

$$\begin{aligned} \left\{ {\varvec{f}}\right\} =\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\} \end{aligned}$$

(76)

Fig. 15b illustrates the matrix form (76) and Fig. 15a illustrates that vector $\left\{ {\varvec{f}}\right\}$ contains the sum of the resisting forces from the different elements. One notes that each column $k$ of matrix $\left[ {\varvec{A}}\right]$:

• Contains the direction cosines of element $k$.

• Can be interpreted physically as the external loads in equilibrium with a unit axial forces $t_{k} = 1$ in element $k$ (and zero forces in all the others elements).

By backsubstitution of Eq. (76) into Eq. (75),  one obtains the following condition of static equilibrium:

$$\begin{aligned} \left\{ {\varvec{f}}^{ext}\right\} -\underbrace{\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\} }_{\left\{ {\varvec{f}}\right\} } =\left\{ \textbf{0}\right\} \end{aligned}$$

(77)

However, given that the axial forces $\left\{ {\varvec{t}}\right\}$ are unknown, the structure may not be in equilibrium. In this case, one obtains the residual (out-of-balance) forces:

$$\begin{aligned} \left\{ {\varvec{f}}^{res}\right\} =\left\{ {\varvec{f}}^{ext}\right\} -\underbrace{\left[ {\varvec{A}}\right] \left\{ {\varvec{t}}\right\} }_{\left\{ {\varvec{f}}\right\} } \end{aligned}$$

(78)

which will produce, by second Newton’s law, the motion and the acceleration of the nodes until an equilibrium is achieved or until collapse. Note that the Dynamic Relaxation Method [67, 164] tracks this movement due to the residual forces $\left\{ {\varvec{f}}^{res}\right\}$ until the structure comes at rest (with $\left\{ {\varvec{f}}^{res}\right\} =\left\{ \textbf{0}\right\}$ for all free DoF) through damping.

Assuming the $b$ axial forces $\left\{ {\varvec{t}}\right\}$ have been obtained, the $c$ reaction forces $\left\{ {\varvec{f}}^{fix}\right\}$ at the supports can be obtained through Eq. (74) which can be rewritten $\left\{ {\varvec{f}}^{fix}\right\} = -\left\{ {\varvec{f}}\right\} +\left[ {\varvec{A}}^{fix}\right] \left\{ {\varvec{t}}\right\}$. This ends the computation and interpretation of the equilibrium conditions in a general pin-jointed structure.

1.3 Appendix A.3: Force Density Formulation

The equilibrium matrix $\left[ {\varvec{A}}\right]$ (which was redeveloped here above) differs from the one introduced in ref. [14] which is called here $\left[ {\varvec{A}}^{FDM}\right]$. The matrix $\left[ {\varvec{A}}^{FDM}\right]$ is a distinct formulation of the equilibrium matrix which is based on the so-called Force Density Method (FDM) [65, 68, 94]. FDM relies on the definition of a force density $q_{k} =\frac{t_{k}}{l_{k}}$ in each element $k$. Restarting the derivation from equation (73) using this time the definition of a force density, one obtains:

$$\begin{aligned} \left[ {\varvec{A}}^{FDM}\right] \left\{ {\varvec{q}}\right\} =\left\{ {\varvec{f}}\right\} \end{aligned}$$

(79)

Where:

• The vector $\left\{ {\varvec{q}}\right\}$ contains the force densities $q_{k} =\frac{t_{k}}{l_{k}}$ of each element $k$.

• The matrix $\left[ {\varvec{A}}^{FDM}\right]$ contains the differences of (length-dimensional) coordinates $\varDelta x_{k} =\left( x_{2}-x_{1}\right)$, $\varDelta y_{k} =\left( y_{2}-y_{1}\right)$ and $\varDelta z_{k} =\left( z_{2}-z_{1}\right)$ of the elements (whereas $\left[ {\varvec{A}}\right]$ contains the dimensionless direction cosines $c_{x,k} =\frac{\varDelta x_{k}}{l_{k}}$, $c_{y,k} =\frac{\varDelta y_{k}}{l_{k}}$ and $c_{z,k} =\frac{ \varDelta z_{k}}{l_{k}}$).

Using the diagonal matrix $\left[ {\varvec{l}}\right]$ (that contains the current lengths $l_{k}$ of the elements on the diagonal), one obtains the relations between both equilibrium matrices $\left[ {\varvec{A}}\right]$ and $\left[ {\varvec{A}}^{FDM}\right]$:

$$\begin{aligned} \underbrace{\left[ {\varvec{A}}^{FDM}\right] \left[ {\varvec{l}}\right] ^{-1}}_{\left[ {\varvec{A}}\right] }\left\{ {\varvec{t}}\right\} =\left\{ {\varvec{f}}\right\} \Leftrightarrow \left[ {\varvec{A}}^{FDM}\right] \underbrace{\left[ {\varvec{l}}\right] ^{-1}\left\{ {\varvec{t}}\right\} }_{\left\{ {\varvec{q}}\right\} } =\left\{ {\varvec{f}}\right\} \end{aligned}$$

This ends the reinterpretation of the static equilibrium conditions from the Force Density Method viewpoint. This is further discussed in section 4.1.

1.4 Appendix A.4: Systematic Way to Compute the Equilibrium Matrix

Filling in the entries of the equilibrium matrix $\left[ {\varvec{A}}\right]$ is a rather cumbersome process because it requires several nested “for loops” with tricky referencing to the correct indexes (see Fig. 16). Therefore, ref. [71, 77] proposed a systematic way to compute the equilibrium matrix following the formulation $\left[ {\varvec{A}}^{FDM}\right]$ introduced in ref. [14]. This systematic way is here redeveloped for the computation of matrix $\left[ {\varvec{A}}\right]$ (rather than $\left[ {\varvec{A}}^{FDM}\right]$) and physically interpreted.

Fig. 16

Systematic computation of the equilibrium matrix $\left[ {\varvec{A}}\right]$ using the connectivity matrix $\left[ \overrightarrow{{\varvec{C}}}\right]$

The procedure starts with the computation of the connectivity matrix $\left[ \overrightarrow{{\varvec{C}}}\right]$ [65, 68] which reflects that elements are defined with a direction from a start node to an end node (cfr “Appendix A.1”). Fig. 16 shows that each entry $kj$ of the connectivity matrix $\left[ \overrightarrow{{\varvec{C}}}\right]$ (size $b\times n$) is equal to 0 if node (j) do not belong to element $k$, $-1$ if node (j) is the start node of element $k$ and 1 if it is the end node.

Then, given the vectors (size $n\times 1$) of the node coordinates $\left\{ {\varvec{x}}\right\}$, $\left\{ {\varvec{y}}\right\}$, $\left\{ {\varvec{z}}\right\}$, one finds the differences of coordinates $\left\{ \varDelta {\varvec{x}}\right\}$, $\left\{ \varDelta {\varvec{y}}\right\}$, $\left\{ \varDelta {\varvec{z}}\right\}$ (size $b\times 1$) between the element ends by:

$$\begin{aligned} \left\{ \varDelta {\varvec{x}}\right\} {\varvec{ = }}\left[ \overrightarrow{{\varvec{C}}}\right] \left\{ {\varvec{x}}\right\} \end{aligned}$$

(80)

The current length of each element k can then be easily computed by $l_{k} =\sqrt{\varDelta x_{k}^{2}+\varDelta y_{k}^{2}+\varDelta z_{k}^{2}}$ and stored in the vector $\left\{ {\varvec{l}}\right\}$ or in the diagonal matrix $[{\varvec{l}}]$. The vectors of the direction cosines $\left\{ {\varvec{c}}_{x}\right\}$, $\left\{ {\varvec{c}}_{y}\right\}$ and $\left\{ {\varvec{c}}_{z}\right\}$ of the elements are then obtained by:

$$\begin{aligned} \left\{ {\varvec{c}}_{x}\right\} {\varvec{ = }}\left[ {\varvec{l}}\right] ^{-1}\left\{ \varDelta {\varvec{x}}\right\} \end{aligned}$$

(81)

After reshaping under diagonal matrix forms $\left[ {\varvec{c}}_{x}\right]$, $\left[ {\varvec{c}}_{y}\right]$, $\left[ {\varvec{c}}_{z}\right]$, the equilibrium matrices $\left[ {\varvec{A}}_{x}\right]$, $\left[ {\varvec{A}}_{y}\right]$, $\left[ {\varvec{A}}_{z}\right]$ (sizes $n\times b$) are finally obtained and contain the direction cosines for each element end as follow :

$$\begin{aligned} \left[ {\varvec{A}}_{x}\right] =\left[ \overrightarrow{{\varvec{C}}}\right] ^{T}\left[ {\varvec{c}}_{x}\right] \Leftrightarrow \left[ {\varvec{A}}_{x}\right] =\left[ \overrightarrow{{\varvec{C}}}\right] ^{T}diag\left( \left[ {\varvec{l}}\right] ^{-1}\left[ \overrightarrow{{\varvec{C}}}\right] \left\{ {\varvec{x}}\right\} \right) \end{aligned}$$

(82)

Repeating Eq. (82) in the two other directions $\left\{ {\varvec{y}}\right\}$ and $\left\{ {\varvec{z}}\right\}$ leads to $\left[ {\varvec{A}}_{y}\right]$, $\left[ {\varvec{A}}_{z}\right]$. Then the three matrices $\left[ {\varvec{A}}_{x}\right]$, $\left[ {\varvec{A}}_{y}\right]$, $\left[ {\varvec{A}}_{z}\right]$ are grouped in a single matrix $\left[ {\varvec{A}}\right]$ and the rows are rearranged arbitrarily according to the arbitrarily chosen order of the DoF (see Fig. 16). Finally, the DoF fixed by a support are removed from matrix $\left[ {\varvec{A}}\right]$ and stored in a matrix $\left[ {\varvec{A}}^{fix}\right]$.

This ends the systematic computation of the equilibrium matrix [A] as well as its physical interpretation. This article aims at solving the equilibrium and compatibility conditions (1) and (3), to which the reader is invited to refer.