1 Introduction

The design of tensegrity structures passes through three steps: form-finding, structural stability and load analysis (Schenk 1983). A key step in the design of tensegrity structures is the determination of their equilibrium configuration, known as form-finding (Tibert and Pellegrino 2003). As pioneering work in form-finding, the force density method was first proposed by Schek (1974) for cable structures. The force density method is widely used in the form-finding of tensegrity literature, such as Tibert and Pellegrino (2003). Estrada et al. (2006) presented a multi-parameter form-finding procedure for tensegrity structures using the force-density method. Masic et al. (2005) extended the force-density method by explicitly incorporating shape constraints for general and symmetric tensegrity structures. Zhang and Ohsaki (2006) offered an adaptive force density method for form-finding problems of tensegrity structures. Most recently, Lee et al. (2014) proposed force identification of tensegrity grid structures according to external loads by using a force density method.

Most of form-finding methods assume given topologies, symmetry conditions, and try to find equilibrium configurations using some given constraints (Chen et al. 2015). A different approach is to find the topology with a genetic algorithm. There have been several researches that dealt with optimum designs using the genetic algorithm (Liu X et al. 2012; Hao et al. 2012; Le Riche and Haftka 1995). Recently, several studies have researched the form-finding methods of tensegrity structures using genetic algorithms for searching self-equilibrium topology. Paul et al. (2005) used genetic algorithms to develop an initial arbitrary topology into a stable one. Xu and Luo (2010) presented a form-finding method of irregular tensegrities based on a genetic algorithm. Yamamoto et al. (2011) proposed a genetic algorithm based form-finding method to obtain tensegrity structures with fewer design variables. Most recently, Koohestani (2012) provided an efficient form-finding method using a genetic algorithm that is used as an optimisation technique. Instead, Chen et al. (2012) used a ant colony system to build the form-finding method.

Most of the available methods have dealt with the form-finding of tensegrities for only the case of a single self-stress state. Recently, however, one numerical methods is presented for form-finding of tensegrity structures with multiple states of self-stress (Tran and Lee 2011). Tran and Lee (2011) used appropriate number of member groups that are employed to determine a single integral feasible force density vector; the members are grouped based on the geometrical symmetry properties. However, in this case, member grouping is not systematic and rather arbitrary. In this regard, the automatic member grouping method is developed in this paper in order to determine single integral feasible self-stress state of tensegrity structures.

The present study aims at determining the self-equilibrium and stability properties of tensegrity structures using the force density method combined with genetic algorithm. Also, the final goal of this paper is to present an automatic grouping method and equally present minimum number of groups that can be achieved the regular shapes of the tensegrities. Tensegrity structures can be highly efficient in terms of regular form, provided that the minimum number of groups is applied to the system. There has been increasing in a topic of grouping in recent years (Chen and Feng 2012; Koohestani 2015). The best situation is one in which the tensegrity structure is divided into two groups (cables and struts). Since not all systems can be divided into two groups, it is important that the systems have the appropriate minimum number of groupings. The results of these efforts indicated that regular tensegrity structures can be drawn.

This procedure requires only the topology and the types of members (i.e., either compression or tension). Both the eigenvalue decomposition of the force density matrix and the singular value decomposition of the equilibrium matrix are iteratively executed to find the range of feasible sets of the nodal coordinates and the force densities. When combined with a genetic algorithm, the standard deviation of the force densities in the cables is used to uniquely define a single integral feasible set of force densities. In contrast to prior existing methods, the proposed method can easily determine the feasible sets of the force densities with automatic grouping. In this paper, Section 2 gives the theoretical basis for the equilibrium equations. Section 3 will describe the formulation of form-finding with a genetic algorithm theory. The examples of tensegrity structures will be analysed in Sections 4 and 5 will conclude the paper.

2 Formulation of self-equilibrium equations

2.1 Force density method

The force density method uses a linear equation in the nodal coordinates: this equation can be linearised with notation (1), known as force density (Tibert and Pellegrino 2003).

$$\begin{array}{@{}rcl@{}} q_{k}=\frac{f_{k}}{l_{k}} \end{array} $$
(1)

where any member k has a member force f k and a length of element l k (k = 1,2,3,⋯ , b). For a d-dimensional (d = 2 or 3) tensegrity structure with b members and n free nodes can be expressed by a connectivity matrix \(\textbf {C} (\in \mathbb {R}^{b\times n})\) as discussed in (Schek 1974). If member k connects nodes i and j (i < j), then the i th and j th elements of the k th row of a connectivity matrix C are set to 1 and -1, respectively, as follows:

$$\begin{array}{@{}rcl@{}} \textbf{C}_{(k,p)}= \left\{ \begin{array}{rl} 1 & \text{for p} = \text{i} \\ -1 & \text{for p} = \text{j} \\ 0 & \textit{otherwise} \end{array} \right. \end{array} $$
(2)

Let \(\textbf {x}, \textbf {y}, \textbf {z} (\in \mathbb {R}^{n})\) denote the nodal coordinate vectors of the free node, in x, y and z directions. When the external load and self-weight are ignored, the equilibrium equations can be written as follows:

$$\begin{array}{@{}rcl@{}} \textbf{D}[\textbf{x} \; \textbf{y} \; \textbf{z}] = \textbf{C}^{T} diag(\textbf{q}) \textbf{C}[\textbf{x} \; \textbf{y} \; \textbf{z}]&=&\left[\textbf{0} \; \textbf{0} \; \textbf{0}\right] \end{array} $$
(3)

where \(\textbf {D} (\in \mathbb {R}^{n \times n})\) is the force density matrix (Tibert and Pellegrino 2003; Estrada et al. 2006), or stress matrix (Connelly 1982).

Instead of using the connectivity matrix C and force density vector q, the force density matrix D can be written directly by Vassart and Motro (1999); Connelly and Terrell (1995) as

$$\begin{array}{@{}rcl@{}} \textbf{D}_{(i,j)}= \left\{ \begin{array}{ll} -q_{k} & \text{if nodes i and j are connected by member k} \\ \displaystyle\sum\limits_{k\in\Omega} q_{k} & \text{for i} = \text{j} \\ 0 & \textit{otherwise} \end{array} \right.{} \end{array} $$
(4)

in which Ω denotes the set of members connected to node i. Equation (4) indicates that the force density matrix D is always square and symmetric. D of the tensegrity structure is semi-definite due to the existence of compression members (struts), with q k < 0. Using a second term of (3), the equilibrium equation can be expressed as

$$\begin{array}{@{}rcl@{}} \textbf{C}^{T} diag(\textbf{q}) \textbf{C} \textbf{x}&=&0 \end{array} $$
(5a)
$$\begin{array}{@{}rcl@{}} \textbf{C}^{T} diag(\textbf{q}) \textbf{C} \textbf{y}&=&0 \end{array} $$
(5b)
$$\begin{array}{@{}rcl@{}} \textbf{C}^{T} diag(\textbf{q}) \textbf{C} \textbf{z}&=&\textbf{0} \end{array} $$
(5c)

Equation (5a) can be reorganized as

$$\begin{array}{@{}rcl@{}} \textbf{A} \textbf{q}&=&\textbf{0} \end{array} $$
(6)

where A (\(\in \mathbb {R}^{dn \times b}\)) is known as the equilibrium matrix, defined by

$$\begin{array}{@{}rcl@{}} \textbf{A}&=& \left( \begin{array}{c} \textbf{C}^{T} diag(\textbf{Cx})\\ \textbf{C}^{T} diag(\textbf{Cy})\\ \textbf{C}^{T} diag(\textbf{Cz}) \end{array} \right) \end{array} $$
(7)

Equation (3) shows the relationship between force density matrix D and nodal coordinates, and (6) illustrates the relationship between the equilibrium matrix A and force densities.

2.2 Rank deficiency conditions

The form-finding procedure of tensegrity structures requires rank deficiency conditions of force density and equilibrium matrices. The rank deficiency of D (n D ) has at least one state of self-stress, since the sum of the elements of the row or column of force density matrix (D) always equals zero. Furthermore, in a d-dimensional tensegrity structure, the rank deficiency of D has at least d useful particular solutions. Therefore, the rank deficiency condition is defined as

$$\begin{array}{@{}rcl@{}} n_{\textbf{D}}\geq d+1 \end{array} $$
(8)

The second rank deficiency condition is related to a dimension of null space of the equilibrium matrix A. The dimension of null space of the equilibrium matrix A is identical to ”s”, known as the number of independent states of self-stress. A tensegrity structure ensures the existence of at least one state of self-stress and can be stated as

$$\begin{array}{@{}rcl@{}} s \; = \; n_{\textbf{A}} \; \geq \; 1 \end{array} $$
(9)

3 Form-finding process

3.1 Formulation

This proposed method does not require initial geometry or symmetrical conditions of the tensegrity structure. The dimension size, the connectivity of nodes and the type of each member are only required for a form-finding procedure. Based on the type of individual member, the initial force density coefficients of cables and struts are automatically assigned as +1 and -1, respectively, as follows:

$$\begin{array}{@{}rcl@{}} \textbf{q}^{0}&=&\{\underbrace{+1 \; +1 \; {\cdots} \; +1}_{cables} \quad \underbrace{-1 \; -1 \; {\cdots} \; -1}_{struts}\}^{T} \end{array} $$
(10)

Firstly, the force density matrix is calculated from the initial force density vector by (10) and the nodal coordinates are adopted from the eigenvalue decomposition of the force density matrix D. The square force density matrix D can be factorized as follows by using the eigenvalue decomposition (Meyer CD 2000).

$$\begin{array}{@{}rcl@{}} \textbf{D}&=&\Phi \Lambda{\Phi}^{T} \end{array} $$
(11)

where \(\Phi (\in \mathbb {R}^{n \times n})\) is the orthogonal matrix (ΦΦT = I n , in which \(\textbf {I}_{n} \in \mathbb {R}^{n \times n}\) is the unit matrix) whose i th column is the eigenvector basis \(\phi _{i} (\in \mathbb {R}^{n})\) of D. \(\Lambda (\in \mathbb {R}^{n \times n})\) is the diagonal matrix whose diagonal elements are the corresponding eigenvalues, i.e., Λ i i = λ i . The eigenvector ϕ i of Φ corresponds to eigenvalue λ i of Λ. The eigenvalues are in increasing order as

$$\begin{array}{@{}rcl@{}} \lambda_{1} \; \leq \lambda_{2} \; \leq \; {\cdots} \; \leq \lambda_{n} \end{array} $$
(12)

It is clear that the number of zero eigenvalues of D is equal to the dimension of its null space. The first d + 1 eigenvectors of \(\bar {\Phi }\), corresponding to the first d + 1 smallest eigenvalues, respectively, are chosen as nodal coordinates [x, y, z] for d-dimensional tensegrity structure.

Subsequently, these nodal coordinates are substituted into (6) to select the candidates for a set of force densities by the singular value decomposition of the matrix A.

$$\begin{array}{@{}rcl@{}} \textbf{A} &=& \textbf{U} \textbf{V} \textbf{W}^{T} \end{array} $$
(13)

where \(\textbf {U} (\in \mathbb {R}^{dn \times dn})=[\textbf {u}_{1} \; \textbf {u}_{2} \; {\cdots } \; \textbf {u}_{dn}]\) and \(\textbf {W} (\in \mathbb {R}^{b \times b})=[\textbf {w}_{1} \; \textbf {w}_{2} \; \cdots \; \textbf {w}_{b}]\) are orthogonal matrices. \(\textbf {V} (\in \mathbb {R}^{dn \times b})\) is a diagonal matrix with non-negative singular values of A in decreasing order as

$$\begin{array}{@{}rcl@{}} \sigma_{1} \; \geq \; \sigma_{2} \; \geq \; {\cdots} \; \geq \; \sigma_{b} \; \geq \; 0 \end{array} $$
(14)

The matrices U and W from (13) can be expressed, respectively, as (Pellegrino 1993)

$$\begin{array}{@{}rcl@{}} \textbf{U}=[\textbf{u}_{1} \textbf{u}_{2} \cdot \cdot \cdot \textbf{u}_{r_{\textbf{A}}} \mid \textbf{m}_{1} \cdot \cdot \cdot \textbf{m}_{m}] \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} \textbf{W}=[\textbf{w}_{1} \textbf{w}_{2} \cdot \cdot \cdot \textbf{w}_{r_{\textbf{A}}} \mid \textbf{q}_{1} \cdot \cdot \cdot \textbf{q}_{s}] \end{array} $$
(16)

where the vectors \(\textbf {m}_{i} \in \mathbb {R}^{dn} (i=1,2,\cdots ,m)\) denote m (= d n − r A ) inextensional mechanisms including both possible infinitesimal mechanisms and rigid body motions, while the vector \(\textbf {q}_{j} \in \mathbb {R}^{b} (j=1,2,\cdots ,s)\) are s independent states of self-stress that satisfy the linear homogeneous (6).

Regarding s = 1 (one state of self-stress), the vector \(\textbf {q}_{1} (\in \mathbb {R}^{b})\) in (16) matching in signs with q 0 is indeed the single state of self-stress that satisfies the homogeneous (6). However, the proposed form-finding algorithm continues iterating until (8) and (9) are met.

Where s ≥ 2, the bases of the vector spaces of force densities and mechanisms of any tensegrity structure are calculated from the null space of the equilibrium matrix (Pellegrino 1993). As a result, the general solution \(\bar {\textbf {q}}\) of (6) that lies in the null space of A is formulated as

$$\begin{array}{@{}rcl@{}} \bar{\textbf{q}}=\sum\limits_{i=1}^{d + 1}c_{i} \textbf{q}^{i} \end{array} $$
(17)

where the coefficients c i are arbitrary values and \(\textbf {q}_{i} \in \mathbb {R}^{b} (i=1,2,...,s)\) are the particular solutions of (6). A genetic algorithm is then used to obtain the general solution \(\bar {\textbf {q}}\) that satisfies (3). Finally, the eigenvalue decomposition of the force density matrix and the single value decomposition of the equilibrium matrix are performed iteratively to find the range of feasible sets of nodal coordinates and force densities that satisfy the required rank deficiency of the force density and equilibrium matrices, respectively. Figure 1 shows the flowchart of solving the form-finding problem by using the genetic algorithm.

Fig. 1
figure 1

The flowchart of solving the form-finding problem by using the genetic algorithm

Full size image

3.2 Fitness function

In this study, the form-finding algorithm is formulated using constrained optimization problems combined with the standard deviation of the force density in the cables as follows:

$$\begin{array}{@{}rcl@{}} \text{Minimize } \sqrt{\frac{\sum\limits_{k=1}^{m}{{q_{k}^{2}}}}{m}-\left( \frac{\sum\limits_{k=1}^{m}q_{k}}{m}\right)^{2}} (q_{k}\in {\Gamma}_{c}) \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} \text{Subject to} & &\\ &&\text{i)} \left( \begin{array}{c} 0<q_{i}<1 (q_{i}\in {\Gamma}_{c})\\ -1<q_{j}<0 (q_{j}\in {\Gamma}_{s}) \end{array} \right) \end{array} $$
(19a)
$$\begin{array}{@{}rcl@{}} &&\text{ii)} \frac{q_{i} -nq_{j}}{q_{i}}\leq \epsilon_{0} \end{array} $$
(19b)

in which Γ denotes the total set of the force density and m is the number of cables. Γ c and Γ s are the set of the force densities for cable members and strut members, respectively. q i and q j are a component of \(\bar {\textbf {q}}\). Subscript (i and j) denotes element numbers, and 𝜖 0 is used to define the tolerance. Equation (19a) indicates unilateral conditions for tensegrity grid structures, which are necessary in order to have a unique value of initial self-stress forces. On the other hand, (19b) are optional constraints for drawing the desired grouping of the tensegrity from the optimization problem and for two distinct members that are in a linear relationship to each other.

3.3 Automatic grouping scheme

The standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of data values (Bland and Altman 1996). In this study, a role of the standard deviation is to make uniform force density values so that the value of fitness function can be minimized. We aim to solve the minimisation problem with a genetic algorithm, this logic ensures that the standard deviation of force densities for cables converges to minimum value as much as possible. By using these uniform values, the proposed method leads regular geometries of tensegrity structures to be formed. As a result of this algorithm, a feasible set of force densities with a suitable grouping is easily obtained.

Figure 2 shows comparison of two systems which have a non-uniform and uniform force density sets, respectively. The structures possessing the non-uniform force density sets lead to irregular geometries. However, with the iterative processes of the genetic algorithms, the force densities of the elements are uniformly distributed by using the proposed fitness function.

Fig. 2
figure 2

A role of the standard deviation is to make uniform the force density values. The proposed method leads regular geometries of tensegrity structures to be formed; A two-dimensional two-strut tensegrity structure

Full size image

4 Numerical example

The tensegrity structures with one state of self-stress, a two-dimensional hexagonal tensegrity structure, a three-dimensional three-strut octahedral cell and a three-dimensional six-strut tensegrity are illustrated to demonstrate the capability of the proposed method. Based on the algorithm developed, both the nodal coordinates and the single integral feasible force density vector are simultaneously defined with limited information of the nodal connectivity and the type of each member. We have fixed a maximum of 100 iterations using a population size of 200. The algorithms of all numerical examples were terminated when the terminating conditions were reached prior to the maximum iterations. Note that all of the force densities given in tables are normalized with respect to the force density coefficient of Element 1. The main parameters of the proposed genetic algorithm is set as:

  • Population size : 200

  • Maximum generations : 100

  • Child : One child per pair of parents

  • Bounds of variables : [-1, 0] for struts / [0, 1] for cables

  • Inner loop : 20

4.1 2D four-strut tensegrity

In this and next sections, two tensegrity structures with one state of self-stress (s = 1) are demonstrated to verify the accuracy of the proposed method. The 2-dimensional four-strut tensegrity has been selected from (Tran and Lee 2010). This structure is composed of four cables and four struts (Fig. 3). In prior studies, all members have been grouped into two sets, including one group of cable members and the other group of strut members. The proposed method does not use a grouping constraint and the feasible sets of the force densities with automatic grouping can be easily determined. The calculated force density value after normalizing with respect to the force density coefficient of the Element 1 is as presented in Table 1. These results agree well with those of prior studies. The calculated force density value after normalizing with respect to the force density coefficient of the Element 1 is as presented in Table 1. These results agree well with those of previous study. Since the fitness function of the proposed method tends to make uniform the force density values of cables, the algorithm works effectively in these examples which group members into two sets. After investigating the rank deficiency of the force density matrix, the 2-dimensional four-strut tensegrity is formed to have one self-stress state (s = 1) and no infinitesimal mechanism (m = 0) (Pellegrino 1993).

Fig. 3
figure 3

The initial topology of the 2D four-strut tensegrity structure

Full size image
Table 1 Comparison of the force densities obtained by the proposed method with other paper(2D four-strut tensegrity)
Full size table

4.2 3D expandable octahedron

The three-dimensional expandable octahedron has been selected from (Guest 2011); and this system consists of 24 cables and six struts (Fig. 4). The obtained three-dimensional expandable octahedron possesses one state of self-stress (s = 1) and one infinitesimal mechanism (m = 1). Table 2 shows a force density set of the elements. The result in Table 2 indicates that the same results as those of previous study can be yielded. We must note that the results were obtained without a grouping condition.

Fig. 4
figure 4

The initial topology of the 3D expandable octahedron

Full size image
Table 2 Comparison of the force densities obtained by the proposed method with other paper(3D expandable octahedron)
Full size table

4.3 2D hexagonal tensegrity structures

We consider two 2D hexagonal tensegrity structures which are composed of 9 elements and 11 elements, respectively, this examples have been selected from (Tran and Lee 2010) and (Tran and Lee 2011). Figure 5a and b show the initial topologies of the 2D hexagonal tensegrity structure with six cables and eight cables, and cables (struts) are depicted by thin (thick) lines. The distinction between the number of cables of two structures, leads to different self-stress states. The 2D hexagonal tensegrity structure with six cables has one self-stress state (s = 1), whereas the 2D hexagonal tensegrity structure with eight cables has s = 2.

Fig. 5
figure 5

The initial topologies of the 2D hexagonal tensegrity structure with; a six cables (s = 1), and b eight cables (s = 2)

Full size image

While six cables case automatically obtained the results with two groups (The force densities for cable and strut equal 1.0 and −0.5, respectively.), such as those of previous study, the case of eight cables obtained the new force density values, as presented in Table 3. Table 3 shows a comparison of the results of previous study (Tran and Lee 2011) with grouping and the results of the proposed method with automatic grouping. The previous method requires appropriate grouping in order to obtain a single feasible pre-stressed mode. The authors repeated the analysis eight times to obtain the appropriate group of the two-dimensional three-strut tensegrity structure. Accordingly, trial and error should be employed to find the appropriate five groups. Contrastingly, the proposed method required only one analysis to yield the feasible set of force densities. The results of the proposed method show the same group classification with those of previous studies without any grouping constraint. In spite of enough iteration steps in the genetic algorithm processes, the reason why the proposed method is actually more dfficient is that EVD and SVD analyses are the most computationally intensive unlike the genetic algorithm.

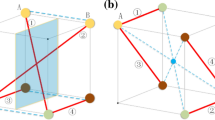
Table 3 Comparison of the force densities obtained by the proposed method with other paper (the 2D hexagonal tensegrity structure with eight cables)
Full size table

Figure 6 shows the obtained geometry of previous study and present study. In the previous study, in order to obtain a single integral feasible prestressed mode, a linear relation between member 2 and 3 is imposed as q 3 = 1.5q 2. As a consequence of the linear relation, this process obtained one geometry as indicated in Fig. 6a. However, in this study, a different result can be obtained without grouping conditions or linear relationships as shown in Fig. 6b.

Fig. 6
figure 6

The obtained geometry of the 2D hexagonal tensegrity structure; a Tran and Lee (2011), and b Present study

Full size image

4.4 3D three-strut octahedral cell

As the next example, a three-dimensional three-strut octahedral cell that has three struts and 12 cables as shown in Fig. 7 is considered. The input parameters for this example are n = 6, b = 15, and d = 3. After investigating the rank deficiency of the force density matrix, the tensegrity is formed to have three self-stress states (s = 3) and no infinitesimal mechanism (m = 0).

Fig. 7
figure 7

The initial topology of the 3D three-struct octahedral cell

Full size image

In Table 4, comparison of the results of previous study (Tran and Lee 2011) with grouping and the results of the proposed method with automatic grouping is presented. In the prior study, based on the symmetry properties, the members were divided into four groups. The proposed method, however, does not require any symmetry properties of the structure or grouping constraint. Applying the proposed form-finding method, the range of feasible sets of the nodal coordinates and the force densities is obtained, divided into two groups. A difference in the number of grouping is caused by fitness functions of the genetic algorithms. Thus, the appropriate minimum groups for tensegrity structures that satisfy the rank deficiency conditions of force density and equilibrium matrices can be easily obtained through the proposed algorithm. The geometries of three case are obtained as shown in Fig. 8. This shows that the geometry result of present study with two groups is formed into regular shape as compared with the previous studies.

Table 4 Comparison of the force densities obtained by the proposed method with other paper(3D three-strut octahedral cell)
Full size table
Fig. 8
figure 8

The obtained geometry of the 3D three-strut octahedral cell; a Previous study (Tran and Lee 2011) with grouping, b Present study with automatic grouping

Full size image

4.5 3D six-strut tensegrity

A 3-dimensional six-strut tensegrity has six struts and 24 cables, and the initial topology is composed of 12 nodes and 30 elements Fig. 9. After investigating rank deficiency, the structure obtained two states of self-stress (s = 2), and two infinitesimal mechanisms (m = 2).

Fig. 9
figure 9

The initial topology of the 3D six-strut tensegrity

Full size image

In Table 5, a comparison of the results of previous studies (Tran and Lee 2011) with grouping and the results of the proposed method with automatic grouping is presented. In previous studies, four groups were chosen through trial and error. Applying the proposed form-finding method, the seven groups obtained differ from those of the previous study. The results are appropriately grouped by using the proposed algorithm, however, it is not minimum groups for this system. To obtain the minimum number of grouping, a specific force density ratio constraint of Element 1 and Element 2 (q 1 = q 2) is additionally imposed to the fitness function. As a result, the results obtained again agree fairly with those of the previous study and the minimum number of groups (four groups) can be achieved. This indicates that a suitable minimum number of groups is easily obtained using the proposed method. For the purpose of obtaining fewer number of groupings, with a new constraint condition where all force densities of cables are set as unified is provided for the algorithm, equilibrium configurations cannot be obtained. Eventually, this means that four groups are the optimum number of groupings.

Table 5 Comparison of the force densities obtained by the proposed method with other paper(3D six-strut tensegrity)
Full size table

5 Conclusion

In this study, an automatic grouping method for the form-finding of tensegrity is presented to find the self-equilibrium and the stability properties of the structures. For tensegrities with multiple self-stress states (s > 1), all the members must be manually grouped in accordance with the geometrical symmetry in order to have the unique feasible solution in most previous investigation. However, present study automatically generates the member group of the tensegrity by simply providing the unilateral conditions of the members. The standard deviation of the force densities in the cables is used to uniquely define a single integral feasible set of force densities. The fitness function using the standard deviation can be significant in creating uniform force density values. Five examples of tensegrity structures are performed, and a very good performance of the proposed method has been shown in the numerical examples. In all the numerical examples, minimum number of member groups are easily obtained automatically with only unilateral condition except for 3D six-strut tensegrity case. In 3D six-strut tensegrity case, the specific force density ratio constraint was used additionally to obtain the minimum number of member groups. Form-finding with minimum number of member groups was achieved in the present study that is, the regular shapes of the tensegrity was obtained.