1 Introduction

In recent years, as a hot issue of many fields, blind source separation (BSS) techniques have been applied to speech signal processing [1], biomedical engineering [2], array signal processing [3], mechanical fault diagnosis [4], image processing [5], and so on. BSS can be classified into normal blind source separation (NBSS), overdetermined blind source separation (OBSS) and under-determined blind source separation (UBSS) based on the number of sources and sensors. In NBSS, the number of sources is equal to that of sensors. In OBSS, there are more sensors than sources. In UBSS, there are less sensors than sources. Independent component analysis (ICA) [6, 7] is a main method to handle BSS problems. The ICA algorithms solving the OBSS problems and those solving the UBSS problems are called overdetermined ICA and under-determined ICA, respectively. ICA is always applied to solve OBSS problems and NBSS problems [8–13] that include image processing, biomedical application and speech recognition. ICA is also applied to UBSS problems [14–16]. However, ICA is usually unsatisfactory for solving UBSS problems, so the research on UBSS receives more attention. As the most representative method of UBSS, sparse component analysis (SCA) [17, 18] can yield better separation results than traditional ICA. The SCA method includes two steps: mixing matrix estimation and sources recovery. The mixing matrix estimation is the basis of sources recovery. In other words, the estimation precision of the mixing matrix has an important effect on sources recovery. Therefore, the mixing matrix estimation gets particularly important. In SCA methods, the performance is up to the sparsity of signals. A signal is sparse if only a small number of samples have valid values and other samples are nearly zero. However, many signals are not sparse in real life. We must make transformations such as short-time Fourier transform (STFT) [19, 20] and wavelet transform (WT) [21] to make signals sparser. This paper focuses on complex mixing matrix estimation of UBSS problems by utilizing the sparse time-frequency (TF) representations that are obtained by STFT.

Many methods have been proposed to estimate the mixing matrix. In these algorithms, the algorithms based on single source points where only one source occurs can improve the accuracy of estimating the mixing matrix and then receive more attention. Some scholars [22–26] detected single source points with various methods and then estimated the mixing matrix by utilizing single source points. Xu [27] extended the algorithm of single source points to images and estimated the mixing matrix faster and more accurately. The above methods based on single source points can obtain good performance for estimating the mixing matrix, and they are all applicable to UBSS. However, these methods aim at real mixing matrix estimation. In other words, they are invalid for estimating the complex mixing matrix. If the mixing model of BSS is the instantaneous mixing model, the mixing matrix is real. However, if the mixing model is the anechoic mixing model, the mixing matrix is complex. The instantaneous mixing model is sometimes restrictive, and the anechoic mixing model is closer to the actual application. Some algorithms consider the complex mixing matrix estimation. The algorithm in Li et al. [28] estimated the complex mixing matrix with more sources than sensors. It utilized the probability density distribution of single source points and the K-means clustering algorithm. In [29], the mixing matrix was estimated based on single source points and agglomerative hierarchical clustering. These two algorithms proposed the similar and specific model about single source points. In this paper, we propose a more general model to transform complex mixing matrix estimation to real mixing matrix estimation. As a result, all detection algorithms of single source points for real matrix estimation can be applied. What is more, we combine the single source points detection with the potential function clustering algorithm to improve the algorithm performance.

The rest of this paper is organized as follows. In Sect. 2, we introduce the basic model of our method. Our algorithm is derived in Sect. 3. Section 4 describes the simulation results and analysis, and conclusions are drawn in Sect. 5.

2 The basic model

In the algorithms described in Li et al. [28] and Zhang et al. [29], the mixing matrix is estimated when the antenna array is the uniform linear array. In order to present our algorithm better and compare with other algorithms more intuitively, we take the uniform linear array as the research priority.

This paper assumes that sources come from the far-field of the array. Assume there are M sources \(\mathbf{{s}}(t) = {[{s_1}(t),{s_2}(t),\ldots ,{s_M}(t)]^\mathrm{T}}\) and N mixed signals \(\mathbf{{x}}(t) = {[{x_1}(t),{x_2}(t),\ldots ,{x_N}(t)]^\mathrm{T}}\). \({s_i}(t)(i = 1,\ldots ,\) M) denotes the ith source signal at the time instant t. \({x_i}(t)(i = 1,\ldots ,N)\) denotes the ith mixed signal at the time instant t. M is larger than N. The linear mixing model of UBSS can be described as

$$\begin{aligned} \mathbf{{x}}(t) = \mathbf{{Hs}}(t) \end{aligned}$$
(1)

where the mixing matrix \(\mathbf{{H}}\) can also be written as

$$\begin{aligned} \mathbf{{H}} = \left[ {\begin{array}{*{20}{c}} {{h_{11}}}&{}{{h_{12}}}&{} \cdots &{}{{h_{1M}}}\\ {{h_{21}}}&{}{{h_{22}}}&{} \cdots &{}{{h_{2M}}}\\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ {{h_{N1}}}&{}{{h_{N2}}}&{} \cdots &{}{{h_{NM}}} \end{array}} \right] \end{aligned}$$
(2)

The distance between two sensors is d, and the angle between the mth source and the normal is \({\theta _m}( -\pi /2<{\theta _m} < \pi /2)\). The schematic of the uniform linear array is shown in Fig. 1.

Fig. 1
figure 1

Schematic of the uniform linear array

Full size image

If the first sensor is chosen as the reference, the delay from the nth sensor to the first sensor for the mth source can be denoted as

$$\begin{aligned} \varDelta {\tau _m} = \frac{{2\pi (n-1)d\sin {\theta _m}}}{{\lambda w}} \end{aligned}$$
(3)

where \(\lambda \) is the signal wavelength and w is the signal frequency. If the complex expression of the mth source is denoted as \({s_m}(t) = {a_m}(t){e^{j[wt + \varphi (t)]}}\), the mth source received by the nth sensor can be written as

$$\begin{aligned}&{x_{nm}}(t) = {H_{nm}}{s_m}(t + \varDelta {\tau _m})\nonumber \\&\quad ={H_{nm}}{a_m}(t + \varDelta {\tau _m}){e^{j[wt + w\varDelta {\tau _m} + \varphi (t + \varDelta {\tau _m})]}} \end{aligned}$$
(4)

where \({H_{nm}}\) is called amplitude dis-accommodation factor. If we assume that the modulation components \({a_m}(t)\) and \(\varphi (t)\) are narrow-band signals and take no account of the effect of the amplitude fading, the above formula can be simplified as

$$\begin{aligned}&{x_{nm}}(t) \approx {a_m}(t){e^{j[wt + w\varDelta {\tau _m} + \varphi (t)]}}\nonumber \\&\quad ={a_m}(t){e^{j[wt + \varphi (t)]}} \cdot {e^{jw\varDelta {\tau _m}}}\nonumber \\&\quad ={s_m}(t) \cdot {e^{jw\varDelta {\tau _m}}}\nonumber \\&\quad ={s_m}(t) \cdot {e^{j\frac{{2\pi d}}{\lambda }(n - 1)\sin {\theta _m}}}\nonumber \\&\quad ={h_{nm}}{s_m}(t) \end{aligned}$$
(5)

Based on the above formula, the mixed signal that includes M sources in the nth sensor can be denoted as

$$\begin{aligned} {x_n}(t) = \sum \limits _{m = 1}^M {{x_{nm}}(t)} = \sum \limits _{m = 1}^M {{h_{nm}}{s_m}(t)} \end{aligned}$$
(6)

It can also be written with the matrix form

$$\begin{aligned}&\left[ \begin{array}{*{20}{c}} {{x_1}(t)}\\ {{x_2}(t)}\\ \vdots \\ {{x_N}(t)} \end{array} \right] \nonumber \\&\quad =\left[ {\begin{array}{*{20}{c}} 1&{}\quad \cdots &{}\quad 1\\ {{e^{j\frac{{2\pi d}}{\lambda }\sin {\theta _1}}}}&{}\quad \cdots &{}\quad {{e^{j\frac{{2\pi d}}{\lambda }\sin {\theta _M}}}}\\ \vdots &{}\quad \cdots &{}\quad \vdots \\ {{e^{j\frac{{2\pi d}}{\lambda }(N - 1)\sin {\theta _1}}}}&{}\quad \cdots &{}\quad {{e^{j\frac{{2\pi d}}{\lambda }(N - 1)\sin {\theta _M}}}} \end{array}} \right] \, \left[ \begin{array}{*{20}{c}} {{s_1}(t)}\\ {{s_2}(t)}\\ \vdots \\ {{s_M}(t)} \end{array} \right] \nonumber \\ \end{aligned}$$
(7)

For the uniform linear array, the corresponding mixing matrix is

$$\begin{aligned} \mathbf{{H}} = \left[ {\begin{array}{*{20}{c}} 1&{}\quad \cdots &{}\quad 1\\ {{e^{j\frac{{2 \pi d}}{\lambda }\sin {\theta _1}}}}&{}\quad \cdots &{}\quad {{e^{j\frac{{2\pi d}}{\lambda }\sin {\theta _M}}}}\\ \vdots &{}\quad \cdots &{}\quad \vdots \\ {{e^{j\frac{{2\pi d}}{\lambda }(N - 1)\sin {\theta _1}}}}&{} \cdots &{}{{e^{j\frac{{2\pi d}}{\lambda }(N - 1)\sin {\theta _M}}}} \end{array}} \right] \end{aligned}$$
(8)

In order to guarantee that there is no ambiguity in DOA estimation, the assumption \(d \le \lambda /2\) is usually satisfied. Meanwhile, the angle measurement error gets lower when d gets larger. Therefore, d is usually equal to \(\lambda /2\). Besides, the articles [28, 29] assume d as \(\lambda /2\). In order to compare our algorithm with other algorithms, d is set to \(\lambda /2\) in this paper. Equation (8) can be simplified as

$$\begin{aligned} \mathbf{{H}} = \left[ {\begin{array}{*{20}{c}} 1&{} \cdots &{}1\\ {{e^{j\pi \sin {\theta _1}}}}&{}\quad \cdots &{}\quad {{e^{j\pi \sin {\theta _M}}}}\\ \vdots &{}\quad \cdots &{}\quad \vdots \\ {{e^{j\pi (N - 1)\sin {\theta _1}}}}&{}\quad \cdots &{}\quad {{e^{j\pi (N - 1)\sin {\theta _M}}}} \end{array}} \right] \end{aligned}$$
(9)

3 The proposed algorithm

In order to make signals sparser, STFT is adopted. The STFT of the nth mixed signal is as follows

$$\begin{aligned} X_n'(t,f) = \int _{ - \infty }^\infty {{x_n}(\tau )h(t - \tau ){e^{ - j2\pi f\tau }}{\text {d}}\tau } \end{aligned}$$
(10)

where \(h(\;)\) denotes the window function. Similarly, the STFT of the mth source signal is denoted as

$$\begin{aligned} {S_m}(t,f) = \int _{ - \infty }^\infty {{s_m}(\tau )h(t - \tau ){e^{ - j2\pi f\tau }}{\text {d}}\tau } \end{aligned}$$
(11)

Applying STFT on Eq. (1), we can obtain the following formula

$$\begin{aligned} {\mathbf{{X}}'}(t,f) = \mathbf{{HS}}(t,f) \end{aligned}$$
(12)

where \({\mathbf{{X}}'}(t,f) = {[X_1'(t,f),X_2'(t,f),\ldots ,X_N'(t,f)]^\mathrm{T}}\) and \(\mathbf{{S}}(t,f) = {[{S_1}(t,f), {S_2}(t,f),\ldots ,{S_M}(t,f)]^\mathrm{T}}\) refer to the STFT coefficients of mixtures and sources, respectively.

Two assumptions need to be satisfied like other UBSS algorithms. On one hand, any \(N \times N\) sub-matrix of the mixing matrix should be of full rank. Even if we only estimate the mixing matrix, the condition that any two columns of the mixing matrix are uncorrelated is also needed. On the other hand, some TF points where only one source occurs must exist.

We consider two mixed signals that include the mixed signal \({x_1}(t)\) received by the first sensor and the mixed signal \({x_n}(t)\) received by the nth sensor. Combining Eq. (7), we can obtain

$$\begin{aligned} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {X_1'(t,f)}\\ {X_n'(t,f)} \end{array}} \right] \\ \quad = \left[ {\begin{array}{*{20}{c}} 1&{}\quad \cdots &{}\quad 1\\ {{e^{j\pi (n - 1)\sin {\theta _1}}}}&{}\quad \cdots &{}\quad {{e^{j\pi (n - 1)\sin {\theta _M}}}}\\ \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{S_1}(t,f)}\\ {{S_2}(t,f)}\\ \vdots \\ {{S_M}(t,f)} \end{array}} \right] \end{array} \end{aligned}$$
(13)

If \({\psi _m} = \pi (n - 1)\sin {\theta _m}(m = 1,2,\ldots ,M)\) is assumed, Eq. (13) can be simplified as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {X_1'(t,f)}\\ {X_n'(t,f)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{}\quad \cdots &{}\quad 1\\ {{e^{j{\psi _1}}}}&{}\quad \cdots &{}\quad {{e^{j{\psi _M}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{S_1}(t,f)}\\ {{S_2}(t,f)}\\ \vdots \\ {{S_M}(t,f)} \end{array}} \right] \end{aligned}$$
(14)

Because the above mixing matrix is complex, most algorithms based on single source points are not applicable. In other words, the algorithms cannot present the linear clustering feature. Therefore, the goal of this paper is getting the linear clustering feature through transformation and then estimating the mixing matrix.

A matrix \(\mathbf{{T}}\) is denoted as

$$\begin{aligned} \mathbf{{T}} = \left[ {\begin{array}{*{20}{c}} {{e^{jb}}}&{}1\\ 1&{}{{e^{jb}}} \end{array}} \right] \end{aligned}$$
(15)

where b is an angle. Utilizing Eqs. (14) and (15), we obtain the following formula

$$\begin{aligned} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{X_1}(t,f)}\\ {{X_n}(t,f)} \end{array}} \right] = \mathbf{{T}}\left[ {\begin{array}{*{20}{c}} {X_1'(t,f)}\\ {X_n'(t,f)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e^{jb}} + {e^{j{\psi _1}}}} &{} \cdots &{}{{e^{jb}} + {e^{j{\psi _M}}}}\\ {1 + {e^{j(b + {\psi _1})}}} &{} \cdots &{}{1 + {e^{j(b + {\psi _M})}}}\\ \end{array}} \right] \\ \times {\left[ {\begin{array}{*{20}{c}} {{S_1}(t,f)}&{} \cdots &{}{{S_M}(t,f)} \end{array}} \right] ^\mathrm{T}} \end{array}\nonumber \\ \end{aligned}$$
(16)

After this procedure, the new STFT coefficients of mixtures \(\mathbf{{X}}(t,f) = [X_1(t,f),X_2(t,f),\ldots ,X_N(t,f)]\) are obtained. When only one source \({s_1}\) occurs at some TF point \(\left( {{t_p},{f_p}} \right) \), Eq. (16) can be denoted as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{X_1}({t_p},{f_p})}\\ {{X_n}({t_p},{f_p})} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e^{jb}} + {e^{j{\psi _1}}}}\\ {1 + {e^{j(b + {\psi _1})}}} \end{array}} \right] {S_1}({t_p},{f_p}) \end{aligned}$$
(17)

From the above formula, we can get

$$\begin{aligned}&\frac{{{X_n}({t_p},{f_p})}}{{{X_1}({t_p},{f_p})}} = \frac{{[1 + {e^{j(b + {\psi _1})}}]{S_1}({t_p},{f_p})}}{{({e^{jb}} + {e^{j{\psi _1}}}){S_1}({t_p},{f_p})}} = \frac{{[1 + {e^{j(b + {\psi _1})}}]}}{{({e^{jb}} + {e^{j{\psi _1}}})}}\nonumber \\&\quad = \frac{{[1 + {e^{j(b + {\psi _1})}}]{e^{ - j(b + {\psi _1})/2}}}}{{({e^{jb}} + {e^{j{\psi _1}}}){e^{ - j(b + {\psi _1})/2}}}}\nonumber \\&\quad = \frac{{{e^{j(b + {\psi _1})/2}} + {e^{ - j(b + {\psi _1})/2}}}}{{{e^{j(b - {\psi _1})/2}} + {e^{ - j(b - {\psi _1})/2}}}}\nonumber \\&\quad = \frac{{[{e^{j(b + {\psi _1})/2}} + {e^{ - j(b + {\psi _1})/2}}]/2}}{{[{e^{j(b - {\psi _1})/2}} + {e^{ - j(b - {\psi _1})/2}}]/2}} = \frac{{\cos \frac{{b + {\psi _1}}}{2}}}{{\cos \frac{{b - {\psi _1}}}{2}}} \end{aligned}$$
(18)

Because the above ratio is real, two equations can be obtained based on Eq. (18)

$$\begin{aligned} \begin{array}{l} {\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_p},{f_p})] = \left\{ {\begin{array}{*{20}{c}} {{\mathop {\mathrm{Re}}\nolimits } [{X_1}({t_p},{f_p})]}\\ {{\mathop {\mathrm{Re}}\nolimits } [{X_n}({t_p},{f_p})]} \end{array}} \right\} \\ \quad =\left[ {\begin{array}{*{20}{c}} {{\mathop {\mathrm{Re}}\nolimits } [{X_1}({t_p},{f_p})]}\\ {\left( \cos \frac{{b + {\psi _1}}}{2}/\cos \frac{{b - {\psi _1}}}{2}\right) {\mathop {\mathrm{Re}}\nolimits } [{X_1}({t_p},{f_p})]} \end{array}} \right] \end{array} \end{aligned}$$
(19)
$$\begin{aligned} \begin{array}{l} {\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_p},{f_p})] = \left\{ {\begin{array}{*{20}{c}} {{\mathop {\mathrm{Im}}\nolimits } [{X_1}({t_p},{f_p})]}\\ {{\mathop {\mathrm{Im}}\nolimits } [{X_n}({t_p},{f_p})]} \end{array}} \right\} \\ \quad =\left[ {\begin{array}{*{20}{c}} {{\mathop {\mathrm{Im}}\nolimits } [{X_1}({t_p},{f_p})]}\\ {\left( \cos \frac{{b + {\psi _1}}}{2}/\cos \frac{{b - {\psi _1}}}{2}\right) {\mathop {\mathrm{Im}}\nolimits } [{X_1}({t_p},{f_p})]} \end{array}} \right] \end{array} \end{aligned}$$
(20)

Utilizing the above two equations and forcing the sign of the first element of the two vectors to be positive, we can get

$$\begin{aligned} \frac{{{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_p},{f_p})]}}{{\left\| {{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_p},{f_p})]} \right\| }} = \frac{{{\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_p},{f_p})]}}{{\left\| {{\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_p},{f_p})]} \right\| }} \end{aligned}$$
(21)

Consider some TF point \(({t_q},{f_q})\) where two sources \({s_1}\) and \({s_2}\) occur. If we want to realize

$$\begin{aligned} \frac{{{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]}}{{\left\| {{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]} \right\| }} = \frac{{{\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]}}{{\left\| {{\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]} \right\| }} \end{aligned}$$
(22)

the following conditions must be satisfied

$$\begin{aligned}&\frac{{{\mathop {\mathrm{Re}}\nolimits } [{S_1}({t_q},{f_q})]}}{{{\mathop {\mathrm{Im}}\nolimits } [{S_1}({t_q},{f_q})]}} = \frac{{{\mathop {\mathrm{Re}}\nolimits } [{S_2}({t_q},{f_q})]}}{{{\mathop {\mathrm{Im}}\nolimits } [{S_2}({t_q},{f_q})]}} \end{aligned}$$
(23)
$$\begin{aligned}&{\mathop {\mathrm{sgn}}} \{ {\mathop {\mathrm{Re}}\nolimits } [{S_1}({t_q},{f_q})]\} = {\mathop {\mathrm{sgn}}} \{ {\mathop {\mathrm{Im}}\nolimits } [{S_1}({t_q},{f_q})]\} \end{aligned}$$
(24)
$$\begin{aligned}&{\mathop {\mathrm{sgn}}} \{ {\mathop {\mathrm{Re}}\nolimits } [{S_2}({t_q},{f_q})]\} = {\mathop {\mathrm{sgn}}} \{ {\mathop {\mathrm{Im}}\nolimits } [{S_2}({t_q},{f_q})]\} \end{aligned}$$
(25)

These conditions are so strict that the probability of Eq. (22) is very low. Meanwhile, when three or more sources occur at some TF point, the probability of similar equations will get lower. For identifying single source points, the authors in [26] develop a rule as

$$\begin{aligned} \left| {\frac{{{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]}}{{\left\| {{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]} \right\| }} - \frac{{{\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]}}{{\left\| {{\mathop {\mathrm{Im}}\nolimits } [\mathbf{{X}}({t_q},{f_q})]} \right\| }}} \right| < \varepsilon _1 \end{aligned}$$
(26)

where \({\varepsilon _1}\) is a threshold value that is close to 0. After single source points detection, the points that are close to the origin still have bad effect on estimation. In order to improve performance, these points should be removed if they satisfy the following formula

$$\begin{aligned} \left\| {{\mathop {\mathrm{Re}}\nolimits } [\mathbf{{X}}(t,f)]} \right\| < {\varepsilon _2} \end{aligned}$$
(27)

where \({\varepsilon _2}\) is a threshold value. After above procedures, we use the residual points to estimate the mixing matrix. In this paper, we adapt a potential function clustering algorithm. The number and the set of the residual single source points are set to T and B, respectively. We first normalize the data in the set B and then define the potential function as

$$\begin{aligned} J({\mathbf{{b}}_k}) = \sum \limits _{j = 1}^{T} {{{\left[ {\exp \left( {\beta {{\cos }^2}(\widehat{{\mathbf{{b}}_k},{\mathbf{{b}}_j}})} \right) } \right] }^\gamma }} \end{aligned}$$
(28)

where \({\mathbf{{b}}_k}\) and \({\mathbf{{b}}_j}\) are the elements of the set B, \(\widehat{{\mathbf{{b}}_k},{\mathbf{{b}}_j}}\) denotes the included angle of \({\mathbf{{b}}_k}\) and \({\mathbf{{b}}_j}\), \(\beta \) and \(\gamma \) are the parameters that adjust the attenuation of the objective function at the non-maximum points. \({\mathbf{{b}}_k}\) can be denoted as \(({b_{k1}},{b_{k2}})\), so we can calculate the potential function values of different \({\mathbf{{b}}_k}\) and get the three-dimensional scatter plot of \(J({\mathbf{{b}}_k})\). In the figure, there are some peaks occurring and the number of the peaks is equal to that of sources. The amplitude of each point is \(P(k)(k = 1,\ldots ,T)\). Because of the effect of noises, there will be some false peaks. In order to remove these false peaks, the normalization is first adopted as follows

$$\begin{aligned} \hat{P}(k) = P(k)/\max [P(k)] \end{aligned}$$
(29)

where \(\max [\;]\) denotes the maximum and \(\hat{P}(k)\) is the normalization amplitude. Then, the smooth function is utilized and defined as

$$\begin{aligned} {p_k}= & {} [\hat{P}(k - 2) + 2 * \hat{P}(k - 1) \nonumber \\&+\,4 * \hat{P}(k) + 2 * \hat{P}(k + 1) + \hat{P}(k + 2)]/10 \end{aligned}$$
(30)

where \({{p_k}}\) is the new amplitude. In order to get the locations of the peaks accurately, the following rules are set

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{p_{k - 1}}< {p_k}{\;\;{\mathrm{and }}\;\;}{p_{k + 1}}< {p_k}}\\ {{p_{k - 2}}< {p_k}{\;\;{\mathrm{and }}\;\;}{p_{k + 2}} < {p_k}} \end{array}} \right. \end{aligned}$$
(31)

Based on the above rules, corresponding peak locations help us find the corresponding \({\mathbf{{b}}_k}\) that are considered to be clustering centers. After these procedures, we get M clustering centers \(\left( {{Y_m},{Z_m}} \right) (1 \le m \le M)\). Combining with Eq. (18), we obtain the following formula

$$\begin{aligned} \frac{{{Y_m}}}{{{Z_m}}} = \frac{{\cos \frac{{b + {\psi _m}}}{2}}}{{\cos \frac{{b - {\psi _m}}}{2}}} \end{aligned}$$
(32)

According to the above equation, we need to exchange positions of the numerator and the denominator if \(\cos [(b - {\psi _m})/2]\) is equal to 0. In order to calculate simply, we set b as \(\pi /2\). Then, Eq. (32) can be simplified as

$$\begin{aligned} \frac{{{Y_m}}}{{{Z_m}}} = \tan \left( \frac{\pi }{4} - \frac{{{\psi _m}}}{2}\right) \end{aligned}$$
(33)

Based on the above description, \({\psi _m} = \pi (n - 1)\sin {\theta _m}(1 < n \le N)\) and \( - \pi /2< {\theta _m} < \pi /2\) are known. For a uniform linear array, the least number of sensors is 2. Meanwhile, only utilizing two sensors can help us estimate the mixing matrix. Therefore , we can only set n as 2 and obtain

$$\begin{aligned} {\psi _m} = \pi \sin {\theta _m} \end{aligned}$$
(34)

According to Eqs. (32) and (33), we can know

$$\begin{aligned} - \frac{\pi }{4}< \frac{\pi }{4} - \frac{{{\psi _m}}}{2} < \frac{{3\pi }}{4} \end{aligned}$$
(35)

Through the calculation, \({\psi _m}\) is denoted as

$$\begin{aligned} {\psi _m} = \left\{ {\begin{array}{*{20}{c}} {\frac{\pi }{2} - 2\arctan \left( \frac{{{Y_m}}}{{{Z_m}}}\right) {\quad \;\;{\mathrm{if}}\;\; }\frac{{{Y_m}}}{{{Z_m}}} > - 1}\\ { - \frac{{3\pi }}{2} - 2\arctan \left( \frac{{{Y_m}}}{{{Z_m}}}\right) \,\, {\mathrm{if}}\;\; \frac{{{Y_m}}}{{{Z_m}}} < - 1} \end{array}} \right. \end{aligned}$$
(36)

Based on Eq. (34) and the range of \({\theta _m}\), \({\theta _m}\) is calculated as

$$\begin{aligned} {\theta _m} = \arcsin ({\psi _m}/\pi ) \end{aligned}$$
(37)

After getting all \({\theta _m}\), we can get the final mixing matrix.

In this paper and some other papers, there is permutation ambiguity in the algorithms of estimating the mixing matrix. However, sources recovery is not affected by this permutation ambiguity.

The steps of our algorithm are as follows:

  • Step 1 Transform the problem of complex mixing matrix estimation to the problem of real mixing matrix estimation.

  • Step 2 Detect single source points and remove the points that are close to the origin.

  • Step 3 Get the clustering centers through the potential function clustering algorithm.

  • Step 4 Calculate the corresponding angles and then get the mixing matrix.

4 Simulation results and analysis

In the simulation, four females speech sources are chosen from the Web page of SiSEC2011. The angles of sources and the normal are \( - \pi /12\), \( - \pi /36\), \(5\pi /36\) and \(\pi /18\). The number of sampling points is 80,000. The STFT size is 1024. The overlapping is 256. The Hanning window is chosen as the weighting function. The signals are received by a uniform linear array whose sensors interval is the half of the wavelength. The number of the sensors is 2, so the mixing matrix \(\mathbf{{H}}\) can be written as

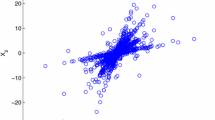
$$\begin{aligned} \mathbf{{H}} = {\left[ {\begin{array}{*{20}{c}} 1&{}{{e^{j\pi \sin ( - \pi /12)}}}\\ 1&{}{{e^{j\pi \sin ( - \pi /36)}}}\\ 1&{}{{e^{j\pi \sin (5\pi /36)}}}\\ 1&{}{{e^{j\pi \sin ( \pi /18)}}} \end{array}} \right] ^\mathrm{T}} \end{aligned}$$

In noiseless case, the scatter plot based on the above equations is shown in Fig. 2.

Fig. 2
figure 2

Scatter plot before detecting single source points

Full size image

It is shown that the points present obvious clustering property, but some multiple source points affect this property. Direct clustering will lead to bad performance because of the influence of multiple source points. The measure of detecting single source points aims at eliminating the multiple source points and getting better performance. Meanwhile, eliminating the points that are close to the origin has good effect on improving the performance. Figure 3 is the scatter plot after detecting single source points and eliminating the points that are close to the origin.

Fig. 3
figure 3

Scatter plot after detecting single source points and eliminating the points that are close to the origin

Full size image

It is shown from Fig. 3 that the points that affect the performance have been removed. In order to lay the foundation for the clustering process, we make the normalizing procedure and force the sign of the first element of the normalized point to be positive for the points in Figs. 2 and 3. After these procedures, the scatter plot comparison before detecting single source points and after detecting single source points is shown in Figs. 4 and 5.

Fig. 4
figure 4

Scatter plot through the normalizing procedure and the sign procedure before detecting single source points

Full size image
Fig. 5
figure 5

Scatter plot through the normalizing procedure and the sign procedure after detecting single source points

Full size image

From Figs. 4 and 5, It is easy to find the superiority of detecting single source points and eliminating the points that are close to the origin. After above procedures, necessary clustering is needed. A potential function clustering algorithm is utilized to process these points in this paper. Figure 6 is the three-dimensional plot of \(J({\mathbf{{b}}_k})\).

Fig. 6
figure 6

Three-dimensional plot of \(J({\mathbf{{b}}_k})\)

Full size image

As shown in Fig. 6, several peaks occur and the number of the peaks is equal to that of sources. The locations of the peaks correspond to the clustering centers. Finally, through this clustering algorithm, the final complex mixing matrix can be estimated as

$$\begin{aligned} {\tilde{\mathbf{H}}} = {\left[ {\begin{array}{*{20}{c}} 1&{}{0.6946 - 0.7194{{i}}}\\ 1&{}{0.9637 - 0.2671{{i}}}\\ 1&{}{0.2431 + 0.9700{{i}}}\\ 1&{}{0.8542 + 0.5200{{i}}} \end{array}} \right] ^\mathrm{T}} \end{aligned}$$

The original mixing matrix is as follows

$$\begin{aligned} \mathbf{{H}} = {\left[ {\begin{array}{*{20}{c}} 1&{}{0.6872 - 0.7264{{i}}}\\ 1&{}{0.9627 - 0.2704{{i}}}\\ 1&{}{0.2407 + 0.9706{{i}}}\\ 1&{}{0.8549 + 0.5189{{i}}} \end{array}} \right] ^\mathrm{T}} \end{aligned}$$

Comparing \({\tilde{\mathbf{H}}}\) with \(\mathbf{{H}}\), we can know that the proposed algorithm is effective and accurate in the noiseless situation.

To demonstrate that this algorithm is also suitable for other sources and other mixing matrix, three speech utterances are selected referring to Reju et al. [24]. The angles of sources and the normal are \( - \pi /18\),\(\pi /9\) and \(\pi /36\). The other conditions remain unchanged. The original mixing matrix and the estimated mixing matrix are as follows.

$$\begin{aligned} \mathbf{{H}}= & {} {\left[ {\begin{array}{*{20}{c}} 1&{}{0.8549 - 0.5189{{i}}}\\ 1&{}{0.4762 - 0.8793{{i}}}\\ 1&{}{0.9627 + 0.2704{{i}}} \end{array}} \right] ^\mathrm{T}}\\ {\tilde{\mathbf{H}}}= & {} {\left[ {\begin{array}{*{20}{c}} 1&{}{0.8570 - 0.5154{{i}}}\\ 1&{}{0.4732 - 0.8809{{i}}}\\ 1&{}{0.9625 + 0.2714{{i}}} \end{array}} \right] ^\mathrm{T}} \end{aligned}$$

According to \(\mathbf{{H}}\) and \({\tilde{\mathbf{H}}}\), we can know that the algorithm is also effective for other sources.

In the noisy situation, an index must be chosen in order to measure the performance of the proposed algorithm and other algorithms. Mean square error (MSE) is suitable for these purposes. It is described as

$$\begin{aligned} {\mathrm{MSE}} = \frac{1}{M}\sum \limits _{m = 1}^M {{{\left( {\theta _m} - {{\tilde{\theta }}_m}\right) }^2}} \end{aligned}$$
(38)

where \({\tilde{\theta }_m}\) is the estimated value of \({\theta _m}\).

Gaussian white noise is used to demonstrate the robustness of the proposed algorithm and the comparison algorithms that include Li’s algorithm in [28] and Zhang’s algorithm in [29]. In this paper, \({\varepsilon _1}\) is 0.02 and \({\varepsilon _2}\) is 0.1. All parameters of the comparison algorithms are selected based on the references. The average results of 100 Monte Carlo trials about three algorithms are shown in Fig. 7.

Fig. 7
figure 7

Performance comparison of the proposed algorithm with other algorithms

Full size image

From Fig. 7, we can know that our algorithm has better performance than the comparison algorithms.

5 Conclusions

In this paper, a new algorithm is proposed to estimate the complex mixing matrix in the UBSS problem. The algorithms based on single source points can get good performance in the estimation of the real mixing matrix. However, the detection method of single source points cannot be directly applied to the estimation of the complex mixing matrix. In this paper, we first transform complex mixing matrix estimation to real mixing matrix estimation through modeling and calculating. Following that, a detection algorithm of single source points is adopted to get the single source points and remove the points that are close to the origin. Then, we propose a potential function clustering process in order to get better clustering results. Finally, the complex mixing matrix is obtained through derivation and calculation. The simulation experiments show efficiency and practicability of the proposed algorithm. Meanwhile, they show that our algorithm owns higher accuracy than other algorithms. The paper is about the estimation problem of the complex mixing matrix. The problem belongs to the anechoic mixing model of BSS. The research of this mixing model is meaningful and promising.