Fast and incoherent dictionary learning algorithms with application to fMRI

Abstract

In this paper, the problem of dictionary learning and its analogy to source separation is addressed. First, we extend the well-known method of K-SVD to incoherent K-SVD, to enforce the algorithm to achieve an incoherent dictionary. Second, a fast dictionary learning algorithm based on steepest descent method is proposed. The main advantage of this method is high speed since both coefficients and dictionary elements are updated simultaneously rather than column-by-column. Finally, we apply the proposed methods to both synthetic and real functional magnetic resonance imaging data for the detection of activated regions in the brain. The results of our experiments confirm the effectiveness of the proposed ideas. In addition, we compare the quality of results and empirically prove the superiority of the proposed dictionary learning methods over the conventional algorithms.

1 Introduction

In dictionary learning (DL) framework, the aim is to find a dictionary that can sparsely represent a signal or image subject to availability of a set of training data. This problem is traditionally modeled by $\mathbf{y}_i=\mathbf{D}\mathbf x _i+{\varvec{\epsilon }}_i$, where $\mathbf{y}_i$ is the $i$-th training vector, $\mathbf{x}_i$ is the $i$-th sparse coefficient vector, and $\mathbf{D}$ is the so-called dictionary. Furthermore, ${\varvec{\epsilon }}_i$ represents the decomposition error. A dictionary is normally defined as an overcomplete matrix (less rows than columns) in which the columns (also called atoms) describe the features of the given training signals/images. In signal processing, the term sparse refers to signals with small number of nonzero samples. Numerous applications are benefited using this framework some of which are compression [1], denoising [2], and inpainting [3].

Majority of dictionary learning techniques are inspired by the well-known sparse recovery problem and the recently emerged field of compressed sensing [4, 5]. One of the well-established dictionary learning methods is called K-SVD [2] which is an extension of K-means clustering and works based on singular value decomposition (SVD). Method of optimal directions (MOD) [6] is another method which finds the dictionary using the pseudo-inverse of the training matrix. There also have been reported maximum a porteriori estimation (MAP)-based [7] and maximum likelihood (ML)-based methods [8]. A dictionary learning method using LARS sparse coding, coined “online dictionary learning”, has been proposed in [9]. This method is based on stochastic approximations designed for large datasets.

In general, it is of particular importance to learn a dictionary that can sparsely represent the given (normally huge) data within a reasonable time. More importantly, the dictionary atoms are required to be incoherent meaning to be nearly orthogonal. This property guarantees that the dictionary is designed efficiently and encompasses maximum possible information of the training signals. There are several existing works in the literature imposing incoherence into the dictionary atoms. Ramirez et al. [10] define a universal DL model based on MAP estimation. They add a low mutual coherence constraint in addition to the column normalization constraint to the dictionary columns. In [11], the authors attempt to exploit both mutual and cumulative coherence and the Gram matrix norm to improve the efficiency and performance of sparse coding algorithms. In another work [12], a constraint is used to find a structured dictionary promoting reduced correlation among the atoms. A clustering approach based on sparse modeling and dictionary learning is proposed in [13]. The authors use an incoherence penalty encouraging dictionaries associated with different classes to be as independent as possible. This procedure allows them to use their method both in the supervised and unsupervised settings. Very recently [14, 15], a decorrelation strategy is proposed which iteratively computes a dictionary close to a given one. This procedure leads to a dictionary with incoherent atoms.

Viewing from a different angle, the problem of matrix decomposition has been also studied in another well-known framework called blind source separation (BSS). In BSS, given mixtures of several sources, e.g., speech signals ($\mathbf{y}_i$’s), the aim is to estimate the mixing matrix ($\mathbf{D}$) and sources ($\mathbf{x}_i$’s), subject to some a priori such as independency, sparsity, or non-negativity of the sources. BSS has various applications in speech processing, communications, and biomedical signal and image processing [16, 17]. One of the most popular methods in BSS framework is independent component analysis (ICA) [16] which takes advantage of statistical independency between the components as a criterion for decomposition. A recent paper [18] has addressed the equivalence between dictionary learning and blind source separation to design fast and efficient probabilistic ICA-based dictionary learning method for inpainting and denoising of natural images. Nevertheless, many recent researches attempt to exploit sparsity for BSS problems [17, 19], revealing encouraging results. Therefore, it would be reasonable and beneficial to explore the performance of DL-based methods, which mainly exploit sparsity, for BSS problems. As an example, we consider in this paper the problem of active-region detection in functional magnetic resonance imaging (fMRI). While ICA has been widely studied and applied in this regard, recent preliminary results have revealed the advantages of exploiting sparsity for this application [20, 21]. In fact, it was shown that most hemodynamic effects in the brain are hardly independent due to complicated structure and strong neural connectivity in the brain. In contrast, biological findings of sparse coding in the brain support the effectiveness of sparsity compared to independency. This claim can be validated by looking at the Olshausen et al. work [8] showing that a set of receptive fields learned by maximizing sparseness in the output of a neural network model is spatially localized, oriented, and selective to spatial structure at a specific scale, similar to cortical simple cells. In another relevant work, a data-driven sparse general linear model (GLM) framework based on a maximum likelihood (ML) estimation is proposed [22, 23]. The authors incorporate a dictionary learning method (K-SVD [2]) to find the design matrices (see [23] for more details) as a subset of atoms of the learned dictionary.

In this paper, we first extend the standard K-SVD dictionary learning to incoherent K-SVD (coined as IK-SVD) by imposing incoherence of the atoms into the dictionary learning procedure. Our proposed method here differs from the method in [14, 15] as we use a simple gradient descent technique for decreasing the coherence. As our second contribution in this paper, we propose a computationally inexpensive algorithm for learning overcomplete dictionaries. We use a steepest descent strategy for updating both the coefficient matrix and the dictionary. The proposed method is fast and does not require any prior knowledge about the level of sparsity. Finally, due to the existing analogy between dictionary learning and source separation, we aim to validate the proposed approaches for BSS problems with sparsity constraint. Hence, we choose fMRI application to detect active brain regions, known as Blood Oxygenation Level Dependent (BOLD), admitting sparse events [20, 21]. Our experimental results and comparisons with relevant methods for both real and synthetic signals confirm the effectiveness of the proposed methods for the purpose of BOLD detection.

The rest of the paper is organized as follows. In the next section, we first describe the K-SVD followed by the proposed incoherent K-SVD algorithm. Then, a fast dictionary learning algorithm using steepest descent technique is proposed. In Sect. 3, the similarities between the two frameworks, i.e., DL and BSS, are described. Section 4 is devoted to analyzing the experimental results, and Sect. 5 concludes the paper.

2 Dictionary learning problem

To mathematically express a generic DL problem, assume that the signal $\mathbf{y}\in \mathbb R ^{n}$ can be represented as a linear combination of a few atoms $\{\mathbf{d}_i\}_{i=1}^K$ in dictionary $\mathbf{D}\in \mathbb R ^{n\times K}$ such that $\mathbf{y}=\mathbf Dx$. We normally consider overcomplete dictionaries in which $n<K$. Assume that we are going to learn a dictionary from $N$ training signals. By slightly changing the notations, vectors $\mathbf{y}$ and $\mathbf{x}$ are replaced with matrices $\mathbf{Y}=\{\mathbf{y}_i\}_{i=1}^N$ of size $n\times N$ and $\mathbf{X}=\{\mathbf{x}_i\}_{i=1}^N$ of size $K\times N$, respectively. Therefore, the DL problem can be expressed as:

$$\begin{aligned} \min _{\mathbf{D},\mathbf X }\left\Vert\mathbf{Y}-\mathbf DX \right\Vert^2_F \ \ \mathrm{s.t.} \ \ \ \ \ \left\Vert\mathbf{x}_{i}\right\Vert_0\le \tau \ \ \ \forall \, i\in [1\ldots N]. \end{aligned}$$

(1)

Here and throughout the paper, $\mathbf{x}_i$ denotes the $i$-th column of $\mathbf{X}$, $\mathbf{x}^i$ indicates the $i$-th row, and $x_{ij}$ refers to the $ij$-th element of it. Furthermore, $\left\Vert.\right\Vert_F^2$ is the Frobenius norm equivalent to $\mathrm Tr (\mathbf{X}^T\mathbf X )$, where $\mathrm Tr (.)$ denotes the matrix trace and $(.)^T$ is matrix transpose symbol. The term $\left\Vert.\right\Vert_0$ is $\ell _0$-norm which counts the number of nonzeros and indicates the level of sparsity. $\tau$ is the maximum allowed number of nonzeros of $\mathbf{x}_i$ and should satisfy $\tau <<K$. Most of the DL techniques tackle (1) by alternately estimating one of the variables while keeping the other one fixed. This is called “alternating minimization” which is extensively discussed in the following subsections.

2.1 Incoherent K-SVD

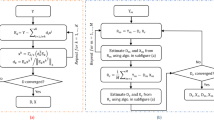
High incoherence between the dictionary atoms is desired in almost all dictionary learning methods. This guarantees that the atoms are as discriminative as possible. As a leading dictionary learning method, we adopt K-SVD method. This method by itself lacks the incoherence flavor, and hence, we propose a remedy for that. We first briefly describe the original K-SVD method and then propose the incoherent K-SVD method.

Updating process for $\mathbf{X}$ (while keeping $\mathbf{D}$ fixed) is known as sparse coding due to sparsity constraint on $\mathbf{X}$. Sparse coding can be cast as applying one of the common sparse recovery algorithms such as orthogonal matching pursuit (OMP) [24], basis pursuit (BP) [25], or FOCUSS [26] to all $\{\mathbf{y}_i\}_{i=1}^N$, independently, and recovering $\{\mathbf{x}_i\}_{i=1}^N$. Here, we assume that $\tau$ is known and apply OMP to solve¹:

$$\begin{aligned} \min _{\mathbf{x}_i}\left\Vert\mathbf{y}_i-\mathbf{Dx}_i\right\Vert_2 \ \ \mathrm{s.t.} \ \ \ \ \ \Vert \mathbf{x}_{i}\Vert _0\le \tau . \end{aligned}$$

(2)

The second step is updating $\mathbf{D}$. In K-SVD, both sparse coefficients and dictionary columns are updated at the same time. The dictionary update step is carried out column-by-column for $\{\mathbf{d}_i\}_{i=1}^K$. By expanding the Frobenius norm in (1), we reach to:

$$\begin{aligned} \left\Vert\mathbf{Y}-\mathbf D \mathbf{X}\right\Vert^2_F&= \left\Vert\left(\mathbf{Y}-\sum _{j\ne k}\mathbf{d}_j\mathbf x ^j\right)-\mathbf{d}_k\mathbf x ^k\right\Vert^2_F \nonumber \\&= \left\Vert\mathbf{E}_k-\mathbf{d}_k\mathbf x ^k\right\Vert_F^2. \end{aligned}$$

(3)

where $\mathbf{E}_k$ is the error incurred by all columns of $\mathbf{D}$ and all rows of $\mathbf{X}$ except $\mathbf{d}_k$ and $\mathbf{x}^k$. In order to minimize (3), Aharon and Elad [2] apply SVD to $\mathbf{E}_k$ and simultaneously update $\mathbf{d}_k$ and $\mathbf{x}^k$ using the strongest eigenvector and eigenvalue of $\mathbf{E}_k$. This process should be applied after removing the dictionary atoms corresponding to zero coefficients in $\mathbf{X}$ (full details can be found in [2]). This alternating update of dictionary and sparse coefficients are repeated until reaching to a local minimum.

Standard K-SVD method does not include any constraint to achieve incoherent atoms, and thus, we modify it with the aim of adding incoherence. A suitable tool for evaluating the coherence between the atoms is Gram matrix which is defined as $\mathbf{G}=\mathbf D ^T\mathbf{D}$. Matrix $\mathbf{G}$ is $K\times K$ and symmetric with unit diagonal elements (note that $\mathbf{D}$ is column-normalized). The absolute values of off-diagonal elements of $\mathbf{G}$ represent the degree of coherence between any pair of atoms in $\mathbf{D}$ and therefore are desired to be very small. In order to decrease the coherence among the updated atoms in original K-SVD algorithm, we shall design a method to enforce the off-diagonals of $\mathbf{G}$ to zero. Next, we define a cost function toward this goal and then suggest to apply a simple steepest descent method to minimize it. We call this new algorithm IK-SVD, standing for incoherent K-SVD, and can be described as follows. Assume that $\mathbf{D}$ is the updated dictionary at one iteration of original K-SVD. In order to decrease the coherence between the columns of $\mathbf{D}$, the following minimization problem is proposed²:

$$\begin{aligned} \widehat{\mathbf{D}}= \arg \min _{\mathbf{D}}\parallel \mathbf{D}^T \mathbf{D}-\mathbf I \parallel ^2_F. \end{aligned}$$

(4)

Here, $\mathbf{I}$ is the identity matrix of size $K\times K$. In order to minimize the above problem, we first take the gradient of $\mathcal F =\parallel \mathbf{D}^T \mathbf{D}-\mathbf I \parallel ^2_F$ which is computed as:

$$\begin{aligned} \nabla _{\mathbf{D}}\mathcal F = 4\mathbf{D}\left(\mathbf{D}^T\mathbf D -\mathbf{I}\right). \end{aligned}$$

(5)

Then, inserting (5) into $\mathbf{D}\leftarrow \mathbf{D}-\xi \nabla _{\mathbf{D}} \mathcal F$ results in:

$$\begin{aligned} \mathbf{D}_{(k+1)} = \mathbf{D}_{(k)} - \gamma \mathbf{D}_{(k)}(\mathbf{D}_{(k)}^{T} \mathbf{D}_{(k)}-\mathbf{I}), \end{aligned}$$

(6)

where $\gamma =4\xi >0$ is the step size controlling the convergence behavior of the algorithm, and $k$ is the iteration counter of the incoherence constraint stage. The above update should be executed for several times after each update of $\mathbf{D}$ in the standard K-SVD algorithm. We consider a fixed number of iterations as the stopping criterion of this step. Moreover, we chose a variable step size with respect to the number of iterations, $k$, based on $\gamma _k=\gamma _0\frac{1-\alpha }{1-\alpha ^k}$ for $\gamma _0=0.1$. A smaller $\alpha$ causes faster changes of $\gamma _k$ and vice versa. We have found $\alpha =0.1$ an appropriate choice in our experiments. Furthermore, as the iterations proceed (increasing $k$), the value of $\gamma _k$ decreases.

After updating all dictionary columns in the original K-SVD, the above update rule is applied to optimize the dictionary. The columns of $\mathbf{D}$ are also normalized to one, after implementing (6). The pseudo-code of the proposed method is given in Algorithm 1.

Regarding the convergence of both K-SVD and IK-SVD, we shall state that it highly depends on the performance of the sparse coding step, as mentioned in [2]. In fact, both algorithms are suboptimal and may get stuck in local minima. However, since the dictionary update step reduces (3), it is always observed that a successful sparse coding (using OMP, here) leads the algorithms to converge. Successful sparse coding means correct recovery of all nonzero coefficients. We empirically observed that IK-SVD converges to local minima when $\gamma$ is chosen appropriately. The above described variable $\gamma$ has shown to be an appropriate strategy based on our experiments. Furthermore, we select a fixed number of iterations as stopping criterion for both loops in Algorithm 1.

2.2 Fast incoherent dictionary learning (FIDL)

Although K-SVD is shown to be a leading DL method, it is computationally expensive for learning large dictionaries, that is, because of involving SVD, which is a complex operation, and also the column-by-column operation for updating $\mathbf{D}$, which is time consuming in large-scale scenarios. Additionally, our extended IK-SVD method, proposed in previous section, incurs more complexity to the original K-SVD which makes it inappropriate for large-scale problems. In what follows, we propose a fast incoherent dictionary learning algorithm, called FIDL. As its name implies, it is designed to be fast and at the same time exploits the incoherence of atoms. In order to do this, the following cost function is defined:

$$\begin{aligned} \mathcal J (\mathbf{D},\mathbf X )=\overbrace{\left\Vert \mathbf{Y}-\mathbf D \mathbf{X}\right\Vert^2_F+\mu \Vert \mathbf{D}^T\mathbf D -\mathbf{I}\Vert ^2_F}^\mathcal{P (\mathbf{D},\mathbf X )} +\overbrace{\lambda \Vert \mathbf{X}\Vert _1}^\mathcal{Q (\mathbf{X})}. \end{aligned}$$

(7)

which has to be minimized (we will talk about $\mathcal P$ and $\mathcal Q$ later). Note the differences between the problem (7) and (1). Firstly, we use $\ell _1$-norm of the entire matrix $\mathbf{X}$ defined as $\left\Vert\mathbf{X}\right\Vert_1=\sum _i\sum _j|x_{ij}|$, instead of forcing individual vectors $\{\mathbf{x}_i\}$ to be sparse. This allows us to update the coefficients, simultaneously rather than column-by-column. Moreover, the sparsity bounds of all $\{\mathbf{x}_i\}_{i=1}^N$ are not necessarily the same. Secondly, replacing $\ell _0$-norm of $\mathbf{X}$ with $\ell _1$-norm makes the problem convex in $\mathbf{X}$. Finally, the incoherence constraint on $\mathbf{D}$ is also added to the cost function, where the regularization parameters $\mu$ and $\lambda$ control the trade-off between decomposition error and effects of penalty terms. It is noteworthy to mention that problem (7) has been previously studied in [28] with non-negativity constraint and also in [29] without incoherence constraint. However, we do not impose the non-negativity constraint here and propose a Gradient descent-based approach (different from [29]) which alternately updates $\mathbf{X}$ and $\mathbf{D}$ to minimize (7).

2.2.1 Coefficient update (sparse coding)

If we assume $\mathbf{D}$ to be fixed, then, problem (7) will be convex with respect to (w.r.t.) $\mathbf{X}$. We aim at using gradient descent method as a fast approach for solving it. However, problem (7) is non-smooth w.r.t. $\mathbf{X}$, and hence, standard steepest descent cannot be directly applied. To resolve this issue, we use a proximal step called fowardbackward (FB) splitting algorithm [30, 31]. Consider the cost function (7), split into the sum of a smooth and a nonsmooth sub-cost function, represented by $\mathcal P$ and $\mathcal Q$, respectively. We define two following steps:

• Gradient descent step:

  $$\begin{aligned} \tilde{\mathbf{X}}_{(k)}\!=\!\mathbf{X}_{(k)}\!-\!\beta \nabla _{\mathbf{X}} \mathcal P (\mathbf{X}_{(k)})\!=\!\mathbf{X}_{(k)}\!-\!2\beta \mathbf{D}^T\left(\mathbf{D}\mathbf X _{(k)}\!-\!\mathbf{Y}\right)\!, \nonumber \\ \end{aligned}$$

  (8)

  where scalar $\beta >0$ is the step size, and $k$ indicates the $k$-th iteration.

• Proximal step:

  $$\begin{aligned} \mathbf{X}_{(k+1)}&= Prox_\beta \mathcal Q (\tilde{\mathbf{X}}_{(k)}):=\min _{\mathbf{X}_{(k)}}\mathcal Q (\mathbf{X}_{(k)})\nonumber \\&+\frac{1}{2\beta }\left\Vert \mathbf{X}_{(k)}-\tilde{\mathbf{X}}_{(k)}\right\Vert_F^2. \end{aligned}$$

  (9)

The proximal function here is defined using soft-thresholding ($Shrink\{.\}$) due to $\ell _1$-norm in (7), which ultimately leads to:

$$\begin{aligned} \mathbf{X}_{(k+1)}&= Prox_\beta \mathcal Q (\tilde{\mathbf{X}}_{(k)}) = Shrink\{\tilde{\mathbf{X}}_{(k)},\beta \lambda \}\nonumber \\&= \max \left\{ 0,1-\frac{\beta \lambda }{|\tilde{x}_{{ij}_{(k)}}|}\right\} \tilde{\mathbf{X}}_{(k)}. \end{aligned}$$

(10)

where $|\tilde{x}_{{ij}_{(k)}}|$ denotes absolute value of each element of $\tilde{\mathbf{X}}_{(k)}$. Updating $\mathbf{X}$, using (8) and (10), should be alternately executed with dictionary update stage, which will be described shortly. It is important to note that the step size should satisfy $\beta <2/\Vert \mathbf{D}^T\mathbf D \Vert _2$, as the stability condition of the algorithm. We found out based on our experiments that choosing $\beta \simeq 1/\Vert \mathbf{D}^T\mathbf D \Vert _2$ leads the algorithm to perform well.

2.2.2 Dictionary update

Now we aim at updating the dictionary elements while keeping $\mathbf{X}$ fixed. In contrast to the previous section, the gradient descent approach can be directly applied here. That is due to the fact that (7) is convex and smooth w.r.t. $\mathbf{D}$. Taking the gradient of (7), w.r.t. $\mathbf{D}$, leads to:

$$\begin{aligned} \nabla _{\mathbf{D}}\mathcal J (\mathbf{D},\mathbf X )=2 (\mathbf{DX}-\mathbf Y )\mathbf{X}^T+4\mu \mathbf{D} (\mathbf D ^T\mathbf{D}-\mathbf I ). \end{aligned}$$

(11)

The update rule for $\mathbf{D}$ can then be obtained as:

$$\begin{aligned} \mathbf{D}\leftarrow \mathbf{D}-2\eta (\mathbf{DXX}^T-\mathbf{YX}^T+2\mu \mathbf{D} (\mathbf D ^T\mathbf{D}-\mathbf I )). \end{aligned}$$

(12)

Scalar $\eta$ is the step size which should satisfy $0<\eta <2/\Vert \mathbf{X}\mathbf X ^T\Vert _2$ to guarantee the convergence. Hence, we choose $\eta =1/\Vert \mathbf{X}\mathbf X ^T\Vert _2$ which has empirically shown to lead to stable results. In addition, a column normalization is applied to all columns of $\mathbf{D}$, after executing (12), to preserve the column norms of the dictionary. Although direct column normalization is applied in several dictionary learning algorithms [6, 8], it may increase the mean square error (MSE). This issue does not significantly affect the performance and is negligible. However, it can be further investigated by adding a column-norm-constraint penalty term to the cost function which we leave it for future work. The pseudo-code of the proposed algorithm is shown in Algorithm 2.

Regarding the convergence of the proposed method, we shall state that here we minimize the cost function first with respect to $\mathbf{D}$ and then to $\mathbf{X}$ which includes a FB-splitting step. Dictionary update step follows a gradient descent which is guaranteed to reduce the cost function in overall, but not necessarily to a global minimum. Here, the functions with respect to $\mathbf{X}$ are convex and non-smooth, and thus, the convergence behavior follows the results of [32, Lemma 3.1 and Theorem 4.1(b)], as also seen in related works such as [9, 33]. In fact, under the assumptions stated in [9], convergence to a stationary point is guaranteed. Algorithm 2 illustrates a pseudo-code of the proposed FIDL method.

2.2.3 Selection of regularization parameters

While we consider a fixed $\mu$, the sparsity regularization parameter, i.e., $\lambda$, should be selected with care. Manual selection of a fixed $\lambda$ is not an optimal choice as it is independent of the actual sparsity level of $\mathbf{S}$ which is assumed to be unknown. Instead, a variable (decreasing) $\lambda$ has shown to yield better results in several previous works [33, 34]. Here, we consider a more advanced strategy and that is adaptively varying $\lambda$ while minimizing (7). To estimate an appropriate $\lambda$, at every iteration of Algorithm 2, the following gradient descent method [35, 36] is adopted:

$$\begin{aligned} \lambda _{(l+1)} = \lambda _{(l)} - \rho \frac{\partial \mathcal J (\mathbf{X}_{(l+1)}, \mathbf{D}_{(l+1)})}{\partial \lambda _{(l)}}, \end{aligned}$$

(13)

where $\rho$ is a small constant chosen manually. Index $l$ refers to the iteration counter for the outer loop in Algorithm 2. For clarity, we note that $\mathbf{X}_{(l+1)}$ and $\mathbf{D}_{(l+1)}$ indicate, respectively, the values of $\mathbf{X}$ and $\mathbf{D}$ at $(l+1)$-th iteration, and after full execution of both inner loops in Algorithm 2. The same rules apply for $\mathbf{X}_{(l)}$ and $\mathbf{D}_{(l)}$ as well. In order to determine the differentiation in (13), we first modify (7) by replacing (10) into it and obtain:

$$\begin{aligned}&\frac{\partial \mathcal J (\mathbf{X}_{(l+1)},\mathbf{D}_{(l+1)})}{\partial \lambda _{(l)}}\nonumber \\&\quad =\frac{\partial }{\partial \lambda _{(l)}}\left[ \left\Vert\mathbf{Y}-\mathbf D _{(l+1)}\left(\tilde{\mathbf{X}}_{(l)}-\beta _{(l)} \lambda _{(l)}\mathrm sgn (\tilde{\mathbf{X}}_{(l)})\right)\right\Vert_F^2\right.\nonumber \\&\qquad \left. + \lambda _{(l)}\left\Vert\tilde{\mathbf{X}}_{(l)}-\beta _{(l)}\lambda _{(l)} \mathrm sgn (\tilde{\mathbf{X}}_{(l)})\right\Vert_1\right]. \end{aligned}$$

(14)

Note that since the learning rule for $\mathbf{D}_{(l+1)}$, i.e., (12), does not depend on $\lambda$ we did not expand $\mathbf{D}_{(l+1)}$ in (14) to keep the notations simple. For the same reason, the term $\mu \Vert \mathbf{D}^T\mathbf D -\mathbf{I}\Vert ^2_F$ does not appear in (14) as its derivative w.r.t. $\lambda$ is zero. In addition, we considered the fact that $\max \{0,1-\frac{\beta _{(l)}\lambda _{(l)}}{|\tilde{x}_{{ij}_{(l)}}|}\} \tilde{\mathbf{X}}_{(l)}=\tilde{\mathbf{X}}_{(l)}-\beta _{(l)} \lambda _{(l)}\mathrm sgn (\tilde{\mathbf{X}}_{(l)})$, in deriving (14), where $\mathrm sgn (.)$ is the element-wise signum function. Then, by dropping all subscripts $(l)$ (for notational simplicity), and after appropriate manipulations, we reach to:

$$\begin{aligned}&\!\!\!\!\frac{\partial \mathcal J (\mathbf{X}_{(l+1)},\mathbf{D}_{(l+1)})}{\partial \lambda _{(l)}}\nonumber \\&\!=2\beta \mathrm Tr \left(\mathrm sgn (\tilde{\mathbf{X}})^T\mathbf{D}^T \left(\mathbf{Y}-\mathbf D \tilde{\mathbf{X}}\right)\right)\\\nonumber&\!\!\quad +2\beta ^2\lambda \mathrm Tr \left(\mathrm sgn (\tilde{\mathbf{X}})^T \mathbf{D}^T\mathbf D \mathrm sgn (\tilde{\mathbf{X}})\right)\\ \nonumber&\!\!\quad +\sum _i\sum _j \mathrm sgn \left(\tilde{x}_{ij}-\beta \lambda \mathrm sgn (\tilde{x}_{ij})\right)\cdot \left(\tilde{x}_{ij}-2\beta \lambda \mathrm sgn (\tilde{x}_{ij})\right). \end{aligned}$$

(15)

The above equation should then be plugged into (13), giving the update rule for $\lambda$, which should be executed within Algorithm 2. In general, $\lambda$ is initialized with a large value, e.g., $\lambda _{(0)}\in [0.5\;\;0.9]$, which then adaptively varies as the iterations proceed.

3 Analogy to blind source separation

The analogy of DL to BSS has already been pointed out in few researches [18, 37]. However, we believe that there are still rooms to study and recognize those DL methods which can be successfully utilized in source separation applications. This analogy is quite straightforward; in instantaneous blind source separation, we are given $n$ observations $\{\mathbf{y}^i\}_{i=1}^n$ which are linear mixtures of $K$ unknown sources $\{\mathbf{x}^i\}_{i=1}^K$. The desire is to decompose $\mathbf{Y}$ into $\mathbf{D}$ and $\mathbf{X}$ with smallest error and possibly subject to some constraints on $\mathbf{D}$ or $\mathbf{X}$. If the sources are assumed to be sparse in time/pixel domain, then the source separation problem can be described similarly as the aforementioned dictionary learning problems. Particularly, the incoherence penalty would be effective for applications where orthogonality (or at least near-orthogonality) of the mixing matrix is crucial [38, 39], such as in MIMO communications [40]. Therefore, the techniques which solve (1) or minimize (7) can be used for source separation, as well. However, if the sources are assumed to be sparse in a different domain, then techniques such as morphological component analysis (MCA) [33, 34] can be used. In the result section, we apply the proposed methods to synthetic and real auditory fMRI data and show that they can successfully detect the BOLD regions in the brain.

Beside the similarities between the two frameworks, there are some differences in the interpretations of $\mathbf{Y}$, $\mathbf{D}$, and $\mathbf{X}$ which are listed in Table 1. We also note that in dictionary learning framework, $\mathbf{D}$ is normally considered as a complete ($n=K$) or an overcomplete ($n<K$) matrix, while in blind source separation, the case of $n>K$ is also considered. This, however, does not affect the above problem formulations, and the DL methods are still valid even for ($n>K$).

Table 1 Differences in terminology between DL and BSS

4 Results

Extensive experiments have been conducted to examine the performance of the proposed methods in both synthetic and real scenarios.

4.1 Simulated data

4.1.1 Experiment 1

In the first experiment, we generated a set of artificial mixtures based on the under-determined model $\mathbf{Y}=\mathbf D \mathbf{X}$, with ($n<K$). The nonzero entries of the 20$\,\times \,$1,000 sparse matrix $\mathbf{X}$ were generated randomly (from Gaussian distribution). $\mathbf{D}$ was selected as a random overcomplete full-rank matrix of size $15\times 20$ with all columns normalized to one. We applied the proposed IK-SVD and FIDL algorithms to estimate $\mathbf{D}$ and $\mathbf{X}$. The parameters of IK-SVD were $\gamma _0=0.1$, $\alpha =0.1$, $k_{max}=20$, and $50$ iterations as stopping criterion. For FIDL, we selected $k_{max}=20$, $\rho =10^{-7}$, $\mu =0.1$, $\lambda _{(0)}=0.5$, and $\epsilon =0.001$. This experiment was repeated for 1,000 random ensembles of $\mathbf{D}$ and $\mathbf{X}$ while varying sparsity level of $\mathbf{X}$. We varied the number of nonzeros of each column of $\mathbf{X}$ from $1$ to $10$. For comparison purposes, three other algorithms, namely original K-SVD,³ INK-SVD,⁴ and Ramirez’s method⁵ were also involved in this experiment. We used $50$ number of iterations for these methods. Quantitative results are given in Fig. 1. The average correlation between the recovered sources and the original ones (i.e. $\{\mathbf{x}^i\}_{i=1}^K$) is shown in Fig. 1a. The same measure for dictionary columns (i.e. $\{\mathbf{d}_i\}_{i=1}^K$) is depicted in Fig. 1b. Note that these results are obtained after multiplying the recovered matrices with a proper scaling and permutation matrix. According to Fig. 1, FIDL has the best performance among all other methods. IK-SVD shows weaker behavior than FIDL and yet better than INK-SVD and Ramirez’s method. Moreover, based on Fig. 1, the average correlation of recovered sources and dictionary atoms using IK-SVD, at $6$ number of nonzeroes, are $0.9566$ and $0.9783$, respectively. However, we observed that if a fixed $\gamma =0.1$ is used, these values are $0.8921$ and $0.9003$ respectively. This is an indication of improvement when variable $\gamma$ is used.

Fig. 1

Recovery performance: average correlation of recovered a sources and b dictionary atoms versus the number of nonzeros

4.1.2 Experiment 2

In the next experiment, we learned an overcomplete dictionary of size $64\times 256$ over 14,000 noisy image patches of size $8\times 8$ extracted from Barbara image. The variations in SNR of the denoised images (using the same procedure as in [2]), based on dictionaries with different coherence levels, are shown in Fig. 2. The mutual coherence in this figure is calculated using $\mu =\max _{i\ne j} \left|g_{ij}\right|$, where $g_{ij}$ stands for entries of the Gram matrix. As seen from Fig. 2, K-SVD gives the best SNR at $\mu =0.94$, however, INK-SVD, IK-SVD, and FIDL show maximum SNRs at $\mu =0.88$, $\mu =0.81$, and $\mu =0.74$, respectively. This indicates that FIDL can find a suitable dictionary at a smaller coherence level.

Fig. 2

Signal to noise ratio at different coherence levels. The dashed line shows minimum possible mutual coherence calculated via $\sqrt{(K-n)/{n(K-1)}}$

4.1.3 Experiment 3

In the next experiment, the aim was to investigate the robustness of the proposed methods against variations in the input noise. We considered noisy model $\mathbf{Y}=\mathbf D \mathbf{X}+\mathbf V$, where $\mathbf{V}$ was Gaussian noise with zero mean. All matrices were drawn randomly (from Gaussian distribution) with $n=15$, $K=20$, and $N$ = 1,000. The number of nonzeros at each column of $\mathbf{X}$ was set to five. For IK-SVD, we chose $\gamma _0=0.1$, $\alpha =0.1$, $k_{max}=20$, and $50$ iterations. For FIDL, we selected $k_{max}=20$, $\rho =10^{-7}$, $\mu =0.1$, $\lambda _{(0)}=0.5$, and $\epsilon =0.001$. K-SVD, INK-SVD, and Ramirez’s method were run for $50$ iterations. After applying different methods, the SNR of $\widehat{\mathbf{X}}$ (estimated matrix after considering scaling and permutation) was calculated using $20\log _{10}\Vert \mathbf{X}\Vert _F/\Vert \mathbf{X}-\widehat{\mathbf{X}}\Vert _F$. The same evaluation was carried out for the estimated dictionary. The average SNRs over 1,000 trials at different input noise levels are shown in Fig. 3. As seen from Fig. 3, FIDL outperforms other methods for all noise levels. Also, the performance of IK-SVD is comparable with that of INK-SVD in Fig. 3a, whereas it outperforms INK-SVD in Fig. 3b.

Fig. 3

Average SNR of a the estimated source matrix and b dictionary, against changes in input noise level

Table 2 The overall execution time (in seconds) for different methods at different dictionary dimensions

4.1.4 Experiment 4

In another experiment, we set up a simulation for evaluating the computational cost of the proposed methods and comparing these methods with other well-known algorithms. The parameters for the algorithms were similar to the first experiment. However, we increased the dictionary size from $5\times 10$ to 500 $\times$ 1,000 for a fixed level of sparsity $\tau =2$. The following algorithms were applied: original K-SVD, IK-SVD, FIDL, INK-SVD, and Ramirez’s method. A laptop computer with a Core i7 $2.7$ GHz and $6$ GB of RAM was used for this experiment. The overall computation time for all algorithms for total $50$ iterations was recorded. Table 2 shows these values in second. It is seen from the table that FIDL algorithm performs significantly faster than other methods. This indicates that FIDL can be a suitable approach for large-scale problems.

4.2 Synthetic fMRI data

In this experiment, we investigate the performance of the proposed methods in separating the sources from a set of artificially generated fMRI mixtures. The synthetic data for this experiment were taken from MLSP-Lab [41] which have been created using the basic knowledge of the statistical characteristics of the underlying sources involving in the activation procedure in the brain. The simulations started by forming $\mathbf{X}$ of size 5$\,\times \,$3,600 using five vectorized source images of size $60\times 60$ (Fig. 4a). Then, the mixtures were generated by multiplying column-normalized $\mathbf{D}$ of size $100\times 5$ (Fig. 5a) by $\mathbf{X}$. We applied FastICA [42] (with Gauss nonlinearity), IK-SVD, FIDL, and the relevant K-SVD-based method proposed in [23] to separate the sources and the corresponding mixing matrix. For IK-SVD, we chose $\gamma _0=0.1$, $\alpha =0.1$, $k_{max}=20$, and $50$ iterations. For FIDL, we selected $k_{max}=10$, $\rho =10^{-7}$, $\mu =0.1$, $\lambda _{(0)}=0.5$, and $\epsilon =0.001$. The estimated sources and mixing matrix columns are given in Figs. 4 and 5, respectively. It is seen from the figures that both IK-SVD and FIDL are able to recover the sources and mixing matrix columns with higher SNRs. Enforcing sparsity to the entire matrix $\mathbf{X}$ leads FIDL to perform better than other methods (Fig. 4e, third row). However, one can still see some low-SNR spurious sources in Figs. 4 and 5. A solution to improve these results can be adding extra constraints (if available) about the sources of interests (e.g., prior knowledge in the form of a template or a reference signal) to the original cost function.

Fig. 4

The separated source images from synthetic fMRI mixtures: a original images, results of applying b K-SVD-based method [23], c IK-SVD, d FastICA, and e FIDL

Fig. 5

The estimated mixing matrix columns of synthetic fMRI data: a original columns, results of applying b K-SVD based method [23], c IK-SVD, d FastICA, and e FIDL

Also, in order to demonstrate the effect of adaptive $\lambda$ for FIDL, the convergence curves of this experiment are plotted in Fig. 6. It is seen from this figure that $\lambda$ is evolved in a way to stabilize the convergence trend and leads to a very small decomposition error.

Fig. 6

Decomposition error: $\left\Vert\mathbf{Y}-\mathbf D \mathbf{X}\right\Vert_F$ (left), and evolution of adaptive $\lambda$ (right), versus number of iterations

4.3 Real fMRI data

A real auditory fMRI dataset was considered for this experiment. This dataset was taken from [43] and contains brain images acquired by a 2 Tesla scanner (more details about the dataset is available on the website [43]). We applied different methods to the fMRI data and chose $K=35$ sources to be separated, which was already shown to be a suitable choice [21]. For IK-SVD, we chose $\gamma _0=0.1$, $\alpha =0.1$, $k_{max}=50$, and $100$ iterations. Also, we considered denoising-based IK-SVD which assumes no prior knowledge of underlying sparsity level. For FIDL, we selected $k_{max}=50, \rho =10^{-8}, \mu =0.05, \lambda _{(0)}=0.5$, and $\epsilon =0.01$. For FastICA, tanh nonlinearity was used. For the method in [23], the sparsity level $\tau =2$ was used as suggested in the paper. As another relative method, we considered the $\ell _p$-norm NMF factorization method proposed in [44] for this experiment.⁶ In this method, we set $p=0.5$ and $\delta =0.5$. All the results in Fig. 7a–e are based on data-driven methods that estimate both BOLD regions and time-courses. The result of Fig. 7f is obtained using model-based method of statistical parameter mapping (SPM) [43]. Since the canonical hemodynamic response function (HRF), i.e., the periodic curve in Fig. 7f, is a ground truth for time-course we calculated the correlation of the estimated time-courses with it. These values are given at the top of each time-course in Fig. 7. It can be seen that the proposed FIDL and IK-SVD achieved the highest correlations among other methods. This value is very similar for IK-SVD and the method in [23] as expected (Fig. 7b, c).

Fig. 7

Detected BOLD regions and their corresponding time-courses using a FIDL, b IK-SVD, c KSVD-based method [23], d FastICA, e $\ell _p$-norm-based method [44], and f SPM

5 Discussions and conclusions

In this paper, the problem of dictionary learning and its analogy to blind source separation was discussed. Two different dictionary learning methods were proposed: an extension of K-SVD with the objective of learning incoherent atoms and a fast gradient based dictionary learning suitable for large-scale problems. The proposed FIDL method has the advantage of updating both the dictionary and sparse coefficients simultaneously rather than column-by-column. These methods and other well-established techniques were applied to both synthetic and real data. The results of our experiments confirmed the superiority of the proposed methods. In another part of the paper, we stated the similarities between the two frameworks of dictionary learning and blind source separation, and then applied the proposed dictionary learning methods to a set of auditory fMRI mixtures. The results of BOLD detection revealed that the proposed techniques are capable of being used for blindly separating sparse sources, even for noisy data such as fMRI. However, further research is to be carried out to extend the proposed methods for other applications and more complicated data.