Rescheduling for machine disruption to minimize makespan and maximum lateness

Abstract

We consider a scheduling problem where a set of jobs has already been scheduled to minimize some cost objective on a single machine when the machine becomes unavailable for a period of time. The decision-maker needs to reschedule the jobs without excessively disrupting the original schedule. The disruption is measured as the maximum time deviation, for any given job, between the original and new schedules. We examine a general model where the maximum time disruption appears both as a constraint and as part of the cost objective. For a scheduling cost modeled as the makespan or maximum lateness, we provide a pseudopolynomial time optimal algorithm, a constant factor approximation algorithm, and a fully polynomial time approximation scheme. The approximation algorithm has an asymptotically achievable worst-case performance ratio of 2 and has average performance close to optimal. Managerial insights are given on how scheduling costs are affected by machine disruption and the approximation algorithm.

1 Introduction

The topic of rescheduling has garnered much attention in recent years. When considering the dynamic nature and unforeseen changes that can occur in modern production and service environments, a scheduling system must be able to efficiently alter an existing schedule (Vieira et al. 2003). Disruptions that create the necessity for rescheduling include due date changes, labor strikes, machine breakdowns, materials shortages, order cancelations, and the like.

Many rescheduling applications have been reported. Bean et al. (1991) introduce a matchup scheduling approach for an automotive industry application that compensates for the presence of disruptions. Zweben et al. (1993) use iterative repair heuristics in a rescheduling system that supports the space shuttle. In a shipyard application, Clausen et al. (2001) describe a model for rescheduling the storing of steel plates for efficient access as well as the assigning of stacker crates to berths at different container ports. Yu et al. (2003) investigate a short-range airline planning problem and present an optimization-based rescheduling approach in the presence of disruptions caused by crew unavailability, inclement weather, and air traffic. In a typical health care setting, when scheduling patients to operating rooms, regular patients are scheduled in advance, but operating rooms may later become unavailable due to the arrival of urgent medical cases, creating the need for rescheduling (Thompson et al. 2009).

The purpose of this paper is to investigate how to reschedule jobs from a previously optimized schedule in a production environment that experiences a disruption. Initially, we assume that an optimal schedule for a set of jobs on a single machine exists that minimizes a cost objective. However, the processing of most of these jobs has not yet been initiated. This type of situation can exist when schedules are created prior to the work start date; in practice, this could typically be several weeks prior to initiation of job processing. Based on this optimal schedule, commitments to customers and allocation of resources have already been determined. Then, due to an unforeseen disruption prior to execution of the schedule, the machine becomes unavailable for a window of time, requiring rescheduling of the previously optimized schedule. This situation can create havoc for the already existing resource allocation. Thus, with any rescheduling, it is important to adhere to the cost objective utilized in the original schedule, while minimizing disruption with respect to the original schedule. In this paper, we develop mathematical models that take into account the tradeoff between scheduling cost and severity of disruption.

The degree of disruption over an existing schedule is often modeled as a constraint or part of a cost objective. In some cases, the cost of disruption is difficult to gauge, such as loss of reputation or customer goodwill. For example, this can occur when patients are rescheduled to different surgery times. Thus, controlling the severity of disruption is captured as a constraint (Hall and Potts 2004; Hall et al. 2007; Yuan and Mu 2007). In some other cases, it is easier to estimate the costs of disruption, as in the case where a disruption primarily increases internal production costs. Thus, modeling the disruption as part of a cost objective, in essence, considers the tradeoff between disruption and scheduling costs (Unal et al. 1997; Hall and Potts 2004; Qi et al. 2006; Yang 2007). In this work, we model disruption both as a constraint and as part of a cost objective function.

Due to its importance, scholars have proposed divergent approaches to rescheduling for a variety of scheduling environments. Vieira et al. (2003), Aytug et al. (2004), Herroelen and Leus (2005), and Yang et al. (2005) provide extensive reviews of the rescheduling literature, including taxonomies, strategies, and algorithms, in both deterministic and stochastic environments. Also, Yu and Qi (2004) demonstrate the framework, models, and applications in disruption management, with specific focus on scheduling problems. Pinedo (2012), in his treatise on scheduling theory, provides a broad set of descriptions of rescheduling problems. A review of the literature on problems similar to that described in this paper follows.

Single machine rescheduling with newly arrived jobs is considered by Unal et al. (1997), Hall and Potts (2004), Hall et al. (2007), Yang (2007), and Yuan and Mu (2007). Unal et al. (1997) investigate the problem where new jobs with type-dependent setup times are inserted into an existing schedule with jobs having due dates to meet, to minimize the disruption cost plus the makespan or the total weighted completion time of the new jobs. Hall and Potts (2004) study the case where a set of new jobs is inserted into an existing schedule, where either total scheduling cost is minimized subject to a limit on disruption cost, or a total cost is minimized that incorporates both scheduling and disruption costs. Hall et al. (2007) examine a situation with multiple arrivals of new jobs, where maximum lateness is minimized, subject to a limit on maximum time disruption. Yang (2007) considers the problem with new jobs having time compression cost, where the objective is to minimize the total of compression costs, disruption costs, and scheduling costs. Yuan and Mu (2007) examine rescheduling with new jobs, where jobs have release dates, and the objective is to minimize makespan subject to a limit on maximum sequence disruption.

Single machine rescheduling with job unavailability is studied by Hall and Potts (2010). These authors consider a situation where a set of jobs is available later than expected, with an objective to minimize total scheduling cost, subject to a limit on maximum time disruption.

Single-machine rescheduling with changed job characteristics is investigated by Wu et al. (1993). These authors consider a case where after a schedule has been determined, the release dates of jobs are changed. The problem is modeled using bicriteria optimization, with maximum lateness as one criterion, and total time or sequence disruption as the other criterion.

Rescheduling for machine disruption is examined by Leon et al. (1994), Azizoǧlu and Alagöz (2005), and Qi et al. (2006). Leon et al. (1994) propose a method to find a schedule for a job shop that is robust to an unforeseen period of machine unavailability, where robustness is defined over makespan and delay of job processing. Azizoǧlu and Alagöz (2005) investigate a problem with identical parallel machines, where rescheduling occurs when one machine becomes unavailable for a period of time. Total completion time and number of jobs processed on different machines in the original and new schedules are minimized using bicriteria optimization. Qi et al. (2006) investigate a rescheduling problem with machine unavailability in both single and two-machine settings, with an objective to minimize total completion time plus different measures of time disruption.

In light of the existing literature on rescheduling, our work considers a new rescheduling model with machine disruption. While Leon et al. (1994) focus on the design of a robust schedule, we consider how to adjust an existing schedule in the event of a machine disruption. The scheduling cost used by Azizoǧlu and Alagöz (2005) and Qi et al. (2006) is total completion time, while we use makespan and maximum lateness. Also, we use maximum time disruption, instead of a measure of total disruption, to model the disruption cost over the original schedule.

This paper proceeds as follows. In Sect. 2, we formally define our models. In Sect. 3, we develop structural results and optimization algorithms. In Sect. 4, we provide a constant factor approximation algorithm, and evaluate average performance of the algorithm using a computational study. In Sect. 5, a fully polynomial time approximation scheme is designed. Finally, the paper is concluded with Sect. 6, which also sets forth recommendations for future research.

2 Definitions

We begin by introducing relevant definitions, notations, and classifications. Let $J=\{1,\ldots ,n\}$ denote a set of jobs that are to be processed nonpreemptively on a single machine. It is assumed that the jobs have been previously sequenced in an optimal schedule minimizing some classical objective and that $\pi ^*$ represents an already optimized schedule with no idle time between jobs. Let $T_1$ and $T_2$ ($T_2\ge T_1$) denote the beginning and end of a time period, during which the machine is unavailable for processing jobs. We assume that both $T_1$ and $T_2$ are known at time zero, prior to processing, but after scheduling the jobs of $J$. There is no loss of generality to this assumption: If after time zero $T_1$ and $T_2$ are both known, then the jobs of $J$ having already been processed are removed from the problem, and partially processed jobs, at most one, can either be processed to completion and removed, or processing can be halted immediately and started again from the beginning at a later time, with $J$ and $n$ updated accordingly. Let $p_j$ denote the processing time of job $j, d_j$ its due date, for $j = 1,\ldots ,n$. We assume throughout our model that all values of $p_j$ and $d_j$ are known integers. Lastly, we let $p_{\min }=\min _{j\in J}\{p_j\}$ and $P= \sum _{j\in J} p_j$.

For a feasible schedule $\sigma$ of the jobs of $J$, we define the following terms:

$$\begin{aligned} \begin{array}{lll} S_j(\sigma ) &{}=&{} \text{ the } \text{ start } \text{ time } \text{ of } \text{ job } j, \text{ for } j\in J; \\ C_j(\sigma ) &{}=&{} S_{j}(\sigma )+p_j, \text{ the } \text{ time } \text{ at } \text{ which } \text{ job } \\ &{}&{}\quad j \text{ is } \text{ completed, } \text{ for } j\in J; \\ L_j(\sigma ) &{}=&{} C_j(\sigma )\!-\!d_j, \text{ the } \text{ lateness } \text{ of } \text{ job } j, \text{ for } j\in J; \\ \Delta _j(\pi ^*,\sigma ) &{}=&{} |C_j(\sigma ) - C_j(\pi ^*)|, \text{ the } \textit{time disruption}\\ &{}&{}\quad \text{ of } \text{ job } j, \text{ for } j \in J. \\ \end{array} \end{aligned}$$

Let the maximum time disruption $\Delta _{\max }(\pi ^*,\sigma )=\max _{j \in J}$ $\{\Delta _j(\pi ^*,\sigma )\}$. When no ambiguity is present, we simplify the terms $S_j(\sigma ), C_j(\sigma ), L_j(\sigma ), \Delta _j(\pi ^*,\sigma )$ and $\Delta _{\max }(\pi ^*,\sigma )$ to $S_j, C_j, L_j, \Delta _j$ and $\Delta _{\max }$, respectively. The time disruption models any penalties that result from changing of delivery times of jobs to customers, as well as the cost associated with the rescheduling of resources so that they are available when needed. Also, let $\sigma ^*$ denote an optimal schedule after the rescheduling.

Graham et al. (1979) establish a standard $\alpha |\beta |\gamma$ classification scheme for scheduling problems. For the $\alpha$ term, we use $\alpha = 1,h_1$ to denote a single machine with a single unavailable time period. For the $\beta$ term, we denote $\Delta _{\max } \le k$ to indicate that the maximum time disruption is no more than $k$, where $k$ is a constant integer set by managers to provide a maximum allowable disruption to the rescheduling process. When considering the $\gamma$ term, we denote $\mathcal{S}$ as scheduling cost and $\mu$ as the relative cost of one unit of disruption compared to scheduling cost, where $\mu \ge 0$. In our models, $\mathcal{S} \in \{C_{\max },L_{\max }\}$, where $C_{\max } = \max _{j \in J}\{C_j\}$ denotes makespan, i.e., the maximum completion time, of the jobs, and $L_{\max } = \max _{j \in J}\{L_j\}$ represents the maximum lateness of the jobs. Subsequently, the objective functions considered under $\gamma$ require that the term $\mathcal{S}+\mu \Delta _{\max }$ be minimized.

In total, considering that the problems $1,h_1|\Delta _{\max } \le k|\mathcal{S}+\mu \Delta _{\max }$ encompasses three special cases: (1) the ordinary scheduling problem with machine unavailability $1,h_1||\mathcal{S}$ when $k$ is sufficiently large and $\mu =0$; (2) the constrained problem $1,h_1|\Delta _{\max } \le k|\mathcal{S}$ when $\mu =0$; and (3) the total cost problem $1,h_1||\mathcal{S}+\mu \Delta _{\max }$ when $k$ is sufficiently large.

Table 1 provides a summary of our computational complexity and approximation results for the rescheduling problems studied. The first column indicates which of the two classical scheduling objectives is being considered. The second column provides the time complexity of our optimal algorithm in each case. The third column indicates the value of the worst-case performance ratio for our approximation algorithm. In the appropriate cells, readers can find a reference to the corresponding proof for each result.

Table 1 Results for rescheduling problems

3 Optimization

In Sect. 3.1 we describe the structural properties that reduce the solution space requiring enumeration for finding an optimal schedule for each problem. In Sect. 3.2, we develop an optimal dynamic programming algorithm for solving each problem, following the structural properties established in Sect. 3.1.

3.1 Structural properties

In this section, we present and prove several properties of an optimal schedule that will be used later to construct the optimization algorithms. Note that multiple optimal schedules may exist for the scheduling problem considered. The properties we present are just for the purpose of finding an optimal schedule using dynamic programming algorithms, and may not be satisfied by every optimal schedule.

Consider the original optimal schedule $\pi ^*$ before the machine becomes unavailable. Selecting $\pi ^*$ depends on what the objective function is chosen to be. For the makespan objective $C_{\max }$, the original optimal schedule $\pi ^*$ is defined by an arbitrarily arranged job sequence. For the maximum lateness objective $L_{\max }$, schedule $\pi ^*$ is defined by an earliest due date (EDD) sequence, where jobs are in a nondecreasing order of due dates (Jackson 1955). For both cases, we assume that the jobs are indexed in such a way that the schedule $\pi ^*$ is defined by the sequence $(1,\ldots ,n)$ with no idle time between jobs. For convenience, we denote $\pi ^* = (1,\ldots , n)$. Let $j_1 = \min \{j | C_j(\pi ^*)>T_1\}$, and $j_2=\min \{j|S_j(\pi ^*)> T_2\}$. Here, $j_1$ is the first job in $\pi ^*$ completed after $T_1$, and $j_2$ is the first job in $\pi ^*$ to start after $T_2$.

The constraint $\Delta _{\max }\le k$ implies that, in a feasible schedule $\sigma , S_j(\sigma ) \ge S_j(\pi ^*)-k$ and $C_j(\sigma ) \le C_j(\pi ^*)+k$, for $j=1,\ldots ,n$. After rescheduling, the partial schedule of jobs that finish their processing at time $T_1$ or earlier is referred to as the earlier schedule, and of jobs that begin their processing at time $T_2$ or later is referred to as the later schedule.

Next, we consider the values of $T_1, T_2$, and $k$ that are practical for study. First, if $T_1< p_{\min }$, then by moving schedule $\pi ^*$ to start at $T_2$, we can obtain schedule $\sigma ^*$. Second, if $T_1\ge P$, then $\sigma ^*=\pi ^*$. Thus, we assume that $p_{\min }\le T_1 <P$. Third, by the definition of $j_1$, at least one of jobs $1,\ldots ,j_1$ in $\pi ^*$ needs to be scheduled in the later schedule. If $k<T_2-S_{j_1}(\pi ^*)$, then it is not feasible to schedule any of jobs $1,\ldots ,j_1$ in the later schedule. Therefore, we proceed to assume that $k \ge T_2-S_{j_1}(\pi ^*)$. Throughout, we assume each job in $\sigma ^*$ is processed as early as possible.

Note that processing jobs following the same sequence as $\pi ^*$, each as early as possible, is not necessarily optimal. This is because such rescheduling may waste a long period of machine idle time immediately preceding the start time $T_1$ of the machine disruption. This suboptimality is shown by the following example.

Example 1

$n = 2$; $p_1 = 1, p_2 = r$; $T_1 = r, T_2=r+1$; $k=r+1$; $\mu =0$. The scheduling cost is the makespan. If jobs are scheduled in the same sequence as $\pi ^*$, each as early as possible, then jobs 1 and 2 are scheduled in intervals $[0,1]$ and $[r+1,2r+1]$, respectively, with a makespan of $2r+1$. In an optimal schedule, however, jobs 1 and 2 are scheduled in intervals $[r+1,r+2]$ and $[0,r]$, respectively, with a makespan of only $r+2$.

Next, we show that even though not exactly, the job sequence of $\pi ^*$ can be inherited in a certain degree by an optimal schedule $\sigma ^*$ after rescheduling.

Lemma 1

There exists an optimal schedule $\sigma ^*$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$ in which (a) the jobs in the earlier schedule are sequenced in the same order as in $\pi ^*$; (b) the jobs in the later schedule are sequenced in the same order as in $\pi ^ *$.

Proof

(a) First, we consider the earlier schedule in $\sigma ^*$. If property (a) is not met, then let $j$ and $i$ be the first pair of jobs $(j,i)$ for which $i$ precedes $j$ in $\pi ^*$ but $j$ immediately precedes $i$ in $\sigma ^*$. We then generate a new schedule $\sigma '$ by interchanging jobs $j$ and $i$, where job $i$ starts at time $S_j(\sigma ^*)$ and job $j$ starts at time $S_j(\sigma ^*)+p_i$. If $C_j(\sigma ') \ge C_j(\pi ^*)$ (note that this indicates $C_i(\sigma ') \ge C_i(\pi ^*)$), then $\Delta _i(\pi ^*,\sigma ')<\Delta _i(\pi ^*,\sigma ^*)$ and $\Delta _j(\pi ^*,\sigma ')<\Delta _i(\pi ^*,\sigma ^*)$, and therefore $\Delta _{\max }(\pi ^*,\sigma ')\le \Delta _{\max }(\pi ^*,\sigma ^*)$. Alternatively, consider the case where $C_j(\sigma ') < C_j(\pi ^*)$. If $C_i(\sigma ') \le C_i(\pi ^*)$, then $\Delta _i(\pi ^*,\sigma ')\le \Delta _j(\pi ^*,\sigma ')< \Delta _j(\pi ^*,\sigma ^*)$; if $C_i(\sigma ') > C_i(\pi ^*)$, then $\Delta _i(\pi ^*,\sigma ')< \Delta _i(\pi ^*,\sigma ^*)$ and $\Delta _j(\pi ^*,\sigma ')< \Delta _j(\pi ^*,\sigma ^*)$. Hence we have $\Delta _{\max }(\pi ^*,\sigma ')\le \Delta _{\max }(\pi ^*,\sigma ^*)$ under all conditions. Further, since $\pi ^*$ is obtained by a priority index rule, we have $\mathcal{S}(\sigma ') \le \mathcal{S}(\sigma ^*)$, making $\sigma '$ an optimal schedule. A finite number of repetitions of this argument establishes part (a).

(b) The sequence of jobs in the latter schedule is established by the identical interchange argument given in part (a).$\square$

A period of machine idle time is called inserted idle time period if it immediately precedes the processing of a job. Note that after rescheduling, a job processed in the earlier schedule of $\sigma$ might be completed earlier than in $\pi ^*$. In this case, due to the maximum disruption constraint, the job might be immediately preceded by an inserted idle time period. We next establish properties of an optimal schedule for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$ regarding inserted idle time periods, which will make it easier to find an optimal schedule using our algorithms. We consider the earlier schedule first.

Lemma 2

There exists an optimal schedule $\sigma ^*$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$, supposed to be with a maximum time disruption of $l$ time units, in which (a) the jobs in the earlier schedule are processed with at most one inserted idle time period; (b) each job processed in the earlier schedule after an inserted idle time period is processed exactly $l$ time units earlier than in $\pi ^*$; (c) the jobs processed in the earlier schedule after an inserted idle time period are processed consecutively in $\pi ^*$.

Proof

Let us assume an optimal schedule $\sigma ^*$ with more than a single inserted idle time period in the earlier schedule. We then show that schedule $\sigma ^*$ can be adjusted to satisfy (a), (b), and (c), without increasing the scheduling cost or the maximum time disruption.

According to Lemma 1, we assume that jobs in the earlier schedule of $\sigma ^*$ are processed in the same sequence as in $\pi ^*$. Let job $i$ be the job immediately following the first inserted idle time period in the earlier schedule of $\sigma ^*$. Let $j_3(l)=\max \{j|C_j(\pi ^*)-l\le T_1\}$. Note that job $j_3(l)$ is the last processed job in $\pi ^*$ that can be scheduled in the earlier schedule of $\sigma ^*$ with a time disruption no more than $l$ time units. By our definition of $i$ and $j_3(l)$, there are no other jobs besides $i,i+1,\ldots ,j_3(l)$ that can be scheduled in the earlier schedule after an inserted idle time period without increasing the maximum time disruption. We further note that $S_{i}(\sigma ^*)=S_{i}(\pi ^*)-l$, otherwise job $i$ could be processed earlier to reduce the length of the idle time period it follows, without increasing the maximum time disruption or its scheduling cost. Note that there is no inserted idle time in $\pi ^*$. Therefore, scheduling jobs $i,i+1,\ldots ,j_3(l)$ after the first idle time period consecutively with no inserted idle time between them is feasible, where each job is scheduled exactly $l$ time units earlier than in $\pi ^*$. Obviously, such scheduling of jobs $i,i+1,\ldots ,j_3(l)$ will neither increase the scheduling cost or the maximum time disruption from schedule $\sigma ^*$. This constructs an optimal schedule that satisfies (a), (b), and (c).$\square$

The inserted idle time period considered by Lemma 2, as by definition, must immediately precede the processing of a job. In the earlier schedule of an optimal schedule, there might exist another idle time period that immediately precedes the start of the machine disruption. Example 2 illustrates how an inserted idle time period occurs and how the properties in Lemma 2 are met by an optimal schedule of the rescheduling problem.

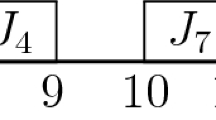
Example 2

$n=3$; $p_1=3,p_2=7,p_3=4$; $T_1=6,T_2=7$; $k=9$; $\mu =0$. The scheduling cost is the makespan. Schedules $\pi ^*$ and $\sigma ^*$ are depicted in Fig. 1, where the processing time is specified in each task, and UN refers to the unavailable period of the machine.

Fig. 1

Gantt chart for Example 2

Next, we consider the property of the job immediately preceded by an inserted idle time period in the earlier schedule of an optimal schedule.

Lemma 3

There exists an optimal schedule $\sigma ^*$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$ in which if a job is immediately preceded by an idle time period in the earlier schedule, then in $\pi ^*$ the job has a start time later than $T_2$.

Proof

According to Lemma 1, we assume that jobs in the earlier schedule of $\sigma ^*$ are processed in the same sequence as in $\pi ^*$. Assume that job $j$ immediately follows an idle time period in the earlier schedule of $\sigma ^*$. By parts (a) and (b) of Lemma 2, we assume that the time disruption of job $j$ is $l$, which is also the maximum time disruption of schedule $\sigma ^*$. By contradiction, let us assume job $j$ has a start time no later than $T_2$ in $\pi ^*$, i.e., $S_j(\pi ^*)\le T_2$.

By assumptions, we have $S_j(\sigma ^*)+l=S_j(\pi ^*)\le T_2$, i.e., $l\le T_2-S_j(\sigma ^*)$. However, since no idle time period exists in $\pi ^*$, the time interval $[0,S_j(\sigma ^*)]$ is insufficient for the processing of all jobs that are scheduled from 0 to $S_j(\sigma ^*)$ in $\pi ^*$. Note that jobs in the earlier schedule of $\sigma ^*$ are processed in the same sequence as in $\pi ^*$, and thus there must exist a job, denoted by $j'$, that starts before $S_j(\sigma ^*)$ in $\pi ^*$ and is processed in the later schedule of $\sigma ^*$, i.e., starts at time $T_2$ or later in $\sigma ^*$. Therefore, the time disruption of job $j'$ is $\Delta _{j'}(\pi ^*,\sigma ^*)>T_2-S_j(\sigma ^*)\ge l$. This contradicts the assumption that the maximum time disruption of schedule $\sigma ^*$ is $l$.$\square$

Now, we consider the existence of an inserted idle time period in the later schedule of an optimal schedule.

Lemma 4

There exists an optimal schedule $\sigma ^*$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$, in which the jobs in the later schedule are processed without any inserted idle time period.

Proof

According to Lemma 1, we assume that jobs in both the earlier and later schedules of $\sigma ^*$ are processed in the same sequence as in $\pi ^*$, each as early as possible. By contradiction, let us assume an optimal schedule $\sigma ^*$ with at least one inserted idle time period in the later schedule.

Suppose job $i$ is scheduled in the later schedule and is preceded immediately by an inserted idle time period. Note that all jobs processed earlier than $i$ in $\pi ^*$ are still processed earlier than $i$ in $\sigma ^*$. Therefore, due to the machine disruption, in $\sigma ^*$ job $i$ is processed no earlier than in $\pi ^*$. Thus, the time disruption of job $i$ is nondecreasing with job completion time. Also, the scheduling cost of job $i$ is also nondecreasing with job completion time. Therefore, scheduling job $i$ one time unit earlier, without changing the schedule of any other jobs, will result in a feasible schedule with total scheduling cost no less than that of $\sigma ^*$, which results in a contradiction with the assumption that in $\sigma ^*$ each job is processed as early as possible in the current sequence.$\square$

We next provide a property regarding the maximum time disruption of jobs in the later schedule of an optimal schedule.

Lemma 5

There exists an optimal schedule $\sigma ^*$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$, in which among all the jobs in the later schedule, the first processed job has the maximum time disruption.

Proof

We assume that schedule $\sigma ^*$ satisfies Lemmas 1 and 4. Under these assumptions, observe that no job in the later schedule of $\sigma ^*$ can be completed earlier than in $\pi ^*$. Suppose job $j$ is processed the first in the later schedule of $\sigma ^*$ and is completed $l$ time units later than in $\pi ^*$. By contradiction, let us assume a job $j'$ processed later than $j$ in $\sigma ^*$ is competed $l'$ time units later than in $\pi ^*$, where $l'>l$.

By Lemma 1, we have that in both $\pi ^*$ and $\sigma ^*$, job $j$ is processed earlier than $j'$. Since there is no inserted idle time period in the later schedule of $\sigma ^*, l'>l$ means that the total processing time of jobs between $j$ and $j'$ in $\sigma ^*$ is larger than the total processing time of jobs between $j$ and $j'$ in $\pi ^*$. This contradicts the assumption that the jobs in the later schedule of $\sigma ^*$ are in the same sequence as in $\pi ^*$.$\square$

Note that $\sigma ^*$ in Example 2 satisfies properties in Lemmas 1–5. Next, we consider how large the value of $k$ in the maximum time disruption constraint should be to make problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$ degenerate to problem $1,h_1||\mathcal{S}+\mu \Delta _{\max }$.

Lemma 6

In problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$, if $k\ge \max \{T_2,P-p_{\min }\}$, then an optimal schedule is found by solving problem $1,h_1||\mathcal{S}+\mu \Delta _{\max }$.

Proof

Let us consider the value of $\Delta _{\max }(\pi ^*,\sigma ^*)$, where $\sigma ^*$ is an optimal schedule of problem $1,h_1||\mathcal{S}+\mu \Delta _{\max }$ and satisfies Lemmas 1 and 2. We first consider jobs with $C_j(\sigma ^*)>C_j(\pi ^*)$. If $C_j(\sigma ^*)\le T_2$, then $\Delta _j\le T_2$; otherwise, Lemma 1 indicates that all the jobs completed after time $T_2$ and before job $j$ in $\sigma ^*$ are processed before job $j$ in $\pi ^*$, and thus $\Delta _j\le T_2$. Alternatively, when $C_j(\sigma ^*)\le C_j(\pi ^*)$, we have $\Delta _j\le P-p_{\min }$, since the makespan of $\pi ^*$ is $P$. Thus, $\Delta _{\max }(\pi ^*,\sigma ^*)\le \max \{T_2,P-p_{\min }\}$, and therefore, $\sigma ^*$ is an optimal schedule for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$ with $k\ge \max \{T_2,P-p_{\min }\}$.$\square$

In view of Lemma 6, we assume that $k \le \max \{T_2,P-p_{\min }\}$ in the following studies. The case $k = \max \{T_2,P-p_{\min }\}$ addresses problem $1,h_1 || S + \mu \Delta _{\max }$.

3.2 Optimal algorithms

The rescheduling problems occurring under both objective functions $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$ with $\mathcal{S} \in \{C_{\max },L_{\max }\}$ are binary NP-hard, as follows from the complexity results for special cases of $1,h_1||C_{\max }$ and $1,h_1||L_{\max }$ (Lee 1996). We focus on the design of pseudopolynomial time optimal algorithms in this section.

3.2.1 Makespan

We develop a dynamic programming algorithm to solve problem $1,h_1|\Delta _{\max } \le k|C_{\max }+\mu \Delta _{\max }$ optimally. The algorithm does not directly track the makespan of a schedule. Instead, the algorithm finds the length of the inserted idle time period of the schedule; then, the makespan can be calculated using the length of the inserted idle time period, the maximum completion time of jobs in the earlier schedule, and the total processing time of all jobs.

Algorithm Makespan (M)

Input

Given $p_1,\ldots ,p_n, \pi ^*=(1,\ldots ,n)$ where jobs are indexed arbitrarily, $T_1, T_2$ and $k$.

Initialization

Find $j_1 = \min \{j | C_j >T_1\}$. Let $z^*=\infty$ and $l=k$.

Value Function

$f_l(j,t)$ = the minimum value of the length of inserted idle time period within the earlier schedule in a schedule for jobs $1,\ldots ,j$ that has an earlier schedule with makespan of $t$, under the constraint that the maximum time disruption is no greater than $l$ time units.

Boundary Condition

$f_l(0,t)= \left\{ \begin{array}{ll}t,&{} \hbox {if } 0\le t\le T_1,\\ \infty ,&{} \hbox {otherwise.}\end{array}\right.$

Optimal Solution Value for Given $l$

$\min \limits _{0 \le t \le T_1} \{P+T_2-t+f_l(n,t)\}$, and let $\sigma _l$ denote the corresponding schedule.

Recurrence Relation

$$\begin{aligned}&f_l(j,t) \\&\quad = \min \left\{ \begin{array}{lll} f_l(j-1,t), &{} \hbox {if } S_j(\pi ^*)+l\ge T_2,&{} (1)\\ f_l(j-1,t-p_j), &{} \hbox {if } C_j(\pi ^*)-l< t, &{}(2)\\ \min \limits _{0 \le t' \le t-p_j}\{f_l(j-1,t')+S_j(\pi ^*)-l-t'\}, &{} \hbox {if } C_j(\pi ^*)-l=t,&{} (3)\\ \infty , &{} \hbox {otherwise.}&{}(4)\end{array}\right. \end{aligned}$$

The sequence of jobs considered by the recurrence relation is verified by Lemma 1. In the recurrence relation, Eq. (1) places job $j$ in the later schedule, under the condition that job $j$ has a time disruption not exceeding $l$ time units. All jobs satisfying $S_j(\pi ^*)+l\ge T_2$ can be feasibly scheduled after machine disruption, since they are scheduled sequentially in $\pi ^*$ with different start times. By Lemma 5, among jobs in the later schedule, the first processed job has the maximum time disruption. Eq. (2) places job $j$ in the earlier schedule with start time $t-p_j$ and a completion time $t$, with no idle time preceding it, where condition $C_j(\pi ^*)-l< t$ guarantees that job $j$ has a time disruption strictly less than $l$ time units. Eq. (3) also places job $j$ in the earlier schedule, but allows idle time to precede it, under condition that job $j$ is completed exactly $l$ time units earlier than in $\pi ^*$. When none of the three conditions holds, job $j$ cannot be feasibly scheduled and a prohibitively large cost is assigned by Eq. (4). Note that for Eqs. (1–3) in the recurrence relation, the condition of each job $j$ is necessary, but not sufficient. For example, a job satisfying $S_j(\pi ^*)+l\ge T_2$ in Eq. (1) may not necessarily be scheduled in the later schedule. In other words, a job $j$ may satisfy more than one equation of Eqs. (1–3), and the recurrence relation schedules $j$ in a way that leads to an optimal schedule.

Termination Test

Let $z_l=C_{\max }(\sigma _l)+\mu \Delta _{\max }(\pi ^*,\sigma _l)$. If $z_l<z^*$, then update $z^*=z_l$. If $\Delta _{\max }(\pi ^*,\sigma _l)>T_2-S_{j_1}(\pi ^*)$, then update $l=\Delta _{\max }(\pi ^*,\sigma _l)-1$ and recalculate the Optimal Solution Value; otherwise, backtrack to find an optimal schedule with total cost $z^*$.

Note that even though the makespan is nonincreasing with $l$, the disruption cost is increasing with $l$. Therefore, it is hard to find an optimal $l$ without an implicit enumeration as used by the termination test. Further, note that part (b) of Lemma 2 plays an important role in the recurrence relation. By part (b) of Lemma 2, given that $\Delta _{\max }=l$, inserted idle time only needs to be considered under the condition $C_j(\pi ^*)-l=t$, and hence we need to consider inserted idle time only for one $t$ value for each pair of $l$ and $j$, which greatly saves computing time. Lemma 4 is used by the recurrence relation in that no inserted idle time is considered when a job is processed in the later schedule. Parts (a) and (c) of Lemma 2 are not used by the recurrence relation. But it is not difficult to justify that for an optimal schedule found, there is at most one inserted idle time period in the earlier schedule, otherwise removing the idle time in the earlier schedule can reduce makespan without increasing the maximum time disruption, and thus the schedule cannot be optimal.

In the Optimal Solution Value step, makespan is equal to $P+T_2-t$ plus the length of the inserted idle time period within the earlier schedule. In the Termination Test step, the cost of the maximum time disruption is added to total cost, and variant values of the maximum time disruption are implicitly enumerated.

Theorem 1

Algorithm M finds an optimal schedule for problem $1,h_1|\Delta _{\max } \le k|C_{\max }+\mu \Delta _{\max }$ in $O(nT_1k)$ time.

Proof

Algorithm M uses structural properties justified in Lemmas 1, 2, 4 and 5. Since the costs of all possible state transitions are compared, Algorithm M generates optimal schedules for problem $1,h_1|\Delta _{\max }\le l|C_{\max }$ for all considered values of $l$. Therefore, $\sigma _l$ is an optimal schedule for problem $1,h_1|\Delta _{\max }(\pi ^*,\sigma _l)\le \Delta _{\max }\le l|C_{\max }+\mu \Delta _{\max }$. The values of $l$ considered in the Termination Test step ensure that an optimal schedule for problem $1,h_1|T_2-S_{j_1}(\pi ^*)\le \Delta _{\max }\le k|C_{\max }+\mu \Delta _{\max }$ is found, which is also optimal for problem $1,h_1|\Delta _{\max }\le k|C_{\max }+\mu \Delta _{\max }$ given that $\Delta _{\max }(\pi ^*,\sigma )\ge T_2-S_{j_1}(\pi ^*)$ for any feasible schedule $\sigma$.

Now, we consider the time complexity of Algorithm M. Since $j \le n, t \le T_1$ and $l\le k$, the number of possible values for the state variables is $O(nT_1k)$. Eqs. (1–2) in the recurrence relation require only constant time. Eq. (3) requires $O(T_1)$ time, but is computed for just one value of $t$ for each corresponding pair of $l$ and $j$, i.e., when $C_j(\pi ^*)-l=t$. Therefore, the overall time complexity of Algorithm M is $O(nT_1k)$. $\square$

Corollary 1

Algorithm M finds an optimal schedule for problem $1,h_1|\Delta _{\max } \le k|C_{\max }$ in $O(nT_1)$ time, and for problem $1,h_1||C_{\max }+\mu \Delta _{\max }$ in $O(nT_1\max \{T_2,P\})$ time.

Proof

Note that when $\mu =0$, it suffices to consider a single value of $l=k$, so the result of the first part follows Theorem 1. The result of the second part follows Lemma 6 and Theorem 1.$\square$

3.2.2 Maximum lateness

We design a dynamic programming algorithm that solves problem $1,h_1|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$ optimally.

Under the assumption that in $\sigma ^*$ jobs in the earlier schedule are processed in the same sequence as in $\pi ^*$, as verified by Lemma 1, and are processed as early as possible in that sequence, we have that in $\sigma ^*$ any job in the earlier schedule is processed no later than in $\pi ^*$. Hence, only the maximum lateness of jobs in the later schedule is considered by our algorithm. If the maximum lateness of jobs in the later schedule is greater than or equal to $L_{\max }(\pi ^*)$, then this value is the maximum lateness of the new schedule. Otherwise, $L_{\max }(\pi ^*)$ is the maximum lateness of the new schedule, since the maximum lateness of a new schedule will never be less than $L_{\max }(\pi ^*)$.

To find the maximum lateness, we track total processing time of jobs in the earlier schedule, to ensure that they are feasibly scheduled, and the completion time of each job in the later schedule, to determine its lateness. The possible inserted idle time periods in the earlier schedule further complicate the problem. Using pseudopolynomial terms to enumerate these values will greatly increase time complexity relative to Algorithm M. Fortunately, in view of Lemma 2, in the earlier schedule, after one inserted idle time period, if it exists, jobs are processed consecutively and each earlier than in $\pi ^*$ by exactly the amount of the maximum time disruption, until there is no room for processing any additional job no later than time $T_1$. That is, once the job immediately following an inserted time period is known, the remaining jobs processed after the idle time period in the earlier schedule are determined. Below, our algorithm uses a state variable, job $i$, to enumerate the job immediately following the inserted idle time period, if it exists, in the earlier schedule.

Algorithm Maximum Lateness (ML)

Input

Given $p_1,\ldots ,p_n, d_1,\ldots ,d_n, \pi ^*=(1,\ldots ,n)$ where jobs are indexed according to an EDD order, $T_1, T_2$ and $k$.

Initialization

Find $j_1 = \min \{j | C_j(\pi ^*) >T_1\}$ and $j_2=\min \{j|S_j(\pi ^*)> T_2\}$. Let $z^*=\infty$. Let $l=k$, and find $j_3(l)=\max \{j|C_j(\pi ^*)-l\le T_1\}$, which is the last processed job in $\pi ^*$ that can be scheduled in the earlier schedule with a time disruption no more than $l$ time units.

Value Function

$f_{l,i}(j,t) =$ the minimum value for the maximum lateness of the jobs in the later schedule of a schedule for jobs $\{1,\ldots ,j\}$ in which

• (a) Maximum time disruption is no greater than $l$ time units.

• (b) Job $i$, if scheduled, is processed exactly from time $S_i(\pi ^*)-l$ to $C_i(\pi ^*)-l$ in the earlier schedule, with an idle time period immediately preceding it. By definition of our value function, we require that the time disruption of job $i$ is no more than $l$ time units when completed at time $T_1$, i.e., $C_{i}(\pi ^*)-l\le T_1$. Also, according to Lemma 3, it suffices to consider $i\ge j_2$. Further, to model the case where there is no inserted idle time in the earlier schedule, a special case where $i=n+1$ is also considered; in this case job $i$ is artificial and not really scheduled.

• (c) Jobs $i+1,\ldots ,j_3(l)$, if scheduled, are processed immediately following job $i$ in the earlier schedule, with no idle time among them. The sufficiency of such scheduling of jobs $i,\ldots ,j_3(l)$ to find an optimal schedule is verified by Lemma 2.

• (d) The maximum completion time of jobs processed before $i$ in the earlier schedule is $t$, where $t\le S_{i}(\pi ^*)-l$. We specifically define $S_{n+1}(\pi ^*)=T_1+l$ to model the case where there is no inserted idle time in the earlier schedule.

Given the definition of the value function, the maximum completion of jobs in the later schedule is $T_2+\sum _{m=1}^jp_m-t-\sum _{m=i}^{\min \{j,j_3(l)\}}p_m$, from which the lateness of jobs in the later schedule can be tracked.

Boundary Condition

$$\begin{aligned} f_{l,i}(0,t)=\left\{ \begin{array}{ll}t, &{} \hbox {if } 0\le t\le T_1,\\ \infty , &{} \hbox {otherwise},\end{array}\right. \end{aligned}$$

where $T_2-S_{j_1}(\pi ^*)\le l \le k$; $C_{i}(\pi ^*)-l\le T_1$ and $i\ge j_2$, or $i=n+1$. Note that if $l < T_2-S_{j_1}(\pi ^*)$, then there exists no feasible schedule and thus such an $l$ does not need to be considered.

Optimal Solution Value for Given $l$

$\min \limits _{i,t}\{\max \{f_{l,i}(n,t),L_{\max }(\pi ^*)\}\},$ where $i\ge j_2$ and $C_{i}(\pi ^*)-l\le T_1$, or $i=n+1$; $0\le t< S_{i}(\pi ^*)-l$ when $i\ne n+1$ and $t\le T_1$ when $i=n+1$. For any schedule, the value of $L_{\max }(\pi ^*)$ is selected as the maximum lateness cost if it is larger than the maximum lateness of the later schedule, as discussed earlier in this section. Let $\sigma _l$ denote the schedule found.

Recurrence Relations

$$\begin{aligned}&f_{l,i}(j,t) \\&\quad = \min \left\{ \begin{array}{lll} \max \{f_{l,i}(j-1,t),C_j-d_j\},&{} \hbox {if } C_j(\pi ^*)+l\ge C_j \hbox {and}&{} \\ &{}\quad j\notin \{i,\ldots ,j_3(l)\},&{} (5)\\ f_{l,i}(i-1,t), &{} \hbox {if } j=j_3(l) \hbox { and } i\ne n+1,&{} (6)\\ f_{l,i}(j-1,t-p_j), &{} \hbox {if } t-p_j\ge 0, C_j(\pi ^*)-l\\ &{}\quad \le t \hbox { and } j<i,&{} (7)\\ \infty , &{}\quad \hbox {otherwise},&{} (8)\end{array}\right. \end{aligned}$$

where $C_j=T_2+\sum _{m=1}^jp_m-t-\sum _{m=i}^{\min \{j,j_3(l)\}}p_m$ is the completion time of job $j$ in the later schedule.

The sequence of jobs considered by the recurrence relation is verified by Lemma 1. Eq. (5) places job $j$ in the later schedule with completion time $C_j$, and the maximum lateness of the later schedule for jobs $1,\ldots ,j$ is updated if the lateness of job $j, C_j-d_j$, is greater than the maximum lateness of jobs in the later schedule of jobs $1,\ldots ,j-1$, under condition that the time disruption of job $j$ is no greater than $l$ time units, and that job $j$ cannot be from jobs $i,\ldots ,j_3(l)$. Here, no inserted idle time period needs to be considered, as verified by Lemma 4. Eq. (6) schedules job $i,\ldots ,j_3(l)$ consecutively in the earlier schedule from time $S_i(\pi ^*)-l$ to $C_{j_3(l)}(\pi ^*)-l$, as prescribed by the definition of the value function, unless $i=n+1$. The feasibility and sufficiency of this equation is verified by Lemma 2. Eq. (7) places jobs $j$ in the earlier schedule, under condition that its start time $t-p_j$ is no earlier than 0, its time disruption is no more than $l$ time units when completed at time $t$, and that job $j$ is processed earlier than job $i$ in $\pi ^*$. Finally, if none of the three sets of conditions is met, then job $j$ cannot be feasibly scheduled and a prohibitively high cost is assigned. As in Algorithm M, for Eqs. (5) and (7) in the recurrence relation, the conditions of each job $j$ are necessary, but not sufficient.

Termination Test

Let $z_l=L_{\max }(\sigma _l)+\mu \Delta _{\max }(\pi ^*,\sigma _l)$. If $z_l<z^*$, then update $z^*=z_l$. If $\Delta _{\max }(\pi ^*,\sigma _l)>T_2-S_{j_1}(\pi ^*)$, then update $l=\Delta _{\max }(\pi ^*,\sigma _l)-1$ and recalculate the optimal solution value; otherwise, backtrack to find an optimal schedule with total cost $z^*$. Note that there is no need to consider schedules with maximum time disruption strictly between $\Delta _{\max }(\pi ^*,\sigma _l)-1$ and $l$, since they will also have maximum lateness equal to $\Delta _{\max }(\pi ^*,\sigma _l)$.

Theorem 2

Algorithm ML finds an optimal schedule for problem $1,h_1|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$ in $O(n^2T_1k)$ time.

Proof

Algorithm ML implicitly enumerates all schedules satisfying properties established by Lemmas 1–5, subject to the maximum disruption constraint, through state transition of dynamic programming, as explicitly explained in each step of the algorithm, hence finding an optimal schedule.

Now, we consider the time complexity of Algorithm ML. In the value function $f_{l,i}(j,t), l$ is in the order $k, i$ and $j$ are both in the order of $n$, and $t$ is in the order of $T_1$, and hence the number of possible state values is $O(n^2T_1k)$. In the recurrence relation, each equation and its conditions take only constant time. Therefore, the overall time complexity of Algorithm ML is $O(n^2T_1k)$.$\square$

Note that it is more straightforward to use the maximum completion time of jobs in the later schedule as a state variable, instead of the maximum completion time of jobs in the earlier schedule not followed by an inserted idle time period; but such a method requires $O(n^2Pk)$ in time complexity, and hence is not as efficient as Algorithm ML.

Corollary 2

Algorithm ML finds an optimal schedule for problem $1,h_1|\Delta _{\max } \le k|L_{\max }$ in $O(n^2T_1)$ time, and for problem $1,h_1||L_{\max }+\mu \Delta _{\max }$ in $O(n^2T_1\max \{T_2,P\})$ time.

Proof

The proof of Corollary 2 is similar to that of Corollary 1.$\square$

4 Approximation algorithm

In this section, a constant factor approximation algorithm for both rescheduling problems is described as follows.

Algorithm H

Step 0 Given the job data, $\pi ^*=(1,\ldots ,n), T_1, T_2$ and $k$.

Step 1 Find $j_1=\min \{j | C_j(\pi ^*)> T_1\}$.

Step 2 Schedule jobs $1,\ldots ,j_1-1$ in that order in the interval $[0,\sum _{j=1}^{j_1-1} p_j]$, and schedule job $j_1,\ldots ,n$ in that order in the interval $[T_2,T_2+\sum _{j=j_1}^np_j]$.

Step 4 Output the resulting schedule, $\sigma ^H$, and its cost, $z^H$.

Since Algorithm H considers the schedule of each job in a single position only, the time required to create a schedule by this algorithm is $O(n)$ when the sequence of $\pi ^*$ is given. If the complete time of each job in $\pi ^*$ is given and sorted, then job $j_1$ can be found by using a binary search over jobs $1,\ldots ,n$ and the complexity of Algorithm H is reduced to $O(\log n)$. Note that we assume $T_1 < P$ and $k\ge T_2-S_{j_1}(\pi ^*)$. By the definition of $j_1$, jobs $1,\ldots ,j_1$ cannot all be scheduled within the interval $[0,T_1]$. As a result, the maximum time disruption of any feasible schedule must be no less than $T_2-S_{j_1}(\pi ^*)$, which is achieved by schedule $\sigma ^H$ generated via Algorithm H; hence schedule $\sigma ^H$ is feasible. In the literature, Algorithm H is applied to problem $1,h_1||L_{\max }$ (Lee and Liman 1992 and Lee 1996).

In analyzing the performance of Algorithm H, we let $z^*$ denote the optimal cost for a given problem instance. By establishing an upper bound on the value of the ratio $z^H/z^*$ over all instances, the worst-case performance of Algorithm H can be explored.

Lemma 7

For $\mathcal{S} \in \{C_{\max }, L_{\max }\}$, if Algorithm H has an asymptotically achievable worst-case performance ratio of $r$ for problem $1,h_1||\mathcal{S}$, then the algorithm also has an asymptotically achievable worst-case performance ratio of $r$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$.

Proof

First, the maximum time disruption of any feasible schedule is at least $T_2-S_{j_1}(\pi ^*)$, which is of schedule $\sigma ^H$. Hence, we have $\Delta _{\max }(\pi ^*,\sigma ^H)\le \Delta _{\max }(\pi ^*,\sigma ^*)$. Consequently, if $z^H\le rz^*$ for problem $1,h_1||\mathcal{S}$, then $z^H\le rz^*$ for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$. And since any instance of problem $1,h_1||\mathcal{S}$ is also an instance of problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$, an asymptotically achievable worst-case performance ratio for problem $1,h_1||\mathcal{S}$ is also asymptotically achievable for problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$.$\square$

Theorem 3

For problem $1,h_1|\Delta _{\max } \le k|C_{\max }+\mu \Delta _{\max }$, Algorithm H has an asymptotically achievable worst-case performance ratio of 2 as $P\rightarrow \infty$.

Proof

According to Lemma 7, it suffices to consider problem $1,h_1||C_{\max }$. We have $z^H\le T_2+P$. Also, it is evident that $z^*\ge T_2$ and $z^*\ge P$. Therefore, $z^H/z^*\le (T_2+P)/\max \{T_2,P\}\le 2$.

In Example 1 in Sect. 2, we have $z^H = 2r+1$ and $z^* = r+2$. Therefore, $\lim \limits _{r \rightarrow \infty } z^H/z^* = \lim \limits _{r \rightarrow \infty } (2r+1)/(r+2) = 2$, which shows that ratio 2 is asymptotically achievable. $\square$

We next analyze the performance of Algorithm H for the maximum lateness problem. Note that the lateness of a job can be negative.

Lemma 8

For problem $1,h_1|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$, it is binary NP-hard to determine whether an instance has an optimal schedule with a total cost less than or equal to zero.

Proof

The proof is by reduction from partition: Given $2m$ elements with integer sizes $a_1,\ldots ,a_{2m}$, where $\sum _{i=1}^{2m} a_i= 2A$, does there exist a partition $S_1, S_2$ of the index sets $\{1,\ldots ,2m\}$ such that $\sum _{i \in S_1} a_i = \sum _{i \in S_2} a_i = A$?

Given an instance of partition, we construct an instance of the rescheduling problem where $n=2m, p_i=a_i$ and $d_i=2A+1$ for $i = 1,\ldots ,n$. Further, let $T_1=A, T_2=A+1, k=\infty$ and $\mu =0$. Then, the rescheduling problem has an optimal schedule with total cost less than or equal to zero if and only if the instance of partition has a solution.$\square$

In view of Lemma 8, approximation algorithm does not exist for problem $1,h_1|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$, unless $P=NP$. Lemma 8 indicates that problem $1,h_1|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$ is APX-hard. Thus, we assume that $d_j \le 0$, for $j=1,\ldots ,n$, and denote the modified problem by $1,h_1,d_j\le 0|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$. Subtracting a common constant from all due dates does not change the nature of the problem, so the assumption is not restrictive. This assumption is used by Hall et al. (2007) and Hall and Potts (2010).

Theorem 4

For problem $1,h_1,d_j\le 0|\Delta _{\max } \le k|L_{\max }+\mu \Delta _{\max }$, Algorithm H has an asymptotically achievable worst-case performance ratio of 2.

Proof

According to Lemma 7, it suffices to consider problem $1,h_1||L_{\max }$. Consider a schedule $\sigma '$ of jobs $1,\ldots ,j_1-1,j_1+1,\ldots ,n$ where jobs $1,\ldots ,j_1-1$ are scheduled in that order in the interval $[0,\sum ^{j_1-1}_{j=1}p_j]$ and jobs $j_1+1,\ldots ,n$ are scheduled in that order in the interval $[T_2,T_2+\sum ^{n}_{j=j_1+1}p_j]$. Let $z'$ denote the cost of schedule $\sigma '$. It is evident that $z'\le z^*$, and $z'\ge z^H-p_{j_1}$. Therefore, we have that $z^H-z^*<p_{j_1}\le P \le z^*$, where $P \le z^*$ follows from our assumption that $d_j \le 0$ for $j=1,\ldots ,n$, and then conclude that $z^H/z^*\le 2$. Example 1 in Sect. 2 with $d_1=d_2=0$ shows that the ratio is asymptotically achievable.$\square$

Algorithm H is easy to implement, but it is practically useful in that it might be the most natural response to a machine disruption. Next, we generate a set of random problem instances to evaluate (1) how the minimum rescheduling cost is affected by the machine disruption; (2) the average performance of Algorithm H; and (3) how the average performance of Algorithm H is affected by different parameter values of the rescheduling problem. Following the guidelines posited by Hall and Posner (2001), (a) we create a broad range of parameter specifications, (b) all the parameters may be rescaled without significantly affecting the performance of the algorithm, and (c) the experimental design varies only the parameters that could affect the analysis.

Algorithm H is tested on ten randomly generated problem instances for each combination of the specifications for five parameters, $n, T_1, D=T_2-T_1, k$, and $\mu$. First, we randomly generate $p_j \sim UI[1,\ldots ,100]$, and $d_j \sim UI[p_j,\ldots ,\lfloor P/2 \rfloor ]$, which guarantee that the maximum lateness of an optimal schedule is at least $\lfloor P/2 \rfloor >0$, and thus a relative percentage gap from optimality can be used. Second, we use $n \in \{$20, 40, 60, 80, 100, 150, 200$\}$. Third, we have $T_1\in \{\lfloor P/4\rfloor ,\lfloor P/2\rfloor ,\lfloor 3P/4\rfloor \}$. Fourth, we consider $D \in \{\lfloor P/50\rfloor ,\lfloor P/25\rfloor ,\lfloor P/10\rfloor \}$. Finally, for the specifications for $k$ and $\mu$, we consider three types of problem: (1) for the constrained problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}$, we have $k\in \{D+100,D+\lfloor 2.5P/n \rfloor , D+\lfloor 3P/n \rfloor , D+\lfloor 3.5P/n \rfloor , D+\lfloor 4P/n \rfloor \}$; (2) for the total cost problem $1,h_1||\mathcal{S}+\mu \Delta _{\max }$, we use $\mu \in \{.5,1,2\}$; (3) for the general problem $1,h_1|\Delta _{\max }\le k|\mathcal{S}+\mu \Delta _{\max }$, we consider $k\in \{D+100,D+\lfloor 2.5P/n \rfloor , D+\lfloor 3P/n \rfloor , D+\lfloor 3.5P/n \rfloor , D+\lfloor 4P/n \rfloor \}$ and $\mu \in \{.5,1,2\}$. Overall, $7*3*3*(5+3+5*3)=1,449$ combinations are considered.

Tables 2, 3 and 4 summarize the computational results. In each table, the first column shows values of the input parameters $n, T_1, D, k$, and $\mu$. For both problems with costs $C_{\max }$ and $L_{\max }$, column APO (resp., MPO) contains the average (resp., maximum) percentage difference of the cost of an optimal schedule after the machine disruption relative to that of the original schedule; column APE (resp., MPE) shows the average (resp., maximum) relative percentage error of the schedule obtained by Algorithm H relative to an optimal schedule; column PI shows the percentage of instances for which Algorithm H finds an optimal schedule.

Table 2 Effect of parameters on performance of Algorithm H for constrained problems

Table 3 Effect of parameters on performance of Algorithm H for total cost problems

Table 4 Effect of parameters on performance of Algorithm H for general problems

Regarding the total extra cost of rescheduling, as a percentage of the original scheduling cost, caused by machine disruption, Tables 2, 3 and 4 show that the extra cost (1) increases with duration of the machine disruption, but is insensitive to disruption start time; (2) is insensitive to the number of jobs when the maximum time disruption does not appear in the cost objective; (3) deceases with the number of jobs and increases with the relative cost of time disruption compared to the scheduling cost when the maximum time disruption is part of the cost objective; and (4) decreases with the maximum allowable time disruption $k$, but becomes insensitive to $k$ when $k$ is large.

Regarding the performance of Algorithm H, we find that (1) Algorithm H finds close-to-optimal schedules with APE values less than 1.2 % except in problem $1,h_1|\Delta _{\max }\le k|L_{\max }$, where the average APE is 2.14 %; and (2) Algorithm H is more likely to find an optimal schedule when the maximum time disruption is part of the cost objective, which may be explained by the fact that Algorithm H finds a schedule with the minimum $\Delta _{\max }$ among all feasible schedules.

Next, we consider how parameter values affect the performance of Algorithm H. First, with a larger number of jobs, Algorithm H finds schedules with smaller APE values, but fewer optimal schedules. Second, the start time and duration of the machine disruption do not significantly affect the performance of Algorithm H. Third, Algorithm H exhibits better relative performance when the maximum allowable time disruption is small. This is because Algorithm H finds the same schedule for different values of $k$, but with the greater flexibility provided by larger values of $k$, the total cost of an optimal schedule decreases. Fourth, on average, Algorithm H performs better with larger values of $\mu$. This is because Algorithm H minimizes $\Delta _{\max }$ for every instance, where $\Delta _{\max }$ plays a larger role in the cost objective with larger $\mu$.

5 Approximation scheme

Approximation can be achieved by a fully polynomial time approximation scheme (FPTAS), which is a family of algorithms $\{A_{\epsilon }\}$ such that for any $\epsilon > 0, A_{\epsilon }$ delivers a solution that is within a factor $1+\epsilon$ of optimality and possesses a running time polynomial in problem input size and $1/\epsilon$ (Schuurman and Woeginger 2001). In this section, we provide an FPTAS for modified problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }+\mu \Delta _{\max }$, which contains $1,h_1|\Delta _{\max }\le k|C_{\max }+\mu \Delta _{\max }$ as a special case when $d_1=\ldots =d_n=0$. Since the problem is NP-hard, this is the strongest type of an approximation result.

Lemma 9

If there exists an FPTAS for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }$ with $O(X)$ running time that is independent of $k$, then there exists an FPTAS for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }+\mu \Delta _{\max }$ with $O((X\log k)/\epsilon )$ running time.

Proof

Let $\Delta _0=T_2-S_{j_1}(\pi ^*)$, i.e., the minimum value of $\Delta _{\max }$ for any feasible schedule. Let $\delta _i=2^i\Delta _0\epsilon$, for $i=0,\ldots ,m$, where $m=\max \{i|2^i\Delta _0<k\}$. Note that $m< \log _2(k/\Delta _0)$. Apply the existing FPTAS to solve instances $1,h_1,d_j\le 0|\Delta _{\max }\le l|L_{\max }$, with $l=k$, and $l=2^i\Delta _0,2^i\Delta _0+\delta _i,\ldots ,2^i\Delta _0+\lfloor 2/\epsilon \rfloor \delta _i$ excluding instances where $l > k$, for $i=0,\ldots ,m$. The running time for these computations is $O((X\log k)/\epsilon )$. Note that all the schedules found are feasible for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }+\mu \Delta _{\max }$, and among these schedules, we choose the one with the minimum total cost, denoted by $z^H$.

Let $\sigma ^*$ denote an optimal schedule for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }+\mu \Delta _{\max }$ with total cost $z^*$. Next we show that $z^H\le (1+\epsilon )z^*$. Suppose that schedule $\sigma ^*$ has $\Delta _{\max }(\pi ^*,\sigma ^*)=k^*\le k$, and hence, $\sigma ^*$ is also an optimal schedule for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k^*|L_{\max }+\mu \Delta _{\max }$. Let $k'=2^i\Delta _0+l\delta _i$, where $2^i\Delta _0+(l-1)\delta _i< k^* \le k'$. Suppose the existing FPTAS finds a schedule $\sigma '$ for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k'|L_{\max }$, with a total cost $z'=L_{\max }(\sigma ')+\mu \Delta _{\max }(\pi ^*,\sigma ')$. First, note that $z^H \le z'$. Second, we have $L_{\max }(\sigma ')\le (1+\epsilon )L_{\max }(\sigma ^*)$ since $k'\ge k^*$. Third, we have $k'\le k^*+\delta _i = k^*+2^i\Delta _0\epsilon \le k^*+k^*\epsilon$. Therefore, we have $z'\le (1+\epsilon )z^*$, and then $z^H \le z' \le (1+\epsilon )z^*$. $\square$

Next we design an FPTAS for problems $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }$. In our approximation scheme, a lower bound of $L_{\max }(\sigma ^*)$ is used, as defined below. Consider a preemptive schedule $\sigma ^{LB}$, in which jobs are sequenced as in $\pi ^*$. Specifically, job $j_1$ is processed with preemption beginning at time $S_{j_1}(\pi ^*)$ and completed at time $C_{j_1}(\pi ^*)+T_2-T_1$, and all other jobs are processed without preemption in the same sequence as in $\pi ^*$. We have $L_{\max }(\sigma ^{LB})\le L_{\max }(\sigma ^*)$, since $\sigma ^{LB}$ is optimal for the corresponding rescheduling problem with preemption.

We develop a family of algorithms {ML$_{\epsilon }\}$ such that for any given $\epsilon > 0$, Algorithm ML$_{\epsilon }$ delivers a schedule ${\sigma }^{\epsilon }$ with $L_{\max }({\sigma }^{\epsilon })/L_{\max }(\sigma ^*) \le 1+\epsilon$. Similar to Algorithm ML, we minimize the maximum lateness in the later schedule. Our algorithm ensures that the generated schedule will be with maximum lateness equal to $L_{\max }(\pi ^*)$ if maximum lateness does not occur in the later schedule. It should be noted that $\pi ^*$ indexes jobs in an EDD order.

Algorithm ML $_{\varvec{\epsilon }}$

Input

Given $p_1,\ldots ,p_n, d_1,\ldots ,d_n, \pi ^*=(1,\ldots ,n), T_1, T_2$, and $\epsilon$.

Initialization

Find schedule $\sigma ^{LB}$. Compute $L_{\max }(\sigma ^{LB}), \delta =\epsilon L_{\max }(\sigma ^{LB})$, and $j_3=\max \{j|C_j(\pi ^*)-k\le T_1\}$.

State Variables

$(j,t,v)_i$ corresponds to a partial schedule containing jobs $1,\ldots ,j$ where (a) jobs $i,i+1,\ldots ,j_3$, if scheduled, occupy the time interval $[S_{i}(\pi ^*)-k,C_{j_3}(\pi ^*)-k]$; (b) the time interval $[0,t]$ with $t\le S_{i}(\pi ^*)-k$ is occupied by jobs from $1,\ldots ,\min \{j,i\}$ without idle time; (c) the maximum lateness of jobs in the later schedule is $v$.

Initial State

$(0,0,0)_i$, for $S_{i}(\pi ^*)-k>0$ and $C_{i}(\pi ^*)>T_2$.

Trial State Generation

For each state $(j,t,v)_i$, generate at most four trial states: (1) $(j+1,t,\max \{v,C_{j+1}-d_{j+1}\})_i$, if $C_{j+1}(\pi ^*)+k\ge C_{j+1}$ and $j+1\notin \{i,\ldots ,j_3\}$, where $C_{j+1}=T_2+\sum _{m=1}^{j+1}p_m-t-\sum _{m=i}^{\min \{j+1,j_3\}}p_m$ is the completion time of job $j+1$ in the later schedule; (2) $(j_3+1,t,v)_i$ if $j+1=i$; and (3) $(j+1,t+p_{j+1},v)_i$ if $j+1< i$ and $C_{j+1}(\pi ^*)-k\le t+p_{j+1}\le S_{i}(\pi ^*)-k$; and (4) $(j+1,t,\infty )_i$, if none of the first three trial states applies.

Trial State Rounding

For each trial state $(j+1,t,v')_i$ except for $v'=\infty$, replace it with $(j+1,t,\lfloor v'/\delta \rfloor \delta )_i$.

Rounded Trial State Elimination

For each pair of rounded trial states $(j+1,t',v)_i$ and $(j+1,t'',v)_i$ (where $v$ is an integer multiple of $\delta$), eliminate the second state if $t' \le t''$, and eliminate the first state otherwise.

Termination Test

If $j+1<n$, then set $j=j+1$ and return to the Trial State Generation step. Otherwise, select a state $(n,t,\hat{v})_i$ for which $\hat{v}$ is smallest, and backtrack to find the corresponding schedule ${\sigma }^{\epsilon }$.

Theorem 5

The family of algorithms {ML$_{\epsilon }$}, for $\epsilon > 0$, is an FPTAS for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }$, with $O(n^2/\epsilon )$ running time.

Proof

Similar to Algorithm ML, Algorithm ML$_{\epsilon }$ constructs a schedule according to the properties given by Lemmas 1–5. Thus, an optimal schedule is obtained without Trial State Rounding. Since no rounding is applied to the state variable $t$, the Trial State Generation step ensures feasibility of the schedule found.

Now, we analyze the maximum lateness of the schedule found by Algorithm ML$_{\epsilon }$. The Termination Test step selects the state $(n,t,\hat{v})_i$ and schedule ${\sigma }^{\epsilon }$. First, since state variable $v$ is always rounded down, we have $\hat{v}\le L_{\max }(\sigma ^*)$. Also, in each execution of the Trial State Rounding step, replacing $v'$ by $\lfloor v'/\delta \rfloor \delta$ decreases the value of the state variable from its true value by at most $\delta$. Also, no subsequent decrease occurs since $v$ either remains unchanged or is replaced by $C_{j+1}-d_{j+1}$ after the Trial State Generation and Trial State Rounding steps. Therefore, the effect is that $L_{\max }({\sigma }^{\epsilon })\le \hat{v}+\delta$. We deduce that $L_{\max }({\sigma }^{\epsilon })\le \hat{v}+\delta \le L_{\max }(\sigma ^*)+\delta =L_{\max }(\sigma ^*)+\epsilon L_{\max }(\sigma ^{LB})\le (1+\epsilon )L_{\max }(\sigma ^*)$.

It remains to analyze the time complexity of Algorithm ML$_{\epsilon }$. First, we consider the number of values of the state variables that remain after the Rounded Trial State Elimination step. States are generated for $n$ values of $j$ and at most $n$ values of $i$. Next, we show that the number of values of the state variable $v$ is $O(1/\epsilon )$. Algorithm H finds a schedule that defines an upper bound of $v$ that needs to be considered, which is supposed to be $z^H$. It is evident that $z^H-z^{LB}\le p_{j_1}\le z^{LB}$, and thus $z^H\le 2z^{LB}$. Therefore, the maximum number of values of state variable $v$ is $1+\lfloor z^H/\delta \rfloor \le 1+2/\epsilon =O(1/\epsilon )$. For each $j$, each rounded value of $v$, and each $i$, only a single value of $t$ remains after the Rounded Trial State Elimination step. Thus, the overall number of values of state variables that remain after the Rounded Trial State Elimination step is $O(n^2/\epsilon )$. Since each value of these state variables generates at most four trial states, the Rounded Trial State Elimination step requires constant time for each trial state. Therefore, the overall time complexity of Algorithm ML$_{\epsilon }$ is $O(n^2/\epsilon )$. $\square$

Algorithm ML$_{\epsilon }$ applies the same idea as Algorithm ML, and solves problem $1,h_1|\Delta _{\max }\le k|C_{\max }$ as a special case. One may wonder whether we can apply the idea behind Algorithm M to design a more efficient FPTAS for problem $1,h_1|\Delta _{\max }\le k|C_{\max }$. Unfortunately, we are unable to deliver such an algorithm. We explain this difficulty as follows. We find upper and lower bounds for the maximum lateness of an optimal schedule for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }$ with a ratio of no more than 2, as discussed in the proof of Theorem 5. Algorithm M essentially minimizes the length of machine idle times in the earlier schedule, and this length can be zero in an optimal schedule for a nontrivial instance. We are unable to find an upper and a lower bound of this length with a bounded ratio, which creates difficulty for approximation. Of course, one can directly minimize the makespan for problem $1,h_1|\Delta _{\max } \le k|C_{\max }$, but we apparently do not have an algorithm more efficient than Algorithm ML$_{\epsilon }$.

Combining Lemma 9 and Theorem 5, we have the below result.

Corollary 3

There exists an FPTAS for problem $1,h_1,d_j\le 0|\Delta _{\max }\le k|L_{\max }+\mu \Delta _{\max }$ with $O((n^2\log k)/\epsilon ^2)$ running time.

6 Conclusions

In this paper, we study a single machine rescheduling problem under machine disruption. Two classical scheduling cost measures are considered: makespan and maximum lateness. For each measure, we provide a pseudopolynomial time optimal dynamic programming algorithm. Also, we design an approximation algorithm with a worst-case performance ratio of 2, and demonstrate computationally that the algorithm performs near-optimally, on average, for both problems. We also develop an FPTAS for the two rescheduling problems.

There are several interesting extensions of our study for future research. First, it would be interesting to study the rescheduling problem in a multiple machine situation, where a disruption cost may be incurred when a job is moved from one machine to another. Second, additional constraints, such as the capacity limit for shipping jobs from their original positions to new positions, needs detailed investigation. Third, it is useful to optimize the design of preventive schedules that are robust to fallible machines. Finally, when modeling the unavailability of operating rooms in a health care setting, more practical details should be subject to careful exploration.