Specification testing of partially linear single-index models: a groupwise dimension reduction-based adaptive-to-model approach

Abstract

This paper develops a groupwise dimension reduction-based adaptive-to-model test for partially linear single-index models. The test behaves as a local smoothing test would if the model were bivariate. The test statistic under the null hypothesis is asymptotically normally distributed. The test can detect local alternatives distinct from the null hypothesis at the rate that existing local smoothing tests can achieve when the regression model contains bivariate covariates. Therefore, the curse of dimensionality is largely alleviated. Numerical studies, including two real data examples, are conducted to examine the finite sample performance of the proposed test.

1 Introduction

Consider the following partially linear single-index model (PLSIM):

$$\begin{aligned} Y = \beta ^{\top }X + g(\alpha ^{\top }Z) + \epsilon , \end{aligned}$$

(1.1)

where Y is the scale response, $W=(X^{\top },Z^{\top })^{\top }\in {\mathbb {R}}^{p_1+p_2}$ is the $(p_1+p_2)-$dimensional covariate, $g(\cdot )$ an unknown smooth functions, $\beta$ and $\alpha$ are unknown vectors of parameters, and $\epsilon$ is the error term such that $E(\epsilon |X, Z)=0$. For identifiability, $\alpha$ satisfies $||\alpha ||=1$. Typically, model (1.1) is a reasonable compromise between fully parametric and fully nonparametric modelling. The literature on PLSIM estimation is enormous. For example, Carroll et al. (1997) first proposed a maximum quasi-likelihood method to estimate the generalised PLSIM, Xia and Härdle (2006) extended the minimum average variance estimation (MAVE) approach developed by Xia et al. (2002), Zhu and Xue (2006) proposed empirical-likelihood-based inference for the PLSIM, Wang et al. (2010) developed a two-step method to estimate the model, Liang et al. (2010) proposed the semi-parametrically efficient profile least-squares estimators of coefficients, and Lu et al. (2019) devised a method to consistently estimate the biased PLSIM. Zhao et al. (2020) considered PLSIMs of panel data with errors correlated in space and time and proposed a generalised F-type test method to check index parameters. It is not all so easy to determine whether a real data set corresponds to the given statistical formalisation. Therefore, it is crucial to perform a suitable and efficient model checking before further statistical analysis.

Many efforts have been devoted to checking parametric models since the 1980s. The two most popular methodologies in the literature are local and global smoothing methods. Local smoothing methods are sensitive to high-frequency/oscillating alternative models in low-dimensional cases. However, they suffer from slow convergence rates due to nonparametric estimation and thus are greatly affected by the curse of dimensionality. For examples of local smoothing methods based on nonparametric estimation, see Härdle and Mammen (1993), Zheng (1996), Fan and Li (1996), Dette (1999), Fan et al. (2001), Fan and Huang (2001), Koul and Ni (2004) and Van Keilegom et al. (2008).

Globally smoothing methods involve empirical process-based tests that are typically functions of the averages of weighted sums of residuals. These tests converge to their weak limits at the rate of $n^{-1/2}$, which is the fastest possible rate at which they can detect local alternatives at the fastest possible rate of $n^{-1/2}$. Thus, they have theoretical advantages over local smoothing tests. However, when the dimension is greater than 1, the intractability of the limiting null distributions requires a resampling approximation such as the wild bootstrap to determine critical values. Practical evidence shows that these type of tests are less sensitive to oscillating alternatives models. For examples of these methods, see Stute (1997), Stute et al. (1998), Zhu (2003), Khmaladze and Koul (2004), and Stute et al. (2008). González Manteiga and Crujeiras (2013) provided a comprehensive review of the studies in this domain.

A direct way to alleviate the curse of dimensionality is to project the high-dimensional covariates onto one-dimensional spaces. Escanciano (2006) and Lavergne and Patilea (2008, 2012) proposed tests based on projected covariates. Zhu (2003) and Stute et al. (2008) used residual processes to construct tests that can also be considered dimension reduction types. These tests typically require Monte Carlo approximations to determine critical values (e.g. Escanciano 2006; Lavergne and Patilea 2008), although some of them, such as that of Lavergne and Patilea (2012), are asymptotically distribution-free. All these tests use one-dimensional projections to overcome the curse of dimensionality. However, the computational of the test statistics is a serious burden. The computations become even more elaborate if we further need to use a re-sampling approximation such as the bootstrap to determine critical values. Recently, Guo et al. (2016) developed the innovative model-adaptive local smoothing methodology to test the specification of parametric single-index models, thus alleviating the dimensionality problem. Zhu et al. (2017), Tan et al. (2018), Tan and Zhu (2019), Zhu et al. (2021) and Zhu et al. (2022) extended this strategy to use other parametric dimension reduction models. Li et al. (2021) proposed an adaptive-to-model hybrid of tests for parametric regression models, which fully inherits the merits of nonparametric estimation-based tests and empirical process-based tests and while avoiding their shortcomings. However, few studies have considered model checking for PLSIMs based on dimension reduction. In this paper, we construct a groupwise dimension reduction-based adaptive-to-model test for PLSIMs, to mitigate the curse of dimensionality. First, the groupwise dimension reduction method ensures that the proposed test statistic is automatically adaptive to the underlying model under the respective null and alternative hypotheses. It can thus alleviate the dimensionality problem, and simultaneously achieve the omnibus property under the alternative hypothesis. Under the null hypothesis, in probability, the test statistic only involves the bivariate covariates $\beta ^{\top }X$ and $\alpha ^{\top }Z$. The null distribution of the proposed test statistic converges to the limiting null distribution at a faster rate $O_p(nh)$, where h is being a bandwidth converging to zero at a certain rate. Moreover, by fully utilising the information of the low-dimensional null model, the proposed test can detect the local alternatives distinct from the null hypothesis at a faster rate $O_p(n^{-1/2}h^{-1/2})$ than the convergence rate $O_p(n^{-1/2}h^{-(p_{1}+p_{2})/4})$ of existing local smoothing tests for parametric models, where $p_1+p_2$ is the dimension of the complete set (X, Z), for example, as in the tests developed by Fan and Li (1996). Therefore, when the dimensions of X and Z are large, the new test is superior to existing local smoothing tests in terms of significance level maintenance and power enhancement.

The rest of the paper is organised as follows. In Sect. 2, we construct the test statistic. Because growpwise sufficient dimension reduction techniques play a crucial role in the proposed test, we also review groupwise least-squares (GLS) estimation. Section 3 discusses some asymptotic properties of the new test. Section 4 includes simulation studies and the analyses for two real data sets. The regularity conditions and all of the proofs of the theoretical results are presented in the Appendix.

2 Model-adaptive test construction

2.1 Basic construction

As we often have no knowledge of the model structure under the alternative hypothesis, the general alternative hypothesis takes the following form:

$$\begin{aligned} Y = m(X,Z) + \epsilon , \end{aligned}$$

(2.1)

where $m(X,Z)=E(Y|X,Z)$ with $m(\cdot ,\cdot )$ being an unknown smoothing function. For any $p_1\times p_1$ orthogonal matrix $B_1$ and $p_2\times p_2$ orthogonal matrix $B_2$, we have $m(X,Z)=m(B_1B^{\top }_1X,B_2B^{\top }_2Z)\equiv : {\tilde{m}}(B^{\top }_1X,B^{\top }_2Z)$ with ${\tilde{m}}(\cdot ,\cdot )=m(B_1\cdot ,B_2\cdot )$ as the function m is unknown. Therefore, any purely nonparametric regression model (2.1) can be reformulated as the groupwise dimension reduction model:

$$\begin{aligned} Y = m(B^{\top }_1X,B^{\top }_2Z) + \epsilon , \end{aligned}$$

(2.2)

where $B_1$ is a $p_1 \times q_1$ matrix with $q_1$ orthogonal columns and $B_2$ is a $p_2 \times q_2$ matrix with $q_1$ orthogonal columns, $q_1$ and $q_2$ are unknown numbers such that $1 \le q_1 \le p_1$ and $1 \le q_2 \le p_2$. For identifiability, we assume that the matrixes $B_1$ and $B_2$ satisfy $B^{\top }_1B_1=I_{q_1}$ and $B^{\top }_2B_2=I_{q_2}$. Based on this observation, we consider an alternative model (2.2) that covers more model structures and is widely used in the sufficient dimension reduction field. We reformulate the hypotheses as

$$\begin{aligned}&H_0:\ E(Y|X, Z) = \beta ^{\top }X + g(\alpha ^{\top }Z)\ {\text { for some }} \beta \in {\mathbb {R}}^{p_1}, \alpha \in {\mathbb {R}}^{p_2},\\&H_1:\ E(Y|X, Z) = m(B^{\top }_1X,B^{\top }_2Z) \ne \beta ^{\top }X + g(\alpha ^{\top }Z) \ \mathrm{{for\ any\ }} \beta \in {\mathbb {R}}^{p_1}, \alpha \in {\mathbb {R}}^{p_2}. \end{aligned}$$

The null and alternative models can then be unified. Under the null hypothesis, $q_1=1$, $q_2=1$, $B_1=\beta /||\beta ||_2$ and $B_2=\alpha$. $||A||_2$ denotes the $L_2$-norm of a vector A throughout this paper. Under the alternative hypothesis, $q_1\ge 1$ and $q_2\ge 1$. Therefore, we can construct a test that is automatically adaptive to the null and alternative models by consistently estimating $q_1$, $q_2$, $B_1$ and $B_2$ under the null and the alternative models, respectively.

Let $\epsilon =Y-\beta ^{\top }X-g(\alpha ^{\top }Z)$. Under the null hypothesis $H_0$, $B_1=\kappa \beta$ with $\kappa =1/||\beta ||_2$, and $B_2=\alpha$. Thus, we have

$$\begin{aligned} E(\epsilon |X, Z)=0 \Rightarrow E(\epsilon |X, Z) =E(\epsilon | B^{\top }_1X,B^{\top }_2Z)= 0. \end{aligned}$$

such that

$$\begin{aligned}&E(\epsilon E(\epsilon |B^{\top }_1X,B^{\top }_2Z)f(B^{\top }_1X,B^{\top }_2Z))=E(E^2(\epsilon |B^{\top }_1X,B^{\top }_2Z)f(B^{\top }_1X,B^{\top }_2Z))=0, \end{aligned}$$

where $f(\cdot )$ denotes the density function of $(B^{\top }_1X,B^{\top }_2Z)$. Under the alternative hypothesis $H_1$, as

$$\begin{aligned} E(Y|X, Z)=E(\epsilon |B^{\top }_1X,B^{\top }_2Z)=m(B^{\top }_1X,B^{\top }_2Z)-\beta ^{\top }X - g(\alpha ^{\top }Z)\ne 0, \end{aligned}$$

we have

$$\begin{aligned} E\left[ \epsilon E(\epsilon |B^{\top }_1X,B^{\top }_2Z)W(B^{\top }_1X,B^{\top }_2Z)\right] =E\left[ E^2(\epsilon |B^{\top }_1X,B^{\top }_2Z)\right] >0. \end{aligned}$$

(2.3)

The above argument implies that we can construct a consistent test based on the left term in (2.3). The null hypothesis $H_0$ is rejected for large values of the test statistic.

Let $\{(x_1,z_1,y_1), \cdots , (x_n,z_n,y_n)\}$ denote independent and identically distributed (i.i.d.) samples. We estimate $E(\epsilon |B^{\top }_1X,B^{\top }_2Z)$ using the kernel estimate:

$$\begin{aligned}&{{\hat{E}}}({\hat{\epsilon }}_i|{B_{1n}}^\top x_i,{B_{2n}}^\top z_i )=\frac{\frac{1}{n-1}\sum _{j\ne i}^nK_{h}(B^{\top }_{1n} x_j-B^{\top }_{1n} x_i,B^{\top }_{2n} z_j-B^{\top }_{2n} z_i){\hat{\epsilon }}_j}{\frac{1}{n-1}\sum _{j\ne i}^n K_{h}(B^{\top }_{1n} x_j-B^{\top }_{1n} x_i,B^{\top }_{2n} z_j-B^{\top }_{2n} z_i)}, \end{aligned}$$

where $K_{h}=K(\cdot /h)/h^{{\hat{q}}_1+{\hat{q}}_2}$ with $K(\cdot )$ being a $({\hat{q}}_1+{\hat{q}}_2)$-dimensional product kernel function with univariate kernel function $k(\cdot )$ and h being a bandwidth, $B_{1n}$ and $B_{2n}$ are estimates of $B_1$ and $B_2$ with estimated structural dimensions ${\hat{q}}_1$ and ${\hat{q}}_2$, respectively, which we discuss in the next subsection. Here, ${\hat{\epsilon }}_i$ denotes the estimate of the residual term $\epsilon _i$, and ${\hat{\epsilon }}_i = y_i-{\hat{\beta }}^{\top }_1x_i-{\hat{g}}({\hat{\alpha }}^{\top } z_i)$, where ${\hat{\beta }}^{\top }_1$, ${\hat{\alpha }}$ and ${\hat{g}}(\cdot )$ denote the estimators of $\beta$, $\theta$ and $g(\cdot )$, respectively. More details are presented in the Appendix.

The density function $f({B}^{\top }_{1n} x_i,{B}^{\top }_{2n} z_i)$ for $i=1,2,...,n$, can be estimated by the following kernel form:

$$\begin{aligned} {\hat{f}}_{i}=\frac{1}{n-1}\sum _{j\ne i}^n K_{h}({B}^{\top }_{1n}x_j-{B}^{\top }_{1n} x_i,{B}^{\top }_{2n} z_j-{B}^{\top }_{2n} z_i). \end{aligned}$$

Therefore, a non-standardised test statistic is defined by

$$\begin{aligned} S_{n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}^n {\hat{\epsilon }}_i{\hat{\epsilon }}_j K_{h}({B}^{\top }_{1n} x_j-{B}^{\top }_{1n}x_i,{B}^{\top }_{2n}z_j-{B}^{\top }_{2n}z_i). \end{aligned}$$

(2.4)

Remark 2.1

The nonparametric kernel-based test in Zheng (1996) can also be extended to check the PLSIM, and its test statistic can be defined as:

$$\begin{aligned} S_{ZHn} = \frac{1}{n(n-1)} \sum _{i=1}^{n} \sum _{\begin{array}{c} j=1 \\ j \ne i \end{array}}^{n} \frac{1}{h^{p_1+p_2}} {\tilde{K}}\left( \frac{x_{i}-x_{j}}{h}, \frac{z_{i}-z_{j}}{h} \right) \hat{\epsilon _{i}} \hat{\epsilon _{j}}, \end{aligned}$$

(2.5)

where ${\tilde{K}}_{h}={\tilde{K}}(\cdot /h,\cdot /h)/h^{p_1+p_2}$ with ${\tilde{K}}(\cdot )$ being a $(p_1+p_2)-$dimensional kernel function. There are two differences between the formulae (2.4) and (2.5). First, we use $K_h(\cdot )$ in $S_n$ instead of ${\tilde{K}}_h(\cdot ,\cdot )$ in $T_{ZH}$. We prove that under $H_0$, ${\hat{q}}_1={\hat{q}}_2= 1$, ${B}_{1n}\rightarrow \beta /||\beta ||_2$ and ${B}_{2n}\rightarrow \alpha /||\alpha ||_2$ in probability, implying that our test reduces the dimension $p_1+p_2$ to 2. Under the alternative hypothesis, we show that $B_{1n}$ and $B_{2n}$ are automatically consistently estimated. Second, it can be easily shown that for the test statistic $S_{ZHn}$ to have a finite limiting distribution under the null hypothesis, the standardising constant must be $nh^{(p_1+p_2)/2}$ to obtain $nh^{(p_1+p_2)/2}S_{ZHn}$. We will see that the standardising form $nhS_n$ has a finite limit under $H_0$ and diverges to infinity much faster than the typical rate $nh^{(p1+p2)/2}$ of the test in Zheng (1996) under $H_1$. The results are presented in Sect. 3.

2.2 A review of groupwise least squares estimation

In general, matrices $B_1$ and $B_2$ are not identifiable. For any $q_1 \times q_1$ orthogonal matrix $C_1$ and $q_2 \times q_2$ orthogonal matrix $C_2$, as the $\sigma$-fields generated by the random variable $(B^{\top }_1X,B^{\top }_2Z)$ are equivalent to those generated by $({\tilde{B}}^{\top }_1X,{\tilde{B}}^{\top }_2Z)$ with ${\tilde{B}}_1=B_1\times C_1$ and ${\tilde{B}}_2=B_2\times C_2$, we have

$$\begin{aligned} E(\epsilon |B^{\top }_1X,B^{\top }_2Z)=E(\epsilon |{\tilde{B}}^{\top }_1X,{\tilde{B}}^{\top }_2Z). \end{aligned}$$

However, it is sufficient to identify the spaces spanned by $B_1$ and $B_2$ when we construct an adaptive-to-model test in Sect. 2.1. Groupwise dimension reduction (Li 2009) can be used to identify the subspaces spanned by the column vectors of matrices $B_1$ and $B_2$.

There are several groupwise dimension reduction approaches available in the literature. Li (2009) proposed a framework for grouped sufficient dimension reduction. Motivated by the MAVE method in Xia et al. (2002), Li et al. (2010) proposed an estimator to incorporate group information into dimension reduction. Guo et al. (2015) developed groupwise dimension reduction based on the “direct sum envelope". Zhou et al. (2016) discussed overlapped groupwise dimension reduction. Generally, these methods are computationally demanding because the resulting estimators need to be solved by an iterative procedure. This procedure involves iteratively estimating the nonparametric and the parametric component. Zhu et al. (2021) proposed a GLS estimation method for groupwise dimension reduction to avoid the iterative procedure. Thus, we recommend the GLS method in Zhu et al. (2021) to estimate $B_1$ and $B_2$.

According to Zhu et al. (2021), GLS estimation proceeds as follows:

• 1. Consider some transformation functions of the response variable, $f_1(Y),\ldots ,f_t(Y)$ satisfying $E(f_k(Y))=0$, where t is a prespecified number, and the least-squares estimates of regressing $f_k(Y)$ on $W=(X^{\top },Z^{\top })^{\top }$ is

  $$\begin{aligned} \beta _{k}=\arg \min _{\beta _k}E\{f_k(Y)-W^{\top }\beta _k\}^2, \end{aligned}$$

  for $k=1,\cdots , t$. Then the target matrix M can be constructed as follows:

  $$\begin{aligned} M=(M^{\top }_1, M^{\top }_2)^{\top }=\left( \frac{\beta _{1}}{1+||\beta _{1}||},\ldots , \frac{\beta _{t}}{1+||\beta _{t}||}\right) , \end{aligned}$$

  (2.6)

  where $M_1$ and $M_2$ are $p_1\times t$ and $p_2\times t$ matrixes, respectively.

• 2. Then $M_iM^{\top }_i$ is a $p_i\times p_i$ positive semi-definite matrix satisfying $\mathrm{{Span}}(M_iM^{\top }_i) =\mathrm{{Span}}(B_i)$, for $i=1,2$.

• 3. When the observations $\{w_i, y_i\}_{i=1}^n$ are available, $\beta _k$ can be estimated by the least squares estimates as:

  $$\begin{aligned} \beta _{kn}=\arg \min _{\beta _k}\sum _{i=1}^n\left\{ f_k(y_i)-w^{\top }_i\beta _k\right\} ^2. \end{aligned}$$

  The target matrix M in (2.6) can be estimated by:

  $$\begin{aligned} M_n=(M^{\top }_{1n}, M^{\top }_{2n})^{\top }=\left( \frac{\beta _{1n}}{1+||\beta _{1n}||},\ldots , \frac{\beta _{tn}}{1+||\beta _{tn}||}\right) . \end{aligned}$$

  When $q_i$ is given, an estimate $B_{in}$ of $B_i$ consists of the eigenvectors associated with the $q_i$ largest eigenvalues of $M_iM^{\top }_i$, for $i=1,2$. For more details, refer to Zhu et al. (2021).

2.3 Dimensionality estimation

As illustrated above, the two structure dimensions $q_1$ and $q_2$ are essential to estimating matrices $B_1$ and $B_2$. We adopt the thresholding double ridge ratio criterion proposed by Zhu et al. (2020). To address the special case $q_i=p_i$, we define some artificial eigenvalues ${\hat{\lambda }}_{i(p_i+1)}={\hat{\lambda }}_{i(p_i+2)}=0$. Let

$$\begin{aligned} {\hat{r}}_{ij}=\frac{{\hat{s}}^*_{i(j+1)}+c_{2n}}{{\hat{s}}^*_{ij}+c_{2n}} \ \ \mathrm{{with }}\ \ {\hat{s}}^*_{ij}=\frac{{\hat{\lambda }}_{i(j+1)}+c_{1n}}{{\hat{\lambda }}_{ij}+c_{1n}}-1, \end{aligned}$$

(2.7)

where $c_{1n}$ and $c_{2n}$ are the two ridges converging to 0, and $0 \le {\hat{\lambda }}_{ip_i} \le \ldots \le {\hat{\lambda }}_{i1}$ are the eigenvalues of matrix $M_{in}M^{\top }_{in}/t$. The dimension $q_i$ can be estimated by:

$$\begin{aligned} {\hat{q}}_i:= \left\{ \begin{array}{ll} 0, &{} \mathrm{{\ if}}\ {\hat{r}}_{ij}> \tau , \ \mathrm{{\ for\ all}}\ 1\le j\le p_i,\\ \arg \max _{1\le j \le p_i}\left\{ j: \ {\hat{r}}_{ij}\le \tau \right\} , &{} \mathrm{{otherwise}}, \end{array}\right. \end{aligned}$$

(2.8)

where $0<\tau <1$. Based on the rule of thumb in Zhu et al. (2020), we set $\tau =0.5$ to avoid overestimation with a large $\tau$ or underestimation with small $\tau$. As the target matrix here differs from that in Zhu et al. (2020), we recommend the ridge values $c_{1n}=0.4\log (n)/\sqrt{n}$ and $c_{2n}=0.8\log (n)/\sqrt{n}$, based on some numerical studies.

The following proposition presents the consistency of the estimators ${\hat{q}}_k$, for $k=1,2$.

Proposition 2.1

Under conditions A1 and A2 in the Appendix, assume that $c_{1n} \rightarrow 0$, $c_{2n} \rightarrow 0$ and $c_{1n}c_{2n}n \rightarrow \infty$. Then we have

$$\begin{aligned} \lim _{n \rightarrow \infty }P\left( {\hat{q}}_1=q_1,{\hat{q}}_2=q_2\right) =1. \end{aligned}$$

3 Asymptotic properties

3.1 Limiting null distribution

First, we provide some notation. Let

$$\begin{aligned} s^2 = 2\int {}K^2(u,v)dudvE\{[Var(\varepsilon ^2|B^{\top }_1X,B^{\top }_2Z)]^2p(B^{\top }_1X,B^{\top }_2Z)\}, \end{aligned}$$

(3.1)

and

$$\begin{aligned} {\hat{s}}^2 = \frac{2h^2}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^nK^2_{h}({B}^{\top }_{1n} x_j-{B}^{\top }_{1n} x_i,{B}^{\top }_{2n} z_j-{B}^{\top }_{2n} z_i){\hat{\epsilon }}^2_i{\hat{\epsilon }}^2_j. \end{aligned}$$

(3.2)

Next, we state the result for the null limiting distribution.

Theorem 3.1

Under $H_0$ and the regularity conditions in the Appendix, we have

$$\begin{aligned} nhS_n {\mathop {\longrightarrow }\limits ^{d}} N(0, {s^2}). \end{aligned}$$

Furthermore, ${s^2}$ can be consistently estimated by ${\hat{s}}^2$.

From Theorem 3.1, we have the standardised test statistic $T_n$:

$$\begin{aligned} T_n=nhS_n / {\hat{s}} {\mathop {\longrightarrow }\limits ^{d}} N(0,1). \end{aligned}$$

3.2 Power study

To study how sensitive the new test statistic is against the alternative hypothesis, we consider the following sequence of local alternative models:

$$\begin{aligned} H_{1n} : Y=\beta ^{\top }X + g(\alpha ^{\top }Z)+ C_nf(B^{\top }_1X,B^{\top }_2Z)+\eta , \end{aligned}$$

(3.3)

where the function $f(\cdot ,\cdot )$ is continuous and differentiable and satisfies $E[f^2(B^{\top }_1X,B^{\top }_2Z)] < \infty$, $E(\eta |X,Z)=0$, and $\beta$ and $\theta$ are the linear combination of the columns of $B_1$ and $B_2$, respectively.

Lemma 3.1

Under the local alternative $H_{1n}$ in (3.3) with $C_n = n^{-1/2}h^{-1/2}$ and the same conditions in Proposition 2.1 except that $C_n^2\log {n} \le c_n \rightarrow 0$, we have

$$\begin{aligned} \lim _{n \rightarrow \infty }P\left( {\hat{q}}_1=q_1,{\hat{q}}_2=q_2\right) =1. \end{aligned}$$

Next, we state the results of the power performance of the test statistic.

Theorem 3.2

Under the regularity conditions in the Appendix, we have the following results.

• (i) Under $H_{1n}$ with a fixed $C_n >0$

  $$\begin{aligned} T_{n}/(n h) {\mathop {\longrightarrow }\limits ^{P}} {Constant} >0. \end{aligned}$$

• (ii) Under the sequence of local alternative hypotheses $H_{1n}$ in (3.3), $T_n$ has different asymptotic properties based on the rates of $C_n$ as follows.

  • (a) If $q_1=q_2=1$ and $C_n = n^{-1/2}h^{-1/2}$,

    $$\begin{aligned} T_n {\mathop {\longrightarrow }\limits ^{d}} N(u, 1), \end{aligned}$$

    where

    $$\begin{aligned} u=E\{f^2(B^{\top }_1X,B^{\top }_2Z)p_{B_1B_2}(B^{\top }_1X,B^{\top }_2Z)\}/s \end{aligned}$$

    with $s^2$ defined by (3.1);

  • (b) if $q_1+q_2>2$, $C_nn^{1/2} h^{1/2}\rightarrow c_0>0$ for some constant $c_{0}$ or $C_nn^{1/2} h^{1/2}\rightarrow \infty$ and $C_nn^{1/2} h^{(q_1+q_2)/4}\rightarrow 0$, we have

    $$\begin{aligned} T_n/h^{(q_1+q_2-2)/2} {\mathop {\longrightarrow }\limits ^{\mathrm {d}}} N(0,1); \end{aligned}$$

  • (c) if $q_1+q_2>2$ and, $C_n=n^{-1/2} h^{-(q_1+q_2)/4}$, we have

    $$\begin{aligned} T_n/h^{(q_1+q_2-2)/2} {\mathop {\longrightarrow }\limits ^{\mathrm {d}}} N(u,1); \end{aligned}$$

  • (d) if $q_1=q_2=1$ and $C_n n^{1/2}h^{1/2} \rightarrow \infty$, or $q_1+q_2>2$ and $C_nn^{1/2} h^{(q_1+q_2)/4}\rightarrow \infty$, we have

    $$\begin{aligned} T_n/(C^2_nnh){\mathop {\longrightarrow }\limits ^{\mathrm {P}}} {u} >0. \end{aligned}$$

4 Numerical studies

4.1 Simulations

In this subsection, we examine the finite-sample performance of the proposed test using several numerical examples. Each experiment is repeated 1000 times to compute the empirical sizes and powers at the significance level $\alpha = 0.05$. The parametrical vectors $\beta$ and $\alpha$ are estimated using the MAVE method in Xia and Härdle (2006) (see the Appendix). In some applications, the asymptotic normal approximation does not work well in finite sample settings. Thus, re-sampling techniques are often used in finite samples. We apply the wild bootstrap algorithm adopted by Guo et al. (2016). Consider the bootstrap observations $y_{i}^{*}={{\hat{\beta }}}^{T} x_i +g({\hat{\alpha }}^{T}z_i)+\epsilon _{i}^{*},$ where $\epsilon _{i}^{*}={\hat{\epsilon }}_{i} \times U_{i}$. $\left\{ U_{i}\right\} _{i=1}^{n}$ can be chosen to be i.i.d. Bernoulli variates with

$$\begin{aligned} P\left( U_{i}=\frac{1-\sqrt{5}}{2}\right) =\frac{1+\sqrt{5}}{2 \sqrt{5}}, \quad P\left( U_{i}=\frac{1+\sqrt{5}}{2}\right) =1-\frac{1+\sqrt{5}}{2 \sqrt{5}} \text{. } \end{aligned}$$

Let $T^*_n$ be the bootstrap version of $T_n$, based on the bootstrap samples $\{(x_1,z_1,y^*_1)$, $\cdots , (x_n,z_n,y^*_n)\}$. The null hypothesis is rejected if $T_n$ is larger than the corresponding quantile of the bootstrap distribution of $T^*_n$.

For our test, we select the kernel function $K(\cdot )$ to be Gaussian, and set the bandwidths as $h_1=0.8n^{-1 /(1+4)}$ and $h=0.8n^{-1 /\left( {\hat{q}}_{1}+{\hat{q}}_{2}+4\right) }$ with the estimated dimensions ${\hat{q}}_{1}$ and ${\hat{q}}_{2}$ of $B_{1 n}^{\top } X$ and $B_{2 n}^{\top } Z$, where $h_1$ is used to estimate $\beta$, $\alpha$ and the function $g(\cdot )$ and h is used to construct the test statistics.

As in Remark 2.1, we extend the test in Zheng (1996) to check the PLSIMs for comparison and write the test statistic as $T^{ZH}_n$. For the test in Zheng (1996), we set the bandwidth as $h=1.5 n^{-1 / (4+p_1+p_2)}$ and select the quartic kernel function $K(u)=\frac{15}{16}\left( 1-u^{2}\right) ^{2}$, if $|u| \le 1$ and 0, otherwise. We compare the results of these two test statistics computed from the 500 wild bootstrap samples.

The observations $\left\{ x_i\right\} ^n_{i=1}$ and $\left\{ z_i\right\} ^n_{i=1}$ are generated i.i.d. from multivariate normal distributions $N(0_{p_1}, \Sigma _{1})$ and $N(0_{p_2}, \Sigma _{2})$, respectively, and independent of the standard normal errors. Here, $\Sigma _{1}=I_{p_1 \times p_1}$ and $\Sigma _{2}=I_{p_2 \times p_2}$. The sample sizes are set as n = 200, 400 and the dimensions are $p_{1} = p_{2} = 4, 8$.

Example 1

Consider the model

$$\begin{aligned} Y=\beta ^\top X+ (\alpha ^\top Z+1)^2+a(0.4 \beta ^\top X+1)^2 +\epsilon , \end{aligned}$$

where $\beta$ and $\alpha$ are set using the following two cases:

• Case 1: $\beta =(\underbrace{1, \ldots , 1}_{p_{1} / 2}, 0, \ldots , 0)^{\top } / \sqrt{p_{1} / 2}$, and $\alpha =(0, \ldots , 0, \underbrace{1, \ldots , 1}_{p_{2} / 2})^{\top } / \sqrt{p_{2} / 2}$;

• Case 2: $\beta =(\underbrace{1, \ldots , 1}_{p_{1}}) / \sqrt{p_{1}}$, and $\alpha =(\underbrace{1, \ldots , 1}_{p_{2}}) / \sqrt{p_{2}}$.

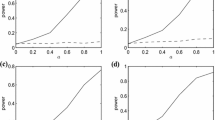
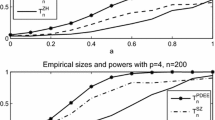
The error term $\epsilon$ follows the standard normal distribution. In this example, $a=0$ and $a \ne 0$ correspond to the null and the alternative hypothesis, respectively. The results of the empirical sizes and powers are displayed in Table 1. From Table 1, we make the following observations:

First, the proposed $T_n$ can control the empirical sizes well. $T^{ZH}_n$ tends to be conservative, especially when $p_1=p_2=4$, but when $p_1 =p_2= 8$, the significance level can be better maintained. Second, the empirical powers of the proposed test $T_n$ increase reasonably with larger a, and thus the test is significantly and uniformly more powerful than $T^{ZH}_n$. $T^{ZH}_n$ is invalid when detecting the alternative hypothesis with a large dimension $p_1=p_2=8$. For $p_1=p_2=4$ and $p_1=p_2=8$, the dimensions of X and Z have less influence for $T_n$ than they do for $T^{ZH}_n$. $T_n$ performs uniformly better than $T^{ZH}_n$ in the above two cases.

Table 1 Empirical sizes and powers of the tests for Example 1

Example 2

In this example, we examine the finite sample performance of the proposed method under the following model:

$$\begin{aligned} Y=\beta ^\top X+ exp(\alpha ^\top Z) +0.6(\alpha ^\top Z)^2+a(\beta ^\top X)^2 +\epsilon , \end{aligned}$$

where all parameter values are set to be the same as those in Example 1. $a = 0$ corresponds to the null hypothetical model. The empirical sizes and powers are presented in Table 2.

We observed that the power performances of $T_n$ in Example  1 and Example 2 are similar by comparing Tables 1, 2 and 3. The proposed test can maintain the significance level as well as in the previous example, and its power performs significantly and uniformly better than that of the test in Zheng (1996).

Table 2 Empirical sizes and powers of the tests for Example 2

Example 3

In this example, we examine the finite sample performance of the proposed method under the model:

$$\begin{aligned} Y=\beta ^\top X+ 0.9(\alpha ^\top Z)^3 + a(X_1+0.5X_2^2) +\epsilon , \end{aligned}$$

where $X_i$ and $Z_i$ denote the $i-$th components of X and Z, respectively. All parameters values are the same as those used in Example 1. The related results are displayed in Table 3.

From Table 3, both tests still control the size well. When $p_1=p_2=4$, the empirical powers of $T_{n}$ increase faster than those of $T^{ZH}_n$ as a increase. For $T^{ZH}_n$, the empirical sizes and powers are close to the significance level $\alpha =0.05$ when $p_1=p_2=8$. $T_{n}$ is significantly better than $T^{ZH}_n$ at detecting the alternative hypothesis because dimension reduction mitigates the curse of dimensionality.

Table 3 Empirical sizes and powers of the tests for Example 3

Example 4

To examine the stability of powers against the structure dimension, we consider a more complex model with higher structure dimensions $q_1$ and $q_2$:

$$\begin{aligned} Y= & {} \beta ^\top X+ \sin (\alpha ^\top Z)+2\alpha ^\top Z+a(X_1^3+0.3X_2^2+\exp (X_3)+|X_4| \\&+0.2Z_1^2+Z_2^2+\cos (Z_3)+Z_4^3)/4 +\epsilon , \end{aligned}$$

where $X_i$ and $Z_i$ denote the $i-$th components of X and Z, respectively. All parameters values are the same as those used in Example 1. $a = 0$ corresponds to the null hypothetical model. Under the alternative hypotheses, the structural dimensions $q_1$ and $q_2$ of the alternative models are equal to 4. The results are presented in Table 4.

We observe that the performances of empirical powers and sizes in Example 4 and Examples 1–3 are similar by comparing Table 4 and Tables 1, 2 and 3. The empirical sizes of the two tests are close to the significance level. However, the proposed test has significantly higher power than $T_{n}^{ZH}$, especially when $p_1=p_2=8$. We also find that the structural dimensions have a negligible effect on the empirical sizes and powers of our test.

Table 4 Empirical sizes and powers of the tests for Example 4

4.2 Real data analysis

4.2.1 Body fat data

We now apply the proposed method to the analysis of the body fat data, which can be found at http://lib.stat.cmu.edu/datasets/bodyfat. Chen et al. (2016) analysed this dataset, which provides estimates of the percentage of body fat determined by underwater weighing and various body circumference measurements. The dataset contains 251 samples with 14 attributes. Consistent with Chen et al. (2016), we select the following 12 attributes: $\mathrm height^4/weight^2$, age, and circumferences of 10 body parts, namely, neck, chest, abdomen, hip, thigh, knee, ankle, biceps, forearm, and wrist. We set the knee, ankle, and forearm circumferences as $X=(X_1, X_2, X_3)$. The other predictors are set as $Z=(Z_1,Z_2,\cdots ,Z_9)$. The response variable is the logarithm of the percentage of body fat (Y). We delete one observations in which the percentage of body fat is equal to 0.

The value of the test statistic is $T_n=18.2261$ and the $p-$value is approximately 0. Therefore, there is enough evidence to reject the null hypothesis at the significance level $\alpha = 0.05$. The residual plot of the PLSIM fitted against ${\hat{\beta }}^{\top }X$ and ${\hat{\alpha }}^{\top }Z$ in Fig. 1 shows a linear relationship between ${\hat{\beta }}^{\top }X$ and the residuals.

Fig. 1

Plot of the residuals against the linear part and single-indexing direction in the body fat data

4.2.2 Auto MPG

This data set is obtained from the Machine Learning Repository at the University of California-Irvine (http://archive.ics.uci.edu/ml/datasets/Auto+MPG). Xia (2007) and Guo et al. (2016) analysed this data set. It has 406 samples and 8 attributes. The predictors are cylinders, engine displacement, horsepower, vehicle weight, time to accelerate from 0 to 60 mph, model year, and the origin of the car. Miles per gallon (Y) is the response variable. Consistent with Xia (2007), we set cylinders, engine displacement, horsepower, vehicle weight, time to accelerate from 0 to 60 mph, and model year as $Z_1,Z_2,\cdots ,Z_6$. $X_1=1$ if a car is from America, and 0 otherwise. $X_2=1$ if a car is from Europe and 0 otherwise.

The value of the proposed test statistic is $T_n= -1.1447$, and the p-value is 0.2523. Hence, the null hypothesis should be accepted at the significance level $\alpha = 0.05$. We plot the residual plot against the single-indexing direction in Fig. 2, and the plot shows no pattern. Thus, it is reasonable to fit this dataset based on the PLSIM.

Fig. 2

Plot of the residuals against the single-index direction in the Auto MPG data

Appendix

1.1 Brief review of the minimum average variance estimation of the PLSIM

As stated previously, the proposed test procedure needs to estimate the parameter vectors $\beta$ and $\alpha$ and the function g. Therefore, we briefly review the MAVE approach developed by Xia and Härdle (2006) to estimate the PLSIM. The basic algorithm is based on the minimum average variance:

$$\begin{aligned} \left( \beta , \alpha \right) =\arg \min _{\beta , \alpha } E\left[ Y-\beta ^{\top } X-g\left( \alpha ^{\top } Z\right) \right] ^{2} \end{aligned}$$

subject to $||\alpha ||=1$. A two-step iterative algorithm to estimate the PLSIM. Given $(\beta , \theta )$, we have:

$$\begin{aligned} \left( \begin{array}{l} a_{j} \\ d_{j} \end{array}\right) =\left\{ \sum _{i=1}^{n} w_{i j}\left( \begin{array}{c} 1 \\ z_{i j}^{\top } \alpha \end{array}\right) \left( \begin{array}{c} 1 \\ z_{i j}^{\top } \alpha \end{array}\right) ^{T}\right\} ^{-1} \sum _{i=1}^{n} w_{i j}\left( \begin{array}{c} 1 \\ z_{i j}^{\top } \alpha \end{array}\right) \left( y_{i}-\beta ^{\top } z_{i}\right) . \end{aligned}$$

Given $\left( a_{j}, d_{j}\right)$, we have:

$$\begin{aligned} \begin{aligned} \left( \begin{array}{l} {\hat{\beta }} \\ {\hat{\alpha }} \end{array}\right) =&\left\{ \sum _{j=1}^{n} G\left( \alpha ^{\top } z_{j}\right) I_{n}\left( z_{j}\right) \sum _{i=1}^{n} w_{i j}\left( \begin{array}{c} X_{i} \\ d_{j} z_{i j} \end{array}\right) \left( \begin{array}{c} x_{i} \\ d_{j} z_{i j} \end{array}\right) ^{T}\right\} ^{-1} \\&\times \sum _{j=1}^{n} G\left( \alpha ^{\top } z_{j}\right) I_{n}\left( Z_{j}\right) \sum _{i=1}^{n} w_{i j}\left( \begin{array}{c} x_{i} \\ d_{j} Z_{i j} \end{array}\right) \left( y_{i}-a_{j}\right) , \end{aligned} \end{aligned}$$

where $z_{ij}=z_i-z_j$, $w_{i j}$, for $i,j=1,2,\cdots , n$, are some weights with $\sum _{i=1}^nw_{i j}=1$, and $G(\cdot )$ is another weight function that controls the contribution of $(X_j , Z_j , Y_j )$ to the estimation of $\beta$ and $\theta$. The function g can be estimated using the following kernel estimate:

$$\begin{aligned} {{\hat{g}}}({ B_{2n}}^\top z_i)=\frac{\frac{1}{n-1}\sum _{j\ne i}^nQ_{h_1}(B^{\top }_{2n} z_j-B^{\top }_{2n} z_i)(y_i-{\hat{\beta }}^{\top }x_i)}{\frac{1}{n-1}\sum _{j\ne i}^n Q_{h_1}(B^{\top }_{2n} z_j-B^{\top }_{2n} z_i)}, \end{aligned}$$

where $Q_{h_1}=K(\cdot /h_1)/h_1$ with $Q(\cdot )$ being some univariate kernel function.

In our numerical studies, the MAVE method is implemented by using the first column vector of $B_{1n}$ and $B_{2n}$ as the initial estimators for $\beta$ and $\alpha$ and setting the maximum number of iterations to 100. More details can be found in Xia and Härdle (2006).

1.2 Regularity conditions

• A1 Let $W=(X,Z)$. Assume that $E(W|B^\top W)$ is a linear function of $B^{\top } W$ with the columns of $B \in {\mathbb {R}}^{p \times q}$ being any basis of the central space ${\mathcal {S}}_{Y|W}$, where $p=p_1+p_2$ and q denotes the dimension of ${\mathcal {S}}_{Y|W}$.

• A2 $f_i(Y)$’s satisfy $E[f_i(Y)]=0$ and $E[f^2_i(Y)]<\infty$ for $i=1,\cdots , t$ and the coverage condition holds, namely, the target matrix M defined in (2.6) is such that $\mathrm{{Span}}(M) ={\mathcal {S}}_{Y|W}$. Additionally, the second moment of W exists.

• A3 The density function $p_{B_1,B_2}(\cdot ,\cdot )$ of $(B^{\top }_1X,B^{\top }_2Z)$ is continuous with a bounded first-order derivative and satisfies, on its support ${\mathbb {C}}_1$,

  $$\begin{aligned} 0<\inf _{(B^{\top }_1 x,B^{\top }_2 z) \in {\mathbb {C}}_2} p_{B_1,B_2}(B^{\top }_1x,B^{\top }_2z)\le & {} \sup _{(B^{\top }_1 x,B^{\top }_2 z) \in {\mathbb {C}}_2} p_{B_1,B_2}(B^{\top }_1x,B^{\top }_2z)< \infty . \end{aligned}$$

• A4 The function $g(\cdot )$ is $\eta -$order partially differentiable for some positive integer $\eta$, and the $\eta$th partially derivative of $g(\cdot )$ is bounded.

• A5 The kernel function $Q(\cdot )$ is symmetric and second-order continuously differentiable, and satisfies

  $$\begin{aligned} \int u^{i}Q(u)du= & {} \delta _{i0}, \ \ (i=0, 1,\ldots , \eta -1 ),\\ Q(u)= & {} O((1+|u|^{\eta +1+\gamma })^{-1}), \ \text{ some }\ \gamma >0, \end{aligned}$$

  where $\delta _{ij}$ is the Kronecker delta with $\eta$ given in Condition A4.

• A6 The kernel function $K(\cdot )$ is a bounded, symmetric kernel function. It is first order continuously differentiable and satisfies $\int K(u)du = 1$.

• A7 $n \rightarrow \infty$, $h_1 \rightarrow 0$, $h \rightarrow 0$,

  • 1) under the null or local alternative hypotheses with $C_n = n^{-{1}/{2}}h^{-{1}/{2}}$, $nh_1\rightarrow \infty$, $nh^{2}\rightarrow \infty$ and $nh^{2\eta }_1h\rightarrow 0$;

  • 2) under the global alternative hypothesis, $nh_1\rightarrow \infty$, $nh^{q_1+q_2}\rightarrow \infty$ and $nh^{2\eta }_1h^{(q_1+q_2)/2}\rightarrow 0$,

where $\eta$ is given in Condition A6.

Remark 5.1

Conditions A1 and A2 are necessary for obtaining consistent estimators of matrixes $B_1$ and $B_2$. The linearity condition A1 holds when W follows an elliptically contoured distribution, see Li (1991), and it is mild in high-dimensional scenarios (see Hall and Li 1993). The coverage condition $\mathrm{{Span}}(M) ={{\mathcal {S}}}_{Y|W}$ in Condition A2 in the literature is widely adopted to overcome technical issues, see Wu and Li (2011). Conditions A3, A4, A5 and A6 are widely used in the literature for nonparametric estimation. The four conditions ensure that the test is well-behaved, see Fan and Li (1996) and Zheng (1996). It is worth pointing out that Condition A5 pertaining to the higher-order kernel plays a critical role in bias reduction, see Robinson (1988) and Fan and Li (1996). We use different bandwidths $h_1$ and h to estimate the function ${\hat{g}}(\cdot )$ and construct the test statistic $T_n$, because they involve the various covariates under the alternative hypothesis. This phenomenon has been discussed in several studies. For example Stute and Zhu (2005) stated that the optimal bandwidth for estimation should be different from that for test statistic construction. For more details on Conditions A3-A7 refer to Fan and Li (1996), Zhu and Zhu (2018) and Zhu et al. (2021).

1.3 The proofs of the theoretical results

Proof of Proposition 2.1

Employing the same justification procedure to that for Theorem 2.1 in Zhu et al. (2020), we can get the results. Then we omit the detail here.

Proof of Theorem 3.1

Define the events $A_{1n} = \{T_n \le c\}$ for any constant c and $A_{2n} = \{{\hat{q}}_1 = 1, {\hat{q}}_2 = 1\}$. Proposition 2.1 shows that under the null hypothesis, $\lim _{n\rightarrow \infty }P(A_{2n}) = 1$, where P(A) denotes the probability that event A happens. Then we have $\lim _{n\rightarrow \infty }P(A_{2n}) = \lim _{n\rightarrow \infty }P(A_{1n} \cap A_{2n})$. This result ensures that under the null hypothesis, in an asymptotic sense we only need to consider the properties of the test statistic on the event that ${\hat{q}}_1=1$ and ${\hat{q}}_2=1$.

For notation simplicity, define $K_{B_{1n}B_{2n}ij} = K((B^{\top }_1x_i -B^{\top }_1x_j)/h, (B^{\top }_2z_i -B^{\top }_2z_j)/h)$, $K^1_{B_{1}B_{2}ij}=\frac{\partial {K}(B^{\top }_{1}(x_i-x_j)/h,B^{\top }_{1}(z_i-z_j)/h)}{\partial (B^{\top }_{1}(x_i-x_j)/h)}$, $K^1_{B_{1}B_{2}ij}=\frac{\partial {K}(B^{\top }_{1}(x_i-x_j)/h,B^{\top }_{1}(z_i-z_j)/h)}{\partial (B^{\top }_{2}(z_i-z_j)/h)}$, $g_i = g(\theta ^{\top }z_i)$, ${\hat{g}}_i ={\hat{g}}({\hat{\theta }}^{\top }z_i)$, $\epsilon _{i}=y_i-\beta ^{\top }_1x_j-g_i$, ${\hat{\epsilon }}_{i}=y_i-{\hat{\beta }}^{\top }_1x_j-{\hat{g}}_i$, $p_i = p_{B_2}(B^{\top }_2z_i)$ and ${\hat{p}}_i = {\hat{p}}_{B_{2n}}(B^{\top }_{2n}z_i)$, ${\tilde{y}}_i=y_i-\beta ^{\top }x_i$. Throughout the proof of this theorem, $E_i(\cdot )=E(\cdot |B^{\top }_1x_i, B^{\top }_2w_i)$.

Noted that ${\hat{\epsilon }}_i = y_i-{\hat{\beta }}^{\top }_1x_i-{\hat{g}}({\hat{\alpha }}^{\top } z_i)=\epsilon _{i}+ [\beta ^{\top }x_i- {\hat{\beta }}^{\top }x_i]+[g(\alpha ^{\top } z_i) -{\hat{g}}({\hat{\alpha }}^{\top } z_i)]$. We then decompose the term $S_n$ as

$$\begin{aligned} S_n= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}\epsilon _{i}\epsilon _{j} \nonumber \\&+ \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}[\beta ^{\top }_1x_i- {\hat{\beta }}^{\top }_1x_i][\beta ^{\top }_1x_j- {\hat{\beta }}^{\top }_1x_j] \nonumber \\&+\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}[g_i-{\hat{g}}_i][g_j -{\hat{g}}_j]\nonumber \\&+\frac{2}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}[\beta ^{\top }x_i- {\hat{\beta }}^{\top }x_i]\epsilon _{j} \nonumber \\&+\frac{2}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}[g_i -{\hat{g}}_i]\epsilon _{j} \nonumber \\&+\frac{2}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}[\beta ^{\top }x_i- {\hat{\beta }}^{\top }x_i][g_j -{\hat{g}}_j]\nonumber \\&\equiv :&S_{1n}+S_{2n}+S_{3n}+2S_{4n}+2S_{5n}+2S_{6n}. \end{aligned}$$

(5.1)

We now prove that both the terms $n hS_{n}$ and $n hS_{1n}$ have the same limiting null distribution, $n hS_{2n}=o_p(1)$, $n hS_{3n}=o_p(1)$, $n hS_{4n}=o_p(1)$, $n hS_{5n}=o_p(1)$ and $n hS_{6n}=o_p(1)$.

Consider the term $S_{1n}$. The first order Taylor expansion for $S_{1n}$ with respect to $B_1$ and $B_2$ yields

$$\begin{aligned} S_{1n} =: S_{11n} + S_{12n}+S_{13n}, \end{aligned}$$

where $S_{11n}$ and $S_{12n}$ have the following forms:

$$\begin{aligned} S_{11n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1}B_{2}ij}\epsilon _{i}\epsilon _{j},\\ S_{12n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n\frac{1}{h^{3}}K^1_{{\tilde{B}}_{1}{\tilde{B}}_{2}ij} ({B}_{1n}-B_1)^{\top }(x_i-x_j)\epsilon _{i}\epsilon _{j},\\ S_{13n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n\frac{1}{h^{3}}K^1_{{\tilde{B}}_{1}{\tilde{B}}_{2}ij} ({B}_{2n}-B_2)^{\top }(z_i-z_j)\epsilon _{i}\epsilon _{j}, \end{aligned}$$

with ${\tilde{B}}_1=\{{\tilde{B}}_{1ij}\}_{p_1\times q_1}$, ${\tilde{B}}_{1ij} \in [\min \{B_{1ij}, B_{1nij}\}, \max \{B_{1ij}, B_{1nij}\}]$, $B_{1}=\{B_{1ij}\}_{p_1\times q_1}$ and $B_{1n}=\{B_{1nij}\}_{p_1\times q_1}$. Due to the facts that $||B_{1n}-B_1||=O_p(1/\sqrt{n})$ and the kernel function $K(\cdot )$ has a continuous and bounded first-order derivative, we infer that replacing ${\tilde{B}}_1$ by $B_1$ does not influence the convergence rates of $S_{12n}$ and $S_{13n}$. Similarly, we can infer that replacing ${\tilde{B}}_2$ by $B_2$ does not influence the convergence rates of $S_{12n}$ and $S_{13n}$.

It is obvious that $S_{11n}$ is an $U-$statistic with the kernel as:

$$\begin{aligned} H(v_i, v_j)=\frac{1}{h^{2}}K_{B_{1}B_{2}ij}\epsilon _{i}\epsilon _{j}, \end{aligned}$$

where $v_i=(x_i,z_i, y_i)$. Under null hypothesis, as $E[H(v_i, v_j)|v_j]=0$, $S_{11n}$ is a degenerate U-statistic. Under Conditions A3–A7, adapting the similar arguments as that for Lemma 3.3 in Zheng (1996), we can obtain

$$\begin{aligned} nhS_{11n}{\mathop {\longrightarrow }\limits ^\mathrm{d}} N(0,s^2). \end{aligned}$$

We now prove that the second term $nhS_{12n}$ and $nhS_{13n}$ tend to zero. As $K(\cdot )$ is spherically symmetric, the term $S_{12n}$ can be rewritten as an U-statistic with the kernel:

$$\begin{aligned} H(v_i,v_j)= & {} \frac{1}{h^{3}}K^1_{B_{1}B_{2}ij} ({B}_{1n}-B_1)^{\top }(x_i-x_j)\epsilon _{i}\epsilon _{j}\\&+\frac{1}{h^{3}}K^1_{B_{1}B_{2}ij} ({B}_{1n}-B_1)^{\top }(x_j-x_i)\epsilon _{i}\epsilon _{j}. \end{aligned}$$

It is obvious that $E[H(v_i,v_j)|v_i]=0$. Thus, the term $S_{12n}$ is a degenerate $U-$statistic. Applying the arguments used for handling the term $S_{11n}$, together with $||B_{1n}-B_1||=O_p(1/\sqrt{n})$, it yields that $nhS_{12n}=o_p(1)$. Similarly, we can get that $nhS_{13n}=o_p(1)$.

Therefore, together with the results about $S_{11n}$, $S_{12n}$ and $S_{13n}$, we have

$$\begin{aligned} nhS_{1n}{\mathop {\longrightarrow }\limits ^\mathrm{d}} N(0,s^2). \end{aligned}$$

Now we turn to prove that $nhS_{2n}=o_p(1)$. Note that

$$\begin{aligned} S_{2n}= & {} (\beta _1- {\hat{\beta }}_1)^{\top }\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}(x_i- x_i)(x_j- x_j)^{\top }(\beta _1- {\hat{\beta }}_1) \nonumber \\&\equiv :&(\beta _1- {\hat{\beta }}_1)^{\top }{\tilde{S}}_{2n}(\beta _1- {\hat{\beta }}_1). \end{aligned}$$

Due to the fact ${\tilde{S}}_{2n}$ is a $U-$statistic, it is easy to conclude that ${\tilde{S}}_{2n}=O_p(1)$. Because $\beta _1- {\hat{\beta }}_1=O_p(1/\sqrt{n})$ and $h\rightarrow 0$, we get $nhS_{2n}=O_p(h)=o_p(1)$.

Consider the term $S_{3n}$ that can be written as:

$$\begin{aligned} S_{3n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}\frac{{\hat{p}}_{i}}{p_{i}}\frac{{\hat{p}}_{j}}{p_{j}} [{\hat{g}}_i-g_i(u)][{\hat{g}}_j-g_j]\\&+\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\frac{1}{h^{2}}K_{B_{1n}B_{2n}ij}\left[ \frac{{\hat{p}}_{i}-p_{i}}{p_{i}}\frac{{\hat{p}}_{j}-p_{j}}{p_{j}} -2\frac{({\hat{p}}_{i}-p_{i}){\hat{p}}_{j}}{p_{i}p_{j}}\right] \\&[{\hat{g}}_i-g_i(u)][{\hat{g}}_j-g_j]\\=: & {} {\tilde{S}}_{3n} + o_p({\tilde{S}}_{3n}). \end{aligned}$$

Substituting the kernel estimators ${\hat{g}}_i$ and ${\hat{p}}_i$ into ${\tilde{S}}_{3n}$, we have

$$\begin{aligned} {\tilde{S}}_{3n}= & {} \frac{1}{n(n-1)^3}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{l\ne i}^n\sum _{k\ne j}^n \frac{1}{h^{2}}\frac{1}{h^{2}_1}\frac{1}{p_{i}p_{j}}K_{B_{1n}B_{2n}ij}Q_{B_{2n}il}Q_{B_{2n}jk}\\&[y_l-{\hat{\beta }}^{\top }x_l-g_i][y_k-{\hat{\beta }}^{\top }x_k-g_j]. \end{aligned}$$

Due to the facts $B_{1n}-B_1=O_p(1/\sqrt{n})$, $B_{2n}-B_2=O_p(1/\sqrt{n})$ and $\beta _n-\beta =O_p(1/\sqrt{n})$, adapting the similar statement for dealing with the term $S_{1n}$, we can infer that replacing $B_{1n}$, $B_{2n}$ and ${\hat{\beta }}$ by $B_{1}$, $B_{2}$ and $\beta$ respectively does not influence the convergence rates of ${\tilde{S}}_{3n}$, namely,

$$\begin{aligned} {\tilde{S}}_{3n}= & {} {\tilde{S}}_{31n}+o_p({\tilde{S}}_{31n}), \end{aligned}$$

where

$$\begin{aligned} {\tilde{S}}_{31n}= & {} \frac{1}{n(n-1)^3}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{l\ne i}^n\sum _{k\ne j}^n \frac{1}{h^{2}}\frac{1}{h^{2}_1}\frac{1}{p_{i}p_{j}}K_{B_{1}B_{2}ij}Q_{B_{2}il}Q_{B_{2}jk}\\&[{\tilde{y}}_l-g_i][{\tilde{y}}_k-g_j]. \end{aligned}$$

Following the similar idea of justifying Proposition A.1 in Fan and Li (1996), we will show $nh{\tilde{S}}_{31n}=o_p(1)$ by proving that $E({\tilde{S}}^2_{31n})=o(n^{-2}h^{-2}).$ However, it is difficult and tedious to directly calculate $E({\tilde{S}}^2_{31n})$ since it contains eight summations. We first show $E({\tilde{S}}_{31n})= o(n^{-1}h^{-1})$. Then we use this result and a symmetry argument to show $E({\tilde{S}}^2_{31n})=o(n^{-2}h^{-2}).$

Decompose $E({\tilde{S}}_{31n})$ with two terms with two subsets of subscripts as:

• ${\mathcal {A}}_1=$ {i, j, l, k are all different from each other};

• ${\mathcal {A}}_2=$ {i, j, l, k take no more than three different values}.

Then ${\tilde{S}}_{31n}$ can be decomposed as ${\tilde{S}}_{31n} = {\tilde{S}}_{311n}+ {\tilde{S}}_{312n}$, where the summation indices of ${\tilde{S}}_{311n}$ and ${\tilde{S}}_{312n}$ are associated with ${\mathcal {A}}_1$ and ${\mathcal {A}}_2$, respectively.

Under the assumption that $nh^{2{\eta }}_1h=o(1)$, by applying Lemma B.1, Lemmas 2 and 3 in Robinson (1988), we have

$$\begin{aligned} E({\tilde{S}}_{311n})= & {} \frac{1}{hh^{2}_1}E\bigg (K_{B_1B_213}E_1\left\{ \frac{1}{p_{1}}Q_{B_112}[g_2-g_1]\right\} \\&E_3\left\{ \frac{1}{p_{3}}Q_{B_134}[g_4-g_3]\right\} \bigg )\\\le & {} C\frac{h^{2{\eta }}_1}{h^{q_1}}E\left[ D_F(B^{\top }_2z_1,u)D_F(B^{\top }_2z_3,u)K_{B_1B_213}\right] \\= & {} O(h^{2{\eta }}_1)=o(n^{-1}h^{-1}). \end{aligned}$$

Next we consider subset ${\mathcal {A}}_2$. It can be divided into three groups: case (I) $l=k$; case (II) $l=j$; case (III) $k=i$. Then ${\tilde{S}}_{312n}$ can be further decomposed as ${\tilde{S}}_{312n}= {\tilde{S}}_{3121n}+ {\tilde{S}}_{3122n}+ {\tilde{S}}_{3123n}$ associated with the above three sub-events. For ${\tilde{S}}_{3121n}$ with the sub-event (I),

$$\begin{aligned} E({\tilde{S}}_{3121n})= & {} \frac{1}{n(n-1)^3}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{k\ne i,k\ne j}^n \frac{1}{hh^{2}_1}E\bigg (\frac{1}{p_{i}p_{j}}K_{B_1B_2ij}Q_{B_2ik}Q_{B_2jk}\\&\times [g_k-g_i][g_k-g_j]\bigg ). \end{aligned}$$

By applying Lemma B.1, Lemmas 2 and 3 in Robinson (1988) and Fubini’s theorem, we have

$$\begin{aligned} E({\tilde{S}}_{3121n})= & {} \frac{n(n-1)(n-2)}{n(n-1)^3hh^{2}_1}E\bigg (\frac{1}{p_{1}p_{2}}K_{B_1B_212}Q_{B_2 13}Q_{B_2 23}[g_3-g_1][g_3-g_2]\bigg )\\= & {} \frac{(n-2)}{(n-1)^2hh^{2}_1}E\bigg (\frac{1}{p_{1}p_{2}}K_{B_1B_212}E_1\big \{[g_3-g_1]Q_{B_2 13}\big \}Q_{B_2 23}[g_3-g_2]\bigg )\\= & {} O(n^{-1}h^{\eta }_1h^{-1})=o(n^{-1}h^{-1}). \end{aligned}$$

The same argument can be applied to the terms $E({\tilde{S}}_{3122n})$ and $E({\tilde{S}}_{3123n})$ to obtain the upper bound $o(n^{-1}h^{-1}).$ Hence, altogether we have $E({\tilde{S}}_{31n})=E({\tilde{S}}_{311n}) + E({\tilde{S}}_{312n})=o(n^{-1}h^{-1})$.

Now we consider $E({\tilde{S}}^2_{31n})$ by using the similar decomposition of $E({\tilde{S}}_{31n})$ although it is much more complicated. Note that

$$\begin{aligned} E({\tilde{S}}^2_{31n})= & {} E\bigg \{\frac{1}{n^3(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{l\ne i}^n\sum _{k\ne j}^n \frac{1}{hh^{2}_1}\frac{1}{p_{i}p_{j}}K_{B_1B_2ij}Q_{B_2il}Q_{B_2jk}\\&\qquad [g_l-g_i][g_k-g_j]\bigg \}^2\\&=\frac{1}{n^6(n-1)^2}\frac{1}{h^{2}h^{4}_1}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{l\ne i}^n\sum _{k\ne j}^n\sum _{i'=1}^n\sum _{j' \ne i'}^n\sum _{l'\ne i'}^n\sum _{k'\ne j'}^n\\&\qquad E\Bigg (\Bigg \{\frac{1}{p_{i}p_{j}}K_{B_1B_2ij}Q_{B_2 il}Q_{B_2 jk} [g_l-g_i][g_k-g_j]\Bigg \}\\&\qquad \Bigg \{\frac{1}{p_{i'}p_{j'}}K_{B_1B_2i'j'} Q_{B_2i'l'}Q_{B_2j'k'} [g_{l'}-g_{i'}][g_{k'}-g_{j'}]\Bigg \}\Bigg )\\&=:LA_1+LA_2 +LA3, \end{aligned}$$

where the summation indices of $LA_1$, $LA_2$ and $LA_3$ respectively associated with three subsets of subscripts ${\mathcal {B}}_1$, ${\mathcal {B}}_2$ and ${\mathcal {B}}_3$ as:

• ${\mathcal {B}}_1=$ {i, j, l, k are all different from $i',j',l',k'$ };

• ${\mathcal {B}}_2=$ {exactly one index from i, j, l, k equals one of subscripts $i',j',l',k'$};

• ${\mathcal {B}}_3=$ {the eight summation indices $i,j,l,k, i',j',l',k'$ take no more than six different values}.

With ${\mathcal {B}}_1$, the sums in $LA_1$ with i, j, l, k and $i',j',l',k'$ are independent of each others. Thus $LA_1$ is equal to the square of $E({\tilde{S}}_{21n})$. Hence we can obtain that $LA_1=o(n^{-2}h^{-q_1})$. Next we consider $LA_2$ with the subset ${\mathcal {B}}_2$. By symmetry, we only need to compute three cases: case (I) $i=i'$; case (II) $i=l'$; case (III) $l=l'$, and $LA_2$ can be further decomposed as $LA_2= LA_{21}+ LA_{22}+ LA_{23}$ associated with the above three subsets.

Under case (I),

$$\begin{aligned}&LA_{21}\\&\quad =\frac{1}{n^2(n-1)^6h^{2}h^{4}_1}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{l\ne i}^n\sum _{k\ne j}^n E\bigg [\frac{1}{p_{i}p_{j}}K_{B_1B_2ij}Q_{B_2 il}Q_{B_2 jk}[g_l-g_i][g_k-g_j]\\&\qquad \sum _{j' \ne i}^n\sum _{l'\ne i}^n\sum _{k'\ne j}^n\frac{1}{p_{i}p_{j'}}K_{B_1B_2ij'}Q_{B_2il'}Q_{B_2j'k'} [g_{l'}-g_{i}][g_{k'}-g_{j'}]\bigg ]. \end{aligned}$$

Via an application of the Fubini’s theorem and Lemma B.1, Lemmas 2 and 3 in Robinson (1988), we have

$$\begin{aligned}&LA_{21}\\&\quad =\frac{1}{nh^{2}h^{4}_1}E\bigg [\frac{1}{p_{1}p_{2}}K_{B_1B_212}Q_{B_2 13}Q_{B_2 24} [g_3-g_1][g_4-g_2]\\&\qquad \frac{1}{p_{1}p_{5}}K_{B_1B_215}Q_{B_2 16}Q_{B_2 57} [g_6-g_1][g_7-g_5]\bigg ]\\&\quad =\frac{1}{nh^{2}h^{4}_1}E\bigg (\frac{1}{p_{1}p_{2}} E_1\big \{[g_3-g_1]Q_{B_2 13}\big \}E_2\big \{[g_4-g_2]Q_{B_2 24}\big \}\\&\qquad \frac{1}{p_{1}p_{5}}E_1\big \{[g_6-g_1]Q_{B_2 16}\big \}E_5\big \{[g_7-g_5]Q_{B_2 57}\big \}K_{B_1B_212}K_{B_1B_215}\bigg )\\&\quad \le \frac{h^{4\eta }_1}{nh^{2}}E\bigg [\frac{1}{p_{1}p_{2}p_{1}p_{5}}K_{B_1B_212}D_F(B^{\top }_2z_{1})D_F(B^{\top }_2z_{2}) D(B^{\top }_2z_{1})D(B^{\top }_2z_{5})K_{B_1B_215}\bigg ]\\&\quad =O(h^{4\eta }_1n^{-1})=o(n^{-2}h^{-2}). \end{aligned}$$

In case (II),

$$\begin{aligned}&LA_{22}\\&\quad =\frac{1}{n^2(n-1)^6h^{2}h^{4}_1}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{l\ne i}^n\sum _{k\ne j}^n E\bigg (\frac{1}{p_{i}p_{j}}K_{B_1B_2ij}Q_{B_2 il}Q_{B_2 jk}[g_l-g_i][g_k-g_j]\\&\qquad \sum _{i' \ne i}^n\sum _{j' \ne i'}^n\sum _{k'\ne j'}^n\frac{1}{p_{i'}p_{j'}}K_{B_1B_2i'j'}Q_{B_2i'i}Q_{B_2j'k'}[g_i-g_{i'}][g_{k'}-g_{j'}]\bigg ). \end{aligned}$$

The application of Fubini’s theorem and Lemma B.1, Lemmas 2 and 3 in Robinson (1988) again yields

$$\begin{aligned}&LA_{22}\\&\quad =\frac{1}{nh^{2}h^{4}_1}E\bigg (\frac{1}{p_{1}p_{2}}K_{B_1B_212}Q_{B_2 13}Q_{B_2 24}[g_3-g_1][g_4-g_2]\\&\qquad \frac{1}{p_{5}p_{6}}K_{B_1B_256}Q_{B_2 15}Q_{B_2 67}[g_1-g_5][g_7-g_6]\bigg )\\&\quad =\frac{1}{nh^{2}h^{4}_1}E\bigg (K_{B_1B_212}\frac{1}{p_{1}p_{2}} E_1\big \{[g_3-g_1(u_1)]Q_{B_2 13}\big \} E_2\big \{[g_4-g_2Q_{B_2 24}\big \}\\&\qquad \frac{1}{p_{5}p_{6}}K_{B_1B_256}[g_1-g_5]Q_{B_2 15}E_6\big \{[g_7-g_6]Q_{B_2 67}\big \}\bigg )\\&\quad \le \frac{h^{3\eta }_1}{nh^{2}}E\bigg [\frac{1}{p_{1}p_{2}p_{1}p_{5}}K_{B_{1}B_212}D_F(B^{\top }_2z_{1})D_F(B^{\top }_2z_{2})\\&\qquad [g_1-g_5]Q_{B_2 15}D_F(B^{\top }_2z_{6})K_{B_{1}B_256}\bigg ]\\&\quad =O(h^{3\eta }_1n^{-1})=o(n^{-2}h^{-2}). \end{aligned}$$

For case (III), the similar argument as above for case (II) can be used to justify $LA_{23}=o(n^{-2}h^{-q_1})$. Altogether, we have $LA_2=o(n^{-2}h^{-q_1})$.

Last, consider the sum $LA_3$ with the subset ${\mathcal {B}}_3$ in which the eight summation indices $i,j,l,k, i',j',l',k'$ take no more than six different values. As it is easy to show that $LA_3=o(n^{-2}h^{-2})$ by the similar arguments used above, we then omit the detail. Altogether, we conclude that $E({\tilde{S}}^2_{31n})=o(n^{-2}h^{-2})$. The application of Chebyshiev’s inequality implies ${\tilde{S}}_{31n}=o_p(n^{-1}h^{-1})$.

Using the similar process as those for the term ${\tilde{S}}_{31n}$, under Conditions A3−A7 in Appendix, we can justify that the terms ${\tilde{S}}_{321n}$, ${\tilde{S}}_{322n}$ and ${\tilde{S}}_{323n}$ have the following converging rates:

$$\begin{aligned} E(||{\tilde{S}}_{321n}||^2)= & {} O(\max \{h^{2\eta }_1, h^{2\eta }_1n^{-1}, h^{\eta }_1n^{-1}\})=o(n^{-1}h^{-1});\\ E(||{\tilde{S}}^2_{322n}||^2)= & {} O(\max \{h^{2\eta }_1, h^{2\eta }_1n^{-1}, h^{\eta }_1n^{-1}\})=o(n^{-1}h^{-1});\\ E(||{\tilde{S}}^2_{323n}||^2)= & {} O(\max \{h^{4\eta }_1, h^{4\eta }_1n^{-1}, h^{3\eta }_1n^{-1}\})=o(n^{-1}h^{-1}). \end{aligned}$$

To save the space, we omit some more detailed deductions. The Chebyshiev’s inequality yields that

$$\begin{aligned} {\tilde{S}}_{321n}=o_p(n^{-1/2}h^{-1});\ {\tilde{S}}_{322n}=o_p(n^{-1/2}h^{-1});\ {\tilde{S}}_{323n}=o_p(n^{-1/2}h^{-1}). \end{aligned}$$

As $||B_{1n}-B_1||=O_p(n^{-1/2})$, together with the above convergence rates, we have ${\tilde{S}}_{32n}=o_p(n^{-1}h^{-1})$. Combining the convergence rates of ${\tilde{S}}_{31n}$ and ${\tilde{S}}_{32n}$, we conclude ${\tilde{S}}_{3n}=o_p(n^{-1}h^{-q_1/2})$.

Now we discuss the convergence rate of the term $S_{5n}$. Note that

$$\begin{aligned} S_{5n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h}K_{B_{1n}B_{2n}ij}\epsilon _{i}[{\hat{g}}_j-g_j]\frac{{\hat{p}}_{j}}{p_{j}}\\&+\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n \frac{1}{h}K_{B_{1n}B_{2n}ij}\epsilon _{i}[{\hat{g}}_j-g_j]\left( \frac{{\hat{p}}_{j}-p_{j}}{p_{j}}\right) \\=: & {} {\tilde{S}}_{5n} + o_p({\tilde{S}}_{5n}). \end{aligned}$$

Substituting the kernel estimators ${\hat{g}}_j$ and ${\hat{p}}_j$ into ${\tilde{S}}_{5n}$, we have

$$\begin{aligned} {\tilde{S}}_{5n}= & {} \frac{1}{n(n-1)^2}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{k\ne j}^n\frac{1}{hh_1}\frac{1}{p_{j}}K_{B_{1n}B_{2n}ij}\epsilon _{i}Q_{B_{2n}jk}[g_k-g_j]. \end{aligned}$$

Adopting the similar process for dealing with the term $S_{1n}$ and $S_{3n}$, we can infer that replacing $B_{1n}$, $B_{2n}$ and ${\hat{\beta }}$ by $B_{1}$, $B_{2}$ and $\beta$ respectively does not influence the convergence rates of ${\tilde{S}}_{3n}$, namely,

$$\begin{aligned} {\tilde{S}}_{5n}= & {} {\tilde{S}}_{51n}+o_p({\tilde{S}}_{51n}), \end{aligned}$$

where

$$\begin{aligned} {\tilde{S}}_{51n}= & {} \frac{1}{n(n-1)^2}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{k\ne j}^n\frac{1}{hh_1}\frac{1}{p_{j}}K_{B_1B_2ij}\epsilon _{i}Q_{B_2jk}[{\tilde{y}}_k-g_j]. \end{aligned}$$

As $E[\epsilon _{i}|x_i,z_i]=0$, Fubini’s theorem and the properties of conditional expectation yield $E({\tilde{S}}_{51n})=0$. We then consider the second order moment of ${\tilde{S}}_{51n}$ as:

$$\begin{aligned}&E({\tilde{S}}^2_{51n})\\&\quad =E\bigg \{\frac{1}{n(n-1)^2}\sum _{i=1}^n\sum _{j \ne i}^n\sum _{k\ne j}^n \frac{1}{hh_1}\frac{1}{p_{j}}K_{B_1B_2ij} \epsilon _{i}Q_{B_2jk}[{\tilde{y}}_k-g_j]\bigg \}^2\\&\quad =E\bigg \{\frac{1}{n^2(n-1)^4}\frac{1}{h^{2}h^{2}_1}\sum _{i=1}^n\sum _{i \ne j}^n\sum _{k\ne j}^n\sum _{i'=1}^n\sum _{i' \ne j'}^n\sum _{k'\ne j'}^n\\&\qquad \frac{1}{p_{j}p_{j'}}K_{B_1B_2ij}K_{B_1B_2i'j'}Q_{B_2jk}Q_{B_2j'k'} \epsilon _{i}[{\tilde{y}}_k-g_j] \epsilon _{i'}[{\tilde{y}}_{k'}-g_{j'}]\bigg \}\\&\quad =E\bigg \{\frac{1}{n^2(n-1)^4}\frac{1}{h^{2}h^{2}_1}\sum _{i=1}^n\sum _{i \ne j}^n\sum _{k\ne j}^n\sum _{i'=1}^n\sum _{i' \ne j'}^n\sum _{k'\ne j'}^n \\&\qquad \frac{1}{p_{j}p_{j'}}K_{B_1B_2ij}Q_{B_2jk}K_{B_1B_2i'j'}Q_{B_2j'k'} \epsilon _{i}[g_{k}-g_j] \epsilon _{i'}[g_{k'}-g_{j'}]\bigg \} +o(n^{-2}h^{-2}). \end{aligned}$$

Note that $E[\epsilon _{i}\epsilon _{i'}|w_i, w_{i'}] \ne 0$ if and only if $i = i'$. Fubini’s theorem and the Lemma B.1, Lemmas 2 and 3 in Robinson (1988) altogether yields:

$$\begin{aligned}&E({\tilde{S}}^2_{51n})\\&\quad =\frac{1}{nh^{2}h^{2}_1}E\bigg \{ \frac{1}{p_{2}p_{4}}K_{B_1B_212}Q_{B_223}K_{B_1B_214}Q_{B_245}E[\epsilon ^2_{1}|w_1][g_{3}-g_2][g_{5}-g_{4}]\bigg \}\\&\quad =\frac{1}{nh^{2}h^{2}_1}E\bigg (\frac{1}{p_{2}p_{4}}K_{B_1B_212}K_{B_1B_214}E[\epsilon ^2_{1}|w_1]\\&\quad E_2\big \{Q_{B_123}[g_{3}-g_2]\big \}E_4\big \{Q_{B_145}[g_{5}-g_{4}]\big \}\bigg )\\&\quad \le \frac{h^{2\eta }_1}{nh^{2}}E\bigg [\frac{1}{p_{2}p_{4}}K_{B_1B_212}K_{B_1B_214} D_F(B^{\top }_2z_{2})D_{F}(B^{\top }_2z_{4})\bigg ]\\&\quad =O(h^{2\eta }_1n^{-1})=o(n^{-2}h^{-1}). \end{aligned}$$

The Chebyshiev’s inequality implies that ${\tilde{S}}_{51n}=o_p(n^{-1}h^{-1})$. Thus $S_{5n}=o_p(n^{-1}h^{-1})$.

Using the similar statement to deal with the terms $S_{1n}$, $S_{2n}$ and $S_{5n}$, we can conclude that $S_{4n}=o_p(n^{-1}h^{-1})$ and $S_{6n}=o_p(n^{-1}h^{-1})$.

To sum up, together with all the results about the terms $S_{in}$ for $i=1,\cdots ,6$, we conclude that

$$\begin{aligned} n hS_n {\mathop {\longrightarrow }\limits ^\mathrm{d}} N(0, s^2). \end{aligned}$$

To complete the proof of this theorem, we justify the consistency of $s^{2}_{n}$ to $s^2$, where $s^2_{n}$ is

$$\begin{aligned} s^2_{n}=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}^n\frac{1}{h^{2}}K^2_{B_{1n}B_{2n}ij}{\hat{\epsilon }}^2_{i}{\hat{\epsilon }}^2_{j}. \end{aligned}$$

Under the null hypothesis, since $B_{1n}$, $B_{2n}$ and ${\hat{g}}$ are uniformly consistent to $B_1$, $B_2$ and g, respectively, some elementary computations yield an asymptotic presentation:

$$\begin{aligned} s^2_{n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}^n \frac{1}{h^2} K^2_{B_1B_2ij}\epsilon ^2_{i}\epsilon ^2_{j} + o_p(1)=: {\tilde{s}}^2_{n}+ o_p(1). \end{aligned}$$

It is clear that ${\tilde{s}}^2_{n}$ is an $U-$statistic with kernel:

$$\begin{aligned} H(w_i,y_i, w_j, y_j)=\frac{1}{h^2} K^2_{B_1B_2ij}\epsilon ^2_{i}\epsilon ^2_{j}. \end{aligned}$$

We can easily show that the condition of lemma 3.1 of Zheng (1996) is satisfied. Based on U-statistic theory, it is easy to justify ${\tilde{s}}^2_{n}= E({\tilde{s}}^2_{n})+o(1)$, where

$$\begin{aligned} E({\tilde{s}}^2_{n})= & {} s^2+o(1)\\= & {} 2\int {}K^2(u,v)dudvE\{[Var(\varepsilon ^2|B^{\top }_1X,B^{\top }_2Z)]^2p(B^{\top }_1X,B^{\top }_2Z)\}+o(1). \end{aligned}$$

The more details can be found in Fan and Li (1996) and Zheng (1996). $\square$

Proof of Theorem 3.2

Here we use the similar notations as those in Theorem 3.1 of the main body. Define $K_{B_{1n}B_{2n}ij} = K((B^{\top }_1x_i -B^{\top }_1x_j)/h, (B^{\top }_2z_i -B^{\top }_2z_j)/h)$, $g_i = g(\theta ^{\top }z_i)$, ${\hat{g}}_i ={\hat{g}}({\hat{\theta }}^{\top }z_i)$, $\epsilon _{i}=y_i-\beta ^{\top }_1x_j-g_i$, ${\hat{\epsilon }}_{i}=y_i-{\hat{\beta }}^{\top }_1x_j-{\hat{g}}_i$, $p_i = p_{B_2}(B^{\top }_2z_i)$ and ${\hat{p}}_i = {\hat{p}}_{B_{2n}}(B^{\top }_{2n}z_i)$, ${\tilde{y}}_i=y_i-\beta ^{\top }x_i$. Throughout the proof of this theorem, $E_i(\cdot )=E(\cdot |B^{\top }_1x_i, B^{\top }_2z_i)$. Define the events $A_{1n} = \{T_n \le c\}$ for any constant c and $A_{2n} = \{{\hat{q}}_1 = q_1, {\hat{q}}_2 = q_2\}$. Proposition 2.1 and Lemma 3.1 purport that under the global and local alternative hypothesis, we have $\lim _{n\rightarrow \infty }P(A_{2n}) = \lim _{n\rightarrow \infty }P(A_{1n} \cap A_{2n})$. This result ensures that under the global and local alternative hypotheses, in an asymptotic sense it is only needed to consider the events ${\hat{q}}_1=q_1$ and ${\hat{q}}_2=q_2$.

Proof of Part (I). Under Conditions A1 and A2 in Appendix, due to the facts $||B_{1n}-B_1||=O_p(1/\sqrt{n})$ and $||B_{2n}-B_2||=O_p(1/\sqrt{n})$, ${\hat{g}}$ is an uniformly consistent estimator of g, see Fan and Gijbels (1996). It is easy to prove that under the global alternative hypothesis, we have

$$\begin{aligned} S_n= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}^n\frac{1}{h^{q_1+q_2}} K_{B_{1n}B_{2n}ij} {\hat{\epsilon }}_{i}{\hat{\epsilon }}_{j}\\= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}\frac{1}{h^{q_1+q_2}}K_{B_{1}B_{2}ij} \epsilon _{i}\epsilon _{j}+o_p(1), \end{aligned}$$

where $\epsilon _{i}=y_i-\beta ^{\top }_0x_i - g(\alpha ^{\top }_0z_i)$ with $(\beta _0, \alpha _0)=\arg \min _{\beta , \alpha } E[Y-\{\beta ^{\top } X+g(\alpha ^{\top } Z)\}]^{2}$. It is obvious that the term

$$\begin{aligned} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n\frac{1}{h}^{q_1+q_2}K_{B_{1}B_{2}ij} \epsilon _{i}\epsilon _{j} \end{aligned}$$

is an $U-$statistic with the kernel $\frac{1}{h^{q_1+q_2}}K_{B_{1}B_{2}ij} \epsilon _{i}\epsilon _{j}$.

Using the element properties of $U-$statistic and Fubini’s theorem, we have

$$\begin{aligned} S_n= & {} E\left\{ \frac{1}{h^{q_1+q_2}}K_{B_{1}B_{2}12} \epsilon _{1}\epsilon _{2}\right\} +o_p(1)\\= & {} E\{f^2(B^{\top }_1X,B^{\top }_2Z)p_{B_1B_2}(B^{\top }_1X,B^{\top }_2Z)\}+o_p(1)>0, \end{aligned}$$

where $p_{B_1B_2}$ stands for the density function of $(B^{\top }_1X,B^{\top }_2Z)$.

Additionally, applying the same argument as that in the justification of Theorem 3.1, we can prove that in probability $s^2_{n}$ converges to some positive value which may be different from $s^2$ in Theorem 3.1. Thus, altogether, we have

$$\begin{aligned} T_{n}/(n h) {\mathop {\longrightarrow }\limits ^{\mathrm {p}}} {Constant} >0. \end{aligned}$$

Proof Part (II): As the description as the proof of Part (I) in this theorem, here it is also only needed to consider the events ${\hat{q}}_1=q_1$ and ${\hat{q}}_2=q_2$ in an asymptotic sense. Under the local alternative hypotheses $H_{1n}$, using the similar statement as that used to justify Theorem 3.1, we can conclude that:

$$\begin{aligned} S_n= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j\ne i}^n \frac{1}{h^{q_1+q_2}} K_{B_{1n}B_{2n}ij} {{\hat{\epsilon }}_{i}{\hat{\epsilon }}_{j}}\\=: & {} Q_{n}+o_p(Q_n), \end{aligned}$$

where

$$\begin{aligned} Q_{n}=\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i \ne j}^n\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij} {\epsilon _{i}\epsilon _{j}}, \end{aligned}$$

with $\epsilon _{i}=y_i-\beta ^{\top }_0x_i + g(\alpha ^{\top }_0z_i)$. Let $\varepsilon _i=y_i-\beta ^{\top }_0x_i - g(\alpha ^{\top }_0z_i)-C_n f(B^{\top }_1x_i,B^{\top }_2z_i)$. Then we have $\epsilon _{i}=\varepsilon _i+C_n f(B^{\top }_1x_i,B^{\top }_2z_i)$ and $E[\varepsilon _i|w_i]=0$. Furthermore, $Q_{n}$ is decomposed as:

$$\begin{aligned} Q_{n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij}[\varepsilon _i+C_n f(B^{\top }_1x_i,B^{\top }_2z_i)]\\&[\varepsilon _j+C_n f(B^{\top }_1x_j,B^{\top }_2z_j)]\\=: & {} Q_{1n}+C_nQ_{2n}+C^2_nQ_{3n}, \end{aligned}$$

where $Q_{1n}$, $Q_{2n}$ and $Q_{3n}$ have the following forms as:

$$\begin{aligned} Q_{1n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij} \varepsilon _i\varepsilon _j;\\ Q_{2n}= & {} \frac{2}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij} f(B^{\top }_1x_i,B^{\top }_2z_i)\varepsilon _j;\\ Q_{3n}= & {} \frac{1}{n(n-1)}\sum _{i=1}^n\sum _{j \ne i}^n\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij}f(B^{\top }_1x_i,B^{\top }_2z_i)f(B^{\top }_1x_j,B^{\top }_2z_j). \end{aligned}$$

Again following the similar argument to that in the justification of Theorem 3.1, we can easily obtain that $nh^{\frac{q_1+q_2}{2}}Q_{1n}{\mathop {\longrightarrow }\limits ^{\mathrm {d}}} N(0,s^2)$ and thus $Q_{1n}=O_p(n^{-1}h^{-\frac{q_1+q_2}{2}}).$

Then we consider the term $Q_{2n}$. In fact, $Q_{2n}$ can be written as $U-$statistic with the kernel:

$$\begin{aligned} H_n(t_i,t_j)=\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij} \{f(B^{\top }_1x_i,B^{\top }_2z_i)\varepsilon _j+f(B^{\top }_1x_j,B^{\top }_2z_j)\}\varepsilon _i\}, \end{aligned}$$

where $t_i=(x_i, z_i, y_i)$. Since $E[\varepsilon _j|x_i, z_i]=0$, then $E[H(t_i,t_j)]=0$. To use the properties of a non-degenerate U-statistic (Serfling 1980), it is essential to prove $E[H^2(t_i,t_j)] = o(n)$. Note that

$$\begin{aligned} E[H^2_n(t_i, t_j)]\le & {} 4E[\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij}f(B^{\top }_1x_i,B^{\top }_2z_i)\varepsilon _j]^2\\= & {} \frac{4}{h^{q_1+q_2}}E[\frac{1}{h^{q_1+q_2}}K_{B_{1}B_{2}12}f^2(B^{\top }_1x_1,B^{\top }_2z_1)E(\varepsilon ^2_2|B^{\top }_1x_2,B^{\top }_2z_2)]. \end{aligned}$$

By the application of Fubini’s theorem and the change of the original variables to be $v_1=(B^{\top }_1x_2-B^{\top }_1x_1)/h$ and $v_2=(B^{\top }_2z_2-B^{\top }_2z_1)/h$ yield

$$\begin{aligned} E[H^2_n(t_i, t_j)]= & {} \frac{4}{h^{q_1+q_2}}\int _{{\mathbb {R}}^{q_1+q_2}} K(v)dv E[ f^2(B^{\top }_1x_1,B^{\top }_2z_1)\\&E(\varepsilon ^2_2|B^{\top }_1x_2,B^{\top }_2z_2)] +o\left( \frac{1}{h^{q_1+q_2}}\right) \\ {}= & {} O\left( \frac{1}{h^{q_1+q_2}}\right) =o(n). \end{aligned}$$

We now turn to discuss the conditional expectation of $H_n(t_i, t_j)$. By Fubini’s theorem, it is easy to calculate $r_n(t_i)=E\{H_n(t_i, t_j)|t_i\}$ to be

$$\begin{aligned} r_n(t_i)= & {} \frac{1}{h^{q_1+q_2}} E\{K_{B_{1}B_{2}ij}f(B^{\top }_1x_j,B^{\top }_2z_j)\varepsilon _i|t_i\}\\= & {} \varepsilon _i \int _{{\mathbb {R}}^{q_1}} \int _{{\mathbb {R}}^{q_2}} K(v_1,v_2)f(B^{\top }_1x_i-hv_1,B^{\top }_2z_i-hv_2)\\&p_{B_1B_2}(B^{\top }_1x_i-hv_1,B^{\top }_2z_i-hv_2)dv_1dv_2du\\= & {} \varepsilon _if(B^{\top }_1x_i,B^{\top }_2z_i)p_{B_1B_2}(B^{\top }_1x_i,B^{\top }_2z_i)+l_n(t_i)\\=: & {} m(t_i)+l_n(t_i). \end{aligned}$$

Let ${\tilde{Q}}_{2n}$ denote the “projection" of the statistic $Q_{2n}$ as:

$$\begin{aligned} {\tilde{Q}}_{2n}= & {} \frac{1}{n}\sum _{i=1}^nr_n(t_i)=\frac{1}{n}\sum _{i=1}^nm(t_i)+\frac{1}{n}\sum _{i=1}^nl_n(t_i)\\=: & {} Q_{21n}+Q_{22n}. \end{aligned}$$

Central-limit theorem yields that $\sqrt{n}Q_{21n}=O_p(1)$. As the functions $g(\cdot ,\cdot )$ and $p_{B_1B_2}(\cdot ,\cdot )$ satisfy the Lipschitz condition, we have $E\{l^2_n(t_i)\}=O(h^2)\rightarrow 0$. Note that $E\{l_n(t_i)\}=0$. We can conclude that $\sqrt{n}Q_{22n}=o_p(1)$. Therefore, altogether, $Q_{2n}=O_p(1/\sqrt{n})$. Under the local alternative hypothesis, $C_nQ_{2n}=O_p(C_n/\sqrt{n})$.

Finally consider the term $C^2_nQ_{3n}$. It is obvious that $Q_{3n}$ is also an $U-$statistic with the kernel:

$$\begin{aligned} H_n(t_i,t_j)=\frac{1}{h^{q_1+q_2}} K_{B_{1}B_{2}ij}f(B^{\top }_1x_i,B^{\top }_2z_i)f(B^{\top }_1x_j,B^{\top }_2z_j) \end{aligned}$$

with $t_i=(x_i,z_{i}, y_i)$. Using the element characteristic of $U-$statistic, we have

$$\begin{aligned} Q_{3n}= & {} E(H_n(t_i,t_j))+o_p(1)\\= & {} \frac{1}{h^{q_1+q_2}} E[K_{B_{1}B_{2}ij} f(B^{\top }_1x_i,B^{\top }_2z_i)f(B^{\top }_1x_j,B^{\top }_2z_j)]+o_p(1). \end{aligned}$$

Again, we can derive that $E\{H_n(t_i,t_j)\}=\mu _1+o(1)$ with

$$\begin{aligned} \mu _1=E\{f^2(B^{\top }_1X,B^{\top }_2Z)p_{B_1B_2}(B^{\top }_1X,B^{\top }_2Z)\}. \end{aligned}$$

Therefore, we have $Q_{3n}=\mu _1+o_p(1)$. The above equation implies $C^2_nQ_{3n}=O_p(C^2_n)$. Altogether, we have

$$\begin{aligned} Q_{1n}=O_p(n^{-1}h^{-\frac{q_1+q_2}{2}});\ \ C_nQ_{2n}=O_p(C_n/\sqrt{n});\ \ C^2_nQ_{3n}=O_p(C^2_n). \end{aligned}$$

Additionally, following the similar arguments for proving Theorem 3.1, $s^2_{n} {\mathop {\longrightarrow }\limits ^{\mathrm {p}}} s^2$. Therefore, we have the following conclusions.

If $q_1=q_2=1$ and $C_n = n^{-1/2}h^{-1/2}$, $Q_{1n}$ and $Q_{3n}$ are the leading terms of $Q_n$, which yields that

$$\begin{aligned} T_n {\mathop {\longrightarrow }\limits ^{d}} N(u, 1), \end{aligned}$$

where $u=E\{f^2(B^{\top }_1X,B^{\top }_2Z)p_{B_1B_2}(B^{\top }_1X,B^{\top }_2Z)\}/s$.

If $q_1=q_2=1$ and $C_n n^{1/2}h^{1/2} \rightarrow \infty$, $Q_{3n}$ is the leading term of $Q_n$. This implies that

$$\begin{aligned} T_n/(C^2_nnh){\mathop {\longrightarrow }\limits ^{\mathrm {P}}} {u} >0. \end{aligned}$$

If $q_1+q_2>2$, if $C_nn^{1/2} h^{1/2}\rightarrow c_0>0$ for some constant $c_{0}$ or $C_nn^{1/2} h^{1/2}\rightarrow \infty$ and $C_nn^{1/2} h^{(q_1+q_2)/4}\rightarrow 0$, $Q_{1n}$ is the leading term of $Q_n$, then we have

$$\begin{aligned} T_n/h^{(q_1+q_2-2)/2} {\mathop {\longrightarrow }\limits ^{\mathrm {d}}} N(0,1). \end{aligned}$$

If $q_1+q_2>2$, if $C_n=n^{-1/2} h^{-(q_1+q_2)/4}$, $Q_{1n}$ and $Q_{3n}$ are the leading terms of $Q_n$, thus, we have

$$\begin{aligned} T_n/h^{(q_1+q_2-2)/2} {\mathop {\longrightarrow }\limits ^{\mathrm {d}}} N(u,1). \end{aligned}$$

If $q_1+q_2>2$ and $C_nn^{1/2} h^{(q_1+q_2)/4}\rightarrow \infty$, $Q_{3n}$ is the leading term of $Q_n$. This implies that

$$\begin{aligned} T_n/(C^2_nnh){\mathop {\longrightarrow }\limits ^{\mathrm {P}}} {u} >0. \end{aligned}$$

The proof is finished. $\square$