1 Introduction

Testing the validity of a specified model up to some unknown parameters is an important issue in statistical inference. A long-standing focus for this model checking problem is their sensitivity to outlying observations or heavy-tailed distributions. This is because these observations may have destructive effects even though with small violation in usual observations. However, in the past decades, researchers have made more efforts on robust estimation, but paid less attention to robust hypothesis testing. Therefore, it is critical to develop a robust test that can be against outlier contamination.

Sample containing outliers or contaminated data is not uncommon and an ubiquitous problem in many disciplines, for example clinical trials, medical research, longitudinal studies, and so forth. When there exist outliers in the data, robust statistical inference procedures can improve the accuracy and reliability of statistical analyses. The purpose of robust hypothesis testing is twofold, just as stated in Heritier and Ronchetti (1994): One is that under small and arbitrary departures from the null hypothesis, the level of a test should be stable, which is called the robustness of validity; the other is that the test can still make a good power performance under small and arbitrary departures from specified alternatives, that is called the robustness of efficiency. Wang and Qu (2007) suggested a robust version of Zheng’s (1996) test. Their numerical studies also showed the necessity of using a robust testing procedure: the effect of outliers on Zheng’s original test is dramatic and destructive so that it cannot maintain the significance level.

Many efforts have been devoted to the development of robust testing procedures. For linear regression models, Schrader and Hettmansperger (1980) proposed the \(\rho _c\) test based on Huber’s M estimators; Markatou and Hettmansperger (1990) introduced an aligned generalized M test for testing subhypotheses in general linear models, which is a robustification of the well-known F test and can be viewed as a generalization of Sen’s (1982) M test for linear models. Afterward, Heritier and Ronchetti (1994) and Markatou and Manos (1996) presented robust versions of the Wald, score and drop-in-dispersion tests for general parametric models and nonlinear regression models, respectively. Wang and Qu (2007) developed a robust approach for testing the parametric form of a regression function versus an omnibus alternative, which can be viewed as a robustification of a smoothing-based conditional moment test. Feng et al. (2015) recommended a robust testing procedure to make comparison of two regression curves through combining a Wilcoxon-type artificial likelihood function with generalized likelihood ratio test.

There are a number of proposals available in the literature on testing consistently the correct specification of a parametric regression model. Most of existing test procedures can be classified into two categories: global smoothing tests and local smoothing tests. As mentioned in a comprehensive review paper of González-Manteiga and Crujeiras (2013), the global smoothing tests mainly involve empirical process, which can avoid subjective selection of the smoothing parameter, such as bandwidth; the local smoothing tests are based on nonparametric smoothing techniques such as Nadaraya–Watson kernel estimation (Nadaraya 1964; Watson 1964), smoothing spline estimation or other local smoothing techniques. Examples of global smoothing tests include Bierens (1990), Bierens and Ploberger (1997), Stute (1997), Stute et al. (1998b), Whang (2000), Escanciano (2006a), among many others. This class of methods enjoys fast convergence rate of order \(O(n^{-1/2})\) (see Stute et al. (1998a)). However, this type of tests is often less sensitive to high-frequency models. To certain extent, this shortcoming makes their practical limitation since it is not uncommon to have high-order or high-frequency models. Also, in higher than 2-dimensional scenarios, the limiting null distribution is usually intractable which requires the assistance from resampling approximation to determine critical values. Further, the power performance in high-dimensional cases is not very encouraging.

As for local smoothing tests, examples include the tests suggested by Härdle and Mammen (1993), Zheng (1996), Fan et al. (2001), Horowitz and Spokoiny (2001), Koul and Ni (2004), and Van Keilegom et al. (2008). Since they must involve multivariate nonparametric function estimation procedures and thus inevitably and severely suffer from the curse of dimensionality when the number of covariates is large, even moderate. This typical problem is a big obstacle for local smoothing tests to well maintain the significance level and to sense the alternative models. Because of the data sparseness in multi-dimensional space, the behavior of nonparametric smooth estimators very quickly deteriorates as the dimension increases, see Stone (1980). Further, even when there are no outliers, local smoothing tests have the typical slow convergence rate of order \(O(n^{-1/2}h^{-p/4})\) to their limits when p is large where p is the number of covariates. Besides, a suitable choice of smooth parameter is difficult but necessary for these tests. Although existing empirical studies show that the effect of bandwidth selection is not too profound in small p situations, how to make a practically suitable bandwidth choice is still a long-standing problem when the dimension p is relatively large.

The above observations suggest that a common difficulty both global and local smoothing test procedures suffer from is the data sparseness in high-dimensional space even for large sample sizes (see Escanciano (2007)). To attack this challenge, a representative method documented as projection-pursuit technique was proposed and experimented. The significant feature of this method is to employ the projections of original data onto one-dimensional subspaces: first projecting the original high-dimensional covariates to one-dimensional space to form a linear combination and a test can be obtained as an average of tests based on these selected combinations, see Huber (1985) for detail. Escanciano (2006b) proposed a consistent test for the goodness of fit of parametric regression models, which applied a residual marked empirical process. Some earlier references include Zhu and Li (1998) who suggested a test that is based on an unweighted integral of expectations with respect to all one-dimensional directions. Zhu and An (1992) could be an earlier reference that had already used this idea to deal with a relevant testing problem. Zhu (2003) constructed a lack-of-fit test via seeking for a good projection direction for plotting to achieve the dimension reduction aim. Lavergne and Patilea (2008) introduced the projection-pursuit technique to local smoothing-based tests to avoid the effect of dimension. Afterward, Lavergne and Patilea (2012) suggested a smooth integrated conditional moment (ICM) test. This test is an omnibus test based on the kernel estimation that performs against a sequence of directional nonparametric alternatives as if there were only one covariate whatever the number of covariates is. All of these tests either have no tractable sampling and limiting null distributions or have tractable limiting null distributions that are not useful for the significance level maintenance if critical values are determined by them. Thus, resampling/bootstrap approximations are commonly resorted to determine critical values. However, the algorithm of approximation is very computationally intensive when all projections are involved. Stute and Zhu (2002) simply used a one-dimensional projected covariate that is a linear combination of all covariates to alleviate this typical dimensionality problem. But the disadvantage is also obvious: it is a directional rather than an omnibus test which cannot detect general alternatives. Another relevant reference is Stute et al. (2008) who also suggested a dimension reduction test that is based on the residual empirical process marked by a set of functions of covariates. This test relies solely on selecting proper functions for the significance level maintenance and power enhancement. A data-driven selection procedure would be in demand.

Recently, a dimension reduction model–adaptive test is proposed by Guo et al. (2016), which is an omnibus test against global alternative models. This local smoothing test procedure introduces a novel model–adaptation concept in model checking for parametric regression models. The test statistic under the hypothetical model can converge to its limit at the rate of order \(O(n^{-1/2}h^{-1/4})\) and detect local alternatives distinct from the null model at this rate, which is not affected by the number of covariates. Their test behaves like a local smoothing test as if the number of covariates were one. Another superiority is that it owns tractable limiting null distribution and can work very well even with moderate sample sizes without the assistance of resampling approximation to determine critical values.

All of the above tests can avoid the curse of dimensionality to some extent; they are, however, not robust against outliers, and their efficiency is adversely affected by outlying observations. Our subsequent numerical analysis suggests that the test proposed by Guo et al. (2016) fails to work when there exist outliers because a linear local average of the responses is not robust, as elaborated in Härdle (1992). To tickle this problem, we incorporate the idea in Guo et al. (2016) into a robust model–adaptive smoothing-based conditional moment test. It can possess the robustness property and simultaneously solve the dimensionality problem.

The hypothetical model is the following with a dimension reduction structure:

$$\begin{aligned} Y=g(\beta ^\top X,\theta )+\varepsilon , \end{aligned}$$
(1)

where Y is the response with the covariate vector \(X\in \mathbf R ^p\). The random error term \(\varepsilon \) and X are independent. \(\beta \) and \(\theta \) are unknown parameter vectors of dimensions p and d, respectively. In addition, \(g(\cdot )\) is a known function and the superscript \(\top \) denotes transposition. As we often have no much information in advance on model structure when this parametric structure assumption is false, a general alternative model is considered as follows:

$$\begin{aligned} Y=m(B^\top X)+\varepsilon , \end{aligned}$$
(2)

where \(m(\cdot )\) is an unknown smooth function and \(\varepsilon \) denotes the error. Here, \(\varepsilon \) is independent of X. B is an unknown \(p\times q\) orthonormal matrix for an unknown integer q with \(1\le q\le p\). This model treats the nonparametric regression \(Y=m(X)+\varepsilon \) as a special case in which the matrix \(B=I_p\) with \(q=p\).

In this paper, we construct a robust dimension reduction adaptive-to-model test (R-DREAM). It sufficiently invokes the information in both the null and alternative models to get rid of curse of dimensionality and employs centered asymptotic rank transformation technique to achieve the goal of robustness. We further study the local robustness via influence function analysis, which indicates that our R-DREAM has first-order influence function of zero and second-order influence function bounded in the response direction. Therefore, it is argued that our test can have more stable and robust performance when there are outliers in responses than existing local smoothing tests. It is worthwhile to point out that our test is mainly robust against the error’s distribution and does not need to impose strong conditions on it. However, as the test is for the regression mean function, the second moments of X is required to derive the asymptotic properties. Thus, like Wang and Qu (2007) and Feng et al. (2015), it cannot handle models without moments of covariates. This deserves a further investigation.

The rest of this article is organized as follows. In Sect. 2, the test is constructed. The approaches to estimate the matrix B and to identify its structure dimension q are also stated in this section. Section 3 presents the large sample properties under the null, global and local alternative hypothesis. The local robustness properties through the Hampel influence function analysis are also discussed in this section. Numerical studies including simulation studies and a real data analysis are, respectively, reported in Sects. 4 and 5. All of the proofs are relegated to “Appendix”.

2 A robust dimension reduction adaptive-to-model test

As discussed before, the hypotheses of interest are:

$$\begin{aligned}&H_0: Y=g(\beta ^\top X,\theta )+\varepsilon ~\text{ for } \text{ some }~\beta \in R^p, \theta \in R^d;\nonumber \\&H_1: Y=m(B^\top X)+\varepsilon ~\text{ and }~m(B^\top X)\ne g(\beta ^\top X,\theta )~\text{ for } \text{ any }~\beta \in R^p, \theta \in R^d,~~~~~~~~~ \end{aligned}$$
(3)

where \(g(\cdot )\) is a known link function and \(m(\cdot )\) is an unknown link function. \(\beta \) and \(\theta \) are, respectively, the parameter vectors of p and d dimensions. \(\varepsilon \) denotes the error, which is independent of X. B is a \(p\times q\) orthonormal matrix where \(B^\top B=I_q\) and \(1\le q\le p\).

2.1 Test statistic construction

Denote \(e=Y-g(\beta ^\top X,\theta )\) and let \(e^\star =H(e)-1/2\), where \(H(\cdot )\) is the cumulative distribution function of e and H(e) follows uniformly distributed on (0, 1). Under the null hypothesis \(H_0\),

$$\begin{aligned} E(e^\star |X)=E\left\{ H(e)-\frac{1}{2}|X\right\} =0. \end{aligned}$$
(4)

In this case, the model (1) is with \(q=1\), and

$$\begin{aligned} E(e^\star |X)=0\Rightarrow E(e^\star |\beta ^\top X)=E(e^\star |B^\top X)=0. \end{aligned}$$

Further, the following formula

$$\begin{aligned} E\{e^\star E(e^\star |B^\top X)f(B^\top X)\}=E\left\{ \left( E(e^\star |B^\top X)\right) ^2 f(B^\top X)\right\} =0 \end{aligned}$$
(5)

holds under \(H_0\), where \(f(\cdot )\) is the probability density function of \(B^\top X\).

Under \(H_1\), we have \(e=Y-g(\beta ^\top X,\theta )=m(B^\top X)-g(\beta ^\top X,\theta )+\varepsilon \). The conditional expectation \(E(e^\star |X)\) is

$$\begin{aligned} E(e^\star |X) =E\left\{ H\left( m(B^\top X)-g(\beta ^\top X,\theta )+\varepsilon \right) -\frac{1}{2}\Big |X\right\} . \end{aligned}$$
(6)

When \(P(m(B^\top X)-g(\beta ^\top X,\theta )=C)=1\), the conditional expectation \(E(e^\star |X)\) reduces to the unconditional expectation \(E(e^\star )=E(H(e)-1/2)=0\). Here, the event that \(E(e^\star |X)\) equals to zero occurs only when \(P(m(B^\top X)-g(\beta ^\top X,\theta )=C)=1\) for some constant C, which only holds under the null hypothesis \(H_0\). Since we can enlarge the null class of models by including some location shifts, if \(g(\beta ^\top X,\theta )\) belongs to the null class of models, then so does \(g(\beta ^\top X,\theta )+C\). In other words, it is reasonable to assume that the null class of models is sufficiently general to contain all location shifts in the Y direction. However, under \(H_1\), \(P(m(B^\top X)-g(\beta ^\top X,\theta )=C)\ne 1\) holds. Hence, the conditional expectation \(E(e^\star |X)\) is not equal to zero but relates to X. Different values of X would make different values of the conditional expectation \(E(e^\star |X)\). Therefore, when \(H_1\) holds, \(E(e^\star |X)\) is not equal to zero; further,

$$\begin{aligned} E(e^\star |X)\ne 0\Rightarrow E(e^\star |B^\top X)\ne 0. \end{aligned}$$

Thus, we have

$$\begin{aligned} E\{e^\star E(e^\star |B^\top X)f(B^\top X)\}=E\left\{ \left( E(e^\star |B^\top X)\right) ^2 f(B^\top X)\right\} >0. \end{aligned}$$
(7)

Based on the different performances of \(E\{e^\star E(e^\star |B^\top X)f(B^\top X)\}\) under \(H_0\) and \(H_1\) in (5) and (7), respectively, its empirical version can be used as a test statistic. The null hypothesis \(H_0\) is rejected for large values of the test statistic.

Given a random sample \(\{(y_1,x_1), (y_2,x_2),\ldots ,(y_n,x_n)\}\), define the asymptotic rank transform of \(\hat{e}_i=y_i-g(\hat{\beta }^\top x_i,\hat{\theta })\) as \(n^{-1}\sum _{l=1}^n I(\hat{e}_l\le \hat{e}_i)\) where \(\sum _{l=1}^n I(\hat{e}_l\le \hat{e}_i)\) is the rank of \(\hat{e}_i\) among all of the n residuals. Here, \(\hat{\beta }\) and \(\hat{\theta }\) come from robust estimates of \(\beta \) and \(\theta \). Further, the corresponding centered asymptotic rank transform of residuals is as follows

$$\begin{aligned} \hat{e}_i^\star =\frac{1}{n}\sum _{l=1}^n I(\hat{e}_l\le \hat{e}_i)-\frac{n+1}{2n},~~l=1,\ldots ,n, \end{aligned}$$
(8)

where \(I(\cdot )\) is the indicator function.

Once an estimator of \(\hat{B}(\hat{q})\) is available, a kernel estimator of the regression function \(E(e^\star _i|B^\top X_i)\) can be estimated as follows:

$$\begin{aligned} \hat{E}(e^\star _i|\hat{B}(\hat{q})^\top x_i)=\frac{\frac{1}{n-1}\sum _{j\ne i}^n \hat{e}_j^\star {\mathcal {K}}_h\{\hat{B}(\hat{q})^\top (x_i-x_j)\}}{\hat{f}(\hat{B}(\hat{q})^\top x_i)}, \end{aligned}$$

where \(\hat{e}_j^\star \) has been defined in (8). \(\hat{B}(\hat{q})\) is an sufficient dimension reduction (SDR) estimate of the matrix B with an estimated structural dimension \(\hat{q}\) of q and the estimates will be specified later. Besides, \({\mathcal {K}}_h(\cdot )={\mathcal {K}}(\cdot /h)/h^{\hat{q}}\), where \({\mathcal {K}}(\cdot )\) is a \(\hat{q}\)-dimensional kernel function and h is the bandwidth, and \(\hat{f}(\hat{B}(\hat{q})^\top x_i)\) is a kernel estimator of the density function of \(f(B^\top x_i)\),

$$\begin{aligned} \hat{f}(\hat{B}(\hat{q})^\top x_i)=\frac{1}{n-1}\sum _{j\ne i}^n {\mathcal {K}}_h\{\hat{B}(\hat{q})^\top (x_i-x_j)\}. \end{aligned}$$

Further, a robust dimension reduction adaptive-to-model test (R-DREAM) can be constructed as follows:

$$\begin{aligned} V_n=\frac{1}{n(n-1)} \sum _{i=1}^n\sum _{j\ne i}^n {\mathcal {K}}_h\{\hat{B}(\hat{q})^\top (x_i-x_j)\}\hat{e}_i^\star \hat{e}_j^\star . \end{aligned}$$
(9)

Remark 1

From the above construction of \(V_n\) in (9), it seems that except for the estimates of the matrix B and structural dimension q, the test statistic makes no difference with the test proposed by Wang and Qu (2007) as follows:

$$\begin{aligned} \tilde{V}_n=\frac{1}{n(n-1)} \sum _{i=1}^n\sum _{j\ne i}^n \tilde{{\mathcal {K}}}_h (x_i-x_j)\hat{e}_i^\star \hat{e}_j^\star , \end{aligned}$$
(10)

where \(\tilde{{\mathcal {K}}}_h(\cdot )=\tilde{{\mathcal {K}}}(\cdot /h)/h^p\) with \(\tilde{{\mathcal {K}}}(\cdot )\) being a p-dimensional kernel function. Comparing the test statistic in (9) with that in (10), we note that \(\hat{q}\)-dimensional kernel function (\(\hat{q}\le p\)) is required in \(V_n\). The result in Sect. 3 shows that under the null hypothesis \(H_0\), \(\hat{q} = 1\) with a probability going to one, which can avoid the curse of dimensionality greatly. Another superiority of the new test is the model–adaptive property, that is, through estimating the matrix B, the test can automatically adapt the hypothetical and alternative model such that it can have better performance in the significance level maintenance and power enhancement. To be specific, under \(H_0\), \(\hat{B}(\hat{q})\rightarrow c\beta \) for a constant c, and under \(H_1\) \(\hat{q}= q\ge 1\) with a probability going to one, \(\hat{B}(\hat{q})\rightarrow BC\) for a \(q\times q\) orthogonal matrix C, adaptive to the alternative model (2).

Remark 2

Another related test is the dimension reduction model–adaptive test \(T_n^\mathrm{GWZ}\) proposed by Guo et al. (2016):

$$\begin{aligned} T_n^\mathrm{GWZ}=\frac{1}{n(n-1)} \sum _{i=1}^n\sum _{j\ne i}^n {\mathcal {K}}_h\{\hat{B}(\hat{q})^\top (x_i-x_j)\}\hat{e}_i\hat{e}_j. \end{aligned}$$
(11)

In Sect. 3.3, we will show through Hampel influence function analysis that R-DREAM has more stable and robust behavior than \(T_n^\mathrm{GWZ}\) when the response is contaminated.

2.2 Identification and estimation of B

As the estimates of the matrix B and structural dimension q are crucial for our R-DREAM, we first specify the estimate for the matrix B under given q and then study how to select q consistently. The method to estimate B is inspired by sufficient dimension reduction technique. In fact, B is not identifiable since for any \(q\times q\) orthogonal matrix C, \(m(B^\top X)\) can always be rewritten as \(\tilde{m}(C^\top B^\top X)\). Therefore, what we can identify is the space spanned by B via sufficient dimension reduction technique, or in other words, we can identify q base vectors of the space spanned by B. In view of easy operation, good performance and robustness of DEE, we consider to employ it to estimate B. One can read Zhu et al. (2010) to get the details on SIR-based DEE method and Guo et al. (2016) also gives a simple review of it.

Compared with SIR, DEE can avoid selecting the number of slices as there is no optimal solution. Define the new response variable \({\mathcal {U}}(t)=I(Y\le t)\) for any t, where the indicator function \(I(Y\le t)\) takes the value 1 if \(Y\le t\) and 0, otherwise. When SIR is applied, the original related matrix \({\mathcal {M}}(t)\) based on SIR is a \(p\times p\) positive semi-definite matrix such that \(span\{{\mathcal {M}}(t)\}={\mathcal {S}}_{{\mathcal {U}}(t)|X}\). Here, \({\mathcal {S}}_{{\mathcal {U}}(t)|X}\) is the central subspace of \({\mathcal {U}}(t)|X\). Given \({\mathcal {M}}=E\{{\mathcal {M}}(T)\}\), according to Theorem 1 in Zhu et al. (2010), \(span\{{\mathcal {M}}\}={\mathcal {S}}_{Y|X}\). In our paper, since \({\varepsilon }\bot \!\!\!\bot X\) is assumed and thus we get \({\mathcal {S}}_{Y|X}={\mathcal {S}}_{E(Y|X)}\), where the later is the central mean subspace of Y given X.

Based on the above description, estimating \({\mathcal {S}}_{E(Y|X)}\) amounts to estimating \({\mathcal {M}}\). Given the sample \(\{(y_1,x_1), (y_2,x_2),\ldots ,(y_n,x_n)\}\), we define the dichotomized responses as \(u_i(y_j)=I(y_i\le y_j),\,\,i,j=1,\ldots ,n\). Thus, for each fixed \(y_j\), we can obtain a new sample \(\{(u_1(y_j),x_1), (u_2(y_j),x_2),\ldots ,(u_n(y_j),x_n)\}\) and the estimate \({\mathcal {M}}_n(y_j)\) of \({\mathcal {M}}(y_j)\) can be gained with SIR. Thus, \({\mathcal {M}}\) can be estimated as

$$\begin{aligned} {\mathcal {M}}_{n,n}=n^{-1}\sum _{j=1}^n{\mathcal {M}}_n(y_j), \end{aligned}$$
(12)

which has been proved to be root-n consistent to \({\mathcal {M}}\) by Zhu et al. (2010). The q eigenvectors of \({\mathcal {M}}_{n,n}\) corresponding to its q largest eigenvalues are applied to estimate B. For this method, a mild linearity condition is assumed: \(E(X|B^\top X=z)\) is linear in z (Li 1991).

2.3 Identification of B and Estimation of the structural dimension q

In order to get R-DREAM in (9), the estimate of structural dimension q is necessary for the above method of identifying B. Here, a ridge-type ratio estimate (RRE) method, which is inspired by Xia et al. (2015), is suggested to determine q for DEE. It is based on the ratios of the eigenvalues with an artificially added ridge value c. Denote \(\hat{\lambda }_1\ge \hat{\lambda }_2\ge \cdots \ge \hat{\lambda }_p\) to be the eigenvalues of \({\mathcal {M}}_{n,n}\) in (12). \(\hat{q}\) can be obtained as

$$\begin{aligned} \hat{q}=\arg \min _{k=1,\ldots ,p-1}\frac{\lambda _{k+1}+c}{\lambda _k+c}, \end{aligned}$$

where the constant \(c=1/\sqrt{nh}\) is recommended. The consistencies of \(\hat{q}\) under the null hypothesis (1) and global alternative hypothesis (2) are shown in the following lemma.

Lemma 1

Assume that the DEE-based matrix \({\mathcal {M}}_{n,n}\) is root-n consistent to \({\mathcal {M}}\). Then, the corresponding estimate \(\hat{q}= q\) (under \(H_0\), \(q=1\)) with a probability going to one as \(n\rightarrow \infty \). Therefore, for a \(q\times q\) orthogonal matrix C, \(\hat{B}(\hat{q})\) is a root-n consistent estimate of \(BC^\top \).

3 Asymptotic properties

In this section, the large sample properties of the R-DREAM test statistic \(V_n\) in (9) are investigated via its asymptotic distributions under the null hypothesis, global alternative hypothesis and local alternative hypothesis. The robustness properties of our proposed test are also studied through Hampel influence function analysis.

3.1 Limiting null distribution

The asymptotic normality discussed in the following requires that the regression parameter is root-n consistently estimated under \(H_0\) and the residuals must come from a robust fit. Let \(Z=B^\top X\) and

$$\begin{aligned} Var=\frac{1}{72}\int {\mathcal {K}}^2(u)\mathrm{d}u\int p^2(z)\mathrm{d}z, \end{aligned}$$

where p(z) is the probability density function of Z. Moreover, Var can be consistently estimated by:

$$\begin{aligned} \widehat{Var}=\frac{1}{72n(n-1)}\sum _{i=1}^n\sum _{j\ne i}^n \frac{1}{h^{\hat{q}}}{\mathcal {K}}^2\left\{ \frac{\hat{B}(\hat{q})^\top (x_i-x_j)}{h}\right\} . \end{aligned}$$

We first state the asymptotic property of the R-DREAM test statistic in (9) under the null hypothesis \(H_0\) as follows:

Theorem 1

Suppose that conditions (C1)–(C8) in Appendix hold. Under \(H_0\), we have

$$\begin{aligned} nh^{1/2}V_n\Rightarrow N(0, Var). \end{aligned}$$

Plugging in a consistent estimator of Var, a standardized version of \(V_n\) can be defined as

$$\begin{aligned} S_n=\frac{n-1}{n}\frac{nh^{1/2}V_n}{\sqrt{\widehat{Var}}}. \end{aligned}$$
(13)

The following corollary can be easily obtained.

Corollary 1

Under \(H_0\) and Conditions (C1)–(C8) in Appendix, we have

$$\begin{aligned} S_n^2\Rightarrow \chi _1^2, \end{aligned}$$

where \(\chi _1^2\) is the Chi-square distribution with one degree of freedom.

Theorem 1 and Corollary 1 characterize the asymptotic properties of the test statistic \(V_n\). Based on Corollary 1, p-values of R-DREAM can be easily determined by the quantiles of the Chi-square distribution with one degree of freedom. The null hypothesis \(H_0\) is rejected when \(S_n\ge \chi ^2_{1-\alpha }(1)\) where \(\chi ^2_{1-\alpha }(1)\) is the \(1-\alpha \) upper quantile of the Chi-square distribution.

3.2 Power study

We are now in the position to examine the power performance of our R-DREAM under alternative hypothesis. More specifically, the following sequence of alternative models is under consideration:

$$\begin{aligned} H_{1n}: \quad Y=g(\tilde{\beta }^\top X,\tilde{\theta })+C_n m(B^\top X)+\varepsilon , \end{aligned}$$
(14)

where \(E[m^2(B^\top X)]<\infty \) and \(\{C_n\}\) is a constant sequence. When \(C_n=C\) for a nonzero constant C, the model is a global alternative model, while when \(C_n\) goes to zero, it is a sequence of local alternative models. In this sequence of models, \(\beta \) is one of the columns in B. Denote \(\tilde{\alpha }=(\tilde{\beta }^\top ,\tilde{\theta }^\top )^\top \). For a robust estimate \(\hat{\alpha }\), we have \(\hat{\alpha }-\tilde{\alpha }=O_p(1/\sqrt{n})\). We first discuss the consistency of \(\hat{q}\) under the local alternative hypothesis (14). When \(n\rightarrow \infty \), the local alternative models converge to the null model, \(\hat{q}\)s under the local alternative models are expected to converge to \(\hat{q}\) under the null model, which finally converge to the structural dimension \(q=1\) under the null model.

Lemma 2

Assume conditions (C1)–(C8) in Appendix hold, and under the local alternative hypothesis (14) with \(C_n=n^{-1/2}h^{-1/4}\), we have \(\hat{q}=1\) as \(n\rightarrow \infty \) with a probability going to one, where \(\hat{q}\) is the DEE-based estimate.

The asymptotic properties under global and local alternative hypotheses are concluded in the following theorem.

Theorem 2

Under Conditions (C1)–(C8) in Appendix, we have:

(i) Under the global alternative of (2) or equivalently the above model with \(C_n=C>0\),

$$\begin{aligned} S_n/(nh^{1/2})\Rightarrow Constant>0; \end{aligned}$$

(ii) Under the local alternative hypothesis (14) with \(C_n=n^{-1/2}h^{-1/4}\), we have

$$\begin{aligned} nh^{1/2}V_n\Rightarrow N(\mu , Var)~~~\text{ and }~~~S_n^2\Rightarrow \chi _1^2(\mu ^2/Var), \end{aligned}$$

where

$$\begin{aligned} \mu =E[h^2(\varepsilon )m^2(B^\top X)p(X)], \end{aligned}$$

\(h(\cdot )\) denotes the probability density function of \(\varepsilon \) and \(\chi _1^2(\mu ^2/Var)\) is a non-central Chi-squared random variable with one degree of freedom and the non-centrality parameter \(\mu ^2/Var\).

The above theorem indicates that under the global alternative hypothesis, the R-DREAM test is consistent with the asymptotic power 1, and it can also detect the local alternatives distinct from the null hypothesis at a nonparametric rate of order \(n^{-1/2}h^{-1/4}\), which is the optimal rate with one-dimensional predictor for the test \(\tilde{V}_n\) in (10).

Remark 3

From the above theorem, we can observe that under the null hypothesis, the use (automatically) of lower-order kernel function in \(V_n\) in (9) makes a very significant improvement than \(\tilde{V}_n\) in (10). Based on Theorem 1, \(V_n\) owns a much faster convergence rate of order \(nh^{1/2}\) and \(nh^{1/2}V_n\) is asymptotically normal under the null, whereas the rate of order \(nh^{p/2}\) is for \(\tilde{V}_n\). Further, according to Theorem 2, the conclusion can be made that \(V_n\) is much more sensitive than Wang and Qu’s test \(\tilde{V}_n\) in the sense that \(V_n\) can detect the local alternatives distinct from the null at the rate of \(n^{-1/2}h^{-1/4}\), whereas \(\tilde{V}_n\) is only workable at the rate of order \(n^{-1/2}h^{-p/4}\). Therefore, the power performance of the proposed test can be much enhanced.

Remark 4

Our original simulation results based on \(S_n\) in (13) with DEE-based estimate suggest the conservative sizes of tests. Thus, the following size adjustment is needed for the test statistics with the DEE-based estimate:

$$\begin{aligned} \tilde{S}_n=(1+4n^{-4/5})S_n, \end{aligned}$$
(15)

The size adjustment constant is chosen through intensive simulation with various different values, and this one is recommended. With such a size adjustment, our new test \(\tilde{S}_n\) can better control type I errors. It is worth noting that the size adjustment is asymptotically negligible when \(n\rightarrow \infty \) since \(\tilde{S}_n- S_n\) tends to zero at the rate of order \(n^{-4/5}\) as \(n\rightarrow \infty \).

3.3 Robustness property

In this section, we investigate the local stability of R-DREAM under infinitesimal local contamination through Hampel influence function, which was introduced by Hampel (1974). The Hampel influence analysis reveals that R-DREAM has the desired local robustness property. In the following, we first give von Mises functional expansion of R-DREAM and further derive the Hampel influence function. Compared with Wang and Qu (2007), the key difference is between the used covariate X and \(\hat{B}(\hat{q})^\top X\) in the respective test statistics, and \(\hat{B}(\hat{q})^TX\) is automatically 1- and q-dimensional under the null and alternative hypothesis. Thus, we only give some brief descriptions about the results.

The von Mises analysis (see Fernholz (1983)) can provide the basis of the Hampel influence function calculation. We first discuss the von Mises functional expansion. Let \( Z= B^\top X\), \(\hat{Z}=\hat{B}(\hat{q})^\top X\) and denote \(\hat{H}_n\) as the empirical distribution function of \(Y_1-g(\hat{\beta }^\top X_1,\hat{\theta }), \ldots ,Y_n-g(\hat{\beta }^\top X_n,\hat{\theta })\). When \(H_0\) holds, \(B=c\beta \), and \(\hat{B}(\hat{q})\) is an estimator of \(\beta \) up to a scalar constant c. The R-DREAM statistic \(V_n\) in (9) can be asymptotically expressed as

$$\begin{aligned} T(\hat{F}_h,F_n)=: & {} \int \int \left[ \hat{H}_n(y-g((\beta ^\top x)(F_n),\theta (F_n)))-\frac{1}{2}\right] \times \\&\left( \int \left[ \hat{H}_n(y_1-g((\beta ^\top x)(F_n),\theta (F_n))) -\frac{1}{2}\right] \times \hat{f}_h(\hat{z},y_1)\mathrm{d}y_1\right) d F_n(\hat{z},y), \end{aligned}$$

where \(F_n(\cdot )\) is the empirical distribution function of \((\hat{Z}_i, Y_i)\)’s, \(((\beta ^\top x)(F_n),\theta (F_n))^\top \) is an estimator of \((\beta ^\top x,\theta )^\top \), which can be rewritten as a functional of the empirical distribution \(F_n\), and \(\hat{f}_h(z_i,y_i)\) is a smoothing kernel estimation of the joint density function of \((\hat{Z},Y)\), which has the following form:

$$\begin{aligned} \hat{f}_h(\hat{z}_i,y_i)=\frac{1}{n-1}\sum _{i\ne j}^n {\mathcal {K}}_{1,h}(y_i-y_j) {\mathcal {K}}_{2,h}(\hat{z}_i-\hat{z}_j), \end{aligned}$$

where \({\mathcal {K}}_{1}(\cdot ),{\mathcal {K}}_{2}(\cdot )\) are two kernel functions and satisfy \({\mathcal {K}}_{1,h}(\cdot )={\mathcal {K}}_{1}(\cdot /h)/h\) and \({\mathcal {K}}_{2,h}(\cdot )={\mathcal {K}}_{2}(\cdot /h)/h^{\hat{q}}\), respectively. An appropriate functional for R-DREAM is bivariate with the form

$$\begin{aligned} T(F,F)=: & {} \int \int \left[ H(y-g((\beta ^\top x)(F),\theta (F)))-\frac{1}{2}\right] \times \nonumber \\&\left( \int \left[ H(y_1-g((\beta ^\top x)(F),\theta (F)))-\frac{1}{2}\right] \times f(z,y_1)\mathrm{d}y_1\right) d F(z,y),\nonumber \\ \end{aligned}$$
(16)

here, \(F(\cdot )\) is the distribution function of (Z, Y) and \(H(\cdot )\) is the distribution function of \(Y-g(\beta ^\top X,\theta )\): \(H(v)=\int \int _{y\le g((\beta ^\top x)(F),\theta (F))+v}\mathrm{d}F(z,y)\).

Now we are in the position to analyze Hampel influence function (Hampel 1974). When the second-order influence function in the response direction is bounded, the regression functions is robustly estimated. The detailed derivations for the first-order and the second-order influence function of \(\tilde{V}_n\) in (10) are given in Wang and Qu (2007). Here, we only report the properties for influence functions of T(F, F) in (16) at the point \((z_0,y_0)\), and the detailed proofs are left into Appendix.

Theorem 3

Suppose the conditions (C1)–(C8) in Appendix hold, we have

(i) R-DREAM has a degenerate first-order influence function.

(ii) The second-order influence function of R-DREAM is bounded in the response direction.

For the purpose of comparison, the first-order and second-order influence functions for the test \(T^\mathrm{GWZ}_n\) in (11) are derived. The first-order influence function is also zero and the second-order influence function are given by (26) in Appendix. Based on this formulation, we can see that the second-order influence function in the y-direction is not bounded. The above influence function analysis indicates R-DREAM possesses more stable and robust performance than the test \(T_n^\mathrm{GWZ}\) when the response is under contamination.

Remark 5

In order to have the above desired robustness property, a robust method must be used to implement the parameter estimation. In our paper, the popular Tukey bisquare M-estimate method (P.29, Maronna et al. 2006) is used to estimate the parameters. The robust estimate \((\hat{\beta }^\top ,\hat{\theta }^\top )^\top \) is obtained by solving the following minimization problem:

$$\begin{aligned} (\hat{\beta }^\top ,\hat{\theta }^\top )=\arg \min _{\beta ,\theta }\sum _{i=1}^n \rho (y_i-g(\beta ^\top x_i,\theta )), \end{aligned}$$

where

$$\begin{aligned} \rho (u)=\left\{ \begin{array}{ccc} 1-[1-(u/k)^2]^3&{} ~~\text{ if }~~|u|\le k, \\ 1&{}~~\text{ if }~~ |u|> k. \end{array}\right. \end{aligned}$$

Here, \(k=4.685\sigma _\varepsilon \) is the tuning constant and \(\sigma _\varepsilon \) is the standard deviation of the error \(\varepsilon \). In this way, the \(\sqrt{n}\) consistent estimates of the parameters can be derived. Note that using \(k=4.685\sigma _\varepsilon \) can achieve the good estimation efficiency. However, the \(\sqrt{n}\) consistency holds for any fixed value in the place of \(\sigma _\varepsilon \) if we do not consider the estimation efficiency. In our case, we can simply use \(k=4.685\) to avoid estimating the unknown \(\sigma _\varepsilon \). It is worth mentioning that the other robust estimation methods can also be applicable for estimating the parameters as long as the \(\sqrt{n}\) consistent estimates of the parameters can be obtained.

4 Simulation studies

In this section, two simulation studies are conducted to examine the theory and the finite-sample performance of the proposed R-DREAM. The purpose of the simulation studies is twofold: to check the usefulness of dimension reduction strategy to overcome the curse of dimensionality and to check how much it would lose in the cases without outliers when compared to existing non-robust tests.

Study 1: Consider the following models

$$\begin{aligned}&H_{11}: Y=\beta _1^\top X+0.75a(\beta _2^\top X+1.2)^3+\varepsilon ,\\&H_{12}: Y=\beta _1^\top X+a\times \left\{ 3.8\exp (1.2\beta _2^\top X)-10\right\} +\varepsilon ,\\&H_{13}: Y=\beta _1^\top X+1.2a\times \exp (-1.3\beta _1^\top X)+\varepsilon , \end{aligned}$$

where \(\beta _1=(1,\ldots ,1)^\top /\sqrt{p}\), \(\beta _2=(\underbrace{1,\ldots ,1}_{p/2},0,\ldots ,0)^\top /\sqrt{p/2}\), \(p=4,2\) and \(n=100\). The covariates \(X=(X_1,\ldots ,X_p)^\top \) are generated from multivariate normal distributions \(N(0,\Sigma _k),~k=1,2\) with \(\Sigma _1=I_p\) and \(\Sigma _2=\{0.2^{|i-j|}\}_{p\times p}\). Two kinds of errors are considered: \(\varepsilon \sim N(0,1)\) and \(\varepsilon \sim t(1)\). For \(H_{11}\) and \(H_{12}\), when \(a\ne 0\), we have \(q=2\) and \(B=(\beta _1,\beta _2)\). However, for \(H_{13}\), \(q=1\) and \(B=\beta _1\). For the first two alternative models \(H_{11}\) and \(H_{12}\), \(10\%\) of the responses are randomly added by observations from the two following nonlinear models, respectively:

$$\begin{aligned}&\text{ Case } \text{1: }~~Y=8\exp \{-|\beta _1^\top X|\}+10+\varepsilon ,\\&\text{ Case } \text{2: }~~Y=8\exp \{-|\beta _1^\top X|\}+48+\varepsilon . \end{aligned}$$

As to the last alternative model \(H_{13}\), two outlier situations are considered: Case 3: 10% of the responses are randomly added by an outlying value of 5; Case 4: 10% of the responses are randomly added by an outlying value of 15. We set \(a=0,0.2,\ldots ,1.0\) where \(a=0\) corresponds to the null hypothesis and \(a\ne 0\) to the alternative hypothesis. We intend to apply these alternative models to examine the effect of dimensionality on the proposed test \(\tilde{S}_n\) and \(T_n^{WQ}\) of Wang and Qu (2007).

Table 1 Empirical sizes and powers of \(\tilde{S}_n\) and \(T_n^{WQ}\) for \(H_{10}\) versus \(H_{11}\) and \(H_{12}\) at the significance level \(\alpha =0.05\) with \(n=100\)
Full size table

Throughout these simulations, unless otherwise specified, the kernel function is taken to be \({\mathcal {K}}(u)=15/16(1-u^2)^2\) if \(|u|\le 1\) and 0, otherwise. Our experience in the simulations suggests that \(\tilde{S}_n\) is not very sensitive to the choice of kernel function. The bandwidth is recommended as \(h=0.5n^{-1/(\hat{q}+4)}\) through intensive numerical computation. The significance level is set to be \(\alpha =0.05\) and the sample size \(n=100\) is considered. Every simulation result is the average of 4000 replications.

The simulation results under models \(H_{11}\) and \(H_{12}\) are reported in Table 1 for \(a=0,0.2,\ldots ,1\) at the significance level \(\alpha =0.05\). From this table, we can observe that in all the cases we conduct, the two tests have empirical sizes close to the significance level. Also, the simulated powers of the tests become higher with increase in the parameter a. It can be seen clearly that the test \(\tilde{S}_n\) works very well in power performance and is not significantly affected by the dimension of X. However, \(T_n^{WQ}\) severely suffers from the curse of dimensionality. When the dimension of X gets larger, \(T_n^{WQ}\) completely fails to detect the alternatives. In addition, our proposed test \(\tilde{S}_n\) shows robust performance to the correlated covariates and the heavy tail error distribution t(1). Figure 1 reports the simulated power curves under \(H_{13}\) for different values of a and sample sizes \(n=100\). The similar conclusion can be arrived.

Study 2: We generate the data from the following model:

$$\begin{aligned} H_{21}: Y=\beta ^\top X+0.5a(\beta ^\top X+1)^3+\varepsilon , \end{aligned}$$

where \(\beta =(1,\ldots ,1)^\top /\sqrt{p}\) and \(p=8,12\). Here, \(X\sim N(0,I_p)\) and \(\varepsilon \sim N(0,1)\). In this study, we investigate two issues: One is whether the test \(T_n^\mathrm{GWZ}\) can maintain the significance level when there exist some outlier values in the responses and the other is how much \(\tilde{S}_n\) loses in power when there are not outliers. \(\varrho \) is the percentage of which the responses are randomly replaced by the observations from a nonlinear model \(Y=(3\beta ^\top X+5)^2+\varepsilon \). Here, we only consider \(T_n^\mathrm{GWZ}\) with SIR-based DEE estimate.

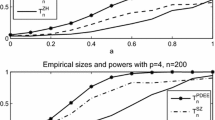
Figure 2 presents the empirical size curves or “significance trace” of the three tests for different values of the ratio \(\varrho \) and sample sizes \(n=100\). In this case, the ratio \(\varrho =0,0.02,\ldots ,0.1\). From this figure, we can see that when \(\varrho =0\), all of the three tests can control empirical sizes very well which are all close to the pre-specified significance level 0.05. However, with the increase in the percentage \(\varrho \), our robust test \(\tilde{S}_n\) outperforms the test \(T_n^\mathrm{GWZ}\). The simulation results indicate that \(\tilde{S}_n\) is not affected by the outlier values and it is more robust, whereas \(T_n^\mathrm{GWZ}\) fails to work when outliers exist.

Fig. 1
figure 1

Empirical sizes and powers of \(\tilde{S}_n\) and \(T_n^{WQ}\) for \(H_{10}\) versus \(H_{13}\) at the significance level \(\alpha =0.05\) with \(n=100\), \(p=4\) and \(\varepsilon \sim N(0,1)\). In four plots, the solid line and the dashed line are for \(\tilde{S}_n\) and \(T_n^{WQ}\), respectively. a Powers for Case 3 under \(H_{13}\) with \(X\sim N(0,\Sigma _{1})\), b powers for Case 4 under \(H_{13}\) with \(X\sim N(0,\Sigma _{2})\), c powers for Case 4 under \(H_{13}\) with \(X\sim N(0,\Sigma _{1})\), d powers for Case 4 under \(H_{13}\) with \(X\sim N(0,\Sigma _{2})\)

Full size image
Fig. 2
figure 2

Empirical sizes of \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\) for \(H_{20}\) versus \(H_{21}\) at the significance level \(\alpha =0.05\) with \(X\sim N(0,I_p)\), \(\varepsilon \sim N(0,1)\) and different values of \(\varrho \). In two plots, the solid line and the dash-dotted line are for \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\), respectively. a Empirical sizes for \(H_{21}\) with \(p=8\), b empirical sizes for \(H_{21}\) with \(p=12\)

Full size image
Fig. 3
figure 3

Simulated powers of \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\) for \(H_{20}\) versus \(H_{21}\) at the significance level \(\alpha =0.05\) with \(X\sim N(0,I_p)\) and \(\varepsilon \sim N(0,1)\). In two plots, the solid line and the dash-dotted line are for \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\), respectively. a Simulated powers for \(H_{21}\) with \(p=8\), b simulated powers for \(H_{21}\) with \(p=12\)

Full size image

We display the simulated power curves for different values of a in Fig. 3. Here, we consider \(\varrho =0\) and \(n=100\). In other words, there are no outliers in the data. The parameter a is set to be \(0,0.2,\ldots ,1\). From the figure, we can see that compared with \(T_n^\mathrm{GWZ}\), it is anticipated that \(T_n^\mathrm{GWZ}\) has higher powers since their test employs more value information, whereas the robust tests only utilize the rank information of the responses. However, the powers of \(\tilde{S}_n\) are still acceptable.

The sensitivity analysis in this study is also considered under the same settings of Study 1 without outliers. Here, \(p=8\), \(X\sim N(0,\Sigma _2)\) with \(\Sigma _2=\{0.2^{|i-j|}\}_{p\times p}\) and \(\varepsilon \sim N(0,1)\) are considered. Figure 4 reports the simulated results of \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\). From this figure, we can see that for the three alternatives \(H_{11}, H_{12}\) and \(H_{13}\) without outliers, the simulated power curves for \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\) have the common sigmoidal shape. Although the powers for \(T_n^\mathrm{GWZ}\) are slightly higher, the performance of our proposed test \(\tilde{S}_n\) remains accredited.

Fig. 4
figure 4

Simulated powers of \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\) for \(H_{10}\) versus \(H_{11},H_{12},H_{13}\) at the significance level \(\alpha =0.05\) with \(X\sim N(0,\Sigma _2)\) and \(\varepsilon \sim N(0,1)\). In three plots, the solid line and the dash-dotted line are for \(\tilde{S}_n\) and \(T_n^\mathrm{GWZ}\), respectively. a Simulated powers for \(H_{11}\), b simulated powers for \(H_{12}\), c simulated powers for \(H_{13}\)

Full size image

5 Real data analysis

In this section, we consider the CARS data to illustrate our test which was collected by Ernesto and David in the year of 1982. After that, this dataset was adopted by the committee on Statistical Graphics of the American Statistical Association (ASA) in its Second Exposition of Statistical Graphics Technology in 1983 and can be found in http://lib.stat.cmu.edu/datasets/cars.data. Recently, Guo et al. (2016) analyzed this dataset with their proposed test and drew the conclusion that it is appropriate to describe this dataset by single-index model rather than simple linear regression model. This dataset includes 406 observations on the following 8 variables: miles per gallon (Y), number of cylinders (\(X_1\)), engine displacement (cu. inches, \(X_2\)), horsepower (\(X_3\)), vehicle weight (lbs. \(X_4\)), time to accelerate from 0 to 60 mph (sec. \(X_5\)), model year (modulo 100, \(X_6\)) and origin of car (1. American, 2. European, 3. Japanese). Since the origin of car is classified into three categories, we refer to Xia (2007) to define two new indicator variables, that is, denote \(X_7=1\) if a car is from America and 0 otherwise and \(X_8=1\) if one is from Europe and 0 otherwise. Here, 392 complete observations are applied to implement our real data analysis. Before analysis, all the covariates are standardized separately and the responses are centered.

It is our interest to test whether the data (Y, X) can be fitted with linear regression models where \(X=(X_1,\ldots ,X_8)^\top \), that is,

$$\begin{aligned}&H_{0}: Y=\beta _0^\top X+\varepsilon ~\text{ for } \text{ some }~\beta _0\in R^8,\nonumber \\&H_{1}: Y=m(B_1^\top X)+\varepsilon ~\text{ and }~m(B_1^\top X)\ne \beta ^\top X~\text{ for } \text{ any }~\beta \in R^8 \end{aligned}$$
(17)

The same kernel function and bandwidth are adopted as simulation section. For the original data, the value of the test statistic \(T_n^\mathrm{GWZ}\) with SIR-based DEE estimate proposed by Guo et al. (2016) is 9.704 and the corresponding p-value is 0. With our proposed R-DREAM, we can obtain that our test statistic \(\tilde{S}_n\) is 8.2744 and the corresponding p-value is 0. Both of results indicate that the original real data cannot be fitted by linear regression models.

Table 2 The values of test statistics and the corresponding p-values for the real data analysis
Full size table

To investigate the influence of outlier values in the response space, the two following situations are considered: a). Case 5: we artificially add the first \(5\%\) and the last \(5\%\) responses of this dataset by an outlying value 50; b). Case 6: we artificially add the first \(3\%\) responses by the observations from the model: \(Y=\tilde{\beta }^\top X+\eta \), where \(p=8\), \(\tilde{\beta }=(1,1,\ldots 1)^\top /\sqrt{p}\) and \(\eta \sim N(0,1)\). The values of test statistics and the corresponding p-values for \(T_n^\mathrm{GWZ}\) and \(\tilde{S}_n\) are reported in Table 2. From this table, we can see that for both cases, our robust test \(\tilde{S}_n\) still suggests to reject the null hypothesis \(H_0\), whereas \(T_n^\mathrm{GWZ}\) cannot reject \(H_0\). The similar conclusion with original data can be made with our test, on the contrary, \(T_n^\mathrm{GWZ}\) tends to make a wrong conclusion, which indicates that our test method is more robust.