An adaptive-to-model test for partially parametric single-index models

Abstract

Residual marked empirical process-based tests are commonly used in regression models. However, they suffer from data sparseness in high-dimensional space when there are many covariates. This paper has three purposes. First, we suggest a partial dimension reduction adaptive-to-model testing procedure that can be omnibus against general global alternative models although it fully use the dimension reduction structure under the null hypothesis. This feature is because that the procedure can automatically adapt to the null and alternative models, and thus greatly overcomes the dimensionality problem. Second, to achieve the above goal, we propose a ridge-type eigenvalue ratio estimate to automatically determine the number of linear combinations of the covariates under the null and alternative hypotheses. Third, a Monte-Carlo approximation to the sampling null distribution is suggested. Unlike existing bootstrap approximation methods, this gives an approximation as close to the sampling null distribution as possible by fully utilising the dimension reduction model structure under the null model. Simulation studies and real data analysis are then conducted to illustrate the performance of the new test and compare it with existing tests.

1 Introduction

Consider the partially parametric single-index model in the form:

$$\begin{aligned} Y = G(\beta ^{\top }X, W, \theta ) + \epsilon , \end{aligned}$$

(1)

where Y is the response variable, (X, W) is the covariate vector in $\mathbb {R}^{p_1+p_2}$, $G(\cdot )$ is a known smooth function that depends not only on the covariate $\beta ^{\top }X$ but also on the covariate W, $\beta$ and $\theta$ are the unknown regression parameter vectors and the error $\epsilon$ follows a continuous distribution and is independent with the covariates (X, W). The model (1) reduces to the parametric single-index model in the absence of the covariate W and to the general parametric model in the absence of the covariate $\beta ^{\top }X$. This structure is often meaningful, as in many applications, $p_1$ is large while $p_2$ is not. See the relevant dimension reduction literature, such as Feng et al. (2013).

However, it is less clear whether a real data set fits the above statistical formalisation. It is worthwhile performing suitable and efficient model checking before any further statistical analysis. As we often have no idea about the model structure under the alternative hypothesis, the general alternative model is considered in the following form:

$$\begin{aligned} Y = g(X, W) + \epsilon , \end{aligned}$$

(2)

where $g(\cdot )$ donates an unknown smooth function.

Several methods for testing the parametric single-index model that removes the covariate W from the model (1), and the general nonlinear model in the absence of the covariate $\beta ^{\top }X$ can be found in the literature. Two prevalent classes of method are locally and globally smoothing tests. A locally smoothing test involves a nonparametric smoothing technique in the estimation, whereas a globally smoothing test only requires a set of sample averages with respect to an index set to form an empirical process or an average over the set of sample averages. For examples, Härdle and Mammen (1993) suggested a locally smoothing test based on the $L_2$ distance between the parametric and nonparametric estimate of the conditional expectation of Y given (X, W) in our notation. Zheng (1996) and Fan and Li (1996) independently developed tests based on second order conditional moments. Dette (1999) proposed a consistent test that depended on the difference between the variance estimate under the null and alternative hypotheses. Fan et al. (2001) developed a generalised likelihood ratio test. For other developments, see the Neyman threshold test (Fan and Huang 2001), a class of minimum distance tests (Koul and Ni 2004) and the distribution distance test (Keilegom et al. 2008). González-Manteiga and Crujeiras (2013) is a comprehensive review. However, locally smoothing tests have two obvious shortcomings. First, those methodologies have the subjective constraint choice of tuning parameters such as bandwidth. Unlike estimation, finding an optimal bandwidth choice for hypothesis testing is still an open problem (Stute and Zhu 2005). Although practical evidence suggests that this issue is not critical when the number p of covariates is small, a proper choice is not easy at all when p is large, even moderate. This problem often results in poor performance on the type I error control. A more serious problem is the typical slow convergence rates of locally smoothing tests, that is $O(n^{-1/2}h^{-p/4})$ under the null hypothesis, where h is the bandwidth tending to zero. In the present setup, $p=p_1+p_2.$ In other words, locally smoothing tests suffer severely from the curse of dimensionality.

For globally smoothing tests, examples include Bierens (1990), Stute (1997) and Khmaladze and Koul (2004). Stute et al. (1998) used bootstrap approximation to determine the critical values of the residual-marked empirical process-based test. Resampling approximation is particularly required when p is larger than 2 as its limiting null distribution is intractable. Escanciano (2007) is also a relevant reference in this class of tests. The typical convergence rate of globally smoothing tests is $O(n^{-1/2})$. Thus, they have the theoretical advantages over locally smoothing tests. However, the data sparseness in high-dimensional space means that most globally smoothing tests suffer from the dimensionality problem, even for large sample sizes (see Escanciano 2006). Practical evidence shows that the power of globally smoothing tests deteriorates and maintaining the significance level becomes more difficult when the dimension p of X is large, or even moderate. This is particularly the case when the alternative model is high-frequency.

A direct way to alleviate this problem is to project the high-dimensional covariates onto one-dimensional spaces first, and a test can be an average of tests that are based on the projections. This is a typical method called the projection-pursuit. Huber (1985) is a comprehensive reference. Zhu and Li (1998) suggested using the projection pursuit technique to define a test based on an unweighted integral of expectations with respect to all one-dimensional directions. Zhu and An (1992) has already used this idea to deal with a relevant testing problem. Lavergne and Patilea (2008) adopted this idea and further developed a dimension-reduction nonparametric method by exploring an optimal direction. Lavergne and Patiliea (2012) advised a smooth version of the integrated conditional moment test over all projection directions. All of these tests partly overcome the curse of dimensionality with use of one-dimensional projections. However, the computational burden is a serious issue. Computing the values of the test statistics is very time-consuming, and becomes even more serious if we further need to use re-sampling approximation such as the bootstrap to determine critical values. Based on our very limited numerical studies, which we do not report in this paper, the CPU time of computing such tests is more than 100 times of computing the test statistic developed in the present paper, even when p is only 4. Wong et al. (1995) discussed the relevant computational issue that involved the integral over all projection directions in a test statistic and suggested a number-theoretical method to reduce the computational workload. Xia (2009) also constructed a test that involved searching for an optimal direction, but the test had no way of controlling type I error.

Stute and Zhu (2002) considered a naive method to handle the curse of dimensionality when testing the parametric single-index model: $Y=G({\beta }^{\top }X)+\epsilon$. Stemming from the fact that under the null hypothesis, $E[\{Y-G({\beta }^{\top }X)\} I(X\le t)]=0$ for all $t \in R^p$ leads to $E[\{Y-G({\beta }^{\top }X)\} I(\beta ^{\top }X\le t)]=0$ for all $t \in R$, the test statistic is based on the empirical process:

$$\begin{aligned} R_{n}(x)= n^{-1/2}\sum _{i=1}^n\left\{ y_i-G({\hat{\beta }}^{\top }x_i)\right\} I({\hat{\beta }}^{\top }x_i \le x), \end{aligned}$$

where ${\hat{\beta }}$ is, under the null hypothesis, a root-n consistent estimate of $\beta$. It has been proven to be powerful in many cases. However, this test is a directional test rather than an omnibus test. Thus, the general alternative of (2) cannot be detected. This phenomenon can be easily illustrated by the following alternative model: $Y=\beta ^{\top }_1X+ c\sin (\beta ^{\top }_2X)+\epsilon$, where X is normally distributed $N(0, I_p)$ with a $p\times p$ identity matrix $I_p$, and $\beta _1$ and $\beta _2$ are two orthogonal vectors. The value $c=0$ corresponds to the null hypothesis. However, for any c, $E(Y-\beta ^{\top }_1X|\beta ^{\top }_1X)=0$. In other words, this conditional mean cannot distinguish between models under the null and alternative hypotheses.

However, the advantage of the SZ’s test (Stute and Zhu 2002) under the null hypothesis is very important particularly in high-dimensional paradigms as under the null hypothesis it solely uses the dimension reduction structure and thus it helps well maintain the significance level. Guo et al. (2015) recently proposed an adaptive-to-model dimension-reduction test that can be used to test for the model $Y=G({\beta }^{\top }X, \theta )+\epsilon$ against the general alternative model $Y=g(X)+\epsilon$. The main idea is to fully utilize the dimension reduction structure about X under the null hypothesis as Stute and Zhu (2002) did, but to adapt the alternative model such that the test is still omnibus. Their test is based on a locally smoothing technique. The improvement over existing locally smoothing tests is significant. The test has a much faster convergence rate of $O(n^{-1/2}h^{-1/4})$ than the typical rate of $O(n^{-1/2}h^{-p/4})$ and can detect local alternatives distinct from the null hypothesis at the rate of $O(n^{-1/2}h^{-1/4})$ that is also much faster than the typical rate of $O(n^{-1/2}h^{-p/4})$ that locally smoothing tests can achieve. In other words, asymptotically, the test works as if X was univariate. Thus, the test can significantly avoid the curse of dimensionality. The numerical studies in their paper also indicated its advantages in cases with moderate sample size.

To facilitate more general alternative models, a key idea in their methodology development is to treat the purely nonparametric regression model (2) as a special multi-index regression model as follows:

$$\begin{aligned} Y = g(B^{\top }X, W) + \epsilon , \end{aligned}$$

(3)

where B is a $p_1\times q$ matrix with q orthogonal columns for an unknown number q with $1\le q \le p_1$ and $g(\cdot )$ is still an unknown smooth function. We assume that the matrix B satisfies $B^{\top }B=I_{q}$ for identifiability. This model covers many popular models in the literature, such as the single-index models with $B=\beta$, the multi-index models with the absence of W, and partial single-index models with the mean function $g_1(\beta ^{\top }X)+g_2(W)$. Here $\beta$ is considered to be a column of B. When $q=p_1$ and $B=I_{p_1}$, the model (3) is reduced to the usual nonparametric alternative model  (2). This is still true even when B is not equal to $I_{p_1}$, but the rank is equal to $p_1$. This is because when $q=p_1$, $g(X, W) = g(BB^{\top }X,W) \equiv : {\tilde{g}}(B^{\top }X,W),$ where B is any $p_1\times p_1$ orthonormal matrix. This persuasively demonstrates that the model (2) can be treated as a special case of (3). Based on this, a test can be constructed by noticing that under the null hypothesis, $E\{Y-g(\beta ^{\top }X, W,\theta )I(B^{\top }X\le t,W \le \omega )\}=0$ for all $(t,\omega )$ and under the alternative hypothesis, it is nonzero for some vector $(t, \omega )$.

To define an empirical version of this function as the basis for constructing a test statistic, an adaptive estimate of B is crucial for ensuring the test to have the adaptive-to-model property. That is, we wish an estimate of B to be consistent to $\kappa \beta$ for a constant $\kappa$ under the null and to B under the alternative. Then, under the null hypothesis, the test can only rely on the dimension-reduced covariates $(\beta ^{\top }X, W)$, and is still omnibus to detect the general alternative model (3). As mentioned above, when W is absent, the test in Guo et al. (2015) has the adaptiveness property to the alternative model. To identify B and its structural dimension, various dimension reduction approaches such as minimum average variance estimation (MAVE, Xia et al. 2002) and discretization-expectation estimation (DEE, Zhu et al. 2010) have been suggested. However, when W is present, these methods fail to work. Furthermore, due to the existence of W, even when the dimension $p_1=1$, the corresponding locally smoothing test still has a slow convergence rate in the order of $O(n^{-1/2}h^{-(p_2+1)/4})$ where $p_2$ is the dimension of W.

In this paper, we consider a globally smoothing test that keeps the advantage of SZ’s test, fully uses the dimension reduction structure and utilises an adaptive-to-model strategy to get the test omnibus. As mentioned above, the key is to identify B adaptive to the null and alternative hypothesis. To be precise, under the null hypothesis, B is identified to be a vector proportional to $\beta$ to make the test dimension-reduced. While, under the alternative hypothesis, B is adaptively identified such that the constructed test is still omnibus. To this end, the partial sufficient dimension reduction approach (e.g. Chiaromonte et al. 2002; Feng et al. 2013) has to be applied. To achieve the above goal, we also need to identify and estimate the structural dimension q of B. Under the null hypothesis, $q=1$ is automatically identified and estimated. We then suggest a ridge-type eigenvalue ratio estimate. The details are presented in the next section. Another issue is critical value determination. In the present setting, the limiting null distribution is intractable, as it is for all globally smoothing tests. A resampling approximation is required. We then propose a Monte Carlo approximation that also fully utilises the information in the hypothetical model so that the approximation can be as close to the sampling null distribution as possible.

The rest of the paper is organised as follows. In Sect. 2, a dimension-reduction method, the partial discretization-expectation estimation, is reviewed, and is then used to identify or estimate B. The ridge-type eigenvalue ratio is also defined and its asymptotic properties are investigated in this section. Based on these, a test is constructed in Sect. 3. The asymptotic properties under the null and local alternative hypotheses are also presented in this section. As the limiting null distribution is intractable, the Monte Carlo test approximation is described in Sect. 4. In Sect. 5, the simulation results are reported and a real data analysis is conducted for illustration. Section 6 is a discussion section and also contains a remark about a limitation of the proposed test due to the inconsistency of the structure dimension estimation under the local alternatives. Regularity conditions and technical proofs are found in the online supplementary material.

2 Partial discretization-expectation estimation and structural dimension estimation

2.1 A brief review on partial discretization-expectation estimation

As discussed above, identifying or estimating B is important for constructing an adaptive test. To this end, sufficient dimension reduction techniques can be applied. According to the sufficient dimension reduction theories, we can identify the space spanned by the columns of the matrix B (see, Chiaromonte et al. 2002). Write ${\tilde{B}}$ as the $p\times q$ matrix consisting of these q basis vectors. We call ${\tilde{B}}$ the basis matrix. Note that B is also a basis matrix of the space. Thus it is easy to see that for a $q\times q$ nonsingular matrix C, ${\tilde{B}}=B \times C^{\top }$. When $q=1$, C is a constant and thus ${\tilde{B}}$ is a vector proportional to the vector $\beta$ under the null hypothesis. In Sect. 3 we show that identifying ${\tilde{B}}$ is enough for the testing problem described herein.

In this subsection, we focus on identifying a basis matrix ${\tilde{B}}$. Without confusion, we still write it as B. This is equivalent to identify the space spanned by the columns of the matrix B which is called the partial central subspace ( see, Chiaromonte et al. 2002), and is written as $S ^{(W)}_{Y|X}$. By their definition, it is the intersection of all subspaces $S$ such that

where stands for ‘independent of’ and $P_{(\cdot )}$ indicates a projection operator with respect to the standard inner product. dim{$S ^{(W)}_{Y|X}$} is called the structural dimension of $S ^{(W)}_{Y|X}$. In our setup, the structural dimension is 1 under the null model and q under the alternative hypothesis. Chiaromonte et al. (2002) and Wen and Cook (2007) developed estimation methods for $S ^{(W)}_{Y|X}$ when W is discrete. Li et al. (2010) proposed groupwise dimension reduction (GDR), which can also deal with this case. Feng et al. (2013) proposed partial discretization-expectation estimation (PDEE) by extending discretization-expectation estimation (DEE) in Zhu et al. (2010). All of those estimations use the root-n consistency with the partial central subspace. In this paper, we adopt PDEE because PDEE is computationally inexpensive, and can be easily used to determine the structural dimension q. Also, when W is absent, PDEE can naturally reduce to DEE without any changes in the algorithm.

From Feng et al. (2013), the following are the basic estimation steps.

• 1. Discretise the covariate $W= (W_1, \ldots , W_{p_2})$ into a set of binary variables by defining $W(\mathbf t )= (I\{W_1 \le t_1\},\ldots , I\{W_{p_2} \le t_{p_2}\})$ where $\mathbf t =(t_1,\ldots , t_{p_2})$ and the indicator functions $I\{W_i \le t_i\}$ take value 1 if $W_i \le t_i$ and 0 otherwise, for $i=1,\ldots , p_2$.

• 2. Let $S ^{(W(\mathbf t ))}_{Y|X}$ denote the partial central subspace of $Y|\{X, W(\mathbf t )\}$, and $M(\mathbf t )$ be a $p_1\times p_1$ positive semi-definite matrix satisfying ${\mathrm{Span}}\{M(\mathbf{t })\} =S ^{(W(\mathbf t ))}_{Y|X}$.

• 3. Let $T={\tilde{W}}$ where ${\tilde{W}}$ is an independent copy of W. The target matrix is $M=E\{M({\tilde{W}})\}$. B consists of the eigenvectors that are associated with the nonzero eigenvalues of $M=E\{M({\tilde{W}})\}$.

• 4. Let ${w}_1,\ldots , {w}_{n}$ be the n observations of W. Define an estimate of M as

  $$\begin{aligned} M_{n}=\frac{1}{n}\sum ^{n}_{i=1}M_n({w}_i), \end{aligned}$$

where $M_n({w}_i)$ is the partial sliced inverse regression matrix estimate defined in Chiaromonte et al. (2002) with sliced inverse regression proposed by Li (1991). Then when q is given, an estimate $B_n(q)$ of B consists of the eigenvectors that are associated with the q largest eigenvalues of $M_{n}$. $B_n(q)$ can be root-n consistent for B. For more details, readers may refer to Feng et al. (2013).

2.2 Structural dimension estimation

The structural dimension q is unknown in general. Interestingly, even when it is given, we still want to estimate adaptively according to its values under the null and alternative hypotheses because of its importance for the adaptive-to-model construction for the test. To estimate q, Feng et al. (2013) advised the BIC-type criterion that is an extension of that in Zhu et al. (2006). However, all practical uses show that selecting a proper penalty is not easy. In this paper, we suggest a ridge-type eigenvalue ratio estimate to determine q as:

$$\begin{aligned} {\hat{q}}=\arg \min _{1\le j \le p}\left\{ \frac{{{\hat{\lambda }}}^2_{j+1}+c_n}{{\hat{\lambda }}^2_j+c_n}\right\} , \end{aligned}$$

(4)

where ${\hat{\lambda }}_{p} \le \cdots \le {\hat{\lambda }}_{1}$ are the eigenvalues of the matrix $M_{n}$. This method is motivated by Xia et al. (2015). The basic idea is as follows. Let $\lambda _j$ be the eigenvalues of the target matrix M. When $j\le q$, the eigenvalue $\lambda _j>0$ and thus, the ratio $r_{j-1}=\lambda _{j}/\lambda _{j-1}>0$; when $j> q$ $\lambda _j=0$. Therefore, $r_{q}=\lambda _{q+1}/\lambda _q=0$; and $\lambda _{j+1}/\lambda _{j}=0/0$. To define all ratios well, we can add a ridge in the ratio as $r_{j}=(\lambda _{j+1}+c_n)/(\lambda _{j}+c_n)$ for $1\le j\le p-1$. As ${\hat{\lambda }}_j^2$ converges to $\lambda _j^2$ at the rate of order $1/\sqrt{n}$ for $1\le j\le q$, and to 0 at the rate of order 1 / n for $q+1\le j\le p$, then $c_n=\log n/n$ can be a good choice. Compared with the BIC criterion in Feng et al. (2013) that requires to choose a suitable penalty, we also need to choose a good ridge constant $c_n$. But we do find that the estimation can be much more stable against the ridge selection than the penalty selection in the BIC criterion. As this is beyond the score of this paper, we do no give the detail in this paper. The algorithm is very easy to implement and the estimation consistency can be guaranteed. The result is stated in the following.

Theorem 1

Under Conditions A1 and A2 in the Appendix, the estimate ${\hat{q}}$ of (4) with $c_n=\log {n}/n$ has the following consistency:

• (i) under the null hypothesis (1), $P({\hat{q}}= 1)\rightarrow 1$;

• (ii) under the alternative hypothesis (3), $P({\hat{q}}= q)\rightarrow 1$.

From our justification presented in the Appendix, the choice of $c_n$ can be in a relatively wide range to ensure consistency under the null and alternative hypotheses. However, to avoid the arbitrariness of its choice, we find that $c_n=\log n /n$ is a proper choice. The above identification of q is very important for ensuring that the test statistic is adaptive to the underlying models. Finally, an estimate of B is $B_n=B_n({\hat{q}}).$ This estimate is used in the following test statistic construction.

3 A partial dimension reduction adaptive-to-model test and its properties

3.1 Test statistic construction

The hypotheses of interest can now be restated. The null hypothesis is

$$\begin{aligned} H_0{:} E(Y|X,W)= & {} G(\beta ^{\top }X,W, \theta ) \quad \hbox {for some}\\&\beta \in \mathbb {R}^{p_1},\ \theta \in \Theta \in \mathbb {R}^d, \end{aligned}$$

against the alternative hypothesis: for any $\beta$ and $\theta$

$$\begin{aligned} H_1{:} E(Y|X,W)= g(B^{\top }X,W) \ne G(\beta ^{\top }X,W, \theta ). \end{aligned}$$

In this subsection, let $\epsilon =Y-G(\beta ^{\top }X,W, \theta )$ denote the error term under the null hypothesis. Under $H_0$, $q=1$, and $B= \kappa \beta$ for some constant $\kappa$, then we have:

$$\begin{aligned} E(\epsilon |X,W)=0\Leftrightarrow & {} E(\epsilon |B^{\top }X,W)=0 \\\Leftrightarrow & {} E[\epsilon I\{(B^{\top }X,W) \le (u,\omega )\}]=0 \end{aligned}$$

for all $(u,\omega )$. Under $H_1$, $E\{Y - G(\beta ^{\top }X,W,\theta )|X,W\}=g(B^{\top }X,W)-G(\beta ^{\top }X,W,\theta ) \ne 0$, we then have:

$$\begin{aligned}&E\{Y-G(\beta ^{\top }X,W,\theta )|X,W\} \ne 0\\&\quad \Leftrightarrow E\{Y-G(\beta ^{\top }X,W,\theta )|B^{\top }X,W\}\ne 0. \end{aligned}$$

Before proceeding to the test statistic construction, recall that what we can identify is ${\tilde{B}}=B\times C$ for a $q\times q$ orthogonal matrix C. Thus, we need to make sure this non-identifiability does not affect the equivalence between $E\{Y-G(\beta ^{\top }X,W,\theta )|{\tilde{B}}^{\top }X, W\}\ne 0$ and $E\{Y-G(\beta ^{\top }X,W,\theta )|B^{\top }X, W\} \ne 0$. This is easy to check. Note that ${\tilde{B}}=B\times C^{\top }$ with C being a non-singular matrix and thus B and ${\tilde{B}}$ map one-to-one. Then

$$\begin{aligned} E\{Y-G(\beta ^{\top }X,W,\theta )|X, W\}= & {} E\{g(B^{\top }X,W)\\&-G(\beta ^{\top }X,W,\theta )|X, W\}\\= & {} E\{{\tilde{g}}({\tilde{B}}^{\top }X,W)\\&-G(\beta ^{\top }X,W,\theta )|X, W\}, \end{aligned}$$

where ${\tilde{g}}(\cdot , \cdot )=g(C^{-1}\cdot , \cdot ).$ It is equivalent between $E\{Y-G(\beta ^{\top }X,W,\theta )|B^{\top }X, W\}\ne 0$ and $E\{Y-G(\beta ^{\top }X,W,\theta )|{\tilde{B}}^{\top }X, W\}\ne 0$. Therefore, identifying B itself is not necessary. As mentioned, we simply write ${\tilde{B}}$ as B.

Now we are in the position to define a residual-marked empirical process. Let

$$\begin{aligned} V_{n}(u,\omega )= & {} n^{-1/2}\sum _{i=1}^n\{y_i- G(\beta ^{\top }_{n}x_i,w_i,\theta _n)\}\nonumber \\&\times I\{(B_{n}({\hat{q}})^{\top }x_i,w_i)\le (u,\omega )\}, \end{aligned}$$

(5)

where $\beta _n$ and $\theta _n$ are the nonlinear least squares estimates respectively, and $B_n({\hat{q}})$ was defined before.

Therefore, we use $V_{n}$ as the basis for constructing a test statistic:

$$\begin{aligned} T_n = \int {V^2_{n}(B_n({\hat{q}})^{\top }x,\omega )} dF_{ n}(B_n({\hat{q}})^{\top }x,\omega ), \end{aligned}$$

(6)

where $F_{ n}(\cdot )$ denotes the empirical distribution based on the samples $\{B_n({\hat{q}})^{\top }x_i, w_i\}_{i=1}^n$. Therefore, the null hypothesis is rejected for large values of $T_n$.

It is clear that this test statistic is not scale-invariant and thus usually a normalizing constant is required. This constant needs to be estimated which involves many unknowns. In this paper, a Monte Carlo test procedure is recommended which can automatically make the test scale-invariant so that normalisation is not necessary. Additionally, it can mimic the sampling null distribution better than existing approximations such as that in Stute et al. (1998). The details can be found in Sect. 4.

3.2 Limiting null distribution

To study the properties of the process $V_{n}(\cdot ,\cdot )$ and the test statistic $T_n$, here we define a process for the purpose of theoretical investigation: for u and $\omega$,

$$\begin{aligned} V^0_{n}(u,\omega )= & {} n^{-1/2}\sum _{i=1}^n\Big \{y_i- G(\beta ^{\top }x_i,w_i,\theta )\}I\{(B^{\top }x_i,w_i) \nonumber \\&\le (u,\omega )\Big \}. \end{aligned}$$

(7)

When $E(Y^2) < \infty$, take the conditional variance of Y given $B^{\top }X=u$ and $W= \omega$,

$$\begin{aligned} \sigma ^2(u,\omega ) = Var(Y|B^{\top }X=u, W= \omega ), \end{aligned}$$

and put

$$\begin{aligned} \psi (u,\omega ) = \int ^\omega _{-\infty }\int ^u_{-\infty }{\sigma ^2(v_1,v_2)}dF_{B^{\top }X,W}(v_1,v_2), \end{aligned}$$

where $F_{B^{\top }X,W}(\cdot ,\cdot )$ denotes the distribution function of $(B^{\top }X,W)$. It is easy to see that under $H_0$,

$$\begin{aligned} \mathrm{{Cov}} \{V^0_{n}(u_1,\omega _1),V^0_{n}(u_2,\omega _2)\}= \psi (u_1 \wedge u_2,\omega _1 \wedge \omega _2). \end{aligned}$$

By Theorem 1.1 in Stute (1997), we can assert that under $H_0$:

$$\begin{aligned} V^0_{n} \longrightarrow V_{\infty } \quad \hbox {in distribution}, \end{aligned}$$

(8)

where $V_{\infty }$ is a continuous Gaussian process with mean zero and covariance kernel as follows:

$$\begin{aligned} K\{(u_1,\omega _1),(u_2,\omega _2)\}=\psi (u_1 \wedge u_2, \omega _1 \wedge \omega _2). \end{aligned}$$

Theorem 2

Under $H_0$ and the regularity conditions A1–A4 in the Appendix, we have the distribution

$$\begin{aligned} V_{n} \longrightarrow V_{\infty }-G^{\top }V \equiv V^1_{\infty }, \end{aligned}$$

where $V_{\infty }$ is the Gaussian process defined in (8) and the vector-valued function $G^{\top }=(G_1,G_2,\ldots ,G_{p+d})$ is defined as

$$\begin{aligned} G_i(u,\omega )=E\left[ m_i(X,W, \beta , \theta )I\{(B^{\top }X,W) \le (u,\omega )\}\right] , \end{aligned}$$

where $B = \kappa \beta$ and V is a $(p_{1}+d)$-dimensional normal vector with mean zero and covariance matrix $L(\beta , \theta )$ which is defined in the Appendix.

Remark 1

From this theorem, we can see that the test statistic has the same convergence rate of order $n^{-1/2}$ to its limit as that of existing globally smoothing tests. In other words, in an asymptotic sense, there is no room for globally smoothing tests to improve their convergence rate. Locally and globally smoothing tests differ in this feature, as $n^{-1/2}h^{p/4}$ can be much improved (Guo et al. 2015). However, as in Stute and Zhu (2002), the new test can largely avoid the effect of dimensionality such that the test is powerful for relatively large p. The simulations in Sect. 5 demonstrate this.

3.3 Power study

First, we present the asymptotic property under the global alternative hypothesis.

Theorem 3

Under Conditions A1, A2, A3 and A4 and $H_{1n}$ with $C_n=c$ a fixed constant, we have in probability

$$\begin{aligned}&n^{-1/2}V_{n}(u,\omega ) \longrightarrow E[\{g(B^{\top }X,W)\\&\quad -G({\tilde{\beta }}^{\top }X,W,{\tilde{\theta }})\}I\{(B^{\top }X,W) \le (u,\omega )\}] \end{aligned}$$

where $({\tilde{\beta }},{\tilde{\theta }})$ may be different from the true value $(\beta ,\theta )$ under the null hypothesis. Then $T_n\rightarrow \infty$ in probability.

To study how sensitive our new method is to the alternative hypotheses, consider the following sequence of local alternative hypotheses:

$$\begin{aligned} H_{1n}{:} Y=G(\beta ^{\top }X, W, \theta )+ C_n g(B^{\top }X, W)+\varepsilon , \end{aligned}$$

(9)

where $C_n$ goes to zero.

Under the local alternatives with $C_n\rightarrow 0$, we also need to estimate the structural dimension q. Recall that under the global alternative hypothesis in Sect. 2, the estimate ${\hat{q}}=q$ had a probability going to zero, which could be larger than 1 when B contains more than one basis vector. However, under the above local alternative models, when $C_n$ goes to zero, the models converge to the hypothetical model that has one vector $\beta$. Thus, we anticipate that ${\hat{q}}$ also converges to 1 under the local alternative hypotheses. The following lemma confirms this.

Lemma 1

Under $H_{1n}$ in (9), $C_n = n^{-1/2}$ and the regularity conditions in Theorem 2, the estimate ${\hat{q}}$ by (4) satisfies that as $n\rightarrow \infty$, $P({\hat{q}}= 1)\rightarrow 1$.

To further study the power performance of the test, assume an additional regularity Condition A5 in the Appendix.

Theorem 4

Under $H_{1n}$ and Conditions A1, A2, A4 and A5, when $C_n=n^{-1/2}$, we have in distribution

$$\begin{aligned}&V_{n}(u,\omega ) \longrightarrow V_{\infty }(u,\omega ) \nonumber \\&\quad +\,E[g(B^{\top }X, W) I\{(\kappa \beta ^{\top }X,W) \le (u,\omega )\}]\nonumber \\&\quad +\,G^{\top }(\eta -V)(u,\omega ) \end{aligned}$$

where $V_{\infty }$, G and V are defined as those in Theorem 2 and $\eta$ is a $(p_{1}+d)$-dimensional constant vector, which are defined in Appendix. Then $T_n$ has a finite limit.

Remark 2

This theorem shows that under the local alternative models, the test would also be directional, because ${\hat{q}}$ is not a consistent estimate of q. This is caused by the difficulty of estimating q when the alternative models are too close to the null model. If the estimation of q could be improved, it is likely that the omnibus property would still hold under the local alternative hypotheses. We discuss this further in Sect. 6.

4 A Monte-Carlo test procedure

As the limiting null distribution of the test statistic $T_n$ is not tractable, the nonparametric Monte Carlo test procedure is suggested to approximate the sampling null distribution, which is similar in spirit to the wild bootstrap, see Stute et al. (1998) and Zhu and Neuhaus (2000). However, to enhance the power of the test, we have a modified version that fully uses the model structure under the null model.

A magical algorithm is developed to determine the p values as follows:

Step 1 :

Generate a sequence of i.i.d variables $\mathbf U =\{U_i\}^n_{i=1}$ from the standard normal distribution N(0, 1). Then construct the following process:

$$\begin{aligned} \Delta _n(u,\omega , \mathbf U ) = n^{-1/2} \sum ^n_{i=1} {\hat{\varrho }}(x_i, w_i, y_i, \beta , \theta )U_i, \end{aligned}$$

where ${\hat{\varrho }}(x_i, w_i, y_i, \beta , \theta )$ is an estimate of $\varrho (x_i, w_i, y_i, \beta , \theta )$ with the following notations:

$$\begin{aligned}&\varrho (x_i, w_i, y_i, \beta , \theta )= \epsilon _i I\{(B^{\top }_1x_i,w_i) \le (u,\omega )\} - G^{\top }v_i,\\&{\hat{\varrho }}(x_i, w_i, y_i, \beta , \theta )= {\hat{\epsilon }}_i I\{(B^{\top }_{1n}x_i,w_i) \le (u,\omega )\} - \hat{G}^{\top }\hat{v}_i,\\&G(u,\omega )=E\left[ m(X,W, \beta , \theta )I\{(B^{\top }_1X,W) \le (u,\omega )\}\right] ,\\&\hat{G}= n^{-1}\sum ^n_{i=1}m(x_i,w_i, \beta _n, \theta _n)I\{(B^{\top }_{1n}X,W) \le (u,\omega )\},\\&v_i=l(x_i,w_i, y_i,\beta , \theta ),\quad \hat{v}_i=l(x_i,w_i, y_i,\beta _n, \theta _n),\\&{\hat{\epsilon }}_i= y_i-G(\beta ^{\top }_{n}x_i, w_i, \theta _n), \end{aligned}$$

with $l(\cdot )$ being a $(p_{1}+d)$-dimensional vector function defined in Appendix, and $B_1$ and $B_{1n}$ being respectively the first column vectors of B and $B_{n}({\hat{q}})$. The resulting Monte Carlo test statistic is

$$\begin{aligned} {\tilde{T}}_n(\mathbf U ) = \int {\Delta ^2_n(B^{\top }_{1n}x,w, \mathbf U )}dF_{B_{1n}}(x,w), \end{aligned}$$

where $F_{B_{1n}}(\cdot )$ denotes the empirical distribution based on the samples $\{B^{\top }_{1n}x_i, w_i\}_{i=1}^n$.

Step 2 :

Generate m sets of $\mathbf U$, $\mathbf U _j$, $j=1,\ldots , m$, and get m values of ${\tilde{T}}_n(\mathbf U )$, say ${\tilde{T}}_n(\mathbf U _j)$, $j=1,\ldots , m$.

Step 3 :

The p value is estimated by

$$\begin{aligned} {\hat{p}} = m^{-1}\sum _{j=1}^mI\{{\tilde{T}}_n(\mathbf U _j)\ge T_n\}, \end{aligned}$$

where $T_n$ is defined in (6). Whenever ${\hat{p}} \le \alpha$, reject $H_0$, for a given significance level $\alpha$, or the critical value is determined as the $(1-\alpha )100\,\%$ upper percentile of all $\mathbf U _j$’s.

As mentioned before, this test procedure is scale-invariant although $T_n$ is not, because the resampling procedure does not need to involve test statistic normalisation and ${\hat{p}} = m^{-1}\sum _{j=1}^mI\{{\tilde{T}}_n(\mathbf U _j)\ge T_n\}= m^{-1}\sum _{j=1}^mI\{{\tilde{T}}_n(\mathbf U _j)/c\ge T_n/c\}$ for any $c>0$.

Remark 3

It is worth pointing out that the algorithm is different from traditional wild bootstrap or nonparametric Monte Carlo test procedures that use the vector $B({\hat{q}})_{n}^{\top }X$. More details can be found in Stute et al. (1998) and Zhu (2005). When we only use the vector $B_{1n}$, which is associated with the largest eigenvalue of the target matrix $M_n$ defined in Sect. 2, we only use univariate covariate $B_{1n}^{\top }X$, which is $\beta ^{\top }X$ under the null asymptotically. This makes the approximation as close to the sampling null distribution as possible.

The following theorem states the consistency of the conditional distribution approximation even under local alternative hypotheses.

Theorem 5

Under the conditions in Theorem 2 and the null hypothesis or the local alternative hypotheses with $C_n=n^{-1/2}$, we know that for almost all sequences $\{(y_1, x_1, w_1), \ldots , (y_n, x_n, w_n), \ldots \},$ the conditional distribution of ${\tilde{T}}_n(\mathbf U )$ converges to the limiting null distribution of $T_n$.

5 Numerical studies

5.1 Simulations

In this subsection, we conduct simulations to examine the finite-sample performance of the proposed test. The simulations are based on 2000 Monte Carlo test replications to compute the critical values or p values. Each experiment is then repeated 1000 times to compute the empirical sizes and powers at the significance level $\alpha = 0.05$. To estimate the central subspace spanned by B, we use the SIR-based PDEE/DEE procedure according to the cases with and without the variate W in the model. In these two cases, we call the test $T^{ PDEE }_{n}$.

We choose the ZH’s test (Zheng 1996) and the SZ’s test (Stute and Zhu 2002) as the representatives of local and and globally smoothing tests, respectively, to compare with our test. We choose these tests because (1) the ZH’s test has the explicitly and tractable limiting null distribution that can be used to determine the critical values; (2) like other locally smoothing tests, the re-sampling version helps improve its performance (we then also include the re-sampling version of the ZH’s test); and (3) the SZ’s test is asymptotically distribution-free and powerful in many situations, but is not an omnibus test. We will demonstrate this. Further, we also compare our test to The GWZ’s test (Guo et al. 2015), because it is based on the ZH’s test but also has the adaptive-to-model property, and can be much more powerful. We respectively write the proposed test, the ZH’s, the SZ’s and the GWZ’s tests as $T^ PDEE _{n}$, $T^ ZH _{n}$, $T^ SZ _{n}$ and $T^ GWZ _{n}$.

In this section, we first design four examples to examine the performance in four scenarios without the random variable W. The first example has the same projection direction in both the hypothetical and alternative models. The second example is used to check the adaptiveness of our test to omnibus testing even when dimension reduction structure under the null hypothesis is fully adopted, showing that the SZ’s test is directional and thus has much less power. The third example is used to check the effect of dimensionality from X for locally smoothing tests, and to compare our test with the ZH’s and the GWZ’s test. The fourth example is used to assess the effect of correlations among the components of X. In the first three examples, the data $(x_i,w_i)$ are generated from the multivariate standard normal distribution $N(0, I_p)$, independent of the standard normal errors $\epsilon _i$.

Example 1

Consider the following regression model:

$$\begin{aligned} Y= & {} \beta ^{\top }_0X + a \times cos(0.6 \pi \beta ^{\top }_0X)\\&+\,0.5\times \epsilon \quad \hbox {and}\quad \beta _0 = (0, 0,1,1)/\sqrt{2}. \end{aligned}$$

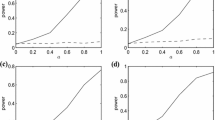
The values $a=0, 0.2,0.4,0.6,0.8, 1$ are used. The value $a = 0$ corresponds to the null hypothesis and $a\ne 0$ to the alternative hypothesis. The power function is plotted in Fig. 1. Some findings are as follows. The power increases reasonably with larger a. The proposed test $T^{PDEE}_{n}$ is significantly and uniformly more powerful than $T^{ZH}_{n}$ and $T^{SZ}_{n}$. When a is not large, $T^{SZ}_{n}$ works better than $T^{ZH}_{n}$, and when a is large, $T^{ZH}_{n}$ slightly outperforms $T^{SZ}_{n}$ in power.

Fig. 1

The empirical size and power curves of $T^{ PDEE }_n$, $T^{ SZ }_n$ and $T^{ ZH }_n$ in Example 1

Example 2

To further check the omnibus property of the proposed test to detect general alternative models, a comparison with the SZ’s test and the ZH’s test is again carried out. In this example, we generate the data from the following regression model:

$$\begin{aligned} Y= \beta ^{\top }_0X + a \times 0.125\exp (0.3\beta ^{\top }_1X) + 0.5\times \epsilon ; \end{aligned}$$

where $\beta _0 = (1, 1,0,0)/\sqrt{2}$ and $\beta _1 = (0, 0, 1, 1)/\sqrt{2}$. The values $a=0,0.1, 0.2,0.3,0.4,$ 0.5, 0.6, 0.7, 0.8, 0.9, 1 are used. In this model, $B=(\beta ^{\top }_0, \beta ^{\top }_1)^{\top }$ and $\beta ^{\top }_0X$ is orthogonal to the functions under the alternative hypotheses. We can see that the SZ’s test cannot detect such alternative hypotheses. The results are reported in Fig. 2. The results clearly show that the SZ’s test $T^ SZ _n$ and the ZH’s test $T^ SZ _n$ are not very sensitive to the alternative hypotheses. In particular, when the sample size is small ($n=100$), the SZ’s test $T^ SZ _n$ has almost no power.

Fig. 2

The empirical size and power curves of $T^{ PDEE }_n$, $T^{ SZ }_n$ and $T^{ ZH }_n$ in Example 2

Example 3

To gain further insights into our test, we consider the effect of the dimensionality of X. When the number of dimensions is large, the ZH’s test does not maintain the significance level or power performance, due to slow convergence. Thus, the wild bootstrap is applied to approximate the sampling null distribution. The re-sampling time is 2000 in this simulation study. The bootstrap version is written as $T^ ZHB _{n}$. the GWZ’s test is also compared.

Consider the models:

$$\begin{aligned} Y= \beta ^{\top }_0X + a \times \{0.3(\beta ^{\top }_1X)^3+0.3(\beta ^{\top }_1X)^2\} + 0.5\times \epsilon ; \end{aligned}$$

Fig. 3

The empirical size and power curves of $T^{ PDEE }_n$, $T^{ ZHB }_n$, $T^{ ZH }_n$ and $T^{ GWZ }_n$ in Example 3

where $\beta _0 = (1, 1,1, 1,0,0,0,0)/2$ and $\beta _1 = (0,0,0,0, 1, 1,1, 1)/2$. Then the dimension $p=8$. The results are presented in Fig. 3. We first examine the significance level maintainance of different methods. $T^{ ZH }_{n}$ does not maintain the significance level well, especially when $n=50$, the empirical sizes of $T^{ ZH }_{n}$ is only 0.024 when the critical value is determined by the limiting null distribution, but its bootstrap version $T^{ ZHB }_{n}$ can do. the test $T^{ GWZ }_{n}$ can also well maintain the significance level. $T^ {PDEE} _{n}$ performs uniformly the best among all competitors and the absolute differences between the significance level and empirical sizes are less than 0.005. From Fig. 3, we can clearly see that the test $T^ {GWZ} _{n}$ has advantage over its competitor $T^ {ZH} _{n}$ in gaining power, and $T^ {PDEE} _{n}$ uniformly works better than the others. The comparison between $T^ {GWZ} _{n}$ and $T^ {PDEE} _{n}$ further substantiates the theoretical advantage that the globally smoothing test is more sensitive to alternative hypotheses than the locally smoothing test when both are constructed via the dimension reduction technique. The results reported in Fig. 1 present that when the sample size is larger, the performance of all methods becomes better reasonably. Compared with the results in Figs. 1 and 2 with $p=4$, the dimension p has little effect for $T^ {PDEE} _n$. However, it has a very significant effect for $T^ {ZHB} _{n}$ and $T^ {ZH} _{n}$. When the dimension of the covariates is higher, the performance of $T^ {ZH} _{n}$ and $T^ {ZHB} _{n}$ is worse. For space saving, We do not include the detail of the simulation results.

Example 4

To further assess the performance of the test $T^ {PDEE} _{n}$, we examine the effect of the correlated covariate X and the distribution of the error term $\epsilon$. Consider the following model:

$$\begin{aligned} y=\beta _0^{\top }X + a\times \exp (-(\beta _0^{\top }X)^2/2)/2 + 0.5\times \epsilon ; \end{aligned}$$

where X follows a normal distribution $N(0, \Sigma )$ with the covariance matrix $\Sigma _{ij}=I(i=j)+ \rho ^{|i-j|} I(i \ne j)$ for $\rho =0.5$, $i,j =1, 2,\ldots , p$, $\beta _0=(1, 1, -1, -1)/2$ and $\epsilon$ follows the student’s t distribution with 4 degrees of freedom.

Table 1 Empirical sizes and powers of $T^{\textit{PDEE}}_{n}$, $T^{\textit{SZ}}_{n}$, $T^{\textit{ZH}}_{n}$ and $T^{\textit{GWZ}}_{n}$ for Example 4 with $p=4$ and correlated covariates

The results are listed in Table 1. Comparing the results in this table with those in Figs. 1 and 2, it is clear that with the correlated covariate X, we arrive at similar conclusions to those in Examples 1 and 2. $T^ {PDEE} _{n}$ easily maintains the significance level. We also find that when the structural dimension $q=1$ under the alternative hypothesis, the power performance of $T^ {GWZ} _{n}$ is very similar to that of $T^ {PDEE} _{n}$. Comparing Example 3 in Fig. 3 with Example 4 in Table 1, we can see that the lower structural dimension increases $T^ {GWZ} _{n}$’s empirical power. This suggests that the structural dimension q still has a negative effect on $T^ {GWZ} _{n}$ although it is not very much. However, the power of $T^ {PDEE} _n$ does not deteriorate when the the structural dimension is increased. Further, $T^ {PDEE} _n$ can control type I error very well and is significantly more powerful than the ZH’s and the SZ’s tests. It is evident that $T^ {PDEE} _{n}$ is robust to the error term.

In summary, the globally smoothing-based dimension reduction adaptive-to-model test inherits the advantages of classical globally smoothing tests and has the adaptive-to-model property when the dimension reduction structure is adopted.

Now we consider the parallel models in Examples 1, 2, 3 and 4 when the covariate W is included. However, we present only the results for $T^{PDEE}_n$ because based on the results in the above examples and comparisons, the performance of the competitors is even worse when there are $q_1$ more dimensions in the model (meaning that $q_1$ more dimensions are added when W is $q_1$-dimensional).

Example 5

The four models are:

Case 1 :

$Y= \beta ^{\top }_0X + W + a \times cos(0.6 \pi \beta ^{\top }_0X) + 0.5\times \epsilon$;

Case 2 :

$Y= \beta ^{\top }_0X + \sin (W) + a\times \{0.5(\beta ^{\top }_1X)^2 + 2\sin (W)\}+0.5\times \epsilon$;

Case 3 :

$Y= \beta ^{\top }_0X + \cos (W) + a \times \{0.3(\beta ^{\top }_1X)^3+0.3(\beta ^{\top }_1X)^2\} + 0.5\times \epsilon$;

Case 4 :

$y=\beta _0^{\top }X + \sin (W) + a\times \exp (-(\beta _0^{\top }X)^2/2)\times W + 0.5\epsilon$.

All of the settings are the same as the respective settings in Examples 1, 2, 3 and 4 except for the additional W following the normal distribution N(0, 1). The results are reported in Table 2.

Table 2 Sizes and powers of $T^{ PDEE }_{n}$ for Example 5

The reported results clearly indicate that when W is presented, $T^ {PDEE} _n$ still works well in maintaining the significance level and detecting general alternative models.

5.2 Real data analysis

In this subsection, for illustration we perform the regression modelling of the well-known Boston Housing Data, initially studied by Harrison and Rubinfeld (1978). The data set contains 506 observations and 14 variables, as follows: the median value of owner-occupied homes in $1000’s (MEDV), per capita crime rate by town (CRIM), proportion of residential land zoned for lots over 25,000 sq.ft. (ZN), proportion of non-retail business acres per town (INDUS), Charles River dummy variable (1 if tract bounds river; 0 otherwise) (CHAS), nitric oxides concentration (parts per 10 million) (NOX), average number of rooms per dwelling (RM), proportion of owner-occupied units built prior to 1940 (AGE), weighted distances to five Boston employment centres (DIS), index of accessibility to radial highways (RAD), full-value property-tax rate per 10, 000 (TAX), pupil-teacher ratio by town (PTRATIO), the proportion of black people by town (B) and lower status of the population (LSTAT).

As suggested by Feng et al. (2013), we take the logarithm of (MEDV) as the response variable, the predictor CRIM as W and the other 11 predictors as X, except CHAS, because it has little influence on the housing price as advised by Wang et al. (2010), and is thus excluded from this data analysis. In this data analysis, we standardise the predictors for ease of explanation. Here a simple linear model is considered to be the hypothetical model. The SIR-based PDEE procedure is applied to determine the partial central subspace $S ^{(W)}_{Y|X}$. A total of 2000 Monte Carlo test replications are implemented to compute the p value that is about 0. Hence, the null hypothesis is rejected. Moreover, ${\hat{q}}$ is 2. Thus, a partial multi-index model would be plausible.

6 Discussions

In this paper, we propose an adaptive-to-model dimension reduction test based on a residual marked empirical process for partially parametric single-index models. The test can fully utilise the dimension reduction structure to reduce dimensionality problems, while remaining an omnibus test. Comparisons with existing local and globally smoothing tests suggest that (1) model-adaptation enhances the power performance, also maintaining the significance level; and (2) the globally smoothing-based adaptive-to-model test outperforms the locally smoothing-based adaptive-to-model test. Thus, a globally smoothing test is worthy of recommendation. This method can be readily applied to other models and problems when a dimension reduction structure is presented. The research is on-going.

In the hypothetical and alternative models, the independence between the error and the covariates is assumed. This condition is fairly strong. The condition can be weakened to handle the testing problem for the following hypothetical and alternative models:

$$\begin{aligned} Y= & {} G(\beta ^{\top }X, W, \theta ) + \delta (\beta ^{\top }X, W)\epsilon ,\\ Y= & {} g(B^{\top }X, W) + \delta (B^{\top }X, W)\epsilon . \end{aligned}$$

Here, all of the settings are the same as those considered in the paper, except that the function $\delta (\cdot )$ is an unknown smooth function. $B_n({\hat{q}})$ estimated by the SIR-based PDEE/DEE procedure is still a root-n consistent estimate of B. Thus, the proposed test can still be feasible.

From the asymptotic properties of the proposed test, we also find a limitation. Under the local alternatives that converge to the null hypothesis at a certain rate, the proposed test, unlike existing omnibus tests, cannot be powerful. This is because of the inconsistency of the estimator ${\hat{q}}$ of q under the local alternatives with $C_n= 1/\sqrt{n}$. The method can only estimate q to be 1. Thus, the estimate ${\hat{B}}$ converges to $\beta$, and when the other directions in B are orthogonal to $\beta$ and the function has some special structure, our test may not have good power. However, this does not mean that our test cannot detect any local alternative models. When the convergence rate $C_n$ becomes slower, the ridge-type eigenvalue ratio estimate can still well estimate B by choosing a suitable ridge value $c_n$ and then local alternative hypotheses can be detected. Thus, to make the test omnibus under local alternatives, the key is to develop a good method to well estimate q. The research is ongoing.