Classification of Weld Seam Width Based on Detrended Fluctuation Analysis, t-Distributed Stochastic Neighbor Embedding, and Support Vector Machine

Abstract

The droplet behavior of welding is chaotic and fractal, and thus is significant for diagnosis of weld quality. To study the long-range correlation of fractals, detrended fluctuation analysis (DFA) is introduced for current and voltage signals. The DFA curve obviously has crossover and can be expressed by a two exponent model, including a short-term exponent (α1) at small scale and a long-term exponent (α2) at large scale. However, the relationship between the weld seam width and the two exponent model is not obviously linear. A high-dimensional feature is generated on basis of all points of the DFA curve, t-distributed stochastic neighbor embedding is used for dimension reduction. Then, a low-dimensional feature combined with support vector machine is used to predict weld seam width, which achieves higher classification accuracy than the two exponent model. This study provides a new attempt about the chaotic and fractal characteristics in welding.

Introduction

Gas metal arc welding (GMAW) is an advanced manufacturing technology in which metals are joined by high-temperature heating, and has many advantages, such as low cost, and high deposition efficiency (Ref 1). However, when process parameter mismatching or weld distortion occurs, the arc stabilty and thereby weld seam width and depth will change (Ref 2, 3). Unstable arc will result in defect of weld quality, such as porosity, burn-through and undercut. Therefore, it is of great significance to monitor the welding by the arc signal (Ref 4, 5). Adolfsson et al. extracted the repeated sequential probability ratio of voltage signal to evaluate welding stability (Ref 6). Wei et al. used the probability density distribution of current signal combined with linear discriminant analysis to classify porosity defects (Ref 7). Wang et al. extracted the low frequency feature of voltage signal to predict the penetration of weld seam (Ref 8). Pal et al. extracted the root mean square of current signal combined with a radial basis function network to predict weld distortion (Ref 9, 10). He et al. applied local mean decomposition to extract the time-frequency features of current signal, and combined with support vector machine to classify weld defects (Ref 11). However, since statistical analysis and time-frequency analysis cannot describe the inherent correlation and complexity of signal, fully depicting the relationship between electrical signal and welding is difficult.

Recently, the chaos and fractal have been applied to depict the inherent correlation and complexity of signal. Lv et al. systematically proved that the droplet behavior is chaotic and fractal, and extracted the correlation dimension, Lyapunov exponent and approximate entropy of current signal to classify the weld quality (Ref 12). He et al. applied the largest Lyapunov exponent of current signal to quantify welding stability (Ref 13). Yao et al. extracted the sample entropy of current signal for pulse GMAW to quantify welding stability (Ref 14). Nevertheless, it is significant to further study the chaotic and fractal characteristics for diagnosis of weld quality.

In terms of chaos and fractal, long-range correlation is important for understanding the self-similarity of fractal. To depict the long-range correlation of non-stationary time series, Peng et al. proposed detrended fluctuation analysis (DFA) (Ref 15). DFA can effectively eliminate the false long-range correlation caused by the non-stationary factor, so as to truly reveal the long-range correlation of complex systems (Ref 16, 17). Generally, the long-range correlation of time series is described by a single scale exponent $\alpha$. The $\alpha$ of DFA is estimated as the overall slope of a fluctuation function $\mathrm{lg}(F\left(s\right))$ and different scales $\mathrm{lg}(s)$. However, a single scale exponent cannot fully describe the characteristics of non-stationary time series in many practical applications. A two-coefficient model was proposed, which involves a short-term exponent α1 and a long-term exponent α2 (Ref 18). Moura et al. carried out DFA of vibration signals to classify the imbalance level of wind turbines (Ref 19). Lin et al. extracted the feature of the crossover of DFA in rotary machinery, and identified fault diagnosis (Ref 20).

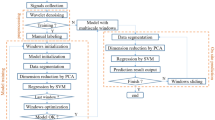
In the welding, the weld seam width is important for overlaying welding or additive manufacturing based on arc. In this study, the scale exponent based on DFA is used to analyze the inherent dynamic behavior of current and voltage signals of welding. The relationship between the scale exponent and weld seam width is studied, and t-distributed stochastic neighbor embedding (t-SNE) and support vector machine (SVM) are combined to classify weld seam width.

The paper is organized as follows: in section 2, the DFA is introduced. In section 3, the current and voltage signals are analyzed by DFA. In section 4, the t-SNE and SVM are applied to classify the weld seam width. Finally, the conclusions are drawn.

DFA

DFA can effectively eliminate irrelevant trends and reveal the long-range correlation that reflects the dynamic behavior of non-stationary time series. The DFA algorithm for time series $x\left( i \right)\left( {i = 1,2, \ldots ,N} \right)$ is conducted as follows:

• (1) A summation sequence of de-mean values $Y\left( k \right)$ is constructed:

  $$Y\left( k \right) = \mathop \sum \limits_{i = 1}^{k} \left( {x\left( i \right) - \left\langle x \right\rangle } \right)$$

  (1)

  $\left\langle x \right\rangle$ is taken over all points,

  $$\left\langle x \right\rangle = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} x\left( i \right)$$

  (2)

• (2) $Y\left( k \right), k = 1,2, \ldots ,N$ is divided into non-overlapping data of N_s-segments by the size s, and $N_{s} \equiv {\text{int}}\left[ {N/s} \right]$. Because $s$ is barely an aliquot part of the length N, a small part of data at the end of $x\left( i \right)$ will remain. To take maximal advantage of the data, the same operation is carried out again from the opposite end. Hence, 2N_s segments are obtained in all.

• (3) In each segment, a least squares line is fitted to the data, which is regarded as the local trend and denoted by $y_{\nu } \left( k \right)$ (${\upnu }$ is the current segment number). The degree of polynomial can be varied to eliminate linear, quadratic or higher order trends. Then, the local trend in each segment is subtracted to get $Y_{s} \left( k \right)$:

  $$Y_{s} \left( k \right) = Y\left( k \right) - y_{\nu } \left( k \right)$$

  (3)

  Then, the variance of the detrended time series $Y_{s} \left( k \right)$ is calculated by averaging over all data points $k$ in the ${\upnu }$th segment:

  $$F_{s}^{2} \left( \nu \right) = Y_{s}^{2} \left( k \right) = \frac{1}{s}\mathop \sum \limits_{k = 1}^{s} Y_{s}^{2} \left[ {\left( {\nu - 1} \right)s + k} \right]\quad {\upnu } \in 1,N_{s}$$

  (4)
  $$F_{s}^{2} \left( \nu \right) = \frac{1}{s}\mathop \sum \limits_{k = 1}^{s} Y_{s}^{2} \left[ {N - \left( {\nu - N_{s} } \right)s + k} \right]\quad {\upnu } \in N_{s} + 1,2N_{s}$$

  (5)

• (4) The fluctuation $F_{s}^{2} \left( \nu \right)$ is used to calculate the fluctuation function $F\left( s \right)$:

  $$F\left( s \right) = \left[ {\frac{1}{{2N_{s} }}\mathop \sum \limits_{\nu = 1}^{{2N_{s} }} F_{s}^{2} \left( \nu \right)} \right]^{1/2}$$

  (6)

• (5) For different segment size $s$ (different scale), its fluctuation function $F\left( s \right)$ can be obtained. In general, $F\left( s \right)$ obeys a power-law behavior with respect to $s$:

  $$F\left( s \right)\sim s^{\alpha }$$

  (7)

where $\alpha$ is the scale exponent of $x\left( i \right)$.

The $\alpha$ is applied to depict the long-range correlation and self-similarity of the time series. At $\alpha = 0.5$, the time series shows short-range correlation, such as constitutes white noise. At $\alpha < 0.5$, the time series displays anti-persistence long-range correlation, and smaller ${\upalpha }$ indicates stronger anti-persistence. At $\alpha > 0.5$, the time series shows persistent long-range correlation, and larger $\alpha$ implies stronger persistence. Especially, when at $\alpha = 1$, the time series is a $1/f$ processes, and at $\alpha = 1.5$, the time series represents a Brownian motion. To verify the algorithm, the time series of white noise (Fig. 1a) and $1/f$ processes (Fig. 1b) are obtained. The $\alpha$ of white noise is 0.5119 (Fig. 1c), and the $\alpha$ of $1/f$ processes is 1.002 (Fig. 1d).

Fig. 1

The $\alpha$ of white noise and $1/f$ processes signals

Experiment and Analysis

The 316L stainless steel (00Cr17Ni14Mo2) plates are experimentally welded with different process parameters, and the equipment consists of two parts, which are an ABB robot and a Fronius CMT welding machine (Fig. 2). Other conditions include the plate size of 20 * 600 * 300 mm³, the contact tip-to-work distance of 15 mm, the shielding gas of 1.5% O₂ + 5% N₂ + 93.5% Ar, and the weld wire of high nitrogen stainless steel (HNS0.99) in diameter of 1.2 mm.

Fig. 2

Robot and CMT welding equipment

To obtain varying weld quality, the process parameters are changed, and the droplet transition is cold metal arc transfer mode which is developed on the basis of short-circuiting transition. With the increase of wire feed speed, the wire melting also increases in unit time, and it causes the weld seam width increases gradually (Table 1 and Fig. 3). In the welding, the current and voltage signals are sampled at a rate of 1 kHz.

Table 1 The process parameters and seam width of tests 1-6

Fig. 3

Weld seam at different wire feed speeds

DFA of Current and Voltage Signals

The current and voltage signals of welding in the data length of 1000, are characteristic of obvious quasi-periodic fluctuation (Fig. 4). Generally, the quasi- periodicity of signal is directly related to the periodicity of droplet transfer of welding. The maximum peak frequency of power spectrum of signal is mainly about 54.7 Hz (Fig. 5), meaning that the number of points of each period is about 18, which is basically consistent with the number of droplet transfer per second. Other peaks appear at frequency of 48.8, 103.5 and 158.2 Hz, indicating the current and voltage signals are complex with multiple frequencies.

Fig. 4

The current and voltage signals of welding

Fig. 5

The power spectrum of current and voltage signals

To depict the long-range correlation of time series of welding, the current voltage signals are calculated by DFA, with the segment size $s$ set as $s \in \left[ {10,N/4} \right]$ and the total data length N = 1000. In the actual calculation, s is equal to [10, 12, 15, 17, 20, 22, 25, 27, 29, 32, 34, 37, 39, 42, 44, 46, 49, 51, 54, 56, 58, 61, 63, 66, 68, 71, 73, 75, 78, 80, 83, 85, 88, 90, 92, 95, 97, 100, 102, 105, 107, 109, 112, 114, 117, 119, 122, 124, 126, 129, 131, 134, 136, 138, 141, 143, 146, 148, 151, 153, 155, 158, 160, 163, 165, 168, 170, 172, 175, 177, 180, 182, 185, 187, 189, 192, 194, 197, 199, 202, 204, 206, 209, 211, 214, 216, 218, 221, 223, 226, 228, 231, 233, 235, 238, 240, 243, 245, 248, 250] and its length is 100. The relationship between fluctuation function $\lg \left( {F\left( s \right)} \right)$ and segment size $\lg \left( s \right)$ is nonlinear (Fig. 6) and cannot be fully expressed by a single exponent. Due to the existence of obvious crossover, it is a typical two exponent model. The crossover point is at about 22, which is almost equal to the number of droplet transfer per second. That is to say, different correlations are observed at small scale and large scale. For the current signal, the scale exponent $\alpha 1$ at small scale is greater than 0.5, indicating the current signal is not independent and has continuous long-range correlation at small scale. The scale exponent $\alpha 2$ at large scale is smaller than 0.5, indicating the current signal shows anti-persistence correlation.

Fig. 6

The two scale exponents of DFA

The Reason of Crossover Phenomenon of Welding Signal

The crossover of DFA is closely related to the component of signal, and the current signal has some peaks at frequency 48.8, 54.7, 103.5 and 158.2 Hz. This means the signal contains some periodic components, so the effect of peak frequency on the scale exponent should be discussed. A low-pass filter is used to filter out the corresponding high-frequency components and the filter frequencies are set as 30, 70, 110 and 170 Hz. The current signal is filtered by a low-pass filter, and then the DFA is conducted (Fig. 7). At the filter frequencies of 70, 110 and 170 Hz, the DFA of the filtered signal also exits obvious crossover (Fig. 8). However, at the filter frequency of 30 Hz, the relationship between fluctuation function $\lg \left( {F\left( s \right)} \right)$ and segment size $\lg \left( s \right)$ is almost linear, and the crossover phenomenon is not obvious. Hence, the frequency components of 48.8 and 54.7 Hz are important factors affecting the occurrence of crossover, which also means the crossover is affected by the droplet transfer of welding.

Fig. 7

Current signals of different filtering frequency

Fig. 8

The scale exponent of different filtering frequencies

The Scale Exponent of Welding Signal at Different Wire Feeding Speeds

In the welding, the wire feed speed parameters are close to the weld seam width. With the increase of wire feed speed, it means that the wire melting also increases in unit time, it will cause the weld seam width increases gradually. Figure 9, 10 and 11 show the original current signals at different wire feeding speeds (1.0-6.0 m/min in Table 1 and Fig. 3), while other parameters are kept constant. With the rise of wire feed speed, the amplitude of current signal increases, and its frequency distribution changes. The current signals of different wire feeding speeds are analyzed by DFA (Fig. 12). The value of fluctuation function $\lg \left( {F\left( s \right)} \right)$ increases with the acceleration of wire feeding speed, and the scale exponents obey a two exponent model ($\alpha 1$ and $\alpha 2$).

Fig. 9

Current signals at wire speed of 1.0 and 2.0 m/min

Fig. 10

Current signals at wire speed of 3.0 and 4.0 m/min

Fig. 11

Current signals at wire speed of 5.0 and 6.0 m/min

Fig. 12

DFA of current signals

To depict the relationship of two scale exponents ($\alpha 1$ and $\alpha 2$) with wire feed speed, 10 sets of data sample of current signal are calculated. The mean and variance values of $\alpha 1$ and $\alpha 2$ are also computed (Table 2). The mean value of scale exponent at small scale $\left( {E\left( {\alpha 1} \right)} \right)$ is larger than 0.5, and increases with the increase of wire feeding speed. This result indicates the current signal is not independent and has continuous long-range correlation at small scale. The mean value of exponent at large scale $\left( {E\left( {\alpha 2} \right)} \right)$ is small than 0.5, indicating the current signal is close to anti-persistence correlation.

Table 2 The two scale exponents of current signal at different wire speeds

Furthermore, the voltage signals of different wire feeding speeds are analyzed by DFA (Fig. 13). About 10 sets of data samples of voltage signals are calculated, and the mean and variance values of two scale exponents ($\alpha 1$ and $\alpha 2$) are obtained (Table 3). The mean value of exponent at small scale $\left( {E\left( {\alpha 1} \right)} \right)$ is larger than 0.5, and increases with the increase of wire feeding speed. This result indicates the voltage signal is not independent and has continuous long-range correlation at small scale. The mean value of exponent at large scale $\left( {E\left( {\alpha 2} \right)} \right)$ is smaller than 0.5 and rises with the increase of wire feeding speed, indicating the voltage signal is close to anti-persistence correlation.

Fig. 13

DFA of voltage signals

Table 3 The two scale exponents of voltage signal at different wire speeds

Classification of Weld Seam Width Based on t-SNE and SVM

The weld seam width will increase gradually with the acceleration of wire feed speed, so it may be classified by using the current and voltage signals. Based on the two exponent model ($\alpha 1$ and $\alpha 2$) of DFA of current and voltage signals, a 4-dimensional feature vector can be obtained to depict the changes of weld seam width. However, the linear relationship of $\alpha 1$ or $\alpha 2$ with weld seam width is unclear (Tables 2 and 3). Since the scale exponent is estimated as the overall slope of fluctuation function $\lg \left( {F\left( s \right)} \right)$ and different scales $\lg \left( s \right)$ of the DFA curve, all the points of the DFA curve are used as the feature vector. A 200-dimensional feature vector will be determined to depict the change of weld seam width, and a feature reduction method is needed to improve the generalizing performance of penetration status classification.

Recently, a manifold learning called t-distributed stochastic neighbor embedding (t-SNE) is proposed to reduce feature dimensions and its mainly steps can be described as follows (Ref 21, 22):

• (1) For the original data $X = \left\{ {x_{1} , x_{2} , \ldots ,x_{n} } \right\}$, the conditional probability $p_{j|i}$ with perplexity (Perp, a cost function parameter) of $x_{j}$ to $x_{i}$ can be calculated by Eq 8:

  $$p_{j|i} = \frac{{{\text{exp}}\left( { - \left\| x_{i} - x_{j} \right\|^{2} /2\delta_{i}^{2} } \right)}}{{\mathop \sum \nolimits_{k \ne i} {\text{exp}}\left( { - \left\| x_{i} - x_{k} \right\|^{2} /2\delta_{i}^{2} } \right)}}$$

  (8)

  where $\delta_{i}$ is the variance of the Gaussian that is centered on data point $x_{i}.$

• (2) The joint probability $p_{ij}$ is the symmetrical conditional probability in the high-dimensional space, so it is defined as $p_{ij} = \frac{{p_{j|i} + p_{i|j} }}{2n}$, where n is the total number of data points.

• (3) Then, the initial low-dimensional data is set as $y^{\left( 0 \right)} = \left\{ {y_{1} ,y_{2} , \ldots , y_{n} } \right\}$ from $N\left( {0,10^{ - 4} } \right)$.

• (4) In the low-dimensional space, the joint probability $q_{ij}$ is defined using a Student t-distribution with one degree of freedom:

  $$q_{ij} = \frac{{\left( {1 + \left\| y_{i} - y_{j} \right\|^{2} } \right)^{ - 1} }}{{\mathop \sum \nolimits_{k \ne l} \left( {1 + \left\| y_{k} - y_{l} \right\|^{2} } \right)^{ - 1} }}$$

  (9)

• (5) To measure the similarity between the joint probability distributions P of high-dimensional space and joint probability distribution Q of low-dimensional space, and using a gradient descent algorithm to minimize cost function $C = \mathop \sum \limits_{i} {\text{KL}}(P_{i} ||Q_{i} ) = \mathop \sum \limits_{i} \mathop \sum \limits_{j} p_{j|i} \log \frac{{p_{j|i} }}{{q_{j|i} }}$ that Kullback-Leiblerhe divergence between P and Q, the gradient $\delta C/\delta y_{i}$ is calculated by:

  $$\frac{\delta C}{{\delta y_{i} }} = 4\mathop \sum \limits_{j} \left( {p_{ij} - q_{ij} } \right)\left( {y_{i} - y_{j} } \right)\left( {1 + \left\| y_{i} - y_{j} \right\|^{2} } \right)^{ - 1}$$

  (10)

• (6) The low-dimensional space data can be obtained by Eq 11

  $$y^{\left( t \right)} = y^{{\left( {t - 1} \right)}} + \eta \frac{\delta C}{{\delta y}} + \alpha \left( t \right)\left( {y^{{\left( {t - 1} \right)}} - y^{{\left( {t - 2} \right)}} } \right)$$

  (11)

  where learning rate $\eta$ and momentum $\alpha \left( t \right)$ are optimization parameters.

• (7) Steps (4) to (6) are repeated from t = 1 to T, where T is maximum number of iterations that should be pre-set. At last, the low-dimensional data $y^{\left( T \right)} = \left\{ {y_{1} ,y_{2} , \ldots , y_{n} } \right\}$ are obtained.

Thus, t-SNE is used to decrease the 200-dimensional feature of the DFA curve of current and voltage signals to a 3-dimensional feature, and then a three-dimensional histogram is adopted to visualize data (Fig. 14b). At the same time, the 4-dimensional feature vector of double scale exponents is processed by t-SNE (Fig. 14a). The six kinds of weld seam width are almost completely separated, which showed that the 200-dimensional feature vector of the DFA curve is more effective than the double-exponent model for classification of weld seam width.

Fig. 14

Three-dimensional visualization of the results of t-SNE

The SVM classification model is selected to characterize the effect of t-SNE data quantitatively (Ref 23, 24). From totally 480 samples, 240 samples are selected into the SVM model for training, and the other 240 samples for testing (Fig. 15). At last, the recognition accuracy is 100% from the all points of DFA curve, and is about 86.25% from the double-exponent model. This result indicates the all points of DFA curve is more accurate than the double-exponent model in classification of weld seam width.

Fig. 15

The SVM classification model

Conclusions

The DFA of current and voltage signals in welding is analyzed. When the feature of DFA is used to classify weld width, the all points of DFA curve can obtain higher accuracy compared to the double-exponent model.

• (1) The DFA of current and voltage signals is characteristic of multi-scale exponents and shows crossover. The crossover point is about equal to the count of droplet transition per second.

• (2) The scale exponent of current and voltage signals is greater than 0.5 at small scale, which indicates the signal is not independent and has continuous long-range correlation. At large scale, the scale exponent is smaller than 0.5 and tends to be relatively stable, indicating the signal is close to anti-persistence long-range correlation.

• (3) Compared to the double-exponent model, the all points of DFA curve can obtain higher accuracy rate up to 100% in classifying the weld width combined with t-SNE.