Introduction

The application of a lightweight car body is an effective means for improving fuel efficiency and reducing exhaust emissions. In recent years, aluminum alloys have become one of the classes of materials that effectively reduce the weight of automotive parts and have attracted great attention from original equipment manufacturers (OEMs) worldwide. As the first step in automotive manufacturing, the rapid and efficient evaluation of the stamping product geometry and forming process is a concept that is inseparable from the extensive application of numerical simulation technologies (Ref 1, 2). To obtain reliable numerical analysis results, an appropriate yield criterion and hardening curve should be input.

The uniaxial tensile test is the simplest experimental method for obtaining a hardening curve, but due to the occurrence of local necking in the experimental process, most aluminum alloys can only be used to collect effective stress–strain data in the logarithmic strain range of 0.15-0.25 (Ref 3). In the automotive industry, the actual strain of sheet metal may be far above this range. To predict the stress response under large strain conditions, it is necessary to extrapolate the hardening curve to a higher level of plastic strain. However, if flow stress models, such as the Hollomon, Swift and Voce models, are used to infer the subsequent stress and are used as inputs, the simulation results may have large errors (Ref 4). Therefore, the best way to accurately measure the flow stress at large strain is through testing. The hydraulic bulging test (HBT) and viscous pressure bulge (VPB) test are popular methods for obtaining the hardening curve of a blank under large plastic deformation. Both tests require that the bulging medium between the blank and mold cavity be filled. The only difference (quasi-static state) between these tests is that the former uses hydraulic oil, while the latter uses high-viscosity polyurethane. Gutscher et al. (Ref 5) proposed that the hardening curve could be expressed based on the VPB test. However, after undergoing rolling deformation and recrystallization annealing, the crystal orientations show inhomogeneous distributions. Therefore, the anisotropies of sheet metals should be considered. Smith et al. (Ref 6) assumed that a blank was in-plane isotropic, and considering the Hill48 yield criterion (Ref 7), they proposed a formula for calculating the hardening curve by using the average normal anisotropy. Nasser et al. (Ref 8) considered the idea that the isotropic assumption may lead to inaccurate hardening curves from bulging tests, so they proposed a method for modifying the equivalent stress of the hardening curve based on the Hill90 yield criterion (Ref 9). In recent years, the digital image correlation (DIC) technique has been widely used in deformation measurement and strain analysis via the HBT (Ref 10). Sigvant et al. (Ref 3) converted the hydraulic bulging curve into a hardening curve in the reference direction through the equivalent plastic work principle. The good conversion accuracy proves the effectiveness of this method. In 2014, a standardized program based on an optical measurement method was published, and a method was proposed for extending the uniaxial stress–strain curve beyond uniform elongation through the HBT. Since then, the International Organization for Standardization (ISO) 16808: 2014 standard has been widely used by many scholars (Ref 11,12,13). Note that in the above methods, whether the anisotropic yield criterion or equivalent plastic work principle is used to modify the hydraulic bulging curve, it is assumed that the plastic work contour is the same at all strain levels. This may not match the actual situation. Therefore, it is necessary to discuss both the evolution of the plastic work contour and the description accuracy of the yield criterion in the deformation process.

To date, many researchers have proposed many yield criteria. Usually, it is necessary to use the Lankford coefficient (r-value) and/or the normalized yield stress to calculate the material parameters. However, with increasing plastic work or equivalent plastic strain, the normalized flow stress may change significantly. As some researchers have reported for various common engineering materials, such as copper alloys (Ref 14), steel (Ref 15), pure titanium (Ref 16), aluminum alloys (Ref 17) and magnesium alloys (Ref 18), this phenomenon is called different work hardening. Although the mechanical properties determined at some specific equivalent plastic strain levels may better reflect the deformation behavior of the blank than the initial yield point, it is difficult to reflect the anisotropic behavior of the blank during the whole deformation process. Yoon et al. (Ref 19) pointed out that the degree of anisotropy change is relatively small compared to the thermal processing history, and although the assumption of isotropic hardening is reasonable, the anisotropy caused by deformation must be considered for a more stringent approach. In short, the plastic processing of sheet metal should not only account for the orthotropy caused by the rolling and heat treatment processes but should also consider the deformation anisotropy caused by the subsequent forming process. The evolution of the crystallographic texture and dislocation changes during the forming process may be very complex, and it is impossible to characterize all the crystallographic features. Therefore, it is necessary to establish a phenomenological material model to describe the anisotropy. Aretz (Ref 20) constructed the Yld2003 yield criterion with anisotropic hardening and solved the yield surface shape evolution problem. Wang et al. (Ref 21) defined the material parameters of the Yld2000-2d yield criterion as a sixth-order polynomial function, and the improved yield criterion was shown to accurately predict the ear contour of the deep drawing test. Peters et al. (Ref 22) developed a strain rate-related Yld2000-2d yield criterion via anisotropic hardening for low-carbon steels with strong strain rate sensitivity. Yoon et al. (Ref 23) calculated the material parameters for the Yld2000-2d and CPB06ex2 yield criteria and found that considering the evolution of the anisotropic coefficients can improve the accuracy of predicting the inhomogeneity of the cup height distribution. In addition, no yield criterion is applicable for describing the anisotropic behavior of all engineering materials, and strict experimental verification is necessary. Sheet metal undergoes various multiaxial stress conditions in the stamping production; therefore, the validity of the constitutive model should be verified by the results of a multiaxial stress test (Ref 24, 25). In the field of experimental plasticity of sheet metal, the application of the HBT is very common, but a single stress state is not enough to verify the constitutive model. To obtain more stress or strain paths, cruciform specimen tests can be used for biaxial tensile tests (Ref 17, 26, 27).

In this paper, a material model (BBC05-DWH yield criterion) considering different work hardening behaviors of blanks is developed by improving the BBC2005 yield criterion. According to elastoplastic theory and the generalized form of Hooke’s law, the hardening curves of the Hill48, Barlat89 and BBC2005 yield criteria under different load ratios are deduced. The BBC05-DWH yield criterion is compared with the Hill48, Barlat89 and BBC2005 yield criteria, and the prediction accuracy of the hardening curves for the cruciform specimen biaxial tensile test is analyzed considering different yield criteria and material parameter identification methods. The validity of this new model is further verified by the plastic strain directions, which are measured at different equivalent plastic strain levels, and the uniaxial hardening curves, which are measured at different angles. The new material model was also successfully applied to correct the HBT stress–strain curve, systematically considering the influences of different yield criteria, material parameter identification methods and work hardening behaviors on the extrapolated hardening curve.

Establishing the Biaxial Tensile Hardening Relationship

In the sheet metal forming process, most materials are in the biaxial loading stage. Therefore, the validity of the material model can be verified by biaxial tensile testing.

According to Drucker’s formula (Ref 28), we have

$${\varvec{d}}\varepsilon_{ij}^{{\varvec{p}}} = {\varvec{d}}\lambda \frac{\partial f}{{\partial \sigma_{ij} }}$$
(1)

where \({\varvec{d}}\varepsilon_{ij}^{{\varvec{p}}}\) is the increment of the plastic strain, \({\varvec{d}}\lambda\) is a proportionality factor, and \(f\) is the yield function expression. It assumes that the rolling direction (RD) and transverse direction (TD) of the sample are represented by “1” and “2”, respectively. The ratio of the stresses in two directions under the biaxial loading path is expressed as

$$\sigma_{{2}} { = }\alpha \sigma_{{1}}$$
(2)

According to the equivalent plastic work principle, we have

$${\varvec{d}}\overline{\varepsilon }_{ij}^{{\varvec{p}}} = \frac{{\sigma_{{1}} {\varvec{d}}\varepsilon_{1}^{{\varvec{p}}} + \sigma_{2} {\varvec{d}}\varepsilon_{2}^{{\varvec{p}}} }}{{\overline{\sigma }}}$$
(3)

where \(\sigma_{{1}}\) and \(\sigma_{2}\) represent the stress in the x and y directions of the biaxial tensile test, respectively, and \({\varvec{d}}\overline{\varepsilon }_{ij}^{{\varvec{p}}}\) is the equivalent plastic strain increment. Based on the generalized form of Hooke's law, the elastic strains in the RD and TD under plane stress conditions are

$$\varepsilon_{1}^{{\varvec{e}}} = (\sigma_{1} - \mu \sigma_{2} )/E$$
(4a)
$$\varepsilon_{2}^{{\varvec{e}}} = (\sigma_{2} - \mu \sigma_{1} )/E$$
(4b)

where Poisson's ratio \(\mu\) is equal to 0.33 and Young's modulus \(E\) is 70 GPa, in this study.

Hill48 Yield Criterion

The Hill48 yield criterion (Ref 7) in the plane of the principal stress state is simplified to

$$f = (G + H)\sigma_{1}^{2} + (H + F)\sigma_{2}^{2} - 2H\sigma_{1} \sigma_{2} = \overline{\sigma }^{2}$$
(5)

From Eq 2 and 5, the corresponding relationship between the equivalent stress and principal stress can be defined as

$$\sigma_{{1}} = \overline{\sigma }{/}A_{{1}}$$
(6a)
$$\sigma_{{2}} = \alpha \overline{\sigma }{/}A_{{1}}$$
(6b)
$$A_{{1}} = \sqrt {H(\alpha - 1)^{2} + F\alpha^{2} + G}$$
(6c)

This relationship can be obtained from Eq 1 and 5, namely

$${\varvec{d}}\varepsilon_{1}^{{\varvec{p}}} = {\varvec{d}}\lambda \left[ {2(G + H)\sigma_{1} - 2H\sigma_{2} } \right]$$
(7a)
$${\varvec{d}}\varepsilon_{2}^{{\varvec{p}}} = {\varvec{d}}\lambda \left[ {2(H + F)\sigma_{1} - 2H\sigma_{1} } \right]$$
(7b)

According to proportional loading and Eq 2 and 7, we have

$$\frac{{{\varvec{d}}\varepsilon_{1}^{{\varvec{p}}} }}{{{\varvec{d}}\varepsilon_{2}^{{\varvec{p}}} }} = \frac{{\varepsilon_{1}^{{\varvec{p}}} }}{{\varepsilon_{2}^{{\varvec{p}}} }} = \frac{(G + H) - \alpha H}{{\alpha (H + F) - H}}$$
(8)

For the same stress ratio, \(\alpha\) is a constant, so the two sides of Eq 3 are integrated at the same time. Upon combination with Eq 2, we obtain

$$\varepsilon_{1}^{{\varvec{p}}} + \alpha \varepsilon_{2}^{{\varvec{p}}} = A_{{1}} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(9)

By combining Eq 8 and 9, the corresponding relationship between the strain in the RD and the TD and the equivalent strain is computed as

$$\varepsilon_{1}^{{\varvec{p}}} = A_{{1}} \cdot \frac{(G + H - \alpha H)}{{A_{2} }} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(10a)
$$\varepsilon_{2}^{{\varvec{p}}} = A_{{1}} \cdot \frac{(H + F)\alpha - H}{{A_{2} }} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(10b)
$$A_{2} = \alpha^{2} (F + H) - 2\alpha H + G + H$$
(10c)

Then, according to Eq 2, 4, 6 and 10, the true strain \(\varepsilon_{1}\) and \(\varepsilon_{{2}}\) can be further computed by

$$\varepsilon_{1} = \varepsilon_{1}^{{\varvec{p}}} + \frac{1}{E} \cdot \frac{{\overline{\sigma }}}{{A_{1} }} \cdot (1 - \alpha \mu )$$
(11a)
$$\varepsilon_{2} = \varepsilon_{2}^{{\varvec{p}}} + \frac{1}{E} \cdot \frac{{\overline{\sigma }}}{{A_{1} }} \cdot (\alpha - \mu )$$
(11b)

Barlat89 Yield Criterion

In the principal stress state, the Barlat89 yield criterion (Ref 29) can be simplified to

$$\phi = a\left| {T_{1} + T_{2} } \right|^{M} + a\left| {T_{1} - T_{2} } \right|^{M} + c\left| {2T_{2} } \right|^{M} = 2\sigma_{e}^{M}$$
(12a)
$$T_{1} = (\sigma_{1} + h\sigma_{2} )/2$$
(12b)
$$T_{2} = \sqrt {\left( {\frac{{\sigma_{1} - h\sigma_{2} }}{2}} \right)^{2} }$$
(12c)

By substituting Eq 2 into Eq 12, the principal stresses \(\sigma_{{1}}\) and \(\sigma_{2}\) are given by

$$\sigma_{{1}} = B_{1}^{{{1/}M}} \cdot \sigma_{e}$$
(13a)
$$\sigma_{2} = \alpha B_{1}^{1/M} \cdot \sigma_{e}$$
(13b)
$$B_{1} = \frac{2}{{a\left| {t_{1} + t_{2} } \right|^{M} + a\left| {t_{1} - t_{2} } \right|^{M} + c\left| {2t_{2} } \right|^{M} }}$$
(13c)
$$t_{1} = (1 + h\alpha )/2$$
(13d)
$$t_{2} = \sqrt {\left( {\frac{1 - h\alpha }{2}} \right)^{2} }$$
(13e)

By combining Eq 1 and 12, we obtain

$$\begin{aligned} {\varvec{d}}\varepsilon_{1}^{{\varvec{p}}}& = {\varvec{d}}\lambda \left\{ {M\left[ {a(T_{1} + T_{2} )\left| {T_{1} + T_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} + \frac{{\sigma_{1} - h\sigma_{2} }}{{4T_{2} }}} \right)} \right.} \right. \hfill \\ & \left. \quad{ + a(T_{1} - T_{2} )\left| {T_{1} - T_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} - \frac{{\sigma_{1} - h\sigma_{2} }}{{4T_{2} }}} \right)\left. { + 2^{M} cT_{2}^{M - 1} \cdot \frac{{\sigma_{1} - h\sigma_{2} }}{{4T_{2} }}} \right]} \right\} \hfill \\ \end{aligned}$$
(14a)
$$\begin{aligned} {\varvec{d}}\varepsilon_{2}^{{\varvec{p}}} &= {\varvec{d}}\lambda \left\{ {Mh\left[ {a(T_{1} + T_{2} )\left| {T_{1} + T_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} - \frac{{\sigma_{1} - h\sigma_{2} }}{{4T_{2} }}} \right)} \right.} \right. \hfill \\ &\left. \quad { + a(T_{1} - T_{2} )\left| {T_{1} - T_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} + \frac{{\sigma_{1} - h\sigma_{2} }}{{4T_{2} }}} \right)\left. { - 2^{M} cT_{2}^{M - 1} \cdot \frac{{\sigma_{1} - h\sigma_{2} }}{{4T_{2} }}} \right]} \right\} \hfill \\ \end{aligned}$$
(14b)

Substituting Eq 2 into Eq 14 gives

$$\frac{{\varepsilon_{1}^{{\varvec{p}}} }}{{\varepsilon_{2}^{{\varvec{p}}} }} = \frac{{B_{2} }}{{hB_{3} }}$$
(15a)
$$\begin{aligned} B_{2} &= a(t_{1} + t_{2} )\left| {t_{1} + t_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} + \frac{1 - h\alpha }{{4t_{2} }}} \right) \hfill \\ &\quad + a(t_{1} - t_{2} )\left| {t_{1} - t_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} - \frac{1 - h\alpha }{{4t_{2} }}} \right) + 2^{M} ct_{2}^{M - 1} \cdot \frac{1 - h\alpha }{{4t_{2} }} \hfill \\ \end{aligned}$$
(15b)
$$\begin{aligned} B_{3} &= a(t_{1} + t_{2} )\left| {t_{1} + t_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} - \frac{1 - h\alpha }{{4t_{2} }}} \right) \hfill \\ &\quad + a(t_{1} - t_{2} )\left| {t_{1} - t_{2} } \right|^{M - 2} \cdot \left( {\frac{1}{2} + \frac{1 - h\alpha }{{4t_{2} }}} \right) - 2^{M} ct_{2}^{M - 1} \cdot \frac{1 - h\alpha }{{4t_{2} }} \hfill \\ \end{aligned}$$
(15c)

and applying Eq 2 and 3, we have

$$\varepsilon_{1}^{{\varvec{p}}} + \alpha \varepsilon_{2}^{{\varvec{p}}} = B_{1}^{ - 1/M} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(16)

According to Eq 15 and 16, \(\varepsilon_{1}^{{\varvec{p}}}\) and \(\varepsilon_{{2}}^{{\varvec{p}}}\) are solved as

$$\varepsilon_{1}^{{\varvec{p}}} { = }\frac{{B_{2} }}{{B_{1} (B_{2} + \alpha hB_{3} )}} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(17a)
$$\varepsilon_{{2}}^{{\varvec{p}}} { = }\frac{{hB_{3} }}{{B_{1} (B_{2} + \alpha hB_{3} )}} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(17b)

Through Eq 2, 4, 13 and 17, the true strains \(\varepsilon_{1}\) and \(\varepsilon_{{2}}\) are expressed as

$$\varepsilon_{1} = \varepsilon_{1}^{{\varvec{p}}} + \frac{{\sigma_{e} }}{E} \cdot B_{{1}}^{{{1/}M}} \cdot (1 - \alpha \mu )$$
(18a)
$$\varepsilon_{2} = \varepsilon_{2}^{{\varvec{p}}} + \frac{{\sigma_{e} }}{E} \cdot B_{1}^{1/M} \cdot (\alpha - \mu )$$
(18b)

BBC2005 yield criterion

The equivalent stress of the BBC2005 yield criterion (Ref 12, 30) in the principal stress state is given by

$$\Phi = \left[ {a(\Lambda + \Gamma )^{2k} + a(\Lambda - \Gamma )^{2k} + b(\Lambda + \Psi )^{2k} + b(\Lambda - \Psi )^{2k} } \right]^{\frac{1}{2k}} = \overline{\sigma }$$
(19a)
$$\Gamma = L\sigma_{1} + M\sigma_{2}$$
(19b)
$$\Lambda = \sqrt {(N\sigma_{1} - P\sigma_{2} )^{2} }$$
(19c)
$$\Psi = \sqrt {(Q\sigma_{1} - R\sigma_{2} )^{2} }$$
(19d)

By substituting Eq 2 into Eq 19, \(\sigma_{1}\) and \(\sigma_{{2}}\) can be written as

$$\sigma_{{1}} = \overline{\sigma }/C_{1}$$
(20a)
$$\sigma_{2} = \alpha \overline{\sigma }/C_{1}$$
(20b)
$$C_{1} = \left[ {a(\Lambda_{\alpha } + \Gamma_{\alpha } )^{2k} + a(\Lambda_{\alpha } - \Gamma_{\alpha } )^{2k} + b(\Lambda_{\alpha } + \Psi_{\alpha } )^{2k} + b(\Lambda_{\alpha } - \Psi_{\alpha } )^{2k} } \right]^{\frac{1}{2k}}$$
(20c)
$$\Gamma_{\alpha } = L + \alpha M$$
(20d)
$$\Lambda_{\alpha } = \sqrt {(N - \alpha P)^{2} }$$
(20e)
$$\Psi_{\alpha } = \sqrt {(Q - \alpha R)^{2} }$$
(20f)

According to Eq 1 and 19, we have

$${\varvec{d}}\varepsilon_{1}^{{\varvec{p}}} = {\varvec{d}}\lambda \left[ {\frac{\partial \Phi }{{\partial \Gamma }}\frac{\partial \Gamma }{{\partial \sigma_{1} }} + \frac{\partial \Phi }{{\partial \Lambda }}\frac{\partial \Lambda }{{\partial \sigma_{1} }} + \frac{\partial \Phi }{{\partial \Psi }}\frac{\partial \Psi }{{\partial \sigma_{1} }}} \right]$$
(21a)
$${\varvec{d}}\varepsilon_{2}^{{\varvec{p}}} = {\varvec{d}}\lambda \left[ {\frac{\partial \Phi }{{\partial \Gamma }}\frac{\partial \Gamma }{{\partial \sigma_{2} }} + \frac{\partial \Phi }{{\partial \Lambda }}\frac{\partial \Lambda }{{\partial \sigma_{2} }} + \frac{\partial \Phi }{{\partial \Psi }}\frac{\partial \Psi }{{\partial \sigma_{2} }}} \right]$$
(21b)
$$\frac{\partial \Phi }{{\partial \Gamma }} = \frac{a}{{\overline{\sigma }^{2k - 1} }}\left[ {(\Lambda + \Gamma )^{2k - 1} - (\Lambda - \Gamma )^{2k - 1} } \right]$$
(21c)
$$\frac{\partial \Phi }{{\partial \Lambda }} = \frac{1}{{\overline{\sigma }^{2k - 1} }}\left\{ {a\left[ {(\Lambda + \Gamma )^{2k - 1} + (\Lambda - \Gamma )^{2k - 1} } \right]} \right. + \left. {b\left[ {(\Lambda + \Psi )^{2k - 1} + (\Lambda - \Psi )^{2k - 1} } \right]} \right\}$$
(21d)
$$\frac{\partial \Phi }{{\partial \Psi }} = \frac{b}{{\overline{\sigma }^{2k - 1} }}\left[ {(\Lambda + \Psi )^{2k - 1} - (\Lambda - \Psi )^{2k - 1} } \right]$$
(21e)
$$\frac{\partial \Gamma }{{\partial \sigma_{1} }} = L$$
(21f)
$$\frac{\partial \Gamma }{{\partial \sigma_{2} }} = M$$
(21g)
$$\frac{\partial \Lambda }{{\partial \sigma_{1} }} = \frac{{N(N\sigma_{1} - P\sigma_{2} )}}{\Lambda }$$
(21h)
$$\frac{\partial \Lambda }{{\partial \sigma_{2} }} = - \frac{{P(N\sigma_{1} - P\sigma_{2} )}}{\Lambda }$$
(21i)
$$\frac{\partial \Psi }{{\partial \sigma_{1} }} = \frac{{Q(Q\sigma_{1} - R\sigma_{2} )}}{\Psi }$$
(21j)
$$\frac{\partial \Psi }{{\partial \sigma_{2} }} = - \frac{{R(Q\sigma_{1} - R\sigma_{2} )}}{\Psi }$$
(21k)

Applying Eq 2 to Eq 21, according to the characteristics of proportional loading, there are

$$\frac{{\varepsilon_{1}^{{\varvec{p}}} }}{{\varepsilon_{2}^{{\varvec{p}}} }} = \frac{{C_{2} \cdot L + C_{3} \cdot \frac{Q(Q - \alpha R)}{{\Psi_{\alpha } }} + C_{4} \cdot \frac{N(N - \alpha P)}{{\Lambda_{\alpha } }}}}{{C_{2} \cdot M + C_{3} \cdot \left[ { - \frac{R(Q - \alpha R)}{{\Psi_{\alpha } }}} \right] + C_{4} \cdot \left[ { - \frac{P(N - \alpha P)}{{\Lambda_{\alpha } }}} \right]}}$$
(22a)
$$C_{2} = a\left[ {(\Lambda_{\alpha } + \Gamma_{\alpha } )^{2k - 1} - (\Lambda_{\alpha } - \Gamma_{\alpha } )^{2k - 1} } \right]$$
(22b)
$$C_{3} = b\left[ {(\Lambda_{\alpha } + \Psi_{\alpha } )^{2k - 1} - (\Lambda_{\alpha } - \Psi_{\alpha } )^{2k - 1} } \right]$$
(22c)
$$C_{4} = a\left[ {(\Lambda_{\alpha } + \Gamma_{\alpha } )^{2k - 1} + (\Lambda_{\alpha } - \Gamma_{\alpha } )^{2k - 1} } \right] + b\left[ {(\Lambda_{\alpha } + \Psi_{\alpha } )^{2k - 1} + (\Lambda_{\alpha } - \Psi_{\alpha } )^{2k - 1} } \right]$$
(22d)

By substituting Eq 2 into Eq 3, we have

$$\varepsilon_{1}^{{\varvec{p}}} + \alpha \varepsilon_{2}^{{\varvec{p}}} = C_{1} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(23)

According to Eq 22 and 23, \(\varepsilon_{1}^{{\varvec{p}}}\) and \(\varepsilon_{{2}}^{{\varvec{p}}}\) are solved as

$$\varepsilon_{1}^{{\varvec{p}}} = \frac{{C_{1} \cdot \varepsilon_{1}^{{\varvec{p}}} /\varepsilon_{2}^{{\varvec{p}}} }}{{\alpha + \varepsilon_{1}^{{\varvec{p}}} /\varepsilon_{2}^{{\varvec{p}}} }} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(24a)
$$\varepsilon_{2}^{{\varvec{p}}} = \frac{{C_{1} }}{{\alpha + \varepsilon_{1}^{{\varvec{p}}} /\varepsilon_{2}^{{\varvec{p}}} }} \cdot \overline{\varepsilon }^{{\varvec{p}}}$$
(24b)

Then, by combining Eq 2, 4, 20 and 24, the true strains \(\varepsilon_{1}\) and \(\varepsilon_{{2}}\) are calculated as

$$\varepsilon_{1} = \varepsilon_{1}^{{\varvec{p}}} + \frac{1}{E} \cdot \frac{{\overline{\sigma }}}{{C_{1} }} \cdot (1 - \alpha \mu )$$
(25a)
$$\varepsilon_{2} = \varepsilon_{2}^{{\varvec{p}}} + \frac{1}{E} \cdot \frac{{\overline{\sigma }}}{{C_{1} }} \cdot (\alpha - \mu )$$
(25b)

When the material parameters of the BBC2005 yield criterion are related to the equivalent plastic strain, the above derivation process is also applicable to the BBC05-DWH yield criterion.

Experimental Procedure

Material

The tested blank is 5182-O aluminum alloy with a thickness of 1.2 mm, as produced by Kobelco. The corresponding chemical composition is shown in Table 1.

Table 1 Chemical composition of 5182-O aluminum alloy (wt.%)
Full size table

Uniaxial Tensile Test

Uniaxial tensile specimens were prepared by a wire electrical discharge machining (EDM) process at 15° increments in the RD, and the sample size was consistent with the ISO 6892-1:2016 standard, as shown in Fig. 1. The test was finished on a Zwick/Roell Z150 universal electronic testing machine at room temperature with a strain rate of 10-3/s-1.

Fig. 1
figure 1

Sampling angles and sample size

Full size image

Biaxial Tests

Hydraulic Bulging Test

The HBT was finished on an Erichsen universal testing machine, the model type of which was 142-basic. The hole diameter d of the die was 100 mm, and the fillet radius R was 5 mm. A circular sample was clamped between the die and blank holder. The diameter of the sample was 170 mm, and the blank holder force was 135 kN. Due to the large blank holder force used, no material inflow was observed during the test. In addition, a random pattern of black and white matte spray paint was applied to the outer surface, and imaging of the deformed sample was recorded with a DIC system (ARAMIS®, GOM) at a frequency of 10 Hz. During the test, the speed of the hydraulic fluid medium was constant, and the bulging speed was 0.7029 mm/s. A schematic diagram of the HBT is shown in Fig. 2(a).

Fig. 2
figure 2

(a) Schematic diagram of the HBT and (b) geometry of the cruciform specimen

Full size image

Biaxial Tensile Test of Cruciform Specimens

The biaxial tensile test of the cruciform specimens was completed on a biaxial tensile testing machine controlled by a servo motor. Extensometers were installed on both sides of the samples along the RD and TD, and testing was carried out at different loading ratios (\(\alpha\)= 4:1, 2:1, 4:3, 1:1, 3:4, 1:2 and 1:4). Here, \(\alpha\) is the ratio of loading in the RD and TD, and the loading rate is 0.1 mm/s. The geometry of the cruciform specimen is shown in Fig. 2(b). The total specimen length was 350 mm, the design of the center part was consistent with the ISO 16842: 2014 standard, and the measurement area was 60 mm×60 mm. Each arm had seven equally spaced gaps, prepared by laser cutting, with lengths of 60 mm and widths of 0.2 mm. The purpose of making gaps on the cruciform specimens is to make the stress in the central area more uniform.

Table 2 lists the mechanical properties required for different yield criteria and material parameter identification methods, and the numbers in brackets represent the number of mechanical properties employed. The hardening curves tested in all the above experiments will be used in the “Validation and discussion” section to check the validity and applicability of different material models describing the plastic anisotropy behavior of 5182-O aluminum alloy. In addition, because the hardening curve of the pure shear stress state is not obtained through the experiments, \(\tau_{s1}\) (0°) and \(\tau_{s2}\) (45°) are calculated by the Hill90 yield criterion.

Table 2 Mechanical properties required by different yield criteria and material parameter identification methods
Full size table

Results and Discussion

In the HBT, the stress change at the dome of the sample cannot be directly measured, and the flow stress is usually determined by membrane theory (Ref 5, 8).

$$\frac{{\sigma_{{1}} }}{{\rho_{1} }} + \frac{{\sigma_{2} }}{{\rho_{2} }} = \frac{p}{t}$$
(26)

The HBT is regarded as axisymmetric, assuming that principal stresses are equal (\(\sigma_{b} = \sigma_{1} = \sigma_{2}\)), and the instantaneous radii of the dome are similarly equivalent (\(\rho = \rho_{1} = \rho_{2}\)). Considering that the normal stress was ignored, the expression of flow stress is rewritten as

$$\sigma_{b} = \frac{p \times \rho }{{2 \times t}}$$
(27)

The dome normal strain \(\varepsilon_{t}\) can be determined by

$$\varepsilon_{t} = - \varepsilon_{3} = \varepsilon_{1} + \varepsilon_{2} = \ln \frac{{t_{0} }}{t}$$
(28)

From Eq 4 and 28, the normal true plastic strain can be given as

$$\varepsilon_{t}^{{\varvec{p}}} = - \varepsilon_{1} - \varepsilon_{2} + \frac{2(1 - \mu )}{E}\sigma_{b}$$
(29)

where \(\varepsilon_{t}^{{\varvec{p}}}\) is a negative number, meaning that the blank continues to thin during the bulging process, and the instantaneous geometric conditions and the in-plane principal strain are measured by the DIC system.

For the cruciform specimen test, as shown in Fig. 3, the central area with an initial thickness of \(t_{0}\) is uniformly deformed from a square to a rectangle. The loads in the orthogonal directions of the biaxial tensile test can be directly obtained from the testing machine. Since the four axes of the tensile testing machine (each direction contains two axes) are independently controlled, the average load in the same direction at the same time is taken as the total load in each direction. The extensometer clamped on the test sample can measure the elongation \(\Delta s_{1}\) and \(\Delta s_{2}\) in the RD and TD so that engineering stresses \(\sigma_{{1,{\kern 1pt} E}}\) and \(\sigma_{{2,{\kern 1pt} E}}\) in different directions and engineering strains \(\varepsilon_{{1,{\kern 1pt} E}}\) and \(\varepsilon_{{2,{\kern 1pt} E}}\) can be expressed as

$$\sigma_{{1,{\kern 1pt} E}} = \frac{{F_{1} }}{{s_{0} \cdot t_{0} }}$$
(30a)
$$\sigma_{{2,{\kern 1pt} E}} = \frac{{F_{2} }}{{s_{0} \cdot t_{0} }}$$
(30b)
$$\varepsilon_{{1,{\kern 1pt} E}} = \frac{{\Delta s_{1} }}{{s_{0} }}$$
(31a)
$$\varepsilon_{{2,{\kern 1pt} E}} = \frac{{\Delta s_{2} }}{{s_{0} }}$$
(31b)

Then, the expressions of true stresses \(\sigma_{{1,{\kern 1pt} T}}\)/\(\sigma_{{2,{\kern 1pt} T}}\) and true strains \(\varepsilon_{{1,{\kern 1pt} T}}\)/\(\varepsilon_{{2,{\kern 1pt} T}}\) in different directions can be calculated by

$$\sigma_{{1,{\kern 1pt} T}} = \frac{{F_{1} }}{{s_{0} \cdot t_{0} }}\left(1 + \frac{{\Delta s_{1} }}{{s_{0} }}\right)$$
(32a)
$$\sigma_{{2,{\kern 1pt} T}} = \frac{{F_{2} }}{{s_{0} \cdot t_{0} }}\left(1 + \frac{{\Delta s_{2} }}{{s_{0} }}\right)$$
(32b)
$$\varepsilon_{{1,{\kern 1pt} T}} = \ln \left( {1 + \frac{{\Delta s_{1} }}{{s_{0} }}} \right)$$
(33a)
$$\varepsilon_{{2,{\kern 1pt} T}} = \ln \left( {1 + \frac{{\Delta s_{2} }}{{s_{0} }}} \right)$$
(33b)

By combining the constant volume principle of plastic deformation with Eq 4, the true plastic strains \(\varepsilon_{{1,{\kern 1pt} T}}^{{\varvec{p}}}\) and \(\varepsilon_{{2,{\kern 1pt} T}}^{{\varvec{p}}}\) can be given as

$$\varepsilon_{{1,{\kern 1pt} T}}^{{\varvec{p}}} = \ln \left( {1 + \frac{{\Delta s_{1} }}{{s_{0} }}} \right) - \frac{{F_{1} (1 + \frac{{\Delta s_{1} }}{{s_{0} }}) - \mu F_{2} (1 + \frac{{\Delta s_{2} }}{{s_{0} }})}}{{E(s_{0} \cdot t_{0} )}}$$
(34a)
$$\varepsilon_{{2,{\kern 1pt} T}}^{{\varvec{p}}} = \ln \left( {1 + \frac{{\Delta s_{2} }}{{s_{0} }}} \right) - \frac{{F_{2} (1 + \frac{{\Delta s_{2} }}{{s_{0} }}) - \mu F_{1} (1 + \frac{{\Delta s_{1} }}{{s_{0} }})}}{{E(s_{0} \cdot t_{0} )}}$$
(34b)
Fig. 3
figure 3

Illustration of the biaxial tensile deformation of the cruciform specimen

Full size image

Hardening Curves and r-Value

Figure 4 shows the hardening curves for different directions in 5182-O aluminum alloy. A sharp fluctuation was observed in the hardening curves, which can be attributed to the Portevin–Le Chatelier (PLC) effect. Due to the repeated pinning and depinning behavior between the solute atoms and movable dislocations, the hardening curve exhibited increasingly clear strain localization and stress drop phenomena with an increasing degree of plastic deformation (Ref 31, 32). Therefore, the modified Hocket–Sherby hardening law (35) was employed to smooth the hardening curve, and the adjusted R-squared value is more than 99.78%.

$$\sigma = Y_{0} + K\varepsilon^{{\varvec{p}}} { + }Q\left\{ {1 - \exp \left[ { - b(\varepsilon^{{\varvec{p}}} )^{a} } \right]} \right\}$$
(35)

Figure 5(a) and (b) shows the curves of the hydraulic pressure, thickness at the dome apex, bulge radii and dome height in the HBT. The hardening curve from the HBT is shown in Fig. 5(c). The HBT provides a larger hardening area at the later stage of deformation (red range), and the strain range is more than twice that of the uniaxial tensile test. The PLC effect was also observed in the HBT, and the modified Hocket–Sherby hardening law was employed to smooth the hardening curve. The adjusted R-squared value of the fitted curve was 99.96%, which was well correlated with the experimental curve. Table 3 lists the fitting parameters of the modified Hocket–Sherby hardening law for the above tests.

Fig. 4
figure 4

Engineering stress–strain curves: (a) the RD, DD and TD and (b) 15°, 30°, 60° and 75° directions. True stress–true plastic strain curves: (c) the RD, DD and TD and (d) 15°, 30°, 60° and 75° directions

Full size image
Fig. 5
figure 5

(a) Hydraulic pressure–dome height curve, (b) bulge radii–dome height curve and thickness at the dome apex–dome height curve and (c) true stress–true plastic strain curve

Full size image
Table 3 Fitting parameters of the modified Hocket–Sherby hardening law
Full size table

The hardening curves of the biaxial tensile test under different loading ratios are shown in Fig. 6. Among these results, the loading ratios of 1:0 and 0:1 have uniaxial tensile curves (the strain range is 0-0.10). The hardening curves under different loading ratios are clearly different, and the maximum strains in each direction are also clearly different. The results show that the biaxial tensile curves are higher than those of the uniaxial tensile curves in the direction with a larger loading ratio (such as the RD with a loading ratio of 2:1 and TD with a loading ratio of 1:2). Moreover, with an ordered change in \(\alpha\), the hardening curve increases continuously and reaches its highest value in the balanced biaxial stress state.

Fig. 6
figure 6

Biaxial tensile test of cruciform specimens: (a) the hardening curves in the RD and (b) the hardening curves in the TD

Full size image

Figure 7(a) shows the change in the r-value with plastic strain \(\varepsilon_{l}^{{\varvec{p}}}\). Overall, the trend of the r-value change is constant. In the range of the yield platform (\(0 \le \varepsilon_{l}^{{\varvec{p}}} \le 0.008\)), the r-value first increases and then decreases. After exceeding the yield platform (\(\varepsilon_{l}^{{\varvec{p}}} > 0.008\)), the r-value gradually returns to the stable state and exhibits little change with the increase in uniform plastic deformation. The method used to determine the r-value in this study is shown in Fig. 7(b). In the tensile strain range of 1%-12%, the slope of each width strain–thickness strain curve is the r-value. The equal biaxial r-value (\(r_{b}\)) is determined by a similar method. Note that some studies have shown that the HBT is usually not suitable for determining \(r_{b}\) (Ref 33). Therefore, \(r_{b}\) is determined by performing biaxial tensile testing on cruciform specimens with a loading ratio of 1:1, the slope of plastic strain in the TD and RD is fitted for the entire range of uniform deformation, and the measured \(r_{b}\) is 1.032. Table 4 lists the mechanical properties of the uniaxial tensile test in seven directions, including the yield strength Rp0.2, tensile strength Rm, uniform elongation Ag, r-value, average normal anisotropy \(\overline{r}\) and planar anisotropy \(\Delta r\).

Fig. 7
figure 7

(a) Instantaneous r-value-logarithmic plastic strain curve and (b) width plastic strain–normal plastic strain curve, where the illustration shows the TD plastic strain–RD plastic strain curve of a cruciform specimen under balanced biaxial tensile stress

Full size image
Table 4 Material properties of the 5182-O aluminum alloy measured by uniaxial tensile tests
Full size table

Experimental Plastic Work Contours

The RD is selected as the reference direction. The plastic work W (N/mm2) and equivalent stress \(\sigma_{0}\) are determined first. Then, the \(\sigma_{90}\) and the balanced biaxial stress components \(\sigma_{11}\) and \(\sigma_{22}\) under the same plastic work conditions are determined. By drawing the calculated stress points (\(\sigma_{0}\), 0), (0, \(\sigma_{90}\)) and (\(\sigma_{11}\), \(\sigma_{22}\)), work contours related to equivalent plastic strain and plastic work are formed. Figure 8(a) shows the plastic work contour, as measured experimentally. The maximum equivalent plastic strain including the full load ratios obtained from the cruciform specimen test is 0.075. When the \(\overline{\varepsilon }^{{\varvec{p}}}\) is 0.1, the balanced biaxial stress point is obtained by the HBT. To compare the plastic work contours under different strains, the stress component is normalized by the equivalent stress related to its respective work contour, as shown in Fig. 8(b). Note that even though the different work hardening behaviors of the blank selected in this paper are not significant, to accurately capture the trend of plastic work contour change, the anisotropy caused by deformation should be considered.

Fig. 8
figure 8

(a) Plastic work contours measured under different equivalent plastic strain levels and (b) normalized plastic work contours

Full size image

Evolution of Normalized Flow Stress

In the presence of deformation anisotropy, the blank exhibits different work hardening characteristics. To overcome the limitation of describing deformation anisotropy, the stress anisotropy data \(\sigma_{{\varvec{0}}} /\sigma_{{\varvec{0}}}\), \(\sigma_{{{\varvec{45}}}} /\sigma_{{\varvec{0}}}\), \(\sigma_{{{\varvec{90}}}} /\sigma_{{\varvec{0}}}\) and \(\sigma_{b} /\sigma_{{\varvec{0}}}\) measured under the same plastic work conditions are expressed as equivalent plastic strain-related functions. Since the r-value anisotropy data remain unchanged overall (as shown in Fig. 7), their changes are not considered in this work. Figure 9 shows the trend of the normalized flow stress change with the equivalent plastic strain, and the \(\sigma_{{{\varvec{45}}}} /\sigma_{{\varvec{0}}}\), \(\sigma_{{{\varvec{90}}}} /\sigma_{{\varvec{0}}}\) and \(\sigma_{b} /\sigma_{{\varvec{0}}}\) ratios at each equivalent plastic strain level are measured in increments of 0.005. The normalized flow stress in the diagonal direction (DD) shows a trend of rising first and then slowly decreasing, while the TD shows a trend of continuously rising. For the normalized flow stress of balanced biaxial hardening, the equivalent plastic strain exhibits a very evident curvature change in the hydraulic bulging curve before 0.07 and returns to the normalized state of slowly increasing after 0.07. The reason for this phenomenon may be due to the lack of pressure signal collection in the elastic stage, and the error in reconstruction for the bulge radii, inducing a hardening relationship measurement that does not truly reflect the deformation behavior of the blank (Ref 30). As the degree of plastic deformation increases, this effect gradually decreases and can be ignored. The cruciform specimen test is an effective method for reconstructing the stress in the low strain stage, and can compensate for the above problems (Ref 34). Therefore, in the range of \(0 \le \overline{\varepsilon }^{{\varvec{p}}} < 0.09{5}\), the average value of the stress components is regarded as \(\sigma_{{\varvec{b}}}\) by using the test data of cruciform specimens under balanced biaxial tension. In the range of \(\overline{\varepsilon }^{{\varvec{p}}} \ge 0.09{5}\), the HBT test data are used for this calculation. Wang et al. (Ref 21) used sixth-order polynomial function fitting to characterize the relationship between the material parameters and the equivalent plastic strain. However, when the material deformation exceeds the uniform deformation range of uniaxial tensile testing, there is a very evident end jumping phenomenon that occurs. Therefore, to improve the applicability of the fitting method and the stability of the results, an exponential function is used for fitting. Since a linear evolution trend is observed at the end, the addition of a linear term should be considered in the function. Now, the normalized flow stress can be fitted under different levels of equivalent plastic strain, where these levels of fittings are represented by the following functional relationship.

$$\sigma_{{N{\text{ormali}}zed}} = N_{0} + N_{1} \exp \left( { - \frac{{\overline{\varepsilon }^{{\varvec{p}}} }}{{t_{1} }}} \right) + N_{2} \exp \left( { - \frac{{\overline{\varepsilon }^{{\varvec{p}}} }}{{t_{2} }}} \right) + K\overline{\varepsilon }^{{\varvec{p}}}$$
(36)

where \(N_{0}\), \(N_{1}\), \(t_{1}\), \(N_{2}\), \(t_{2}\) and \(K\) are fitting parameters for Eq 36, and their values are listed in Table 5.

Fig. 9
figure 9

Normalized yield stress–equivalent plastic strain curve in the (a) DD and TD and (b) cruciform specimen test \((0 \le \overline{\varepsilon }^{{\varvec{p}}} < 0.095)\) and HBT \((\overline{\varepsilon }^{{\varvec{p}}} \ge 0.09{5})\)

Full size image
Table 5 Fitting parameters N0, N1, t1, N2, t2 and K
Full size table

Validation and Discussion

The effectiveness of the developed material model is verified by uniaxial tensile hardening curves, biaxial tensile hardening curves and directions of plastic strains. Before that comparison is conducted, the exponents \(M\) and \(k\) in the Barlat89 and BBC2005 yield criteria are determined by comparing the exponents commonly used for BCC and FCC materials. This comparison is shown in Fig. 10, where the \(\overline{\varepsilon }^{{\varvec{p}}}\) values are 0.0023, 0.0353 and 0.0751. A method for quantitatively evaluating the error between the theoretical plastic work contour and experimental data points is proposed, as shown in Eq 37.

$$\delta_{ave}^{yl} = \frac{1}{{N_{yl} }}\left\{ {\sum\limits_{i = 1}^{{N_{yl} }} {\frac{{\sqrt {\left[ {\sigma_{11}^{cal} (i) - \sigma_{11}^{\exp } (i)} \right]^{2} + \left[ {\sigma_{22}^{cal} (i) - \sigma_{22}^{\exp } (i)} \right]^{2} } }}{{\sqrt {\left[ {\sigma_{11}^{\exp } (i) + \sigma_{22}^{\exp } (i)} \right]^{2} } }}} } \right\}$$
(37)

where \(N_{yl}\) is the number of experimental data points and \(i\) is the \(i{\text{th}}\) stress ratio. The calculated data points are the same as the stress ratio of the experimental data points. Figure 10(e) shows the error analysis results for different exponents. For the Barlat89 yield criterion, \(M = 6\) generates a smaller error than \(M = 8\) in determining the yield locus using either stress anisotropy data or r-value anisotropy data. For the BBC05-DWH yield criterion, the error for \(k = 3\) is approximately 0.01, while the error for \(k = {4}\) is less than 0.005 at each of the three plastic strain levels. Therefore, for material parameter identification, the exponent \(M\) is equal to 6, and the exponent \(k\) is equal to 4. The normalized yield stress for \(\overline{\varepsilon }^{{\varvec{p}}}\)= 0.0023 is listed in Table 6. The material parameters based on different yield criteria and parameter identification methods are shown in Tables 7, 8, 9 and Fig. 11, which will be used for the stress–strain curve calculation.

Fig. 10
figure 10

Results of the comparisons between the predicted and measured plastic work contours of the Hill(a) Hill48-σ and Hill48-r, (b) Barlat89-σ, (c) Barlat89-r, (d) BBC05-DWH yield criteria (\(\overline{\varepsilon }^{{\varvec{p}}}\) = 0.0023, 0.0353 and 0.0751) and (e) average error of different yield criteria and exponents

Full size image
Table 6 Normalized yield stresses (\(\overline{\varepsilon }^{{\varvec{p}}} = 0.0023\))
Full size table
Table 7 Material parameters for the Hill48 yield criterion (\(\overline{\varepsilon }^{{\varvec{p}}} = 0.0023\))
Full size table
Table 8 Material parameters for the Barlat89 yield criterion (\(\overline{\varepsilon }^{{\varvec{p}}} = 0.0023\))
Full size table
Table 9 Material parameters for the BBC2005 yield criterion (\(\overline{\varepsilon }^{{\varvec{p}}} = 0.0023\))
Full size table
Fig. 11
figure 11

Evolution of the material parameters for the BBC05-DWH yield criterion (a) \(0 \le \overline{\varepsilon }^{{\varvec{p}}} < 0.095\) and (b) \(\overline{\varepsilon }^{{\varvec{p}}} \ge 0.09{5}\)

Full size image

The experimental curves are compared to the uniaxial tensile hardening curves predicted based on different yield criteria and material parameter identification methods at 15° intervals along the RD, as shown in Fig. 12(a-g). The prediction error \(\delta_{ave}^{uni}\) between the theoretical and experimental uniaxial loading stresses is calculated by

$$\delta_{ave}^{uni} = \frac{1}{{N_{\varphi } }}\left[ {\sum\limits_{i = 1}^{{N_{\varphi } }} {\frac{{\sqrt {\left[ {\sigma_{\varphi }^{cal} (i) - \sigma_{\varphi }^{\exp } (i)} \right]^{2} } }}{{\sigma_{\varphi }^{\exp } (i)}}} } \right]$$
(38)

where \(\varphi\)= {15°, 30°, 45°, 60°, 75°, 90°}. \(N_{\varphi }\) represents the number of experimental points at different angles. Under uniaxial stress status, for the Hill48 and Barlat89 yield criteria, the prediction accuracy using stress anisotropy data is higher than that using r-value anisotropy data, as shown in Fig. 12(h). The prediction result of the BBC05-DWH for the RD, DD and TD is almost zero, which is reasonable because material parameter identification uses the normalized flow stress related to equivalent plastic strain in these three directions. For other directions, the BBC05-DWH yield criterion can still provide good prediction accuracy, and shows the least prediction error. However, overall, all the yield criteria examined in this paper seem to be able to describe the hardening relationship under uniaxial loading conditions well. Considering that sheet metal is subjected to complex stress states during the forming process, the effectiveness of different material models under biaxial loading conditions should continue to be checked.

Fig. 12
figure 12

Theoretical and experimental hardening curves for the uniaxial tensile test at 15° intervals along the RD and average error \(\delta_{ave}^{uni}\): (a) RD, (b) 15°, (c) 30°, (d) DD, (e) 60°, (f) 75°, (g) TD and (h) \(\delta_{ave}^{uni}\)

Full size image

Figure 13 shows the theoretical prediction hardening curves in the RD and TD under biaxial tensile stress at different loading ratios. For different loading ratios, the BBC2005 and BBC05-DWH yield criteria can be used to accurately predict the test results in both the RD and TD. In addition, when the loading ratios are 4:1 and 1:4, the Hill48-r and Barlat89-r yield criteria can also be used to obtain higher prediction accuracies. When the loading ratios are 2:1 and 1:2, the Barlat89-r yield criterion is accurate. When the loading ratios are 4:3 and 3:4, neither the Hill48 nor Barlat89 yield criterion can accurately predict the hardening trends. When the loading ratio is 1:1, the Hill48-σ yield criterion can be employed to accurately predict the hardening curve.

Fig. 13
figure 13

Theoretical and experimental hardening curves for the biaxial tensile test at different loading ratios: (a) \({4:1 - }\sigma_{x}\), (b) \({1:4 - }\sigma_{y}\), (c) \({2:1 - }\sigma_{x}\), (d) \({1:2 - }\sigma_{y}\), (e) \({4:3 - }\sigma_{x}\), (f) \({3:4 - }\sigma_{y}\), (g) \({1:}1{ - }\sigma_{x}\) and (h) \({1:1 - }\sigma_{y}\)

Full size image

To further analyze the effectiveness of different material models in predicting the biaxial tensile hardening relationship, it is necessary to perform quantitative evaluation. In the uniform deformation range for a certain loading ratio, the following function can be defined to calculate the relative error between the predicted stress and the experimental stress.

$$\delta_{\alpha > 1}^{bia} = \frac{1}{{N_{x} }}\left[ {\sum\limits_{i = 1}^{{N_{x} }} {\frac{{\sqrt {\left[ {\sigma_{11}^{cal} (i) - \sigma_{11}^{\exp } (i)} \right]^{2} } }}{{\sigma_{11}^{\exp } (i)}}} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\alpha > 1)$$
(39a)
$$\delta_{\alpha = 1}^{bia} = \frac{1}{2}\left\{ {\frac{1}{{N_{x} }}\left[ {\sum\limits_{i = 1}^{{N_{x} }} {\frac{{\sqrt {\left[ {\sigma_{11}^{cal} (i) - \sigma_{11}^{\exp } (i)} \right]^{2} } }}{{\sigma_{11}^{\exp } (i)}}} } \right] + \frac{1}{{N_{y} }}\left[ {\sum\limits_{i = 1}^{{N_{y} }} {\frac{{\sqrt {\left[ {\sigma_{22}^{cal} (i) - \sigma_{22}^{\exp } (i)} \right]^{2} } }}{{\sigma_{22}^{\exp } (i)}}} } \right]} \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\alpha = 1)$$
(39b)
$$\delta_{\alpha < 1}^{bia} = \frac{1}{{N_{y} }}\left[ {\sum\limits_{i = 1}^{{N_{y} }} {\frac{{\sqrt {\left[ {\sigma_{22}^{cal} (i) - \sigma_{22}^{\exp } (i)} \right]^{2} } }}{{\sigma_{22}^{\exp } (i)}}} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\alpha < 1)$$
(39c)

where \(N_{x}\) and \(N_{y}\) represent the number of experimental points in the RD and TD. By calculating the average value of the relative errors for all loading ratios and denoting this value \(\delta_{ave}^{bia}\), the final errors of different material models can be quantitatively analyzed.

Figure 14 shows the error distribution of the theoretical prediction and experimental curves for different loading ratios. For all loading ratios, the Barlat89 yield criterion using the r-value anisotropy data has higher prediction accuracy than the hardening curve calculated from the stress anisotropy data. The results from the Hill48 yield criterion, in addition to a 1:1 loading ratio, are also consistent with this regular pattern. It is generally believed that material parameter identification using stress anisotropy data is a more accurate approach for describing the hardening relationship that is directly related to stress and the springback calculation. When r-value anisotropic data are used to identify material parameters, the resulting parameters can accurately describe the plastic deformation relationship, such as the earing problem of deep drawing parts (Ref 35, 36). Only the test results shown based on the uniaxial loading state seem reasonable, as shown in Fig. 12 and 15. If r-value anisotropic data are not used in material parameter identification, the prediction results for the r-values in different directions are not satisfactory. In contrast, if stress anisotropy data are not used in this identification, the prediction accuracy for the flow stress is also reduced. However, for more complex loading conditions, the overall prediction accuracy for the hardening relationship prediction based on stress anisotropy data is not as good as that based on r-value anisotropy data. As the only special case, the Hill48-σ yield criterion shows accurate prediction accuracy for a loading path of 1:1 because balanced biaxial stress is used in the corresponding parameter identification. Therefore, for the Hill48 and Barlat89 yield criteria that are often used in the engineering field, the approach for choosing appropriate material parameter identification methods needs to be judged according to actual needs, relevant problems and multiaxial load test results. It is not sufficient to consider only the test results for a typical uniaxial or balanced biaxial loading state when judging the accuracy of a material model. In the practical forming applications, the Hill48 and Barlat89 yield criteria can each use only one method to identify the material parameters. However, regardless of whether r-value anisotropic data or stress anisotropic data are used, these criteria cannot be used to accurately describe the biaxial hardening relationships for different loading paths at the same time. The reason for this above phenomenon is that there is no use of balanced biaxial data to identify material parameters in the Hill48-r, Barlat89-r and Barlat89-σ yield criteria. Because the mechanical properties of balanced biaxial stress status are in a very special position on the yield surface (the cusp of the yield surface), it plays an important role in constraining the shape of the yield locus under the associated flow rule. However, in the Hill48-σ yield criterion, although balanced biaxial data are used, there are still obvious errors in the prediction accuracy of biaxial hardening relationships, which can be attributed to the lack of flexibility of the quadratic order model, and can lead to inevitable limitations in describing the complex stress state. This also explains why the Hill48 and Barlat89 yield criteria can be used to describe the uniaxial stress state and obtain high-precision prediction results, while when extended to the biaxial stress state, the prediction results are not satisfactory. To improve the accuracy of theoretical predictions or numerical analyses, it is necessary to choose a yield criterion with a higher flexibility.

Fig. 14
figure 14

Comparison between the biaxial hardening curves predicted with different yield criteria and material parameter identification methods and the experimental curves: (a) error distributions for different loading paths and (b) average error \(\delta_{ave}^{bia}\)

Full size image
Fig. 15
figure 15

Calculated (a) r-values and (b) uniaxial flow stresses in different angles based on various yield criteria

Full size image

However, for the biaxial hardening relationship at any loading ratio, even if a more advanced yield criterion is used, the BBC05-DWH yield criterion that considers different work hardening behaviors of the blank still yields a more accurate prediction than the traditional BBC2005 yield criterion. Furthermore, under these conditions, the average error is reduced by more than 26%. As mentioned in the Sect. 1, it is almost impossible to fully describe the deformation characteristics of materials in the entire strain range depending on the corresponding material properties measured under the specific equivalent plastic strain. Therefore, the BBC05-DWH yield criterion shows the best prediction accuracy, indicating the effectiveness of the developed material model.

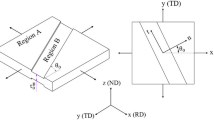
In addition, the ability to accurately reproduce the plastic strain directions related to the reference plastic strain of the work contour is an important standard that is used to verify the material model (Ref 37, 38). Figure 16 shows the measured directions of the plastic strains \(\beta\) compared to those calculated using the BBC05-DWH yield criterion. Within the defined strain range, the predicted strain direction based on the BBC05-DWH yield criterion is close to the measured data. The distance between the theoretical prediction value and the actual measurement data is defined as the error. The maximum deviation among all the loading ratios occurs at a loading ratio of 4:3, and the error is 7.8°.

Fig. 16
figure 16

Measured plastic strain directions compared to those calculated using the BBC05-DWH yield criterion

Full size image

Correction of the Hardening Curve for the HBT

In early research, the hardening curve measured by the HBT was directly applied as the equivalent curve (Ref 5, 39), and the stress of the experimental curve was calculated through the isotropic yield criterion. However, it is possible to make serious mistakes in such a calculation if the anisotropy of the blank is ignored. Therefore, it is generally accepted by most researchers that the hydraulic bulging curve is regarded as the hardening curve to describe the balanced biaxial stress state. Based on the equivalent plastic work principle or anisotropic yield criterion, this curve is modified to an equivalent stress–equivalent strain curve and used for numerical analysis. In this section, a BBC05-DWH yield criterion, in which different work hardening behaviors are considered, is used to modify the hydraulic bulging curve and is compared with the in-plane isotropic Hill48 yield criterion modified method that was proposed by Smith et al. (Ref 6), the Hill90 yield criterion modified method that was proposed by Nasser et al. (Ref 8), and the equivalent plastic work principle modified method that was suggested based on the ISO 16808: 2014 standard. Note that for the convenience of comparison, the data for the ISO 16808 standard correction curve in the small plastic deformation stage are not replaced with the RD data. The different correction methods are as follows:

$$\overline{\sigma }_{{{\varvec{Hill48}}}} = \sigma_{{\varvec{b}}} \left[ {2 - \frac{{2\overline{r}}}{{(\overline{r} + 1)}}} \right]^{\frac{1}{2}}$$
(40)
$$\overline{\sigma }_{{{\varvec{Hill90}}}} = \sigma_{{\varvec{b}}} \left[ {\frac{{r_{0} + r_{90} }}{{(1 + r_{0} )r_{90} }}} \right]^{\frac{1}{2}}$$
(41)
$$\overline{\sigma }_{{{\varvec{ISO}}}} = \sigma_{{\varvec{b}}} \cdot \frac{{\sigma_{{\user2{f - ref}}} }}{{\sigma_{{\user2{B - ref}}} }}$$
(42)
$$\begin{aligned} \overline{\sigma }_{{\user2{BBC05 - DWH}}} &= \sigma_{{\varvec{b}}} \left\{ {a(\overline{\varepsilon }^{{\varvec{p}}} )\left[ {\sqrt {\left[ {N(\overline{\varepsilon }^{{\varvec{p}}} ) - P(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2} } + L(\overline{\varepsilon }^{{\varvec{p}}} ) + M(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2k} } \right. \hfill \\ &\quad + a(\overline{\varepsilon }^{{\varvec{p}}} )\left[ {\sqrt {\left[ {N(\overline{\varepsilon }^{{\varvec{p}}} ) - P(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2} } - L(\overline{\varepsilon }^{{\varvec{p}}} ) - M(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2k} \hfill \\ &\quad +b(\overline{\varepsilon }^{{\varvec{p}}} )\left[ {\sqrt {\left[ {N(\overline{\varepsilon }^{{\varvec{p}}} ) - P(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2} } + \sqrt {\left[ {Q(\overline{\varepsilon }^{{\varvec{p}}} ) - R(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2} } } \right]^{2k} \hfill \\& \left.\quad +{ b(\overline{\varepsilon }^{{\varvec{p}}} )\left[ {\sqrt {\left[ {N(\overline{\varepsilon }^{{\varvec{p}}} ) - P(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2} } - \sqrt {\left[ {Q(\overline{\varepsilon }^{{\varvec{p}}} ) - R(\overline{\varepsilon }^{{\varvec{p}}} )} \right]^{2} } } \right]^{2k} } \right\}^{\frac{1}{2k}} \hfill \\ \end{aligned}$$
(43)

where \(\sigma_{{\user2{f - ref}}}\) is the last effective flow stress point in the uniform strain range of the RD, and \(\sigma_{{\user2{B - ref}}}\) is the flow stress in the HBT under the same plastic work conditions. The equivalent stress formula calculated based on the Hill48 anisotropic yield criterion and r-value anisotropic data is consistent with the method proposed by Nasser et al. (Ref 8). Therefore, this method can be regarded as an improvement in the in-plane isotropic Hill48 yield criterion method. Figure 17 shows the hardening curves, as corrected based on the four methods. The hardening curves calculated by the Smith et al. (Ref 6) and Nasser et al. (Ref 8) methods seem to be consistent because the 5182-O aluminum alloy tested in this paper shows a low in-plane anisotropy. Additionally, these two methods overestimate the hardening degree of the material compared to the RD curve, which is actually the same as the prediction results shown in Fig. 13(g, h). Because the hardening curve of 1:1 predicted based on the Hill48-r yield criterion is lower than the experimental results, it is intuitive to expect that the reverse prediction of the hardening curve based on the HBT will inevitably lead to higher correction results. The prediction results from the BBC05-DWH method and ISO16808 standard method are very similar. Although the two methods apply different correction ideas, in essence, the material parameter identification processes in the anisotropic yield criteria are also through plastic work, so the difference between the two methods is that the former considers different work hardening, while the latter assumes that the material isotropically hardens. In the small deformation stage, the hardening curves calculated by the two methods are almost the same, but when the strain exceeds 0.35, the ISO16808 standard method that ignores the different work hardening behavior of the blank predicts a higher-level hardening trend. In the automotive stamping industry, considering the actual strain range of sheet metals, the influence of different work hardening behavior on the correction of the hydraulic bulging curve should be considered, especially for engineering materials with significantly different work hardening behavior.

Fig. 17
figure 17

Correction of the hydraulic bulging curve based on different methods

Full size image

In general, the hydraulic bulging curve is modified through the yield criterion. First, it is necessary to ensure that the selected yield function can accurately predict \(\sigma_{b}\). Although using r-value anisotropic data to identify material parameters shows a lower level of average error in describing the biaxial loading relationship, as shown in Fig. 14, the use of such data is clearly not satisfactory for the prediction of the \(\sigma_{b}\). Furthermore, the different work hardening behaviors need to be characterized by evolved normalized flow stresses and r-values. However, experimental data measured under large plastic strain are not easy to obtain, especially through the standard uniaxial tensile test. Therefore, for different engineering materials, it is necessary to choose a more appropriate method for predicting the normalized flow stress and r-value according to the material characteristics. Alternatively, the multiaxial tube expansion test (Ref 37), reverse identification method (Ref 40) and virtual field method (Ref 41) can also be used to measure and predict the hardening curve at the highest possible strain levels.

Conclusion

A material model BBC05-DWH yield criterion was developed considering different work hardening behaviors. The difference between this model and the traditional model is that the material parameters were expressed as a function of the equivalent plastic strain. Uniaxial and biaxial tensile tests and HBT tests were carried out on a 5182-O aluminum alloy to verify the effectiveness of the developed material model. The conclusions are as follows:

  1. 1.

    The hardening relationship of biaxial tensile stress for different loading ratios was deduced by using the Hill48-σ, Hill48-r, Barlat89-σ, Barlat89-r, BBC2005 and BBC05-DWH yield criteria. These results show the importance of selecting suitable material parameter identification methods and considering deformation anisotropy in the forming process.

  2. 2.

    The use of only stress anisotropy data to identify material parameters under uniaxial loading can reasonably predict flow stress in different directions. Furthermore, the use of only r-value anisotropy data to identify material parameters can more accurately predict the r-values in different directions. However, this conclusion may not be applicable to complex loading conditions.

  3. 3.

    The HBT is a popular method used to measure the equal biaxial tensile hardening curve over a large plastic strain range, but it may not be accurate enough for measuring the hardening curve in a small plastic deformation stage. Therefore, to determine the balanced biaxial stress in a small strain range, cruciform specimen tests should be carried out.

  4. 4.

    The modification of the hydraulic bulging curve should ensure that the yield criterion accurately describes the balanced biaxial stress. For a more stringent treatment, because different work hardening behaviors can provide more accurate correction results, the deformation anisotropy of the materials should at least be considered in the strain range that can be measured through testing.

  5. 5.

    The function of the fitted normalized flow stress used in this work can describe the deformation behavior of 5182-O aluminum alloy well, especially after the uniform plastic deformation stage, and no end jumping phenomenon induced. The hardening curve calculated with this function can be used as the input for the constitutive model in a large deformation state.