Accuracy improvement of FLD prediction for anisotropic sheet metals using BBC 2008 advanced yield criterion

Abstract

In this paper, a theoretical framework was developed to incorporate BBC 2008 advanced yield criterion into the classical Marciniak–Kuczynski theory to compute limit strains of anisotropic metallic sheets. The classical Hill’s 48 yield function was also utilized to compare with the results obtained by BBC 2008. The anisotropy parameters contained in BBC 2008 yield function were identified by minimizing an error function using Levenberg–Marquardt method. The data from uniaxial and plane strain tensile testings were employed to establish the error function. All the experimental tests were performed on AA 3003-H19 aluminum sheets. The yield criteria were assessed from the standpoint of predicting material properties and the yield locus by comparing theoretical findings and experimental data. The influence of the use and non-use of the plane strain yield stresses in the identification procedure on the FLD calculation was also investigated. To verify the theoretical predictions of the FLD, a series of Nakajima tests were accomplished. Comparing the experimental results and theoretical predictions revealed that the best agreement was found when BBC 2008-16p yield function was utilized to express the yield locus. Failure to use the plane strain yield stresses in the calibration procedure of the BBC 2008-16p criterion also causes overpredicting the limit strains for positive strain ratios.

1 Introduction

The formability of metallic sheets can be effectively assessed using a forming limits diagram, abbreviated as FLD. This diagram contains all combinations of the principal minor and major strains that metallic sheets can undergo without necking during plastic deformation. The FLD concept was initially presented by Keeler [1] and then developed by Goodwin [2]. There have been numerous attempts to acquire FLD during the previous decades using experimental, numerical, and theoretical methods. Due to the high cost and time-consuming nature of the experimental methods, numerical and theoretical approaches for determining limit strains have received more attention from several researchers. Hence, numerous theories have been proposed to predict limit strains, such as diffuse necking [3], localized necking [4], Marciniak–Kuczynski model [5,6,7], bifurcation theory [8], and maximum modified force criterion (MMFC) [9,10,11,12,13]. Another technique to determine the limit strains is to use a ductile fracture criterion. In this method, stress and strain histories calculated by theoretical analysis or numerical simulations are transferred to the ductile failure criteria to investigate whether necking has occurred. The criteria GTN [14, 15], Xue [16], Bao and Wierzbicki [17], and Mohr–Marcadet 2015 [18], DF2016 [19] are examples of the ductile fracture criteria. Among the theoretical models, the proposed model by Marciniak–Kuczynski, abbreviated as M–K, is the most preferred in the theoretical prediction of FLD due to its simplicity and ability to incorporate different yield criteria and constitutive laws analytically.

In the analysis of the sheet metal’s formability, the yield criterion is the most significant element because it determines the transition conditions from elastic to plastic stress state as well as the anisotropic behavior of the material. Depending on the yield function used, different results may be obtained. Due to this fact, several investigations have been performed to evaluate the effect of various yield criteria on the forming limits prediction.

Lian et al. [20] calculated the right-hand side of the FLD using Hill’s 79 yield criterion. The effect of Barlat–Lian 1989 and Hill’s 79 yield functions on the calculation of forming limits was studied by Lian et al. [21]. They demonstrated that the FLDs of a large number of materials could be characterized by selecting the yield function exponent M in the range of 5–10 in the Barlat–Lian 1989 criterion. Xu and Weinmann [22] performed an investigation on the FLD calculation of metallic sheets using MK model and Hill’s 1993 yield criterion. Xu and Weinmann [22] showed that limit strains are significantly affected by the shape of the yield locus. They concluded that increasing the yield surface sharpness in the biaxial tension zone reduces the forming limits for positive strain ratios. Cao et al. [23] studied the FLD of sheet metals for linear and nonlinear strain paths using M–K model and Karafillis and Boyce yield criterion. They found that the calculated FLD for AA 6111-T4 and AA 2008-T4 matched well with the experimental data. Banabic and Dannenmann [24] combined Hill’s 1993 yield function with M–K and diffuse necking theories to calculate FLD for positive strain ratios. They introduced the parameter of the ratio of uniaxial yield stress over biaxial yield stress and showed that an enhancement of this parameter gives higher limit strains in biaxial tension region. Butuc et al. [25] released a more general program for computing FLD using M–K approach. They implemented Hill’s 48, Hill’s 79, and YLD 96 yield functions as well as the Voce and Swift constitutive equations into the developed code for AA 6xxx-T4 sheets. The performances of YLD 96 and BBC 2000 yield functions on the FLD prediction for AA 5xxx aluminum alloy sheet were assessed by Butuc et al. [26]. They found a high degree of conformity between experimental FLDs and theoretical findings when the yield surface and hardening law are characterized by Yld96 Voce equation, respectively. Ávila and Vieira [27] examined the influence of von Mises, Hill’s 48, Hill’s 79, Hill’s 93, and Hosford–Logan yield criteria on the calculation of forming limits for biaxial tension using M–K theory. They demonstrated that the yield function has a predominant influence on the theoretical results. Dariani and Azodi [28] incorporated Hill’s 79 yield criterion into the M–K model and demonstrated that theoretical results of FLD prediction are dependent upon the exponent of the yield function. They obtained the optimum exponent of Hill’s 79 yield function for different materials in the case that the best agreement was reached between the experimental and the predicted FLD. Banabic et al. [29] combined the BBC 2000 yield function and classical M–K theory to compute the forming limits for AA2008-T4 aluminum alloy sheet. Ganjiani and Assempour [30] studied the effect of Hosford and BBC 2000 yield criterion on the prediction of FLDs using M–K theory. Ganjiani and Assempour [30] revealed that using BBC 2000 yield criterion leads to the best correlation between the experimental FLD and theoretical results for AA5XXX alloy. As well, the use of exponents 6 and 8 for the Hosford criterion leads to the appropriate prediction of FLD for AK steel and AA5XXX alloy, respectively. Ahmadi et al. [31] employed BBC2000, BBC2002, and BBC2003 yield criteria combined with the Voce and Swift constitutive laws to calculate forming limits by MK model. Their results showed that utilizing BBC 2003 yield criterion and the Voce constitutive law gives the best theoretical results for AA3003-O aluminum alloy sheet. The effect of Hill’s 48, 90, 93, YLD 89, and Plunkett yield functions on the FLD prediction of Al 5754 sheets were assessed by Dasappa et al. [32]. The results revealed that the computed limit strains are significantly influenced by the method used to identify the anisotropy coefficients of the yield criteria and the shape of the yield surface. Panich et al. [33] applied YLD 2000, Hill’s 48, and Von Mises yield functions along with modified Voce and Swift constitutive laws for FLD and FLSD computation of DP780 and TRIP780 sheets. They deduced that the best agreement between experimental data and predicted forming limits can be achieved using YLD 2000 yield function in combination with Swift constitutive law. Basak and Panda [34] employed Bao–Wierzbicki ductile damage criterion and classical M–K theory in combination with Hill’s 48 and YLD 2000 yield functions to calculate the forming and fracture limit diagrams of AA5052 and EDD metallic sheets. They showed that utilizing Yld2000-2d yield criterion in the theoretical models gives the best description of experimental data. Djavanroodi et al. [35] investigated FLD prediction of Ti–6Al–4V and AA7075 sheets theoretically and numerically using Hill’s 93 and BBC 2000 yield functions. They demonstrated that implementing Hill’s 93 and BBC 2000 yield functions in the numerical computation of FLD yields better results for Ti–6Al–4V and AA7075, respectively. The effect of the yield function exponent on the calculation of FLD was assessed by Lei et al. [36]. They acquired the optimal value of the exponent for Barlat–Lian 1989 yield function so that the calculated limit strains were in the best agreement with experimental FLD for SZA6 zirconium alloy. The proposed analytical models are not limited to single-layer sheets, but also for multilayer sheets. For example, Jalali et al. [37, 38] examined the formability of bimetals utilizing M–K model combined with Hill’s 79 yield.

The reviewed literature revealed that the degree of agreement between the computed FLD based on the theoretical models and experimental results strongly depends on the utilized yield function. Consequently, the incorporation of a proper yield criterion that can accurately capture the anisotropic properties of the metallic sheets improves the FLD prediction accuracy.

The anisotropic yield functions can be divided into two categories: classical anisotropic yield functions and advanced yield criteria. Hill's family criteria [39,40,41,42] are one of the best examples of the classical anisotropic yield function. These types of yield criteria have been used by many researchers so far due to their simple formulation and ease of determining the anisotropy coefficients utilized in them. The main disadvantage of classical criteria is their inability to accurately describe the yield surface and properties of highly anisotropic sheet metals, particularly aluminum alloys. Another type of yield criterion, the so-called advanced yield criterion, incorporates several coefficients that may be identified based on experimental data. Because of the large number of input data required to determine the parameters used in the advanced yield criteria, they can accurately describe the planar distribution of the plastic behavior (i.e., plastic anisotropy coefficient and yield stress) and yield locus [43]. BBC yield criteria family [44,45,46,47], YLD yield criteria family [48,49,50], Yoon 2014 [51], Lou and Yoon 2018 [52], and Cazacu 2019 [53, 54] are the best examples of the advanced yield functions. The advanced yield criteria differ in their mathematical formulation and accuracy in describing the anisotropic behavior of materials. The simpler the formulation of the yield criterion, the higher its computational efficiency.

Comsa and Banabic [47] introduced the most recent edition of the BBC yield criterion family called ‘BBC 2008’ as a finite series. The amount of experimental data available determines the number of terms in the series. BBC 2008 has more flexibility than other versions of this yield criterion family (i.e., BBC 2000, BBC 2003, and BBC 2005). BBC 2008 does not apply linear stress tensor transformations, unlike other advanced yield criteria published in the literature, such as the YLD yield criterion family [48,49,50]. As a result, its computing efficiency should be higher in the theoretical and numerical analysis. Additionally, some studies [55, 56] have demonstrated that using the BBC 2008 yield criterion improves the results of numerical simulations and analytical models in analyzing sheet metal forming processes. Hence, the authors employed BBC 2008 yield criterion in their theoretical model in the present research.

In this paper, BBC 2008 yield criterion was incorporated into the M–K theory to compute the FLD of AA 3003-H19 anisotropic sheets. Hill’s 48 is the most common yield function employed in the theoretical and numerical analysis of sheet metal formability so far. For this reason, it was implemented into the theoretical model to compare with the results obtained by BBC 2008. To calibrate the anisotropy parameters of BBC 2008 yield function, an error function was built and minimized by Levenberg–Marquardt method. The Lankford coefficients and yield stresses at angles 0, 15, 30, 45, 60, 75, and 90° to the rolling direction and plane strain yield stresses in the rolling and transverse directions obtained from experiments were utilized in the calibration procedure. By comparing the experimental data with the theoretical findings, the performances of Hill’s 48 and BBC 2008 (8 and 16 parameters) yield functions were examined from the point of view of reproducing material properties as well as FLD prediction.

2 Theoretical model

2.1 Explanation of yield criteria

The yield criterion is typically formulated by an implicit function of the stress components as follows:

$$\Phi =\tilde{\sigma }\left({\sigma }_{ij}\right)-Y(\overline{\varepsilon })=0$$

(1)

where $\tilde{\sigma }\left({\sigma }_{ij}\right)\ge 0$ is the equivalent stress, $\overline{\varepsilon }$ is equivalent plastic strain, $Y(\overline{\varepsilon })$ is the material’s yield strength and ${\sigma }_{ij}= {\sigma }_{ji}$ (i, j = 1, 2, 3) are the stress components expressed in the plastic orthotropy axes. The rolling direction (RD), transverse direction (TD), and normal direction (ND) of the sheet are denoted by subscripts 1, 2, and 3, respectively. The equivalent stress is determined by yield function as well as the yield strength of a material is characterized by hardening law as a function of equivalent plastic strain.

2.1.1 Hill’s 48 yield criterion

Hill [39] presented a quadratic function as a yield criterion for the anisotropic materials. The equivalent stress of Hill’s 48 yield criterion is expressed as

$$2{\tilde{\sigma }}^{2}=F{\left({\sigma }_{22}-{\sigma }_{33}\right)}^{2}+G{\left({\sigma }_{33}-{\sigma }_{11}\right)}^{2}+H{\left({\sigma }_{11}-{\sigma }_{22}\right)}^{2}+2L{{\sigma }_{23}}^{2}+2M{{\sigma }_{13}}^{2}+2N{{\sigma }_{12}}^{2}$$

(2)

where F, G, H, L, M, and N are parameters that characterize the material's anisotropy state. The anisotropy parameters are determined through the following relations

$$\begin{aligned} F & = \frac{{2r_{0} }}{{r_{90} \left( {1 + r_{0} } \right)}} , \quad G = \frac{2}{{1 + r_{0} }} , \quad H = \frac{{2r_{0} }}{{1 + r_{0} }} \\ N & = \frac{{2\left( {r_{0} + r_{90} } \right)\left( {r_{45} + 0.5} \right)}}{{r_{90} \left( {1 + r_{0} } \right)}} , \quad L = M = 3. \\ \end{aligned}$$

(3)

In Eq. (3), the Lankford coefficients are denoted by r, and its subscript determines the orientation angle to the rolling direction.

2.1.2 BBC 2008 yield criterion

The yield criterion suggested by Comsa and Banabic [47] is in the form of a finite series under plane stress conditions for plastically orthotropic metallic sheets. The following formula describes the equivalent stress for the BBC 2008 yield criterion.

$$\begin{aligned} & \frac{{\overline{\sigma }^{2k} }}{w - 1} = \mathop \sum \limits_{i = 1}^{s} \left\{ {w^{i - 1} \left\{ {\left[ {L^{\left( i \right)} + M^{\left( i \right)} } \right]^{2k} + \left[ {L^{\left( i \right)} - M^{\left( i \right)} } \right]^{2k} } \right\} + w^{s - i} \left\{ {\left[ {M^{\left( i \right)} + N^{\left( i \right)} } \right]^{2k} + \left[ {M^{\left( i \right)} - N^{\left( i \right)} } \right]^{2k} } \right\}} \right\} \\ & k,s \in N \\ & w = \left( \frac{3}{2} \right)^{1/s} > 1 \\ & L^{\left( i \right)} = l_{1}^{\left( i \right)} \sigma_{11} + l_{2}^{\left( i \right)} \sigma_{22} \\ & M^{\left( i \right)} = \sqrt {\left[ {m_{1}^{\left( i \right)} \sigma_{11} - m_{2}^{\left( i \right)} \sigma_{22} } \right]^{2} + \left[ {m_{3}^{\left( i \right)} \left( {\sigma_{12} + \sigma_{21} } \right)} \right]^{2} } \\ & N^{\left( i \right)} = \sqrt {\left[ {n_{1}^{\left( i \right)} \sigma_{11} - n_{2}^{\left( i \right)} \sigma_{22} } \right]^{2} + \left[ {n_{3}^{\left( i \right)} \left( {\sigma_{12} + \sigma_{21} } \right)} \right]^{2} } \\ & l_{1}^{\left( i \right)} , l_{2}^{\left( i \right)} , m_{1}^{\left( i \right)} , \text{'} m_{2}^{\left( i \right)} , m_{3}^{\left( i \right)} , n_{1}^{\left( i \right)} , n_{2}^{\left( i \right)} , n_{3}^{\left( i \right)} \in R \\ \end{aligned}$$

(4)

where $l_{1}^{\left( i \right)} , l_{2}^{\left( i \right)} , m_{1}^{\left( i \right)} ,text{'} m_{2}^{\left( i \right)} , m_{3}^{\left( i \right)} , n_{1}^{\left( i \right)} , n_{2}^{\left( i \right)} , n_{3}^{\left( i \right)}$ are anisotropy parameters may be calibrated by experimental data. The value of k is determined by the sheet metal’s crystalline structure so that its values for BCC and FCC materials are 3 and 4, respectively. Obviously, whenever s = 1 and s = 2, the yield function includes 8 (BBC 2008-8p) & 16 (BBC 2008-16p) coefficients to describe the anisotropy, respectively.

2.1.2.1 Identification procedure

There are two distinct approaches to calibrating the anisotropy parameters contained in the advanced yield criteria. The first approach is to solve a set of equations where the number of equations equals the number of anisotropy coefficients. In this case, the number of experimental data should be equal to the number of anisotropy parameters. The failure risk of this method grows as the number of parameters increases. Another efficient approach is to minimize an error function. The greatest benefit of this strategy is that the number of experimental data does not need to match the number of anisotropy parameters. In other words, it is possible to obtain the anisotropy coefficients with fewer experimental data. It is worth noting that the greater the number of experiments, the greater the accuracy of the identification procedure. Comsa and Banabic [47] presented an error function to characterize the anisotropic coefficients utilized in the BBC 2008 yield function as follows:

$$\begin{aligned} & E\left( {l_{1}^{\left( i \right)} , l_{2}^{\left( i \right)} , m_{1}^{\left( i \right)} , text{'} m_{2}^{\left( i \right)} , m_{3}^{\left( i \right)} , n_{1}^{\left( i \right)} , n_{2}^{\left( i \right)} , n_{3}^{\left( i \right)} } \right) \\ & \quad = \mathop \sum \limits_{i = 1}^{n} \left( {\frac{{Y_{{\varphi_{i} }}^{\exp } }}{{Y_{{\varphi_{i} }} }} - 1} \right)^{2} + \mathop \sum \limits_{i = 1}^{n} \left( {r_{{\varphi_{i} }}^{\exp } - r_{{\varphi_{i} }} } \right)^{2} + \left( {\frac{{Y_{b}^{\exp } }}{{Y_{b} }} - 1} \right)^{2} + \left( {r_{b}^{\exp } - r_{b} } \right)^{2} \\ \end{aligned}$$

(5)

where

• ${r}_{{\varphi }_{i}}$ and ${Y}_{{\varphi }_{i}}$ are the theoretical Lankford coefficient (r value) and uniaxial yield stress predicted by the yield criterion, respectively. The orientation of the specimens relative to RD is denoted by subscript φ.

• ${Y}_{b}$ and ${r}_{b}$ define the theoretical equi-biaxial yield stress and equi-biaxial r value. These quantities are determined by BBC 2008 criterion in the case that the equi-biaxial tensile specimen is oriented along RD and TD.

• The quantities denoted by the ‘exp’ superscript are related to the experimental values. The number of utilized experimental data is defined by ‘n’ as the summation limit.

It is noteworthy that the error function (Eq. (5)) is a function of anisotropy parameters ($l_{1}^{\left( i \right)} , l_{2}^{\left( i \right)} , m_{1}^{\left( i \right)} ,text{'} m_{2}^{\left( i \right)} , m_{3}^{\left( i \right)} , n_{1}^{\left( i \right)} , n_{2}^{\left( i \right)} , n_{3}^{\left( i \right)}$) and is defined based on a squared distance between the experimental data and theoretical values. The required relations for calculating the predicted values are detailed in reference [47]. Two types of experimental data required to establish and minimize the error function are data from uniaxial tensile tests (i.e., ${Y}_{0}, {Y}_{45}, {Y}_{90}, {r}_{0}, {r}_{45}$ and ${r}_{90}$) and data from equi-biaxial tension of cruciform specimen [44] or bulge test (i.e., ${Y}_{b}$ and ${r}_{b}$). Due to the high cost of sample preparation and execution of the biaxial tensile test, as well as the fact that biaxial tensile testing equipment is rarely found in industrial laboratories, Aretz et al. [57] proposed to utilize two yield stresses corresponding to plane strain tensile test along RD and TD instead of using Y_b and r_b in the calibration procedure. In this case, all the required experiments for the calibration can be executed on a universal tensile testing machine. Consequently, the error function (Eq. (5)) can be revised as follows:

$$\begin{aligned} & E\left( {l_{1}^{\left( i \right)} , l_{2}^{\left( i \right)} , m_{1}^{\left( i \right)} ,text{'} m_{2}^{\left( i \right)} , m_{3}^{\left( i \right)} , n_{1}^{\left( i \right)} , n_{2}^{\left( i \right)} , n_{3}^{\left( i \right)} } \right) \\ & \quad = \mathop \sum \limits_{i = 1}^{n} \left( {\frac{{Y_{{\varphi_{i} }}^{\exp } }}{{Y_{{\varphi_{i} }} }} - 1} \right)^{2} + \mathop \sum \limits_{i = 1}^{n} \left( {r_{{\varphi_{i} }}^{\exp } - r_{{\varphi_{i} }} } \right)^{2} + \mathop \sum \limits_{i = 1}^{2} \left( {\frac{{\left( {Y_{{\psi_{i} }}^{{{\text{ps}}}} } \right)^{\exp } }}{{Y_{{\psi_{i} }}^{{{\text{ps}}}} }} - 1} \right)^{2} \\ \end{aligned}$$

(6)

where $\left\{{\psi }_{1}, {\psi }_{2}\right\}=\left\{{0}^{^\circ }, {90}^{^\circ }\right\}$, and the ‘ps’ superscript indicates the plane strain yield stress. Reference [57] details the needed relations for computing the theoretical plane strain yield stress.

Since the error function was constructed in the form of the sum of squares of nonlinear functions, the Levenberg–Marquardt algorithm [58] was used to minimize the error function in this study.

2.1.3 Associated flow rule

The associated flow rule or normality rule determines the plastic strain increments and direction of plastic flow. The associated flow rule is formulated as

$$\mathrm{d}{\varepsilon }_{ij}=\mathrm{d}\overline{\varepsilon } \frac{\partial \tilde{\sigma }}{\partial {\sigma }_{ij}}$$

(7)

where $\mathrm{d}\overline{\varepsilon }>0$ is the equivalent plastic strain increment. Differentiating of $\tilde{\sigma }$ with respect to the stress components for Hill’s 48 yield criterion is relatively simple, but calculating them for the BBC 2008 yield function is more complex and can be determined using the chain rule as follows:

$$\frac{\partial \tilde{\sigma }}{\partial {\sigma }_{ij}}= \sum_{i=1}^{s}\left\{\frac{\partial \tilde{\sigma }}{\partial {L}^{(i)}}\frac{\partial {L}^{(i)}}{\partial {\sigma }_{ij}}+\frac{\partial \tilde{\sigma }}{\partial {N}^{(i)}}\frac{\partial {N}^{(i)}}{\partial {\sigma }_{ij}}+\frac{\partial \tilde{\sigma }}{\partial {M}^{(i)}}\frac{\partial {M}^{(i)}}{\partial {\sigma }_{ij}}\right\}$$

(8)

A more detailed description of each term of Eq. (8) is presented in Appendix A.

2.2 M–K model

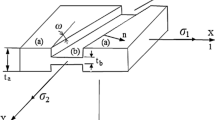
Marciniak and Kuczynski (M–K) [5,6,7] introduced a theoretical model to characterize the FLD of sheet metals. This model was founded on the idea that the sheet has an initial inhomogeneity due to a variation in its thickness. The inhomogeneity is represented as a groove with an inclination angle of ${\theta }_{0}$. Figure 1 illustrates a graphical representation of the M–K model in a schematic form. As can be seen, the sheet metal is partitioned into two areas: uniform and groove, marked by the letters ‘A’ and ‘B,’ respectively. The initial amount of inhomogeneity can be quantified by a variable called the initial imperfection factor through the following relation

Fig. 1

Graphical representation of the M–K model in a schematic form

$${f}_{0}=\frac{{{t}_{0}}^{B}}{{{t}_{0}}^{A}}$$

(9)

where the variable t₀ represents the initial sheet thickness, as well as superscripts A and B are related to the perfect and imperfect regions, respectively.

By applying an increment of equivalent plastic strain to the uniform zone ($\mathrm{d}{\overline{\varepsilon }}^{A}$), both regions are subjected to plastic deformation, but the amounts of deformations in these two regions are different. As deformation progresses, strains begin to concentrate gradually in the groove until the ratio of $\mathrm{d}{\overline{\varepsilon }}^{B}$ to $\mathrm{d}{\overline{\varepsilon }}^{A}$ exceeds 10. When this condition is met, the specimen’s deformation is confined in the groove region, and the limit strains are reached.

2.2.1 Computation of strain and stress in the uniform zone

To analyze stress and strain, a Cartesian reference frame is set so that its x, y, and z axes are parallel to the orthotropy axes RD, TD, and ND of the sheet, as illustrated in Fig. 1. The local coordinate system ntz is also attached to the groove region. The ‘n’ and ‘t’ axis coincide with the normal and longitudinal directions of the groove, respectively.

A plane stress condition and rigid plastic along with isotropic hardening material, are the general assumptions that were employed in this research. It is also assumed that proportional and monotonic strain increments along the orthotropy axes are applied to the uniform area, and therefore the x and y directions are principal. Hollomon’s power law was utilized to describe the material’s work hardening as follows:

$$\tilde{\sigma }=K{\overline{\varepsilon }}^{n}$$

(10)

where n is strain hardening exponent and K is strength coefficient. The strain path in the uniform area is defined by

$$\rho =\frac{{d\varepsilon }_{2}^{A}}{{d\varepsilon }_{1}^{A}}.$$

(11)

The stress ratio in zone ‘A’ is defined as

$$\alpha =\frac{{\sigma }_{2}^{A}}{{\sigma }_{1}^{A}}.$$

(12)

Finally, the strain increment and stress tensor in the uniform region are

$$\begin{aligned} \left[ {{\text{d}}\varepsilon^{A} } \right]_{xyz} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & \rho & 0 \\ 0 & 0 & { - \left( {1 + \rho } \right)} \\ \end{array} } \right]{\text{d}}\varepsilon_{1}^{A} \\ \left[ {\sigma^{A} } \right]_{xyz} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & \alpha & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\sigma_{1}^{A} . \\ \end{aligned}$$

(13)

The equivalent stress must be a homogeneous function of degree one [50]. Therefore, it is possible to rewrite the relation of equivalent stress in terms of stress ratio as follows:

$$\tilde{\sigma }\left({\sigma }_{1} , {\sigma }_{2}\right)={\sigma }_{1}\tilde{\sigma }\left(1 , \alpha \right)={\sigma }_{1}h\left(\alpha \right).$$

(14)

The strain path is also determined in terms of stress ratio by calculating the strain increments from Eq. (7) and substituting them into Eq. (11) as follows:

$$\rho ={\left.\frac{\frac{\partial \tilde{\sigma }}{\partial {{\sigma }_{2}}^{A}}}{\frac{\partial \tilde{\sigma }}{\partial {{\sigma }_{1}}^{A}}}\right|}_{{{\sigma }_{1}}^{A}=1 ,{ {\sigma }_{2}}^{A}=\alpha }=g\left(\alpha \right).$$

(15)

Note that in Eqs. (14) and (15) the homogeneity of the equivalent stress function has been exploited allowing to use of the relative stresses ${{\sigma }_{1}}^{A}=1$ and ${{\sigma }_{2}}^{A}=\alpha$ instead of using absolute stresses. By using a numerical approach to solve the following equation, the stress ratio in the uniform region corresponding to the strain path can be determined.

$$g\left( \alpha \right) - \rho = 0.$$

(16)

The accumulated equivalent plastic strain in each loading step can be calculated by summing the current or imposed equivalent plastic strain increment and the accumulated equivalent plastic strain up to, but not including, the current increment of loading. In the uniform region for a given strain path $\rho$, combining Eqs. (1) and (14) and substituting the values of the stress ratio obtained from Eq. (16) and the accumulated equivalent plastic strain yields

$${{\sigma }_{1}}^{A}=\frac{Y({\overline{\varepsilon }}^{A})}{h\left({\alpha }^{A}\right)}.$$

(17)

The value of ${{\sigma }_{2}}^{A}$ is also determined using the stress ratio relation (Eq. (12)). The strain components in the uniform region are specified by substituting the stress components into the flow rule.

During plastic deformation, the groove orientation evolves as:

$$\mathrm{tan}\left(\theta +\mathrm{d}\theta \right)=\frac{1+{\mathrm{d}\varepsilon }_{1}^{A}}{1+{\mathrm{d}\varepsilon }_{2}^{A}}\mathrm{tan}(\theta ).$$

(18)

The stress and strain tensors are transformed to the ntz coordinate system using the rotation matrix $\left[Q\right]$ through the following relations

$$\begin{aligned} \left[ {\sigma^{A} } \right]_{ntz} & = \left[ Q \right]\left[ {\sigma^{A} } \right]_{xyz} \left[ Q \right]^{T} \\ \left[ {\varepsilon^{A} } \right]_{ntz} & = \left[ Q \right]\left[ {\varepsilon^{A} } \right]_{xyz} \left[ Q \right]^{T} \\ \end{aligned}$$

(19)

where

$$\left[Q\right]= \left[\begin{array}{ccc}\mathrm{cos}\theta & \mathrm{sin}\theta & 0\\ -\mathrm{sin}\theta & \mathrm{cos}\theta & 0\\ 0& 0& 1\end{array}\right].$$

(20)

2.2.2 Computation of strain and stress in the groove zone

In the imperfect zone, ${{\sigma }_{nn}}^{B}$, ${{\sigma }_{nt}}^{B}$, ${{\sigma }_{tt}}^{B}$, and $\mathrm{d}{\overline{\varepsilon }}^{B}$ are the unknown independent parameters. Four independent equations are required to calculate these parameters, which will be explained in the following.

The first equation is obtained by establishing a compatibility condition. The strain increments in both regions are considered to be the same along the groove's longitudinal direction.

$${\mathrm{d}\varepsilon }_{tt}^{B}={\mathrm{d}\varepsilon }_{tt}^{A}.$$

(21)

The second and third equations are provided by the equilibrium condition in the interface of the uniform and groove areas along the normal and longitudinal axis (n, t) as follows:

$${F}_{nn}^{B}={F}_{nn}^{A}$$

(22)

$${F}_{nt}^{B}={F}_{nt}^{A}.$$

(23)

The ratio of current sheet thickness in regions ‘B’ to ‘A’ determines the instantaneous imperfection factor, which is formulated through the following relation

$$f={f}_{0} \mathrm{exp}\left({\varepsilon }_{z}^{B}-{\varepsilon }_{z}^{A}\right).$$

(24)

Combination of the equilibrium equations and Eq. (24) gives

$$f{\sigma }_{nn}^{B}={\sigma }_{nn}^{A}$$

(25)

$$f{\sigma }_{nt}^{B}={\sigma }_{nt}^{A}.$$

(26)

Finally, the plastic work relation is expressed as

$${{\sigma }_{nn}}^{B}{\mathrm{d}\varepsilon }_{nn}^{B}+2{{\sigma }_{nt}}^{B}{\mathrm{d}\varepsilon }_{nt}^{B}+{{\sigma }_{tt}}^{B}{\mathrm{d}\varepsilon }_{tt}^{B} {= \tilde{\sigma }}^{B}\mathrm{d}{\overline{\varepsilon }}^{B}$$

(27)

where ${\tilde{\sigma }}^{B}$ is calculated by hardening law.

To determine the unknown variables, the nonlinear system of Eqs. (21), (25), (26), and (27) must be solved numerically. In this research, the well-known Newton–Raphson method was utilized.

2.3 Numerical procedure for FLD calculation

In order to calculate the limit strains, a parametric program was written in MATLAB software. The material constants (K, n), strain path ($\rho$), the initial imperfection factor (${f}_{0}$), and the yield function’s anisotropy parameters are considered input variables. The flowchart in Fig. 2 depicts the calculation procedure. Initially, the stress ratio $\alpha$ corresponding to the strain path in region ‘A’ is found by numerical solving of Eq. (16). All stress and strain components and increments are set to zero. Then, a small equivalent strain increment ($\mathrm{d}{\overline{\varepsilon }}^{A}=0.0001$) is imposed to the uniform region. The stress tensor in this region is identified using Eqs. (17) and (13). The strain increments are also computed by substituting the obtained stresses into the associated flow rule (Eq. (7)). The band orientation (θ) is updated at each increment of the plastic deformation through Eq. (18). By transforming the obtained stress and strain increments to ntz coordinate system (Eq. (19)), the system of nonlinear equations (Eqs. (21), (25), (26) and (27)) can be established. The unknown parameters (${{\sigma }_{nn}}^{B}$, ${{\sigma }_{nt}}^{B}$, ${{\sigma }_{tt}}^{B}$, and $\mathrm{d}{\overline{\varepsilon }}^{B}$) of the groove region are determined by numerical solving of the system of equations using the Newton–Raphson method. This incremental calculation procedure continues until the condition $\frac{\mathrm{d}{\overline{\varepsilon }}^{B}}{\mathrm{d}{\overline{\varepsilon }}^{A}}\ge 10$ is met. With attaining the necking point, the minor and major strains of the uniform region are stored. By varying the necking band angle (θ) from 0° to 90°, the calculation procedure is repeated. Finally, among the calculated major and minor strains, the ordered pair (${\varepsilon }_{1}^{A}$, ${\varepsilon }_{2}^{A}$) is reported as a point on the FLD whose major strain ${\varepsilon }_{1}^{A}$ is minimal relative to θ. The FLD is fully characterized by changing the strain ratio from uniaxial tension ($\rho =-0.5$) to equi-biaxial tension ($\rho =1$) and repeating the calculation procedure.

Fig. 2

Flowchart of limit strains calculation

3 Experiments

In this research, an AA3003-H19 sheet with a thickness of 1 mm was used in the experiments. Prior to mechanical testing, the samples were annealed at 415 °C for 2 h to increase formability.

3.1 Uniaxial tensile test

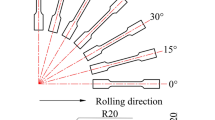
The uniaxial tensile tests were accomplished to identify the strain hardening properties of AA3003-H19 metallic sheet as well as to acquire the input data for calibration of the BBC2008 yield criterion. The specimens for tensile testing were made in line with ASTM E8M at each 15° relative to the rolling direction (i.e., 0, 15, 30, 45, 60, 75, and 90). Figure 3 shows the schematic geometry of dog-bone shape samples for uniaxial tension. The length and width of the gauge section of the specimens are 70 and 12.5 mm, respectively. Tensile testing was performed using a Zwick-Roell universal machine with a capacity of 100 kN at a crosshead speed 1 mm/min. The acquired stress–strain curves at different orientations with respect to the rolling direction are plotted in Fig. 4. The yield stresses were measured at 0.2% plastic strain. The experimental r values and normalized yield stresses obtained are listed in Table 1. The values of n and K reported in Table 1 are the coefficients of Hollomon’s equation, which were characterized according to the calculation method proposed in the ASTM E 646-07 using stress–strain data collected from tensile testing along RD.

Fig. 3

Geometry and dimensions of dog-bone shape samples for uniaxial tension

Fig. 4

Experimental stress–strain curves

Table 1 Mechanical properties of AA 3003-H19

3.2 Plane strain tension test

To characterize the yield stress for the plane strain state, the test procedure presented in [59] was utilized. This method has been developed based on the tension of notched specimens with different widths (W). Figure 5 shows the geometry of plane strain tensile specimens. As can be seen, all dimensions of the specimens except their width are kept constant.

Fig. 5

Geometry of samples for plane strain tensile test

An et al. [59] have demonstrated that in the tension of the notched specimens, if their width is large enough, then the plane strain condition is established in the middle region of them, and the strain distribution in this region is homogeneous. In this case, the distribution of strain in the area close to the notch is also independent of the width of the samples. Therefore, the width of the specimen can be decomposed into two terms as

$$W={W}^{\mathrm{ps}}+2{W}^{e}$$

(28)

where ${W}^{\mathrm{ps}}$ is width of the portion of the sample which is under plane strain condition, and ${W}^{e}$ is width of the notch-affected zone. None of the values ${W}^{\mathrm{ps}}$ and ${W}^{e}$ can be measured directly and accurately. The total measured force can be expressed as follows:

$${F}_{\mathrm{t}}={\sigma }^{\mathrm{ps}}\times t\times {W}^{\mathrm{ps}}+2{F}_{\mathrm{e}}$$

(29)

where F_t is the total force measured experimentally, F_e is the portion of total force which is expended to deform the notch-affected region, t is the material’s nominal thickness, and σ^ps is the yield stress corresponding to the plane strain state. It should be noted that the value of F_e is independent of the width of the specimens [59]. Substituting Eq. (28) into Eq. (29) and some mathematical manipulations yields

$${F}_{\mathrm{t}}={f}^{\mathrm{ps}}\times W+C$$

(30)

where ${f}^{\mathrm{ps}}$ equals to plane strain flow stress multiplied by material thickness, and C is a constant coefficient that represents notch effect. According to Eq. (30), the total measured force is linearly related to the specimen width. Therefore, by performing tension on samples with different widths, the total measured force versus width of specimens can be drawn. By applying a linear regression model to the obtained data, Eq. (30) is fully defined. Finally, the slope of the linear regression (${f}^{\mathrm{ps}}$) represents the flow stress.

In this study, two sets of specimens with a width of 47, 57, 67, and 77 mm in rolling and transverse directions were utilized. To decrease measurement errors, each test was conducted three times, and the average findings were recorded as experimental data. The F_t versus W diagram is plotted for samples in Fig. 6. The obtained plane strain yield stresses are listed in Table 1.

Fig. 6

Force versus width of specimen obtained from plane strain tensile test

3.3 Nakajima test

To specify the experimental limit strains of AA3003-H19 sheet, a series of Nakajima tests were accomplished. In this test, a hemispherical punch is used to stretch the specimens with specific geometries. The stretching continues until the necking phenomenon occurs. A framework for executing the Nakajima test is documented in detail in ISO 12004-2 standard. Figure 7 depicts the standard geometry of the specimens for the Nakajima test. By performing the Nakajima test on specimens of different widths (shown by W in Fig. 7), all points on the FLD from uniaxial (small value of W) to equi-biaxial tension (completely circular specimen) can be determined. In this study, the width of specimens was selected to be 30, 55, 70, 90, 120, 145, and 180 mm, while the rest of the dimensions were maintained constant. The sample with a width of 180 mm was completely circular. Figure 8 illustrates the Nakajima samples after deformation. The specimen’s surface was electrochemically etched using a pattern of circular grids prior to carrying out the Nakajima tests. The diameter of the grids was 2.5 mm. During the stretching process, the circles deform and become ellipses. To determine the limit strains, the minor and major diameters of the ellipses were measured after necking. A portable digital camera was used as a measurement probe. The measurement probe was utilized to capture an image at different locations with appropriate magnification and resolution on the deformed samples, as shown in Fig. 9. Afterward, the minor and major diameters of the ellipse were computed using image processing.

Fig. 7

Geometry of specimens used in the Nakajima testes

Fig. 8

Nakajima samples after necking

Fig. 9

Measurement of deformed grids using a digital camera

4 Results and discussion

4.1 Identifying the coefficients of yield criteria

The anisotropy parameters included in the BBC 2008 yield function were determined by minimizing the error function (Eq. (5)) for AA3003-H19. The obtained parameters for BBC 2008-8p and BBC 2008-16p are tabulated in Tables 2 and 3, respectively. Additionally, the parameters of Hill’s 48 yield criterion for the material are listed in Table 4.

Table 2 Calculated BBC 2008-8p (s = 1) anisotropy parameters for AA3003-H19

Table 3 Calculated BBC 2008-16p (s = 2) anisotropy parameters for AA3003- H19

Table 4 Anisotropy parameters of Hill’s 48 yield function for AA3003-H19

4.2 Performance evaluation of the BBC 2008 and Hill’s 48 yield criteria

The performances of Hill’s 48, BBC 2008-8p, and BBC 2008-16p were evaluated in terms of material behavior prediction. For this purpose, the theoretical normalized yield stresses and r values reproduced by Hill’s 48 and BBC 2008 yield functions were plotted against the experimental data for AA 3003-H19 in Figs. 10 and 11. As shown in Fig. 10, BBC 2008-16p exactly reproduces the experimental normalized yield stresses given in Table 1, while the reproduction using BBC 2008-8p shows small discrepancies. This is because the BBC 2008-16p contains more anisotropy parameters than BBC 2008-8p and is therefore more flexible. However, Hill's 48 cannot give an accurate prediction of yield stresses distribution. According to Fig. 11, only the BBC 2008-16p criterion can accurately capture the r values distribution, whereas none of the BBC 2008-8p and Hill’s 48 criteria can precisely predict it.

Fig. 10

Distribution of theoretical normalized yield stress versus experimental data for AA 3003-H19

Fig. 11

Distribution of theoretical r values versus experimental data for AA 3003-H19

The performances of the yield function were also quantitatively examined using the quality of fit method. This method was first proposed by Wexian [60] and was later developed by Leacock [61] to evaluate the accuracy of yield functions systematically. The comparative or relative root mean square deviation between the experimental data and predicted values is the basis of the quality of fit method and is formulated through the following relations

$$\Delta r=\frac{\sqrt{\sum_{i=1}^{n}{\left({r}_{{\varphi }_{i}}- {{r}_{{\varphi }_{i}}}^{\mathrm{exp}}\right)}^{2}/n }}{\left({{r}_{0}}^{\mathrm{exp}}+2{{r}_{45}}^{\mathrm{exp}}+{{r}_{90}}^{\mathrm{exp}}\right)/4}$$

(31)

and

$$\Delta \sigma =\frac{\sqrt{\sum_{i=1}^{n}{\left({Y}_{{\varphi }_{i}}- {{Y}_{{\varphi }_{i}}}^{\mathrm{exp}}\right)}^{2}/n }}{\left({{Y}_{0}}^{\mathrm{exp}}+2{{Y}_{45}}^{\mathrm{exp}}+{{Y}_{90}}^{\mathrm{exp}}\right)/4}$$

(32)

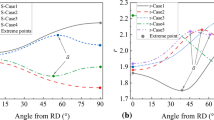
where $\Delta r$ and $\Delta \sigma$ referred to the comparative or relative deviations of r values and uniaxial yield stresses. In Eqs. (31) and (32), theoretical values do not have any superscript, whereas the experimental data are labeled by the ‘exp’ superscript. The number of experimental data is also denoted by ‘n.’ Figure 12 depicts the relative deviations of the r values and uniaxial yield stresses for BBC 2008 and Hill’s 48 yield criteria. As shown in Fig. 12, the relative deviations of r value and yield stress for BBC 2008-16p are lower than those for BBC 2008-8p and Hill’s 48 yield criteria. This evidences that the version with 16 parameters of the BBC 2008 yield criterion describes the anisotropic properties of AA 3003-H19 metallic sheets more accurately than BBC 2008-8p and Hill's 48. Therefore, utilizing the BBC 2008-16p criterion may improve the accuracy of the FLD prediction.

Fig. 12

Relative deviation of yield stress and r values

Figure 13 presents yield loci predicted by BBC 2008-16p, BBC 2008-8p, and Hill’s 48 yield criteria for AA 3003-H19. The experimental uniaxial yield strength along RD and TD is also marked in this figure with a filled black circle. As is seen, the yield surfaces provided by both of BBC 2008-8p and BBC 2008-16p criteria at points RD and TD are consistent with the experimental data. In contrast, Hill’s 48 is consistent with experimental data only in the point of uniaxial tension in the rolling direction. Another interesting observation is the difference between the yield stresses predicted by BBC 2008-8p and BBC 2008-16p yield functions in the equi-biaxial tension region, which requires more experimental data or crystal plasticity simulations to validate this area.

Fig. 13

Yield loci predicted by different yield functions for AA 3003-H19

4.3 Comparison between experimental FLD and theoretical predictions

Figure 14 illustrates experimental and calculated FLD for AA 3003-H19 using various yield criteria and the M–K theory. The initial imperfection factor was chosen so that the theoretical value of limit strain for plane strain condition ($\rho =0$) matched the experimental result. For all strain ratios, the value f₀ = 0.998 was utilized to compute the limit strains.

Fig. 14

Experimental versus theoretical FLD based on different yield functions for AA3003-H19

According to Fig. 14, the predictions made by the M–K model combined with the three yield criteria for the left-hand side of FLD are similar and have good conformity with the experimental data. In the other word, the yield function incorporated into the M–K theory has no impact on the FLD calculation of AA3003-H19 sheets for negative strain ratios ($\rho <0$). This is in line with the findings of prior investigations on the M–K model [25, 32, 62, 63]. On the other hand, a strong dependency between the computed limit strains and the employed yield criterion is observed for positive strain ratios ($\rho >0$). Figure 14 shows that, when yield locus shape was expressed by BBC 2008-16p yield criterion, the best conformity between experimental limit strains and theoretical results was found for the right-hand side of the FLD. This result was to be expected since the BBC 2008-16p yield criterion reproduces the anisotropic behavior of the material more accurately and therefore provides a more accurate prediction of the FLD. On the other hand, the use of the BBC 2008-8p and Hills 48 yield criteria underestimate and overestimate the right-hand side of the FLD, respectively. To justify this phenomenon, it can be referred to the research of Xu et al. [22] and Dasapa et al. [32]. They demonstrated that the curvature of yield surface in biaxial tension region significantly affects the results of FLD prediction for positive strain ratio so that a more round yield locus in biaxial tension region predicts higher limit strains[22, 32]. As illustrated in Fig. 13, Hill’s 48 and BBC 2008-8p yield criteria provide a more rounded and sharper yield surface than BBC 2008-16p in the biaxial tension region, respectively. For this reason, the forming limits for positive minor strains predicted by Hill’s 48 and BBC 2008-8p are higher and lower, respectively, than those calculated by BBC 2008-16p.

4.4 Influence of identification procedure on the prediction of FLD

The BBC 2008-16p was calibrated using two different ways to examine the influence of the identification procedure of anisotropy parameters used in the yield function on the FLD prediction. In the first case, the calibration was done only using r values and yield stresses collected from the uniaxial tensile testings (denoted by ‘without Yps’). In the second case, the plane strain yield stresses are incorporated into the calibration procedure in addition to uniaxial tensile test data (denoted by ‘with Yps’). The effect of the identification procedure on the limit strains calculation is depicted in Fig. 15. As can be seen, BBC 2008-16p calibrated without plane strain yield stresses overestimates the forming limits for negative minor strains, whereas the right-hand side of FLD is not affected by the calibration method. To seek the reason, the predicted yield surface by BBC 2008-16p criterion was plotted in two cases with and without the use of plane strain yield stresses in the calibration procedure in Fig. 16. As is seen, failure to use the plane strain yield stresses in the calibration procedure of BBC 2008-16p criterion gives a more rounded yield surface by this criterion and consequently causes to overpredict the limit strains in this case. According to Fig. 16, however, the use of plane strain yield stress in the calibration procedure has no considerable influence on the prediction of the yield surface in the second and fourth quadrants. It is possible to draw the conclusion the use of material properties acquired from uniaxial tensile testing alone is insufficient to calibrate anisotropy coefficients because the yield surface in the biaxial tension region is not accurately determined in this case [57].

Fig. 15

Effect of identification procedure on the calculation of limit strains

Fig. 16

Impact of the plane strain yield stress on the yield loci shape

5 Conclusions

In this study, the capability of the BBC 2008 (8 and 16 parameters) and Hill's 48 yield functions in computing the forming limits diagram of AA 3003-H19 metallic sheets were evaluated theoretically using the M–K model. The Levenberg–Marquardt approach was employed to optimize an error function for calibrating the anisotropy parameters of BBC 2008 yield function. The required material properties for the calibration procedure were provided by uniaxial and plane strain tensile testings. The ability of BBC 2008 and Hill’s 48 yield criteria to reproduce the anisotropic properties of AA 3003-H19 was evaluated. For this purpose, a comparison was made between the theoretical r values and yield stresses computed by the yield criteria and the experimental data along different orientations relative to the rolling direction. The effect of the calibration procedure on the FLD prediction was also examined. To achieve the experimental FLD and verify the theoretical findings, a set of standard Nakajima tests were accomplished. The results revealed that:

• The 16-parameter version of the BBC 2008 yield criterion can accurately capture the anisotropic properties of AA 3003-H19 metallic sheets, while BBC 2008-8p and Hill's 48 could not precisely describe them.

• For the negative strain ratios, the forming limits of AA3003-H19 sheets are unaffected by the yield criterion incorporated into the M–K model. In contrast, a strong dependency between the calculated limit strains and the employed yield function was found for the positive strain ratios.

• All three criteria of the BBC 2008-8p, BBC 2008-16p, and Hill’s 48 give identical results for the left-hand side of the FLD and correspond well with the experimental data.

• Using BBC 2008-16p yield function in M–K analysis gives the best conformity between experimental and theoretical limit strains for the right-hand side of the FLD. In contrast, BBC 2008-8p and Hills 48 yield criteria underestimate and overestimate the limit strains for positive strain ratios, respectively.

• BBC 2008-16p calibrated without the plane strain yield stresses overestimates the FLD for positive strain ratios, whereas the calibration method has no impact on the left-hand side of the FLD.

Appendix A

A more detailed description of each term of Eq. (8) is presented as follows:

$$\begin{aligned} \frac{{\partial \overline{\sigma }}}{{\partial L^{\left( i \right)} }} & = \frac{{\left( {w - 1} \right)}}{{\overline{\sigma } ^{{\left( {2k - 1} \right)}} }}\left\{ {w^{i - 1} \left\{ {\left[ {L^{\left( i \right)} + M^{\left( i \right)} } \right]^{2k - 1} + \left[ {L^{\left( i \right)} - M^{\left( i \right)} } \right]^{2k - 1} } \right\}} \right\} \\ \frac{{\partial \overline{\sigma }}}{{\partial M^{\left( i \right)} }} & = \frac{{\left( {w - 1} \right)}}{{\overline{\sigma } ^{{\left( {2k - 1} \right)}} }}\left\{ {w^{i - 1} \left\{ {\left[ {L^{\left( i \right)} + M^{\left( i \right)} } \right]^{2k - 1} - \left[ {L^{\left( i \right)} - M^{\left( i \right)} } \right]^{2k - 1} } \right\}} \right. \\ & \quad \left. { + w^{s - i} \left\{ {\left[ {M^{\left( i \right)} + N^{\left( i \right)} } \right]^{2k - 1} + \left[ {M^{\left( i \right)} - N^{\left( i \right)} } \right]^{2k - 1} } \right\}} \right\} \\ \frac{{\partial \overline{\sigma }}}{{\partial N^{\left( i \right)} }} & = \frac{{\left( {w - 1} \right)}}{{\overline{\sigma } ^{{\left( {2k - 1} \right)}} }}\left\{ {w^{s - i} \left\{ {\left[ {M^{\left( i \right)} + N^{\left( i \right)} } \right]^{2k - 1} - \left[ {M^{\left( i \right)} - N^{\left( i \right)} } \right]^{2k - 1} } \right\}} \right\} \\ \frac{{\partial L^{\left( i \right)} }}{{\partial \sigma_{11} }} & = l_{1}^{\left( i \right)} \\ \frac{{\partial L^{\left( i \right)} }}{{\partial \sigma_{12} }} & = \frac{{\partial L^{\left( i \right)} }}{{\partial \sigma_{21} }} = 0 \\ \frac{{\partial L^{\left( i \right)} }}{{\partial \sigma_{22} }} & = l_{2}^{\left( i \right)} \\ \frac{{\partial M^{\left( i \right)} }}{{\partial \sigma_{11} }} & = \frac{{m_{1}^{\left( i \right)} \left[ {m_{1}^{\left( i \right)} \sigma_{11} - m_{2}^{\left( i \right)} \sigma_{22} } \right]}}{{M^{\left( i \right)} }} \\ \frac{{\partial M^{\left( i \right)} }}{{\partial \sigma_{12} }} & = \frac{{\partial M^{\left( i \right)} }}{{\partial \sigma_{21} }} = \frac{{\left( {m_{3}^{\left( i \right)} } \right)^{2} \left( {\sigma_{12} + \sigma_{21} } \right)}}{{M^{\left( i \right)} }} \\ \frac{{\partial M^{\left( i \right)} }}{{\partial \sigma_{22} }} & = - \frac{{m_{2}^{\left( i \right)} \left[ {m_{1}^{\left( i \right)} \sigma_{11} - m_{2}^{\left( i \right)} \sigma_{22} } \right]}}{{M^{\left( i \right)} }} \\ \frac{{\partial N^{\left( i \right)} }}{{\partial \sigma_{11} }} & = \frac{{n_{1}^{\left( i \right)} \left[ {n_{1}^{\left( i \right)} \sigma_{11} - n_{2}^{\left( i \right)} \sigma_{22} } \right]}}{{N^{\left( i \right)} }} \\ \frac{{\partial N^{\left( i \right)} }}{{\partial \sigma_{12} }} & = \frac{{\partial N^{\left( i \right)} }}{{\partial \sigma_{21} }} = \frac{{\left( {n_{3}^{\left( i \right)} } \right)^{2} \left( {\sigma_{12} + \sigma_{21} } \right)}}{{N^{\left( i \right)} }} \\ \frac{{\partial N^{\left( i \right)} }}{{\partial \sigma_{22} }} & = - \frac{{n_{2}^{\left( i \right)} \left[ {n_{1}^{\left( i \right)} \sigma_{11} - n_{2}^{\left( i \right)} \sigma_{22} } \right]}}{{N^{\left( i \right)} }}. \\ \end{aligned}$$

(33)