Introduction

One of the keys for a high prediction accuracy and time effectivity of simulations of deep drawing processes is an accurate mathematical description of the mechanical material behavior [1]. Therefore much effort was put into the development of constitutive models to better describe the mechanical behavior of sheet metal material and thus to increase the accuracy in the prediction of the geometrical and mechanical properties of formed sheet metal parts. Since Hill developed the Hill48 yield criterion [2], numerous other yield criteria to describe plastic anisotropy have been proposed e.g., by Hill [3, 4], Barlat and his co-authors [5–8], Banabic and his co-workers [9, 10] and many others. Also, models that are able to describe tension compression asymmetry (e.g., [11]) as well as models that account for the Bauschinger effect by means of kinematic hardening (e.g., [12, 13]) or distortional hardening (e.g., [14, 15]) have been published. Many of the models above have successfully been implemented into commercial finite element codes which today are a crucial instrument for the development of sheet metal parts, tool layouts and the process designs. Most of the above yield functions have in common, that the model parameters are determined based on standardized mechanical tests like tensile tests. For finding the parameters of more complex models, the experimental effort usually is significantly higher. However, because of the high complexity and the computational cost involved, mainly isotropic hardening models are used in industrial applications. The scalar parameters of these models are assumed to be constant and not to change once they are determined. This causes a homogeneously expanding elastic domain, meaning the yield stress ratios for different stress states stay constant for every level of plastic strain. Typically, the hardening curve in rolling direction (RD) is used as a reference in constitutive models for sheet metal. If an isotropic hardening model is used, the hardening under a stress state different from uniaxial tension in RD cannot be represented correctly as long as the hardening under this stress state is not proportional to the one in RD. Experiments for different materials have shown, that this proportionality is not given in most of the cases. The assumption of isotropic strain hardening breaks down even for monotonic uniaxial loading. This has also been reported e.g., in [16, 17]. A plausible explanation for this phenomenon is a differently changing microstructure under different loading directions [17]. To also account for such effects in a phenomenological model, a simple approach is to introduce a dependency of the model parameters on the equivalent plastic strain. In this way, the hardening in the directions that are used to fit the model parameters can be independently described. In the present work Barlat’s Yld2000-2d [8] model, which involves eight material parameters forms the basis. Based on tensile and hydraulic bulge test results, the parameters are varied with increasing equivalent plastic strain in order to predict the RD, transversal direction (TD) and 45° as well as the equibiaxial hardening curve correctly. Similar ideas were proposed by [18, 19].

Material model

Original Yld2000-2d

In 2003 Barlat et al. published the so-called Yld2000-2d yield criterion [8]. It was mainly developed to overcome some problems of the Yld96 [7] yield criteria, namely the lack of a proof of convexity as well as the the difficulty to obtain the analytical derivatives. The Yld2000-2d criterion is an extension of the criterion of Hershey [20] and Hosford [21] to orthotropic anisotropy based on two linear transformations of the deviatoric stress tensor. It has eight parameters that are determined based on eight mechanical properties. These are the uniaxial yield stress in RD, TD and diagonal direction ( σ 0, σ 45, σ 90) and the yield stress under equibiaxial condition σ b as well as the Lankford parameters in the three directions ( r 0, r 45, r 90) and the biaxial r-value r b . The yield criterion is given as

$$ \phi = \phi'+\phi''=2\bar{\sigma}^a $$
(1)

where the exponent a is a material coefficient and

$$\begin{array}{@{}rcl@{}} \phi' &=& |X_1'-X_2'|^{a} \notag\\ \phi'' &=& |2X_2''+X_1''|^a+|2X_1''+X_2''|^a \end{array} $$
(2)

where \(X_{i}^{'}\) and \(X_{j}^{''}\) are the principal values of the matrices X ′ and X ″

$$\begin{array}{@{}rcl@{}} X_{i}^{'} &=&\frac{1}{2} \left(X_{11}^{'}+X_{22}^{'}\pm \sqrt{(X_{11}^{'}-X_{22}^{'} )^{2}+4X_{12}^{'2}}\right)\notag\\ X_{j}^{''} &=&\frac{1}{2} \left(X_{11}^{''}+X_{22}^{''}\pm \sqrt{(X_{11}^{''}-X_{22}^{''} )^{2}+4X_{12}^{''2}}\right) \end{array} $$
(3)

whose components are obtained from the following linear transformation

$$\begin{array}{@{}rcl@{}} \mathbf{X}' &=&\mathbf{L}'{\sigma} \notag\\ \mathbf{X}'' &=&\mathbf{L}''{\sigma} \end{array} $$
(4)

where

$$ \left[ \begin{array}{l} L_{11}' \\ L_{12}' \\ L_{21}' \\ L_{22}' \\ L_{66}' \end{array} \right] = \left[ \begin{array}{llllll} &2/3 & & 0 & &0 \\ -&1/3 & & 0 & &0 \\ & 0 & -& 1/3 & &0 \\ & 0 & & 2/3 & &0 \\ & 0 & & 0 & &1 \end{array} \right] \left[ \begin{array}{l} \alpha_{1} \\ \alpha_{2} \\ \alpha_7 \end{array} \right] $$
(5)

and

$$ \left[ \begin{array}{l} L_{11}'' \\ L_{12}'' \\ L_{21}'' \\ L_{22}'' \\ L_{66}'' \end{array} \right] =\frac{1}{9} \left[ \begin{array}{llllllllll} -& 2 & & 2 & & 8 & -& 2 & & 0 \\ & 1 & -& 4 & -& 4 & & 4 & & 0 \\ & 4 & -& 4 & -& 4 & & 1 & & 0 \\ -& 2 & & 8 & & 2 & -& 2 & & 0 \\ & 0 & & 0 & & 0 & & 0 & & 9 \\ \end{array} \right] \left[ \begin{array}{l} \alpha_{3} \\ \alpha_{4} \\ \alpha_{5} \\ \alpha_{6} \\ \alpha_{8} \\ \end{array} \right] $$
(6)

In the equations above, σ is the Cauchy stress and α 1 − α 8 are the eight anisotropy coefficients. To determine the coefficients, Barlat et al. propose the minimization of eight functions representing the difference between measured and predicted yield stresses or Lankford parameters respectively. The exponent m is assumed to be a real number between 2 and ∞. By setting all α parameters equal to 1, and the exponent a equal to 2, the yield criterion is reduced to the von Mises criterion while an exponent a of ∞ leads to the Tresca criterion. By comparing the phenomenological model with yield loci calculated with a polycrystal model, [22] stated, that an exponent of a = 6 is best suited for a body centered cubic (BCC) material, while for a face centered cubic (FCC) material, an exponent a = 8 should be chosen. Kuwabara and his co-workers [23] recommend to determine the exponent a based on yield stresses under biaxial loading with different ratios σ 1 / σ 2. For this purpose they designed a testing apparatus for the biaxial testing of cruciform specimen [24]. Because such a testing machine was not available, the exponent a is set to 6 for the steel and to 8 for the aluminum material.

Modifications on Yld2000-2d

As mentioned in the Section “Introduction”, constant parameters α 1 to α 8 lead to constant ratios σ xx / σ yy for every level of plastic strain, when σ xx and σ yy are the yield stresses in RD and TD under two arbitrary stress states. To overcome this limitation, the parameters are expressed as a function of the equivalent plastic strain (which is proportional to the equivalent plastic work). In order to obtain the parameters, the yield stress in RD ( σ 0) at different levels of equivalent plastic strain \(\bar {\varepsilon }^{p}_{i}\) is taken. In a second step, the corresponding plastic work W pl is computed according to Eq. 7.

$$ W_{pl} = \int_{0}^{\bar{\varepsilon}^{p}_{i}}\sigma_{y}(\bar{\varepsilon}^p) d\bar{\varepsilon}^p $$
(7)

The remaining yield stresses ( σ 45, σ 90 and σ b ) are taken at the same amount of plastic work. The Lankford parameters were almost constant for both of the materials investigated in this study thus their variation is not taken into account. The four yield stresses in combination with the four r-values build the input for the parameter fitting of the Yld2000-2d function. Now the fitting can be done at different levels of equivalent plastic strain leading to the eight parameters being a function of the equivalent plastic strain. [19] uses a sixth order polynomial function to fit the parameters. In the present study, for both of the materials a suitable description was sought-after. While the parameters for the aluminum material are described with a constant - linear - constant function, the ones for the steel material are fitted with a Hockett-Sherby type function (cf. Section “Laboratory tests”).

In order to account for the strain rate dependency of the DC05 material, a rate dependent hardening model was used. The hardening curve of the material is given as the quasi-static part of the curve multiplied with a scale factor which depends on the rate of the equivalent plastic strain

$$ \sigma_{y} (\bar{\varepsilon}^{p},\dot{\bar{\varepsilon}}^p)=\sigma_{y0} (\bar{\varepsilon}^p) \cdot c(\dot{\bar{\varepsilon}}^p) $$
(8)

Numerical implementation

The numerical implementation of the model described in Section “Modifications on Yld2000-2d” is mainly according to the one given in [25]. However, due to the dependency of the model parameters on the equivalent plastic strain and the incorporation of the strain rate dependency, some consequences for the implementation arise. The hardening curve of the material is given by Eq. 8. Assuming associated flow rule, for a given total strain increment Δε, the plastic strain increment can be computed as

$$ \Delta\varepsilon^{p} = \Delta\bar{\varepsilon}^{p}\frac{\partial\bar{\sigma}}{\partial\boldsymbol{\sigma}}=\gamma\frac{\partial\bar{\sigma}}{\partial\boldsymbol{\sigma}} $$
(9)

where γ is called the plastic multiplier. The yield function is written as

$$\begin{array}{@{}rcl@{}} f(\sigma, \bar{\varepsilon}^{p},\dot{\bar{\varepsilon}}^p) &=& \bar{\sigma}(\sigma, \bar{\varepsilon}^p) -\sigma_{y}(\bar{\varepsilon}^{p},\dot{\bar{\varepsilon}}^p) \notag\\ &=& \left(\frac{\phi}{2}\right)^{\frac{1}{a}}-\sigma_{y0}(\bar{\varepsilon}^p)\cdot c(\dot{\bar{\varepsilon}}^p) \end{array} $$
(10)

The consistency condition then is

$$ f(\sigma+\Delta\sigma, \bar{\varepsilon}^p+\Delta\bar{\varepsilon}^p) = 0 $$
(11)

The strain rate is assumed to stay constant during each incremental step. It is also known that the stress increment Δσ for a total strain increment Δε is given as the product of the elastic stiffness tensor C and the difference of the total strain increment and the plastic strain increment Δε p

$$ \Delta\sigma = \mathbf{C}(\Delta\varepsilon-\Delta\varepsilon^p) $$
(12)

by using Eqs. 8 and 12, the consistency condition (11) can be rewritten as

$$ \bar{\sigma}\left(\sigma^T-\gamma\mathbf{C}\frac{\partial\bar{\sigma}}{\partial\sigma}\right)-\sigma_{y}(\varepsilon+\Delta\varepsilon)\cdot(\dot{\bar{\varepsilon}}^p) = 0 $$
(13)

where σ T = CΔε is the so-called trial stress. A Newton-Raphson based predictor corrector scheme is used to find the solution for Eq. 13. To overcome the difficulty of finding a solution for large strains, a return mapping algorithm as used in [26] is applied. In this algorithm, Eq. 13 is not directly solved for a residuum of zero, but for a prescribed residuum which is lowered step by step. This leads to

$$\begin{array}{@{}rcl@{}} f(\gamma_k) =&& \bar{\sigma}\left(\sigma^T-\gamma_{k}{C}\frac{\partial\bar{\sigma}}{\partial\sigma}, \gamma_{k}\right) \notag\\ && -\sigma_{y}(\bar{\varepsilon}^p+\gamma_k)\cdot(\dot{\bar{\varepsilon}}^p)-F_{k} = 0 \end{array} $$
(14)

where F k is a prescribed value which is lowered continuously until F k becomes 0 for the last step under the condition that ΔF = (F k − 1 − F k ) < σ y . Equation 14 for the k-th substep in the step n + 1 is then written as:

$$ f(\gamma_k)=\bar{\sigma}(\sigma_{k}, \gamma_k)-\sigma_{y0}(\bar{\varepsilon}^p+\gamma_k)\cdot c(\dot{\bar{\varepsilon}}^p)-F_k=0 $$
(15)

where

$$ \sigma_{k} = \sigma^T-\gamma_{k}\mathbf{C}\frac{\partial\bar{\sigma}}{\partial\sigma_{k}} $$
(16)

and

$$ \sigma_{yk} = \sigma_{y}(\bar{\varepsilon}^p+\gamma_k) = \sigma_{yn}+\gamma_{k}\sigma_{yk}' $$
(17)

where \(\sigma _{yk}^{'}\) is the slope of the hardening curve and

$$ c(\dot{\bar{\varepsilon}}^p) = c\left(\frac{\gamma_{k}}{\Delta t}\right) $$
(18)

where Δt is the current time step size. In order to apply the Newton-Raphson based corrector predictor scheme, Eq. 15 has to be linearized around the state variable Δγ. The linearization leads to

$$\begin{array}{@{}rcl@{}} f(\gamma_k+\Delta\gamma_k)=&&f(\gamma_k)+\frac{\partial\bar{\sigma}}{\partial\sigma_{k}}\Delta\sigma_k+\frac{\partial\bar{\sigma}}{\partial\alpha_{i}}\frac{\partial\alpha_{i}}{\partial\bar{\varepsilon}^{p}}\Delta\gamma_{k} \notag\\ &&-\sigma_{yk}'\Delta c_k-c_k'\Delta\sigma_{yk} \end{array} $$
(19)

with

$$ \Delta\sigma_{k} = \left[ \mathbf{E} \Delta\gamma_k + \mathbf{F} \right] \cdot \mathbf{G}^{-1} $$
(20)

where

$$ \mathbf{E} = \mathbf{C}^{-1} \left( \sigma_k-\sigma^T \right)+ \gamma_k \frac{\partial\bar{\sigma}}{\partial\sigma_{k}} $$
(21)
$$ \mathbf{F} = \frac{\partial\bar{\sigma}}{\partial\sigma_{k}} + \gamma_k \frac{\partial^{2}\bar{\sigma}}{\partial\sigma_{k}\partial\bar{\varepsilon}^{p}} $$
(22)
$$ \mathbf{G} = \mathbf{C}^{-1}+ \gamma_k \frac{\partial^{2}\bar{\sigma}}{\partial\sigma_{k}^{2}} $$
(23)
$$ \Delta\sigma_{yk} = \sigma_{yn}-\sigma_{yk}+\sigma_{yk}'\cdot(\gamma_k+\Delta\gamma_k) $$
(24)

Δc k can be expressed as

$$ \Delta c_{k} = \frac{1}{\Delta t}c'\Delta\gamma_k $$
(25)

since the time step Δt, for which the strain increment is given is known from the beginning. The derivatives with respect to \(\bar {\varepsilon }^{p}\) in Eqs. 19 and 22 are due to the dependency of the parameters on the plastic strain. The terms containing c and c′ in Eqs. 19 and 20 are present due to the strain rate dependency. By substituting Δσ k , Δσ y k and Δc k in Eq. 19 with Eqs. 20, 24 and 25, and solving for Δγ k , the following expression is found:

$$ \Delta\gamma_{k} = \frac {f(\gamma_k)-\frac{\partial\bar{\sigma}}{\partial\sigma_{k}}\mathbf{G}^{-1}\mathbf{E} + c\cdot(\sigma_{yk}-\sigma_{yn}-\sigma_{yn}'\cdot\gamma_k)} {\frac{\partial\bar{\sigma}}{\partial\sigma_{k}} \mathbf{G}^{-1} \mathbf{F}- \frac{\partial\alpha_{i}}{\partial\bar{\varepsilon}^{k}} +\sigma_{yk}'\cdot c+\sigma_{yk}\frac{c'}{\Delta t}} $$
(26)

where the definitions (21), (22) and (23) have been used again. The state variables γ k , σ k and σ y are updated after every iteration with

$$\begin{array}{@{}rcl@{}} \gamma_{k}^{new}&=&\gamma_{k}^{old}+\Delta\gamma_{k} \notag\\ \sigma_{k}^{new}&=&\sigma_{k}^{old}+\Delta\sigma_{k} \notag\\ \sigma_{yk}^{new}&=&\sigma_{yk}^{old}+\Delta\sigma_{yk} \end{array} $$
(27)

The rate scale factor c is given as a function of the strain rate \(\dot {\bar {\varepsilon }}^{p}\) and can be evaluated at the actual rate which is given by \(\frac {\gamma }{\Delta t}\). The iteration continues until the consistency condition (19) is fulfilled with a prescribed relative tolerance, which was chosen as 10−5 for this study. After the stress integration is finished (i.e., the procedure has been carried out for all substeps), the thickness strain is updated with

$$ \varepsilon_{zz} = -\frac{\nu}{E}\left(\sigma_{xx}^{(n+1)}+\sigma_{yy}^{(n+1)}\right)-\left(\varepsilon_{xx}^{p(n+1)}+\varepsilon_{yy(n+1)}^{p(n+1)}\right) $$
(28)

The model described in the previous chapter was implemented as a user material model in the explicit finite element code LS-Dyna using the stress integration algorithm given above.

Laboratory tests

In order to characterize the deformation characteristics for the two materials investigated, different material tests were carried out. First, tensile tests in 7 directions were conducted. Every single test was done five times at a strain rate dε / dt = 0.002 before the resulting curves were averaged in order to ensure the measuring accuracy. Since only the stress strain curves in 0°, 45° and 90° to RD have been used in the remainder of this work, these curves are shown in Fig. 1 for Formalex™5x and Fig. 2 for DC05. As is clearly seen on Fig. 2, the 45° and the 90° curve for DC05 cross each other which confirms the statement given in Section “Introduction” about the non-proportional hardening, even for monotonic strain paths. This is less the case for the the aluminum. Furthermore, note that the hardening curves in Fig. 1 show a serrated shape. This is due to the Portevin-Le Chatelier effect [27]. However, this effect was not investigated in this work. For the description of the RD hardening curve, the measured curve were smoothed to avoid numerical instabilities, but no mathematical approximation was used.

Fig. 1
figure 1

Hardening curves for Formalex™5X for different angles to RD

Full size image
Fig. 2
figure 2

Hardening curves for DC05 for different angles to RD

Full size image

The DC05 material exhibits a strain rate dependency of the yield stress, which is typical for mild steel. In order to find an accurate description for this dependency, tensile tests with different velocities were carried out. The results are shown in Fig. 3. Note that the strain rates are only conducted in the range between ≈ 10−5 and ≈ 10−2, since the testing facility did not allow to test at higher rates. A good agreement with the experimental results could be found using the modified Cowper-Symonds [28] approach whose mathematical description is given in Eq. 29. The parameters were determined as \(\dot {\bar {\varepsilon }}^{p}_{0} = 1.48e-4\) and m = 54.99.

$$ \sigma_{y}(\bar{\varepsilon}^{p}, \dot{\bar{\varepsilon}}^p) = \sigma_{y0}(\bar{\varepsilon}^p) \cdot c(\dot{\bar{\varepsilon}}^p) = \sigma_{y0}(\bar{\varepsilon}^p) \cdot \left( 1+\left(\frac{\dot{\bar{\varepsilon}}^{p}}{\dot{\bar{\varepsilon}}^{p}_{0}}\right)\right)^{\frac{1}{m}} $$
(29)

The measured curves as well as the curves predicted by the model are presented in Fig. 3.

Fig. 3
figure 3

DC05 Hardening curves for different strain rates:measured curves and predicted curves (dots)

Full size image

The strain rate dependency was also investigated for Formalex™5x. Since a tensile test carried out at a five time higher strain rate did not show significant differences, it was assumed to be rate-insensitive.

In order to analyze the equibiaxial behavior of the materials, hydraulic bulge tests have been conducted. The tests were evaluated according to [29] to determine the stress-strain relation under equibiaxial loading. Since during a hydraulic bulge test, the material undergoes a wide range of strain rates, strain rate effects have to be compensated. For the DC05 material the equibiaxial hardening curve was corrected based on the strain rate model given in (29) to find a curve that is comparable with the hardening curves given in Fig. 2. The resulting curves, that eventually have been used to find the equibiaxial yield stress σ b as well as to extrapolate the uniaxial hardening curve in RD (reference curve) for strains beyond uniform elongation, are presented in Fig. 4 for DC05 and in Fig. 5 for Formalex™5x.

Fig. 4
figure 4

Measured and corrected equibiaxial hardening curve for DC05

Full size image
Fig. 5
figure 5

Measured equibiaxial hardening cure for Formalex™5x

Full size image

Finally, stack compression tests were carried out to find the biaxial r-value r b . Stacks of nine plates with an initial diameter of 10 mm were compressed to strains between 0.2 and 0.3. Deep drawing foil and lubricant was used to reduce the friction to a minimum. Afterwards, the strains in RD and TD of the central plates were measured and averaged for 5 different tests. By computing the ratio ε TD / ε RD an r b value of 0.89 for DC05 and 1.14 for the Formalex™5x was found. Figure 6 shows a compressed stack of DC05 plates. The picture shows that the stack barely buckled, which is a good indicator for low friction.

Fig. 6
figure 6

compressed stack of nine 10 mm DC05 plates

Full size image

Using the uniaxial and equibiaxial hardening curves, the Yld2000-2d parameters were determined according to the procedure explained in Section “Modifications on Yld2000-2d”. The parameters determined for Formalex™5x are shown in Fig. 7. Since the parameters seem to be unstable before an equivalent strain of approximately 0.04, they have been held constant up to this value. Afterwards, they show an almost linear run, thus a linear slope was used to smooth them between strains of 0.04 and 0.2 (which is the uniform elongation for this material). Beyond uniform elongation, again constant parameters were assumed because there is no data to fit them anymore (Fig. 8).

Fig. 7
figure 7

Determined α parameters as a function of equivalent plastic work \(\bar {\varepsilon }^{p}\) for Formalex™5x

Full size image
Fig. 8
figure 8

Smoothed α parameters as a function of equivalent plastic work \(\bar {\varepsilon }^{p}\) for Formalex™5x

Full size image

For DC05, the determined parameters are presented in Fig. 9. The parameters show a rather steep slope in the beginning, but seem to run to a saturated value after a strain of approximately 0.15. To fit this characteristic, a Hockett-Sherby [30] type of function as given in Eq. 9 was used. The smoothed curves are shown in Fig. 10 while the parameters C 1−4 used to fit α 1 to α 8 are given in Table 1. No further measures have to be taken for strains beyond uniform elongation.

Fig. 9
figure 9

Determined α parameters as a function of equivalent plastic work \(\bar {\varepsilon }^{p}\) for DC05

Full size image
Fig. 10
figure 10

Smoothed α parameters as a function of equivalent plastic work \(\bar {\varepsilon }^{p}\) for DC05

Full size image
Table 1 Hockett-Sherby parameters for smoothing variable α for DC05
Full size table

Figures 11 and 12 show the influence of the varying parameters on the shape of the yield locus for both materials. For the DC05, the influence is stronger than for Formalex™5x. Mainly the equibiaxial yield stress is influenced. However, also the yield stresses in the remaining directions ( σ 45 and σ 90) slightly change.

Fig. 11
figure 11

DC05 yield loci for \(\bar {\varepsilon }^{p}\) = 0, 0.1 and 0.2

Full size image
Fig. 12
figure 12

Formalex™5x yield loci for \(\bar {\varepsilon }^{p}\) = 0, 0.1 and 0.2

Full size image

Validation

Verification

To check whether the model is working properly, the curves shown in the Figs. 1, 2, 3, 4, and 5 have been reproduced using the standard and the modified version of Yld2000-2d. The results are presented in Figs. 13, 14, 15, and 16. It is obvious that the modified version predicts the uniaxial and the equibiaxial stress responses better than the standard version. This was expected because of the way the parameters were determined. For the equibiaxial strain there is a slight difference between the x- and y-stress (stress in RD and TD). The reason is the r b -value that is different from one. Furthermore, also the modified model is not able to exactly predict the curves for DC05 (cf. Fig. 16). These small deviations are due to the used strain rate model, which tends to underestimate stresses at low strains and overestimate them at higher strains (cf. Fig. 3). Nevertheless, good agreement was observed.

Fig. 13
figure 13

Uniaxial and equibiaxial stress strain curves:measurement (solid) and prediction using standard Yld2000-2d (symbols) for Formalex™5x

Full size image
Fig. 14
figure 14

Uniaxial and equibiaxial stress strain curves:measurement (solid) and prediction using modified Yld2000-2d (symbols) for Formalex5x

Full size image
Fig. 15
figure 15

Uniaxial and equibiaxial stress strain curves:measurement (solid) and prediction using standard Yld2000-2d (symbols) for DC05

Full size image
Fig. 16
figure 16

Uniaxial and equibiaxial stress strain curves:measurement (solid) and prediction using modified Yld2000-2d (symbols) for DC05

Full size image

Cross die tests and simulations

For validating the model, the so-called cross-die geometry was used. The cross die shape is a widely used geometry when it comes to validation of material models (e.g., [31, 32]). There are different varieties of cross die shapes, basically with equal side lengths and two different side lengths respectively. In the present study, the latter was used. A test piece with a drawing depth of 75 mm for DC05 and 55 mm for Formalex™5x was drawn. Before drawing, a pattern was applied on the outer surface of both blanks. This pattern is needed to subsequently be able to optically measure the major and minor surface strains with the optical measurement system ARGUS from GOM, which uses digital image correlation techniques to measure displacements of material points between two different stages. After having measured the displacements with ARGUS, the software computes the measured surface points as well as the surface strains. Note that for the steel material, only one half of the real part was measured assuming that the part is drawn symmetrically.

The simulations of the cross die tests have been carried out using the commercial finite element software LS-Dyna in combination with the implemented model described in Section “Material model”. First, the model was used assuming constant α parameters in order to find the correct friction coefficient. For this purpose, the draw-in of the real part and the simulation were compared and the deviation was minimized. In this way, friction coefficients of 0.08 and 0.07 for steel and aluminum respectively were found. Using these friction coefficients, the simulation was carried out again with the varying parameters presented in Section “Laboratory tests”.

After the simulations were finished using both, constant and variable parameters, GOM’s software SView was used to compare the measured strains with those obtained from the simulations.

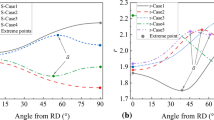
Figures 17, 18, 19, and 20 show the differences between the measured and simulated major and minor surface strains for both materials. Since the modifications affect mainly the equibiaxial region of the yield locus, the biggest influence can be seen at the long side edges of the cross die, where the material is biaxially stretched. Note that the strain in the front flange area of the DC05 part (Figs. 17 and 18) shows worse results with the modified model than with the standard one. This is because the friction was determined based on simulations with the standard formulation. After changing to the modified model, the blank drew in a little further in this region which leads to higher strains. For the aluminum material, the draw in was even slightly better after switching to the variable formulation.

Fig. 17
figure 17

Difference between measured and simulated major strain for DC05 computed with standard (left) and modified (right) version of Yld2000-2d

Full size image
Fig. 18
figure 18

Difference between measured and simulated minor strain for DC05 computed with standard (left) and modified (right) version of Yld2000-2d

Full size image
Fig. 19
figure 19

Difference between measured and simulated major strain for Formalex™5x computed with standard (left) and modified (right) version of Yld2000-2d

Full size image
Fig. 20
figure 20

Difference between measured and simulated minor strain for Formalex™5x computed with standard (left) and modified (right) version of Yld2000-2d

Full size image

To also give a quantitative comparison Figs. 21 and 22 are provided. These Figures show the major and minor strain along a section through the bottom radius of the part (sketched in Figures). The Figures clearly show an improvement in the strain prediction, especially in the edges of the cross die, where the material is biaxially stretched.

Fig. 21
figure 21

Major and minor strains along section for Formalex™5x

Full size image
Fig. 22
figure 22

Major and minor strains along section for DC05

Full size image

Conclusion

A modified version of Barlats Yld2000-2d model was presented. The modifications lie in a dependency of the model parameters on the equivalent plastic strain as well as in the strain rate dependency of the yield stress was incorporated. The model was implemented in LS-Dyna as a user defined material. Laboratory tests to characterize two different materials, a DC05 and Formalex™5x (a 5082 based aluminum alloy) were conducted. The results have been used to fit the model parameters. In a first step, the model was validated by recomputing the uniaxial and equibiaxial stress strain curves. It could be shown, that the quality of the responses could be increased significantly. In a second step, cross die simulations have been carried out. Even though the cross die part turned out not to be the most suitable part to show the advantages of the model, an increase of the strain prediction accuracy could also been confirmed for both materials. An investigation of more complex geometries is part of ongoing work.