Application of Barlat’s Yld 2000-2d Yield Stress Function for Modeling the Anisotropic Plastic Behaviour and the Forming Limit Strain Curve

Abstract

The objective of present paper is to examine the plastic anisotropy behaviour of steel sheet, employing the Barlat´s Yld 2000-2d yield stress criterion and the corresponding non-associated plastic flow rule. New Barlat´s coefficients of anisotropy were defined and calibrated from material experimental data of simple uniaxial tension and equal biaxial stress tests. The new set of coefficients calculated from the experimental Lankford anisotropy coefficients (r-values), normalized yield stress (s-values), equal biaxial stress parameters (r_b and σ_b) were numerically obtained using the Newton-Raphson method. The investigated metal was the highly anisotropic AISI 439 steel sheets found in the literature. In the results analysis and discussion, the new coefficients of anisotropy of the Barlat´s non-associated plastic flow rule were calculated and validated by plotting on the same graph the predicted r-value and s-value curves and the experimental data for the anisotropic steel sheets. The correlations have revealed that the Barlat´s yield criterion and the plastic flow stress potential were not coincident. Furthermore, the predicted limit strain curve of 439 steel correlated better with the experimental FLC_TD transverse curve when using the shear stress fracture criterion and the non-associated plastic potential than the associated flow rule. Therefore, the Barlat´s Yld 2000-2d non-associated plastic flow rule provides a better fit with the experimental Lankford and equal biaxial coefficients of anisotropy and the FLC_TD curve results of AISI 439 steel sheets.

1 Introduction

In sheet metal forming operations practice, it is well-known that the Formability of the blank material is greatly influenced by the strain and strain-rate hardening and the plastic anisotropy coefficients, which can be measured by the Lankford’s coefficients of anisotropy and the equal biaxial anisotropy coefficient. Metal blanks as received exhibits plastic anisotropy with orthotropic symmetry originated from the cold rolling. The three orthotropic axes of plastic anisotropy are mutually perpendicular and are defined in the rolling direction RD, transverse TD and normal or thickness ND directions. These are assumed as the principal axes of orthotropic plastic anisotropy.

One first work to investigate an anisotropic yield stress criterion to describe the plasticity behaviour of sheet metals with orthotropic symmetry was the paper presented by Rodney Hill in 1948 [1]. The phenomenological Hill’s 48 yield stress criterion was an extension of von Mises’s isotropic yield stress criterion. Since then, several other phenomenological anisotropic yield stress criteria have been proposed. A brief review of yield stress criteria can be found in the articles by Barlat et al. [2], Yoon et al. [3] and Bressan et al. [4].

Barlat’s Yld 2000-2d anisotropic yield stress function [5] has been widely applied in numerical simulations and analytical modelling of cup ears and forming limit strains of aluminium and steel alloys in sheet metal shaping operations in plane stress conditions. This yield function was developed from findings of previous works by Hershey [6], Hosford [7] yield stress criteria for isotropic material and the Yld96 anisotropic yield stress criterion proposed by Barlat et al. [8]. In 2003, the Yld 2000-2d anisotropic yield stress criterion applied to sheet metal forming for plane stress condition, pressure independent metals, orthotropic anisotropy was proposed by Barlat et al. [5] and was defined as the sum of two scalar non-quadratic functions, which are generated by two linear transformations of the deviatoric stress tensor.

1.1 Non-associated Plastic Flow Stress Potential

In the modelling of plastic flow behavior of metal, it is commonly postulated and accepted the associated plastic flow rule or normality rule, by which the plastic flow stress potential function is assumed to be coincident with the yield stress criterion. Thus, it is usually assumed that both the yield stress surface and the metal plastic strain increments or strain rate are calculated from a unique yield stress criterion function, which must be a convex function.

In the recent literature, the non-associated plastic flow rule approach has been frequently employed in numerical simulations of sheet metal forming processes. The material yield stress criterion and plastic flow stress potential were defined by two distinct functions [9, 10]. One first work to investigate a non-associated plastic stress potential was presented by Stoughton [9]. The author argued that the associated plastic flow rule postulation is not rigorously true, revealed by comparing the Hill’s 48 yield stress criterion function for both the associated and the non-associated flow rule approaches for the experimental data for mild steel, Al 2008-T4 and Al 2024-T3 aluminium alloys. Employing the tensile test experimental data for uniaxial yield stress and the Lankford coefficient of anisotropy, r-value, at 0°, 45° and 90° to the RD to calibrate the non-associated flow rule modelling, the author found good fittings for other points for different experimental tensile test angles with the predicted curves for yield stress and r-values. The curves fitting was poor or failed to correctly predict the uniaxial yield stress and r-value variations with the angle to RD, using the Hill’s 48 yield criterion as the plastic stress potential or the associated flow rule.

Numerical simulations of cylindrical cup drawing and ears formation and its height profile of highly anisotropic Al 2090-T3 and Al 5042 aluminium sheets were studied by Park and Chung [10]. The authors used the associated and non-associated Barlat’s Yld2000-2D plastic potential. Numerical simulations, using m = 8 and the non-associated plastic potential showed good correlations with the experimental results of ear numbers and height profiles for both materials; better cylindrical cup earing profiles prediction than the associated flow rule and the Hill 48 yield criterion.

The FLC of AISI 439 steel sheet was investigated by Lian et al. [11], employing the non-associated Hill’s 48 plastic flow potential and the yield stress criterion, and the modified maximum force criterion to predict the FLC. The non-associated flow rule model presented better correlation with the experimental FLC curve than the Hill’s 48 associated flow rule model. As well the predicted punch force versus displacement curve of the Nakajima equal biaxial stress test showed good correlation with the experimental data. The authors also presented a short review of recent references that deal with the application of non-associated plastic potentials.

Safei et al. [12] analyzed the non-associated Barlat’s Yld2000-2D flow stress potential model, applying to deformation processes of the highly anisotropic Al 2090-T3 alloy and DC06 steel sheets. The predicted s-value and r-value curves as function of angle to the rolling direction RD have shown good correlation with the experimental data. Although, the numerical simulation of cylindrical cup deep drawing of Al 2090-T3 alloy showed the same number of ears, the simulations revealed poor fitting with the experimental results of the earing height profile.

The objective of present work is to examine the Barlat´s Yld 2000-2d stress function as the anisotropic non-associated plastic flow potential or the flow rule to better describe the plastic anisotropy coefficients of highly anisotropic AISI 409 steel sheets. New generalised and exact equations to calculate the eight coefficients of plastic anisotropy a_i of Barlat´s Yld 2000-2d yield stress function have been proposed by Bressan [4]. Thus, to calibrate the Barlat´s coefficients of plastic anisotropy a_i, eight experimental tests and eight material plastic anisotropy parameters are needed. The plastic anisotropic parameters required are defined as Lankford coefficients of anisotropy r₀, r₄₅, r₉₀; yield stress σ₀, σ₄₅, σ₉₀; balanced biaxial coefficient of anisotropy r_b and balanced biaxial yield stress, σ_b. Newton-Raphson numerical method with relaxation factor were employed to numerically calculate the a_i-values with high accuracy for assumed minimum error. The calculated eight a_i coefficients of anisotropy were validated and calibrated by comparing the predicted r-values and s-values with the experimental data for aluminium alloys [4] and present steel sheets.

2 The Non-Associated Barlat’s Yld 2000-2d Anisotropic Plastic Flow Stress Potential

Defining ${\text{f}} \,\left( {\sigma_{ij} \,,\,\overline{\varepsilon },\dot{\overline{\varepsilon }}} \right)$ as the yield stress function or yield stress surface and Φ(σ_ji) the yield stress criterion, the general loading condition for the onset of plastic straining is,

$${\text{f}} \,\left( {\upsigma_{ij} \,,\,\overline{\varepsilon },\dot{\overline{\varepsilon }}} \right)\,\,\, = \,\,\Phi \left( {\upsigma_{ij} } \right) - \,\,\overline{\upsigma }\,\left( {\varepsilon_{o} ,\overline{\varepsilon },\dot{\overline{\varepsilon }}} \right)\,\,\, = \,\,0\,\,\,$$

(1)

and commonly is a first degree homogeneous function of the Cauchy stress tensor, σ_ji = (1/3) σ_kk δ_ij + S_ij, which defines the yield surface shape (S_ij is the stress deviator), $\overline{\sigma }$ is the current equivalent flow stress and is identified as scalar function of the equivalent plastic strain $\overline{\varepsilon }$, pre-strain $\varepsilon_{o}$ and strain rate $\dot{\overline{\varepsilon }}$. The equivalent flow stress represents the yield stress surface size and material hardening law. The modified Swift equation is: $\overline{\sigma }\,\left( {\varepsilon_{o} ,\overline{\varepsilon },\dot{\overline{\varepsilon }}} \right)\, = \,\sigma_{o} \left( {1 + \overline{\varepsilon }/\varepsilon_{o} } \right)^{n} \left( {\dot{\overline{\varepsilon }}/\dot{\varepsilon }_{o} } \right)^{M}$, where $\sigma_{o}$ is the material yield stress limit. Assuming the existence of a plastic flow potential, the plastic strain increments dε_ij can be calculated from the plastic flow stress potential Ψ(σ_ij) as,

$${\rm d}\varepsilon_{ij} \, = \,\,d\uplambda \,\frac{{\partial \,\Psi \left( {\upsigma_{ij} } \right)}}{{\partial \,\upsigma_{ij} }}$$

(2)

where dλ is the plastic multiplier increment and σ_ij are the stress tensor components. Usually, it is assumed that the plastic potential coincides with the yield stress criterion: Ψ(σ_ij) ≡ Φ(σ_ij).

As mentioned above, the Barlat’s Yld2000-2d anisotropic yield stress criterion [5] applied to sheet metal forming for plane stress condition and orthotropic anisotropy was defined as the sum of two scalar non-quadratic functions, which are generated by two linear transformations of the deviatoric stress tensor S_ij or the Cauchy true stress tensor σ_ij: ${\rm S}^{\prime}_{ij} \, = \,{\rm C}^{\prime}\,{\rm S}_{ij} \, = \,\,{\rm L}^{\prime}_{ij} \,\sigma_{ij}$ and $S^{\prime\prime}_{ij} \, = \,\,C^{\prime\prime}\,S_{ij} = L^{\prime\prime}_{ij} \,\sigma_{ij}$,

$$\Phi \,\, = \,\Phi^{\prime}\,\, + \,\Phi^{\prime\prime}\, = \left| {S^{\prime}_{1} - S^{\prime}_{2} } \right|^{m} + \,\,\left| {2S^{\prime\prime}_{1} + S^{\prime\prime}_{2} } \right|^{m} \, + \,\,\left| {2S^{\prime\prime}_{2} + S^{\prime\prime}_{1} } \right|^{m} = \,2\,\overline{\sigma }^{m} \,$$

(3)

where $\overline{\sigma }$ is the equivalent stress, $S^{\prime}_{j}$ and $S^{\prime\prime}_{k} \,$ are the principal values of the transformed stress tensors $S^{\prime}_{ij}$ and $S^{\prime\prime}_{ij}$. Also, the proposed function Φ is convex for exponent m > 1 [5]. These principal values, in Eq. (3), can be expressed in terms of the Cauchy stress tensor components by the definition of proposed new coefficients of plastic anisotropy, a_i, assuming (x,y)-axis as the material principal cartesian axis of orthotropic anisotropy in the sheet plane and the two matrices ${\mathbf{C^{\prime}}}$ and ${\mathbf{C^{\prime\prime}}}$ expressed as a function of eight coefficients of anisotropy, thus [4],

$$\upsigma^{\prime}_{1} = 2{\rm S}^{\prime\prime}_{1} + {\rm S}^{\prime\prime}_{2} \, = \,\,\left( {{\rm a}_{1} \,\sigma_{\rm xx} + \,{\rm a}_{2} \,\sigma_{\rm yy} } \right)/2 + \,\,\sqrt {\Delta^{\prime}\,}$$

(4a)

$$\upsigma^{\prime}_{2} = 2{\rm S}^{\prime\prime}_{2} + {\rm S}^{\prime\prime}_{1} \, = \left( {{\rm a}_{1} \,\sigma_{\rm xx} + \,{\rm a}_{2} \,\sigma_{\rm yy} } \right)/2 - \,\,\sqrt {\Delta^{\prime}\,} \,$$

(4b)

$$\upsigma^{\prime\prime}_{1} - \upsigma^{\prime\prime}_{2} = {\rm S}^{\prime}_{1} - {\rm S}^{\prime}_{2} = \,\,2\sqrt {\Delta^{\prime\prime}} \,$$

(4c)

where,

$$\begin{gathered} \Delta^{\prime} = \,\,\left( {\frac{{{\rm a}_{3} \,\upsigma_{\rm xx} - \,\,{\rm a}_{4} \,\upsigma_{\rm yy} }}{2}} \right)^{2} \, + \,\,\left( {{\rm a}_{8} \tau_{\rm xy}^{\,} } \right)^{2} \,; \hfill \\ \Delta^{\prime\prime}\, = \,\,\left( {\frac{{{\rm a}_{5} \,\sigma_{\rm xx} - \,\,{\rm a}_{6} \,\upsigma_{\rm yy} }}{2}} \right)^{2} \, + \,\,\left( {{\rm a}_{7} \tau_{\rm xy}^{\,} } \right)^{2} \, \hfill \\ \end{gathered}$$

(4d,e)

where a_i are the proposed eight new coefficients of material plastic anisotropy [4], which are related to the original linear transformation coefficients α_i. Material plastic isotropy is when a_i = α_i = 1. The two anisotropy matrices $L^{\prime}_{ij} \,$ and $L^{\prime\prime}_{ij} \,$ can be expressed as a function of eight new coefficients of material plastic anisotropy [4],

$${\rm a}_{ij} = \,\,\left[ \begin{gathered} {\rm a}_{1} \,\,\,\,\,{\rm a}_{2} \,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ {\rm a}_{3} \,\,\,\,\,{\rm a}_{4} \,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ {\rm a}_{5} \,\,\,\,\,{\rm a}_{6} \,\,\,\,\,0\,\,\,\,\,\,\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,{\rm a}_{7} \,\,\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,0\,\,\,\,\,\,{\rm a}_{8} \hfill \\ \end{gathered} \right]\, = \,\left[ \begin{gathered} 3\left( {{\rm L}^{\prime\prime}_{11} + {\rm L}^{\prime\prime}_{21} } \right)\,\,\,\,\,3\left( {{\rm L}^{\prime\prime}_{22} + {\rm L}^{\prime\prime}_{12} } \right)\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ \,\,\,\left( {{\rm L}^{\prime\prime}_{11} - {\rm L}^{\prime\prime}_{21} } \right)\,\,\,\,\,\,\,\,\left( {{\rm L}^{\prime\prime}_{22} - {\rm L}^{\prime\prime}_{12} } \right)\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ \,\,\,\left( {{\rm L}^{\prime}_{11} - {\rm L}^{\prime}_{21} } \right)\,\,\,\,\,\,\,\,\left( {{\rm L}^{\prime\prime}_{22} - {\rm L}^{\prime\prime}_{12} } \right)\,\,\,\,\,\,0\,\,\,\,\,\,\,\,0 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm L}^{\prime}_{66} \,\,\,\,\,0\,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,{\rm L}^{\prime\prime}_{66} \hfill \\ \end{gathered} \right]$$

(5)

Substituting Eqs. (4a-e) into Eq. (3), Barlat’s Yld 2000-2d anisotropic yield stress function can be written in terms of Cauchy stress tensor components and the coefficients of plastic anisotropy. The non-associated Barlat’s Yld 2000-2d flow potential is assumed to be similar to the yield stress criterion function. However, the anisotropy parameters a_i-values will be substituted by ã_i-values [4], assuming material with M = 0,

$$\begin{gathered} \Psi (\sigma _{{{\text{xx}}}} ,{\mkern 1mu} \sigma _{{{\text{yy}}}} ,{\mkern 1mu} \tau _{{{\text{xy}}}} ,\;{\tilde{\text a}_{\text i}} ){\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} \frac{1}{{2^{{\text{m}}} }}\left| {\;{\tilde{\text a}_{1}} \sigma _{{{\text{xx}}}} + {\mkern 1mu} \;{\tilde{\text a}_{2}} \sigma _{{{\text{yy}}}} + {\mkern 1mu} {\mkern 1mu} \left[ {\left( {\;{\tilde{\text a}_{3}} \sigma _{{{\text{xx}}}} - {\mkern 1mu} \;{\tilde{\text a}_{4}} \sigma _{{{\text{yy}}}} } \right)^{2} + {\mkern 1mu} {\mkern 1mu} \left( {2\;{\tilde{\text a}_{8}} \tau _{{{\text{xy}}}} } \right)^{2} } \right]^{{1/2}} {\mkern 1mu} } \right|^{{\text{m}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\mkern 1mu} {\mkern 1mu} \frac{1}{{2^{{\text{m}}} }}\left| {{\mkern 1mu} \;{\tilde{\text a}_{1}} {\mkern 1mu} \sigma _{{{\text{xx}}}} + {\mkern 1mu} \;{\tilde{\text a}_{2}} {\mkern 1mu} \sigma _{{{\text{yy}}}} - {\mkern 1mu} {\mkern 1mu} \left[ {\left( {\;{\tilde{\text a}_{3}} {\mkern 1mu} \sigma _{{{\text{xx}}}} - {\mkern 1mu} \;{\tilde{\text a}_{4}} \sigma _{{{\text{yy}}}} } \right)^{2} {\mkern 1mu} + {\mkern 1mu} {\mkern 1mu} \left( {2\;{\tilde{\text a}_{8}} \tau _{{{\text{xy}}}} } \right)^{2} } \right]^{{1/2}} {\mkern 1mu} } \right|^{{\text{m}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left| {\left( {\;{\tilde{\text a}_{5}} \sigma _{{{\text{xx}}}} - {\mkern 1mu} \;{\tilde{\text a}_{6}} \sigma _{{{\text{yy}}}} } \right)^{2} + {\mkern 1mu} \left( {2\;{\tilde{\text a}_{7}} \tau _{{{\text{xy}}}} } \right)^{2} } \right|^{{{\text{m}}/2}} = 2\bar{\sigma }^{{\text{m}}} = 2\sigma _{{\text{o}}}^{{\text{m}}} \left( {1 + \bar{\varepsilon }/\varepsilon _{o} } \right)^{{{\text{nm}}}} \hfill \\ \end{gathered}$$

(6)

2.1 Coefficients of Anisotropy from the Non-associated Plastic Potential

For a standard tensile test specimen cut at angle θ to RD, loading in uniaxial tensile stress σ_θ in the x’-axis of tensile direction and y’-axis the width direction, for plane stress condition, the stress components and strain increments in the anisotropy (x,y)-axis or (RD,TD)-axis can be obtained. For a standard tensile test specimen under a uniaxial tensile stress σ_θ, the equivalent stress can be expressed as $\,\overline{\sigma }\,\, = \,\,A\,\,\sigma_{\theta }$, where $A\, = \left\{ {2^{m} F + \left| {B + \,\,C\,} \right|^{m} + \,\left| {B - \,\,C\,} \right|^{m} } \right\}^{1/m} /2^{1\, + \,1/m}$. Then, assuming Barlat´s non-associated flow rule and applying the Euler’s identity theorem for a homogeneous stress function of degree ‘m’ to the Barlat’s yield stress criterion function $\,\Psi \,\,\left( {\sigma_{xx} ,\sigma_{yy} ,\tau_{xy} ,\,\tilde{a}_{i} } \right)$, after rearranging, the Lankford´s coefficient of anisotropy and the equal biaxial stress coefficient of anisotropy can be calculated by [4],

$${\text{r}}_{\uptheta } = \frac{{{\text{d}}\varepsilon _{{{\text{width}}}} }}{{{\text{d}}\varepsilon _{{{\text{thickness}}}} }} = \frac{{\partial \Psi /\partial \sigma _{{{\text{y}}^{\prime } {\kern 1pt} {\text{y}}^{\prime } }} }}{{\partial \Psi /\partial \sigma _{{{\text{zz}}}} }} = \frac{{{\mkern 1mu} 2{\text{m}}{\mkern 1mu} {\text{A}}^{{\text{m}}} \sigma _{\theta }^{{{\text{m}} - 1}} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} }}{{\frac{{\partial \Psi }}{{\partial {\mkern 1mu} \sigma _{{{\text{xx}}}} }} + \frac{{\partial {\mkern 1mu} \Psi }}{{\partial {\mkern 1mu} \sigma _{{{\text{yy}}}} }}{\mkern 1mu} }} - {\mkern 1mu} 1$$

(7)

$$r_{{\text{b}}} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{{\text{d}}\varepsilon _{{{\text{TD}}}} }}{{{\text{d}}\varepsilon _{{{\text{RD}}}} }} = \frac{{{\text{d}}\varepsilon _{{{\text{yy}}}} }}{{{\text{d}}\varepsilon _{{{\text{xx}}}} }} = \frac{{\partial \Psi /\partial \sigma _{{{\text{yy}}}} }}{{\partial \Psi /\partial \sigma _{{{\text{xx}}}} }}$$

(8)

The derivatives of the stress function $\,\Psi \,\,\left( {\sigma_{xx} ,\sigma_{yy} ,\tau_{xy} ,\,\tilde{a}_{i} } \right)$ seen in Eqs. (7–8) are obtained from Eq. (6), considering the derivative chain rule and the derivative sign for the modulus function, thus, they are calculated by [4],

$$\frac{{\partial \Psi }}{{\partial \sigma _{{{\text{xx}}}} }} = \left\{ {2{\text{mE}}{\mkern 1mu} \;{\tilde{\text{a}}}_{5} {\mkern 1mu} + \frac{{\text{m}}}{{2^{{\text{m}}} }}{\mkern 1mu} \left( {{\text{B}} + {\text{C}}} \right)^{{{\text{m}} - 1}} {\mkern 1mu} \left( {\tilde{\text{a}}_{1} + {\text{D}}{\tilde{\text a}_{3}} } \right) + \frac{{\text{m}}}{{2^{{\text{m}}} }}{\mkern 1mu} \left( {{\text{B}} - {\text{C}}} \right)^{{{\text{m}} - 1}} \left( {\tilde{\text{a}}_{1} - {\text{D}}{\tilde{\text a}_{3}} } \right)} \right\}\sigma _{\theta }^{{{\text{m}} - 1}}$$

(9)

$$\frac{{\partial \Psi }}{{\partial \sigma _{{{\text{yy}}}} }}{\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \left\{ { - 2{\text{mE}}{\mkern 1mu} \;{\tilde{\text{a}}}_{6} + {\mkern 1mu} \frac{{\text{m}}}{{2^{{\text{m}}} }}{\mkern 1mu} \left( {{\text{B}} + {\text{C}}} \right)^{{{\text{m}} - 1}} \left( {\;{\tilde{\text{a}}}_{2} - {\text{D}}{\tilde{\text a}_{4}} } \right) + {\mkern 1mu} \frac{{\text{m}}}{{2^{{\text{m}}} }}{\mkern 1mu} \left( {{\text{B}} - {\text{C}}} \right)^{{{\text{m}} - 1}} \left( {\tilde{{\text{a}}}_{2} + {\text{D}}{\mkern 1mu} {\tilde{\text a}_{4}} } \right)} \right\}\sigma _{\theta }^{{{\text{m}} - 1}}$$

(10)

Finally, substituting into Eqs. (7–8), the generalized Lankford’s coefficient of anisotropy r_θ and the equal biaxial coefficient of anisotropy r_b are calculated by,

$${\text{r}}_{\theta } = \frac{{{\mkern 1mu} 2^{{\text{m}}} {\text{F}} + \left| {{\text{B}} + {\text{C}}} \right|^{{\text{m}}} + {\mkern 1mu} \left| {{\text{B}} - {\text{C}}} \right|^{{\text{m}}} }}{{2^{{{\text{m}} + 1}} {\text{E}}{\mkern 1mu} \left( {\tilde{{\text{a}}}_{5} - {\tilde{\text{a}}}_{6} } \right) + {\mkern 1mu} \left( {{\text{B}} + {\text{C}}} \right)^{{{\text{m}} - 1}} {\mkern 1mu} \left( {{\text{A}} + {\text{D}}_{{34}} } \right){\mkern 1mu} + \left( {{\text{B}} - {\text{C}}} \right)^{{{\text{m}} - 1}} \left( {{\text{A}} - {\text{D}}_{{34}} } \right){\mkern 1mu} {\mkern 1mu} }} - 1$$

(11)

$${\text{r}}_{{\text{b}}} = \frac{{2^{{\text{m}}} \left| {\tilde{{\text{a}}}_{5} - {\tilde{\text{a}}}_{6} } \right|^{{\text{m}}} + \left| {\left( {{\tilde{\text{a}}}_{1} + {\tilde{\text{a}}}_{2} } \right) + \left| {\tilde{{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right|} \right|^{{\text{m}}} + \left| {\left( {{\tilde{\text{a}}}_{1} + {\tilde{\text{a}}}_{2} } \right) - \left| {{\tilde{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right|{\mkern 1mu} } \right|^{{\text{m}}} }}{{2^{{{\text{m}} + 1}} {\text{LB} \tilde{\text{a}}}_{5} + {\text{G}}_{1}^{{{\text{m}} - 1}} \left( {{\tilde{\text{a}}}_{1} + {\text{H}}_{{34}} \,{\tilde{\text{a}}}_{3} } \right) + {\text{G}}_{2}^{{{\text{m}} - 1}} {\mkern 1mu} \left( {{\tilde{\text{a}}}_{1} - {\text{H}}_{{34}} {\tilde{\text{a}}}_{3} } \right)}} - 1$$

(12)

Where,

$${\text{A}} = {\tilde{\text{a}}}_{1} + {\tilde{\text{a}}}_{2} ;{\text{B}} = {\tilde{\text{a}}}_{1} \,{\text{cos}}^{2} \theta + {\tilde{\text{a}}}_{2} \,{\text{sin}}^{2} \theta$$

(13a,b)

$${\text{C}} = \left[ {\left( {{\tilde{\text{a}}}_{3} {\text{cos}}^{2} \theta - {\tilde{\text{a}}}_{4} {\text{sin}}^{2} \theta } \right)^{2} + 4\;{\tilde{\text{a}}}_{8}^{2} {\mkern 1mu} {\text{sin}}^{2} \theta {\text{cos}}^{2} \theta } \right]^{{{\kern 1pt} 1/2}}$$

(13c)

$${\text{D}} = \left( {{\tilde{\text{a}}}_{3} {\text{cos}}^{2} \theta - {\tilde{\text{a}}}_{4} {\mkern 1mu} {\text{sin}}^{2} \theta } \right)/{\text{C}};{\text{D}}_{{34}} = {\text{D}}\left( {{\tilde{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right)$$

(13d,e)

$${\text{E}} = \left( {\left( {\;{\tilde{\text{a}}}_{5} {\mkern 1mu} {\text{cos}}^{2} \theta - {\tilde{\text{a}}}_{6} {\text{sin}}^{2} \theta } \right)^{2} + {\mkern 1mu} {\mkern 1mu} 4\;{\tilde{\text{a}}}_{7}^{2} {\mkern 1mu} {\text{sin}}^{2} \theta {\text{cos}}^{2} \theta } \right)^{{({\text{m}}/2){\kern 1pt} - 1}} \left( {\;{\tilde{\text{a}}}_{5} {\mkern 1mu} {\text{cos}}^{2} \theta - {\mkern 1mu} \;{\tilde{\text{a}}}_{6} {\mkern 1mu} {\text{sin}}^{2} \theta } \right)$$

(13f)

$${\text{F}} = \left| {{\mkern 1mu} \left( {{\tilde{\text{a}}}_{5} {\text{cos}}^{2} \theta {\mkern 1mu} - {\tilde{\text{a}}}_{6} {\text{sin}}^{2} \theta } \right)^{2} + {\mkern 1mu} 4{\tilde{\text{a}}}_{7}^{2} {\mkern 1mu} {\text{sin}}^{2} \theta {\text{cos}}^{2} \theta } \right|^{{{\text{m}}/2}}$$

(13g)

$${\text{G}}_{1} = {\mkern 1mu} \left( {{\tilde{\text{a}}}_{1} + {\tilde{\text{a}}}_{2} } \right) + \left| {{\tilde{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right|;{\text{G}}_{2} = {\mkern 1mu} \left( {{\tilde{\text{a}}}_{1} + {\tilde{\text{a}}}_{2} } \right) - \left| {{\tilde{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right|$$

(13h,i)

$${\text{LB}} = {\mkern 1mu} \left( {{\tilde{\text{a}}}_{5} - {\tilde{\text{a}}}_{6} } \right)^{{{\text{m}} - 1}} ;{\text{H}}_{{34}} = \left( {{\tilde{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right)/\left| {{\tilde{\text{a}}}_{3} - {\tilde{\text{a}}}_{4} } \right|$$

(13k,l)

For a tensile test specimen under uniaxial tensile stress σ_θ, the equivalent stress of Eq. (6) is $\,\overline{\sigma }\,\, = \,\,A\,\sigma_{\theta }$. Consequently, the normalized yield stress at any angle θ to RD is,

$$\frac{{\sigma _{\theta } }}{{\sigma _{{\text{o}}} }} = \frac{{2^{{1 + 1/{\text{m}}}} \left( {1 + \bar{\varepsilon }/\varepsilon _{o} } \right)^{{{\text{n}}{\kern 1pt} }} }}{{\left\{ {2^{{\text{m}}} {\text{F}} + \left| {{\text{B}} + {\text{C}}} \right|^{{\text{m}}} + \left| {{\text{B}} - {\text{C}}{\mkern 1mu} } \right|^{{\text{m}}} } \right\}^{{1/{\text{m}}}} }}$$

(14)

where $\sigma_{o}$ is the material yield stress limit. Assuming the current equivalent flow stress, $\overline{\sigma } = \sigma_{o} \left( {1 + \overline{\varepsilon }/\varepsilon_{o} } \right)^{n}$, at any current yielding condition, hence, the normalized equal biaxial stress, $\sigma_{xx} = \,\sigma_{yy} = \sigma_{b} \,\,and\,\,\tau_{xy} = \,\,0$, is calculated by,

$$\frac{{\sigma _{{\text{b}}} }}{{\sigma _{{\text{o}}} }} = \frac{{2^{{1 + 1/{\text{m}}}} \left( {1 + \bar{\varepsilon }/\varepsilon _{{\text{o}}} } \right)^{{\text{n}}} }}{{\left\{ {2^{{\text{m}}} \left( {{\text{a}}_{5} - {\text{a}}_{6} {\mkern 1mu} } \right)^{{\text{m}}} + \left| {\left( {{\text{a}}_{1} + {\text{a}}_{2} } \right) + \left| {{\text{a}}_{3} - {\text{a}}_{4} } \right|} \right|^{{\text{m}}} + {\mkern 1mu} \left| {\left( {{\text{a}}_{1} + {\text{a}}_{2} } \right) - \left| {{\text{a}}_{3} - {\text{a}}_{4} } \right|{\mkern 1mu} } \right|^{{\text{m}}} } \right\}^{{1/{\text{m}}}} }}$$

(15)

Substituting into Eq. (6) the boundary conditions for a uniaxial tensile test specimen under loading at 0° RD, the stress components are $\sigma_{xx} = \,\,\sigma_{0}$ and $\sigma_{yy} = \,\tau_{xy} = \,0$, thus,

$${\mkern 1mu} \left| {2{\text{a}}_{5} {\mkern 1mu} } \right|^{{\text{m}}} + \left| {{\text{a}}_{1} + {\text{a}}_{3} {\mkern 1mu} } \right|^{{\text{m}}} + \left| {{\mkern 1mu} {\text{a}}_{1} - {\text{a}}_{3} {\mkern 1mu} } \right|^{{\text{m}}} - 2^{{1 + {\text{m}}}} \left( {1 + \bar{\varepsilon }/\varepsilon _{{\text{o}}} } \right)^{{\text{n}}} = 0$$

(16)

Similarly, for a specimen under pure shear stress test, the stress components are $\sigma_{xx} = \,\sigma_{yy} = 0$ and $\tau_{xy} = \,\tau_{o} = k$, where $\tau_{0} = k$ is the material shear yield stress limit, the Eq. (6) is reduced to: $a_{7} \, = \,\, \pm 2^{{\left( {1/m} \right) - 1}} \left( {\sigma_{o} /\tau_{o} } \right) = \pm 2^{{\left( {1/m} \right) - 1}} \sigma_{o} /k$.

2.2 The FLC Strain Path in the MPLS Map

The linear strain path β to calculate the FLC_RD curve in the Map of Principal Surface Limit Strains (MPLS) is obtained from Eqs. (9–10). Assuming the principal coordinate axis coincident with the principal direction of anisotropy axis, (1,2)-axis = (x,y)-axis = (RD,TD), and defining the stress ratio X = σ₂/σ₁, the linear strain path is [4],

$$\beta = \frac{{{\text{d}}\varepsilon _{2} }}{{{\text{d}}\varepsilon _{1} }} = {\mkern 1mu} \frac{{\partial {\mkern 1mu} \Psi /\partial {\mkern 1mu} \sigma _{{{\text{yy}}}} {\mkern 1mu} }}{{\partial {\mkern 1mu} \Psi /\partial {\mkern 1mu} \sigma _{{{\text{xx}}}} }} = \frac{{ - 2^{{{\text{m}} + 1}} {\text{L}}\,{\tilde{\text{a}}}_{6} + \left( {{\text{K}}_{1} } \right)^{{{\text{m}} - 1}} \left( {{\tilde{\text{a}}}_{2} - {\text{M}}_{{34}} {\mkern 1mu} \;{\tilde{\text{a}}}_{4} } \right) + \left( {{\text{K}}_{2} } \right)^{{{\text{m}} - 1}} \left( {\;{\tilde{\text{a}}}_{2} + {\text{M}}_{{34}} {\mkern 1mu} \;{\tilde{\text{a}}}_{4} } \right)}}{{2^{{{\text{m}} + 1}} {\text{L}}\,{\tilde{\text{a}}}_{5} + \left( {{\text{K}}_{1} } \right)^{{{\text{m}} - 1}} \left( {{\tilde{\text{a}}}_{1} + {\text{M}}_{{34}} {\mkern 1mu} \;{\tilde{\text{a}}}_{3} } \right) + \left( {{\text{K}}_{2} } \right)^{{{\text{m}} - 1}} \left( {\;{\tilde{\text{a}}}_{1} - {\text{M}}_{{34}} {\mkern 1mu} \;{\tilde{\text{a}}}_{3} } \right)}}$$

(17)

where,

$$\begin{gathered} {\text{L}} = \left| {{{\tilde{\text a}}}_{5} - {{\tilde {\text a}}}_{6} {\text{X}}} \right|^{{{\text{m}} - 2}} \left( {{{\tilde {\text a}}}_{5} - {{\tilde {\text a}}}_{6} {\text{X}}} \right);{\text{K}}_{1} = \left( {{{\tilde {\text a}}}_{1} + {{\tilde {\text a}}}_{2} {\text{X}}} \right) + \left| {{{\tilde {\text a}}}_{3} - {{\tilde {\text a}}}_{4} {\text{X}}} \right|; \hfill \\ {\text{K}}_{2} = \left( {{{\tilde {\text a}}}_{1} + {{\tilde {\text a}}}_{2} {\text{X}}} \right) - \left| {{{\tilde {\text a}}}_{3} - {{\tilde {\text a}}}_{4} {\text{X}}} \right|{\text{;M}}_{{34}} = \left( {{{\tilde {\text a}}}_{3} - {{\tilde {\text a}}}_{4} {\text{X}}} \right)/\left| {{{\tilde {\text a}}}_{3} - {{\tilde {\text a}}}_{4} {\text{X}}} \right| \hfill \\ \end{gathered}$$

(18a,b,c,d)

2.3 The Shear Stress Fracture Criterion to Predict FLC_TD in the MPLS Map

The Bressan-Williams shear stress fracture criterion [13] was proposed firstly in 1983 to predict ductile local necking in sheet metal forming. It is an instability stress point of maximum in a critical shear stress just when local necking initiate by shear bands formation. This maximum shear stress is a critical value that acts in a plane inclined through the sheet thickness and in the direction of pure shear strain, namely τ_cr, that is a material property which depends on temperature and strain rate. Considering the experimental observations of fast shear rupture without visible local necking in sheet metal shaping of strain-rate-independent materials, M = 0, this approach was modified by Bressan and Barlat [14], using the anisotropic Barlat´s Yld-2000-2d yield criterion.

However, assuming the maximum loading axis of specimen coincident with the transverse direction of anisotropy axis, (2,1)-axis = (TD,RD)-axis, and defining the stress ratio X_T = σ₁ /σ₂, linear strain path is β_T = de₁/de₂, the governing equation of fast shear stress fracture criterion to calculate FLC_TD curve in the MPLS map is [14],

$$\upsigma_{2} = \,\,\left| {\left( {2\, + \upbeta_{\rm T} } \right)/\sqrt {1 + \upbeta_{\rm T} } } \right|\,\uptau_{\rm cr}$$

(19)

where σ₂ > 0 is the maximum principal in-plane true stress coincident with TD, τ_cr the critical shear stress. Assuming materials exhibiting planar anisotropy and strain hardening behavior only, strain rate sensitivity exponent is neglected, M = 0, the equivalent flow stress for linear deformations is described by the Swift’s law, $\overline{\sigma }\, = \,K\,\left( {\varepsilon_{o} \, + \,\overline{\varepsilon }} \right)^{n}$, where K is the material strength coefficient,$\overline{\varepsilon }$ the equivalent strain, $\varepsilon_{o}$ the pre-strain, n the material strain hardening exponent. Assuming the equivalent plastic strain increment calculated from the definition of equivalent plastic work increment, using the previous definition of strain path β_T and stress ratio X_T, is obtained,

$${\rm d}\overline{\varepsilon }\, = \left( {\upsigma_{2} /\overline{\upsigma }} \right)\,\left( {1 + \,{\rm X}_{\rm T} \,\upbeta_{\rm T} } \right){\rm d}\varepsilon_{2}$$

(20)

Assuming linear plastic strain path up to the transverse FLC_TD curve, thus, integrating Eq. (20), the predicted major true plastic strain limit ε_2f is calculated by [14],

$$\begin{gathered} \varepsilon _{{2{\text{f}}}} = \left\{ {\frac{1}{2}\left( {\left| {\frac{{\sigma _{1}^{{\prime \prime }} - \sigma _{2}^{{\prime \prime }} }}{{\sigma _{2} }}} \right|^{{\text{m}}} + \left| {\frac{{\sigma _{1}^{\prime } }}{{\sigma _{2} }}} \right|^{{\text{m}}} + {\mkern 1mu} \left| {\frac{{\sigma _{2}^{\prime } }}{{\sigma _{2} }}} \right|^{{\text{m}}} } \right)} \right\}^{{\frac{{1 + {\text{n}}}}{{{\text{m}}{\kern 1pt} {\text{n}}}}}} \left| {\frac{{2{\mkern 1mu} + \beta _{{\text{T}}} }}{{\sqrt {1 + \beta _{{\text{T}}} } }}} \right|^{{\frac{1}{{\text{n}}}}} \frac{{\left( {\tau _{{{\text{cr}}}} /{\text{K}}} \right)^{{\frac{1}{{\text{n}}}}} }}{{\left( {1 + {\text{X}}_{{\text{T}}} {\mkern 1mu} \beta _{{\text{T}}} } \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left\{ {\frac{1}{2}\left( {\left| {\frac{{\sigma _{1}^{{\prime \prime }} {\mkern 1mu} - \sigma _{2}^{{\prime \prime }} }}{{\sigma _{2} }}} \right|^{{\text{m}}} + {\mkern 1mu} \left| {\frac{{\sigma _{1}^{\prime } }}{{\sigma _{2} }}} \right|^{{\text{m}}} + {\mkern 1mu} \left| {\frac{{\sigma _{2}^{\prime } }}{{\sigma _{2} }}} \right|^{{\text{m}}} } \right)} \right\}^{{\frac{1}{{\text{m}}}}} \frac{{\varepsilon _{{\text{o}}} }}{{\left( {1 + {\text{X}}_{{\text{T}}} {\mkern 1mu} \beta _{{\text{T}}} } \right)}} \hfill \\ \end{gathered}$$

(21)

The non-dimensional critical shear stress parameter τ_cr/K is a material property, which can be obtained and calibrated from experimental bulge test or the plane strain point, FLC_o, in the forming limit strain curve point at the minor true strain ε₁ = 0.

3 Materials and Experimental Anisotropy Parameters

The experimental data of AISI 439 steel available in the literature [11] for simple uniaxial tension and equal biaxial stress tests are shown in Tables 1.. The plastic anisotropy parameters used to calibrate the model were: Lankford coefficient of anisotropy r-values, normalized tensile yield stress s-values (=σ_θ/σ_0.19), and equal biaxial stress parameters r_b and σ_b at strain ε = 0.19, according to Barlat et al. [6, 8].

Table 1. Mechanical plastic anisotropy parameters of studied AISI 439 steel [11].

The plastic strain hardening law of the AISI 439 steel sheet of thickness 1.0 mm were obtained from experimental tests, which was applied to calculate the theoretical transverse FLC_TD curves: the average tensile tests: $\overline{\sigma }\, = \,732\,\left( {0.009\, + \,\overline{\varepsilon }} \right)^{0.235}$ MPa, according to the uniaxial experimental results by Lian et al. [11].

4 Results and Discussions

The system of exact non-linear equations, Eq. (11), Eq. (12), Eq. (14), Eq. (15) and Eq. (16), constitute a set of eight equations with eight experimental anisotropy properties and the unknown variables: the anisotropy coefficients ã_i, i = 1,..8. The details of Newton-Raphson numerical method were presented in the paper by Bressan and Donadon [4]. Therefore, it is necessary to choose among these, eight independents equations and eight experimental parameters to form a system of non-linear equations to find numerically the anisotropy coefficients ã_i. The Newton-Raphson method with a relaxation factor is a robust, accurate and reasonably fast numerical method which was employed to solve this system of non-linear equations within a given tolerance.

Fig. 1.

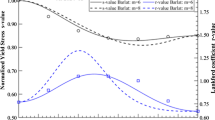
Comparisons of predicted r-ralue and s-value curves for the associated and the non-associated Barlat’s Yld 2000-2d yield stress with experimental results for tensile tests of AISI 439 [11], exponent m = 6, using Newton-Raphson method with experimental calibration parameters: a) associated rule, 4s- and 4r-values: σ₀, σ₄₅, σ₉₀, σ_b, r_o, r₄₅, r₉₀, r_b and b) non-associated plastic potential, 6s- and 2r-values: σ_o, σ₃₀, σ₄₅, σ₇₅, σ₉₀, σ_b, r₄₅, r₉₀; c) non-associated plastic potential, 7r-values and 1s-value: r₀, r₁₅, r₄₅, r₆₀, r₇₅, r₉₀, r_b, σ₄₅.

In Fig. 1, comparison of predicted curves for r-values and s-values versus angle θ to RD with experimental points of AISI 439, using the Barlat’s Yld 2000-2d yield criterion and corresponding associate flow rule and employing the recommended material selection of calibration parameters: 4 r-values and 4 s-values (r₀, r₄₅, r₉₀, r_b, σ₀, σ₄₅, σ₉₀ and σ_b), plotted in the same graph. Although the curve fitting passes exactly through the previously selected 4 r-values and 4 s-values points, for others experimental points the correlation is poor, particularly for s-values points, indicating the necessity of better curve fit. The curve fit is noticeably increased when selecting 6 s-values points for calibration of the normalized yield stress and 7 r-values points for calibration of the Lankford coefficients of anisotropy. Therefore, the yield stress criterion and plastic potential functions are not coincident, but are two distinct functions. The calculated a_i and ã_i plastic anisotropy coefficients of Barlat Yld 2000-2d stress functions for curve fitting of Fig. 1 are seen in Table 2.. Comparison between the calculated and experimental balanced biaxial plasticity parameters are shown in Table 3..

Table 2. The calculated plastic anisotropy coefficients for the Barlat Yld 2000-2d yield stress criterion Φ(σ_ij, a_i) and the independent non-associated Barlat Yld 2000-2d plastic stress potential Ψ(σ_ij, ã_i) of AISI 439 steel, using m = 6 and experimental points.

Table 3. The comparison between the experimental and calculated balanced biaxial plasticity parameters of AISI 439 steel for the numerical cases.

Fig. 2.

Comparisons of the predicted and experimental FLC_TD of AISI 439 steel sheet [11], using the Bressan´s shear stress fracture criterion. The Bartlat´s Yld 2000-2d yield stress function was employed for the associated (4r) and the non-associated plastic stress potential (7r).

Comparisons of the predicted and experimental FLC_TD of AISI 439 steel [11] are seen in Fig. 2. The Bressan-Barlat critical shear stress criterion was calibrated with the experimental data at the plane strain condition point: FLC_o = 0.271 and m = 6. The calibrated normalized critical shear stress obtained was: for associated τ_cr/K = 0.532 and τ_cr/K = 0.335 for the and non-associate Barlat’s plastic potential case. The non-associated Barlat´s Yld 2000-2d plastic flow potential calibrated with 7 r-values provided a better fit with the experimental FLC_TD transverse curve of AISI 439 steel.

5 Conclusions

Prediction of the forming limit strain curve of AISI 439 steel was improved substantially when calibrating the non-associated Barlat´s Yld 2000-2d plastic potential with 7 r-values and using the Bressan-Barlat shear stress fracture criterion. Furthermore, Barlat´s Yld 2000-2d non-associated flow rule provides a better fit with the experimental Lankford and equal biaxial coefficients of anisotropy than the associated rule.