Bifurcation analysis in a diffusive predator–prey system with nonlinear growth rate and protection zone

Abstract

This paper is concerned with the steady-state bifurcations arising from a reaction–diffusion predator–prey system with nonlinear growth rate and a protection zone. Some sufficient conditions for the existence of positive steady-state solutions are given. Our proof is based on the local and global bifurcation theory and some a priori estimates.

1 Introduction

In this paper, we will investigate the following predator-prey model with a protection zone:

$$\begin{aligned} \left\{ \begin{array}{l} u_t=\Delta u+u(a-u)-\dfrac{b(x)uv}{1+mu}, \quad x\in \Omega , t>0, \\[2mm] v_t=\Delta v+v\left( \dfrac{\alpha }{1+\beta v}-d\right) +\dfrac{c(x)uv}{1+mu}, \quad x\in \Omega {\setminus }{\overline{\Omega }}_0, t>0, \\[2mm] \partial _\nu u=0,\quad x\in \partial \Omega , t>0, \quad \partial _\nu v=0, \quad x\in \partial (\Omega {\setminus }{\overline{\Omega }}_0), t>0, \\[2mm] u(x,0)=u_0(x)\ge 0, \quad x\in \Omega , \quad v(x,0)=v_0(x)\ge 0,\quad x\in \Omega {\setminus }{\overline{\Omega }}_0, \end{array}\right. \end{aligned}$$

(1.1)

where $\Omega$ is a bounded domain in the Euclidean space ${\mathbb {R}}^N~(N\ge 2)$ with smooth boundary $\partial \Omega$ and $\Omega _0$ is a subdomain of $\Omega$ with smooth boundary $\partial \Omega _0$. $\Delta =\sum \nolimits ^N_{i=1}\frac{\partial ^2}{\partial x_i^2}$ is the Laplace operator in ${\mathbb {R}}^N$, $\partial _\nu =\partial /\partial \nu$ and $\nu$ is the unit outer normal vector on $\partial \Omega$ or $\partial (\Omega {\setminus }{\overline{\Omega }}_0)$. The homogeneous Neumann boundary condition is assumed so that no individual crosses the habitat boundary. In addition, $a, m, d, \alpha , \beta$ are positive constants; $b(x)\in L^\infty (\Omega ), b(x)\ge 0$ in $\Omega$, $b(x)\equiv 0$ on ${\overline{\Omega }}_0$ and for any compact subset A of $\Omega {\setminus }{\overline{\Omega }}_0$, there exists $\delta _A>0$ such that

$$\begin{aligned} \delta _A\le b(x), \quad \forall x\in A; \end{aligned}$$

$c(x)\in L^\infty (\Omega {\setminus }{\overline{\Omega }}_0)$ and $0<c(x)\le b(x)$ in $\Omega {\setminus }{\overline{\Omega }}_0$.

In (1.1), the predator species v cannot enter the subregion $\Omega _0$ of the habitat $\Omega$, whereas the prey species u can enter and leave $\Omega _0$ freely. Namely, $\Omega _0$ is a predation-free zone for the prey species and such a subregion $\Omega _0$ is called a protection zone. One can think that there is a barrier along $\partial \Omega _0$ that blocks the predator but not the prey (see [1, 2] for further details). The diagrammatic sketches of b(x) and c(x) in (1.1) could be shown by Fig. 1.

Fig. 1

The diagrammatic sketches of b(x) and c(x) in (1.1)

To present the main results, we collect some basic notations and well-known results. Let $q(x)\in C({\overline{\Omega }})$, and denote $\lambda _1^D(q,O)$ and $\lambda _1^{N}(q,O)$ to be the first eigenvalues of $-\Delta +q(x)$ in O subject to the homogeneous Dirichlet boundary condition and Neumann boundary condition, respectively [3,4,5]. It is well known that $\lambda _1^{N}(q,O)$ is increasing in q, that is, $\lambda _1^{N}(q_1,O)<\lambda _1^{N}(q_2,O)$ if $q_1,q_2\in C({\overline{O}}), q_1\le q_2$ and $q_1\not \equiv q_2$ on ${\overline{O}}$. A similar assertion is also true for $\lambda _1^{D}(q,O)$. Moreover,

$\lambda _1^{N}(q,O)<\lambda _1^{D}(q,O)$ for $q\in C({\overline{O}})$,

and

$\lambda _1^{N}(q,\Omega )<\lambda _1^{N}(q,\Omega _0)$, $\lambda _1^{D}(q,\Omega )<\lambda _1^{D}(q,\Omega _0)$ with $q\in C({\overline{\Omega }})$ and $\Omega _0\subset \subset \Omega$.

For convenience, we denote $\lambda _1^D(O)=\lambda _1^D(0,O)$ and $\lambda _1^N(O)=\lambda _1^{N}(0,O)$.

It is well known that the effects of the protection zone on the dynamical behavior are significantly different from non-protection zone case [6,7,8]. Many theoretical results show that there exists a critical patch size $\Omega _0$ for the protection zone. If $\Omega _0$ is below this size, each model behaves similarly to the non-protection zone case, but every model undergoes profound changes in dynamical behavior once $\Omega _0$ is above the critical patch size, and in such a case, the endangered species is always saved from extinction.

In this paper, we study the existence of positive stationary solutions of (1.1) with a protection zone, and mainly investigate the effect of nonlinear growth rate $\left( \dfrac{\alpha }{1+\beta v}\right)$ on the existence of bifurcation of stationary positive solutions. The stationary problem associated with (1.1) is given by

$$\begin{aligned} \left\{ \begin{array}{l} \Delta u+u(a-u)-\dfrac{b(x)uv}{1+mu}=0, \quad x\in \Omega , \\[2mm] \Delta v+v\left( \dfrac{\alpha }{1+\beta v}-d\right) +\dfrac{c(x)uv}{1+mu}=0, \quad x\in \Omega {\setminus }{\overline{\Omega }}_0, \\[2mm] \partial _\nu u=0,\quad x\in \partial \Omega , \quad \partial _\nu v=0, \quad x\in \partial (\Omega {\setminus }{\overline{\Omega }}_0). \end{array}\right. \end{aligned}$$

(1.2)

For convenience, $\Omega {\setminus }{\overline{\Omega }}_0$ will be remembered as $\Omega _1$ below.

The paper is organized as follows. In Sect. 2, we will derive some a priori estimates of positive solutions to the semilinear system (1.2). In Sect. 3, we will obtain positive solutions of the semilinear system by using the local and global bifurcation theory. Finally, the bifurcation stability and global bifurcation are included in Sect. 4.

2 A priori estimates and asymptotic stability of semi-trivial solution

The following lemmas can be helpful to obtain the bounds of positive solutions to (1.2).

Lemma 2.1

(Maximum principle, [9, Proposition 2.2]) Assume that $g\in C({\overline{O}}\times {\mathbb {R}})$.

$\mathrm {(i)}$ If $w\in C^{2}(O)\cap C^{1}({\overline{O}})$ satisfies

$\Delta w(x)+g(x,w(x))\ge 0$ in O, $\partial _\nu w\le 0$ on $\partial O$,

and $w(x_{0})=\max _{{\overline{O}}} w$, then $g(x_{0},w(x_{0}))\ge 0$.

$\mathrm {(ii)}$ If $w\in C^{2}(O)\cap C^{1}({\overline{O}})$ satisfies

$\Delta w(x)+g(x,w(x))\le 0$ in O, $\partial _\nu w\ge 0$ on $\partial O$,

and $w(x_{0})=\min _{{\overline{O}}} w$, then $g(x_{0},w(x_{0}))\le 0$.

Theorem 2.2

Suppose that (u, v) is a positive solution of (1.2). Then:

• (1) If $\alpha <d$, then $\max \{a-\Vert b(x)\Vert _\infty \frac{a(a+d-\alpha )}{d-\alpha },0\}\le u\le a$ in ${\overline{\Omega }}$, $0<v\le \frac{a(a+d-\alpha )}{d-\alpha }$ in $\overline{\Omega _1}$.

• (2) If $\alpha \ge d$, then $\max \{a-\Vert b(x)\Vert _\infty \frac{\alpha -d}{d\beta },0\}\le u\le a$ in ${\overline{\Omega }}$, $\frac{\alpha -d}{d\beta }\le v$ in $\overline{\Omega _1}$. Furthermore, if $d>\frac{a\Vert c(x)\Vert _\infty }{1+am}$, then $v\le \frac{(\alpha -d)(1+am)+a\Vert c(x)\Vert _\infty }{\beta [d(1+am)-a\Vert c(x)\Vert _\infty ]}$ in $\overline{\Omega _1}$.

Proof

(1) Case $\alpha <d$. By adding two equations in (1.2), we have

$$\begin{aligned} \begin{aligned} -\Delta (u+v)&=u(a-u)+v\left( \dfrac{\alpha }{1+\beta v}-d\right) +[c(x)-b(x)]\dfrac{uv}{1+mu} \\&\le au+(\alpha -d)v=au-(d-\alpha )v \\&=(a+d-\alpha )u-(d-\alpha )(u+v) \\&\le a(a+d-\alpha )-(d-\alpha )(u+v) \end{aligned} \end{aligned}$$

By Lemma 2.1, $u+v\le \frac{a(a+d-\alpha )}{d-\alpha }$. Consequently, $v\le \frac{a(a+d-\alpha )}{d-\alpha }$. From the equation for u in (1.2), we get

$$\begin{aligned} -\Delta u=u(a-u)-\dfrac{b(x)uv}{1+mu}\ge u \left[ a-u-\Vert b(x)\Vert _\infty \frac{a(a+d-\alpha )}{d-\alpha }\right] , \end{aligned}$$

and then the maximum principle implies that $u\ge a-\Vert b(x)\Vert _\infty \frac{a(a+d-\alpha )}{d-\alpha }$.

(2) Case $\alpha \ge d$. From the equation for v in (1.2), we obtain

$$\begin{aligned} -\Delta v=v\left( \dfrac{\alpha }{1+\beta v}-d\right) +\dfrac{c(x)uv}{1+mu}\ge v\left( \dfrac{\alpha }{1+\beta v}-d\right) , \end{aligned}$$

which implies that $v\ge \frac{\alpha -d}{d\beta }$. Similarly,

$$\begin{aligned} \begin{array}{l} -\Delta u=u(a-u)-\dfrac{b(x)uv}{1+mu}\ge u(a-u-\Vert b(x)\Vert _\infty \frac{\alpha -d}{d\beta }), \\[2mm] -\Delta v=v\left( \dfrac{\alpha }{1+\beta v}-d\right) +\dfrac{c(x)uv}{1+mu}\le v\left( \dfrac{\alpha }{1+\beta v}-d+\dfrac{a\Vert c(x)\Vert _\infty }{1+am}\right) . \end{array} \end{aligned}$$

Then $u\ge a-\Vert b(x)\Vert _\infty \frac{\alpha -d}{d\beta }$, and $v\le \frac{(\alpha -d)(1+am)+a\Vert c(x)\Vert _\infty }{\beta [d(1+am)-a\Vert c(x)\Vert _\infty ]}$ if $d>\frac{a\Vert c(x)\Vert _\infty }{1+am}$. $\square$

Theorem 2.3

Suppose that (u, v) is a positive solution of (1.2). Then:

• (1) If $\alpha <d$, then $\dfrac{\alpha (d-\alpha )}{(d-\alpha )(1+a\beta )+a^2\beta }\le d \le \alpha -\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$.

• (2) If $\alpha \ge d$, then $a\ge \lambda _1^N\left( \dfrac{(\alpha -d)b(x)}{d\beta (1+am)},\Omega \right)$.

Proof

Suppose that (u, v) is a positive solution of (1.2).

(1) Case $\alpha <d$. From the equation for v in (1.2), we obtain

$$\begin{aligned} -d=\lambda _1^N\left( -\dfrac{\alpha }{1+\beta v}-\dfrac{c(x)u}{1+mu},\Omega _1\right) . \end{aligned}$$

By the monotonicity of eigenvalues,

$$\begin{aligned} \begin{aligned} -d&\le \lambda _1^N\left( -\dfrac{\alpha }{1+\beta \frac{a(a+d-\alpha )}{d-\alpha }},\Omega _1\right) \\&\le \lambda _1^N\left( -\dfrac{\alpha (d-\alpha )}{(d-\alpha )(1+a\beta )+a^2\beta },\Omega _1\right) =-\dfrac{\alpha (d-\alpha )}{(d-\alpha )(1+a\beta )+a^2\beta }, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} -d&\ge \lambda _1^N \left( -\alpha -\dfrac{c(x)u}{1+mu},\Omega _1\right) \\&\ge \lambda _1^N\left( -\alpha -\dfrac{ac(x)}{1+am},\Omega _1\right) =-\alpha +\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right) . \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \dfrac{\alpha (d-\alpha )}{(d-\alpha )(1+a\beta )+a^2\beta }\le d \le \alpha -\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right) . \end{aligned}$$

(2) Case $\alpha >d$. From the equation for v in (1.2), similar to the above, we obtain that

$$\begin{aligned} \begin{aligned} a&=\lambda _1^N \left( u+\dfrac{b(x)v}{1+mu},\Omega \right) \\&\ge \lambda _1^N\left( \dfrac{b(x)\frac{\alpha -d}{d\beta }}{1+am},\Omega \right) =\lambda _1^N\left( \dfrac{(\alpha -d)b(x)}{d\beta (1+am)},\Omega \right) . \end{aligned} \end{aligned}$$

$\square$

Remark 2.4

The results given in Theorem 2.3 lead us directly to the conclusions that:

• (1) Assume that $\alpha <d$. If $d<\dfrac{\alpha (d-\alpha )}{(d-\alpha )(1+a\beta )+a^2\beta }$ or $d>\alpha -\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$, then (1.2) has no positive solution.

• (2) Assume that $\alpha \ge d$. If $a<\lambda _1^N\left( \dfrac{(\alpha -d)b(x)}{d\beta (1+am)},\Omega \right)$, then (1.2) has no positive solution.

Now we start our analysis with a standard linearization argument. For any $\alpha >0$, (1.2) has two semi-trivial solutions: (a, 0) and $(0,\frac{\alpha -d}{d\beta })$ if $\alpha >d$. From the strong maximum principle, any non-negative solution (u, v) of (1.2) is either (0, 0), or semi-trivial, or positive.

The linearized system of (1.2) about the equilibrium point (u, v) can be characterized by the Jacobian matrix

$$\begin{aligned} J(u,v)=\left( \begin{array}{cc} \Delta +a-2u-\dfrac{b(x)v}{(1+mu)^{2}} &{} -\dfrac{b(x)u}{1+mu} \\[2mm] \dfrac{c(x)v}{(1+mu)^{2}} &{} \Delta +\dfrac{\alpha }{(1+\beta v)^{2}}-d+\dfrac{c(x)u}{1+mu} \end{array} \right) . \end{aligned}$$

At the equilibrium point (a, 0) and $(0,\frac{\alpha -d}{d\beta })$ if $\alpha >d$, the corresponding Jacobian matrix J(u, v) are

$$\begin{aligned} J(a,0)=\left( \begin{array}{cc} \Delta -a &{} -\dfrac{ab(x)}{1+am} \\[2mm] 0 &{} \Delta +\alpha -d+\dfrac{ac(x)}{1+am} \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} J(0,\frac{\alpha -d}{d\beta })=\left( \begin{array}{cc} \Delta +a-\frac{\alpha -d}{d\beta }b(x) &{} 0 \\[2mm] \frac{\alpha -d}{d\beta }c(x) &{} \Delta +\dfrac{d(d-\alpha )}{\alpha } \end{array} \right) . \end{aligned}$$

Theorem 2.5

We have the asymptotic stability results of (1.2):

• (1) The semi-trivial solution (a, 0) is locally stable when $\alpha <d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$ and unstable when $\alpha >d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$.

• (2) Assume that $\alpha >d$. The semi-trivial solution $(0, \frac{\alpha -d}{d\beta })$ is locally stable when $a<\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ and unstable when $a>\lambda _1^N\left( \frac{\alpha -d}{d\beta }b(x),\Omega \right)$.

Proof

(1) The linearized eigenvalue problem of (1.2) at (a, 0) is

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta h-ah-\dfrac{ab(x)}{1+am}k+\mu h=0, \quad x \in \Omega , &{} h=0, \quad x\in \partial \Omega , \\[2mm] \Delta k+[\alpha -d+\dfrac{ac(x)}{1+am}]k+\mu k=0, \quad x \in \Omega _1, &{} k=0, \quad x\in \partial \Omega _1, \end{array} \right. \end{aligned}$$

(2.1)

where $\mu$ is eigenvalue and (h, k) is the corresponding eigenfunction.

If $k=0$, then $h\ne 0$, and $\mu \ge a>0$. If $k\ne 0$, then

$$\begin{aligned} \mu \ge \lambda _1^N(d-\alpha -\dfrac{ac(x)}{1+am},\Omega _1)=d-\alpha +\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right) >0 \end{aligned}$$

when $\alpha <d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$. This shows that (a, 0) is locally stable when $\alpha <d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$.

When $\alpha >d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$, we assume that $\mu _0$ and $k_0$ are the principal eigenvalue and the corresponding positive eigenfunction of

$$\begin{aligned} \Delta k+ \left[ \alpha -d+\dfrac{ac(x)}{1+am}\right] k+\mu k=0, \quad x \in \Omega _1, \qquad k=0, x\in \partial \Omega _1. \end{aligned}$$

Then $\mu _0=d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am}\right) -\alpha <0$, and the following problem

$$\begin{aligned} \Delta h-ah-\dfrac{ab(x)}{1+am}k_0+\mu _0 h=0, \quad x \in \Omega , \qquad h=0, x\in \partial \Omega \end{aligned}$$

has a unique solution $h_0$ because the operator $-\Delta +a-\mu _0$ is invertible. This shows that $(\mu _0, h_0, k_0)$ satisfies (2.1), i.e. the eigenvalue problem (2.1) has a negative eigenvalue $\mu _0$ and so (a, 0) is unstable.

(2) The linearized eigenvalue problem of (1.2) at $(0,\frac{\alpha -d}{d\beta })$ is

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta h+(a-\frac{\alpha -d}{d\beta }b(x))h+\mu h=0, \quad x \in \Omega , &{} h=0, \quad x\in \partial \Omega , \\[2mm] \Delta k+\dfrac{d(d-\alpha )}{\alpha }k+\frac{\alpha -d}{d\beta }c(x)h+\mu k=0, \quad x \in \Omega _1, &{} k=0, \quad x\in \partial \Omega _1, \end{array} \right. \end{aligned}$$

(2.2)

where $\mu$ is eigenvalue and (h, k) is the corresponding eigenfunction.

If $h=0$, then $k\ne 0$, and $\mu \ge \dfrac{d(\alpha -d)}{\alpha }>0$. If $h\ne 0$, then

$$\begin{aligned} \mu \ge \lambda _1^N \left( -a+\frac{\alpha -d}{d\beta }b(x),\Omega \right) =-a+\lambda _1^N\left( \frac{\alpha -d}{d\beta }b(x),\Omega \right) >0 \end{aligned}$$

when $a<\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$. This shows that $(0,\frac{\alpha -d}{d\beta })$ is locally stable when $a<\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$.

When $a>\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$, we assume that $\mu _0$ and $h_0$ are the principal eigenvalue and the corresponding positive eigenfunction of

$$\begin{aligned} \Delta h+\left( a-\frac{\alpha -d}{d\beta }b(x)\right) h+\mu h=0, \quad x \in \Omega , \qquad h=0, \quad x\in \partial \Omega . \end{aligned}$$

Then $\mu _0=-a+\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )<0$, and the following problem

$$\begin{aligned} \Delta k+\dfrac{d(d-\alpha )}{\alpha }k+\frac{\alpha -d}{d\beta }c(x)h_0+\mu _0 k=0, \quad x \in \Omega _1, \qquad k=0, \quad x\in \partial \Omega _1 \end{aligned}$$

has a unique solution $h_0$ because of the operator $-\Delta +\frac{\alpha -d}{d\beta }-\mu _0$ is reversible. This shows that $(\mu _0, h_0, k_0)$ satisfies (2.2), i.e. the eigenvalue problem (2.2) has a negative eigenvalue $\mu _0$ and so $(0, \frac{\alpha -d}{d\beta })$ is unstable. $\square$

Remark 2.6

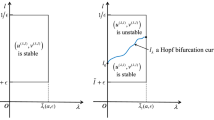
For the two curves of solutions in the space of

$$\begin{aligned} \Gamma _u=\{(\alpha ; a, 0): \alpha>0\}\quad and\quad \Gamma _v=\{(\alpha ; 0, \frac{\alpha -d}{d\beta }): \alpha >d\}, \end{aligned}$$

(2.3)

Theorem 2.5 implies that bifurcation could occur along the semi-trivial branches (2.3), if (1): $\alpha >d+\lambda _1^N\left( -\dfrac{ac(x)}{1+am},\Omega _1\right)$, or (2): $\alpha >d$ and $a>\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$.

3 Bifurcation from semi-trivial solution

In this section, we will investigate the bifurcation solutions of (1.2) by the bifurcation theory. We fix d and take $\alpha$ as the main bifurcation parameter. In order to main bifurcation parameter of (1.2) which bifurcate from semi-trivial solution (a, 0) and $(0,\frac{\alpha -d}{d\beta })$ with $\alpha \ge d$. First, we set up the abstract framework for our bifurcation analysis. For $p>1$, we define

$$\begin{aligned} X=W^{2,p}(\Omega )\times W^{2,p}(\Omega _1)\doteq X_1\times X_2, \quad Y=L^p(\Omega )\times L^p(\Omega _1)\doteq Y_1\times Y_2, \end{aligned}$$

where $W^{2,p}(O)=\{w\in W^{2,p}(O): \partial _\nu w=0\ \text {on}\ \partial O\}$.

For a given operator L, we denote the kernel and range of L with ${\mathcal {N}}(L)$ and ${\mathcal {R}}(L)$, respectively.

Theorem 3.1

We have the results:

• (1) If $d>-\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)$, then

  • (a) $\alpha$ is a bifurcation point where a continuum $\Gamma _1$ of positive solutions to (1.2) bifurcates from $\Gamma _u$ at $({\overline{\alpha }}; a,0)$ if and only if $\alpha =d+\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)\doteq {\overline{\alpha }}$.

  • (b) all positive solutions of (1.2) near $({\overline{\alpha }}; a,0)\in {\mathbb {R}}\times X$ can be expressed as $({\overline{\alpha }}(s); u(s),v(s))$ with $s\in (0,\delta )$, where $({\overline{\alpha }}(s);u(s),v(s))$ is a smooth function with respect to s and satisfies $({\overline{\alpha }}(s);u(s),v(s))=({\overline{\alpha }};a,0)$ and the bifurcation is supercritical.

• (2) If $\alpha >d$ and $\lambda _1^N\left( \dfrac{(\alpha -d)b(x)}{d\beta (1+am)},\Omega \right) \le a<\lambda _1^D(\Omega _0)$, then

  • (a) there exists a unique ${\widehat{\alpha }}(a)$ such that $a=\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$. Moreover, ${\widehat{\alpha }}(a)\rightarrow d$ as $a\rightarrow 0^+$ and ${\widehat{\alpha }}(a)\rightarrow \infty$ as $a\rightarrow \lambda _1^D(\Omega _0)^-$.

  • (b) $\alpha$ is a bifurcation point where an continuum $\Gamma _2$ of positive solutions to (1.2) bifurcates from $\Gamma _v$ at $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })$ if and only if $\alpha ={\widehat{\alpha }}$.

  • (c) all positive solutions of (1.2) near $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })\in {\mathbb {R}}\times X$ can be expressed as $({\widehat{\alpha }}(s); u(s),v(s))$ with $s\in (0,\delta )$, where $({\widehat{\alpha }}(s);u(s),v(s))$ is a smooth function with respect to s and satisfies $({\overline{\alpha }}(s);u(s),v(s))=({\widehat{\alpha }};0, \frac{{\widehat{\alpha }}-d}{d\beta })$ and the bifurcation is supercritical (subcritical), if $m_0>1$ $(<1)$, where

    $$\begin{aligned} m_0=\frac{\int _{\Omega }\frac{m({\widehat{\alpha }}-d)}{d\beta }b(x)\varphi _1^{3} dx-\int _{\Omega }b(x)\varphi _1^2\varphi _2 dx}{\int _{\Omega }\varphi _1^{3}dx}. \end{aligned}$$

• (3) If $a\ge \lambda _1^D(\Omega _0)$, then for any $\alpha >d$, $a>\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ and no bifurcation of positive solutions can occur along $\Gamma _v$.

Proof

(1) Take the variables $w=a-u$ and define $F(\alpha ; w,v): {\mathbb {R}}\times X\rightarrow Y$ by

$$\begin{aligned} F(\alpha ; w,v)=\left( \begin{array}{c} \Delta w+w^{2}-aw+\dfrac{b(x)(a-w)v}{1+m(a-w)} \\[2mm] \Delta v+v\left( \dfrac{\alpha }{1+\beta v}-d\right) +\dfrac{c(x)(a-w)v}{1+m(a-w)} \end{array} \right) . \end{aligned}$$

By using a simple calculation, we obtain

$$\begin{aligned} F_{(w,v)}(\alpha ; 0,0)[h,k]=\left( \begin{array}{c} \Delta h-ah+\dfrac{ab(x)}{1+am}k \\[2mm] \Delta k+[\alpha -d+\dfrac{ac(x)}{1+am}]k \end{array} \right) \\ F_{\alpha (w,v)}(\alpha ; 0,0)[h,k]=\left( \begin{array}{c} 0 \\ k \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} F_{(w,v)(w,v)}(\alpha ; 0,0)[h,k]^{2}=\left( \begin{array}{c} 2h^{2}-\frac{2b(x)}{(1+am)^2}hk \\ -\frac{2c(x)}{(1+am)^2}hk-2\alpha \beta k^{2} \end{array} \right) , \end{aligned}$$

Let $\alpha =d+\lambda _1^N(-\dfrac{ac(x)}{1+am},\Omega _1)\doteq {\overline{\alpha }}$. Then $F_{(w,v)}(\alpha ; 0,0)[h,k]=0$ has a solution with $h>0$. Thus ${\overline{\alpha }}$ is the only bifurcation point along $\Gamma _u$ where positive solutions of (1.2) bifurcates.

It is easy to verify that the kernel ${\mathcal {N}}(F_{(w,v)}({\overline{\alpha }}; 0,0))=span\{(\varphi _1,\varphi _2)\}$, where $(\varphi _1,\varphi _2)\ne (0,0)$ satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \Delta \varphi _1-a\varphi _1+\dfrac{ab(x)}{1+am}\varphi _2=0, \quad x\in \Omega , \\[2mm] \Delta \varphi _2+\left[ {\overline{\alpha }}-d+\dfrac{ac(x)}{1+am}\right] \varphi _2=0, \quad x\in \Omega _1, \\[2mm] \partial _\nu \varphi _1=0, \quad x\in \partial \Omega , \quad \partial _\nu \varphi _2=0, \quad x\in \partial \Omega _1. \end{array}\right. \end{aligned}$$

(3.1)

We can choose $\varphi _2>0$ as the corresponding positive eigenfunction of $\lambda _1^N(d-\dfrac{ac(x)}{1+am},\Omega _1)$ with $\int _{\Omega _1} \varphi _2^2dx=1$, and then $\varphi _1=(-\Delta +a)^{-1}\left( \dfrac{ab(x)}{1+am}\varphi _2\right) >0$.

It is easy to check that the range

$$\begin{aligned} {\mathcal {R}}(F_{(w,v)}({\overline{\alpha }};0,0))=\left\{ (f,g)^{T}\in Y: \int _{\Omega _1}g(x)\varphi _2dx=0 \right\} , \end{aligned}$$

and

$$\begin{aligned} F_{\alpha (w,v)}({\overline{\alpha }}; 0,0)[\varphi _1,\varphi _2]=(0,\varphi _2)^{T}\not \in {\mathcal {R}}(F_{(w,v)}({\overline{\alpha }};0,0)) \end{aligned}$$

since $\int _{\Omega _1} \varphi _2^2dx=1>0$. By applying the results of [10] or [11], the set of solutions to (1.2) near $({\overline{\alpha }}; a,0)$ is a smooth curve

$$\begin{aligned} \Gamma _1=\{({\overline{\alpha }}(s); a-w(s),v(s)): s\in [0,\delta )\}, \end{aligned}$$

with $\delta >0$ small, ${\overline{\alpha }}(0)=d+\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1), w(s)=s\varphi _1+o(|s|), v(s)=s\varphi _2+o(|s|)$. By [12, Corollary 2.3],

$$\begin{aligned} {\overline{\alpha }}'(0)=-\frac{\langle l,F_{(w,v)(w,v)}({\overline{\alpha }};0,0)[\varphi _1,\varphi _2]^{2}\rangle }{2\langle l,F_{\alpha (w,v)}({\overline{\alpha }};0,0)[\varphi _1,\varphi _2]\rangle }=\int _{\Omega _1}\left( \frac{c(x)\varphi _1\varphi _2^2}{(1+am)^2}+\alpha \beta \varphi _2^3\right) dx>0, \end{aligned}$$

where l is a linear functional on $Y^{2}$ defined as $\langle l,[f,g]\rangle =\int _{\Omega _1}g(x)\varphi _2dx$. This yields that the bifurcation $\Gamma _{u}$ at $({\widetilde{\alpha }};0,0)$ is supercritical.

(2) We take the variables $v=\frac{\alpha -d}{d\beta }+w$ and define $G(\alpha ; u,w): {\mathbb {R}}\times X\rightarrow Y$ by

$$\begin{aligned} G(\alpha ; u,w)=\left( \begin{array}{c} \Delta u+u(a-u)-\dfrac{b(x)u(\frac{\alpha -d}{d\beta }+w)}{1+mu} \\[2mm] \Delta w+(\frac{\alpha -d}{d\beta }+w)\left( \dfrac{\alpha }{1+\beta (\frac{\alpha -d}{d\beta }+w)}-d\right) +\dfrac{c(x)u(\frac{\alpha -d}{d\beta }+w)}{1+mu} \end{array} \right) . \end{aligned}$$

By using a simple calculation, we obtain

$$\begin{aligned} G_{(u,v)}(\alpha ; 0,0)[h,k]=\left( \begin{array}{c} \Delta h+ah-\frac{\alpha -d}{d\beta }b(x)h \\[2mm] \Delta k+\dfrac{d(d-\alpha )}{\alpha }k+\frac{\alpha -d}{d\beta }c(x)h \end{array} \right) \\ G_{\alpha (u,v)}(\alpha ; 0,0)[h,k]=\left( \begin{array}{c} -\frac{b(x)}{d\beta }h \\ \frac{c(x)}{d\beta }h+{\overline{C}}k \end{array} \right) , \end{aligned}$$

where ${\overline{C}}=\frac{d^2(\beta -1)(\beta ^2-2\beta +2)({\widehat{\alpha }}-d)-d\alpha ^2\beta ^3}{{\widehat{\alpha }}^3\beta ^3}$, and

$$\begin{aligned} G_{(u,v)(u,v)}(\alpha ; 0,0)[h,k]^{2}=\left( \begin{array}{c} (-2+\frac{2m(\alpha -d)}{d\beta }b(x))h^{2}-2b(x)hk \\ -\frac{2m(\alpha -d)}{d\beta }c(x)h^{2}+2c(x)hk-\frac{2\beta d^3}{\alpha ^3} k^{2} \end{array} \right) . \end{aligned}$$

Let $a=\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$. Then $G_{(u,w)}(\alpha ; 0,0)[h,k]=0$ has a solution with $h>0$.

Let $\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ be the principal eigenvalue of

$$\begin{aligned} -\Delta u+\frac{\alpha -d}{d\beta }b(x)u=\lambda u, \quad x\in \Omega , \qquad \partial _\nu u=0,\quad x\in \partial \Omega . \end{aligned}$$

(3.2)

By the proof of Theorem 2.1 in [1], we obtain that for any $\alpha >d$, $\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ is strictly increasing respect to $\alpha$, $\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )<\lambda _1^D(\Omega _0)$, and

$$\begin{aligned} \lim _{\alpha \rightarrow \infty }\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )=\lambda _1^D(\Omega _0). \end{aligned}$$

Now if $a\ge \lambda _1^D(\Omega _0)$, then for any $\alpha \ge d$, $a>\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$. Hence, by the analyses above, no bifurcation of positive solutions can occur along $\Gamma _v$.

If $a<\lambda _1^D(\Omega _0)$, then there exits a unique ${\widehat{\alpha }}(a)$ such that $a=\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ due to the continuity and monotonicity of $\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$. We easily see that ${\widehat{\alpha }}(a)\rightarrow d$ as a decreases to 0, and ${\widehat{\alpha }}(a)\rightarrow \infty$ as a increases to $\lambda _1^D(\Omega _0)$.

At $(\alpha ; u,w)=({\widehat{\alpha }}; 0,0)$, ${\mathcal {N}}(G_{(w,v)}({\widehat{\alpha }}; 0,0))=span\{(\phi _1,\phi _2)\}$. We can choose $\phi _1>0$ with $\int _{\Omega } \phi _1^2dx=1$ and $\phi _2=(-\Delta +\frac{d(\alpha -d)}{\alpha })^{-1}(\frac{\alpha -d}{d\beta }c(x)\phi _1)>0$. Then

$$\begin{aligned} {\mathcal {R}}(G_{(u,w)}({\widehat{\alpha }};0,0))=\{(f,g)^{T}\in Y: \int _{\Omega }f(x)\phi _1dx=0\}, \end{aligned}$$

and

$$\begin{aligned} G_{\alpha (u,w)}({\widehat{\alpha }}; 0,0)[\phi _1,\phi _2]=\left( -\frac{b(x)}{d\beta }\phi _1,\frac{c(x)}{d\beta }\phi _1+{\overline{C}}\phi _2\right) ^{T}\not \in {\mathcal {R}}(F_{(w,v)}({\widehat{\alpha }};0,0)) \end{aligned}$$

since $-\frac{1}{d\beta }\int _{\Omega } b(x)\phi _1^2dx\ne 0$.

By applying the results of [10] or [11], the set of solutions to (1.2) near $({\widehat{\alpha }}; 0,\frac{{\widehat{\alpha }}-d}{d\beta })$ is a smooth curve

$$\begin{aligned} \Gamma _2=\{({\widehat{\alpha }}(s); u(s),\frac{{\widehat{\alpha }}-d}{d\beta }+w(s)): s\in [0,\delta )\}, \end{aligned}$$

with $\delta >0$ small, ${\widehat{\alpha }}(0)={\widehat{\alpha }}, u(s)=s\phi _1+o(|s|), w(s)=s\phi _2+o(|s|)$. By [12, Corollary 2.3],

$$\begin{aligned} \begin{aligned} {\widehat{\alpha }}'(0)&=-\frac{\langle l,G_{(u,w)(u,w)}({\overline{\alpha }};0,0)[\phi _1,\phi _2]^{2}\rangle }{2\langle l,G_{\alpha (u,w)}({\overline{\alpha }};0,0)[\phi _1,\phi _2]\rangle } \\&=\frac{\int _{\Omega }(\frac{m({\widehat{\alpha }}-d)}{d\beta }b(x)-1)\phi _1^{3} dx-\int _{\Omega }b(x)\phi _1^2\phi _2 dx}{\frac{1}{d\beta }\int _{\Omega } b(x)\phi _1^2dx}, \end{aligned} \end{aligned}$$

where l is a linear functional on $Y^{2}$ defined as $\langle l,[f,g]\rangle =\int _{\Omega }f(x)\phi _1dx$. $\square$

4 Bifurcation stability and global bifurcation

Theorem 4.1

Recall ${\overline{\alpha }}, {\widehat{\alpha }}, (\varphi _1,\varphi _2)$ and $(\phi _1,\phi _2)$ in Theorem 3.1.

• (1) Suppose that $d>-\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)$. If

  $$\begin{aligned} \dfrac{1}{(1+am)^2}\int _{\Omega _1}c(x)\varphi _2^3 dx<{\overline{\alpha }}\beta \int _{\Omega _1}\varphi _1\varphi _2^2dx, \end{aligned}$$

  then the local bifurcation coexistence state (u(s), v(s)) bifurcating from $({\overline{\alpha }}; a, 0)$ is linearly stable.

• (2) If $\alpha >d$, then the local bifurcation coexistence state (u(s), v(s)) bifurcating from $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })$ is nondegenerate and linearly stable.

Proof

For convenience, we use the notation ${\overline{\alpha }}(s)=\alpha ,(u(s),v(s))=(u,v)$ in Theorem 3.1. The linearized problem of (1.2) at (u, v) can be written as

$$\begin{aligned} {\mathcal {L}}(s)(h,k)=\gamma (s)(h,k) \end{aligned}$$

(4.1)

where

$$\begin{aligned} {\mathcal {L}}(s)=\left( \begin{array}{cc} \Delta +a-2u-\dfrac{b(x)v}{(1+mu)^{2}} &{} -\dfrac{b(x)u}{1+mu} \\[2mm] \dfrac{c(x)v}{(1+mu)^{2}} &{} \Delta +\dfrac{\alpha }{(1+\beta v)^{2}}-d+\dfrac{c(x)u}{1+mu} \end{array}\right) . \end{aligned}$$

It easy to see that, as $s\rightarrow 0$,

$$\begin{aligned} {\mathcal {L}}(s)\rightarrow {\mathcal {L}}_0\doteq \left( \begin{array}{cc} \Delta -a &{} -\dfrac{ab(x)}{1+am} \\[2mm] 0 &{} \Delta +{\overline{\alpha }}-d+\dfrac{ac(x)}{1+am} \end{array}\right) . \end{aligned}$$

By the proof in Theorem 3.1, we know that 0 is the principal eigenvalue of ${\mathcal {L}}_0$ with the corresponding eigenfunction $(\varphi _1,\varphi _2)$, where $\varphi _1$ and $\varphi _2$ are defined in Theorem 3.1.

By the perturbation theory of linear operators [13], we know that, when s is sufficiently small, ${\mathcal {L}}(s)$ has a unique eigenvalue $\gamma (s)$ satisfying $\lim _{s\rightarrow 0}\gamma (s)=0$ and all the other eigenvalues of ${\mathcal {L}}(s)$ have negative real parts and are apart from 0. Now we determine the sign of $Re(\gamma (s))$ as $s>0$ is sufficiently small. Let (h, k) be the corresponding eigenfunction to $\gamma (s)$ such that $(h,k)\rightarrow (\varphi _1,\varphi _2)$.

Multiplying the second equation of (4.1) by v and integrating over $\Omega _1$, we get

$$\begin{aligned} \int _{\Omega _1}v\Delta k+\dfrac{\alpha v}{(1+\beta v)^{2}}k-dvk+\dfrac{c(x)uv}{1+mu}k+\dfrac{c(x)v^2}{(1+mu)^{2}}h dx=\int _{\Omega _1}\gamma (s)vk dx.\nonumber \\ \end{aligned}$$

(4.2)

Multiplying the second equation of (1.2) by k integrating over $\Omega _1$, we have

$$\begin{aligned} \int _{\Omega _1}k\Delta v+v\left( \dfrac{\alpha }{1+\beta v}-d\right) k+\dfrac{c(x)uv}{1+mu}k dx=0. \end{aligned}$$

(4.3)

The fact combined with (4.2) and (4.3) to yields

$$\begin{aligned} \gamma (s)\int _{\Omega _1}vk dx=\int _{\Omega _1}\dfrac{c(x)v^2}{(1+mu)^{2}}h-\dfrac{\alpha \beta v^2}{(1+\beta v)^2}k dx. \end{aligned}$$

(4.4)

Note that ${\overline{\alpha }}(0)=d+\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)\doteq {\overline{\alpha }}, w(s)=s\varphi _1+o(|s|), v(s)=s\varphi _2+o(|s|)$. Dividing by $s^2$ and letting $s\rightarrow 0^+$ in (4.4), it is deduced that

$$\begin{aligned} \lim _{s\rightarrow 0^{+}}\frac{\gamma (s)}{s}=\dfrac{1}{(1+am)^2}\int _{\Omega _1}c(x)\varphi _2^3 dx-{\overline{\alpha }}\beta \int _{\Omega _1}\varphi _1\varphi _2^2dx, \end{aligned}$$

which implies that the bifurcation coexistence state (u(s), v(s)) $({\overline{\alpha }}; a, 0)$ is linearly stable, if

$$\begin{aligned} \dfrac{1}{(1+am)^2}\int _{\Omega _1}c(x)\varphi _2^3 dx<{\overline{\alpha }}\beta \int _{\Omega _1}\varphi _1\varphi _2^2dx. \end{aligned}$$

(2) Analogously, multiplying the first equation of (4.1) by u and the first equation of (1.2) by h, integrating over $\Omega$, we get

$$\begin{aligned} \int _{\Omega }u\Delta h+auh-2u^2h-\dfrac{b(x)uv}{(1+mu)^{2}}h-\dfrac{b(x)u^2}{1+mu}k dx=\int _{\Omega }\gamma (s)uh dx, \\ \int _{\Omega }h\Delta u+u(a-u)h-\dfrac{b(x)uv}{1+mu}h dx=0. \end{aligned}$$

Then we have

$$\begin{aligned} \lim _{s\rightarrow 0^{+}}\frac{\gamma (s)}{s}=-\int _{\Omega }b(x)\phi _1^2\phi _2 dx-\int _{\Omega }\phi _1^3dx<0. \end{aligned}$$

This implies that then the local bifurcation coexistence state (u(s), v(s)) bifurcating from $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })$ is nondegenerate and linearly stable. The proof is completed. $\square$

Next, we will investigate the global bifurcation of (1.2). We fix the parameters $a>0$ and $d>\frac{a\Vert c(x)\Vert _\infty }{1+am}$ (See theorem 2.2) and take $\alpha$ as the main bifurcation parameter. By the unilateral global bifurcation theorem developed by L$\mathrm {\acute{o}}$pez-G$\mathrm {\acute{o}}$mez, one can see [11] or [14] for the details, we study the global bifurcation at $({\overline{\alpha }};a,0)$.

Let $P_O=\{w\in W^{2,p}(O): w>0, x\in {\overline{O}}\}$. Then $P^{2}=P_\Omega \times P_{\Omega _1}$ is the nature positive cone in X. From the proof of Theorem 3.1, it follows that all the conditions in [11, Theorem 6.4.3] hold. This yields that there exists a component ${\mathcal {C}}^{+}\supset \Gamma _u$ of solution to (1.2) bifurcating at $({\overline{\alpha }};a,0)$ and ${\mathcal {C}}^{+}$ satisfies one of the following alternatives:

(i) ${\mathcal {C}}^{+}$ is unbounded in ${\mathbb {R}}\times X$;

(ii) There exists a real number ${\widetilde{\alpha }}\ne {\overline{\alpha }}$, such that $({\widetilde{\alpha }};a,0)\in {\mathcal {C}}^{+}$;

(iii) ${\mathcal {C}}^{+}$ contains a point $(\alpha ;u,v)\in \Gamma _v$ or $\in \Gamma _0=\{(\alpha ; 0, 0): \alpha \in R\}$, such that $(\alpha ;u,v)\in {\mathcal {C}}^{+}$.

By Theorems 2.2 and 2.3, the alternative (i) do not occur. By Theorem 3.1 (1)(a), i.e., $\alpha$ is a bifurcation point where an continuum $\Gamma _1$ of positive solutions to (1.2) bifurcates from $\Gamma _u$ at $({\overline{\alpha }}; a,0)$ if and only if $\alpha ={\overline{\alpha }}$, we know that the alternative (ii) don’t occur. So, the alternative (iii) must occur. Now, we claim that ${\mathcal {C}}^{+}$ ends at some point $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })$ on $\Gamma _v$ for some ${\widehat{\alpha }}>d$.

In fact, we assume on the contrary that ${\mathcal {C}}^{+}$ ends at some point $(\alpha ; 0, 0)$. Let $u(s)=s\psi _1(s)+o(s)$ and $v(s)=s\psi _2(s)+o(s)$ for $0<s\ll 1$, then $\lim _{s\rightarrow 0^+}u(s)/s=\psi _1$, $\lim _{s\rightarrow 0^+}u(s)/s=\psi _2$, where $\psi _1$ and $\psi _2$ are the positive functions in $\Omega$ and $\Omega _1$ respectively. By dividing the first equation of (1.2) by s and letting $s\rightarrow 0^+$, we obtain that

$$\begin{aligned} \Delta \psi _1+a\psi _1=0, x\in \Omega , \qquad \partial _\nu \psi _1=0, x\in \partial \Omega . \end{aligned}$$

(4.5)

Thus, we get $a=0$, which contradicts $a>0$.

Combined the arguments above with the local bifurcation results (Theorem 3.1), we obtain the following theorem.

Theorem 4.2

Suppose that $0<a<\lambda _1^D(\Omega _0)$ and $d>\frac{a\Vert c(x)\Vert _\infty }{1+am}$ be fixed. Then there exists a continuum ${\mathcal {C}}^{+}$ of the positive solutions connecting $({\overline{\alpha }}; a, 0)$ to $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })$ with ${\widehat{\alpha }}>d$ and satisfying

$$\begin{aligned} Proj_\alpha {\mathcal {C}}^{+}=({\overline{\alpha }},{\widehat{\alpha }}), \end{aligned}$$

which implies that (1.2) possesses at least a positive solution for any $\alpha \in ({\overline{\alpha }},{\widehat{\alpha }})$.

Remark 4.3

Theorem 3.1) shows that (1) if $d>\frac{a\Vert c(x)\Vert _\infty }{1+am}$, then there exist bifurcation of positive solutions along $\Gamma _u$; (2) if $a>\lambda _1^D(\Omega _0)$, then there exists no bifurcation of positive solutions along $\Gamma _v$.

Remark 4.4

For fixed $a>0$, the term $a>\lambda _1^D(\Omega _0)$ in Remark 4.3 can be interpreted as the fact that the protection zone $\Omega _0$ is large. In addition, if $d>\frac{a\Vert c(x)\Vert _\infty }{1+am}$, then by the same proof process similar to theorem 4.2, there exists a continuum ${\mathcal {C}}^{+}$ of the positive solutions emanating from $({\overline{\alpha }}; a, 0)$ and satisfying $Proj_\alpha {\mathcal {C}}^{+}=({\overline{\alpha }},+\infty )$.

Remark 4.5

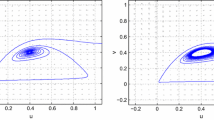
(Numerical example) Letting $\Omega =(0,5\pi )$, we consider the effect of degenerate on the positive solution to (1.1), i.e., the following two cases (See Figure 2):

(1) Functions b(x) and c(x) are independent of x: $b(x)\equiv 0.05$ and $c(x)\equiv 0.03$;

(2) Functions b(x) and c(x) are dependent of x:

$b(x)=\left\{ \begin{array}{ll} 0.05 &{} \pi \le x\le 4\pi \\ 0 &{} otherwise \end{array}\right.$ and $c(x)=\left\{ \begin{array}{ll} 0.03 &{} \pi \le x\le 4\pi \\ 0 &{} otherwise \end{array}\right.$.

Fig. 2

Numerical simulation of the spatio-temporal positive solutions to (1.1) with $a=1.25, m=1, \alpha =0.85, \beta =1$ and $d=0.5$, where the first and second column represent u(x, t) and v(x, t), respectively. a–c–e case 1, the unique positive spatially homogeneous equilibrium (1.2330, 0.7583) is locally asymptotically stable; b–d–f case 2, there exists a spatially heterogeneous positive steady state solution

5 Discussions

In this paper we propose a reaction–diffusion predator–prey model with a protection zone for the prey and nonlinear growth rate for the predator. It is shown that the protection zone will affect the existence of positive steady-state solutions or steady-state bifurcations form (1.1). By Remark 2.4 and Theorem 3.1, the existence and non-existence results are summarized below:

• (A1) Assume that $\alpha <d$. If $d<\dfrac{\alpha (d-\alpha )}{(d-\alpha )(1+a\beta )+a^2\beta }$ or $d>\alpha -\lambda _1^N(-\dfrac{ac(x)}{1+am},\Omega _1)$, then (1.2) has no positive solution.

• (A2) Assume that $\alpha >d$ and $a\ge \min \{\lambda _1^D(\Omega _0),\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )\}$. Then there is no bifurcation of positive solutions to (1.2) can occur along $\Gamma _v$.

• (A3) If $d>-\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)$, then there is a continuum $\Gamma _1$ of positive solutions to (1.2) bifurcates from $\Gamma _u$ at $({\overline{\alpha }}; a,0)$ where $\alpha =d+\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)\doteq {\overline{\alpha }}$.

• (A4) If $\alpha >d$ and $\lambda _1^N(\dfrac{(\alpha -d)b(x)}{d\beta (1+am)},\Omega )\le a<\lambda _1^D(\Omega _0)$, then there a continuum $\Gamma _2$ of positive solutions to (1.2) bifurcates from $\Gamma _v$ at $({\widehat{\alpha }}; 0, \frac{{\widehat{\alpha }}-d}{d\beta })$, where $\alpha ={\widehat{\alpha }}$ and which is a unique ${\widehat{\alpha }}(a)$ such that $a=\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$. Moreover, ${\widehat{\alpha }}(a)\rightarrow d$ as $a\rightarrow 0^+$ and ${\widehat{\alpha }}(a)\rightarrow \infty$ as $a\rightarrow \lambda _1^D(\Omega _0)^-$.

Note that $b(x)\in L^\infty (\Omega ), b(x)\ge 0$ in $\Omega$, $b(x)\equiv 0$ on ${\overline{\Omega }}_0$ and for any compact subset A of $\Omega {\setminus }{\overline{\Omega }}_0$, there exists $\delta _A>0$ such that $\delta _A\le b(x), \forall x\in A;$ $c(x)\in L^\infty (\Omega {\setminus }{\overline{\Omega }}_0)$ and $0<c(x)\le b(x)$ in $\Omega {\setminus }{\overline{\Omega }}_0$. Now, let $b(x)=c(x)=1$ in $\Omega {\setminus }{\overline{\Omega }}_0$ in order to better analyze the affect of protection zone on the dynamics of (1.1).

Since $-\lambda _1^N(-\dfrac{ac(x)}{1+am},\Omega _1)$ is increasing in $\Omega _0$, $\lambda _1^D(\Omega _0)$ and $\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ are decreasing in $\Omega _0$, (A1) and (A2) imply that the smaller the size of protection zone $\Omega _0$, two populations u and v are more likely to coexist. This is also in line with the original intention of constructing ecological nature reserve in reality.

Let ${\overline{\alpha }}=d+\lambda _1^N(-\frac{ac(x)}{1+am},\Omega _1)$ in (A3). Define the unique ${\widehat{\alpha }}(a)$ in (A4) such that $a=\lambda _1^N(\frac{\alpha -d}{d\beta }b(x),\Omega )$ if $\alpha >d$ and $\lambda _1^N(\dfrac{(\alpha -d)b(x)}{d\beta (1+am)},\Omega )\le a<\lambda _1^D(\Omega _0)$. (A3) and (A4) show that there is a circular domain $\Omega _0$, at which there is a continuum $\Gamma _1$ or $\Gamma _2$ of positive solutions to (1.2) bifurcates from $\Gamma _u$ or $\Gamma _v$.

Hence a recommendation for the people setting up the protection zone is to have a circular region with as large as possible area as the protect [15].