Computation of certain topological indices for 2D nanotubes

Abstract

Graph theory has various applications in chemistry and molecular structure research, and its importance has been growing continuously. In molecular graphs, points represent the atoms, and lines represent the chemical bonds between atoms. This article is about to show the precise evaluation for topological descriptors based on the degree sum of the neighbors of end vertices for some molecular structures. We derive for Sanskruti index, Neighborhood inverse sum index, Neighborhood Harmonic index, Fifth $ND_e$ index, and Neighborhood second modified Zagreb index for two-dimensional lattice structure of certain Nanotube and Nanotorus.

1 Introduction

Mathematical chemistry is the study of physical chemistry in that we use mathematical methods to analyze and estimate the molecular structure of a chemical compound. Chemical graph theory is a branch of chemistry that deals with graphs in which graph theory methods have been using to convert chemical phenomena into mathematical models. A topological index is a numerical value for chemical composition, and it correlates chemical structure with biological reaction or chemical reactivity. It is one of some chemical and physical characteristics. Molecular descriptors have been developed from a molecular graph for determining numbers to molecular graphs and then by using those numbers to describe the molecule [12].

A topological descriptor is a form of a molecular descriptor. Quantitative structure-property (QSPR) and structure-activity (QSAR) studies include topological descriptors. A nanostructure is a structure that lies halfway among molecular structures and microscopic in terms of dimension. It is a substance made possible by molecular engineering. It refers to something less than 100 nanometers in physical sizes, such as atom clusters to dimensional layers. Carbon nanotubes (CNTs) [19, 22] are cylindrical carbon allotropes.

Recently Sanskruti index S(G) is proposed by S.M. Hosamani [7, 15, 20] and it is defined by

$$\begin{aligned} S(G)=\sum \limits _{uv \in E(G)} \bigg (\frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)-2}\bigg )^3 \end{aligned}$$

where $\delta _G(u) = \sum _{u' \in N(u)}d(u'), N(u)=\{u':uu' \in E(G)\}$ and the same goes for $\delta _G(v)$.

The Neighborhood inverse sum index NI(G), Neighborhood Harmonic index NH(G) and Neighborhood second modified Zagreb index $M_2^{nm}$[15, 16, 23] is referred to as follows

$$\begin{aligned} NI(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)}\\ NH(G)&=\sum \limits _{uv \in E(G)} \frac{2}{\delta _G(u)+\delta _G(v)}\\ M_2^{nm}(G)&=\sum \limits _{uv \in E(G)} \frac{1}{\delta _G(u)\delta _G(v)} \end{aligned}$$

where $\delta _G(u) = \sum _{uv \in E(G)}d_G(v)$ and $\delta _G(v) = \sum _{uv \in E(G)}d_G(u)$.

The Fifth $ND_e$ index $ND_5$ [15, 17] is defined as

$$\begin{aligned} ND_5(G)=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)^2+\delta _G(v)^2}{\delta _G(u)\delta _G(v)} \end{aligned}$$

where $\delta _G(u) = \sum _{uv \in E(G)}d_G(v)$ and $\delta _G(v) = \sum _{uv \in E(G)}d_G(u)$.

2 Applications of nanostructure

Graph theory has been commonly used to investigate the chemical and physical properties of materials over the last few decades. Chemical graph theory was proposed as a result of the growing interest in this area and following that, numerous topological indices were investigated and described. Chemical graph theory was also used to study nanotechnology, which is a mixture of nanoscience, mathematics, and chemistry. Quantitative structure-property relationship (QSPR) and Quantitative structure-activity relationship (QSAR) are two of these relationships that are studied to estimate nanostructure properties and biological activities. Sanskruti, Neighborhood inverse sum, Neighborhood Harmonic, Fifth $ND_e$, and Neighborhood second modified Zagreb index are used to estimate nanostructure bioactivity in the study of QSAR and QSPR [2, 5, 8, 11].

3 The $HAC_5C_7[p,q]$ nanotube

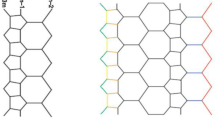
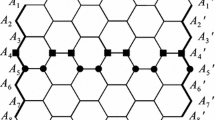
A trivalent decoration has been made by combining $C_5$ and $C_7$ and is known as a $C_5C_7$ net. It has been using to mask both a torus and a tube. As a $C_5C_7$ net, the $HAC_5C_7[p,q]$ nanotube can be studied, and Fig. 1a shows an illustration. In 2007, Iranmanesh and Khormali calculated the vertex-Szeged index of $HAC_5C_7$ nanotube [10]. The two-dimension lattice of $HAC_5C_7$ has been explained consistently in [14]. In the entire lattice, the number of heptagons and periods has been represented by p and q in a row see [13]. In $HAC_5C_7$, there are $8pq + p$ vertices and $12pq - p$ edges, respectively [21]. The three rows of $HAC_5C_7$ is said to be $m^{th}$ period, and as shown in Fig. 1b.

Fig. 1

$HAC_5C_7[p,q]$ nanotube

4 Some topological indices of $HAC_5C_7 [p,q]$ nanotube, $(p,q > 1)$

The general result is determined for $HAC_5C_7[p,q]$ nanotube in this segment by above mentioned topological indices. In addition to these indices, we present a visual analogy as well as their utilization (Fig. 2).

Theorem 1

Let G be the graph of $HAC_5C_7[p,q]$ nanotube. Then,

• 1. $S(G)=1556.956pq - 520.549p$

• 2. $NI(G)=54pq-10.773p$

• 3. $NH(G)=1.333pq+0.079p$

• 4. $ND_5(G)=24pq-1.694p$

• 5. $M_2^{nm}(G)=0.148pq+0.037p$

Proof

Consider the graph of $HAC_5C_7$ is represented by G. The cardinality of vertex set is $8pq+p$ and the edge set is $12pq-p$ for the graph G. According to the degrees of the vertices, the vertices are divide into two groups. The collection of vertices of degree i is designated by the symbol $V_i$. For G, we have $\vert V_2 \vert = 2p + 2$, $\vert V_3 \vert = 8pq-p-2$. The edge set is divide into the following sections corresponding to their sum of the degrees of the neighborhood, which are

$$\begin{aligned} E_{1}&=\{st \in E(SR_n)\mid d_u=9~ and ~d_v=9\}\\ E_{2}&=\{st \in E(SR_n)\mid d_u=9 ~and ~d_v=8\}\\ E_{3}&=\{st \in E(SR_n)\mid d_u=9 ~and ~d_v=7\}\\ E_{4}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=8\}\\ E_{5}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=6\}\\ E_{6}&=\{st \in E(SR_n)\mid d_u=7 ~and ~d_v=6\} \end{aligned}$$

From the graph G, we can see that $\mid E_1 \mid$ = 12pq - 9p, $\mid E_2 \mid$ = 2p, $\mid E_3 \mid$ = p, $\mid E_4 \mid$ = p, $\mid E_5 \mid$ = 2p and $\mid E_6 \mid$ = 2p. Then, by definition S(G) index is calculated as follows by using the edge partition.

$$\begin{aligned} S(G)&=\sum \limits _{uv \in E(G)} \bigg (\frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)-2}\bigg )^3\\&=(12pq-9p)\bigg (\frac{9 \times 9}{9+9-2}\bigg )^3+(2p)\bigg (\frac{9 \times 8}{9+8-2}\bigg )^3\\&\quad +(p)\bigg (\frac{9 \times 7}{9+7-2}\bigg )^3+(p)\bigg (\frac{8 \times 8}{8+8-2}\bigg )^3\\&\quad +(2p)\bigg (\frac{8 \times 6}{8+6-2}\bigg )^3+(2p)\bigg (\frac{7 \times 6}{7+6-2}\bigg )^3 \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} S(G)&=1556.956pq - 520.549p. \end{aligned}$$

By definition, NI(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} NI(G)= & {} \sum \limits _{uv \in E(G)} \frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)}\\= & {} (12pq-9p)\bigg (\frac{9 \times 9}{9+9}\bigg )+(2p)\bigg (\frac{9 \times 8}{9+8}\bigg )+(p)\bigg (\frac{9 \times 7}{9+7}\bigg )\\&+(p)\bigg (\frac{8 \times 8}{8+8}\bigg )+(2p)\bigg (\frac{8 \times 6}{8+6}\bigg )+(2p)\bigg (\frac{7 \times 6}{7+6}\bigg ) \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} NI(G)&=54pq-10.773p. \end{aligned}$$

By definition, NH(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} NH(G)&=\sum \limits _{uv \in E(G)} \frac{2}{\delta _G(u)+\delta _G(v)}\\&=(12pq-9p)\bigg (\frac{2}{9+9}\bigg )+(2p)\bigg (\frac{2}{9+8}\bigg ) +(p)\bigg (\frac{2}{9+7}\bigg )\\&\quad +(p)\bigg (\frac{2}{8+8}\bigg ) +(2p)\bigg (\frac{2}{8+6}\bigg )+(2p)\bigg (\frac{2}{7+6}\bigg ) \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} NH(G)&=1.333pq+0.079p. \end{aligned}$$

By definition, $ND_5(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} ND_5(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)^2+\delta _G(v)^2}{\delta _G(u)\delta _G(v)}\\&=(12pq-9p)\bigg (\frac{9^2 + 9^2}{9 \times 9}\bigg )+(2p)\bigg (\frac{9^2 + 8^2}{9 \times 8}\bigg )+(p)\bigg (\frac{9^2 + 7^2}{9 \times 7}\bigg )\\&\quad +(p)\bigg (\frac{8^2 + 8^2}{8 \times 8}\bigg )+(2p)\bigg (\frac{8^2 + 6^2}{8 \times 6}\bigg )+(2p)\bigg (\frac{7^2 + 6^2}{7 \times 6}\bigg ) \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} ND_5(G)&=24pq-1.694p. \end{aligned}$$

By definition, $M_2^{nm}(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} M_2^{nm}(G)&=\sum \limits _{uv \in E(G)} \frac{1}{\delta _G(u)\delta _G(v)}\\&=(12pq-9p)\bigg (\frac{1}{9 \times 9}\bigg )+(2p)\bigg (\frac{1}{9 \times 8}\bigg )+(p)\bigg (\frac{1}{9 \times 7}\bigg )\\&\quad +(p)\bigg (\frac{1}{8 \times 8}\bigg )+(2p)\bigg (\frac{1}{8 \times 6}\bigg )+(2p)\bigg (\frac{1}{7 \times 6}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} M_2^{nm}(G)&=0.148pq+0.037p. \end{aligned}$$

$\square$

Fig. 2

Graphical representation for $HAC_5C_7[p,q]$ nanotube

5 The $HAC_5C_6C_7[p,q]$ nanotube

A trivalent decoration has been made by combining $C_5$, $C_6$ and $C_7$ is known as a $C_5C_6C_7$ net see [18]. It has been using to mask a torus or a tube. As a $C_5C_6C_7$ net, the $HAC_5C_6C_7[p,q]$ nanotube can be studied, and Fig. 3a shows an illustration. The two-dimension lattice of $HAC_5C_6C_7$ has been studied consistently. In the entire lattice, the number of heptagons and periods has been represented by p and q in a row. In $HAC_5C_6C_7$, there are $8pq + p$ vertices and $12pq - p$ edges see [19]. The development of $HAC_5C_6C_7$ is discussed in [24]. The three rows of $HAC_5C_6C_7$ is said to be $m^{th}$ period, and as shown in Fig. 3b.

Fig. 3

$HAC_5C_6C_7[p,q]$ nanotube

6 Some topological indices of $HAC_5C_6C_7 [p,q]$ nanotube, $(p,q > 1)$

The general result is determined for $HAC_5C_6C_7[p,q]$ nanotube in this segment by above mentioned topological indices. In addition to these indices, we present a visual analogy as well as their utilization (Figs. 4, 5, and 6).

Theorem 2

Let G be the graph of $HAC_5C_6C_7[p,q]$ nanotube. Then,

• 1. $S(G)=3113.9121pq - 1063.4764p$

• 2. $NI(G)=108pq-21.955p$

• 3. $NH(G)=2.667pq+0.174p$

• 4. $ND_5(G)=48pq-3.480p$

• 5. $M_2^{nm}(G)=0.296pq+0.148p$

Proof

Consider the graph of $HAC_5C_6C_7$ is represented by G. The cardinality of vertex set is $8pq + p$ and the edge set is $12pq - p$ for the graph G. The edge set is divide into the following sections corresponding to their sum of the degrees of the neighborhood, which are

$$\begin{aligned} E_{1}&=\{st \in E(SR_n)\mid d_u=9~ and ~d_v=9\}\\ E_{2}&=\{st \in E(SR_n)\mid d_u=9 ~and ~d_v=8\}\\ E_{3}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=8\}\\ E_{4}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=7\}\\ E_{5}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=6\}\\ E_{6}&=\{st \in E(SR_n)\mid d_u=7 ~and ~d_v=6\} \end{aligned}$$

From the graph G, we can see that $\mid E_1 \mid$ = 12pq - 9p, $\mid E_2 \mid$ = 4p, $\mid E_3 \mid$ = 2p, $\mid E_4 \mid$ = 2p, $\mid E_5 \mid$ = 4p and $\mid E_6 \mid$ = 4p. Then, by definition S(G) index is calculated as follows by using the edge partition.

$$\begin{aligned} S(G)&=\sum \limits _{uv \in E(G)} \bigg (\frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)-2}\bigg )^3\\&=(24pq-18p)\bigg (\frac{9 \times 9}{9+9-2}\bigg )^3+(4p)\bigg (\frac{9 \times 8}{9+8-2}\bigg )^3\\&\quad +(2p)\bigg (\frac{8 \times 8}{8+8-2}\bigg )^3+(2p)\bigg (\frac{8 \times 7}{8+7-2}\bigg )^3\\&\quad +(4p)\bigg (\frac{8 \times 6}{8+6-2}\bigg )^3+(4p)\bigg (\frac{7 \times 6}{7+6-2}\bigg )^3 \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} S(G)&=3113.9121pq - 1063.4764p. \end{aligned}$$

By definition, NI(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} NI(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)}\\&=(24pq-18p)\bigg (\frac{9 \times 9}{9+9}\bigg )+(4p)\bigg (\frac{9 \times 8}{9+8}\bigg )+(2p)\bigg (\frac{8 \times 8}{8+8}\bigg )\\&\quad +(2p)\bigg (\frac{8 \times 7}{8+7}\bigg )+(4p)\bigg (\frac{8 \times 6}{8+6}\bigg )+(4p)\bigg (\frac{7 \times 6}{7+6}\bigg ) \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} NI(G)&=108pq-21.955p. \end{aligned}$$

By definition, NH(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} NH(G)&=\sum \limits _{uv \in E(G)} \frac{2}{\delta _G(u)+\delta _G(v)}\\&=(24pq-18p)\bigg (\frac{2}{9+9}\bigg )+(4p)\bigg (\frac{2}{9+8}\bigg )+(2p)\bigg (\frac{2}{8+8}\bigg )\\&\quad +(2p)\bigg (\frac{2}{8+7}\bigg )+(4p)\bigg (\frac{2}{8+6}\bigg )+(4p)\bigg (\frac{2}{7+6}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} NH(G)&=2.667pq+0.174p. \end{aligned}$$

By definition, $ND_5(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} ND_5(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)^2+\delta _G(v)^2}{\delta _G(u)\delta _G(v)}\\&=(24pq-18p)\bigg (\frac{9^2 + 9^2}{9 \times 9}\bigg )+(4p)\bigg (\frac{9^2 + 8^2}{9 \times 8}\bigg )+(2p)\bigg (\frac{8^2 + 8^2}{8 \times 8}\bigg )\\&\quad +(2p)\bigg (\frac{8^2 + 7^2}{8 \times 7}\bigg )+(4p)\bigg (\frac{8^2 + 6^2}{8 \times 6}\bigg )+(4p)\bigg (\frac{7^2 + 6^2}{7 \times 6}\bigg ) \end{aligned} \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} ND_5(G)&=48pq-3.480p. \end{aligned}$$

By definition, $M_2^{nm}(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} M_2^{nm}(G)&=\sum \limits _{uv \in E(G)} \frac{1}{\delta _G(u)\delta _G(v)}\\&=(24pq-18p)\bigg (\frac{1}{9 \times 9}\bigg )+(4p)\bigg (\frac{1}{9 \times 8}\bigg )+(2p)\bigg (\frac{1}{8 \times 8}\bigg )\\&\quad +(2p)\bigg (\frac{1}{8 \times 7}\bigg )+(4p)\bigg (\frac{1}{8 \times 6}\bigg )+(4p)\bigg (\frac{1}{7 \times 6}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} M_2^{nm}(G)&=0.296pq+0.148p. \end{aligned}$$

$\square$

Fig. 4

Graphical representation for $HAC_5C_6C_7[p,q]$ nanotube

7 $TUC_4C_8[p,q]$ nanotorus and nanotube

The two-dimensional lattice and Nanotorus of $TUC_4C_8[p,q]$ has presented in Fig. 5, and we will use documentation and concept of Diudea and Graovac [19]. GTUC[p, q] indicates the nanotube of $TUC_4C_8[p,q]$ see Fig. 7. The overall number of octagons in each row and column of Nanotube of $TUC_4C_8[p,q]$ is equivalent to p and q. The overall number of squares and octagons in Nanotube of $TUC_4C_8[p,q]$ is the same in each row [4, 6, 9]. In 2D-lattice of $TUC_4C_8[p,q]$, the overall number of octagons in each row and column is equivalent to p and q. In [1, 3, 19], two-dimensional lattice of $TUC_4C_8[p,q]$ nanotorus, the overall number of squares of columns and rows are (q + 1) and (p + 1).

In two-dimensional lattice of $TUC_4C_8[p,q]$ nanotorus, the number of vertex set and edge set is $(4p^2+4p)(q+1)$ and $6pq+5p+5q+4$, similarly for GTUC[p, q], vertex set and edge set is $4pq+4p$ and $6pq+5p$.

Fig. 5

a 2D-lattice of $TUC_4C_8[p,q]$, b nanotorus of $TUC_4C_8[p,q]$

8 Some topological indices of 2D-lattice of $TUC_4C_8[p,q]$ nanotorus, $(p,q > 1)$

The general result is determined for 2D-lattice of $TUC_4C_8[p,q]$ nanotorus in this segment by above mentioned topological indices. In addition to these indices, we present a visual analogy as well as their utilization.

Theorem 3

Let G be the graph of 2D-lattice of $TUC_4C_8 [p,q]$ nanotorus. Then,

• 1. $S(G)=240.7033(p+q)+778.4780pq+11.1269$

• 2. $NI(G)=27pq+16.155(p+q)+7.304$

• 3. $NH(G)=0.667pq+0.736(p+q)+0.891$

• 4. $ND_5(G)=12pq+10.389(p+q)-9.022$

• 5. $M_2^{nm}(G)=0.074pq+0.108(p+q)+0.194$

Proof

Consider the graph of 2D-lattice of $TUC_4C_8 [p,q]$ nanotorus is represented by G. The cardinality of vertex set is $(4p^2+4p)(q+1)$ and the edge set is $6pq+5p+5q+4$ for the graph G. The edge set is divide into the following sections corresponding to their sum of the degrees of the neighborhood, which are

$$\begin{aligned} E_{1}&=\{st \in E(SR_n)\mid d_u=9~ and ~d_v=9\}\\ E_{2}&=\{st \in E(SR_n)\mid d_u=9 ~and ~d_v=8\}\\ E_{3}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=8\}\\ E_{4}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=6\}\\ E_{5}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=5\}\\ E_{6}&=\{st \in E(SR_n)\mid d_u=5 ~and ~d_v=5\} \end{aligned}$$

From the graph G, we can see that $\mid E_1 \mid$ = 6pq - 5p - 5q + 4, $\mid E_2 \mid$ = 4(p + q - 2), $\mid E_3 \mid$ = 2(p + q + 2), $\mid E_4 \mid$ = 4(p + q - 2), $\mid E_5 \mid$ = 8 and $\mid E_6 \mid$ = 4. Then, by definition S(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} S(G)&=\sum \limits _{uv \in E(G)} \bigg (\frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)-2}\bigg )^3\\&=(6pq-5p-5q+4)\bigg (\frac{9 \times 9}{9+9-2}\bigg )^3+(4p+4q-8)\bigg (\frac{9 \times 8}{9+8-2}\bigg )^3\\&\quad +(2p+2q+4)\bigg (\frac{8 \times 8}{8+8-2}\bigg )^3+(4p+4q-8)\bigg (\frac{8 \times 6}{8+6-2}\bigg )^3\\&\quad +(8)\bigg (\frac{8 \times 5}{8+5-2}\bigg )^3+(4)\bigg (\frac{5 \times 5}{5+5-2}\bigg )^3 \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} S(G)&=240.7033(p+q)+778.4780pq+11.1269. \end{aligned}$$

By definition, NI(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} NI(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)}\\&=(6pq-5p-5q+4)\bigg (\frac{9 \times 9}{9+9}\bigg )+(4p+4q-8)\bigg (\frac{9 \times 8}{9+8}\bigg )\\&\quad +(2p+2q+4)\bigg (\frac{8 \times 8}{8+8}\bigg )+(4p+4q-8)\bigg (\frac{8 \times 6}{8+6}\bigg )\\&\quad +(8)\bigg (\frac{8 \times 5}{8+5}\bigg )+(4)\bigg (\frac{5 \times 5}{5+5}\bigg ) \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} NI(G)&=27pq+16.155(p+q)+7.304. \end{aligned}$$

By definition, NH(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} NH(G)&=\sum \limits _{uv \in E(G)} \frac{2}{\delta _G(u)+\delta _G(v)}\\&=(6pq-5p-5q+4)\bigg (\frac{2}{9+9}\bigg )+(4p+4q-8)\bigg (\frac{2}{9+8}\bigg )\\&\quad +(2p+2q+4)\bigg (\frac{2}{8+8}\bigg )+(4p+4q-8)\bigg (\frac{2}{8+6}\bigg )\\&\quad +(8)\bigg (\frac{2}{8+5}\bigg )+(4)\bigg (\frac{2}{5+5}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} NH(G)&=0.667pq+0.736(p+q)+0.891. \end{aligned}$$

By definition, $ND_5(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} ND_5(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)^2+\delta _G(v)^2}{\delta _G(u)\delta _G(v)}\\&=(6pq-5p-5q+4)\bigg (\frac{9^2 + 9^2}{9 \times 9}\bigg )+(4p+4q-8)\bigg (\frac{9^2 + 8^2}{9 \times 8}\bigg )\\&\quad +(2p+2q+4)\bigg (\frac{8^2 + 8^2}{8 \times 8}\bigg )+(4p+4q-8)\bigg (\frac{8^2 + 6^2}{8 \times 6}\bigg )\\&\quad +(8)\bigg (\frac{8^2 + 5^2}{8 \times 5}\bigg )+(4)\bigg (\frac{5^2 + 5^2}{5 \times 5}\bigg ) \end{aligned} \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} ND_5(G)&=12pq+10.389(p+q)-9.022. \end{aligned}$$

By definition, $M_2^{nm}(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} M_2^{nm}(G)&=\sum \limits _{uv \in E(G)} \frac{1}{\delta _G(u)\delta _G(v)}\\&=(6pq-5p-5q+4)\bigg (\frac{1}{9 \times 9}\bigg )+(4p+4q-8)\bigg (\frac{1}{9 \times 8}\bigg )\\&\quad +(2p+2q+4)\bigg (\frac{1}{8 \times 8}\bigg )+(4p+4q-8)\bigg (\frac{1}{8 \times 6}\bigg )\\&\quad +(8)\bigg (\frac{1}{8 \times 5}\bigg )+(4)\bigg (\frac{1}{5 \times 5}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} M_2^{nm}(G)&=0.074pq+0.108(p+q)+0.194. \end{aligned}$$

$\square$

Fig. 6

Graphical representation for 2D-lattice of $TUC_4C_8 [p,q]$ nanotorus

9 Some topological indices of GTUC[p, q] nanotube, $(p,q > 1)$

The general result is determined for GTUC[p, q] nanotube in this segment by above mentioned topological indices. In addition to these indices, we present a visual analogy as well as their utilization.

Fig. 7

GTUC[p, q] nanotube with p = 5 and q = 4

Theorem 4

Let G be the graph of GTUC[p, q] nanotube. Then,

• 1. $S(G)=778.4780pq+240.70p$

• 2. $NI(G)=27pq+16.155p$

• 3. $NH(G)=0.667pq+0.736p$

• 4. $ND_5(G)=12pq+10.389p$

• 5. $M_2^{nm}(G)=0.074pq+0.108p$

Proof

Consider the graph of GTUC is represented by G. The cardinality of vertex set is $4pq+4p$ and the edge set is $6pq+5p$ for the graph G. The edge set is divide into the following sections corresponding to their sum of the degrees of the neighborhood, which are

$$\begin{aligned} E_{1}&=\{st \in E(SR_n)\mid d_u=9~ and ~d_v=9\}\\ E_{2}&=\{st \in E(SR_n)\mid d_u=9 ~and ~d_v=8\}\\ E_{3}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=8\}\\ E_{4}&=\{st \in E(SR_n)\mid d_u=8 ~and ~d_v=6\} \end{aligned}$$

From the graph G, we can see that $\mid E_1 \mid$ = 6pq - 5p, $\mid E_2 \mid$ = 4p, $\mid E_3 \mid$ = 2p, $\mid E_4 \mid$ = 4p. Then, by definition S(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} S(G)&=\sum \limits _{uv \in E(G)} \bigg (\frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)-2}\bigg )^3\\&=(6pq-5p)\bigg (\frac{9 \times 9}{9+9-2}\bigg )^3+(4p)\bigg (\frac{9 \times 8}{9+8-2}\bigg )^3\\&\quad +(2p)\bigg (\frac{8 \times 8}{8+8-2}\bigg )^3+(4p)\bigg (\frac{8 \times 6}{8+6-2}\bigg )^3 \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} S(G)&=778.4780pq+240.70p. \end{aligned}$$

By definition, NI(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} NI(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)\delta _G(v)}{\delta _G(u)+\delta _G(v)}\\&=(6pq-5p)\bigg (\frac{9 \times 9}{9+9}\bigg )+(4p)\bigg (\frac{9 \times 8}{9+8}\bigg )\\&\quad +(2p)\bigg (\frac{8 \times 8}{8+8}\bigg )+(4p)\bigg (\frac{8 \times 6}{8+6}\bigg ) \end{aligned} \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} NI(G)&=27pq+16.155p. \end{aligned}$$

By definition, NH(G) index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} NH(G)&=\sum \limits _{uv \in E(G)} \frac{2}{\delta _G(u)+\delta _G(v)}\\&=(6pq-5p)\bigg (\frac{2}{9+9}\bigg )+(4p)\bigg (\frac{2}{9+8}\bigg )\\&\quad +(2p)\bigg (\frac{2}{8+8}\bigg )+(4p)\bigg (\frac{2}{8+6}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} NH(G)&=0.667pq+0.736p. \end{aligned}$$

By definition, $ND_5(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} ND_5(G)&=\sum \limits _{uv \in E(G)} \frac{\delta _G(u)^2+\delta _G(v)^2}{\delta _G(u)\delta _G(v)}\\&=(6pq-5p)\bigg (\frac{9^2 + 9^2}{9 \times 9}\bigg )+(4p)\bigg (\frac{9^2 + 8^2}{9 \times 8}\bigg )\\&\quad +(2p)\bigg (\frac{8^2 + 8^2}{8 \times 8}\bigg )+(4p)\bigg (\frac{8^2 + 6^2}{8 \times 6}\bigg ) \end{aligned} \end{aligned}$$

We obtain our desired outcome after simplifying the above form,

$$\begin{aligned} ND_5(G)&=12pq+10.389p. \end{aligned}$$

By definition, $M_2^{nm}(G)$ index is calculated as follows by using the edge partition,

$$\begin{aligned} \begin{aligned} M_2^{nm}(G)&=\sum \limits _{uv \in E(G)} \frac{1}{\delta _G(u)\delta _G(v)}\\&=(6pq-5p)\bigg (\frac{1}{9 \times 9}\bigg )+(4p)\bigg (\frac{1}{9 \times 8}\bigg )\\&\quad +(2p)\bigg (\frac{1}{8 \times 8}\bigg )+(4p)\bigg (\frac{1}{8 \times 6}\bigg ) \end{aligned} \end{aligned}$$

We obtain the necessary result by reducing the above calculation,

$$\begin{aligned} M_2^{nm}(G)&=0.074pq+0.108p. \end{aligned}$$

$\square$

Fig. 8

Graphical representation for GTUC[p, q] nanotube

10 Graphical comparison and discussion

For the Nanotubes and Nanotorus $HAC_5C_7$, $HAC_5C_6C_7$, 2D-lattice of $TUC_4C_8[p,q]$ nanotorus, and GTUC, we have calculated mentioned topological indices for some various p and q values. We also create the following tables for small p and q values for these topological indices to $HAC_5C_7$, $HAC_5C_6C_7$, 2D-lattice of $TUC_4C_8$, and GTUC, respectively. Tables 1, 2, 3, and 4 show that as the values of p and q increase, the value of all the indices increases correspondingly.

The graphical representations of topological indices using the following tables for $HAC_5C_7$, $HAC_5C_6C_7$, 2D-lattice of $TUC_4C_8$ nanotorus, and GTUC are shown in Figs. 2, 4, 6, and 8 for various p and q values. The comparison graphs for the 2D-lattice structure of certain nanotube and nanotorus are presented in Fig. 9 using the following tables. All the topological indices are highlighted individually in the graphs. In this paper, we derive close formulae for all topological indices, and graphically it is shown that the Sanskruti index is more rapid than all other indices.

Table 1 Comparison table for $HAC_5C_7$[p,q] nanotube

Table 2 Comparison table for $HAC_5C_6C_7$[p,q] nanotube

Table 3 Comparison table for 2D-lattice of $TUC_4C_8 [p,q]$ nanotorus

Table 4 Comparison table for GTUC[p, q] nanotube

Fig. 9

Comparison graphs of topological indices are presented for the 2D-lattice structure and individually highlighted for indices using blue, red, green, violet, and purple, respectively (color figure online)

11 Conclusion

In this paper, we have estimated the Sanskruti index, the Neighborhood inverse sum index, the Neighborhood Harmonic index, the Fifth $ND_e$ index and the Neighborhood second modified Zagreb index for two dimensional lattice structure of certain Nanotube and Nanotorus.