The Graovac–Pisanski index of armchair tubulenes

Abstract

Molecular descriptors play a fundamental role in chemistry and pharmaceutical sciences since they can be correlated with a large number of physico-chemical properties of molecules. The most commonly used molecular descriptor is the Wiener index which is defined as the sum of distances between all the pairs of vertices in a molecular graph. The Graovac–Pisanski index, which is also called the modified Wiener index, considers the symmetries and the distances in molecular graphs. This index already has known correlations with the topological efficiency and the melting points for some molecules and nanostrucures. Carbon nanotubes are molecules made of carbon with a cylindrical structure possessing unusual valuable properties. Because of these properties carbon nanotubes are extremely valuable for nanotechnology and materials engineering. We focus on open-ended single-walled carbon nanotubes, which are also called tubulenes. In a mathematical model we can consider them as a subgraph of a hexagonal lattice embedded on a cylinder with some vertices being identified. In the present paper, we investigate the automorphisms and the orbits of armchair tubulenes and derive the closed formulas for their Graovac–Pisanski index.

1 Introduction

In this paper we model carbon nanotubes in terms of graph theory. A graph G is an ordered pair $G = (V, E)$ of a set V of vertices (also called nodes or points) together with a set E of edges, which are 2-element subsets of V. For some basic concepts about graph theory see [21]. Having a molecule, if we represent carbon atoms by vertices and bonds between them by edges, we obtain a molecular graph.

Theoretical molecular descriptors (also called topological indices) are graph invariants that play an important role in chemistry, pharmaceutical sciences, materials science and engineering, etc. The most famous molecular descriptor is the Wiener index introduced in 1947 [22]. This index is defined as the sum of distances between all the pairs of vertices in a molecular graph. Nowadays this index is used for preliminary screening of drug molecules and also for predicting binding energy of protein-ligand complex at a preliminary stage.

The Graovac–Pisanski index is a molecular descriptor that considers symmetries and distances in a graph. It measures how far the vertices of a graph are moved on the average by its automorphisms. The Graovac–Pisanski index was introduced by Graovac and Pisanski [8] under the name modified Wiener index. However, the name modified Wiener index was later used for different variations of the Wiener index [9, 14, 15]. Therefore, we use the name Graovac–Pisanski index as suggested by Ghorbani and Klavžar [7].

Carbon nanotubes are carbon compounds with a cylindrical structure, first observed in 1991 [10]. The extremely large ratio of length to diameter causes unusual properties of these molecules, which are valuable for nanotechnology, materials science and technology, electronics, and optics. Carbon nanotubes can be open-ended or closed-ended. Open-ended single-walled carbon nanotubes are also called tubulenes.

It was shown in [3] that the quotient of the Wiener index and the Graovac–Pisanski index is strongly correlated with the topological efficiency for some nanostructures. The topological efficiency was introduced in [5, 16] as a tool for the classification of the stability of molecules. Moreover, the effects of the symmetries of a molecule to its melting point were discussed in [17] and correlations between the Graovac–Pisanski index and melting points for alkanes and polyaromatic hydrocarbons were shown in [6].

For recent studies on the Graovac–Pisanski index of some molecular graphs and nanostructures see also [1, 2, 4, 11,12,13, 19]. Moreover, the Graovac–Pisanski index of zig-zag nanotubes was computed in [20]. We use similar ideas to compute this index for armchair nanotubes, but in some places our computation is more difficult and requires some additional insights.

In the present paper we first describe the automorphisms of armchair tubulenes and compute the orbits under the natural action of the automorphism group on the set of vertices of a graph. In the second part, the Graovac–Pisanski index for these nanotubes is computed. For this purpose, different cases according to the number of layers and the width of a nanotube are considered. Final results are then gathered in Table 3.

2 Preliminaries

In this paper we considered simple, finite, and connected graphs. The distance $d_G(x,y)$ (or sometimes d(x, y)) between vertices x and y of a graph G is the length of a shortest path between vertices x and y in G. For a subset $S \subseteq V(G)$ and a vertex $x \in V(G)$, we define the distance from a vertex to a subset as $d(x,S) = \sum _{y \in S}d(x,y)$. A subgraph H of G is isometric if for any two vertices $x,y \in V(H)$ it holds $d_H(x,y) = d_G(x,y)$. Furthermore, if for any two $x,y \in V(H)$ every shortest path between x and y in G is completely included in H then H is called convex.

The Wiener index of a connected graph G is defined as $W(G) = \frac{1}{2} \sum _{u \in V(G)} \sum _{v \in V(G)} d_G(u,v)$. Also, for any $S \subseteq V(G)$ we define $W(S) = \frac{1}{2} \sum _{u \in S} \sum _{v \in S} d_G(u,v)$.

An isomorphism of graphs G and H with $|E(G)|=|E(H)|$ is a bijection $f: V(G)\rightarrow V(H)$ such that for any two $u,v \in V(G)$ it holds that if $uv \in E(G)$ then $f(u)f(v) \in E(H)$. When graphs G and H are the same, then f is called an automorphism. The composition of two automorphisms is another automorphism, and the set of automorphisms of a given graph G, under the composition operation, forms an automorphism group $\mathrm{Aut}(G)$.

The Graovac–Pisanski index of a connected graph G, $\widehat{W}(G)$, is defined as

$$\begin{aligned} \widehat{W}(G) = \frac{|V(G)|}{2 |\mathrm{Aut}(G)|} \sum _{u \in V(G)} \sum _{\alpha \in \mathrm{Aut}(G)} d_G(u, \alpha (u)). \end{aligned}$$

Next, we introduce some basic definitions from group theory. If G is a group and X is a set, then a group action $\phi$ of G on X is a function $\phi :G \times X \rightarrow X$ that satisfies the following: $\phi (e,x) = x$ for any $x \in X$ (here, e is the neutral element of G) and $\phi (gh,x)=\phi (g,\phi (h,x))$ for all $g,h \in G$ and $x \in X$. The orbit of an element x in X is the set of elements in X to which x can be moved by the elements of G, i.e. the set $\lbrace \phi (g,x) \, | \, g \in G \rbrace$. If G is a graph and $\mathrm{Aut}(G)$ the automorphism group, then $\phi : \mathrm{Aut}(G) \times V(G) \rightarrow V(G)$, defined by $\phi (\alpha ,u) = \alpha (u)$ for any $\alpha \in \mathrm{Aut}(G)$, $u \in V(G)$, is called the natural action of the group $\mathrm{Aut}(G)$ on V(G).

Graovac and Pisanski showed in [8] that if $V_1, \ldots , V_t$ are the orbits under the natural action of the group $\mathrm{Aut}(G)$ on V(G), then

$$\begin{aligned} \widehat{W}(G) = |V(G)| \sum _{i=1}^t \frac{1}{|V_i|}W(V_i). \end{aligned}$$

(1)

In addition, let $W'(G) = \sum _{i=1}^t W(V_i)$ be the sum of the Wiener indices of orbits of G.

3 Armchair tubulenes and their automorphisms

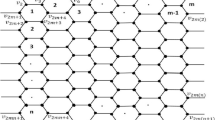
The general definition of a tubulene can be found in [18], but for our purpose it is enough to focus just on armchair tubulenes. Let $n \ge 2$ and $p \ge 1$ be two integers such that n is an even number. An armchair tubulene AT(n, p) is a graph with a cylindrical structure such that it is composed of n vertical layers of hexagons, each containing exactly p hexagons, see Fig. 1. The cycles representing two open ends of an armchair tubulene will be denoted by $c_1$ and $c_2$. Moreover, let $C_1$ and $C_2$ be subgraphs of AT(n, p) induced by $c_1$ and $c_2$, respectively. Obviously, n represents the width of a tubulene and p represents its length. Note that n must be even since otherwise a tubulene is not well defined. In some literature, the number of hexagons in vertical layers of hexagons of an armchair tubulene may not be constant. In such a case, vertical layers have two sizes such that every second vertical layer has one hexagon more with respect to the previous layer. However, in this paper we focus only on the previously defined armchair tubulenes.

Next, we introduce additional notation for the vertices of an armchair tubulene. Obviously, AT(n, p) has $p+1$ layers of vertices and every layer has two types of vertices, i.e. type 0 and type 1. In the figures the vertices in a layer of type 0 always lie lower than the vertices of type 1. The set of vertices of type $k \in \{0,1\}$ in layer $i \in \{0,\ldots ,p\}$ is denoted by $V^k_i$, see Fig. 1 for an example.

Fig. 1

Armchair tubulene AT(6, 4) where the vertices $A_i$ and $A_i'$ are identified. Vertices in $V^0_2$ are denoted with circles and vertices in $V^1_2$ with squares

In this section, we determine the orbits under the natural action of the group $\mathrm{Aut}(AT(n,p))$ on the set V(AT(n, p)). First, one lemma is needed.

Lemma 1

Let $\varphi : V(C_1) \rightarrow V(C_i)$ be an isomorphism between subgraphs $C_1$ and $C_i$, where $i \in \lbrace 1,2 \rbrace$. Then there is exactly one automorphism $\overline{\varphi }: V(AT(n,p)) \rightarrow V(AT(n,p))$ such that $\varphi (x) = \overline{\varphi }(x)$ for any $x \in V(C_1)$.

Proof

Let $\varphi : V(C_1) \rightarrow V(C_i)$ be an isomorphism where $i \in \lbrace 1,2 \rbrace$. For any $x \in V(C_1) = V^0_0 \cup V^1_0$ we define $\overline{\varphi }(x) = \varphi (x)$. In the rest of the proof we will define function $\overline{\varphi }$ step by step such that every edge will be mapped to an edge and $\overline{\varphi }$ will be a bijection.

First let $x \in V^0_1$. Then there is exactly one $y \in V^1_0$ such that x and y are adjacent. Since the degree of y is 3, let $y_1$ and $y_2$ be the other two neighbours of y in AT(n, p). Obviously, $\overline{\varphi }(y), \overline{\varphi }(y_1)$, and $\overline{\varphi }(y_2)$ are already defined and it holds that $\overline{\varphi }(y_1)$ and $\overline{\varphi }(y_2)$ are both adjacent to $\overline{\varphi }(y)$. Since the degree of $\overline{\varphi }(y)$ is 3, we define $\overline{\varphi }(x)$ to be the neighbour of $\overline{\varphi }(y)$, different from $\overline{\varphi }(y_1)$ and $\overline{\varphi }(y_2)$. This can be done for any $x \in V^0_1$.

Now let $x \in V^1_1$. Then there is exactly one vertex $y \in V^0_1$ such that y is adjacent to x. Let $y_1$ and $y_2$ be the other two neighbours of y. It is easy to see that $\overline{\varphi }(y)$, $\overline{\varphi }(y_1)$, and $\overline{\varphi }(y_2)$ are already defined. Also, the degree of $\overline{\varphi }(y)$ is 3. Therefore, we define $\overline{\varphi }(x)$ to be the neighbour of $\overline{\varphi }(y)$, different from $\overline{\varphi }(y_1)$ and $\overline{\varphi }(y_2)$. This can be done for any $x \in V^1_1$.

With the procedure above we have defined function $\overline{\varphi }$ on the set of vertices $V^0_0 \cup V^1_0 \cup V^0_1 \cup V^1_1$ such that for any two adjacent vertices $x,y \in V^0_0 \cup V^1_0 \cup V^0_1 \cup V^1_1$, it holds that $\overline{\varphi }(x)$ and $\overline{\varphi }(y)$ are also adjacent. Using induction, we can define function $\overline{\varphi }$ on the set V(AT(n, p)) such that for any two adjacent vertices $x,y \in V(AT(n,p))$ it holds that $\overline{\varphi }(x)$ and $\overline{\varphi }(y)$ are adjacent. Since $\overline{\varphi }$ is also bijective, it is an automorphism of the graph AT(n, p). It follows from the construction that $\overline{\varphi }$ is also unique. Therefore, the proof is complete. $\square$

Finally, we obtain the orbits under the natural action of the group $\mathrm{Aut}(AT(n,p))$ on the set V(AT(n, p)).

Theorem 1

The orbits under the natural action of the group $\mathrm{Aut}(AT(n,p))$ on the set V(AT(n, p)) are:

• 1. if p is odd

  $$\begin{aligned} O^0_i= & {} V^0_i \cup V^1_{n-i}, \ i \in \Big \lbrace 0, \ldots , \frac{p-1}{2} \Big \rbrace , \\ O^1_i= & {} V^1_i \cup V^0_{n-i}, \ i \in \Big \lbrace 0, \ldots , \frac{p-1}{2} \Big \rbrace . \end{aligned}$$

• 2. if p is even

  $$\begin{aligned} O^0_i= & {} V^0_i \cup V^1_{n-i}, \ i \in \Big \lbrace 0, \ldots , \frac{p-2}{2} \Big \rbrace , \\ O^1_i= & {} V^1_i \cup V^0_{n-i}, \ i \in \Big \lbrace 0, \ldots , \frac{p-2}{2} \Big \rbrace , \\ O_{\frac{p}{2}}= & {} V^0_{\frac{p}{2}} \cup V^1_{\frac{p}{2}}. \end{aligned}$$

Proof

It follows from the Proof of Lemma 1 that for any vertex x of type k in layer i, where $i \in \lbrace 0, \ldots , p \rbrace$, $k \in \lbrace 0,1 \rbrace$, and any vertex y in layer i of type k or in layer $n-i$ of type $1-k$, there is an automorphism that maps x to y. We notice that this also works when p is even and $i = \frac{p}{2}$, which means that if $x \in V^0_{\frac{p}{2}}$ and $y \in V^1_{\frac{p}{2}}$, there is an automorphism that maps x to y.

Also, if x is in layer i and y is in layer j, $j \ne i, j \ne n-i$, the distance from x to the boundary, i.e. $\min \lbrace d(x,u) \, | \, u \in V(C_1) \cup V(C_2) \rbrace$, can not be the same as the distance from y to the boundary, i.e. $\min \lbrace d(y,u) \, | \, u \in V(C_1) \cup V(C_2) \rbrace$. Therefore, there is no automorphism that maps x to y.

Moreover, if $x \in V^0_i$ and $y \in V^1_i$ or $y \in V^0_{n-i}$, where $i \in \lbrace 0, \ldots , p \rbrace$, $i \ne \frac{p}{2}$, then the numbers $\min \lbrace d(x,C_1),d(x,C_2) \rbrace$ and $\min \lbrace d(y,C_1),d(y,C_2) \rbrace$ can not be the same. Again, there is no automorphism that maps x to y.

Therefore, the proof is complete. $\square$

Figure 2 shows armchair tubulene AT(6, 2) where the vertices from orbit $O^0_0$ are denoted with a circle, the vertices from orbit $O^1_0$ are denoted with a square, and the other vertices are from orbit $O_{1}$.

Fig. 2

Armchair tubulene AT(6, 2) with three orbits

In the previous theorem we have only determined the orbits under the natural action of the group $\mathrm{Aut}(AT(n,p))$ on the set V(AT(n, p)). However, it would be interesting to find out which group $\mathrm{Aut}(AT(n,p))$ is. Therefore, we state the following open problem.

Problem 1

Let AT(n, p) be an armchair tubulene. Determine to which group the automorphism group $\mathrm{Aut}(AT(n,p))$ is isomorphic.

4 The Graovac–Pisanski index of armchair tubulenes

In this section, we calculate the Graovac–Pisanski index of armchair tubulenes. We have to consider the following four cases. The first part is explained in details, while for the remaining cases only the important results are given. We always denote by u an arbitrary element of $V^0_0$ and by v an arbitrary element of $V^1_0$.

• 1. p is even and $4 \, | \, n$

  It is enough to compute $W(O^0_0)$ and $W(O^1_0)$ since, for example, $W(O^0_1)$ of the graph AT(n, p) is exactly $W(O^0_0)$ of the graph $AT(n,p-2)$ [the graph $AT(n,p-2)$ is a convex subgraph of the graph AT(n, p)]. Beside that, we need to calculate $W(O_{\frac{p}{2}})$. Since the graph induced on the vertices in $O_{\frac{p}{2}}$ is an isometric cycle of length 2n, we have $W(O_{\frac{p}{2}})=n^3$.

  Next, we need to calculate $d(u,V^0_0)$ and therefore, we consider distances between some vertices on the cycle of length 2n, see Fig. 3. Note that the thick vertices represent the vertices in set $V^0_0$. Therefore,

  $$\begin{aligned} d(u,V^0_0)= & {} \sum _{i=0}^{\frac{n}{4}-1}(3+4i) + \sum _{i=0}^{\frac{n}{4}-1}(4+4i) + \sum _{i=0}^{\frac{n}{4}-1}(1+4i) + \sum _{i=0}^{\frac{n}{4}-2}(4+4i) \\= & {} \frac{n^2}{2}. \end{aligned}$$

  Obviously, $d(v,V^1_0) = d(u,V^0_0) = \frac{n^2}{2}$. To determine $d(u,V^1_p)$ and $W(O^0_0)$, we consider two cases.

Fig. 3

Subgraph $C_1$ when $n=8$ with the distances from vertices in $V^0_0$ to u

• (a) $n \le 4p + 4$

  In this case, we can draw two lines a and b, see Fig. 4. All n vertices of $V^1_p$ are between lines a and b or near lines a and b (at most 4 vertices).

  It is easy to observe that a shortest path from vertex u to some vertex $x \in V^1_p$ can be obtained by joining a path following line a or line b and a vertical path. Therefore, the distance from u to the vertex directly above u equals $2p+1$ and the distance increases by 1 for every next vertex in $V^1_p$ (in both directions). For an example see Fig. 4. Hence, we get

$$\begin{aligned} d(u,V^1_p)= & {} (2p+1) + 2 \sum _{i=1}^{\frac{n-2}{2}}(2p+1+i) + \Big (2p+1 + \frac{n}{2}\Big ) \\= & {} \frac{n^2}{4} + 2np + n. \end{aligned}$$

Fig. 4

Distances from u in AT(8, 4). Curves $L_1$ and $L_2$ are joined

Therefore,

$$\begin{aligned} d(u,O^0_0) = d(u,V^0_0) + d(u,V^1_p) = \frac{3n^2}{4} + 2np + n \end{aligned}$$

and since every vertex in $O^0_0$ has equivalent position, we deduce

$$\begin{aligned} W(O^0_0)= & {} \frac{1}{2} \cdot |O^0_0| \cdot d(u,O^0_0) = \frac{2n}{2}\Big (\frac{3n^2}{4} + 2np + n\Big ) \\= & {} n\Big (\frac{3n^2}{4} + 2np + n\Big ). \end{aligned}$$

Fig. 5

Distances from u in one part of an armchair tubulene

• (b) $n > 4p + 4$

  In this case, we also draw two lines a and b as before. There are exactly 4p vertices of $V^1_p$ between lines a and b, exactly 4 vertices (2 on each side) of $V^1_p$ near lines a and b, and $n - 4p - 4$ other vertices. See Fig. 5. We can notice that the distance from u to the vertex directly above u is $2p+1$ and that the distance from u increases by 1 (in both directions) for every next vertex among other $4p+3$ vertices that are between or near lines a and b. Afterwards, for the rest $n-4p-4$ vertices the increase of the distance from u alternates between 3 and 1 in both directions. Therefore, we get

  $$\begin{aligned} d(u,V^1_p)= & {} (2p+1) + 2 \sum _{i=1}^{\frac{4p+2}{2}}(2p+1+i) + (2p+1 + 2p+2) \\&+\, \sum _{i=0}^{\frac{n-4p-8}{4}}(4p+5 + 4i) + \sum _{i=0}^{\frac{n-4p-8}{4}}(4p+6 + 4i) \\&+\, \sum _{i=0}^{\frac{n-4p-8}{4}}(4p+6 + 4i) + \sum _{i=0}^{\frac{n-4p-8}{4}}(4p+7 + 4i) \\= & {} \frac{n^2}{2} + p(4p+4). \end{aligned}$$

  Consequently,

  $$\begin{aligned} d(u,O^0_0) = d(u,V^0_0) + d(u,V^1_p) =n^2 + 4p^2 + 4p \end{aligned}$$

  and since every vertex in $O^0_0$ has equivalent position, we obtain

  $$\begin{aligned} W(O^0_0)= & {} \frac{1}{2} \cdot |O^0_0| \cdot d(u,O^0_0) = \frac{2n}{2}(n^2 + 4p^2 + 4p) \\= & {} n(n^2 + 4p^2 + 4p). \end{aligned}$$

  To compute $W(O^1_0)$, we also consider two cases.

Fig. 6

Distances from v in AT(8, 4). Curves $L_1$ and $L_2$ are joined

• (a) $n \le 4p$

  Similar as before, we can draw two lines a and b as shown in Fig. 6. All n vertices of $V^0_p$ are between lines a and b or near lines a and b (at most 4 vertices). It is easy to observe that the distance from vertex v to the vertex directly above v equals $2p-1$ and that the distance increases by 1 for every next vertex in $V^0_p$ (in both directions). For an example see Fig. 6. Hence, we get

  $$\begin{aligned} d(v,V^0_p)= & {} (2p-1) + 2 \sum _{i=1}^{\frac{n-2}{2}}(2p-1+i) + \Big (2p-1 + \frac{n}{2}\Big ) \\= & {} \frac{n^2}{4} + 2np - n. \end{aligned}$$

  Therefore,

  $$\begin{aligned} d(v,O^1_0) = d(v,V^1_0) + d(v,V^0_p) = \frac{3n^2}{4} + 2np - n \end{aligned}$$

  and since every vertex in $O^1_0$ has equivalent position, we deduce

  $$\begin{aligned} W(O^1_0)= & {} \frac{1}{2} \cdot |O^1_0| \cdot d(v,O^1_0) = \frac{2n}{2}\Big (\frac{3n^2}{4} + 2np - n\Big ) \\= & {} n\Big (\frac{3n^2}{4} + 2np - n\Big ). \end{aligned}$$

• (b) $n > 4p$

  In this case, we also draw two lines a and b as in the previous case. There are exactly $4p-4$ vertices of $V^0_p$ between lines a and b, exactly 4 vertices (2 on each side) of $V^0_p$ near lines a and b, and $n-4p$ other vertices.

  We can notice that the distance from v to the vertex directly above v is $2p-1$ and that the distance from v increases by 1 (in both directions) for every next vertex among other $4p-1$ vertices that are between or near lines a and b. Afterwards, for the rest $n-4p$ vertices the increase of the distance from v alternates between 3 and 1 in both directions. Therefore, we get

  $$\begin{aligned} d(v,V^0_p)= & {} (2p-1) + 2 \sum _{i=1}^{\frac{4p-2}{2}}(2p-1+i) + (2p-1 + 2p) \\&+\, \sum _{i=0}^{\frac{n-4p-4}{4}}(4p+1 + 4i) + \sum _{i=0}^{\frac{n-4p-4}{4}}(4p+2 + 4i) \\&+\, \sum _{i=0}^{\frac{n-4p-4}{4}}(4p+2 + 4i) + \sum _{i=0}^{\frac{n-4p-4}{4}}(4p+3 + 4i) \\= & {} \frac{n^2}{2} + p(4p-4). \end{aligned}$$

  Consequently,

  $$\begin{aligned} d(v,O^1_0) = d(v,V^1_0) + d(v,V^0_p) =n^2 + 4p^2 - 4p \end{aligned}$$

  and since every vertex in $O^1_0$ has equivalent position, we get

  $$\begin{aligned} W(O^1_0)= & {} \frac{1}{2} \cdot |O^1_0| \cdot d(v,O^1_0) = \frac{2n}{2}(n^2 + 4p^2 - 4p) \\= & {} n(n^2 + 4p^2 - 4p). \end{aligned}$$

  Putting all the results together, we obtain Table 1.

  Table 1 Distances in AT(n, p) with p even and $4 \, | \, n$

  To compute $\widehat{W}(AT(n,p))$, we use Eq. 1 from Sect. 2. First define the following functions:

  $$\begin{aligned} \begin{array}{rcl} f_1(p) &{} = &{} n\Big (\frac{3n^2}{4} + 2np + n\Big ), \\ f_2(p) &{} = &{} n(n^2 + 4p^2 + 4p), \\ g_1(p) &{} = &{} n\Big (\frac{3n^2}{4} + 2np - n\Big ), \\ g_2(p) &{} = &{} n(n^2 + 4p^2 - 4p). \\ \end{array} \end{aligned}$$

  One can notice that $W(O^0_i)=f_1(p-2i)$ if $n \le 4(p-2i)+4 = 4p-8i+4$ and $W(O^0_i)=f_2(p-2i)$ if $n > 4p-8i+4$ (and similar can be done for $W(O^1_i)$). This follows from the fact that the Wiener index of the orbit $O^0_i$ in AT(n, p) is the same as the Wiener index of the orbit $O^0_0$ in $AT(n,p-2i)$ (and the same holds for $W(O^1_i)$). Now consider the following four cases.

• (a) $n > 4p+4$

  It follows

  $$\begin{aligned} {W'}(AT(n,p)) = W(O_{\frac{p}{2}}) + \sum _{i=1}^{\frac{p}{2}}f_2(2i) + \sum _{i=1}^{\frac{p}{2}}g_2(2i). \end{aligned}$$

• (b) $n = 4p+4$

  For $p \ge 4$ it follows

  $$\begin{aligned} {W'}(AT(n,p)) = W(O_{\frac{p}{2}}) + \sum _{i=1}^{\frac{p-2}{2}}f_2(2i) + f_1(p) + \sum _{i=1}^{\frac{p}{2}}g_2(2i). \end{aligned}$$

  The case $p=2$ can be easily computed in a similar way.

• (c) $n \le 4p$ and $8 \, | \, n$

  For $n \ge 16$ it follows

  $$\begin{aligned} {W'}(AT(n,p))= & {} W(O_{\frac{p}{2}}) + \sum _{i=1}^{\frac{n-8}{8}}f_2(2i) + \sum _{i=\frac{n}{8}}^{\frac{p}{2}}f_1(2i) \\&+\, \sum _{i=1}^{\frac{n-8}{8}}g_2(2i) + \sum _{i=\frac{n}{8}}^{\frac{p}{2}}g_1(2i). \end{aligned}$$

  The case $n=8$ can be easily computed in a similar way.

• (d) $n \le 4p$ and $8 \, | \, (n-4)$

  For $n\ge 20$ it follows

  $$\begin{aligned} {W'}(AT(n,p))= & {} W(O_{\frac{p}{2}}) + \sum _{i=1}^{\frac{n-12}{8}}f_2(2i) + \sum _{i=\frac{n-4}{8}}^{\frac{p}{2}}f_1(2i) \\&+\, \sum _{i=1}^{\frac{n-4}{8}}g_2(2i) + \sum _{i=\frac{n+4}{8}}^{\frac{p}{2}}g_1(2i). \end{aligned}$$

  The cases $n=12$ or $n=4$ can be easily computed in a similar way. To compute all the sums from the previous cases, we use a computer program. Since $|V(AT(n,p))| = 2n(p+1)$ and the cardinality of any orbit of AT(n, p) is 2n, it is easy to see that $\widehat{W}(AT(n,P)) = (p+1)W'(AT(n,P))$. The results are presented in the first part of Table 3.

Table 2 Distances in AT(n, p) with p even and $4 \, | \, (n-2)$

• 2. p is even and $4 \, | \, (n-2)$

  All the details are similar to the case 1. Therefore, the important results are presented in Table 2. We also have $W(O_{\frac{p}{2}})=n^3$. The values of the Graovac–Pisanski index in this case are shown in the second part of Table 3.

• 3. p is odd and $4 \, | \, n$

  All the details are similar to the case 1. It turns out that the distances are the same as for even p. Therefore, we can consider Table 1. The values of the Graovac–Pisanski index in this case are shown in the third part of Table 3.

• 4. p is odd and $4 \, | \, (n-2)$

  All the details are similar to the case 1. As above it turns out that the distances are the same as for even p. Therefore, we can consider Table 2. The values of the Graovac–Pisanski index in this case are shown in the last part of Table 3.

Finally, the results for the Graovac–Pisanski index of AT(n, p) are shown in Table 3. The results for some small cases are omitted.

Table 3 Closed formulas for $\widehat{W}(AT(n,p))$

5 Conclusion

In this paper we have presented armchair carbon nanotubes by graphs. Such a mathematical model was used to study the symmetries of these molecules and to compute their Graovac–Pisanski index, for which strong correlations with some physico-chemical properties have already been reported in the literature. Moreover, an open problem regarding the determination of the automorphism group of an armchair tubulene is stated.