Geometry and Topology of Nanotubes and Nanotori

Abstract

A molecular graph is the graph of a molecule in which the vertices are atoms and edges are chemical bonds. We review the recent results on computing symmetry of series of armchair polyhex, zig-zag polyhex and C₄C₈(R/S) nanotubes and nanotori. The topological properties of these nanostructures are also investigated.

6.1 Introduction

A graph G is a pair (V, E) consisting of a set V = V(G) of vertices and a set E = E(G) of unordered pairs {x, y} = xy of distinct vertices of G called edges. Suppose M is a chemical system like a molecule (having dimensionality Δ = 0), a carbon nanotube (Δ = 1), a graphenic lattice (Δ = 2) or a diamond crystal (Δ = 3). The molecular graph of M is a simple graph such that vertices are atoms and edges are chemical bonds. The degree δ of each vertex (the number of chemical bonds) in a molecular graph is assumed to be at most four. Taking into consideration sp² carbon systems, we mention here that in the Hückel theory only pi electron molecular orbitals are included because these determine the general properties of these molecules and the sigma electrons are ignored. Thus, when we are talking about Hückel theory we need the molecule to have a pi network and therefore all molecular graphs should have max degree 3 or less—a vertex of degree 4 represents a saturated carbon atom that cannot be part of a pi system and which is typical of diamond-like bulk structures. The max degree 4 also holds for alkanes, which are not included in the present research.

Being this chapter devoted to the investigation of the structural and topological properties of some families of nanostructures, a few formal tools have to be shortly introduced here starting with a simple recap of the concept of group.

A group is a mathematical structure that is usually used to describe the symmetries characterizing a given set of mathematical objects. It is a set of elements G equipped with a binary operation of multiplication *: G × G → G such that:

• i) it is associative, e.g. for all $x,\text{ }y,\text{ }z\in G,\text{ }x*(y*z )=(x*y )*z;$

• ii) there exists an element e ∈ G such that for an arbitrary element g in $G,g*e=e*g=g;$

• iii) and, for each x ∈ G there exists $y\in G$ such that $x*y=y*x=e.$

A group is then called finite if the underlying set G is finite. The symmetry structure of G can be formalized by the notion of finite group action. To describe it, we assume G is a group and X is a set. We also assume that there is a map $\phi:G\times X\to X$ with the following two properties:

• a. for each $x\in X,\phi (e,x )=x,$

• b. and, for all elements $x\in X$ and $g,\,h\in G,\phi (g,\phi(h,x ) )=\phi (gh,x ).$

In this case, G and X are called a transformation group and a G-set, respectively. The mapping $\phi$ is called a group action. For simplicity it is convenient to define $gx=\phi (g,x ).$

Suppose now G is a group and H is a non-empty subset of G. H is said to be a subgroup of G, if H is closed under group multiplication. A subgroup H of G is called to be normal in G, if for all $g\in G$ we have g ⁻¹ Hg = H. When both H and K are subgroups of G such that H is normal in $G,\,H\cap K=1$, and G = HK, then G is called a semi-direct product of H by K. Here, HK is the set of all elements of G in the form of xy such that $x\in H$ and $y\in K$.

An automorphism of G is a permutation g of V(G) such that g(u) and g(v) are adjacent if and only if u and v are adjacent, where $u,v\in V(G)$. It is well-known that the set of all automorphisms of G, with the operation of composition of permutations, is a permutation group on V(G), denoted Aut(G). The name topological symmetry is also used for this algebraic structure. Randić (1974, 1976) showed that a graph can be depicted in different ways such that its point group symmetry or even the 3D representation may differ, but its automorphism group symmetry remains the same. The topological symmetry of a molecular graph is not usually the same as its point group symmetry but it corresponds to the maximal symmetry the geometrical realization of a given topological structure may possess. This very important topological feature will play an instrumental role in the present investigations.

Computationally, several software packages are may be sourced on line for solving computational problems related to finite groups. GAP is an abbreviation for Groups, Algorithms and Programming (The GAP Team 1995). Since all symmetry elements of a physical object is a group under composition of functions, the package is useful for this topic. Our calculations are based however on three other packages. These are HyperChem (HyperChem package Release 7.5 for Windows 2002), TopoCluj (Diudea et al. 2002) and MAGMA (Bosma et al. 1997).

Calculations reported in this paper are done by using a combination of these packages. We first draw a nanotube or nanotorus by HyperChem. Then we will compute the adjacency matrix by TopoCluj. We then apply MAGMA and GAP for computing symmetry group. All notations are standard and taken from the standard book of group theory. We encourage to reader to consult the celebrated book of Trinajstić (1992) for more information on symmetry.

6.2 Nanotubes and Nanotori Topological Indices

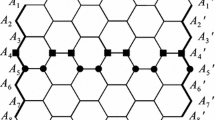
A carbon nanotube is a new allotrope of carbon with a tubular structure at the nanoscale. The molecular graphs of armchair and zig-zag polyhex nanotubes are depicted in Figs. 6.1 and 6.2, respectively. We associate two parameters [r, s] to each armchair and zig-zag polyhex nanotube as follows. In an armchair nanotube, Figs. 6.1 and 6.2, the parameter s denotes the number of vertical zig-zags, while in a zig-zag nanotube, Figs. 6.3 and 6.4, s denotes the number of horizontal zig-zags. On the other hand, the parameter r in an armchair polyhex is the number of rows and in a zig-zag nanotube it returns the number of hexagons in each row.

Fig. 6.1

The molecular graph of an armchair [p, 10] nanotube

Fig. 6.2

The 2D lattice of an armchair [11, 6] nanotube

Fig. 6.3

The molecular graph of a zig-zag [13, 13] nanotube

Fig. 6.4

The 2D lattice of a zig-zag [6, 8] nanotube

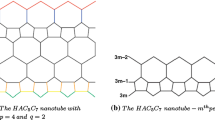
A C ₄ C ₈ net is a trivalent (atom degree 3) decoration made by alternating squares C₄ and octagons C₈. Such a plane covering can be derived from square net by the leapfrog operation, Figs. 6.5 and 6.6. A C₄C₈(R) nanotube is another beautiful mathematical object constructed by squares and octagons. An charming example is shown in Figs. 6.7 and 6.8. A carbon nanotorus is geometrically obtained by connecting the two ends of a carbon nanotube into a ring, Figs. 6.9, 6.10, 6.11 and 6.12.

Fig. 6.5

The molecular graph of a C₄C₈(R) nanotube

Fig. 6.6

The 2D lattice of a C₄C₈(R) nanotube

Fig. 6.7

The molecular graph of a C₄C₈(S) nanotube

Fig. 6.8

The 2D lattice of C₄C₈(S) nanotube

Fig. 6.9

The molecular graph of a C₄C₈(R) nanotorus

Fig. 6.10

The 2D Lattice of C₄C₈(R) Nanotorus

Fig. 6.11

The 2D lattice of C₄C₈(S) nanotorus

Fig. 6.12

The molecular graph of a polyhex nanotorus

The symmetry properties of these nanostructures are one of the main subject of this study.

Suppose $(G,{{\cdot }_{1}})$ and $(H,{{\cdot }_{2}})$ are groups. The cartesian product G × H is the set of all ordered pairs (a, b) where $a\in G$ and $b\in H$, together with the following group structure:

$$ (a\text{ },\text{ }b )*(x,y )=(a{{\cdot }_{1}}x,\text{ }b{{\cdot }_{2}}y) $$

(6.1)

The concept of semi-direct product is a generalization of cartesian product. In the cartesian product of two groups, each component represents in fact a normal subgroup, their intersection is trivial and the components generate the whole group. In the semi-direct product instead we admit one of the subgroup to be non-normal. In mathematical exact phrasing: in semi-direct product a group can be constructed from two subgroups, one of which is a normal subgroup, the intersection of two subgroups is trivial and they generate the group.

It is easy to see that if N and H are groups and φ is a homomorphism of H into the automorphism group of N then the set N × H by operation $({{\text{n}}_{1}},\text{ }{{\text{h}}_{1}})\cdot ({{\text{n}}_{2}},\text{ }{{\text{h}}_{2}})=({{\text{n}}_{\text{1}}}{{{}\varphi{}}_{\text{h}1}}({{\text{n}}_{2}}),\text{ }{{\text{h}}_{1}}{{\text{h}}_{2}}),\text{ }{{\text{n}}_{1}},\text{ }{{\text{n}}_{2}}\in \text{N}$ and h₁, h₂ ∈ H, has a group structure. This group is denoted by N × _φ H and called the semi-direct product of N by H.

A graph invariant is a quantity that is invariant under all graph automorphisms. The topological indices are numerical graph invariants used in theoretical chemistry to encode molecules for the classification an design of chemical compounds with given physico-chemical properties or given pharmacological and biological activities (Trinajstić 1992) (MIHAI). Notice that the bond relations between atoms do not fully determine the molecular geometry and so, in general, topological indices cannot uniquely determine a chemical compound, but they are usually useful to obtain information on some physico-chemical properties of compounds.

We now recall some algebraic definitions used here. Suppose G is a simple graph and $\left\{\text{u,}\,\text{v} \right\}\subseteq \text{V(G)}$. A path connecting u and v in G is a sequence:

$$ \text{u = }{{\text{u}}_{\text{0}}}\text{, }{{\text{e}}_{\text{1}}}\text{, }{{\text{u}}_{\text{1}}}\text{, }{{\text{e}}_{\text{2}}},\,\ldots \text{, }{{\text{e}}_{\text{n}}}\text{, }{{\text{u}}_{\text{n}}}\text{= v}~{} $$

(6.2)

of distinct vertices u₁, …, u_n and distinct edges e₁, …, e_n such that e_i is an edge with end vertices u_i−1 and u_i. The distance d(u, v) is define to be the length of a minimal path connecting u and v. The half-summation of all distances between pairs of vertices in G is called the Wiener index of G which is denoted by W(G). The Wiener index has been the first distance-based graph invariant and it was introduced by an the American chemist Harold Wiener (1947). Suppose e = uv individuates an edge in G. Define quantities m_u(e) and m_v(e) as follows: m_u(e) is defined as the number of edges lying closer to the vertex u than the vertex v, and m_v(e) is defined analogously. The edges equidistant from both ends of the edge uv are not counted. In a similar way, we define n_u(e) to be the number of vertices lying closer to the vertex u than v. The PI index (Khadikar et al. 2001) of G is defined as

$$ \text{PI}(\text{G} )\text{ =}{{\sum }_{\text{e=uv}}}[{{\text{m}}_{\text{u}}}(\text{e} )\text{+ }{{\text{m}}_{\text{v}}}(\text{e} ) ] $$

(6.3)

For acyclic molecular graphs G, Wiener discovered a remarkably simple algorithm for computing W(G). To explain his method, we assume that e = ij is an edge of G, N(i) is the number of vertices of G lying closer to i than to j and N(j) is defined analogously. Thus,

$$ N(i )=\,|\left\{u\in V(G )\text{ }|\text{ }d(u,i )\text{ }<\text{ }d(u,j ) \right\}\left| \quad \text{and}\quad N(j )= \right|\left\{u\in V(G )\text{ }|\text{ }d(u,j )\text{ }<\text{ }d(u,i ) \right\}|~ $$

(6.4)

Then the Szeged index of G is defined as the half-summation of all products N(i)N(j) over all graph edges e = ij. This generalization was conceived by Ivan Gutman (1994) at the Attila Jozsef University in Szeged, and so it was called the Szeged index. It is useful to mention here that Gutman in his 1994 paper proposed the existence of the cyclic index and abbreviated it by W*. In that paper he has not given any name to this index. Khadikar et al. (1995) used the name “Szeged index” and abbreviated as Sz. According to a long-known result in the theory of graph distances, if G is a tree then Sz(G) = W(G), reproducing Wiener’s original method.

Klavžar et al. (1996) proved that for every connected graph G we have W(G) ≤ Sz(G). So it is natural to ask about equality of these graph invariants. To find a characterization of graphs satisfy the equality, we need some notation. A maximal 2-connected subgraph of a connected graph G is called a block of G. The block graphs are those in which every block is a clique. Dobrynin and Gutman (1995) investigated the structure of a connected graph G featuring the property that Sz(G) = W(G). They proved that Sz(G) = W(G) if and only if G is a block graph (Dobrynin et al. 1995). A new proof for this result is recently published (Khodashenas et al. 2011).

The Wiener, PI and Szeged indices are all distance based invariants of a graph. There are some other graph invariants based on degree sequence of the molecular graph under consideration. The first such invariants are Zagreb group indices. The Zagreb indices have been introduced more than forty years ago by Gutman and Trinajstić (1972). They are defined as:

$$ {{M}_{1}}(G )={{\sum }_{v\in V(G )}}deg{{(v )}^{2}}\quad \text{and}\quad {{M}_{2}}(G )={{\sum }_{uv\in E(G )}}deg(u )\times deg(v )~ $$

(6.5)

where deg(u) is the degree of the vertex u of G. A historical background, computational techniques and mathematical properties of Zagreb indices can be found in papers (Gutman and Das 2004; Khalifeh et al. 2009; Zhou 2004; Zhou and Gutman 2005).

The Randić molecular connectivity index, Randić index for short, is a second degree-based topological invariant, introduced in (Randić 1975). It is defined as:

$$ \chi (G)=\sum\nolimits_{uv\in E(G)}{{{(\deg (u)\,\deg (v) )}^{-1/2}}}. $$

(6.6)

It reflects molecular branching and has several applications in chemistry (Klarner 1997).

The atom-bond connectivity (ABC) index is another degree-based topological index introduced by Estrada et al. 1998 to study the stability of alkanes and the strain energy of cycloalkanes. This index is defined as follows:

$$ ABC(G)=\sum\nolimits_{uv\in E(G)}{\sqrt{\frac{\deg (u)+\deg (v)-2}{\deg (u)+\deg (v)}.}}$$

(6.7)

Estrada (2008) presented a new topological approach which provides a good model for the stability of linear and branched alkanes as well as the strain energy of cycloalkanes. He also reported that the heat of formation of alkanes can be obtained as a combination of stabilizing effects coming from atoms, bonds and protobranches. Furtula et al. (2009) studied the mathematical properties of the ABC index of trees. They found chemical trees with extremal ABC values and proved that, among all trees, the star tree S_n, has the maximal ABC index. Das (2010) presented the lower and upper bounds on ABC index of graphs and trees, and characterize graphs for which these bounds are best possible. Fath-Tabar et al. (2011) obtained some inequalities for the atom-bond connectivity index of a series of graph operations and proved that the bounds are tight. They applied their result to compute the ABC indices of C₄ nanotubes and nanotori.

The relationship between degree-based topological indices of graphs is an important problem in chemical graph theory. Das and Trinajstić (2010) compared the GA and ABC indices for chemical trees and molecular graphs and proved some results.

The Balaban index of a molecular graph G is defined by Balaban (1982, 1983) as:

$$J(G) = {{}^{m}\! / \!{}_{{(\mu + 1)\sum_{e = uv} {{{[d(u)d(v)]}^{-0.5}}} }}},$$

(6.8)

where m is the number of edges of G, $\mu (G)=\,|E(G)|-|V(G)|+1$ is the cyclomatic number of G and for every vertex x, d(x) is the summation of topological distances between x and all vertices of G.

In the end of this section the concept of eccentric connectivity index of molecular graphs is presented. Let G be a molecular graph (Sharma et al. 1997; Sardana and Madan 2001). The eccentric connectivity index $\xi (G)$is defined as:

$$ \xi (G)=\sum\nolimits_{u\in V(G)}{{{\deg }_{G}}(u){{\varepsilon }_{G}}(u)} $$

(6.9)

where ${{\deg }_{G}}(u)$ denotes the degree of vertex u and ${{\varepsilon }_{G}}(u)$ is the largest distance between u and any other vertex v of the graph G.

6.3 Symmetry Considerations on Nanotubes and Nanotori

A dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. These groups play an important role in chemistry. Most of point group symmetry of molecules can be described by dihedral groups. It is easy to prove that a group generated by two involutions on a finite domain is a dihedral group. A dihedral group with 2n symmetry elements is denoted by D_n. This group can be presented as follows:

$$ {{\text{D}}_{\text{n}}}\text{=}\left\{\text{x, y}\!\!|\!\!{{\text{x}}^{\text{n}}}\text{= }{{\text{y}}^{\text{2}}}\text{=}{{(\text{xy} )}^{\text{2}}}\text{= 1} \right\} $$

(6.10)

We now consider the molecular graph of a zig-zag and armchair (achiral) polyhex nanotorus . Yavari and Ashrafi (2009) proved in some special cases that the symmetry group of armchair and zig-zag polyhex nanotorus is constructed from a dihedral group and a plane symmetry group of order 2.

Arezoomand and Taeri (2009) presented a generalization of this result. They proved that:

Theorem 1 (Arezoomand and Taeri)

The symmetry group of the molecular graph of a zig-zag and armchair (achiral) polyhex nanotorus is isomorphic to D_4m × Z₂, where Z₂ denotes the cyclic group of order 2.

Hypergraphs are a generalizations of graphs in which an edge can connect more than two vertices. In the graph theoretical language, a hypergraph consists of a set of vertices V and a set of hyper-edges E which is a collection of subsets in V in such a way than the union of hyper-edges are the whole vertices. A k-hypergraph is a hypergraph with the property that any edge connects exactly k vertices. The case of k = 2 corresponds to the usual graphs considered so far. The best generalization of the mentioned result was introduced by Staic and Petrescu-Nita (2013).They studied the symmetry group of two special types of carbon nanotori by using the notion of Cayley hypergraph. To explain this concept, we assume that G is a group and S is a non-empty subset of G such that S = S⁻¹ and $\text{G}=\left\langle \text{S} \right\rangle$. We define a graph Cay(G, S) as follows: (i) V(Cay(G, S)) = G, and, (ii) two vertices a and y are adjacent if and only if $\text{x}{{\text{y}}^{-1}}\in \text{S}$. The graph Cay(G, S) is called the Cayley graph of G constructed by S. If G is a group and T is a generator set for G containing elements of order 3 such that $\text{a}\in \text{T}$ implies that ${{\text{a}}^{-\text{1}}}\notin \text{T}$ then 3-hypergraph Cay₃(G, T) can be defined as follows: take the set of vertices to be G. A cyclically ordered 3-subset {g₁, g₂, g₃} is a hyper-edge if there exists $\text{a}\in \text{T}$ such that g₂ = g₁a and g₃ = g₁a. The main result of Staica and A. Petrescu-Nita is as follows:

Theorem 2 (Staic and Petrescu-Nita)

Suppose T_n is a group presented as follows:

$$ {{\text{T}}_{\text{n}}}\text{=}\{\text{a; b}\!\!|\!\!{{\text{a}}^{\text{3}}}\text{= 1; }{{\text{b}}^{\text{3}}}\text{= 1; }{{(\text{ab} )}^{\text{3}}}\text{= 1; }{{(\text{a}{{\text{b}}^{\text{2}}})}^{\text{n}}}\text{= 1}\}{} $$

(6.11)

Then T_n is a semi-direct product of Z_n × Z_n by Z₃. Moreover, the Cayley hypergraph associated with the group T_n can be placed on a torus.

If SL(2,3) denotes the set of all 2 × 2 matrices over a field of order 3 then a Cayley hypergraph associated with this group can be placed on a torus.

We end this section by a result on the symmetry group of nanotubes. Suppose A[p, q], B[p, q], C(R)[p, q] and C(S)[p, q] are zig-zag polyhex, armchair polyhex, C₄C₈(R) and C₄C₈(S) nanotubes with parameters p and q, respectively.

Theorem 3

The symmetry groups of A[p, q], B[p, q], C(R)[p, q] and C(S)[p, q] are computed as follows:

1. $\text{Aut}(\text{A}[\text{p, q}]{} )=\left\{\begin{array}{*{35}{l}}{{D}_{4p}}& p\not{=}q\\ {{C}_{2}}\times {{D}_{2p}}& p=q\\\end{array}, \right.$

2. $\text{If q is even and p}\ne \text{3 then}\,\text{Aut(B}[\text{p, q}]\text{) = }\left\{\begin{array}{*{35}{l}}{{D}_{2q}}& p\,is\,even\\ \begin{array}{*{35}{l}}{{D}_{2q}}& \frac{q}{2}\,is\,odd\\ {{C}_{2}}\times {{D}_{q}}& \frac{q}{2}\,is\,even\\\end{array} & p\,is\,odd\\\end{array} \right.,$

3. If p ≠ 2 then $\text{Aut}(\text{C}(\text{R} )[\text{p,q} ] )\cong \text{Aut}(\text{C}(\text{S} )[\text{p,q} ] )\cong {{\text{Z}}_{\text{2}}}\times {{\text{D}}_{\text{2p}}}.$ Moreover, if p = 2 then $\text{Aut}(\text{C}(\text{S} )[\text{2,1} ] )\cong {{\text{Z}}_{\text{2}}}{}\times{}\,{{\text{D}}_{8}}$ and $\text{Aut}(\text{C}(\text{S} )[\text{2, q} ] ) ={{\text{C}}_{\text{2}}}{}\times{}{{\text{C}}_{\text{2}}}{}\times{}{{\text{C}}_{\text{2}}},$ when q ≠ 1.

Previous theorems clearly illustrate the power of topological methods in predicting geometrical properties of carbon nanostructures.

6.4 Topology of Nanotubes and Nanotori

The history of computing topological indices of nanotubes and nanotori started by publishing two paper by Diudea and his co-workers (Diudea et al. 2004; John and Diudea 2004) about Wiener index armchair and zig-zag polyhex nanotubes. After publishing these seminal papers, several scientists focus on computing such numbers for the molecular graphs of nanostructures. For the sake of completeness we record the mentioned results of Diudea and his co-workers in Theorem 4.

Theorem 4

Suppose A = A[p, q] and B = B[p, q] are zig-zag and armchair polyhex nanotubes, respectively. Then the Wiener index of these nanotubes can be computed by the following formulas:

1) $\text{W(A)}=\left\{ \begin{aligned}\frac{q{{\text{p}}^{2}}}{24}(4{{\text{q}}^{2}}+3\text{qp}-4)+\frac{{{\text{q}}^{2}}\text{p}}{12}({{\text{q}}^{2}}-1) & \text{q}\le \frac{\text{p}}{2}+1 \\\frac{\text{q}{{\text{p}}^{2}}}{24}(8{{\text{q}}^{2}}+{{\text{p}}^{2}}-6)-\frac{{{\text{p}}^{3}}}{192}({{\text{p}}^{2}}-4) & \text{q}>\frac{\text{p}}{2}+1 \\\end{aligned} \right.,$

2) $\text{W(B)}=\left\{\begin{array}{*{35}{l}}\frac{\text{p}}{\text{12}}[{{\text{p}}^{\text{2}}}(\text{12}{{\text{q}}^{\text{2}}}-\text{2}{{\text{p}}^{\text{2}}}\text{+}\,\text{8} )\text{+8pq}({{\text{p}}^{\text{2}}}\text{+}\,{{\text{q}}^{\text{2}}}-\text{2} )\text{+}\,\text{3}(-\text{1+}\,{{(-\text{1)}}^{\text{p}}}) ] & {} & \text{q}\ge \text{p}\\ \frac{\text{p}}{\text{12}}[\text{24}{{\text{p}}^{\text{2}}}{{\text{q}}^{\text{2}}}\text{+}\,\text{2}{{\text{q}}^{\text{4}}}-\text{8}{{\text{q}}^{\text{2}}}\text{+3}\,{{(-\text{1)}}^{\text{p}}}(\text{1}-{{(-\text{1)}}^{\text{q}}}) ] & {} & \text{q}\le \text{p}\\\end{array} \right..$

In a series of papers (Yousefi and Ashrafi 2006, 2007, 2008a, 2011; Yousefi et al. 2008c, d; Ashrafi and Yousefi 2007a, b) introduced a matrix method to recalculate the Wiener number of armchair, zig-zag polyhex nanotubes, C₄C₈(R/S) nanotube , polyhex nanotorus and C₄C₈(R/S) nanotorus . Choose a zig-zag polyhex nanotube T. The main idea of this matrix method is choosing a base vertex b from the 2-dimensional lattice of a T and then label vertices of hexagon by starting from the hexagon containing b. By computing distances between b and other vertices, we can obtain a distance matrix of nanotubes related to the vertex b. It is clear that by choosing different base vertices, one can find different distance matrices for T, but the summation of all entries will be the same. To explain, we assume that b is a base vertex from the 2-dimensional lattice of T and x_ij is the (i, j)^th vertex of T, Fig. 6.6. Define $D_{m\times n}^{(1,1)}=[d_{i,j}^{(1,1)}],$ where $d_{i,j}^{(1,1)}$ is distance between (1,1) and (i, j), i = 1, 2, …, m and j = 1, 2, …, n. There are two separates cases for the (1,1)^th vertex, where in the first case $d_{1,1}^{(1,1)}=0,\,d_{1,2}^{(1,1)}=d_{2,1}^{(1,1)}=1$ and in the second case $d_{1,1}^{(1,1)}=0,\,d_{1,2}^{(1,1)}=1,\,d_{2,1}^{(1,1)}=3.$ Suppose $D_{m\times n}^{(p,q)}$ is distance matrix of T related to the vertex (p, q) and $s_{i}^{(p,q)}$ is the sum of i^th row of $D_{m\times n}^{(p,q)}$. Then there are two distance matrix related to (p, q) such that $s_{i}^{(p,2k-1)}=s_{i}^{(p,1)}\,;~s_{i}^{(p,2k)}=s_{i}^{(p,2)}\,;~1\le k\le n/2,~1\le i\le m,~1\le p\le m.$ If b varies on a column of T then the sum of entries in the row containing base vertex is equal to the sum of entries in the first row of $D_{m\times n}^{(1,1)}$. On the other hand, one can compute the summation of all entries in other rows by distance from the position of base vertex. Therefore, if 2 | (i + j) then

$$ s_{k}^{(i,j)}=\left\{\begin{matrix} s_{i-k+1}^{(1,1)}\quad \quad 1\le k\le i\le m,\quad 1\le j\le n\\ s_{k-i+1}^{(1,2)}\quad \quad 1\le i\le k\le m,\quad 1\le j\le n\end{matrix} \right. $$

and if 2 $\not{|}$(i + j) then we have$s_{k}^{(i,j)}=\left\{\begin{matrix} s_{i-k+1}^{(1,2)}\quad \quad 1\le k\le i\le m,\quad 1\le j\le n\\ s_{k-i+1}^{(1,1)}\quad \quad 1\le i\le k\le m,\quad 1\le j\le n\end{matrix} \right..$

We now describe our algorithm to compute distance matrix of a zig-zag polyhex nanotube. To do this, we define matrices $A_{m\times (n/2+1)}^{(a)}=[{{a}_{ij}}],~{{B}_{m\times (n/2+1)}}=[{{b}_{ij}}]$ and $A_{m\times (n/2+1)}^{(b)}=[{{c}_{ij}}]$ as follows: (Fig. 6.13).

Fig. 6.13

Two Basically Different Cases for the Vertex b

For computing distance matrix of this nanotube we must compute matrices $D_{m\times n}^{(a)}=[d_{i,j}^{a}]$ and $D_{m\times n}^{(b)}=[d_{i,j}^{b}]$. By these calculations, on can see that

$$ d_{i,j}^{a}=\left\{\begin{matrix} Max\{{{a}_{i,j}},{{b}_{i,j}}\}\quad 1\le j\le n/2\\ {{d}_{i,n-j+2}}\quad \quad \quad j>n/2+1\end{matrix} \right.\quad and\quad d_{i,j}^{b}=\left\{\begin{matrix} Max\{{{a}_{i,j}},{{c}_{i,j}}\}\quad 1\le j\le n/2\\ {{d}_{i,n-j+2}}\quad \quad \quad j>n/2+1\end{matrix} \right.. $$

By continuing this method, the mentioned authors proved that:

Theorem 5

Suppose A and B are an armchair and zig-zag polyhex nanotube, respectively, with exactly m rows and n columns, Fig. 6.2. Moreover, we assume that C is a polyhex nanotorus with similar parameters. Then,

• 1. (Yousefi and Ashrafi 2007)

$$ \text{W(A)}=\left\{\begin{array}{*{35}{l}}\frac{{{\text{m}}^{2}}\text{n}}{12}(3{{\text{n}}^{2}}+{{\text{m}}^{2}}-4 )+\frac{\text{n}}{8}{{(-1)}^{\frac{\text{n}}{2}}}[1-{{(-1)}^{\text{n}}}] & {} & \text{m}\le \frac{\text{n}}{2}+1\\ \frac{\text{m}{{\text{n}}^{2}}}{24}({{\text{n}}^{2}}+4{{\text{m}}^{2}}+3\text{mn}-8 )-\frac{{{\text{n}}^{3}}}{192}({{\text{n}}^{2}}-16 )+\frac{\text{n}}{8}\left[{{(-1)}^{\frac{\text{n}}{2}}}-1 \right] & {} & \text{m}>\frac{\text{n}}{2}+1\\\end{array} \right., $$

• 2. (Ashrafi and Yousefi 2007a)

$$ \text{W(B)}=\left\{\begin{array}{*{35}{l}}\frac{\text{m}{{\text{n}}^{2}}}{24}(4{{\text{m}}^{2}}+3\text{mn}-4 )+\frac{{{\text{m}}^{2}}\text{n}}{12}({{\text{m}}^{2}}-1 ) & {} & \text{m}\le \frac{\text{n}}{2}+1\\ \frac{\text{m}{{\text{n}}^{2}}}{24}(8{{\text{m}}^{2}}+{{\text{n}}^{2}}-6 )-\frac{{{\text{n}}^{3}}}{192}({{\text{n}}^{2}}-4 ) & {} & \text{m}>\frac{\text{n}}{2}+1\\\end{array} \right.. $$

• 3. Yousefi-Azari et al. (2008e)

$$ \text{W(C)}=\left\{\begin{array}{*{35}{l}}\frac{\text{p}{{\text{q}}^{2}}}{24}(6{{\text{p}}^{2}}+{{\text{q}}^{2}}-4 ) & {} & \text{q}<\text{p}\\ \frac{{{\text{p}}^{2}}\text{q}}{24}(3{{\text{q}}^{2}}+3\text{pq}+{{\text{p}}^{2}}-4 ) & {} & \text{q}\ge \text{p}\\\end{array} \right.. $$

Suppose E = TUC₄C₈(R)[m, n], F = TUC₄C₈(S)[m, n] are two different types of C₄C₈ nanotubes and G = TC₄C₈(R)[m, n] is a C₄C₈ nanotorus in terms of the number of rhombs in a fixed row (m) and column (n). We have

Theorem 6

The Wiener indices of E, F, G and H can be computed as follows:

• 1. (Yousefi and Ashrafi 2006)

$$ \text{W(E)}=\left\{\begin{array}{*{35}{l}}\frac{2\text{m}}{3}({{\text{m}}^{2}}-1 )+\text{mn}(\text{m}+3\text{n})-{{\text{k}}_{1}}& {} & \text{m}<\text{n}\\ \frac{2\text{n}}{3}({{\text{n}}^{2}}-1 )+\text{mn}(3\text{m}+\text{n})-{{\text{k}}_{2}}& {} & \text{m}>\text{n}\\ \frac{\text{n}}{3}(14{{\text{n}}^{2}}-{{\text{k}}_{3}}) & {} & \text{m}=\text{n}\\\end{array} \right. $$

in which ${{\text{k}}_{\text{1}}}=\left\{\begin{array}{*{35}{l}}0 & {} & 2|\text{n}\,\And \,2|\text{m}\\ \text{n}-\text{m} & {} & 2|\text{n}\,\And \,2\not{|}\text{m}\\ \text{m} & {} & 2\not{|}\text{n}\,\And \,2|\text{m}\\ \text{n} & {} & 2\not{|}\text{n}\,\And \,2\not{|}\text{m}\\\end{array} \right.~\quad {{\text{k}}_{\text{2}}}=\left\{\begin{array}{*{35}{l}}0 & {} & 2|\text{m}\\ \text{m} & {} & 2\not{|}\text{m}\\\end{array} \right.\quad {{\text{k}}_{\text{3}}}=\left\{\begin{array}{*{35}{l}}2 & {} & 2|\text{n}\\ 5 & {} & 2\not{|}\text{n}\\\end{array} \right..$

• 2. (Ashrafi and Yousefi 2007b)

$$ \text{W(F)}=\left\{\begin{array}{*{35}{l}}\frac{\text{n}{{\text{m}}^{2}}}{6}(6{{\text{m}}^{2}}+3\text{nm}+{{\text{n}}^{2}}-4 ) & {} & \text{n}\le \text{m}\\ \frac{\text{m}{{\text{n}}^{2}}}{6}(6{{\text{n}}^{2}}+3\text{mn}+{{\text{m}}^{2}}-4 ) & {} & \text{m}<\text{n}\\\end{array} \right.. $$

• 3. (Yousefi and Ashrafi 2008b, 2011)

$$ \text{W(G)}=\left\{\begin{array}{*{35}{l}}\frac{2\text{m}{{\text{n}}^{2}}}{3}(4{{\text{m}}^{2}}+9\text{mn}-4 )+\frac{{{\text{m}}^{2}}\text{n}}{6}[16{{\text{m}}^{2}}-7+3{{(-1)}^{\text{n}}}] & {} & \begin{aligned}& \text{m}\le \frac{\text{n}+1}{2} \\& \end{aligned}\\ \begin{aligned}& \frac{2\text{m}{{\text{n}}^{2}}}{3}(12{{\text{m}}^{2}}+3\text{mn}+2{{\text{n}}^{2}}-5 )-\frac{{{\text{n}}^{3}}}{6}({{\text{n}}^{2}}-1 ) \\& -\frac{\text{n}}{8}(8{{\text{m}}^{2}}+{{\text{n}}^{2}}-4\text{mn}-1 )[1-{{(-1)}^{\text{n}}}] \end{aligned} & {} & \begin{aligned}&\\& \text{m}>\frac{\text{n}+1}{2} \end{aligned}\\\end{array} \right.. $$

Suppose e = uv and M(e) denotes the number of edges that are equidistant to the vertices u and v (including the edge e itself), then evidently m_u(e) + m_v(e) + M(e) = m. Therefore, $\text{PI(G)}={{\text{m}}^{2}}-\sum\nolimits_{e=uv}{\text{M(e}).}$ Using this simple equation, it can be proved that if G is an acyclic graph containing n vertices then PI(G) = (n − 1)(n − 2). In particular, PI = 0, for acyclic graphs when n = 1 and 2. Since every acyclic graph with n vertices has exactly m = n−1 edges, the previous result states that in every acyclic graph G with m edges PI(G) = m(m − 1).

The notion of PI partition was introduced by Klavžar (2007) to find a formula for the PI index of product graphs. Suppose G is a graph and X is a subset of V(G). The subgraph of G induced by X will be denoted 〈X〉. Moreover, let ∂X stands for the set of edges of G with one end vertex in X and the other not in X. For an edge e = uv of G, we define V₁(e) and V₂(e) as follows:

$${{\text{V}}_{\text{1}}}\left({\text{e}}\right){\text{ = }}\left\{{{\text{x}}\in {\text{V}}\left({\text{G}}\right){\text{ }|\text{d}}\left({{\text{x,u}}}\right){\text{ < d}}\left({{\text{x,v}}}\right)}\right\}\quad {\text{and}}\quad {{\text{V}}_{\text{2}}}\left({\text{e}}\right){\text{ = }}\left\{{{\text{x}}\in {\text{V}}\left({\text{G}}\right){\text{ }|\text{d}}\left({{\text{x,u}}}\right){\text{> d}}\left({{\text{x,v}}}\right)}\right\}{\text{.}}$$

It is easily seen that if G is bipartite then for any edge e of G, V₁(e) and V₂(e) form a partition of V(G). We say that a partition E₁, …, E_k of E(G) is a PI-partition of G if for any i, 1 ≤ i ≤ k, and for any e, f ∈ E_i we have V₁(e) = V₁(f) and V₂(e) = V₂(f). If e = uv is an edge a G then we define V₃(e) to be the set of all vertices that are at equal distance from u and v. Thus $\text{V(G})={{\text{V}}_{\text{1}}}\text{(e)}\cup {{\text{V}}_{\text{2}}}\text{(e})\cup {{\text{V}}_{\text{3}}}\text{(e})$. Klavžar (2007) proved that if E₁, …, E_k is a PI-partition of a graph G then $\text{PI}(\text{G} )={{\left| \text{E}(\text{G} ) \right|}^{2}}-\sum\nolimits_{\text{i}=1}^{\text{k}}{|{{\text{E}}_{\text{i}}}|(|{{\text{E}}_{\text{i}}}|+|\text{E}(< {{\text{V}}_{3}}(\text{e})>)|+|\partial {{\text{V}}_{3}}(\text{e})| )}$. If G is bipartite then $\partial {{\text{V}}_{3\,}}(\text{e})={{\text{V}}_{\text{3}}}\text{(e})=\varnothing$; and consequently $\text{PI}(\text{G} ) ={{\left| \text{E}(\text{G} ) \right|}^{\text{2}}}-\sum\nolimits_{i=1}^{k}{|{{E}_{i}}{{|}^{2}}.}$

Using the mentioned method of Klavžar or a straightforward calculation by the mentioned simple equation, one can prove the following two results:

Theorem 7

The PI index of armchair polyhex, zig-zag polyhex and polyhex nanotorus nanotubes can be computed as follows:

• 1. (Ashrafi and Loghman 2006a)

$$\text{PI}\left( \text{B}\left[ \text{2p,q} \right] \right)=\left\{ \begin{array}{*{35}{l}} \left\{ \begin{array}{*{35}{l}}\text{X}-\text{p} & \text{q}\le \text{p}+1 \\ \text{Y}-\text{p} & \text{q}\ge \text{p}+1 \\ \end{array} \right. & 2|\text{p}\,\And \,2|\text{q}-1 \\\left\{ \begin{array}{*{35}{l}} \text{X} & \text{q}\le \text{p}+1 \\ \text{Y} & \text{q}\ge \text{p}+1 \\ \end{array} \right. & \text{Otherwise} \\ \end{array} \right.,$$

where $\text{X = 9}{{\text{p}}^{\text{2}}}{{\text{q}}^{\text{2}}}\text{-- 12}{{\text{p}}^{\text{2}}}\text{q -- 5p}{{\text{q}}^{\text{2}}}\text{+ 8pq + 4}{{\text{p}}^{\text{2}}}\text{-- 4p}$ and $\text{Y = 9}{{\text{p}}^{\text{2}}}{{\text{q}}^{\text{2}}}\text{-- 20}{{\text{p}}^{\text{2}}}\text{q --p}{{\text{q}}^{\text{2}}}\text{+ 4pq + 4}{{\text{p}}^{\text{3}}}\text{+ 8}{{\text{p}}^{\text{2}}}\text{-- 4p}.$

• 2. (Ashrafi and Loghman 2006b)

$$\text{PI}(\text{A}[2\text{p,}\,\text{q}]=\left\{\begin{array}{*{35}{l}}{{\text{p}}^{2}}(9{{\text{q}}^{2}}-7\text{q}+2 )-4\text{p}{{\text{q}}^{2}}& {} & \text{q}\le \text{p}\\ {{\text{p}}^{2}}(9{{\text{q}}^{2}}-15\text{q}+4\text{p}-2 )+4\text{pq} & {} & \text{q}\ge \text{p}\\\end{array}. \right.$$

• 3. (Ashrafi and Rezaei 2007)

$$ \text{PI(C) = }\left\{\begin{array}{*{35}{l}}9{{\text{p}}^{2}}{{\text{q}}^{2}}-\text{p}{{\text{q}}^{2}}-12{{\text{p}}^{2}}\text{q}+4\text{pq} & \text{q}\ge 2\text{p} & {}\\ 9{{\text{p}}^{2}}{{\text{q}}^{2}}-7\text{p}{{\text{q}}^{2}}+4\text{pq} & \text{q}<2\text{p} & {}\\\end{array} \right. $$

Theorem 8

The PI index of TUC₄C₈(R/S) nanotubes and TC₄C₈(R/S) nanotori can be computed as follows:

• 1. (Ashrafi and Loghman 2008)

$$\text{PI(E }\!\![\!\!\text{ p,}\,\text{q }\!\!]\!\!\text{ )}=\left\{ \begin{array}{*{35}{l}} \left\{ \begin{array}{*{35}{l}} 36{{\text{p}}^{2}}{{\text{q}}^{2}}-26\text{p}{{\text{q}}^{2}}-2{{\text{p}}^{2}}\text{q}+8\text{pq} & \text{q}<\text{p} \\ 36{{\text{p}}^{2}}{{\text{q}}^{2}}-26{{\text{p}}^{2}}\text{q}-2\text{p}{{\text{q}}^{2}}+8\text{pq} & \text{q}\ge \text{p} \\\end{array} \right. & \text{if} & \text{p}\,\text{ }\!\!\And\!\!\text{ }\,\text{q}\,\text{are}\,\text{even } \\\left\{ \begin{array}{*{35}{l}} 36{{\text{p}}^{2}}{{\text{q}}^{2}}-10\text{p}{{\text{q}}^{2}}-2{{\text{p}}^{2}}\text{q}\quad \quad & \text{q}<\text{p} \\36{{\text{p}}^{2}}{{\text{q}}^{2}}-10{{\text{p}}^{2}}\text{q}-2\text{p}{{\text{q}}^{2}} & \text{q}\ge \text{p} \\\end{array} \right. & \text{if} & \text{p}\,\text{ }\!\!\And\!\!\text{ }\,\text{q}\,\text{are}\,\text{odd} \\\left\{ \begin{array}{*{35}{l}} 36{{\text{p}}^{2}}{{\text{q}}^{2}}-18\text{p}{{\text{q}}^{2}}-2{{\text{p}}^{2}}\text{q} & \text{q}<\text{p} \\36{{\text{p}}^{2}}{{\text{q}}^{2}}-18{{\text{p}}^{2}}\text{q}-2\text{p}{{\text{q}}^{2}}+8\text{pq} & \text{q}>\text{p} \\\end{array} \right. & \text{if} & \text{p}\,\text{is}\,\text{even}\,\text{ }\!\!\And\!\!\text{ }\,\text{q}\,\text{is}\,\text{odd} \\\left\{ \begin{array}{*{35}{l}} 36{{\text{p}}^{2}}{{\text{q}}^{2}}-18{{\text{p}}^{2}}\text{q}-2\text{p}{{\text{q}}^{2}} & \text{q}>\text{p} \\ 36{{\text{p}}^{2}}{{\text{q}}^{2}}-18\text{p}{{\text{q}}^{2}}-2{{\text{p}}^{2}}\text{q}+8\text{pq} & \text{q}<\text{p} \\\end{array} \right. & \text{if} & \text{p}\,\text{is}\,\text{odd}\,\text{ }\!\!\And\!\!\text{ }\,\text{q}\,\text{is}\,\text{even} \\ \end{array} \right.$$

• 2. (Ashrafi and Loghman 2006c)

$$\text{PI}(\text{F}[\text{4p,q} ] )\text{ =}\left\{\begin{array}{*{35}{l}}\text{X} & \text{q}\le \text{p}\\ \text{Y} & \text{q}\ge \text{p}\\\end{array} \right.,$$

where $\text{X = 36}{{\text{p}}^{\text{2}}}{{\text{q}}^{\text{2}}}\text{-- 28}{{\text{p}}^{\text{2}}}\text{q +8}{{\text{p}}^{\text{2}}}\text{-8p}{{\text{q}}^{\text{2}}}$ and $\text{Y = 36}{{\text{p}}^{\text{2}}}{{\text{q}}^{\text{2}}}\text{-- 36}{{\text{p}}^{\text{2}}}\text{q -- 4p}{{\text{q}}^{\text{2}}}\text{+ 4pq + 4}{{\text{p}}^{\text{3}}}\text{+ 4}{{\text{p}}^{\text{2}}}.$

• 3. (Ashrafi et al. 2009)

$$ \text{PI(G}[\text{p,}\,\text{q}]{})=\left\{\begin{array}{*{35}{l}}36{{\text{p}}^{2}}{{\text{q}}^{2}}-8{{\text{p}}^{2}}\text{q}-10\text{p}{{\text{q}}^{2}}+4\text{pq} & {} & \text{q}\le 2\text{p}\\ 36{{\text{p}}^{2}}{{\text{q}}^{2}}-20{{\text{p}}^{2}}\text{q}-4\text{p}{{\text{q}}^{2}}+4\text{pq} & {} & \text{q}>2\text{p}\\\end{array} \right.. $$

We are now ready to investigate the Szeged index of nanotubes and nanotori. Dobrynin and Gutman (1994) proved that if G is a connected bipartite graph with n vertices and m edges, then $Sz(G)=\frac{1}{4}\left( {{n}^{2}}m-\sum\limits_{e\in E(G)}{{{(d(u)-d(v))}^{2}}} \right)$. Using this result Yousefi et al. (2008d) proved that the Szeged index of a polyhex nanotorus is computed by $\text{Sz(C)}=\frac{3}{8}{{\text{p}}^{3}}{{\text{q}}^{3}}.$ Another application of the mentioned result of Dobrynin and Gutman is computing Szeged index of C₄C₈(S) nanotubes. In (Heydari and Taeri 2009) and (Manoochehrian et al. 2008) the Szeged index of TUC₄C₈(S)[p, q] and zig-zag polyhex nanotubes are computed as follows:

Theorem 9

Suppose F denotes the TUC₄C₈(S)[p, q] nanotube. Then

• 1. If q ≤ p, then the Szeged index of F is given by the following formula:

$$ \text{Sz(F)}=\frac{\text{pq}}{3}(-2{{\text{q}}^{4}}+(64{{\text{p}}^{2}}+2 ){{\text{q}}^{2}}-16{{\text{p}}^{2}}). $$

• 2. If q > p, then Szeged index of long TUC₄C₈(S) nanotubes is given by

$${\text{Sz(F)}} = \left\{{\begin{array}{*{20}{l}} {\frac{{\text{p}}}{{15}}\left({12{{\text{p}}^5}-80{\text{q}}{{\text{p}}^4} + \left({160{{\text{q}}^2}-20}\right){{\text{p}}^3} + 200{{\text{q}}^3}{{\text{p}}^2}}\right.}&{}&{} \\ {\left.{ + \left({20{{\text{q}}^4}-60{{\text{q}}^2} + 8}\right){\text{p}}-2{\text{q}}\left({{{\text{q}}^4}-5{{\text{q}}^2} + 4}\right)}\right)}&{}&{{\text{q}}\le 2{\text{p}}} \\ {\frac{{{{\text{p}}^2}}}{{15}}\left({-52{{\text{p}}^4} + 80{\text{q}}{{\text{p}}^3} + 60{{\text{p}}^2} + \left({280{{\text{q}}^3}-120{\text{q}}}\right){\text{p}}-8}\right)}&{}&{{\text{q}}>2{\text{p}}}\end{array}}\right..$$

• 3. The Szeged index of zig-zag polyhex nanotube is as follows.

$$ \text{Sz(A}[\text{p,}\,\text{q}])=\left\{\begin{array}{*{35}{l}}\frac{8}{3}{{\text{p}}^{3}}{{\text{q}}^{3}}-\frac{2}{3}{{\text{p}}^{3}}\text{q}+\frac{1}{6}\text{p}{{\text{q}}^{3}}-\frac{1}{6}\text{p}{{\text{q}}^{5}}& \text{q}\le \text{p}\\ \frac{5}{2}{{\text{p}}^{6}}+\frac{43}{6}{{\text{p}}^{5}}+\frac{35}{6}{{\text{p}}^{4}}+\frac{5}{6}{{\text{p}}^{3}}-\frac{1}{3}{{\text{p}}^{2}}& \text{q}=\text{p}+1\\ \frac{2}{3}{{\text{p}}^{3}}{{\text{q}}^{3}}+\frac{2}{3}{{\text{p}}^{3}}\text{q}-\frac{2}{15}\text{pq}+\frac{2}{15}{{\text{p}}^{2}}-\frac{1}{5}\text{p}{{\text{q}}^{5}}+\frac{4}{3}{{\text{p}}^{2}}{{\text{q}}^{4}}& {}\\ -\frac{5}{3}\text{p}{{\text{q}}^{3}}+\frac{8}{3}{{\text{p}}^{2}}{{\text{q}}^{2}}-\frac{1}{3}{{\text{p}}^{4}}-\frac{4}{3}{{\text{p}}^{5}}\text{q}+\frac{1}{5}{{\text{p}}^{6}}& \text{p}+1<\text{q}<2\text{p}\\ \frac{89}{5}{{\text{p}}^{6}}-\frac{5}{3}{{\text{p}}^{4}}-\frac{1}{15}{{\text{p}}^{2}}& \text{q}=2\text{p}\\ 2{{\text{p}}^{3}}{{\text{q}}^{3}}-\frac{4}{3}{{\text{p}}^{3}}\text{q}-\frac{2}{15}{{\text{p}}^{2}}+\frac{4}{3}{{\text{p}}^{5}}\text{q}-\frac{13}{15}{{\text{p}}^{6}}+{{\text{p}}^{4}}& \text{q}>2\text{p}\\\end{array}. \right. $$

Recently, (Farahani 2012) computed some degree-based topological indices of zig-zag and armchair polyhex nanotubes. His calculations shows that ${}\chi\text{(A}[\text{m,}\,\text{n}])=\text{mn}+2\text{m}\left(\frac{\sqrt{6}-1}{3} \right),$ $\text{ABC(A}[\text{m,}\,\text{n}])=2\text{mn}+2\text{m}\left(\sqrt{2}-\frac{2}{3} \right),$ M₁(A[m, n]) = 18mn + 8, M₂(A[m, n]) = 27mn + 6, ${}\chi\text{(B}[\text{m,}\,\text{n}])=\left(\text{n}+\frac{\sqrt{6}-1}{3}+\frac{1}{2} \right)\text{m,}$ $\text{ABC(B }\!\![\!\!\text{ m,}\,\text{n }\!\!]\!\!\text{ )}=\left( 2\text{n}+\frac{3\sqrt{2}}{2}-\frac{2}{3} \right)\text{m},$ M₁(B[m, n]) = 18mn + 8 and M₂(B[m, n]) = 27mn + 7m. Moreover, (Asadpour et al. 2011) proved that ${}\chi\text{(E}[\text{p,}\,\text{q}])=4\text{pq}$, ${{\text{M}}_{\text{2}}}\text{(E}[\text{p,}\,\text{q}])=108\text{pq}$, $\text{ABC(E}[\text{p,}\,\text{q}]{})=\frac{12\sqrt{2}}{\sqrt{3}}\text{pq}$, ${}\chi\text{(F}[\text{p,}\,\text{q}])=6\text{pq}+\left(\frac{4}{\sqrt{6}}-3 \right)(\text{p}+\text{q})+4-\frac{2}{\sqrt{6}}$, ${{\text{M}}_{\text{2}}}\text{(F}[\text{p,}\,\text{q}])=16(3\text{pq}+\text{p}+\text{q}-1)$ and $\text{ABC(F}[\text{p,}\,\text{q}])=\sqrt{2}(8\text{pq}-3\text{p}-3\text{q}+4)+4\sqrt{\frac{3}{5}(\text{p}+\text{q}-2)}.$

The Balaban index J which is defined as the average distance sum connectivity is the least degenerate single topological index proposed till now. The mathematical properties of this distance-based topological index in the classes of polyhex and TUC₄C₈(R/S) nanotori are investigated by (Iranmanesh and Ashrafi 2007). They proved that:

Theorem 10

Suppose C[m, n], E[m, n] and F[m, n] are polyhex and TUC₄C₈(R/S) nanotori, respectively. Then,

$$ \text{a) J(C}[\text{m,}\,\text{n}]\text{) =}\left\{\begin{array}{*{35}{l}}\frac{12{{\text{m}}^{2}}\text{n}}{(\text{mn}+4)(6{{\text{m}}^{2}}+{{\text{n}}^{2}}-4 )} & \text{n}<\text{m}\\ \frac{12\text{m}{{\text{n}}^{2}}}{(\text{mn}+4)(3{{\text{n}}^{2}}+3\text{mn}+{{\text{m}}^{2}}-4 )} & \text{n}\ge \text{m}\\\end{array}, \right.\text{ } $$

$$ \text{b) J(E}[\text{m,}\,\text{n}]{}=\left\{\begin{array}{*{35}{l}}\frac{108{{\text{m}}^{3}}{{\text{n}}^{3}}}{(\text{mn}+1)[2\text{m}({{\text{m}}^{2}}-1 )+3\text{mn}(\text{m}+3\text{n})-3{{\text{k}}_{1}}]} & \text{m}<\text{n}\\ \frac{108{{\text{m}}^{3}}{{\text{n}}^{3}}}{(\text{mn}+1)[2\text{n}({{\text{n}}^{2}}-1 )+3\text{mn}(3\text{m}+\text{n})-3{{\text{k}}_{2}}]} & \text{m}>\text{n}\\ \frac{108{{\text{m}}^{2}}{{\text{n}}^{3}}}{({{\text{n}}^{2}}+1 )(14{{\text{n}}^{2}}-{{\text{k}}_{3}})} & \text{m}=\text{n}\\\end{array} \right., $$

in which ${{\text{k}}_{\text{1}}}=\left\{\begin{array}{*{35}{l}}0 & \text{if} & 2|\text{n} & \And& 2|\text{m}\\ \text{n}-\text{m} & \text{if} & 2|\text{n} & \And& 2\not{|}\text{m}\\ \text{m} & \text{if} & 2\not{|}\text{n} & \And& 2|\text{m}\\ \text{n} & \text{if} & 2\not{|}\text{n} & \And& 2\not{|}\text{m}\\\end{array} \right.,\quad {{\text{k}}_{\text{2}}}=\left\{\begin{array}{*{35}{l}}0 & \text{if} & 2|\text{m}\\ \text{m} & \text{if} & 2\not{|}\text{m}\\\end{array} \right.,\quad \text{k3}=\left\{\begin{array}{*{35}{l}}2 & \text{if} & 2|\text{n}\\ 5 & \text{if} & 2\not{|}\text{n}\\\end{array}, \right.$ and, “|” denotes the divisibility relation.

$$ \text{c) J(F}[\text{m,}\,\text{n}]\text{) = }\left\{\begin{array}{*{35}{l}}\frac{54\text{m}{{\text{n}}^{2}}}{(\text{mn}+2)(6{{\text{n}}^{2}}+3\text{nm}+{{\text{m}}^{2}}-4 )} & \text{n}\le \text{m}\\ \frac{54\text{m}{{\text{n}}^{2}}}{(\text{mn}+2)(6{{\text{m}}^{2}}+3\text{mn}+{{\text{n}}^{2}}-4 )} & \text{m}<\text{n}\\\end{array} \right. $$

In the end of this chapter we report two recent results in computing eccentric connectivity index of nanotubes and nanotori.

Theorem 11

The eccentric connectivity index of armchair and zig-zag polyhex nanotubes are computed as follows:

• 1. (Saheli and Ashrafi 2010a) The eccentric connectivity index of a zig-zag polyhex nanotube is as follows:

$$ {}\xi\text{(A}[\text{p,}\,\text{q}])=\left\{\begin{array}{*{35}{l}}-\frac{7}{2}\text{pq}+\text{p}+\frac{9}{2}\text{p}{{\text{q}}^{2}}& {} & \text{p}\le \text{q}+1\\ -\frac{1}{2}\text{pq}+\text{p}+\frac{21}{4}\text{p}{{\text{q}}^{2}}-3{{\text{p}}^{2}}+\frac{3}{4}{{\text{p}}^{3}}-\frac{3}{2}\text{q}{{\text{p}}^{2}}+\frac{1-{{(-1)}^{\text{q}}}}{2}3\text{p}\left(\text{p}-\text{q}-\frac{1}{4} \right) & {} & \text{q}+1<\text{p}<2\text{q}\\ -4\text{pq}-2{{\text{p}}^{2}}+\frac{7}{4}\text{p}+\frac{9}{4}\text{p}{{\text{q}}^{2}}+\frac{3}{2}\text{q}{{\text{p}}^{2}}+\frac{1-{{(-1)}^{\text{q}}}}{2}\frac{3}{2}\text{p}(\text{p}+\text{q}+1) & {} & \text{p}\ge 2\text{q}\\\end{array}. \right. $$

• 2. (Saheli and Ashrafi 2010b) The eccentric connectivity index of an armchair polyhex nanotube with parameters p and q is as follows:

$$ {}\xi\text{(B}[\text{p,}\,\text{q}])=\left\{\begin{array}{*{35}{l}}{{\text{q}}^{2}}(3\text{p}-2) & {} & \text{p}\le \frac{\text{q}}{2}+1\\ \frac{3}{4}{{\text{q}}^{3}}+\frac{1}{2}{{\text{q}}^{2}}+2\text{q}-5\text{qp}+3\text{q}{{\text{p}}^{2}}& {} & \frac{\text{q}}{2}+1<\text{p}\le \text{q}\\ \frac{9}{4}\text{q}{{\text{p}}^{2}}-\frac{7}{2}\text{qp}+\frac{3}{2}{{\text{q}}^{2}}\text{p}-{{\text{q}}^{2}}+\frac{5}{4}\text{q} & {} & \text{p}\ge \text{q}+1\\\end{array}. \right. $$

Theorem 12

The eccentric connectivity index of TUC₄C₈(R/S) nanotubes and nanotori can be computed as follows:

• 1. The eccentric connectivity index of E[p, q] is given by

$$ {}\xi\text{(E}[\text{p,}\,\text{q}])=\left\{\begin{array}{*{35}{l}}(\text{p}+1)[(9{{\text{q}}^{2}}+18\text{pq}+15\text{p}+22\text{q}+10 )+R(\text{p},\text{q}) ] & {} & \text{q}<\left[\frac{\text{p}}{2} \right]\\ (\text{p}+1)[6{{\text{p}}^{2}}-(6\text{pq}+33{{\text{q}}^{2}}+5\text{p}+42\text{q}+14 )+R(\text{p},\text{q}) ] & {} & \left[\frac{\text{p}}{2} \right]\le \text{q}<\text{p}\\ (\text{p}+1)[(27{{\text{q}}^{2}}+6\text{pq}+5\text{p}+42\text{q}+14 )+R(\text{p},\text{q}) ] & {} & \text{q}\ge \text{p}\\\end{array}, \right. $$

where $\text{R}[\text{p,}\,\text{q}]{}=\left[(6\text{q}+5)\frac{1-{{(-1)}^{\text{p}}}}{2}+3\frac{1-{{(-1)}^{\text{q}}}}{2} \right].$

• 2. The eccentric connectivity index of F[p, q] is given by

$$ {}\xi\text{(F}[\text{p,}\,\text{q}])=\left\{\begin{array}{*{35}{l}}22\text{pq}+8{{\text{p}}^{2}}+12{{\text{p}}^{2}}\text{q}+18\text{p}{{\text{q}}^{\text{2}}}& \text{p}\le \left[\frac{\text{q}+1}{2} \right]\\ 28\text{pq}-4{{\text{p}}^{2}}+12{{\text{p}}^{3}}+21\text{p}{{\text{q}}^{2}}+8\text{p}+3\text{p}\frac{1-{{(-1)}^{\text{q}}}}{2} & \left[\frac{\text{q}+1}{2} \right]<\text{p}\le \text{q}+1\\ 8\text{pq}+16{{\text{p}}^{2}}+24{{\text{p}}^{2}}\text{q}+9\text{p}{{\text{q}}^{2}}+3\text{p}+3\text{p}\frac{1-{{(-1)}^{\text{q}}}}{2} & \text{p}>\text{q}+1\\\end{array}. \right. $$

• 3. The eccentric connectivity index of G[p, q] is given by

$$ {}\xi\text{(G}[\text{p,}\,\text{q}])=\left\{\begin{array}{*{35}{l}}12\text{p}(\text{q}+1)(\text{p}+\text{q}+1) & \text{p}\le \left\lceil \frac{\text{q}+1}{2} \right\rceil \\ \frac{4\text{p}+\text{q}}{2}+\frac{1-{{(-1)}^{\text{q}}}}{4} & \text{p}>\left\lceil \frac{\text{q}+1}{2} \right\rceil \\\end{array}. \right. $$

6.5 Conclusions

We have presented here a review of topological-based methods for evaluating the symmetry constraints and topological indices for carbon nanostructures such as nanotubes and nanotori. The first task, has been fulfilled by considering the topological symmetry of the graph of a given chemical system; such a symmetry just reflects the symmetry properties of the automorphism group of the graph providing the upper limit—fully rooted in topology—on the geometrical symmetry of the nanostructure. The second goal considers the application of topological indices in characterizing nanostructures. The reported theorems are very useful because they allow a fast computation of the topological indices for complex graphs (nanostructures) starting from their structural building elements, to derive exact algorithms easy to programme on the computer.

While the primary application concerns the description of carbon-networks in chemical compounds, other applications exist to rank for example proteins according to their degree of folding and topological invariants are useful in social-networks description.