Introduction

Electric vehicles have emerged as a crucial direction in the development of environmentally friendly transportation, primarily due to their low emissions and energy-saving attributes [1, 2]. In the realm of electric vehicle power batteries, lithium batteries are extensively utilized owing to their notable advantages, including high specific energy and compact size [3, 4]. Within the battery management system, the state of charge (SOC) serves as a critical parameter, and precise estimation of SOC holds paramount significance in enhancing battery efficiency and safety performance [5, 6]. Nevertheless, in practical applications, the accurate estimation of SOC proves to be a formidable challenge due to the nonlinear characteristics inherent to batteries and the intricate nature of the external operating environment [7,8,9].

Several methods are available for estimating SOC, including the open circuit voltage method, particle filtering algorithm, neural network method, and Kalman filtering algorithm, among others [10,11,12,13,14]. The open-circuit voltage method exhibits high accuracy in estimating SOC during stationary states, but it is not suitable for real-time estimation [15]. On the other hand, the particle filtering algorithm offers accurate results but comes with high computational complexity, consuming significant computational resources [16]. The neural network method demonstrates high accuracy for a specific battery, but its adaptability to different battery types is limited due to variations in battery characteristics at the individual cell level [17]. Currently, the extended Kalman filter algorithm has emerged as a prominent research focus in battery management systems due to its simplicity in computation, high accuracy, and suitability for real-time SOC estimation [18,19,20,21].

Fig. 1
figure 1

Schematic diagram of the second-order RC model

Full size image

In some control systems, such as distillation control and combustion process control, outliers may appear in the measurable data due to sensor failures or interrupted information transmission [22,23,24,25]. Outliers in the system output can significantly decrease the accuracy of parameter identification or even lead to identification failure [26,27,28,29,30]. Therefore, in recent years, numerous scholars have developed a multitude of algorithms to address the issue of outliers. For example, Zhou et al. improved the autoregressive integral moving average (ARIMA) model and applied it to quality control of seafloor observations through sliding windows and cleaning of input modeling data [31]. Su et al. proposed OmniAnomaly, a stochastic recurrent neural network for multivariate time series anomaly detection, which reconstructs the input data through robust representation and uses the reconstruction probability to determine the outliers [32]. Peter et al. approximated the sum of squares of the residuals to create a least median of squares (LMS) algorithm [33].

In practical applications, the state of lithium batteries is prone to being influenced by the external working environment, leading to the presence of outliers in the process information matrix [16]. To address this issue, this paper introduces the APG algorithm, aiming to handle the state matrix that contains outliers [34, 35]. The fundamental concept of the APG algorithm involves iteratively approximating the low-rank structure of the original matrix [36]. The APG algorithm effectively recovers the outliers in the state matrix, transforming them into normal data [37, 38].

The contributions of this study are summarized below.

  1. 1.

    Introduce the APG algorithm to deal with state vectors containing outliers, which can improve the estimation accuracy of SOC.

  2. 2.

    Build the APG-FFRLS-EKF algorithmic framework for online interactive estimation of SOC, which is highly extensible.

The rest of this paper is structured as follows. “Modelderivation” introduces the parameter identification model and the SOC estimation model. “SOC estimation basedon APG-FFRLS-EKF algorithm” presents an APG-FFRLS-EKF algorithm for SOC estimation models with output outliers. In “Examples”, an example for Samsung lithium batteries is provided. “Conclusions” summarizes this paper and gives future directions.

Model derivation

Parameter identification model

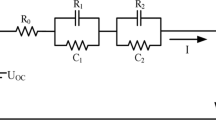
In this paper, we apply the second-order RC equivalent circuit model for the study. It can nicely simulate the charging and discharging behavior of lithium batteries [39, 40]. The basic structure of the model is shown in Fig. 1.

According to Kirchhoff’s voltage-current law, the circuit physical quantities can be described as:

$$\begin{aligned} {\left\{ \begin{array}{ll} i_{L}(t)=C_{1}\dot{u}_{1}+\frac{u_{1}(t)}{R_{1}},\\ i_{L}(t)=C_{2}\dot{u}_{2}+\frac{u_{2}(t)}{R_{2}},\\ u_{L}(t)=u_{ocv}(t)-i_{L}(t)R_{0}-u_{1}(t)-u_{2}(t). \end{array}\right. } \end{aligned}$$
(1)

where \(u_{L}\) denotes the terminal voltage, \(u_{ocv}\) denotes the open circuit voltage, \(R_{0}\) is a series resistance, \(R_{1}\) is a polarization resistance, \(R_{2}\) is a concentration polarization resistance, \(C_{1}\) is a polarization capacitance, and \(C_{2}\) is a concentration polarization capacitance.

Applying the Laplace transform to Eq. 1, yields

$$\begin{aligned} {\left\{ \begin{array}{ll} U_{1}(s)=\frac{I_{L}(s)R_{1}}{1+R_{1}C_{1}s},\\ U_{2}(s)=\frac{I_{L}(s)R_{2}}{1+R_{2}C_{2}s},\\ U_{L}(s)=U_{ocv}(s)-I_{L}(s)R_{0}-U_{1}(s)-U_{2}(s). \end{array}\right. } \end{aligned}$$
(2)

Integrating the above equation, we get

$$\begin{aligned} U_{ocv}(s)=(\frac{R_{1}}{R_{1}C_{1}s+1}+\frac{R_{2}}{R_{2}C_{2}s+1}+R_{0})I_{L}(s)+U_{L}(s). \end{aligned}$$
(3)

Transform the above equation into a differential equation and discretize it, and define

$$\begin{aligned}{} & {} h(k)=u_{ocv}(k)-u_{L}(k), \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \varvec{\varphi } (k)=[h(k-1) \; h(k-2) \; i(k) \; i(k-1) \; i(k-2)]^\textrm{T},\end{aligned}$$
(5)
$$\begin{aligned}{} & {} U_{L}(s)=U_{ocv}(s)-I_{L}(s)R_{0}-U_{1}(s)-U_{2}(s). \end{aligned}$$
(6)

\(\theta _{1}, \theta _{2},\theta _{3}, \theta _{4}\) and \(\theta _{5}\) are expressed as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta _{1}=\frac{8a_{1}-2}{1+2a_{2}+4a_{1}},\\ \theta _{2}=-\frac{1-2a_{2}+4a_{1}}{1+2a_{2}+4a_{1}},\\ \theta _{3}=-\frac{a_{4}+2a_{3}+4a_{1}R_0}{1+2a_{2}+4a_{1}},\\ \theta _{4}=-\frac{2a_{4}-8a_{1}R_0}{1+2a_{2}+4a_{1}},\\ \theta _{5}=-\frac{a_{4}-2a_{3}+4a_{1}R_0}{1+2a_{2}+4a_{1}}, \end{array}\right. } \end{aligned}$$
(7)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} a_{1}=R_1C_1R_2C_2,\\ a_{2}=R_1C_1+R_2C_2,\\ a_{3}=R_1R_2C_2+R_1C_1R_2+R_0(R_1C_1+R_2C_2),\\ a_{4}=R_0+R_1+R_2. \end{array}\right. } \end{aligned}$$
(8)

Then, the battery model is simplified to the following linear form:

$$\begin{aligned} h(k)=\varvec{\varphi } ^\textrm{T}(k)\varvec{\theta }. \end{aligned}$$

Since the open circuit voltage \(u_{ocv}\) is unknown, the parameters in the model cannot be estimated and need to be alternately estimated in conjunction with the SOC model.

SOC estimation model

The establishment of a lithium battery state space model is the fundamental for SOC estimation. The expression for the SOC of lithium batteries is given below:

$$\begin{aligned} SOC(t_{1})=SOC(t_{0})-\frac{1}{C_{r}}\int _{t_{0}}^{t_{1}}\eta i_{L}(t)dt, \end{aligned}$$
(9)

where \(SOC(t_{1})\) denotes the battery SOC at the sampling moment \(t_{1}\), \(C_{r}\) indicates the rated capacity of the battery, \(\eta \) is the Coulomb coefficient, and \(i_{L}(t)\) denotes the current of the battery.

Fig. 2
figure 2

Battery SOC-OCV average curve under intermittent charge and discharge test

Full size image

Combining Eqs. 1 and 7, we can get the state space model of lithium battery as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1}(k+1)=e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}}u_{1}(k)+(1-e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}})R_{1}i_{L}(k),\\ u_{2}(k+1)\!=e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}}u_{2}(k)\!+(1\!-e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}})R_{2}i_{L}(k),\\ SOC(k+1)=SOC(k)-\frac{\eta t}{C_{r}}i_{L}(k),\\ u_{L}(k)=Q(SOC(k))-u_{1}(k)-u_{2}(k)-R_{0}i_{L}(k). \end{array}\right. } \end{aligned}$$
(10)

Considering the noise term, we can obtain the following discretized state space equation for SOC,

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{x}(k+1)=\varvec{A}(k)x(k)+\varvec{B}(k)i_{L}(k)+\varvec{R}(k),\\ y(k)=\varvec{C}(k)\varvec{x}(k)+D(k)i_{L}(k)+V(k), \end{array}\right. } \end{aligned}$$
(11)

where

$$\begin{aligned} \varvec{x}(k)= & {} \begin{bmatrix} SOC(k) \\ u_{1}(k) \\ u_{2}(k) \end{bmatrix}, \varvec{A}(k)= \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} e^{-\frac{\Delta t_{k+1}}{R_1C_1}}&{} 0 \\ 0 &{} 0&{} e^{-\frac{\Delta t_{k+1}}{R_2C_2}} \end{bmatrix},\\ \varvec{B}(k)\!= & {} \begin{bmatrix} -\frac{\eta t}{C_{r}}\\ (1-e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}})R_{1}\\ (1-e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}})R_{2} \end{bmatrix}, \varvec{C}(k)=[\!-1\; \!-\!1 \; \frac{\partial Q(SOC)}{\partial SOC}]^\textrm{T},\\ D(k)= & {} -R_{0}, \qquad \varvec{R}(k)=\begin{bmatrix} R_{1}(k)\\ R_{2}(k)\\ R_{3}(k) \end{bmatrix}. \end{aligned}$$

\(Q(\cdot )\) describes the relationship between SOC and \(u_{ocv}\). At the \(k-th\) moment, the process noise and the measurement noise are \(\varvec{R}(k)\) and V(k), respectively.

The open-circuit voltage \(u_{ocv}\) and SOC of Li-ion batteries have a strong nonlinear relationship [39, 40]. This can be obtained by pulse charge and discharge tests, as shown in Fig. 2.

Remark 1

Batteries follow different curves between charging and discharging due to the hysteresis of the batteries. In this paper, the average of their curves is taken as the true \(SOC-u_{ocv}\) relationship.

SOC estimation based on APG-FFRLS-EKF algorithm

In this section, we give an algorithmic framework for SOC estimation of lithium batteries containing outliers.

Terminal voltage recovery based on accelerated proximal gradient algorithm

In control systems such as chemical process control and network control, the problem of outliers in measured data sets often arises.

In the battery model parameter identification, the current and voltage information of the battery needs to be collected as the input and output of the model. Assume that the collected terminal voltages contain outliers due to operational errors or complex environments. In this paper, the accelerated proximal gradient algorithm is used to process the outliers.

The APG algorithm is commonly used to solve Robust Principal Component Analysis (RPCA) problems [41]. It is widely used in computer vision fields such as face recognition and image recovery [42, 43].

The RPCA problem is mainly the following form.

$$\begin{aligned} \underset{\varvec{A},\varvec{E}}{\text {min}} \quad \left\| \varvec{A} \right\| _{*}+\lambda \left\| \varvec{E} \right\| _{1}\quad s.t.\; \varvec{D}=\varvec{A}+\varvec{E}, \end{aligned}$$
(12)

where \(\varvec{D}\) is the measurable matrix, \(\varvec{A}\) is the recovered low-rank matrix, and \(\varvec{E}\) is the sparse matrix.

The APG algorithm is used to solve the above problem. It is an iterative algorithm commonly used in optimization problems to recover low-rank matrices. The idea is to gradually approximate the optimal solution by alternately updating the matrix and the estimated gradient, combining the most closest estimate and the most closest gradient in each step.

By the definition in “Model derivation”, let \(u_{L}(1),...,u_{L}\)(M) be the collected terminal voltages. In this case, \(\bar{u}_{L}(l_{1}),...,\)\(\bar{u}_{L}(l_{m})\) are the outliers.

First, the terminal voltage vector \(\begin{bmatrix} u_{L}(1),...,u_{L}(M) \end{bmatrix}^\textrm{T}\)is converted to a matrix \(\varvec{\bar{\Phi }}\), where

$$\begin{aligned} \varvec{\bar{\Phi }}=\begin{bmatrix} u_{L}(1) &{} u_{L}(n+1) &{} ... &{} u_{L}(M-n+1)\\ ...&{} ... &{} ... &{} ...\\ u_{L}(n) &{} u_{L}(2n) &{} ... &{} u_{L}(M) \end{bmatrix}. \end{aligned}$$

Then, we can recover the terminal voltage matrix with outliers \(\varvec{\bar{\Phi }}\) to \(\varvec{\Phi }\) by the APG algorithm.

The APG algorithm is intended to solve the following optimization problem.

$$\begin{aligned} \underset{\varvec{\Phi },\varvec{E}}{\text {min}} \quad \left\| \varvec{\Phi }\right\| _{*}+ \lambda \left\| \varvec{E} \right\| _{1}\quad s.t.\; \varvec{\bar{\Phi }}=\varvec{\Phi }+\varvec{E} , \end{aligned}$$
(13)

where \(\varvec{E}\) is a sparse matrix and \(\lambda \) is a penalty factor.

Define \(\varvec{W}=(\varvec{\Phi },\varvec{E})\), \(f(\varvec{W})=\frac{\begin{Vmatrix}\varvec{\bar{\Phi }}-\varvec{\Phi }-\varvec{E}\end{Vmatrix}_{F}^{2}}{2}\) and \(g(\varvec{W})=\mu \begin{Vmatrix}\varvec{\Phi } \end{Vmatrix}_{*}+\lambda \mu \begin{Vmatrix}\varvec{E}\end{Vmatrix}_{1}\). From Eq. 10, we construct the following Lagrangian function.

$$\begin{aligned} G(\varvec{W})= & {} g(\varvec{W})+f(\varvec{W})\\= & {} \mu \begin{Vmatrix}\varvec{\Phi } \end{Vmatrix}_{*}+\lambda \mu \begin{Vmatrix}\varvec{E}\end{Vmatrix}_{1}+\frac{\begin{Vmatrix}\varvec{\bar{\Phi }}-\varvec{\Phi }-\varvec{E}\end{Vmatrix}_{F}^{2}}{2}, \end{aligned}$$

where \(\mu \) is a relaxation factor.

Lemma 1

[44] Approximate \(G(\varvec{W})\) at the point \(\varvec{W}\) using the quadratic separable sequence \(Q(\varvec{W},\varvec{\widetilde{W}})\). The expression for \(Q(\varvec{W},\varvec{\widetilde{W}})\) is:

$$\begin{aligned} Q(\varvec{W},\widetilde{\varvec{W}})= & {} g(\varvec{W})+f(\widetilde{\varvec{W}})+\\< & {} \triangledown f(\widetilde{\varvec{W}}),\varvec{W}-\widetilde{\varvec{W}}> +\frac{L_{f}}{2}\left\| \varvec{W}-\widetilde{\varvec{W}} \right\| ^{2}, \end{aligned}$$

where \(< \triangledown f(\widetilde{\varvec{W}}),\varvec{W}-\widetilde{\varvec{W}}>=tr(\triangledown f^\textrm{T}(\widetilde{\varvec{W}})(\varvec{W}-\widetilde{\varvec{W}}))\) and \(L_{f}\) is the Lipschitz constant of \(f(\varvec{W})\).

Minimizing \(G(\varvec{W})\) is equivalent to minimizing \(Q(\varvec{W},\widetilde{\varvec{W}})\) in Lemma 1. Define \(\varvec{D}\doteq \widetilde{\varvec{W}}-\frac{1}{L_{f}}\triangledown f(\widetilde{\varvec{W}})\), then we have

$$\begin{aligned} \underset{\varvec{W}}{{\text {argmin}}} \; Q(\varvec{W},\widetilde{\varvec{W}})\!=\! \underset{\varvec{W}}{\text {argmin}}\left\{ g(\varvec{W})\!+\!\frac{L_{f}}{2}\left\| \varvec{W}\!-\!\varvec{D} \right\| ^{2} \right\} . \end{aligned}$$
(14)

Remark 2

If \(\widetilde{\varvec{W}}_{k}=\varvec{W}_{k}\), the APG algorithm will degrade to a gradient descent algorithm.

Fig. 3
figure 3

The framework of the APG-FFRLS-EKF algorithm

Full size image
Fig. 4
figure 4

The battery test platform

Full size image

The steps of the APG algorithm contain alternate updates to \(\varvec{\Phi }\) and \(\varvec{E}\). According to Eq. 11, \(\varvec{E}\) can be solved as follows.

$$\begin{aligned} \underset{\varvec{E}}{\text {argmin}} \left\{ \mu \lambda \left\| \varvec{E} \right\| _{1}+\frac{L_{f}}{2}\left\| \varvec{\bar{\Phi }}-\varvec{\Phi }-\varvec{E} \right\| _{F}^{2} \right\} . \end{aligned}$$

Define

$$\begin{aligned} S_{\tau }\left[ i \right] \doteq \left\{ \begin{matrix} i-\tau ,\quad if\;i> \tau ,\\ i+\tau ,\quad if\;i< -\tau ,\\ 0, \quad \quad otherwise, \end{matrix}\right. \end{aligned}$$

where \(i\in \mathbb {R}\) and \(\tau > 0\). According to the definition above, at the (\(k+1\))th iteration, let \(\varvec{D}_{k}=(\varvec{D}_{k}^{A},\varvec{D}_{k}^{E})\), then \(\varvec{E}_{k+1}\) is updated according to the following equation.

$$\begin{aligned} \varvec{E}_{k+1}=S_{\frac{\lambda \mu }{L_{f}}}\left[ \varvec{D}_{k}^{E} \right] . \end{aligned}$$
(15)

Similarly, \(\varvec{\Phi }\) can be computed by

$$\begin{aligned} \underset{\varvec{\Phi }}{\text {argmin}} \left\{ \mu \left\| \varvec{\Phi } \right\| _{*}+\frac{L_{f}}{2}\left\| \varvec{\bar{\Phi }}-\varvec{\Phi }-\varvec{E} \right\| _{F}^{2} \right\} , \end{aligned}$$

let \(\varvec{USV}^\textrm{T}\) be the singular value decomposition of \(\varvec{D}_{k}^{A}\), then

$$\begin{aligned} \varvec{\Phi }_{k+1}=\varvec{U}S_{\frac{\lambda \mu }{L_{f}}}\left[ \varvec{D}_{k}^{A} \right] \varvec{V}^\textrm{T}. \end{aligned}$$
(16)

Remark 3

In the APG algorithm, by setting \(t_{k+1}= \frac{1+\sqrt{4t_{k}^{2}+1}}{2}\), the convergence rate can reach quadratic convergence [45].

We summarize the APG algorithm as Algorithm 1.

Algorithm 1
figure a

APG algorithm.

Full size image

The APG-FFRLS-EKF algorithm for SOC

When there are outliers in the terminal voltages of the output data, traditional identification algorithms have low efficiency and accuracy. The APG-FFRLS-EKF algorithm solves this problem by recovering the outliers in the terminal voltages. Compared with the traditional SOC estimation method, it not only improves the estimation accuracy of the identification model, but also decreases the error of SOC estimation.

Table 1 The parameters of NCR18650PF
Full size table

In this section, the APG-FFRLS-EKF algorithm for SOC estimation of output voltages containing outliers is presented in detail.

First, the APG algorithm is used to recover the terminal voltage outliers. Then, the model parameters \(R_{0},R_{1},R_{2},C_{1},\)\( C_{2}\) are estimated using the FFRLS algorithm. In this case, the open circuit voltage \(u_{ocv}\) in the output data can be obtained from the relationship between SOC and \(u_{ocv}\). The model parameters are identified so that they can be used to alternatively estimate the SOC.

Fig. 5
figure 5

Intermittent current

Full size image
Fig. 6
figure 6

Output estimates and errors with number of outliers 100

Full size image
Fig. 7
figure 7

Output estimates and errors with number of outliers 200

Full size image
Fig. 8
figure 8

Output estimates and errors with number of outliers 500

Full size image
Fig. 9
figure 9

SOC estimates and errors with number of outliers 100

Full size image
Fig. 10
figure 10

SOC estimates and errors with number of outliers 200

Full size image
Fig. 11
figure 11

SOC estimates and errors with number of outliers 500

Full size image

In summary, the steps of the APG-FFRLS-EKF algorithm are as in Algorithm 2.

  1. 1.

    Collect current and terminal voltage data \(\left\{ i_{L}(1),u_{L}(1)\right\} \) \(...\left\{ i_{L}(M),u_{L}(M)\right\} \) from lithium batteries, where \({ \bar{u}_{L}(l_{1}),}\) \({...,\bar{u}_{L}(l_{m})}\) is the sequence of outliers.

  2. 2.

    Expand the terminal voltage vector \([u_{L}(1),...\bar{u}_{L}(l_{1}),...,\) \(\bar{u}_{L}(l_{m}),...u_{L}(M)]^\textrm{T}\) as a matrix \(\varvec{\bar{\Phi } }\).

  3. 3.

    Use the APG algorithm to recover the matrix \(\varvec{\bar{\Phi }}\) into a clean matrix \(\varvec{\Phi }\). \(\varvec{\Phi }\) is then vectorized to \([u_{L}(1),...\hat{u}_{L}(l_{1}),...,\hat{u}_{L}(l_{m}),...u_{L}(M)]^\textrm{T}\), where \([\hat{u}_{L}(l_{1}),...,\hat{u}_{L}\)\((l_{m})]^\textrm{T}\) is the recovered terminal voltage vector.

  4. 4.

    Initialize \(\varvec{\theta }(0)\), \(\varvec{P}(0)\), SOC(0) and \(\varvec{x}(0)\).

  5. 5.

    Get \(u_{ocv}(0)\) from the nonlinear relationship between \(u_{ocv}\) and SOC. Obtain h(k) based on the terminal voltages obtained from step 3 and Eq. 4.

  6. 6.

    Obtain the observation vector \(\varvec{\varphi }(k)\) according to Eq. 5.

  7. 7.

    Compute the gain matrix:

    $$\begin{aligned} \varvec{L}(k)=\frac{\varvec{P}(k-1)\varvec{\varphi } (k)}{\lambda +\varvec{\varphi } ^\textrm{T}(k)\varvec{P}(k-1)\varvec{\varphi }(k)}, \end{aligned}$$
    (17)

    update parameter estimation:

    $$\begin{aligned} \hat{\varvec{\theta }}(k)=\hat{\varvec{\theta } }(k-1)+\varvec{L}(k)[h(k)-\varvec{\varphi } ^\textrm{T}(k)\hat{\varvec{\theta } }(k-1)], \end{aligned}$$
    (18)

    update the covariance matrix:

    $$\begin{aligned} \varvec{P}(k)=[\varvec{I}-\varvec{L}(k)\varvec{\varphi } ^\textrm{T}(k)]\varvec{P}(k-1). \end{aligned}$$
    (19)

    Obtain the battery model parameters \(R_{0},R_{1},R_{2},C_{1},C_{2}\) according to Eqs. 7 and 8.

  8. 8.

    Substitute the battery model parameters obtained from step 7 into Eq. 11.

  9. 9.

    Make predictions about the state vector and the covariance matrix:

    $$\begin{aligned} \hat{\varvec{x}}^{-}(k)= & {} \varvec{A}(k-1)\hat{\varvec{x}}(k-1)+\varvec{B}(k-1)i_{L}(k-1),\end{aligned}$$
    (20)
    $$\begin{aligned} \widetilde{\varvec{P}}^{-}(k)= & {} \varvec{A}(k-1)\widetilde{\varvec{P}}^{-}(k-1)\varvec{A}^\textrm{T}(k-1)+\varvec{V}(k-1). \end{aligned}$$
    (21)
  10. 10.

    Gain Kalman Gain:

    $$\begin{aligned} \varvec{K}(k)=\widetilde{\varvec{P}}^{-}(k)\varvec{C}^\textrm{T}(k)[\varvec{C}(k)\widetilde{\varvec{P}}^{-}(k)\varvec{C}^\textrm{T}(k)+\varvec{V}(k)]^\textrm{T}. \end{aligned}$$
    (22)
  11. 11.

    Update the state vector:

    $$\begin{aligned} \hat{\varvec{x}}(k)=\hat{\varvec{x}}^{-}(k)+\varvec{K}(k)[y(k)-\varvec{C}(k)\hat{\varvec{x}}^{-}(k)-D(k)i_{L}(k)], \end{aligned}$$
    (23)

    where \(\hat{\varvec{x}}(k)=[SOC(k)\;u_{1}(k)\;u_{2}(k)]^\textrm{T}\).

  12. 12.

    Update the covariance matrix:

    $$\begin{aligned} \widetilde{\varvec{P}}(k)=[\varvec{I}-\varvec{K}(k)\varvec{C}(k)]\widetilde{\varvec{P}}^{-}(k). \end{aligned}$$
    (24)
  13. 13.

    If \(k\geqslant M\), then take up the state vector \(\hat{\varvec{x}}(k)\); otherwise, let \(k=k+1\) and go back to step 5.

The framework of the APG-FFRLS-EKF algorithm is shown in Fig. 3.

Examples

The battery tester platform

In order to verify the accuracy of the APG-FFRLS-EKF algorithm in SOC estimation of Li-ion batteries, discharge trial experiments are conducted. As shown in Fig. 4, lithium-ion batteries are tested using the battery experimental platform. The experiments are conducted at room temperature of \(25^{\circ }\textrm{C}\) during the whole process. The battery experiment platform includes a battery tester, a battery holder, Samsung lithium-ion batteries and a host computer. The main parameters of the Samsung lithium-ion battery are shown in Table 1.

Experiments and analysis

Intermittent discharge experiments are conducted on lithium batteries to obtain current and voltage data by sampling. Battery discharge tests were performed at the current profiles shown in Fig. 5.

Generate 100, 200, and 500 random numbers, respectively, to simulate the case of different numbers of outliers in the battery terminal voltage data. The APG-FFRLS-EKF algorithm and FFRLS-EKF algorithm are applied to estimate the output voltage with outliers and SOC.

Under the influence of different numbers of outliers, the output estimates and errors are shown in Figs. 6, 7, and 8. The SOC estimates and errors are shown in Figs. 9, 10, and 11. From Figs. 6, 7, and 8, it can be seen that the terminal voltage data after recovery by the APG algorithm is close to normal. When the percentage of outliers is close to 3%, the data after APG recovery is almost normal. When the percentage of outliers is more than 10%, the data after APG recovery is still close to normal.

From Table 2, it can be seen that the proposed APG-FFRLS-EKF algorithm can obtain high SOC estimation accuracy, with MAE less than 2.0787, and RMSE less than 2.0986.

Table 2 Estimation errors of SOC
Full size table

Conclusions

An APG-FFRLS-EKF algorithm is proposed for the problem of SOC estimation of lithium batteries with output outliers. The APG-FFRLS-EKF algorithm polishes the outlier outputs in advance, which can lead to higher SOC estimation accuracy. Compared with the traditional SOC estimation method, this method has more accurate estimation accuracy and is more robust. It should be noted that the theoretical proof of the convergence analysis of the APG-FFRLS-EKF algorithm is challenging and deserves further study.