Introduction

Electric vehicles have been widely used due to their simple structure, little pollution and high energy efficiency [1,2,3]. As an important component of electric vehicles, lithium-ion batteries have attracted a lot of attentions [4, 5]. The properties of the battery are easily affected by temperature, voltage and current. It is essential to establish an effective battery management system (BMS) to maintain battery health [6,7,8]. The core factor of BMS is the SOC estimation, which reflects the performance of battery. Accurate SOC estimation can maximize battery performance [9, 10].

The nonlinear characteristics of battery system make the SOC estimation difficult. Recently, many algorithms have been proposed in the literature, including the current integration method, data-driven method, and adaptive filtering method [11,12,13,14]. For example, Wang et al. proposed an improved feedforward-long short-term memory (FF-LSTM) modeling method to realize an accurate whole-life-cycle SOC prediction by effectively considering the current, voltage, and temperature variations [15]. Jiao et al. proposed a gated recurrent unit recurrent neural network (GRU-RNN) based momentum gradient method to estimate SOC [16]. However, the data-driven method needs a large amount of training data, which involves heavy computational efforts. The adaptive filtering method considers the battery as a dynamic system and predicts SOC by constructing a state space model. In comparison to the other methods, it can improve estimation accuracy with little computational efforts [17,18,19,20,21].

The recursive least square (RLS) algorithm is a widely used online algorithm for lithium battery equivalent model [22,23,24,25]. Since only one set data are performed to update the estimates, the RLS algorithm has slow convergence rates [26,27,28]. In order to increase the convergence rates, Lao et al. [29] used the forgetting factor recursive least squares algorithm (FFRLS) to estimate unknown model parameters. However, as the number of iterations increases, the past data play less role on the parameter estimates. In [30], Ding proposed a multi-innovation least square (MILS) algorithm, which expands the scalar innovation to vector innovation. Therefore, the MILS algorithm has faster convergence rates [31, 32].

Kalman filter (KF) is a powerful state estimation algorithm [33]. In the last few decades, some novel Kalman filters have been developed, such as the extended Kalman filter (EKF) [34], the unscented Kalman filter (UKF) [35], and the cubature Kalman filter (CKF) [36]. For high-dimensional nonlinear systems, the CKF has higher estimation accuracy and faster convergence rates [37, 38]. However, the covariance matrix does not remain positive definite, it may lead to the divergence of the filter. The square root cubature Kalman filter (SRCKF) algorithm can deal with this problem by performing recursive update in the form of the square root of the covariance matrix [39]. In applications, the state of lithium batteries is easily affected by environmental factors, which leads to outliers in the process noise matrix. To deal with this dilemma, Zhou proposed the strong tracking filter (STF) theory in [40], which makes the residual sequence orthogonal at each step. For this reason, the strong tracking filter theory combining the square root cubature Kalman filter can ensure the filter to track the system states, and has better robustness against model parameter mismatch.

In this paper, we propose two complementary cooperative algorithms for SOC estimation. The proposed square root cubature Kalman filter based multi-innovation least square (SRCKF-MILS) algorithm is used to estimate the battery model parameters and SOC interactively. The strong tracking square root cubature Kalman filter based multi-innovation least square (ST-SRCKF-MILS) algorithm can deal with state vector with outliers. The contributions of this study are summarized as follows.

  1. 1.

    Update SOC by the SRCKF-MILS algorithm, which can achieve more accurate SOC estimates than the HIf algorithm in [43].

  2. 2.

    Improve the SRCKF-MILS algorithm based on STF theory, which can deal with SOC with outliers.

The remaining part of this paper is organized as follows. In the “Online identification of battery model parameters” section, an online identification method of battery model parameters is introduced. In the “Estimating state of charge based on square root cubature Kalman filter” section, the SRCKF-MILS algorithm for SOC is proposed. In the “Improved square root cubature Kalman filter by strong tracking filter theory” section, the ST-SRCKF-MILS algorithm is studied. In the “Examples” section, two examples are provided. Finally, some conclusion remarks are given in the “Conclusions” section.

Online identification of battery model parameters

Battery model parameter estimation

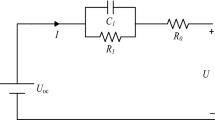
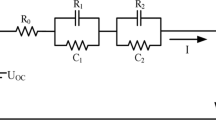
In this paper, a second-order RC model is established to simulate battery charging and discharging behaviors. The basic structure is shown in Fig 1, where U represents the terminal voltage of the circuit, R0 is the series resistance, R1 is the polarization resistance, R2 is the concentration polarization resistance, C1 is the polarization capacitance, C2 is the concentration polarization capacitance, Uocv is the open circuit voltage, and I is the discharge current.

Fig. 1
figure 1

Schematic diagram of the second-order RC model

Full size image

According to the Kirchhoff laws, the circuit equation can be described as follows:

$$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{lll} C_{1}\frac{dU_{1}}{dt}=I(t)-\frac{U_{1}(t)}{R_{1}},\\ C_{2}\frac{dU_{2}}{dt}=I(t)-\frac{U_{2}(t)}{R_{2}},\\ U=U_{ocv}-U_{1}-U_{2}-R_{0}I(t). \end{array}\right. \end{array} $$
(1)

Based on Laplace-transform method, we have

$$ \begin{array}{@{}rcl@{}} U_{ocv}(s)=\left( \frac{R_{1}}{R_{1}C_{1}s+1}+\frac{R_{2}}{R_{2}C_{2}s+1}+R_{0}\right)I(s)+U(s). \end{array} $$
(2)

Define z(t) := Uocv(t) − U(t), Eq. (2) can be transformed into

$$ \begin{array}{@{}rcl@{}} z(t)&=&k_{1}z(t-1)+k_{2}z(t-2)+k_{3}I(t)\\ &&+k_{4}I(t-1)+k_{5}I(t-2), \end{array} $$
(3)

where

$$ \begin{array}{@{}rcl@{}} \begin{cases} k_{1}=\frac{8a-2}{1+2b+4a},\\ k_{2}=-\frac{1-2b+4a}{1+2b+4a},\\ k_{3}=-\frac{d+2c+4aR_{0}}{1+2b+4a},\\ k_{4}=-\frac{2d-8aR_{0}}{1+2b+4a},\\ k_{5}=-\frac{d-2c+4aR_{0}}{1+2b+4a}, \end{cases} \end{array} $$
(4)

and

$$ \begin{array}{@{}rcl@{}} \begin{cases} a=R_{1}C_{1}R_{2}C_{2},\\ b=R_{1}C_{1}+R_{2}C_{2},\\ c=R_{1}R_{2}C_{2}+R_{1}C_{1}R_{2}+R_{0}(R_{1}C_{1}+R_{2}C_{2}),\\ d=R_{0}+R_{1}+R_{2}. \end{cases} \end{array} $$
(5)

The model is simplified as the following general linear model,

$$ \begin{array}{@{}rcl@{}} z(t)=\varphi^{\intercal}(t)\boldsymbol{\theta}, \end{array} $$
(6)

where z(t) is system output, \(\varphi (t)=[z(t-1),z(t-2),I(t),\\ I(t-1),I(t-2)]^{\intercal }\) represents the information vector, and \(\boldsymbol {\theta }=[k_{1},k_{2},k_{3},k_{4},k_{5}]^{\intercal }\) denotes the unknown parameter vector.

Multi-innovation least squares algorithm

The RLS algorithm has several advantages, such as low memory occupation and high precision [30]. However, as the number of iterations increases, the past data have little ability to polish the system parameters. It leads to slow convergence rates. The MILS algorithm expands the information vector into an information matrix, the main steps are as follows:

$$ \begin{array}{@{}rcl@{}} \hat{\boldsymbol{\theta}}(t)&=&\hat{\boldsymbol{\theta}}(t-1)+\boldsymbol{L}(t)\left[\boldsymbol{Y}(p,t)-\boldsymbol{{\varPhi}}^{\intercal}(p,t)\hat{\boldsymbol{\theta}}(t-1)\right],\\ \boldsymbol{L}(t)&=&\boldsymbol{P}(t-1)\boldsymbol{{\varPhi}}(p,t)\left[\boldsymbol{I}_{p}+\boldsymbol{{\varPhi}}^{\intercal}(p,t)\boldsymbol{P}(t-1)\boldsymbol{{\varPhi}}(p,t)\right]^{-1},\\ \boldsymbol{P}(t)&=&\boldsymbol{P}(t-1)-\boldsymbol{L}(t)\boldsymbol{{\varPhi}}^{\intercal}(p,t)\boldsymbol{P}(t-1),\\ \boldsymbol{{\varPhi}}(p,t)&=&\left[\boldsymbol{\varphi}(t),\boldsymbol{\varphi}(t-1),\ldots,\boldsymbol{\varphi}(t-p+1)\right],\\ \boldsymbol{Y}(p,t)&=&\left[y(t),y(t-1),\ldots,y(t-p+1)\right]^{\intercal}, \end{array} $$

where p is the innovation length.

The unknown parameters can be estimated by the MILS algorithm. The battery model parameters R0,R1,R2, C1,C2 can be calculated using Eqs. (4) and (5). Since the output vector of the algorithm contains unmeasured parameter Uocv(t), it can be estimated by SRCKF.

Remark 1

When initializing SOC(0), the corresponding Uocv(0) is obtained by the relationship between the Uocv-SOC data, and in the subsequent iteration process, Uocv is computed by the estimated SOC.

Remark 2

The relationship between the Uocv-SOC data can be obtained through the pulse charge and discharge test. Due to the influence of battery hysteresis, the curves of the battery between charging and discharging are different. This paper takes their average curve as the real Uocv-SOC relationship.

Estimating state of charge based on square root cubature Kalman filter

In this section, the battery state space model is constructed and the derivation of the SRCKF algorithm is presented.

Construction of the battery state space model

By integrating the charging and discharging current of the battery, the obtained integral value is the increase or decrease of the battery’s charge. Assuming that the initial SOC of battery is SOC(t0), the SOC at the sampling time t1 is written by

$$ \begin{array}{@{}rcl@{}} SOC(t_{1})=SOC(t_{0})-\frac{1}{C_{E}}{\int}_{t_{0}}^{t_{1}}\eta I(t)dt, \end{array} $$
(7)

where I(t) represents the battery’s current, η is the Coulomb coefficient, and CE indicates the rated capacity of the battery.

Remark 3

Equation (7) is the current integration method, which has a simple form to calculate SOC. The disadvantage of the current integration method is that if the current measurement is not accurate, the error will gradually accumulate, thus affecting the prediction results of the SOC. In this paper, Eq. (7) is used to construct a state space model to estimate SOC [18].

Combined with Eq. (1), the state space model of the battery is written as

$$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{lll} U_{1,k+1}=e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}}U_{1,k}+\left( 1-e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}}\right)R_{1}I_{k},\\ U_{2,k+1}=e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}}U_{2,k}+\left( 1-e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}}\right)R_{2}I_{k},\\ SOC_{k+1}=SOC_{k}-\frac{\eta t}{C_{E}}I_{k},\\ U_{k}=F(SOC_{k})-U_{1,k}-U_{2,k}-R_{0}I_{k}. \end{array}\right. \end{array} $$
(8)

Considering the noise term, Eq. (8) is transformed into

$$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{ll} \boldsymbol{x}_{k+1}=\boldsymbol{A}_{k}\boldsymbol{x}_{k}+\boldsymbol{B}_{k}\boldsymbol{U}_{k}+\boldsymbol{Q}_{k},\\ y_{k}=F(SOC_{k})-U_{1,k}-U_{2,k}-R_{0}I_{k}+\boldsymbol{R}_{k}, \end{array}\right. \end{array} $$
(9)

where

$$ \begin{array}{@{}rcl@{}} \boldsymbol{x}_{k}&=& \left[\begin{array}{ll} U_{1,k} \\ U_{2,k} \\ SOC_{k} \end{array}\right], \boldsymbol{A}_{k}= \left[\begin{array}{ccc} e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}} & 0& 0 \\ 0 & e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}} & 0\\ 0 & 0& 1 \end{array}\right],\\ \boldsymbol{B}_{k}&=&\left[\begin{array}{ccc} \left( 1-e^{-\frac{\Delta t_{k+1}}{R_{1}C_{1}}}\right)R_{1}\\ \left( 1-e^{-\frac{\Delta t_{k+1}}{R_{2}C_{2}}}\right)R_{2}\\ -\frac{\eta t}{C_{E}} \end{array}\right], \boldsymbol{U}_{k}=\left[\begin{array}{cc} I_{k} \end{array}\right], \boldsymbol{Q}_{k}=\left[\begin{array}{ccc} Q_{1,k}\\ Q_{2,k}\\ Q_{3,k} \end{array}\right]. \end{array} $$

F(x) is the functional relationship between SOC and Uocv, Qk and Rk represent process noise and measurement noise at time k, respectively.

Square root cubature Kalman filter

Since Eq. (9) contains the nonlinear function F(x), the Kalman filter is unavailable for such a model. Here, an improved filtering method, termed as the cubature Kalman filter, is introduced.

Under the Gaussian approximation, the function recursion of the Bayesian filter is simplified to algebraic recursion, i.e., the mean and covariance of the conditional probability density function are calculated during time update and measurement update. It can be seen that the core of the filtering process is to calculate the Gaussian weight product of the integrand in the form of a nonlinear function and a Gaussian probability density function. Then, it follows that

$$ \begin{array}{@{}rcl@{}} I(p)={\int}_{D}p(x)w(x)dx, \end{array} $$
(10)

where p(x) is a nonlinear function, w(x) ≥ 0 is a weight function, \(D\subseteq R^{n}\) indicates the integration area, \(x=[x_{1}\quad x_{2}{\dots } x_{n}]\in D\). The basic idea to solve this problem is to find a series of weighted points xi with weight Wi for approximation,

$$ \begin{array}{@{}rcl@{}} I(p)\approx \sum\limits_{i=1}^{m}W_{i}p(x_{i}). \end{array} $$
(11)

Cubature rule is an effective method to determine these points. However, in the filtering process, the Cholesky factorization of the covariance matrix cannot guarantee its positive definiteness. The SRCKF algorithm can solve this problem by directly performing the recursive update in the form of the square root of the covariance matrix in the filtering process, and has the following advantages over the traditional CKF methods: (1) can reduce the computational complexity; (2) can ensure the positive definiteness of the covariance matrix; (3) can avoid the divergence of the filter; (4) can improve the convergence speed and numerical stability. In summary, the specific steps of the SRCKF are shown in Algorithm 1.

Algorithm 1
figure afigure a

The square root cubature Kalman filter algorithm.

Full size image

The SRCKF-MILS algorithm for SOC

This subsection introduces a complementary cooperative algorithm for estimating SOC. First, the MILS algorithm is used to estimate model parameters R0,R1,R2,C1 and C2, which will be applied to estimate state vector (SOC is one of the states) by the SRCKF. Then, the open circuit voltage Uocv can be obtained by the relationship between Uocv and SOC. The whole process is updated interactively until the SOC is obtained.

The structure diagram of the algorithm is shown in Fig. 2, the relationship between the OCV and the SOC of the battery can be obtained by intermittent charge and discharge test as shown in Fig. 3.

Fig. 2
figure 2

Structure of SOC estimation strategy based on SRCKF-MILS

Full size image
Fig. 3
figure 3

Battery SOC-OCV average curve under intermittent charge and discharge test

Full size image

Improved square root cubature Kalman filter by strong tracking filter theory

Strong tracking filter theory

As shown in Fig. 1, the second-order RC model can reflect the complex electrochemistry, such as polarization reaction and diffusion effect of lithium batteries. However, in applications, the states of lithium batteries change all the time, and are easily affected by environmental factors. This would lead to outliers in the process noise matrix. When using the SRCKF algorithm to estimate the state vector, the noise matrix containing outliers will seriously affect the estimation effect, and even cause the divergence of the filter. Combining the SRCKF algorithm with the STF theory can deal with this problem.

Lemma 1

[40] A sufficient condition for a strong tracking filter is to choose an appropriate time-varying gain matrix such that:

$$ \begin{array}{@{}rcl@{}} Condition \textit{1}: &&\mathrm{E}\left[\boldsymbol{x}(k+1)-\hat{\boldsymbol{x}}(k+1|k+1)\right]\left[\boldsymbol{x}(k\right.\\ &&\left.+1)-\hat{\boldsymbol{x}}(k+1|k+1)\right]^{\intercal}=min, \end{array} $$
(28)
$$ \begin{array}{@{}rcl@{}} Condition \textit{2}: &&\mathrm{E}\left[\boldsymbol{\varepsilon}(k+1+j)\boldsymbol{\varepsilon}^{\intercal}(k+1)\right]=0, \\ &&k=0,1,2,\ldots, j=1,2,\ldots \end{array} $$
(29)

where ε is the output residual sequence φ(xk), \(\boldsymbol {\varepsilon }(k)=\boldsymbol {z}(k)-\hat {\boldsymbol {z}}({k|k-1})\).

Lemma 1 is the orthogonality lemma. Condition 1 is the performance index of Kalman filter, Condition 2 requires that the output residual sequences remain orthogonal. Due to the influence of model uncertainty, the state estimates of the filter may deviate from the real state. It is necessary to adjust the gain matrix Kk, to satisfy Eq. (29).

A time-varying factor λk is introduced to weaken the influence of the old data. The corresponding gain matrix can be obtained by adjusting the prediction error covariance matrix to satisfy the orthogonality theorem. The updated formula of the prediction error covariance matrix is:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{k|k-1}=\boldsymbol{F}_{k}\boldsymbol{P}_{k-1|k-1}\boldsymbol{F}_{k}^{\intercal}+\boldsymbol{Q}_{k}. \end{array} $$
(30)

Adding the fading factor λk, the adjusted prediction error covariance matrix is written as follows:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{k|k-1}=\lambda_{k}\boldsymbol{F}_{k}\boldsymbol{P}_{k-1|k-1}\boldsymbol{F}_{k}^{\intercal}+\boldsymbol{Q}_{k}. \end{array} $$
(31)

Lemma 2

[41] Let \({\Delta }\boldsymbol {x}(k)\triangleq \boldsymbol {x}(k)-\hat {\boldsymbol {x}}(k), \boldsymbol {V}_{0}(k+1)= {E}[\boldsymbol {\varepsilon }(k+1)\boldsymbol {\varepsilon }^{\intercal }(k+1)]\). When O[|Δx(k)2|] ≪ O[|Δx(k)|], the following equality holds,

$$ \begin{array}{@{}rcl@{}} &&\mathrm{E}\left[\boldsymbol{\varepsilon}(k+1+j)\boldsymbol{\varepsilon}^{\intercal}(k+1)\right]\boldsymbol{\approx}\boldsymbol{H}(k+j+1)\cdot\boldsymbol{F}(k+j)\\ &&\left[\boldsymbol{I}-\boldsymbol{K}(k+j)\boldsymbol{H}(k+j)\right]\cdots\boldsymbol{F}(k+2)[\boldsymbol{I}-\boldsymbol{K}(k+2)\\ &&\boldsymbol{H}(k+2)]\cdot\boldsymbol{F}(k+1)[\boldsymbol{P}(k+1|k)\boldsymbol{H}^{\intercal}(k+1)-\\ &&\boldsymbol{K}(k+1)\boldsymbol{V}_{0}(k+1)]. \end{array} $$
(32)

It can be known from Lemma 2 that when the filter has ideal working performance, its output residual sequence is weakly autocorrelated. According to [40], define

$$ \begin{array}{@{}rcl@{}} \boldsymbol{S}(k)=\boldsymbol{P}(k+1|t)\boldsymbol{H}^{\intercal}(k+1)-\boldsymbol{K}(k+1)\boldsymbol{V}_{0}(k+1). \end{array} $$
(33)

The suboptimality of λk+ 1 can be measured by minimizing the following performance indicator:

$$ \begin{array}{@{}rcl@{}} g(k+1)=\sum\limits^{n}_{i=1}\sum\limits^{m}_{j=1}s_{ij}^{2}, \end{array} $$
(34)

where S = (sij). The specific steps are as follows [41]:

$$ \begin{array}{@{}rcl@{}} \lambda_{k}= \left\{\begin{array}{ll} \lambda_{k} \qquad\lambda_{k}\ge1,\\ 1 \qquad\lambda_{k}<1, \end{array}\right. \end{array} $$
(35)

where

$$ \begin{array}{@{}rcl@{}} \lambda_{k}&=&tr(\boldsymbol{N}_{k})/tr(\boldsymbol{M}_{k}), \end{array} $$
(36)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{N}_{k}&=&\boldsymbol{V}_{k}-\boldsymbol{H}_{k}\boldsymbol{Q}_{k-1}\boldsymbol{H}_{k}^{\intercal}-\beta\boldsymbol{R}_{k}, \end{array} $$
(37)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{M}_{k}&=&\boldsymbol{H}_{k}\boldsymbol{F}_{k}\boldsymbol{P}_{k}\boldsymbol{F}_{k}^{\intercal}\boldsymbol{H}_{k}^{\intercal}, \end{array} $$
(38)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{V}_{k}&=& \left\{\begin{array}{ll} \boldsymbol{\varepsilon}_{1}\boldsymbol{\varepsilon}_{1}^{\intercal}\qquad k=1,\\ \\ \frac{\rho\boldsymbol{V}_{k-1}+\boldsymbol{\varepsilon}_{k}\boldsymbol{\varepsilon}_{k}^{\intercal}}{1+\rho}\qquad k>1, \end{array}\right. \end{array} $$
(39)

where Fk is the linearization matrix of the state equation, Hk is the linearization matrix of the measurement equation, tr(⋅) represents the trace of the matrix, εk is the output residual sequence, \(\boldsymbol {\varepsilon }_{k}=\boldsymbol {z}_{k}-\hat {\boldsymbol {z}}_{k|k-1}\), ρ is the forgetting factor, Vk is the covariance matrix of the residual sequence, and β is a weakening factor which can avoid over-regulation.

Strong tracking square root cubature Kalman filter

According to [42], the following equality holds,

$$ \begin{array}{@{}rcl@{}} \boldsymbol{H}_{k}=(\boldsymbol{P}_{xz,k|k-1})^{\intercal}(\boldsymbol{P}_{k|k-1})^{-1}. \end{array} $$
(40)

After introducing the suboptimal fading factor, assume that \(\boldsymbol {P}_{k|k-1}^{e}\), \(\boldsymbol {P}_{zz,k|k-1}^{e}\) and \(\boldsymbol {P}_{xz,k|k-1}^{e}\) represent the new prediction error covariance matrix, prediction output covariance matrix and cross-covariance matrix, respectively.

It is obvious that the following equalities hold,

$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{k|k-1}^{e}&=&\boldsymbol{F}_{k}\boldsymbol{P}_{k-1|k-1}\boldsymbol{F}_{k}^{\intercal}+\boldsymbol{Q}_{k}, \end{array} $$
(41)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{zz,k|k-1}^{e}&=&\boldsymbol{H}_{k}\boldsymbol{P}_{zz,k-1|k-1}\boldsymbol{H}_{k}^{\intercal}+\boldsymbol{R}_{k}. \end{array} $$
(42)

In the SRCKF algorithm, according to QR decomposition, the prediction error covariance matrix Pk|k− 1 and the prediction output covariance matrix Pzz,k|k− 1 can be obtained by updating the corresponding characteristic square roots Sk|k− 1 and Szz,k|k− 1:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{k|k-1}&=&\boldsymbol{S}_{k|k-1}\boldsymbol{S}_{k|k-1}^{\intercal}, \end{array} $$
(43)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{zz,k|k-1}&=&\boldsymbol{S}_{zz,k|k-1}\boldsymbol{S}_{zz,k|k-1}^{\intercal}. \end{array} $$
(44)

In the same way, the following equation can be obtained:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{k|k-1}^{e}&=&\boldsymbol{S}_{k|k-1}^{e}\left( \boldsymbol{S}_{k|k-1}^{e}\right)^{\intercal}, \end{array} $$
(45)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{P}_{zz,k|k-1}^{e}&=&\boldsymbol{S}_{zz,k|k-1}^{e}\left( \boldsymbol{S}_{zz,k|k-1}^{e}\right)^{\intercal}. \end{array} $$
(46)

Therefore, when updating suboptimal fading factor λk, Eqs. (37) and (38) should be transformed into the following form:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{N}_{k}&=&\boldsymbol{V}_{k}-\left( \boldsymbol{P}_{xz,k|k-1}^{e}\right)^{\intercal}\left( \boldsymbol{S}_{k|k-1}^{e}\left( \boldsymbol{S}_{k|k-1}^{e}\right)^{\intercal}\right)^{-1}\boldsymbol{Q}_{k-1}\\ & &\left( \boldsymbol{S}_{k|k-1}^{e}\left( \boldsymbol{S}_{k|k-1}^{e}\right)^{\intercal}\right)^{-1}\left( \boldsymbol{P}_{xz,k|k-1}^{e}\right)^{\intercal}-\beta\boldsymbol{R}_{k}, \end{array} $$
(47)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{M}_{k}&=&\boldsymbol{H}_{k}\boldsymbol{F}_{k}\boldsymbol{P}_{k|k}\boldsymbol{F}_{k}^{\intercal}\boldsymbol{H}_{k}^{\intercal},\\ &=&\boldsymbol{H}_{k}\left( \boldsymbol{P}_{k|k-1}^{e}-\boldsymbol{Q}_{k-1}\right)\boldsymbol{H}_{k}^{\intercal},\\ &=&\boldsymbol{P}_{zz,k|k-1}^{e}-\boldsymbol{R}_{k}-\boldsymbol{H}_{k}\boldsymbol{Q}_{k-1}\boldsymbol{H}_{k}^{\intercal},\\ &=&\boldsymbol{P}_{zz,k|k-1}^{e}+\boldsymbol{N}_{k}-\boldsymbol{V}_{k}+(\beta-1)\boldsymbol{R}_{k},\\ &=&\boldsymbol{S}_{zz,k|k-1}^{e}\left( \boldsymbol{S}_{zz,k|k-1}^{e}\right)^{\intercal}\\ &&+\boldsymbol{N}_{k}-\boldsymbol{V}_{k}+(\beta-1)\boldsymbol{R}_{k}. \end{array} $$
(48)

The ST-SRCKF algorithm can be obtained by introducing the suboptimal fading factor. In Algorithm 1, Eq. (1) needs to be transformed into the following form:

$$ \begin{array}{@{}rcl@{}} S_{k|k-1}&=&\text{qr}{\left( \left[\sqrt{\lambda_{k}} \boldsymbol{X}_{i,k|k-1}^{*}\quad\sqrt{\boldsymbol{Q}_{k}}\right]\right)}. \end{array} $$
(49)

The steps of the ST-SRCKF algorithm are listed as follows.

  1. 1.

    Initialize the posterior error covariance matrix P0, process noise Q0 and measurement noise R0, state vector \(\hat {\boldsymbol {x}}_{0}\), and let k= 1.

  2. 2.

    Predict the state vector \(\hat {x}_{k|k-1}\) by Eqs. (1)–(1) in Algorithm 1.

  3. 3.

    Calculate suboptimal fading factor λk by Eqs. (35), (36), (39), (47), (48).

  4. 4.

    Update the prediction error covariance matrix Sk|k− 1 using Eq. (49).

  5. 5.

    Update the output error covariance matrix Szx,k|k− 1 and the cross-covariance matrix Pzx,k|k− 1 by Eqs. (1)–(1) in Algorithm 1.

  6. 6.

    Update the state vector \(\hat {x}_{k|k}\) by Eqs. (1)–(1) in Algorithm 1.

  7. 7.

    If \(||\hat {x}_{k|k}-\hat {x}_{k-1|k-1}||\le \varepsilon \), obtain the \(\hat {x}_{k|k}\). Otherwise, increase k by 1 and go to step 2.

Examples

The battery tester platform

Referring to Fig. 4, the battery experiment platform is used to detect the Li(NiCoMn)O2 material lithium-ion battery cell, and the experiment is carried out at room temperature 25∘C. The battery experiment platform includes a battery tester (NEWARE CT-4008-5V12A), a battery holder, Samsung ICR18650 (2600 mAh) lithium-ion batteries, and a host computer. The main parameters of the lithium-ion battery are shown in Table 1.

Fig. 4
figure 4

The battery test platform

Full size image
Table 1 The parameters of NCR18650PF
Full size table

Simulation process

Two simulation examples are given to verify the effectiveness of the SRCKF-MILS algorithm and the ST-SRCKF-MILS algorithm.

Apply the EKF-MILS algorithm, the HIf-MILS algorithm and the SRCKF-MILS algorithm to estimate SOC, respectively. The terminal voltage estimation is shown in Fig. 5(a). The terminal voltage estimation errors are shown in Fig. 5(b). Figure 5(c) shows the SOC estimation by different algorithms, and Fig. 5(d) shows the SOC estimation errors. The MAE and RMSE of those algorithms are shown in Table 2.

Fig. 5
figure 5

The errors of SOC estimation under intermittent discharge test

Full size image
Table 2 Estimation errors of SOC
Full size table

In order to verify the robustness of the system state, a strong disturbance is artificially added in the iterative process to simulate the outliers of the state vector.

In the first experiment, take the number of iterations as 200\(\sim \)400, and change the state of the system to a value that deviates from the mean by more than two times of the standard deviations. Figure 6(a) and (b) depict the estimated values and errors of the SRCKF-MILS algorithm, respectively. Figure 6(c) and (d) show the estimated values and errors of the ST-SRCKF-MILS algorithm, respectively. The MAE and RMSE of the SRCKF-MILS algorithm and the ST-SRCKF-MILS algorithm are shown in Table 3.

Fig. 6
figure 6

SOC estimation with state vector outliers

Full size image
Table 3 Estimation errors of SOC with state vector outliers
Full size table

In the second experiment, change the state of the system to a value that deviates from the mean by more than three times of the standard deviations. Figure 7(a) and (b) show the estimated values and errors of the SRCKF-MILS algorithm, respectively. Figure 7(c) and (d) depict the estimated values and errors of the ST-SRCKF-MILS algorithm, respectively. The MAE and RMSE of the SRCKF-MILS algorithm and the ST-SRCKF-MILS algorithm are shown in Table 4.

Fig. 7
figure 7

SOC estimation with state vector serious outliers

Full size image
Table 4 Estimation errors of SOC with state vector serious outliers
Full size table

Ultimately, numerical simulation suggests the following findings:

  1. 1.

    Table 2, Fig. 5(c) and (d) show that the SRCKF-MILS algorithm has the highest estimation accuracy than the EKF-MILS algorithm and the HIf-MILS algorithm.

  2. 2.

    Figure 6 shows that the ST-SRCKF-MILS algorithm is more stable and has smaller estimation errors than the SRCKF-MILS algorithm when the system has state vector outliers.

  3. 3.

    Figure 7 shows that the SRCKF-MILS algorithm diverges when the system has more serious outliers. For the ST-SRCKF-MILS algorithm, although the estimation errors become larger and larger, it remains stable and has a good performance. It illustrates that the ST-SRCKF-MILS algorithm has better robustness.

Conclusions

For the lithium batteries, two complementary cooperative algorithms are proposed to estimate SOC. The first one is the SRCKF-MILS algorithm, which estimates SOC interactively by the MILS algorithm and the SRCKF algorithm. Compared with the classical EKF algorithm and the HIf algorithm in [43], the proposed method improves the accuracy of estimates. In view of the existence of outliers in the state vector, an ST-SRCKF-MILS algorithm is further proposed. Simulation experiments show that the ST-SRCKF-MILS algorithm has better robustness. In addition, the proposed methods can be extended to life prediction for super-capacitors, and can be applied to model block-oriented dynamic systems.