Synchronization control of quaternion-valued memristive neural networks with and without event-triggered scheme

Abstract

In this paper, the real-valued memristive neural networks (MNNs) are extended to quaternion field, a new class of neural networks named quaternion-valued memristive neural networks (QVMNNs) is then established. The problem of master-slave synchronization of this type of networks is investigated in this paper. Two types of controllers are designed: the traditional feedback controller and the event-triggered controller. Corresponding synchronization criteria are then derived based on Lyapunov method. Moreover, it is demonstrated that Zeno behavior can be avoided in case of the event-triggered strategy proposed in this work. Finally, corresponding simulation examples are proposed to demonstrate the correctness of the proposed results derived in this work.

Introduction

Memristor is regarded as the fourth basic circuit element, which was firstly proposed by Chua (1971). However it failed to receive much attention from research area until 2008, the first practical memristor device was invented by HP company (Strukov et al. 2008). Due to its function to depict the relationship between magnetic flux and electric charge, much potential applications of memrister has appeared recently.

One of these application is the memristive neural networks (MNNs), which is formulated by introducing memristor into the connection weights. Based on the ability to memorize the passed quantity of electronics, MNNs has significant potential to be utilized in synapsis and simulate the human brain. Recently, its dynamical behavior has attracted much research attention and a great many important results have been published (Liu et al. xxx; Chen et al. 2014; Bao and Cao 2014; Wu and Zeng 2014; Zhang and Shen 2014; Chen et al. 2015). However, the investigation of MNNs are mainly restricted to the real- or complex-valued fields, the corresponding research in quaternion field are still very few till now. Thus, it gives us the motivation to investigate the quaternion-valued memristive neural networks (QVMNNs).

In 1843, the British mathematician W. R. Hamilton has invented a special type of Clifford algebra named quaternion (Simmons 1992). Different from real value and complex value, an important feature of quaternion is that the commutativity law of multiplication is not applicable for it. Due to this reason, the development of quaternion has been delayed for a long period of time. In recent years, the research for quaternion-valued systems has become a hot topic due to its widespread applications in various fields, including attitude control (Adler 1995), computer graphics (Took and Mandic 2009), image processing (Zou et al. 2016), and prediction of 3-D wind processing (Xia et al. 2015).

Recently, some researchers have introduced quaternion value into traditional NNs (Yang et al. 2018), thus leading to the formulation of quaternion-valued neural networks (QVNNs). The QVNNs can be seen as the generalization of complex-valued NNs (CVNNs), in which the states, connection weights, and activation functions are all quaternion numbers. Compared with RVNNs and CVNNs, the QVNNs shows significant advantage in dealing with multidimensional data. For instance, in image compression (Isokawa et al. 2003), QVNNs can result in a significant reduction in the size of system compared with RVNNs and CVNNs, thus bring about an improvement in calculation efficiency. Moreover, some optimization and estimation problem can be operated by QVNNs with better performance than RVNNs and CVNNs (Qin et al. 2018; Sahoo et al. 2016). Recently, with the rapid development of QVNNs, some remarkable results have been presented (Liu et al. 2017b; Song and Chen 2018; Chen et al. 2017; Liu et al. 2016; Tu et al. 2017; Chen and Song 2017; Liu et al. 2018; Chen et al. 2018), such as global stability (Liu et al. 2017b), multi-stability (Song and Chen 2018), robust stability (Chen et al. 2017), $\mu$-stability (Liu et al. 2016), passivity analysis (Tu et al. 2017), state estimation (Chen and Song 2017). For instance, with the decomposition of the state space, the multi-stability issue for delayed QVNNs were studied in Song and Chen (2018), some dynamical features of the QVNNs are analyzed. In Liu et al. (2018), by applying the approach of decomposition and quaternion-valued LMI, criterion of global $\mu$-stability is derived for the QVNNs. Chen and Song (2017) addresses the state estimation for QVNNs with multiple time delay. Via the quaternion-valued LMI method, some criteria are established. Up to now, the investigation of QVNNs are mainly focus on stability issue, the relative results on synchronization is still few.

Synchronization is an important dynamical behavior in network systems, which has been applied in many different areas, such as associative memory, combinational optimization, and pattern recognition (Ding et al. 2017; Ravishankar 2018; Wei et al. 2018; Bao et al. 2016; Nakamura and Tateno 2019; Dharani et al. 2017). In recent decades, literature for the synchronization of NNs have been widely published. The fixed-time synchronization for uncertain complex-valued neural networks with discontinuous activation functions is investigated in Ding et al. (2017). In Bao et al. (2016), exponential synchronization criteria for coupled stochastic MNNs with probabilistic delay coupling is proposed.

For the purpose to reduce the energy consumption and computation burden in communication networks, a novel sampled control scheme named event-triggered control is proposed. Other than conventional control method, the event-triggered controller only updated at the instants that the measured error exceeds some prescribed threshold. Thus, this control strategy can effectively reduce the control execution times and save the communication resource. Recently, much results on event-triggered control of networks systems have been published (Liu et al. 2017a; Wang et al. 2018; Guo et al. 2018; Li et al. 2016). In Liu et al. (2017a), the state estimation for delayed stochastic MNNs with missing measure is investigated by applying event-triggered method. Finite-time state estimation for recurrent delayed neural networks is discussed in Wang et al. (2018) via component-based event-triggered protocol. In Guo et al. (2018), the synchronization problem of real-valued MNNs has been discussed via a novel event-triggered strategy for the first time. However, the corresponding results for event-triggered synchronization of MNNs has not been extended to quaternion field yet, which gives motivation to this work.

An unavoidable phenomenon in various engineering systems is time delay, which is generated by infinite switching ratio of amplifiers or data processing. Unfortunately, it may lead to instability, oscillation, and other poor performance to the system (Ding et al. 2017; Ravishankar 2018; Wei et al. 2018; Bao et al. 2016; Cao 2019; Cao et al. 2019; Huang et al. 2014, 2019; Huang and Zhang 2019; Huang and Liu 2019; Nakamura and Tateno 2019). Thus, it is necessary to take time delays into the study of dynamical behavior of QVMNNs.

Based on the above discussion, the main purpose of this work is to investigate the synchronization problem of QVMNNs with or without event-triggered strategy. The main contributions of this thesis are presented as below.

• (1) In this paper, the model of QVMNNs is formulated, which combines the features of both MNNs and QVNNs. Thus, our study is the generalization and extension for existing research on NNs, more challenging dynamical characteristics of network systems are dealt with in our work.

• (2) It is the first time that synchronization problem for QVMNNs are investigated by event-triggered control. Two criteria for the master-slave synchronization of QVMNNs are derived, which are convenient to verify.

• (3) The theoretical results in this work may provide new ideas for other quaternion-valued networks in the future.

The structure of this work is presented as below. In part 2, the model is established and some basic preliminaries are given. Main results are achieved in Part 3. In Sect. 5, a numerical example is provided to verity the effectiveness of our theorem. Lastly, conclusion is obtained in Part 5.

Notations. In this work, let R, C and Q stand for the real field, complex field and quaternion field, respectively. $R^{n}, C^{n}$ and $Q^{n}$ represent the space of n dimensional vectors, $R_{n\times n}, C_{n\times n}$ and $Q_{n\times n}$ denotes the space of $n\times n$ dimensional matrices. $C^{(1)}([-\tau , 0], R^{n})$ represents the class of continuous functions from $[-\tau , 0]$ to $R^{n}$. $co\{F_{1}, F_{2}\}$ stands for closure of the convex hull of Q produced by quaternion numbers $F_{1}, F_{2}$. The notation T denotes the transpose of a matrix. For any vector $\chi \in R^{n}$, the vector norm is defined as $\Vert \chi \Vert _{1}=\sum \nolimits _{q=1}^{n}|\chi _{q}|$. For any matrix $A\in R^{n\times n}$, the matrix norm is defined as $\Vert A\Vert _{1}=\max _{1\le q\le n}\{\sum \nolimits _{p=1}^{n}|a_{pq}|\}$, the matrix measure is defined as $\mu _{1}(A)=\lim _{h\rightarrow 0^{+}}\frac{\Vert I+hA\Vert _{1}-1}{h}=\max _{q}\{a_{qq}+\sum _{p=1, p\ne q}^{n}|a_{pq}|\}$.

Model formulation and preliminaries

The quaternion is a kind of supercomplex number formed by one real part and three imaginary parts. A quaternion $q\in Q$ can be described in the form

$$\begin{aligned} q=q^{R}+q^{I}i+q^{J}j+q^{K}k, \end{aligned}$$

where $q^{R}, q^{I}, q^{J}, q^{K}\in R$, the imaginary parts i, j, k obey the Hamilton rule:

$$\begin{aligned} i^{2}&=j^{2}=k^{2}=-1, ij=-ji=k, \\ jk&=-kj=i, ki=-ik=j. \end{aligned}$$

Remark 1

Different from real number and complex number, the commutativity rule does not hold for quaternion multiplication, i.e., for any $x, y\in Q$, it can not be ensured that $xy=yx$. Due to this reason, some good properties in real field and complex field does not hold in quaternion field. Thus, existing approach dealing with RVNNs or CVNNs can not be directly applied to QVNNs, which lead to the need to develop new techniques and theories to cope with QVNNs.

The conjugate of q is denoted by $q^{*}$ or $\bar{q}$, $\bar{q}=q^{R}-q^{I}i-q^{J}j-q^{K}k$. The modulus of q is defined as

$$\begin{aligned} |q|=\sqrt{\bar{q}q}=\sqrt{(q^{R})^{2}+(q^{I})^{2}+(q^{J})^{2}+(q^{K})^{2}}. \end{aligned}$$

For any vector $x=(x_{1},\ldots ,x_{n})^{T}\in Q^{n}$, it is defined that $|x|=(|x_{1}|,\ldots ,|x_{n}|)^{T}$, $x^{*}=\bar{x}=(x^{*}_{1},\ldots ,x^{*}_{n})^{T}$. For any matrix $A=(a_{pq})_{n\times n}\in Q_{n\times n}$, it is defined that $|A|=(|a_{pq}|)_{n\times n}$. For two quaternion $h=h^{R}+h^{I}i+h^{J}j+h^{K}k$ and $q=q^{R}+q^{I}i+q^{J}j+q^{K}k$, the addition between them is defined as

$$\begin{aligned} h+q&=h^{R}+q^{R}+(h^{I}+q^{I})i+(h^{J}+q^{J})j\\&\quad +(h^{K}+q^{K})k. \end{aligned}$$

By Hamilton rule, the product between them is defined as

$$\begin{aligned} hq=\,&(h^{R}q^{R}-h^{I}q^{I}-h^{J}q^{J}-h^{K}q^{K})\\&+(h^{R}q^{I}+h^{I}q^{R}+h^{J}q^{K}-h^{K}q^{J})i\\&+(h^{R}q^{J}+h^{J}q^{R}+h^{K}q^{I}-h^{I}q^{K})j\\&+(h^{R}q^{K}+h^{K}q^{R}+h^{I}q^{J}-h^{J}q^{I})k. \end{aligned}$$

With the introduction of memristive connection weights into QVNNs, the model of QVMNNs is constructed as follows:

$$\begin{aligned} \frac{dx_{p}(t)}{dt}=&-d_{p}x_{p}(t)+\sum \limits _{q=1}^{n}a_{pq}(x_{p}(t))f_{q}(x_{q}(t))\nonumber \\&+\sum \limits _{q=1}^{n}b_{pq}(x_{p}(t))f_{q}(x_{q}(t-\tau (t))), \end{aligned}$$

(1)

where $p=1, 2,\ldots , n$; $x_{p}(t)\in Q$ denotes the state vector of the pth neuron at time t. $d_{p}>0$ is the self-feedback coefficient; $f_{p}(x_{p}(\cdot ))$ denotes the activation function. $a_{pq}(x_{p}(t))$ and $b_{pq}(x_{p}(t))$ stand for the quaternion-valued memristive connection weights. $\tau (t)$ is the time delay satisfying $\dot{\tau }(t)\le \mu <1$ and $0\le \tau (t)<\tau$, where $\mu$ and $\tau$ are positive constants. The initial condition of system (1) is taken as $x_{p}(s)=\phi _{p}(s), -\tau \le s\le 0$, where $\phi _{p}(s)\in C^{(1)}([-\tau , 0], Q)$.

Taking system (1) as the master system and construct the following slave system

$$\begin{aligned} \frac{dy_{p}(t)}{dt}=&-d_{p}y_{p}(t)+\sum \limits _{q=1}^{n}a_{pq}(y_{p}(t))f_{q}(y_{q}(t))\nonumber \\&+\sum \limits _{q=1}^{n}b_{pq}(y_{p}(t))f_{q}(y_{q}(t-\tau (t)))+u_{p}(t), \end{aligned}$$

(2)

where $u_{p}(t)$ is the appropriate controller to be determined later. Define $e_{p}(t)=y_{p}(t)-x_{p}(t)$ as the synchronization error. Our aim is to design proper controller $u_{p}(t)$ to realize the synchronization between system (1) and system (2). The error system of master-slave system is obtained below

$$\begin{aligned} \frac{de_{p}(t)}{dt} =&-d_{p}e_{p}(t)+\sum \limits _{q=1}^{n}a_{pq}(y_{p}(t))g_{q}(e_{q}(t))\nonumber \\&+\sum \limits _{q=1}^{n}b_{pq}(y_{p}(t))g_{q}(e_{q}(t-\tau (t)))\nonumber \\&+\sum \limits _{q=1}^{n}[a_{pq}(y_{p}(t))-a_{pq}(x_{p}(t))]f_{q}(x_{q}(t))\nonumber \\&+\sum \limits _{q=1}^{n}[b_{pq}(y_{p}(t))-b_{pq}(x_{p}(t))]f_{q}(x_{q}(t-\tau (t)))+u_{p}(t). \end{aligned}$$

(3)

According to the current-voltage characteristics and nature of memristor, the memristive weights can be defined as the state-dependent switching case:

$$\begin{aligned} \begin{aligned} a^{R}_{pq}(x^{R}_{p}(t))=&\left\{ \begin{array}{c} \hat{a}^{R}_{pq}, |x^{R}_{p}(t)|\le T_{p}, \\ \check{a}^{R}_{pq}, |x^{R}_{p}(t)|> T_{p}, \end{array}\right. a^{I}_{pq}(x^{I}_{p}(t))=\left\{ \begin{array}{c} \hat{a}^{I}_{pq}, |x^{I}_{p}(t)|\le T_{p}, \\ \check{a}^{I}_{pq}, |x^{I}_{p}(t)|> T_{p}, \end{array}\right. \\ a^{J}_{pq}(x^{J}_{p}(t))=&\left\{ \begin{array}{c} \hat{a}^{J}_{pq}, |x^{J}_{p}(t)|\le T_{p}, \\ \check{a}^{J}_{pq}, |x^{J}_{p}(t)|> T_{p}, \end{array}\right. a^{K}_{pq}(x^{K}_{p}(t))=\left\{ \begin{array}{c} \hat{a}^{K}_{pq}, |x^{K}_{p}(t)|\le T_{p}, \\ \check{a}^{K}_{pq}, |x^{K}_{p}(t)|> T_{p}, \end{array}\right. \\ b^{R}_{pq}(x^{R}_{p}(t))=&\left\{ \begin{array}{c} \hat{b}^{R}_{pq}, |x^{R}_{p}(t)|\le T_{p}, \\ \check{b}^{R}_{pq}, |x^{R}_{p}(t)|> T_{p}, \end{array}\right. b^{I}_{pq}(x^{I}_{p}(t))=\left\{ \begin{array}{c} \hat{b}^{I}_{pq}, |x^{I}_{p}(t)|\le T_{p}, \\ \check{b}^{I}_{pq}, |x^{I}_{p}(t)|> T_{p}, \end{array}\right. \\ b^{J}_{pq}(x^{J}_{p}(t))=&\left\{ \begin{array}{c} \hat{b}^{J}_{pq}, |x^{J}_{p}(t)|\le T_{p}, \\ \check{b}^{J}_{pq}, |x^{J}_{p}(t)|> T_{p}, \end{array}\right. b^{K}_{pq}(x^{K}_{p}(t))=\left\{ \begin{array}{c} \hat{b}^{K}_{pq}, |x^{K}_{p}(t)|\le T_{p}, \\ \check{b}^{K}_{pq}, |x^{K}_{p}(t)|> T_{p}, \end{array}\right. \end{aligned} \end{aligned}$$

(4)

where the switching jump $T_{p}>0$, $\hat{a}^{l}_{pq}, \check{a}^{l}_{pq}, \hat{b}^{l}_{pq}, \check{b}^{l}_{pq}$ are known constants with respect to memristances, $l=R, I, J, K$.

Definition 1

For convenience of later analysis, the following definition is given:

$$\begin{aligned} \acute{a}^{R}_{pq}=&\max \{\hat{a}^{R}_{pq}, \check{a}^{R}_{pq}\}, \acute{a}^{I}_{pq}=\max \{\hat{a}^{I}_{pq}, \check{a}^{I}_{pq}\},\\ \acute{a}^{J}_{pq}=&\max \{\hat{a}^{J}_{pq}, \check{a}^{J}_{pq}\},\\ \acute{a}^{K}_{pq}=&\max \{\hat{a}^{K}_{pq}, \check{a}^{K}_{pq}\}, \grave{a}^{R}_{pq}=\min \{\hat{a}^{R}_{pq}, \check{a}^{R}_{pq}\}, \\ \grave{a}^{I}_{pq}=&\min \{\hat{a}^{I}_{pq}, \check{a}^{I}_{pq}\},\\ \grave{a}^{J}_{pq}=&\min \{\hat{a}^{J}_{pq}, \check{a}^{J}_{pq}\}, \grave{a}^{K}_{pq}=\min \{\hat{a}^{K}_{pq}, \check{a}^{K}_{pq}\},\\ \acute{b}^{R}_{pq}=&\max \{\hat{b}^{R}_{pq}, \check{b}^{R}_{pq}\},\\ \acute{b}^{I}_{pq}=&\max \{\hat{b}^{I}_{pq}, \check{b}^{I}_{pq}\}, \acute{b}^{J}_{pq}=\max \{\hat{b}^{J}_{pq}, \check{b}^{J}_{pq}\}, \\ \acute{b}^{K}_{pq}=&\max \{\hat{b}^{K}_{pq}, \check{b}^{K}_{pq}\},\\ \grave{b}^{R}_{pq}=&\min \{\hat{b}^{R}_{pq}, \check{b}^{R}_{pq}\}, \grave{b}^{I}_{pq}=\min \{\hat{b}^{I}_{pq}, \check{b}^{I}_{pq}\},\\ \grave{b}^{J}_{pq}=&\min \{\hat{b}^{J}_{pq}, \check{b}^{J}_{pq}\},\\ \grave{b}^{K}_{pq}=&\min \{\hat{b}^{K}_{pq}, \check{b}^{K}_{pq}\},\\ \tilde{a}^{R}_{pq}=&\max \{|\hat{a}^{R}_{pq}|, |\check{a}^{R}_{pq}|\}, \tilde{a}^{I}_{pq}=\max \{|\hat{a}^{I}_{pq}|, |\check{a}^{I}_{pq}|\},\\ \tilde{a}^{J}_{pq}=&\max \{|\hat{a}^{J}_{pq}|, |\check{a}^{J}_{pq}|\}, \tilde{a}^{K}_{pq}=\max \{|\hat{a}^{K}_{pq}|, |\check{a}^{K}_{pq}|\},\\ \tilde{b}^{R}_{pq}=&\max \{|\hat{b}^{R}_{pq}|, |\check{b}^{R}_{pq}|\}, \tilde{b}^{I}_{pq}=\max \{|\hat{b}^{I}_{pq}|, |\check{b}^{I}_{pq}|\},\\ \tilde{b}^{J}_{pq}=&\max \{|\hat{b}^{J}_{pq}|, |\check{b}^{J}_{pq}|\}, \tilde{b}^{K}_{pq}=\max \{|\hat{b}^{K}_{pq}|, |\check{b}^{K}_{pq}|\}. \end{aligned}$$

For $\pi =R, I, J, K$, it is noted that

$$\begin{aligned} \acute{A}^{\pi }&=(\acute{a}^{\pi }_{pq})_{n\times n}, \grave{A}^{\pi }=(\grave{a}^{\pi }_{pq})_{n\times n}, \acute{B}^{\pi }=(\acute{b}^{\pi }_{pq})_{n\times n},\\ \grave{B}^{\pi }&=(\grave{b}^{\pi }_{pq})_{n\times n},\tilde{A}^{\pi }=(\tilde{a}^{\pi }_{pq})_{n\times n}, \tilde{B}^{\pi }=(\tilde{b}^{\pi }_{pq})_{n\times n}. \end{aligned}$$

By letting $e(t)=(e_{1}(t),\ldots ,e_{n}(t))^{T}\in Q^{n}$, the compact form of error system (3) can be achieved

$$\begin{aligned} \frac{de(t)}{dt} =&-De(t)+A(y(t))g(e(t))+B(y(t))g(e(t-\tau (t)))\nonumber \\&+(A(y(t))-A(x(t)))f(x(t))\nonumber \\&+(B(y(t))-B(x(t)))f(x(t-\tau (t)))+u(t), \end{aligned}$$

(5)

where $f(x(\cdot ))=(f_{1}(x_{1}(\cdot )),\ldots ,f_{n}(x_{n}(\cdot )))^{T}\in Q^{n}$, $g(e(t))=f(y(t))-f(x(t))$.

Assumption 1

Assume that the function $f(x(t))\in Q^{n}$ can be decomposed into the following form

$$\begin{aligned} f(x(t))&=f^{R}(x^{R}(t))+if^{I}(x^{I}(t))+jf^{J}(x^{J}(t))\nonumber \\&\quad +kf^{K}(x^{K}(t)), \end{aligned}$$

(6)

where functions $f^{R}(x^{R}(t)), f^{I}(x^{I}(t)), f^{J}(x^{J}(t)), f^{K}(x^{K}(t))\in R^{n}$.

Let $e(t)=e^{R}(t)+ie^{I}(t)+je^{J}(t)+ke^{K}(t)$. Then, according to Hamilton rule, the error system (3) can be separated into four real part as below

$$\begin{aligned} \frac{de^{R}(t)}{dt} =&-De^{R}(t)+A^{R}(y)g^{R}(e^{R}(t))-A^{I}(y)g^{I}(e^{I}(t))\nonumber \\&-A^{J}(y)g^{J}(e^{J}(t))\nonumber \\&-A^{K}(y)g^{K}(e^{K}(t))+B^{R}(y)g^{R}(e^{R}(t-\tau (t)))\nonumber \\&-B^{I}(y)g^{I}(e^{I}(t-\tau (t)))\nonumber \\&-B^{J}(y)g^{J}(e^{J}(t-\tau (t)))\nonumber \\&-B^{K}(y)g^{K}(e^{K}(t-\tau (t)))\nonumber \\&+(A^{R}(y)-A^{R}(x))f^{R}(x^{R}(t))\nonumber \\&-(A^{I}(y)-A^{I}(x))f^{I}(x^{I}(t))\nonumber \\&-(A^{J}(y)-A^{J}(x))f^{J}(x^{J}(t))\nonumber \\&-(A^{K}(y)-A^{K}(x))f^{K}(x^{K}(t))\nonumber \\&+(B^{R}(y)-B^{R}(x))f^{R}(x^{R}(t-\tau (t)))\nonumber \\&-(B^{I}(y)-B^{I}(x))f^{I}(x^{I}(t-\tau (t)))\nonumber \\&-(B^{J}(y)-B^{J}(x))f^{J}(x^{J}(t-\tau (t)))\nonumber \\&-(B^{K}(y)-B^{K}(x))f^{K}(x^{K}(t-\tau (t)))+u^{R}(t) \end{aligned}$$

(7)

$$\begin{aligned} \frac{de^{I}(t)}{dt} =&-De^{I}(t)+A^{I}(y)g^{R}(e^{R}(t))+A^{R}(y)g^{I}(e^{I}(t))\nonumber \\&+A^{K}(y)g^{J}(e^{J}(t))\nonumber \\&-A^{J}(y)g^{K}(e^{K}(t))+B^{I}(y)g^{R}(e^{R}(t-\tau (t)))\nonumber \\&+B^{R}(y)g^{I}(e^{I}(t-\tau (t)))\nonumber \\&+B^{K}(y)g^{J}(e^{J}(t-\tau (t)))\nonumber \\&-B^{J}(y)g^{K}(e^{K}(t-\tau (t)))\nonumber \\&+(A^{I}(y)-A^{I}(x))f^{R}(x^{R}(t))\nonumber \\&+(A^{R}(y)-A^{R}(x))f^{I}(x^{I}(t))\nonumber \\&+(A^{K}(y)-A^{K}(x))f^{J}(x^{J}(t))\nonumber \\&-(A^{J}(y)-A^{J}(x))f^{K}(x^{K}(t))\nonumber \\&+(B^{I}(y)-B^{I}(x))f^{R}(x^{R}(t-\tau (t)))\nonumber \\&+(B^{R}(y)-B^{R}(x))f^{I}(x^{I}(t-\tau (t)))\nonumber \\&+(B^{K}(y)-B^{K}(x))f^{J}(x^{J}(t-\tau (t)))\nonumber \\&-(B^{J}(y)-B^{J}(x))f^{K}(x^{K}(t-\tau (t)))+u^{I}(t) \end{aligned}$$

(8)

$$\begin{aligned} \frac{de^{J}(t)}{dt} =&-De^{J}(t)+A^{J}(y)g^{R}(e^{R}(t))+A^{K}(y)g^{I}(e^{I}(t))\nonumber \\&+A^{R}(y)g^{J}(e^{J}(t))\nonumber \\&-A^{I}(y)g^{K}(e^{K}(t))+B^{J}(y)g^{R}(e^{R}(t-\tau (t)))\nonumber \\&+B^{K}(y)g^{I}(e^{I}(t-\tau (t)))\nonumber \\&+B^{R}(y)g^{J}(e^{J}(t-\tau (t)))\nonumber \\&-B^{I}(y)g^{K}(e^{K}(t-\tau (t)))\nonumber \\&+(A^{J}(y)-A^{J}(x))f^{R}(x^{R}(t))\nonumber \\&+(A^{K}(y)-A^{K}(x))f^{I}(x^{I}(t))\nonumber \\&+(A^{R}(y)-A^{R}(x))f^{J}(x^{J}(t))\nonumber \\&-(A^{I}(y)-A^{I}(x))f^{K}(x^{K}(t))\nonumber \\&+(B^{J}(y)-B^{J}(x))f^{R}(x^{R}(t-\tau (t)))\nonumber \\&+(B^{K}(y)-B^{K}(x))f^{I}(x^{I}(t-\tau (t)))\nonumber \\&+(B^{R}(y)-B^{R}(x))f^{J}(x^{J}(t-\tau (t)))\nonumber \\&-(B^{I}(y)-B^{I}(x))f^{K}(x^{K}(t-\tau (t)))+u^{J}(t) \end{aligned}$$

(9)

$$\begin{aligned} \frac{de^{K}(t)}{dt} =&-De^{K}(t)+A^{K}(y)g^{R}(e^{R}(t))-A^{J}(y)g^{I}(e^{I}(t))\nonumber \\&+A^{I}(y)g^{J}(e^{J}(t))\nonumber \\&+A^{R}(y)g^{K}(e^{K}(t))+B^{K}(y)g^{R}(e^{R}(t-\tau (t)))\nonumber \\&-B^{J}(y)g^{I}(e^{I}(t-\tau (t)))\nonumber \\&+B^{I}(y)g^{J}(e^{J}(t-\tau (t)))\nonumber \\&+B^{R}(y)g^{K}(e^{K}(t-\tau (t)))\nonumber \\&+(A^{K}(y)-A^{K}(x))f^{R}(x^{R}(t))\nonumber \\&-(A^{J}(y)-A^{J}(x))f^{I}(x^{I}(t))\nonumber \\&+(A^{I}(y)-A^{I}(x))f^{J}(x^{J}(t))\nonumber \\&+(A^{R}(y)-A^{R}(x))f^{K}(x^{K}(t))\nonumber \\&+(B^{K}(y)-B^{K}(x))f^{R}(x^{R}(t-\tau (t)))\nonumber \\&-(B^{J}(y)-B^{J}(x))\nonumber \\&\cdot f^{I}(x^{I}(t-\tau (t)))+(B^{I}(y)\nonumber \\&-B^{I}(x))f^{J}(x^{J}(t-\tau (t)))\nonumber \\&-(B^{R}(y)-B^{R}(x))f^{K}(x^{K}(t-\tau (t)))+u^{K}(t) \end{aligned}$$

(10)

By making the definition that $E(t)=(e^{R}(t)^{T}, e^{I}(t)^{T}, e^{J}(t)^{T}, e^{K}(t)^{T})^{T}\in R^{4n}$ and $X(t)=(x^{R}(t)^{T}, x^{I}(t)^{T}, x^{J}(t)^{T}, x^{K}(t)^{T})^{T}\in R^{4n}$, then the compact form of (7) can be derived

$$\begin{aligned} \frac{dE(t)}{dt} =&-\bar{D}E(t)+\bar{A}_{y}G(E(t))+\bar{B}_{y}G(E(t-\tau (t)))\nonumber \\&+(\bar{A}_{y}-\bar{A}_{x})F(X(t))\nonumber \\&+(\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))+U(t), \end{aligned}$$

(11)

where

$$\begin{aligned} U(t)&=(u^{R}(t)^{T}, u^{I}(t)^{T}, u^{J}(t)^{T}, u^{K}(t)^{T})^{T}\in R^{4n},\nonumber \\ G(E(t))&=(g^{R}(e^{R}(t))^{T}, g^{I}(e^{I}(t))^{T}, g^{J}(e^{J}(t))^{T}, g^{K}(e^{K}(t))^{T})^{T}\in R^{4n},\nonumber \\ F(X(t))&=(f^{R}(x^{R}(t))^{T}, f^{I}(x^{I}(t))^{T}, f^{J}(x^{J}(t))^{T}, f^{K}(x^{K}(t))^{T})^{T}\in R^{4n},\nonumber \\ \bar{D}&=diag\{D, D, D, D\}\in R^{4n\times 4n}.\nonumber \\ \bar{A}_{y}&=\left( \begin{array}{cccc} A^{R}(y) &\quad -\,A^{I}(y) &\quad -\,A^{J}(y) &\quad -\,A^{K}(y)\\ A^{I}(y) &\quad A^{R}(y) &\quad A^{K}(y) & \quad -\,A^{J}(y)\\ A^{J}(y) &\quad A^{K}(y) &\quad A^{R}(y) &\quad -\,A^{I}(y)\\ A^{K}(y) &\quad -\,A^{J}(y) &\quad A^{I}(y) &\quad A^{R}(y)\\ \end{array} \right) \in R^{4n\times 4n},\nonumber \\ \bar{B}_{y}&=\left( \begin{array}{cccc} B^{R}(y) &\quad -\,B^{I}(y) &\quad -\,B^{J}(y) &\quad -\,B^{K}(y)\\ B^{I}(y) &\quad B^{R}(y) &\quad B^{K}(y) &\quad -\,B^{J}(y)\\ B^{J}(y) &\quad B^{K}(y) &\quad B^{R}(y) &\quad -\,B^{I}(y)\\ B^{K}(y) &\quad -\,B^{J}(y) &\quad B^{I}(y) &\quad B^{R}(y)\\ \end{array} \right) \in R^{4n\times 4n},\nonumber \\ \bar{A}_{x}&=\left( \begin{array}{cccc} A^{R}(x) &\quad -\,A^{I}(x) &\quad -\,A^{J}(x) &\quad -\,A^{K}(x)\\ A^{I}(x) &\quad A^{R}(x) &\quad A^{K}(x) &\quad -\,A^{J}(x)\\ A^{J}(x) &\quad A^{K}(x) &\quad A^{R}(x) &\quad -\,A^{I}(x)\\ A^{K}(x) &\quad -\,{J}(x) &\quad A^{I}(x) &\quad A^{R}(x)\\ \end{array} \right) \in R^{4n\times 4n},\nonumber \\ \bar{B}_{x}&=\left( \begin{array}{cccc} B^{R}(x) &\quad -\,{I}(x) &\quad -\,{J}(x) &\quad -\,{K}(x)\\ B^{I}(x) &\quad B^{R}(x) &\quad B^{K}(x) &\quad -\,{J}(x)\\ B^{J}(x) &\quad B^{K}(x) &\quad B^{R}(x) &\quad -\,{I}(x)\\ B^{K}(x) &\quad -\,{J}(x) &\quad B^{I}(x) &\quad B^{R}(x)\\ \end{array} \right) \in R^{4n\times 4n}, \end{aligned}$$

(12)

Remark 2

Note that the elements of matrices $\bar{A}_{x}, \bar{B}_{x}, \bar{A}_{y}, \bar{B}_{y}$ are variables that switching according to the value x, y. However, each element in these matrices has upper bound.

For the convenience of later discussion, the following notations are made

$$\begin{aligned} \acute{A}&=\left( \begin{array}{cccc} \acute{A}^{R} &\quad \acute{A}^{I} &\quad \acute{A}^{J} &\quad \acute{A}^{K}\\ \acute{A}^{I} &\quad \acute{A}^{R} &\quad \acute{A}^{K} &\quad \acute{A}^{J}\\ \acute{A}^{J} &\quad \acute{A}^{K} &\quad \acute{A}^{R} & \quad \acute{A}^{I}\\ \acute{A}^{K} &\quad \acute{A}^{J} & \quad \acute{A}^{I} &\quad \acute{A}^{R}\\ \end{array} \right) ,\quad \grave{A}&=\left( \begin{array}{cccc} \grave{A}^{R} & \quad \grave{A}^{I} &\quad \grave{A}^{J} &\quad \grave{A}^{K}\\ \grave{A}^{I} &\quad \grave{A}^{R} &\quad \grave{A}^{K} &\quad \grave{A}^{J}\\ \grave{A}^{J} &\quad \grave{A}^{K} & \quad \grave{A}^{R} & \quad \grave{A}^{I}\\ \grave{A}^{K} &\quad \grave{A}^{J} &\quad \grave{A}^{I} &\quad \grave{A}^{R}\\ \end{array} \right) ,\\ \acute{B}&=\left( \begin{array}{cccc} \acute{B}^{R} &\quad \acute{B}^{I} & \quad \acute{B}^{J} &\quad \acute{B}^{K}\\ \acute{B}^{I} &\quad \acute{B}^{R} &\quad \acute{B}^{K} &\quad \acute{B}^{J}\\ \acute{B}^{J} &\quad \acute{B}^{K} & \quad \acute{B}^{R} & \quad \acute{B}^{I}\\ \acute{B}^{K} &\quad \acute{B}^{J} &\quad \acute{B}^{I} &\quad \acute{B}^{R}\\ \end{array} \right) ,\quad \grave{B}&=\left( \begin{array}{cccc} \grave{B}^{R} &\quad \grave{B}^{I} & \quad \grave{B}^{J} & \quad \grave{B}^{K}\\ \grave{B}^{I} &\quad \grave{B}^{R} & \quad \grave{B}^{K} & \quad \grave{B}^{J}\\ \grave{B}^{J} & \quad \grave{B}^{K} &\quad \grave{B}^{R} &\quad \grave{B}^{I}\\ \grave{B}^{K} & \quad \grave{B}^{J} &\quad \grave{B}^{I} & \quad \grave{B}^{R}\\ \end{array} \right) ,\\ \tilde{A}&=\left( \begin{array}{cccc} \tilde{A}^{R} &\quad \tilde{A}^{I} &\quad \tilde{A}^{J} &\quad \tilde{A}^{K}\\ \tilde{A}^{I} &\quad \tilde{A}^{R} &\quad \tilde{A}^{K} &\quad \tilde{A}^{J}\\ \tilde{A}^{J} &\quad \tilde{A}^{K} &\quad \tilde{A}^{R} &\quad \tilde{A}^{I}\\ \tilde{A}^{K} & \quad \tilde{A}^{J} & \quad \tilde{A}^{I} &\quad \tilde{A}^{R}\\ \end{array} \right) ,\quad \tilde{B}&=\left( \begin{array}{cccc} \tilde{B}^{R} &\quad \tilde{B}^{I} &\quad \tilde{B}^{J} &\quad \tilde{B}^{K}\\ \tilde{B}^{I} & \quad \tilde{B}^{R} &\quad \tilde{B}^{K} & \quad \tilde{B}^{J}\\ \tilde{B}^{J} & \quad \tilde{B}^{K} & \quad \tilde{B}^{R} &\quad \tilde{B}^{I}\\ \tilde{B}^{K} &\quad \tilde{B}^{J} &\quad \tilde{B}^{I} &\quad \tilde{B}^{R}\\ \end{array} \right) . \end{aligned}$$

Assumption 2

For any $x,y\in R^{4n}$, there exists positive constants $L_{f}$ and positive scalar $M=(M_{1},\ldots ,M_{4n})^{T}\in R^{4n}$, such that

$$\begin{aligned} \Vert F(x)-F(y)\Vert _{1}\le L_{f}\Vert x-y\Vert _{1}, \quad |F(x)|\le M, \end{aligned}$$

(13)

where $|F(x)|=(|F_{1}(x)|,\ldots ,|F_{4n}(x)|)^{T}\in R^{4n}$.

Definition 2

The quaternion master-slave system (1) and (2) is said to be synchronized if

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert x(t)-y(t)\Vert _{1}=0. \end{aligned}$$

(14)

It is equivalent to that

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert E(t)\Vert _{1}=0. \end{aligned}$$

(15)

Definition 3

The quaternion master-slave system (1) and (2) is said to be quasi-synchronized if there exists a positive constant $\varepsilon$ such that

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert E(t)\Vert _{1}\le \varepsilon . \end{aligned}$$

(16)

It means that the error trajectory can converge to a bounded set.

Lemma 1

(Halanay inequality Halanay 1966) For continuous nonnegative functionV(t), assume that there exists positive constants$\gamma , \beta >0$such that the following conditions hold

$$\begin{aligned} D^{+}V(t)&\le -\beta V(t)+\gamma \sup _{t-\tau \le s\le t}V(s), t\in [t_{0}, +\infty )\nonumber \\&\beta>\gamma >0 \end{aligned}$$

(17)

then we obtain the conclusion

$$\begin{aligned} V(t)\le \sup _{t_{0}-\tau \le s\le t_{0}}V(s)e^{-\mu ^{*}(t-t_{0})}, t\in [t_{0}, +\infty ) \end{aligned}$$

(18)

where$\mu ^{*}>0$is the unique positive solution of equation$\mu -\beta +\gamma e^{\mu \tau }=0$.

Lemma 2

(Generalized Halanay Inequality Wen et al. 2008) For any nonnegative functionV(t), assume that there exists positive constant$\xi$and continuous function$\alpha (t)\ge 0, \beta (t)\le 0, \gamma (t)\ge 0$such that the following conditions hold

$$\begin{aligned} D^{+}V(t)&\le \alpha (t)+\beta (t)V(t)\nonumber \\&\quad +\gamma (t)\sup _{t-\tau \le s\le t}V(s), t\in [t_{0}, +\infty )\nonumber \\&\beta (t)+\gamma (t)\le -\xi , t\in [t_{0}, +\infty ) \end{aligned}$$

(19)

then we obtain the conclusion

$$\begin{aligned} V(t)\le \frac{\alpha ^{*}}{\xi }+\sup _{t_{0}-\tau \le s\le t_{0}}V(s)e^{-\mu ^{*}(t-t_{0})} \end{aligned}$$

(20)

where $\alpha ^{*}=\sup _{-\infty \le s\le t_{0}}\alpha (s), \mu ^{*}=\inf _{t\ge t_{0}}\{\mu (t)| \mu (t)+\beta (t)+\gamma (t)e^{\mu (t)\tau (t)}=0\}.$

Main results

In this part, we first consider the complete synchronization of master-slave system (1) and (2) by choosing the following feedback controller

$$\begin{aligned} U(t)=-KE(t)-\varGamma sgn(E(t)), \end{aligned}$$

(21)

where $K=diag(k_{1},\ldots ,k_{4n}), \varGamma =diag(\gamma _{1},\ldots ,\gamma _{4n})$. Then, the global synchronization of master-slave system (1) and (2) can be obtained by using Halanay inequality.

Theorem 1

Under Assumption2, if there exists control gains matrices$K, \varGamma$such that the following condition holds

$$\begin{aligned}&-d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}-k_{\min }\le 0, \end{aligned}$$

(22)

$$\begin{aligned}&2\cdot 1_{4n}^{T}[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M-\sum _{p=1}^{4n}\gamma _{p}\le 0, \end{aligned}$$

(23)

where$d_{\min }=\min \{d_{1},\ldots ,d_{n}\}, k_{\min }=\min \{k_{1},\ldots ,k_{4n}\}, 1_{4n}=(1,\ldots ,1)^{T}\in R^{4n}$. Then the global synchronization between system (1) and (2) can be achieved under controller (21).

Proof

Considering the Lyapunov functional as below

$$\begin{aligned} V(t)=\Vert E(t)\Vert _{1}+\frac{1}{1-\rho }\int ^{t}_{t-\tau (t)}\Vert \tilde{B}\Vert _{1}\Vert G(E(s))\Vert _{1}ds \end{aligned}$$

(24)

Calculating the derivative of V(t) along the trajectory (11) yields

$$\begin{aligned} \frac{dV(t)}{dt}\le \,&sgnE^{T}(t)\{-\bar{D}E(t)+\bar{A}_{y}G(E(t))\nonumber \\&+\bar{B}_{y}G(E(t-\tau (t)))\nonumber \\&+[(\bar{A}_{y}-\bar{A}_{x})F(X(t))\nonumber \\&+(\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))]-KE(t)\nonumber \\&-\varGamma sgn(E(t))\}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}\Vert G(E(t))\Vert _{1}\nonumber \\&-\Vert \tilde{B}\Vert _{1}\Vert G(E(t-\tau (t)))\Vert _{1}\nonumber \\ \le&\left( -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}\right) \Vert E(t)\Vert _{1}\nonumber \\&+2\cdot 1_{4n}^{T}[(\acute{A}-\grave{A})\nonumber \\&+(\acute{B}-\grave{B})]M-sgnE^{T}(t)\varGamma sgn(E(t))\nonumber \\&-sgnE^{T}(t)KE(t)\nonumber \\ \le&\left( -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}\right) \Vert E(t)\Vert _{1}\nonumber \\&+2\cdot 1_{4n}^{T}[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M\nonumber \\&-\sum _{p=1}^{4n}\gamma _{p}-\sum _{p=1}^{4n}k_{p}|E_{p}(t)|\nonumber \\ \le&\left( -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}\right. \nonumber \\&\left. -k_{\min }\right) \Vert E(t)\Vert _{1}\nonumber \\&+2\cdot 1_{4n}^{T}[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M-\sum _{p=1}^{4n}\gamma _{p}\le 0 \end{aligned}$$

(25)

Based on above analysis, the synchronization between system (1) and (2) can be achieved under the controller (21). $\square$

Remark 3

For the first time, the memistive connection weights are brought into QVNNs. As the extension of memristive RVNNs and CVNNs, the weight connections $a^{R}_{pq}(x_{p}(t)), a^{I}_{pq}(x_{p}(t)), a^{J}_{pq}(x_{p}(t))$ and $a^{K}_{pq}(x_{p}(t))$ are decided by the corresponding imaginary unit of state vector $x_{p}(t)$. Thus, the character of both MNNs and QVNNs are combined in this new model, which lead to more complex dynamical behavior in nonlinear systems. Hence, our work serves as the supplement for the previous results and enrich the theory of QVNNs.

Remark 4

The sign function in controller (21) plays an important role to eliminate the parameter mismatch caused by memristive connection weights. However, this may cause chattering phenomenon to control system. Moreover, the complete synchronization is rather rigorous for many real-life applications Ding et al. (2017), Ravishankar (2018), Wei et al. (2018), Bao et al. (2016). Usually, let the error restricted in an prescribed area is enough Nakamura and Tateno (2019). Thus, another type of synchronization is considered in the next.

In this part, we focus on the quasi-synchronization of master-slave system (1) and (2). Choose the controller below

$$\begin{aligned} U(t)=-KE(t), \end{aligned}$$

(26)

where $K=diag\{k_{1},\ldots ,k_{4n}\}$ is the control gains matrix.

Theorem 2

Under Assumption2, if there exists positive constant$\xi$and control gains matrixKsuch that the following condition holds

$$\begin{aligned} \mu _{1}(-\bar{D}-K)+\Vert \tilde{A}\Vert _{1}L_{f}+\Vert \tilde{B}\Vert _{1}L_{f}\le -\xi <0. \end{aligned}$$

(27)

Then the quasi-synchronization between system (1) and (2) can be achieved under controller (26). The error trajectories will converge to the following set

$$\begin{aligned} \varPsi =\left\{ E(t)\in R^{4n}|\Vert E(t)\Vert _{1}\le \frac{R_{1}}{\xi }\right\} \end{aligned}$$

(28)

where $R_{1}=\Vert (\acute{A}-\grave{A}+\acute{B}-\grave{B})M\Vert _{1}$.

Proof

Considering the Lyapunov functional as below

$$\begin{aligned} V(t)=\Vert E(t)\Vert _{1} \end{aligned}$$

(29)

Computing the derivative along of V(t) along the trajectory (11) yields

$$\begin{aligned} \frac{dV(t)}{dt}=&\lim _{h\rightarrow 0^{+}}\frac{\Vert E(t+h)\Vert _{1}-\Vert E(t)\Vert _{1}}{h}\nonumber \\ =&\lim _{h\rightarrow 0^{+}}\frac{\Vert E(t)+h\dot{E}(t)+o(t)\Vert _{1}-\Vert E(t)\Vert _{1}}{h}\nonumber \\ =&\lim _{h\rightarrow 0^{+}}\frac{1}{h}\{\Vert E(t)+h\{-\bar{D}E(t)+\bar{A}_{y}G(E(t))\nonumber \\&+\bar{B}_{y}G(E(t-\tau (t)))\nonumber \\&+(\bar{A}_{y}-\bar{A}_{x})F(X(t))+(\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))\nonumber \\&-KE(t)\}\Vert _{1}-\Vert E(t)\Vert _{1}\}\nonumber \\ \le&\lim _{h\rightarrow 0^{+}}\frac{1}{h}(\Vert (I-h\bar{D}-hK)E(t)\Vert _{1}-\Vert E(t)\Vert _{1})\nonumber \\&+\Vert \bar{A}_{y}\Vert _{1}\Vert G(E(t))\Vert _{1}\nonumber \\&+\Vert \bar{B}_{y}\Vert _{1}\Vert G(E(t-\tau (t)))\Vert _{1}\nonumber \\&+\Vert (\bar{A}_{y}-\bar{A}_{x})F(X(t))\Vert _{1}\nonumber \\&+\Vert (\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))\Vert _{1}\nonumber \\ \le&\lim _{h\rightarrow 0^{+}}\frac{\Vert (I-h(\bar{D}+K))\Vert _{1}-1}{h}\Vert E(t)\Vert _{1}\nonumber \\&+\Vert \bar{A}_{y}\Vert _{1}L_{f}\Vert E(t)\Vert _{1}\nonumber \\&+\Vert \bar{B}_{y}\Vert _{1}L_{f}\Vert E(t-\tau (t))\Vert _{1}+R_{1}\nonumber \\ \le \,&\mu _{1}(-\bar{D}-K)\Vert E(t)\Vert _{1}+\Vert \tilde{A}\Vert _{1}L_{f}\Vert E(t)\Vert _{1}\nonumber \\&+\Vert \tilde{B}\Vert _{1}L_{f}\Vert E(t-\tau (t))\Vert _{1}+R_{1}\nonumber \\ \le \,&\{\mu _{1}(-\bar{D}-K)+\Vert \tilde{A}\Vert _{1}L_{f}\}\Vert E(t)\Vert _{1}\nonumber \\&+\Vert \tilde{B}\Vert _{1}L_{f}\sup _{t-\tau \le s\le t}\Vert E(s)\Vert _{1}+R_{1} \end{aligned}$$

(30)

According to the Lemma 2, we have

$$\begin{aligned} \Vert E(t)\Vert _{1}\le \frac{R_{1}}{\xi }+\sup _{t-\tau \le s\le t}\Vert E(s)\Vert _{1}e^{-\mu ^{*}t} \end{aligned}$$

(31)

where $\mu ^{*}=\inf _{t\ge 0}\{\mu (t): \mu (t)+\mu _{1}(-\bar{D}-K)+\Vert \tilde{A}\Vert _{1}L_{f}+\Vert \tilde{B}\Vert _{1}L_{f}e^{\sigma \mu (t)}=0\}, \sigma =\mu _{1}(-\bar{D}-K)+\Vert \tilde{A}\Vert _{1}L_{f}.$ Therefore, quasi-synchronization between system (1) and (2) can be achieved under controller (26). $\square$

Remark 5

Compared with complete synchronization, quasi-synchronization is more practical and reasonable in many real applications. Through selecting appropriate control gains matrix K, the convergence field $\varPsi$ can be constrained to any domain that we needed. Moreover, the controller for quasi-synchronization does not contain sign function, thus the chattering phenomenon can be effectively avoided.

In the following part, we focus on the synchronization of master-slave QVMNNs via event-triggered control. Considering the following event-triggered controller

$$\begin{aligned} U(t)=-KE(t_{k})-\varGamma sgn(E(t_{k})), t\in [t_{k},t_{k+1}), \end{aligned}$$

(32)

where the event-triggered instants $t_{k}, k=1,\ldots ,n$ are determined iteratively by the rule below

$$\begin{aligned} t_{k+1}=\inf \{t: t>t_{k}, k_{\max }\Vert \hat{E}(t)\Vert _{1}\ge \alpha (\delta \Vert E(t)\Vert _{1}+\zeta )\}, \end{aligned}$$

(33)

where $\hat{E}(t)=E(t)-E(t_{k})$ for $t\in [t_{k},t_{k+1})$, $\delta =-d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}\Vert L_{f}-k_{\min }, \zeta =-2\cdot 1_{4n}^{T}[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M+\sum _{p=1}^{4n}\gamma _{p}>0$, $\alpha$ is a constant satisfying $0<\alpha <1$, $1_{4n}=(1,\ldots ,1)^{T}\in R^{4n}$.

Theorem 3

Under Assumption2, if the control gains$k_{p}, \gamma _{p}, p=1,\ldots ,4n$satisfy the following conditions

$$\begin{aligned} \gamma _{p}=& \left\{ \begin{array}{ll} -\theta _{p}, &sgnE_{p}(t)sgn(E_{p}(t_{k}))\le 0, \\ \theta _{p}, & sgnE_{p}(t)sgn(E_{p}(t_{k}))> 0, \end{array}\right. \end{aligned}$$

(34)

$$\begin{aligned} -\delta= -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}-k_{\min }<0, \end{aligned}$$

(35)

where$k_{\min }=\min _{p=1,\ldots ,4n}\{k_{p}\}, d_{\min }=\min _{p=1,\ldots ,4n}\{d_{p}\}$. $\theta =(\theta _{1},\ldots ,\theta _{4n})^{T}\in R^{4n}$is an vector satisfying$\theta \ge 2[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M$. Then the synchronization between system (1) and (2) can be achieved under controller (32) and event-triggered strategy (33).

Proof

Considering the Lyapunov functional as below

$$\begin{aligned} V(t)=\Vert E(t)\Vert _{1}+\frac{1}{1-\rho }\int ^{t}_{t-\tau (t)}\Vert \tilde{B}\Vert _{1}\Vert G(E(s))\Vert _{1}ds. \end{aligned}$$

(36)

For $t\in [t_{k},t_{k+1})$, computing the derivative of V(t) along the trajectory (11) yields

$$\begin{aligned} \frac{dV(t)}{dt}\le \,&sgnE^{T}(t)\{-\bar{D}E(t)+\bar{A}_{y}G(E(t))\nonumber \\&+\bar{B}_{y}G(E(t-\tau (t)))\nonumber \\&+[(\bar{A}_{y}-\bar{A}_{x})F(X(t))\nonumber \\&+(\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))]-KE(t_{k})\nonumber \\&-\varGamma sgn(E(t_{k}))\}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}\Vert G(E(t))\Vert _{1}\nonumber \\&-\Vert \tilde{B}\Vert _{1}\Vert G(E(t-\tau (t)))\Vert _{1}\nonumber \\ \le \,&\left( -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}\right) \Vert E(t)\Vert _{1}\nonumber \\&+2\cdot 1^{T}[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M\nonumber \\&-sgnE^{T}(t)\varGamma sgn(E(t_{k}))\nonumber \\&-sgnE^{T}(t)K[E(t_{k})-E(t)+E(t)]\nonumber \\ \le \,&\left( -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}L_{f}-k_{min}\right) \Vert E(t)\Vert _{1}\nonumber \\&-\zeta -sgnE^{T}(t)K[E(t_{k})-E(t)]\nonumber \\ \le&\left( -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{\Vert \tilde{B}\Vert _{1}}{1-\rho }L_{f}-k_{min}\right) \Vert E(t)\Vert _{1}\nonumber \\&-\zeta +k_{\max }\Vert \hat{E}(t)\Vert _{1}\nonumber \\ \le&-\delta \Vert E(t)\Vert _{1}-\zeta +\alpha (\delta \Vert E(t)\Vert _{1}+\zeta )\nonumber \\ =\,&(\alpha -1)(\delta \Vert E(t)\Vert _{1}+\zeta )<0 \end{aligned}$$

(37)

Based on above analysis, the synchronization between system (1) and (2) can be achieved under the controller (32) and event-triggered strategy (33). $\square$

Remark 6

It can be seen that, compared with the control method proposed in [8], Bao and Cao (2014), Ding et al. (2017), Ravishankar (2018), Wei et al. (2018), Bao et al. (2016), Nakamura and Tateno (2019), event-triggered strategy not only ensure the system performance but also reduce the sampled times and computation burden. Thus the network resource is saved and the communication efficiency can be effectively improved. In fact, the traditional feedback controller can be regarded as the special case of the event-triggered controller. Moreover, to ensure the proposed event-triggered control can be applied in real practise, it is important to avoid the condition that event be triggered infinite times during finite time interval, i.e., Zeno behavior.

Later, we prove that the Zeno behavior can be excluded via the event-triggered strategy (33).

Theorem 4

With the condition of Theorem3hold, then there is no Zeno-behavior for the considered system under the event-triggered strategy (33).

Proof

Considering the Lyapunov functional as below

$$\begin{aligned} V(t)=\Vert \hat{E}(t)\Vert _{1}. \end{aligned}$$

(38)

Computing the derivative of V(t) along the trajectory (11) yields

$$\begin{aligned} D^{+}\Vert \hat{E}(t)\Vert _{1}\le \,&\Vert \dot{\hat{E}}(t)\Vert _{1}=\Vert \dot{E}(t)\Vert _{1}\nonumber \\ =\,&\Vert -\bar{D}E(t)+\bar{A}_{y}F(Y(t))-\bar{A}_{x}F(X(t))\nonumber \\&+\bar{B}_{y}F(Y(t-\tau (t)))\nonumber \\&-\bar{B}_{x}F(X(t-\tau (t)))-KE(t_{k})\nonumber \\&-\varGamma sgn(E(t_{k}))\Vert _{1}\nonumber \\ \le \,&\Vert \bar{D}\Vert _{1}\Vert E(t)\Vert _{1}+2(\Vert \tilde{A}\Vert _{1}+\Vert \tilde{B}\Vert _{1})\Vert M\Vert _{1}\nonumber \\&+\Vert K\Vert _{1}\Vert E(t_{k})\Vert _{1}+\sum _{p=1}^{4n}\gamma _{p}\nonumber \\ =\,&\Vert \bar{D}\Vert _{1}\Vert \hat{E}(t)\Vert _{1}+(\Vert \bar{D}\Vert _{1}+\Vert K\Vert _{1})\Vert E(t_{k})\Vert _{1}\nonumber \\&+2(\Vert \tilde{A}\Vert _{1}+\Vert \tilde{B}\Vert _{1})\Vert M\Vert _{1}+\sum _{p=1}^{4n}\gamma _{p}\nonumber \\ =\,&\Vert \bar{D}\Vert _{1}\Vert \hat{E}(t)\Vert _{1}+W, t\in [t_{k},t_{k+1}), \end{aligned}$$

(39)

where $W=2(\Vert \tilde{A}\Vert _{1}+\Vert \tilde{B}\Vert _{1})\Vert M\Vert _{1}+(\Vert \bar{D}\Vert _{1}+\Vert K\Vert _{1})\Vert E(t_{k})\Vert _{1}+\sum _{p=1}^{4n}\gamma _{p}.$ Note that $\Vert \hat{E}(t_{k})\Vert _{1}=0$, solving the inequality (39), we have

$$\begin{aligned} \Vert \hat{E}(t)\Vert _{1}\le \frac{W}{\Vert \bar{D}\Vert _{1}}(e^{\Vert \bar{D}\Vert _{1}(t-t_{k})}-1), t\in [t_{k},t_{k+1}). \end{aligned}$$

(40)

Utilizing the triggered condition (33), it follows that

$$\begin{aligned}&\frac{\alpha (\delta \Vert E(t_{k+1})\Vert _{1}+\zeta )}{k_{\max }}=\Vert \hat{E}(t_{k+1})\Vert _{1}\nonumber \\&\quad \le \frac{W}{\Vert \bar{D}\Vert _{1}}(e^{\Vert \bar{D}\Vert _{1}(t_{k+1}-t_{k})}-1) \end{aligned}$$

(41)

Then, we have

$$\begin{aligned} t_{k+1}-t_{k}\ge \frac{1}{\Vert \bar{D}\Vert _{1}}\ln \left[ \frac{\alpha (\delta \Vert E(t_{k+1})\Vert _{1}+\zeta )\Vert \bar{D}\Vert _{1}}{k_{\max }W}+1\right] \end{aligned}$$

(42)

Due to $\dot{V}(t)\le 0$, it can be obtained

$$\begin{aligned} W&\le (\Vert \bar{D}\Vert _{1}+\Vert K\Vert _{1})V(0)+2(\Vert \tilde{A}\Vert _{1}+\Vert \tilde{B}\Vert _{1})\Vert M\Vert _{1}\nonumber \\&\quad +\sum _{p=1}^{4n}\gamma _{p}=\bar{W}. \end{aligned}$$

(43)

Thus, W is bounded and we can achieve that

$$\begin{aligned} t_{k+1}-t_{k}\ge \frac{1}{\Vert \bar{D}\Vert _{1}}\ln \left[ \frac{\alpha \zeta \Vert \bar{D}\Vert _{1}}{k_{\max }\bar{W}}+1\right] >0 \end{aligned}$$

(44)

Based on above analysis, Zeno behavior can be avoided under the event-triggered strategy (33). $\square$

Remark 7

It can be infer from above proof that if the triggered condition (33) be changed to $t_{k+1}=\inf \{t: t>t_{k}, k_{\max }\Vert \hat{E}(t)\Vert _{1}\ge \alpha \delta \Vert E(t)\Vert _{1}\}$, the synchronization objective can also be achieved. However, Zeno behavior may occur in this case. Hence, the constant $\zeta$ in (33) plays an significant role to eliminate Zeno behavior.

Numerical examples

To show the effectiveness of our theoretical results, some simulation example is given in this section. The principal of Theorem 2 is similar to Theorem 1, thus, we mainly focus on the simulation of Theorems 1 and 3.

Example 1

Consider the QVMNNs with 2 neurons as below

$$\begin{aligned} \frac{dx_{p}(t)}{dt}=&-d_{p}x_{p}(t)+\sum \limits _{q=1}^{2}a_{pq}(x_{p}(t))f_{q}(x_{q}(t))\nonumber \\&+\sum \limits _{q=1}^{2}b_{pq}(x_{p}(t))f_{q}(x_{q}(t-\tau (t)))\,,\,p=1, 2, \end{aligned}$$

(45)

where $d_{1}=1.1, d_{2}=1.1$ and the memristive connection weights are given as below. For convenience, $x^{l}_{p}(t)$ is simplified to $x^{l}_{p}, l=R, I, J, K$.

$$\begin{aligned} \begin{aligned} a^{R}_{11}(x^{R}_{1})=&\left\{ \begin{array}{c} -0.4, |x^{R}_{1}|\le 1, \\ 0.1, |x^{R}_{1}|> 1, \end{array}\right. a^{R}_{12}(x^{R}_{1})=\left\{ \begin{array}{c} 0.1, |x^{R}_{1}|\le 1, \\ -0.1, |x^{R}_{1}|> 1, \end{array}\right. \\ a^{R}_{21}(x^{R}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{R}_{2}|\le 1, \\ 0.1, |x^{R}_{2}|> 1, \end{array}\right. a^{R}_{22}(x^{R}_{2})=\left\{ \begin{array}{c} 0.1, |x^{R}_{2}|\le 1, \\ -0.1, |x^{R}_{2}|> 1, \end{array}\right. \\ \end{aligned}\nonumber \\ \begin{aligned} a^{I}_{11}(x^{I}_{1})=&\left\{ \begin{array}{c} -0.1, |x^{I}_{1}|\le 1, \\ 0.1, |x^{I}_{1}|> 1, \end{array}\right. a^{I}_{12}(x^{I}_{1})=\left\{ \begin{array}{c} 0.1, |x^{I}_{1}|\le 1, \\ -0.1, |x^{I}_{1}|> 1, \end{array}\right. \\ a^{I}_{21}(x^{I}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{I}_{2}|\le 1, \\ 0.2, |x^{I}_{2}|> 1, \end{array}\right. a^{I}_{22}(x^{I}_{2})=\left\{ \begin{array}{c} 0.1, |x^{I}_{2}|\le 1, \\ -0.1, |x^{I}_{2}|> 1, \end{array}\right. \\ \end{aligned}\nonumber \\ \begin{aligned} a^{J}_{11}(x^{J}_{1})=&\left\{ \begin{array}{c} 0.2, |x^{J}_{1}|\le 1, \\ 0.1, |x^{J}_{1}|> 1, \end{array}\right. a^{J}_{12}(x^{J}_{1})=\left\{ \begin{array}{c} 0.1, |x^{J}_{1}|\le 1, \\ -0.1, |x^{J}_{1}|> 1, \end{array}\right. \\ a^{J}_{21}(x^{J}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{J}_{2}|\le 1, \\ 0.2, |x^{J}_{2}|> 1, \end{array}\right. a^{J}_{22}(x^{J}_{2})=\left\{ \begin{array}{c} 0.1, |x^{J}_{2}|\le 1, \\ -0.1, |x^{J}_{2}|> 1, \end{array}\right. \\ a^{K}_{11}(x^{K}_{1})=&\left\{ \begin{array}{c} 0.2, |x^{K}_{1}|\le 1, \\ 0.1, |x^{K}_{1}|> 1, \end{array}\right. a^{K}_{12}(x^{K}_{1})=\left\{ \begin{array}{c} 0.1, |x^{K}_{1}|\le 1, \\ -0.1, |x^{K}_{1}|> 1, \end{array}\right. \\ a^{K}_{21}(x^{K}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{K}_{2}|\le 1, \\ 0.1, |x^{K}_{2}|> 1, \end{array}\right. a^{K}_{22}(x^{K}_{2})=\left\{ \begin{array}{c} 0.1, |x^{K}_{2}|\le 1, \\ 0.2, |x^{K}_{2}|> 1, \end{array}\right. \\ \end{aligned}\nonumber \\ \begin{aligned} b^{R}_{11}(x^{R}_{1})=&\left\{ \begin{array}{c} 0.2, |x^{R}_{1}|\le 1, \\ 0.1, |x^{R}_{1}|> 1, \end{array}\right. b^{R}_{12}(x^{R}_{1})=\left\{ \begin{array}{c} 0.1, |x^{R}_{1}|\le 1, \\ -0.1, |x^{R}_{1}|> 1, \end{array}\right. \\ b^{R}_{21}(x^{R}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{R}_{2}|\le 1, \\ 0.2, |x^{R}_{2}|> 1, \end{array}\right. b^{R}_{22}(x^{R}_{2})=\left\{ \begin{array}{c} 0.1, |x^{R}_{2}|\le 1, \\ -0.1, |x^{R}_{2}|> 1, \end{array}\right. \\ b^{I}_{11}(x^{I}_{1})=&\left\{ \begin{array}{c} 0.2, |x^{I}_{1}|\le 1, \\ 0.1, |x^{I}_{1}|> 1, \end{array}\right. b^{I}_{12}(x^{I}_{1})=\left\{ \begin{array}{c} 0.1, |x^{I}_{1}|\le 1, \\ -0.1, |x^{I}_{1}|> 1, \end{array}\right. \\ b^{I}_{21}(x^{I}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{I}_{2}|\le 1, \\ 0.2, |x^{I}_{2}|> 1, \end{array}\right. b^{I}_{22}(x^{I}_{2})=\left\{ \begin{array}{c} 0.1, |x^{I}_{2}|\le 1, \\ -0.1, |x^{I}_{2}|> 1, \end{array}\right. \\ \end{aligned}\nonumber \\ \begin{aligned} b^{J}_{11}(x^{J}_{1})=&\left\{ \begin{array}{c} -0.1, |x^{J}_{1}|\le 1, \\ 0.1, |x^{J}_{1}|> 1, \end{array}\right. b^{J}_{12}(x^{J}_{1})=\left\{ \begin{array}{c} 0.1, |x^{J}_{1}|\le 1, \\ 0.2, |x^{J}_{1}|> 1, \end{array}\right. \\ b^{J}_{21}(x^{J}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{J}_{2}|\le 1, \\ 0.1, |x^{J}_{2}|> 1, \end{array}\right. b^{J}_{22}(x^{J}_{2})=\left\{ \begin{array}{c} 0.1, |x^{J}_{2}|\le 1, \\ 0.2, |x^{J}_{2}|> 1, \end{array}\right. \\ b^{K}_{11}(x^{K}_{1})=&\left\{ \begin{array}{c} -0.1, |x^{K}_{1}|\le 1, \\ 0.4, |x^{K}_{1}|> 1, \end{array}\right. b^{K}_{12}(x^{K}_{1})=\left\{ \begin{array}{c} 0.1, |x^{K}_{1}|\le 1, \\ 0.2, |x^{K}_{1}|> 1, \end{array}\right. \\ b^{K}_{21}(x^{K}_{2})=&\left\{ \begin{array}{c} -0.1, |x^{K}_{2}|\le 1, \\ 0.1, |x^{K}_{2}|> 1, \end{array}\right. b^{K}_{22}(x^{K}_{2})=\left\{ \begin{array}{c} 0.1, |x^{K}_{2}|\le 1, \\ 0.2, |x^{K}_{2}|> 1, \end{array}\right. \\ \end{aligned} \end{aligned}$$

(46)

where the transmission delay is $\tau (t)=0.5\sin (t)+0.5$, thus $\tau =1, \dot{\tau }(t)\le \rho =0.5\le 1$. The activation function is considered as

$$\begin{aligned} f_{p}(x_{p}(t))&=\frac{1}{1+e^{x^{R}_{p}(t)}}+\frac{1}{1+e^{x^{I}_{p}(t)}}i+\frac{1}{1+e^{x^{J}_{p}(t)}}j\nonumber \\&\quad +\frac{1}{1+e^{x^{K}_{p}(t)}}k, \end{aligned}$$

(47)

which implies that $l^{R}_{1}=l^{R}_{2}=l^{I}_{1}=l^{I}_{2}=l^{J}_{1}=l^{J}_{2}=l^{K}_{1}=l^{K}_{2}=1, M=(1,1,1,1,1,1,1,1)^{T}.$ The slave system is

$$\begin{aligned} \frac{dy_{p}(t)}{dt}=&-d_{p}y_{p}(t)+\sum \limits _{q=1}^{2}a_{pq}(y_{p}(t))f_{q}(y_{q}(t))\nonumber \\&+\sum \limits _{q=1}^{2}b_{pq}(y_{p}(t))f_{q}(y_{q}(t-\tau (t)))\nonumber \\&+u_{p}(t),\quad p=1, 2, \end{aligned}$$

(48)

The corresponding error system can be obtained as

$$\begin{aligned} \frac{dE(t)}{dt} =&-\bar{D}E(t)+\bar{A}_{y}G(E(t))+\bar{B}_{y}G(E(t-\tau (t)))\nonumber \\&+(\bar{A}_{y}-\bar{A}_{x})F(X(t))\nonumber \\&+(\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))+U(t), \end{aligned}$$

(49)

Choose $U(t)=-KE(t)-\varGamma sgn(E(t))$, from the memristive connection weights, it can be obtained that

$$\begin{aligned} \tilde{A}=&\left( \begin{array}{cccccccc} 0.4 &\quad 0.1 &\quad 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.2\\ 0.1 &\quad 0.1 &\quad 0.4 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.2 &\quad 0.1\\ 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.4 &\quad 0.1 &\quad 0.1 &\quad 0.1\\ 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.1 &\quad 0.4 &\quad 0.1\\ 0.1 &\quad 0.2 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.1\\ \end{array} \right) ,\\ \tilde{B}=&\left( \begin{array}{cccccccc} 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 & \quad 0.1 & \quad 0.2 & \quad 0.4 & \quad 0.2\\ 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 & \quad 0.2 & \quad 0.1 & \quad 0.2\\ 0.2 & \quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.2 &\quad 0.1\\ 0.1 &\quad 0.2 &\quad 0.4 &\quad 0.2 &\quad 0.2 & \quad 0.1 &\quad 0.1 &\quad 0.1\\ 0.1 &\quad 0.2 &\quad 0.1 & \quad 0.2 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ 0.4 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.2 &\quad 0.1 & \quad 0.2 & \quad 0.1\\ 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 & \quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ \end{array} \right) ,\\ \acute{A}-\grave{A}=&\left( \begin{array}{cccccccc} 0.5 &\quad 0.2 &\quad 0.2 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2\\ 0.2 &\quad 0.2 &\quad 0.3 &\quad 0.2 &\quad 0.3 & \quad 0.2 & \quad 0.2 & \quad 0.1\\ 0.2 &\quad 0.2 &\quad 0.5 &\quad 0.2 &\quad 0.1 &\quad 0.2 & \quad 0.1 &\quad 0.2\\ 0.3 &\quad 0.2 &\quad 0.2 &\quad 0.2 & \quad 0.2 &\quad 0.1 & \quad 0.3 & \quad 0.2\\ 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.5 &\quad 0.2 &\quad 0.2 &\quad 0.2\\ 0.3 &\quad 0.2 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.2 &\quad 0.3 &\quad 0.2\\ 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.2 & \quad 0.2 &\quad 0.5 &\quad 0.2\\ 0.2 &\quad 0.1 &\quad 0.3 &\quad 0.2 & \quad 0.3 &\quad 0.2 &\quad 0.2 &\quad 0.2\\ \end{array} \right) ,\\ \acute{B}-\grave{B}=&\left( \begin{array}{cccccccc} 0.1 &\quad 0.2 &\quad 0.1 & \quad 0.2 & \quad 0.2 &\quad 0.1 & \quad 0.5 & \quad 0.1\\ 0.3 &\quad 0.2 &\quad 0.3 &\quad 0.2 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.1\\ 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.2 &\quad 0.5 & \quad 0.1 & \quad 0.2 & \quad 0.1\\ 0.3 & \quad 0.2 &\quad 0.3 &\quad 0.2 &\quad 0.2 & \quad 0.1 & \quad 0.2 & \quad 0.1\\ 0.2 &\quad 0.1 &\quad 0.5 &\quad 0.1 & \quad 0.1 & \quad 0.2 & \quad 0.1 &\quad 0.2\\ 0.2 &\quad 0.1 & \quad 0.2 &\quad 0.1 &\quad 0.3 & \quad 0.2 &\quad 0.3 &\quad 0.2\\ 0.5 &\quad 0.1 &\quad 0.2 &\quad 0.1 &\quad 0.1 &\quad 0.2 &\quad 0.1 & \quad 0.2\\ 0.2 &\quad 0.1 & \quad 0.2 &\quad 0.1 & \quad 0.3 &\quad 0.2 &\quad 0.3 & \quad 0.2\\ \end{array} \right) , \end{aligned}$$

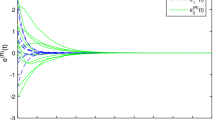
Thus, $\Vert \tilde{A}\Vert _{1}=1.5, \Vert \tilde{B}\Vert _{1}=1.6$. It can be obtained from the condition of Theorem 1 that $k_{\min }\ge -d_{\min }+\Vert \tilde{A}\Vert _{1}L_{f}+\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}\Vert L_{f}=3.6$, $\varGamma \ge 2[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M=(6.4,6.6,6.4,6.6,6.4,6.6,6.4,6.6)^{T}$. Choose $\alpha =0.5, k_{p}=4, \gamma _{p}=7$. Take 20 initial random conditions, Figs. 1 and 2 describes the synchronization errors $e^{R}_{1}, e^{I}_{1}, e^{J}_{1}, e^{K}_{1}, e^{R}_{2}, e^{I}_{2}, e^{J}_{2}, e^{K}_{2}$ between system (45) and (48) with controller (21), respectively. According to the simulation results, the drive system (45) and response system (48) can be synchronized under controller (21), which verify the correctness of Theorem 1. Choosing 10 initial conditions in the interval $[-\,0.3, 0.3]$, the synchronization error between system (45) and (48) is shown in Figs. 1, 2, 3 and 4, which verify the effectiveness of Theorem 1.

Next, we consider the event-triggered case.

Fig. 1

Trajectories of system (49)

Fig. 2

Trajectories of system (49)

Fig. 3

Trajectories of system (49)

Fig. 4

Trajectories of system (49)

Example 2

Consider the same master-slave QVMNNs given in Example 1.

$$\begin{aligned} \frac{dE(t)}{dt} =&-\bar{D}E(t)+\bar{A}_{y}G(E(t))+\bar{B}_{y}G(E(t-\tau (t)))\nonumber \\&+(\bar{A}_{y}-\bar{A}_{x})F(X(t))\nonumber \\&+(\bar{B}_{y}-\bar{B}_{x})F(X(t-\tau (t)))+U(t) \end{aligned}$$

(50)

Choose the event-triggered controller as

$$\begin{aligned} U(t)=-KE(t_{k})-\varGamma sgn(E(t_{k})), t\in [t_{k}, t_{k+1}) \end{aligned}$$

(51)

According to Theorem 3, the event-triggered condition can be calculated as

$$\begin{aligned} t_{k+1}=inf\{t: t>t_{k}, \Vert \hat{E}(t)\Vert _{1}\ge 0.5(0.1\Vert E(t)\Vert _{1}+1)\} \end{aligned}$$

(52)

It can be obtained from the condition of Theorem 3 that $k_{\min }\ge 3.8$, $\theta \ge 2[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M=(6.4,6.6,6.4,6.6,6.4,6.6,6.4,6.6)^{T}$. Choose $\alpha =0.5, k_{p}=4, \theta _{p}=7, \delta =d_{\min }-\Vert \tilde{A}\Vert _{1}L_{f}-\frac{1}{1-\rho }\Vert \tilde{B}\Vert _{1}\Vert L_{f}+k_{\min }=0.4, \zeta =-2\cdot 1^{T}[(\acute{A}-\grave{A})+(\acute{B}-\grave{B})]M+\sum _{p=1}^{4n}\gamma _{p}=4>0$. Thus, the initial condition can be chosen as $x^{l}_{p}(s)\le 0.18, s\in [-\tau , 0], p=1, 2, l=R, I, J, K$. Choosing 10 initial conditions in the interval $[-0.18, 0.18]$, the simulation results are shown in Figs. 5, 6, 7 and 8, which verify the effectiveness of Theorem 3.

Fig. 5

Trajectories of system (50)

Fig. 6

Trajectories of system (50)

Fig. 7

Trajectories of system (50)

Fig. 8

Trajectories of system (50)

Conclusion

In this paper, we introduced the memristive connection weights into QVNNs to construct the QVMNNs, which is a new class of network model with the character of both MNNs and QVNNs. The master-slave synchronization problem of QVMNNs are studied by designing traditional feedback controller and event-triggered controller correspondingly. Applying the Lyapunov method, several criteria guaranteeing the synchronization of drive-response QVMNNs are obtained. Besides, the Zeno behavior can be avoided in event-triggered control. Finally, simulation examples are given to verify the correctness of our results.

Our future research will concentrate on these aspects: 1) The finite-time synchronization of QVMNNs with pinning control. 2) The dynamical behavior of coupled QVMNNs with imperfect communication, such as packet dropout and quantization.