Introduction

Cohen–Grossberg neural network (CGNN) was first introduced by Cohen and Grossberg (1983). In recent years, CGNN, which includes the famous Hopfield neural networks, cellular neural networks and Lotka–Volterra competition models as its special cases, has received extensive attention because of great range of applications in many areas such as optimization, pattern recognition, associative memory, robotics and computer vision. In such application, it is of prime importance to ensure that the designed neural networks is stable (Zhang and Wang 2008; Yang and Cao 2014; Qi et al. 2014; Yang et al. 2014; Li and Xu 2012; Zhou et al. 2007; Li and Song 2008, 2013; Li and Shen 2010; Li et al. 2010).

In implementation of neural networks, time delays are unavoidable due to the finite switching speed of neurons and amplifiers. It has been found that the existence of time delays may lead to instability and oscillation in a neural network (Wang et al. 2006; Li 2010; Pan and Zhong 2010; Zhang et al. 2011; Zhang and Luo 2012; Qiu 2007; Liu et al. 2011; Yang et al. 2010; Li and Li 2009). For example, Wang et al. (2006) considered the asymptotic stability of stochastic CGNNs with mixed time delays by using Lyapunov–Krasovskii functional and LMI technology.

In practice, a real system is usually affected by external perturbations which in many cases are of great uncertainty. Hence, it is necessary to consider the stochastic effects to the stability property of the neural networks. On the other hand, as we have known, artificial neural networks often are subject to impulsive perturbations which can affect dynamical behaviors of the systems. Moreover, those perturbations often may make stable systems unstable or unstable systems stable. Therefore, impulsive effects should also be taken into account (Li et al. 2011; Fu and Li 2011; Li and Xu 2012; Wang and Xu 2009; Zhang et al. 2012; Hespanha et al. 2008; Wan and Zhou 2008; Li and Li 2009). Fu and Li (2011) investigated the asymptotic stability of impulsive stochastic CGNNs with mixed time delays by using Lyapunov–Krasovskii functional and LMI technology.

However, diffusion effects cannot be avoided in the network when electrons are moving in asymmetric electromagnetic fields. Hence, it is essential to consider the state variables are varying with the time and space variables. Some criteria on global exponential stability have been obtained in recent years (Wan and Zhou 2008; Li and Li 2009; Wang and Zhang 2010; Li et al. 2012; Pan et al. 2010; Zhu et al. 2011; Zhou et al. 2012). Wan and Zhou (2008) investigated the exponential stability of stochastic reaction–diffusion CGNNs with delays. Li and Li (2009) and Wang and Zhang (2010) investigated the asymptotic stability of impulsive CGNNs with distributed delays and reaction–diffusion by using M-matrix theory and LMI technology. Li et al. (2012) investigated the mean square exponential stability of impulsive stochastic reaction–diffusion CGNNs with delays. But in their deduction and results the diffusion term does not have any effect.

It is known in the theory of partial differential equations Poincare integral inequality is often used in the deduction of diffusion. Pan et al. (2010), Zhu et al. (2011) and Zhou et al. (2012) studied reaction–diffusion neural networks with Neumann boundary conditions by using Poincare integral inequality.

Motivated by the above discussions, our objective in this paper is to investigated the asymptotic stablity in the mean square of impulsive stochastic CGNNs with mixed delays and Reaction–diffusion terms. By using Lyapunov–Krasovskii functional method, LMI technique (Boyd et al. 1994) and Poincaré inequality, some results are obtained in terms of LMI, which can be easily calculated by MATLAB LMI toolbox.

The rest of the paper is organized as follows. In second section, we introduce the model and some preliminaries. In third section, we give two main results and their proof. And then we give a numerical example to show the effectiveness of the obtained results in forth section. Finally, we conclude our results.

Problem statement and preliminaries

In this paper, we will use the notation \(\fancyscript{A}>0\) or \(\fancyscript{A}<0\) to denote that the matrix \(\fancyscript{A}\) is a symmetric and positive definite or negative definite matrix. The notation \(\fancyscript{A}^T\) and \(\fancyscript{A}^{-1}\) mean the transpose of \(\fancyscript{A}\) and the inverse of a square matrix. If \(\fancyscript{A}\) and \(\fancyscript{B}\) are symmetric matrices, \(\fancyscript{A}>\fancyscript{B}\) means that \(\fancyscript{A}-\fancyscript{B}\) is positive definite matrix. \(I\) denotes the identity matrix. Moreover, the notation \(*\) always denotes the symmetric block in one symmetric matrix.

Consider the following impulsive stochastic CGNNs with mixed delays and reaction–diffusion terms

$$\begin{aligned} dy_i(t,x)&= \sum \limits _{k=1}^m\frac{\partial }{\partial x_k}\left(w_{ik}\frac{\partial y_i(t,x)}{\partial x_k}\right)dt-a_i(y_i(t,x))\left[ b_i(y_i(t,x))-\sum \limits _{j=1}^nc_{ij}f_j (y_j(t,x))\right. \nonumber \\&\quad -\sum \limits _{j=1}^nd_{ij}g_j(y_j(t-\tau (t),x)) -\sum \limits _{j=1}^n\bar{d}_{ij}\int _{t-\mu (t)}^t\bar{g}_j(y_j(s,x))ds\nonumber \\&\quad \left. -\sum \limits _{j=1}^n\tilde{d}_{ij}\int ^t_{-\infty }k_{j}(t-s)\tilde{g} _j(y_j(s,x))ds\right] dt\\&\quad +\sum \limits _{j=1}^n\sigma _{ij}(t,y(t,x),y(t-\tau (t),x))dw_j(t),\quad t\ne t_k,\nonumber \\ y_i(t_k,x)&= y_i(t_k^-,x)+J_{ik}(y_i(t_k^-,x)),\quad t= t_k, \quad x\in X,\quad k\in Z,\nonumber \end{aligned}$$
(1)

where \(i\in N=\{1,2,\ldots, n\}\), corresponds to the number of units in a neural network; \(x=(x_1,\ldots, x_m)^T\in X\), \(X\) is a compact set with smooth boundary \(\partial X\) and \({\textit{mesX}}>0\) in space \(R^m\), where mesX is the measure of the set \(X\); \(y_i(t,x)\) represents the state of the ith neuron at time \(t\) and in space \(x\); \(a_i(y_i(t,x))\) presents an amplification function; \(f_j,g_j,\bar{g}_j,\tilde{g}_j\) denote the activation functions of the \(j\)th neuron at time \(t\) in space \(x\); \(c_{ij},d_{ij},\bar{d}_{ij},\tilde{d}_{ij}\) denote the connection strengths of the \(j\)th unit on the \(i\)th unit, respectively; \(\tau (t)\) corresponds to the transmission delay and satisfies \(0\le \tau (t)\le \tau \), \(\dot{\tau }(t)\le \rho <1,\) and \(0\le \mu (t)\le \mu \), \(\tau, \mu \) are some real constants. \(\omega (t)=(\omega _1(t),\ldots, \omega _n(t))\) is \(n-\)dimensional Brownian motion defined on a complete probability space \((\Omega,\fancyscript{F},P)\) with a natural filtration \(\{\fancyscript{F}\}_{t\ge 0}\) generated by \(\{\omega (s):0\le s\le t\}\), where we associate \(\Omega \) with the canonical space generated by \(\omega (t)\), and denote by \(\fancyscript{F}\) the associated \(\sigma \)-algebra generated by \(\omega (t)\) with the probability measure \(P\). \(w_{ik}\ge 0\) is diffusion coefficient that corresponds to the transmission diffusion coefficient along the \(i\)th neuron.

The Neumann boundary condition and initial conditions of system (1) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial y_i(t,x)}{\partial m}:=0,\quad (t,x)\in [0,+\infty )\times \partial X,\\ y_i(t_0+s,x)=\varphi _i(s,x),\quad (s,x)\in [-\infty,0)\times \partial X. \end{array}\right. } \end{aligned}$$
(2)

Throughout this paper, we make the following assumptions:

  • (H1) Each function \(a_i(u)\) is bounded, positive and continuous, i.e., there exist constants \(\overline{a}_i, \underline{a}_i\), such that \(0<\underline{a}_i\le a_i(u)\le \overline{a}_i\), for \(u\in R, i\in N\).

  • (H2) \(\dfrac{b_i(s_1)-b_i(s_2)}{s_1-s_2}\ge b_i>0,\) for all \(i\in N\) and \(s_1,s_2\in R (s_1\ne s_2)\).

  • (H3) \(f_j,g_j,\bar{g}_j,\tilde{g}_j\) are Lipschitz continuous with Lipschitz constant \(F_j,L_j,\bar{L}_j,\tilde{L}_j\), respectively, for \(j\in N\).

  • (H4) The delay kernel \(k_{j}(\cdot ):[0,+\infty )\rightarrow [0,+\infty ),j\in N\) are real-valued nonnegative continuous functions that satisfy \(\int _0^{+\infty }k_{j}(s)ds=1,\)

  • (H5) The diffusion coefficient \(\sigma (\cdot )=(\sigma _{ij})\) is local Lipschitz continuous and satisfies the linear growth condition. Moreover, there exist \(n\times n\) dimension matrix \(\Gamma _j>0,j=0,1,\ldots,n\) such that

    $$\begin{aligned} trace[\sigma ^T\sigma ]\le y^T(t,x)\Gamma _1 y(t,x)+ y^T(t-\tau (t),x)\Gamma _2 y(t-\tau (t),x). \end{aligned}$$

  • (H6) The impulsive times \(t_k\) satisfy \(0<t_0<t_1<\cdots <t_k<t_{k+1}<\cdots, \lim _{k\rightarrow \infty }t_k=\infty \).

  • (H7) \(b_i(0)=f_j(0)=g_j(0)=\bar{g}_j(0)=\tilde{g}_j(0)=0\), \(\sigma (0,0,0)=0\).

Let \(L^2(X)\) be the space of scalar value Lebesgue measurable function on X and be a Banach space for the \(L_2\)-norm

$$\begin{aligned} \Vert v\Vert _2=\left( \int _X|v|^2dx\right) ^{\frac{1}{2}},\quad v\in L^2(X). \end{aligned}$$

Then for any \(u=(u_1,u_2,\ldots,u_n)^T\), the norm \(\Vert u\Vert \) is defined as

$$\begin{aligned} \Vert u\Vert =\left( \sum \limits _{i=1}^n\Vert u_i\Vert _2^2\right) ^{\frac{1}{2}} \end{aligned}$$

Definition 2.1

The trivial solution of model (1) is said to be globally stochastically asymptotic stable in the mean square if the following condition holds for any initial condition \(\varphi \in C_{\fancyscript{F}}^2\):

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }E\Vert x\Vert ^2=0 \end{aligned}$$

Lemma 2.2

(Poincaré Integral Inequality, Temam 1998) Let \(\Omega \subset R^m(m>2)\) be abounded open set containing the origin. \(v(x)\in H_0^1(\Omega )=\{\omega \vert \omega \vert _{\partial \Omega }=0, \omega \in L^{2}(\Omega ), D_{i}\omega =\frac{\partial \omega }{\partial x_{i}}\in L^{2}(\Omega ), 1\le i\le m\}\) and \(\frac{\partial v(x)}{\partial m}\mid _{\partial \Omega }=0\). Then

$$\begin{aligned} \int _\Omega {| v(x)|}^2dx\le \frac{1}{\lambda _1}\int _\Omega {|\nabla v(x)|}^2dx \end{aligned}$$

where \(\lambda _1\) is the smallest positive eigenvalue of the Neumann boundary problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta \psi (x)=\lambda \psi (x),&\quad x\in \Omega \\ \frac{\partial v(x)}{\partial m}\mid _{\partial \Omega }=0,&\quad x\in \partial \Omega \end{array}\right. } \end{aligned}$$
(3)

Lemma 2.3

(Schur complement, Boyd et al. 1994) For a given matrix

$$\begin{aligned} S=\left( \begin{array}{cc} S_{11} & \quad S_{12}\\ S_{21}&\quad S_{22}\\ \end{array}\right) >0 \end{aligned}$$

where \(S^T_{11}=S_{11},S^T_{22}=S_{22}\), is equivalent to any one of the following conditions:

  1. 1.

    \(S_{22}>0,S_{11}-S_{12}S^{-1}_{22}S^T_{12}>0\);

  2. 2.

    \(S_{11}>0,S_{22}-S_{12}^TS^{-1}_{11}S_{12}>0\);

Lemma 2.4

For any constant matrix \(\Delta \in R^{n\times n},\Delta =\Delta ^T\),scalar a and b with \(a<b\),vector function \(\delta (t):[a,b]\rightarrow R^n\),such that the integrations concerned are well defined, then

$$\begin{aligned} \left( \int ^b_a\delta (s)ds\right) ^T\Delta \left( \int ^b_a\delta (s)ds\right) \le (b-a)\int ^b_a\delta ^T(s)\Delta \delta (s)ds \end{aligned}$$

Lemma 2.5

For any n-dimensional real vectors \(x,y,\varepsilon >0\) and positive definite matrix \(P\in R^{n\times n}\), the following matrix inequality hold.

$$\begin{aligned} 2x^Ty\le \varepsilon ^{-1} x^TPx+\varepsilon y^TP^{-1}y. \end{aligned}$$

Main results

Theorem 3.1

If assumptions (H1)–(H7) hold, and there exist diagonal matrix \(P>0, H>0\) and symmetric matrices \(Q, R>0\), such that the following matrix inequalities hold:

  1. (a)
    $$\begin{aligned} \Xi ^\star =\left( \begin{array}{ccccc} \Sigma & P\overline{A}C+F & P\overline{A}D &P\overline{A}\bar{D} &P\overline{A}\tilde{D}\\ *& -I & 0& 0 & 0\\ *& *& -Q& 0 & 0\\ *& *& *& -R & 0\\ *&*&*& *& -H\\ \end{array}\right) <0 \end{aligned}$$
    (4)

    where \(\lambda _1\) is the smallest positive eigenvalue of the Neumann boundary problem (2),

    $$\begin{aligned} \Sigma&= -2\lambda _1 PW-2P\underline{A}B+\lambda _2\Gamma _1+\frac{\lambda _2}{1-\rho } \Gamma _2+\frac{1}{1-\rho }L^TQL+\mu ^2\bar{L}^TR\bar{L}+\tilde{L}^TH\tilde{L},\\ \lambda _2&= \lambda _{max}(P), \underline{A}={\textit{diag}}\{\underline{a}_1, \underline{a}_2,\ldots,\underline{a}_n\}, \overline{A}={\textit{diag}}\{\overline{a}_1,\overline{a}_2,\ldots,\overline{a}_n\},\\ W&= {\textit{diag}}\{w_1,w_2,\ldots,w_n\},w_i={\textit{min}}_{1\le k\le m}\{w_{ik}\},\\ C&= (c_{ij})_{n\times n},\\ D&= (d_{ij})_{n\times n},\bar{D}=(\bar{d}_{ij})_{n\times n},\quad \tilde{D}=(\tilde{d}_{ij})_{n\times n}. \end{aligned}$$
  2. (b)

    \(J_{ik}(y_i(t_k^-,x))=-r_{ik}y_i(t_k^-,x)\), and \(r_{ik}\in [0,2]\). Then the equilibrium point of system (1) is globally stochastically asymptotically stable in the mean square.

Proof

Construct the following Lyapunov–Krasovskii functional:

$$\begin{aligned} V(t,y(t,x))=V_1+V_2+V_3+V_4+V_5 \end{aligned}$$

where

$$\begin{aligned} V_1&= \int _\Omega y^T(t,x)Py(t,x)dx\\ V_2&= \frac{\lambda _2}{1-\rho }\int _\Omega \int _{t-\tau (t)}^t y^T(s,x)\Gamma _2y(s,x)dsdx\\ V_3&= \frac{1}{1-\rho }\int _\Omega \int _{t-\tau (t)}^t g^T(y(s,x))Qg(y(s,x))dsdx\\ V_4&= \mu \int _\Omega \int _{-\mu }^0\int _{t+\theta }^t \bar{g}^T(y(s,x))R\bar{g}(y(s,x))dsd\theta dx\\ V_5&= \int _\Omega \sum \limits _{j=1}^{n}h_i\int _0^{\infty }k_{j}(\theta )\int _{t-\theta }^t \tilde{g}^2_j(y_j(s,x))dsd\theta dx\\ y(t,x)&= (y_1(t,x),y_2(t,x),\ldots,y_n(t,x))^T,\quad H={\textit{diag}}(h_1,h_2,\ldots,h_n) \end{aligned}$$

Then, we shall compute \(\fancyscript{L}V_1,\fancyscript{L}V_2,\fancyscript{L}V_3,\fancyscript{L}V_4,\fancyscript{L}V_5\) along the trajectories of the model (1), respectively.

$$\begin{aligned} \fancyscript{L}V_1&= 2\int _\Omega y^T(t,x)P\frac{\partial }{\partial t}y(t,x)dx\nonumber \\&= 2\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x) \left\{ \sum \limits _{k=1}^m\frac{\partial }{\partial x_k}\left(w_{ik}\frac{\partial y_i(t,x)}{\partial x_k}\right)-a_i(y_i(t,x))\left[ b_i(y_i(t,x))\right. \right. \nonumber \\&\quad -\sum \limits _{j=1}^nc_{ij}f_j (y_j(t,x)) -\sum \limits _{j=1}^nd_{ij}g_j(y_j(t-\tau _{j}(t),x)) -\sum \limits _{j=1}^n\bar{d}_{ij}\int _{t-\mu (t)}^t\bar{g}_j(y_j(s,x))ds\nonumber \\&\left. \left. \quad -\sum \limits _{j=1}^n\tilde{d}_{ij}\int ^t_{-\infty }k_{j}(t-s)\tilde{g}_j (y_j(s,x))ds\right] \right\} dx +\int _\Omega trace[\sigma ^TP\sigma ]dx\end{aligned}$$
(5)
$$\begin{aligned} \fancyscript{L}V_2&= \frac{\lambda _2}{1-\rho }\int _\Omega \left[ y^T(t,x)\Gamma _2y(t,x) -(1-\dot{\tau }(t))y^T(t-\tau (t),x)\Gamma _2y(t-\tau (t),x)\right] dx\nonumber \\&\le \frac{\lambda _2}{1-\rho }\int _\Omega \left[ y^T(t,x)\Gamma _2y(t,x)-(1-\rho )y^T(t-\tau (t),x)\Gamma _2y(t-\tau (t),x)\right] dx\nonumber \\&\le \frac{\lambda _2}{1-\rho }\int _\Omega y^T(t,x)\Gamma _2y(t,x)dx-\lambda _2\int _\Omega y^T(t-\tau (t),x)\Gamma _2y(t-\tau (t),x)dx \end{aligned}$$
(6)
$$\begin{aligned} \fancyscript{L}V_3&= \frac{1}{1-\rho }\int _\Omega \left[ g^T(y(t,x))Qg(y(t,x))-(1 -\dot{\tau }(t))g^T(y(t-\tau (t),x))Qg(y(t-\tau (t),x)) \right] dx\nonumber \\&\le \frac{1}{1-\rho }\int _\Omega \left[ g^T(y(t,x))Qg(y(t,x))-(1-\rho )g^T(y(t -\tau (t),x))Qg(y(t-\tau (t),x)) \right] dx\nonumber \\&\le \frac{1}{1-\rho }\int _\Omega y^T(t,x)L^TQLy(t,x)dx-\int _\Omega g^T(y(t-\tau (t),x))Qg(y(t-\tau (t),x))dx \end{aligned}$$
(7)

From Lemma 2.4 and the fact that \(0\le \mu (t)\le \mu \), we get

$$\begin{aligned} \fancyscript{L}V_4&= \int _\Omega \left[ \mu ^2 \bar{g}^T(y(t,x))R\bar{g}(y(t,x))dx -\mu \int _{t-\mu }^t \bar{g}^T(y(s,x))R\bar{g}(y(s,x))ds\right] dx\nonumber \\&\le \int _\Omega \left[ \mu ^2 y^T(t,x)\bar{L}^TR\bar{L}y(t,x)dx -\left( \int _{t-\mu }^t \bar{g}(y(s,x))ds\right) ^TR\left( \int _{t-\mu }^t\bar{g}(y(s,x))ds\right) \right] dx \end{aligned}$$
(8)

By well-known Cauchy–Schwarz inequality, we know

$$\begin{aligned} \fancyscript{L}V_5&= \int _\Omega \left[ \sum \limits _{j=1}^{n}h_{j}\int _0^{\infty }k_{j}(\theta ) \tilde{g_j}^2(y_j(t,x))d\theta -\int _\Omega \sum \limits _{j=1}^{n}h_{j}\int _0^{\infty }k_{j}(\theta ) \tilde{g_j}^2(y_j(t-\theta,x))d\theta \right] dx\nonumber \\&= \int _\Omega \left[ \tilde{g}^T(y(t,x))H\tilde{g}(y(t,x))-\sum \limits _{j=1}^{n}h_{j}\int _0^{\infty }k_{j}(\theta )d\theta \int _0^{\infty }k_{j}(\theta ) \tilde{g_j}^2(y_j(t-\theta,x))d\theta \right] dx\nonumber \\&\le \int _\Omega \left[ \tilde{g}^T(y(t,x))H\tilde{g}(y(t,x))-\sum \limits _{j=1}^{n}h_{j}\left( \int _0^{\infty }k_{j}(\theta ) \tilde{g_j}(y_j(t-\theta,x))d\theta \right) ^2\right] dx\nonumber \\&\le \int _\Omega \left[ y(t,x)\tilde{L}^TH\tilde{L}y(t,x)\right. \nonumber \\&\quad \left. -\left( \int _{-\infty }^tk(t-s) \tilde{g}(y(s,x))ds\right) ^TH\left( \int _{-\infty }^tk(t-s) \tilde{g}(y(s,x))ds\right) \right] dx \end{aligned}$$
(9)

By using the Poincaré inequality, the Green formula and the boundary condition, it is easy to calculate that

$$\begin{aligned}&\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x) \sum \limits _{k=1}^m\frac{\partial }{\partial x_k}(w_{ik}\frac{\partial y_i(t,x)}{\partial x_k})dx\nonumber \\&\quad =\sum \limits _{i=1}^{n}p_i\int _{\partial \Omega }(y_i(t,x)w_{ik}\frac{\partial y_i(t,x)}{\partial x_k})_{k=1}^mdx-\sum \limits _{i=1}^{n}p_i\int _{\Omega }\sum \limits _{k=1} ^mw_{ik}(\frac{\partial y_i(t,x)}{\partial x_k})^2dx\nonumber \\&\quad =-\sum \limits _{i=1}^{n}p_i\int _{\Omega }\sum \limits _{k=1}^mw_{ik}(\frac{\partial y_i(t,x)}{\partial x_k})^2dx\nonumber \\&\quad \le -\int _{\Omega }\sum \limits _{i=1}^{n}p_iw_i\sum \limits _{k=1}^m(\frac{\partial y_i(t,x)}{\partial x_k})^2dx=-\int _{\Omega }\sum \limits _{i=1}^{n}p_iw_i(\nabla y(t,x))^2dx\nonumber \\&\quad \le -\lambda _1\int _{\Omega }\sum \limits _{i=1}^{n}p_iw_i |y(t,x)|^2dx=-\lambda _1\int _\Omega y^T(t,x)PWy(t,x)dx\end{aligned}$$
(10)
$$\begin{aligned}&2\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x)a_i(y_i(t,x))b_i(y_i(t,x))dx\ge \int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x)\underline{a}_ib_iy_i(t,x)dx\nonumber \\&\quad =2\int _\Omega y^T(t,x)P\underline{A}By(t,x)dx\end{aligned}$$
(11)
$$\begin{aligned}&2\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x)a_i(y_i(t,x)) \sum \limits _{j=1}^{n}c_{ij}f_j(y_j(t,x))dx \nonumber \\&\quad \le \int _\Omega y^T(t,x)P\bar{A}CC^T\bar{A}^TPy(t,x)dx+\int _\Omega f^T(y(t,x))f(y(t,x))dx\nonumber \\&\quad \le \int _\Omega y^T(t,x)\left[ P\bar{A}CC^T\bar{A}^TP+F^TF\right] y(t,x)dx \end{aligned}$$
(12)

By the same way, we can obtain

$$\begin{aligned}&2\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x)a_i(y_i(t,x))\sum \limits _{j=1}^{n}d_{ij}g_j(y_j(t-\tau (t),x)))dx\nonumber \\&\le \int _\Omega y^T(t,x)P\bar{A}DQ^{-1}D^T\bar{A}^TPy(t,x)dx+\int _\Omega g^T(y(t-\tau (t),x))Qg(y(t-\tau (t),x))dx\end{aligned}$$
(13)
$$\begin{aligned}&2\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x)a_i(y_i(t,x))\sum \limits _{j=1}^{n}\bar{d}_{ij}\int _{t-\mu (t)}^t\bar{g}_j(y_j(s,x)dsdx\nonumber \\&\le \int _\Omega y^T(t,x)P\bar{A}\bar{D}R^{-1}\bar{D}^T\bar{A}^TPy(t,x)dx+\left( \int _{t-\mu }^t \bar{g}(y(s,x))ds\right) ^TR\left( \int _{t-\mu }^t\bar{g}(y(s,x))ds\right) dx\end{aligned}$$
(14)
$$\begin{aligned}&2\int _\Omega \sum \limits _{i=1}^{n}p_iy_i(t,x)a_i(y_i(t,x))\tilde{d}_{ij}\int ^t_{-\infty }k_{j}(t-s)\tilde{g}_j(y_j(s,x))dsdx\nonumber \\&\le \int _\Omega y^T(t,x)P\bar{A}\tilde{D}H^{-1}\tilde{D}^T\bar{A}^TPy(t,x)dx\nonumber \\&+ \left( \int _{-\infty }^tk(t-s) \tilde{g}(y(s,x))ds\right) ^TH\left( \int _{-\infty }^tk(t-s) \tilde{g}(y(s,x))ds\right) dx\end{aligned}$$
(15)
$$\begin{aligned}&\int _\Omega trace[\sigma ^TP\sigma ]dx\nonumber \\&\le \int _\Omega \lambda _2y^T(t,x)\Gamma _1 y(t,x)dx+\int _\Omega \lambda _2 y^T(t-\tau (t),x)\Gamma _2y(t-\tau (t),x)dx\end{aligned}$$
(16)
$$\begin{aligned}&\fancyscript{L}V\le \int _\Omega y^T(t,x)\left[ {-2\lambda _1}PW-2P\underline{A}B+ P\bar{A}CC^T\bar{A}^TP+F^TF\right. \nonumber \\&\quad +P\bar{A}DQ^{-1}D^T\bar{A}^TP+ P\bar{A}\bar{D}R^{-1}\bar{D}^T\bar{A}^TP+P\bar{A}\tilde{D}H^{-1}\tilde{D}^T\bar{A}^TP+ \lambda _2\Gamma _1\nonumber \\&\quad \left. + \frac{\lambda _2}{1-\rho }\Gamma _2+\frac{1}{1-\rho }L^TQL+\mu ^2\bar{L}^TR\bar{L}+\tilde{L}^TH\tilde{L}\right] y(t,x)dx\nonumber \\&= \int _\Omega y^T(t,x)\Xi y(t,x)dx \end{aligned}$$
(17)

where \(\Xi ={-2\lambda _1}PW-2P\underline{A}B+ P\bar{A}CC^T\bar{A}^TP+F^TF+P\bar{A}DQ^{-1}D^T\bar{A}^TP+ P\bar{A}\bar{D}R^{-1}\bar{D}^T\bar{A}^TP+P\bar{A}\tilde{D}H^{-1}\tilde{D}^T\bar{A}^TP+ \lambda _2\Gamma _1+\frac{\lambda _2}{1-\rho }\Gamma _2+\frac{1}{1-\rho }L^TQL +\mu ^2\bar{L}^TR\bar{L}+\tilde{L}^TH\tilde{L}\).

By Lemma 2.3 and our assumption, \(\Xi <0\) if and only if \(\Xi ^\star <0.\) Then, by Dynkin’s formula (Ito and Mckean 1965), for \(t\in (t_k,t_{k+1}],\) we have

$$\begin{aligned} EV(t,y(t,x))-EV(t_k^-,y(t_k^-,x))=E\int _{t_k^-}^t\fancyscript{L}V(s,y(s,x))ds<0, \end{aligned}$$

Hence, for \(t\in (t_k,t_{k+1}],\) \(EV(t,y(t,x))\le EV(t_k^-,y(t_k^-,x))\).

On the other hand, when \(t=t_k^+,\) we have

$$\begin{aligned} V_1(t_k)&= \int _\Omega y^T(t_k,x)Py(t_k,x)dx\nonumber \\&= \int _\Omega \left[ (1-\gamma _{ik})y(t_k^-,x)\right] ^TP(1-\gamma _{ik})(y(t_k^-,x))dx\nonumber \\&\le \int _\Omega y^T(t_k^-,x)Py(t_k^-,x)dx\le V_1(t_k^-) \end{aligned}$$
(18)

Moreover, it is obvious that \(V_2(t_k)=V_2(t_k),V_3(t_k)=V_3(t_k),V_4(t_k)=V_4(t_k^-)\). Hence we get \(V(t_k)\le V(t_k^-), EV(t_k)\le EV(t_k^-).\)

By Lyapnov–Krasovskii stability theorem, we have \(\lim \limits _{t\rightarrow +\infty }E\Vert y\Vert ^2=0\). Then the equilibrium point of (1) is globally stochastically asymptotically stable in the mean square. The proof is completed. \(\square \)

Remark 3.2

From the conditions of Theorem 3.1, we can know that the diffusion coefficient, the Nemman boundary conditions, the delays, the stochastic perturbations and system parameters have key effect on the stability of system 2.1.

Remark 3.3

If we set \(w_{ik}=0\), system 2.1 reduces to the following impulsive stochastic CGNNs with mixed delays:

$$\begin{aligned} dy_i(t,x)&= -a_i(y_i(t,x))[b_i(y_i(t,x))-\sum \limits _{j=1}^nc_{ij}f_j (y_j(t,x)) -\sum \limits _{j=1}^nd_{ij}g_j(y_j(t-\tau (t),x))\nonumber \\&\quad -\sum \limits _{j=1}^n\bar{d}_{ij}\int _{t-\mu (t)}^t\bar{g}_j(y_j(s,x))ds -\sum \limits _{j=1}^n\tilde{d}_{ij}\int ^t_{-\infty }k_{j}(t-s)\tilde{g}_j(y_j(s,x))ds]dt\\&\quad +\sum \limits _{j=1}^n\sigma _{ij}(t,y(t,x), y(t-\tau (t),x))dw_j(t),\qquad \qquad t\ne t_k,\nonumber \\ y_i(t_k,x)&= y_i(t_k^-,x)+J_{ik}(y_i(t_k^-,x)),\quad t= t_k, x\in \Omega, k\in Z,\nonumber \end{aligned}$$
(19)

Constructing Lyapunov functional 3.2 for system (19), by a tiny change, we can obtain the following result.

Corollary 3.4

If assumptions (H1)–(H6) hold, and there exist diagonal matrix \(P>0,H>0\) and a symmetric matrix \(Q,R>0\), such that the following matrix inequalities hold:

  1. 1.
    $$\begin{aligned} \Xi ^\star =\left( \begin{array}{ccccc} \Sigma & P\overline{A}C+F & P\overline{A}D &P\overline{A}\bar{D} &P\overline{A}\tilde{D}\\ *& -I & 0& 0 & 0\\ *& *& -Q& 0 & 0\\ *& *& *& -R & 0\\ *&*&*& *& -H\\ \end{array}\right) <0 \end{aligned}$$
    (20)

    where \(\lambda _1\) is the smallest positive eigenvalue of the Neumann boundary problem (2),

    $$\begin{aligned} \Sigma =-2P\underline{A}B+\lambda _2\Gamma _1+\frac{1}{1-\rho }L^TQL+\mu ^2\bar{L} ^TR\bar{L}+\tilde{L}^TH\tilde{L}, \end{aligned}$$
    $$\begin{aligned} \lambda _2=\lambda _{max}(P),\underline{A}={\textit{diag}}\{\underline{a}_1,\underline{a}_2, \ldots,\underline{a}_n\}, \overline{A}={\textit{diag}}\{\overline{a}_1,\overline{a}_2,\ldots,\overline{a}_n\}, \end{aligned}$$
    $$\begin{aligned} W={\textit{diag}}\{w_1,w_2,\ldots,w_n\},w_i={\textit{min}}_{1\le k\le m}\{w_{ik}\}, C=(c_{ij})_{n\times n}, \end{aligned}$$
    $$\begin{aligned} D=(d_{ij})_{n\times n},\bar{D}=(\bar{d}_{ij})_{n\times n},\tilde{D}=(\tilde{d}_{ij})_{n\times n}. \end{aligned}$$
  2. 2.

    \(J_{ik}(y_i(t_k^-,x))=-r_{ik}y_i(t_k^-,x)\), and \(r_{ik}\in [0,2]\). Then the equilibrium point of system (1) is globally stochastically asymptotically stable in the mean square.

Numerical example

In order to illustrate the feasibility of the present criteria, we provide a concrete example.

Example 4.1

Consider the following impulsive stochastic CGNNs with mixed delays and reaction–diffusion terms

$$\begin{aligned} dy_i(t,x)&= \sum \limits _{k=1}^m\frac{\partial }{\partial x_k}(w_{ik}\frac{\partial y_i(t,x)}{\partial x_k})dt-a_i(y_i(t,x))\left[ b_i(y_i(t,x))-\sum \limits _{j=1}^nc_{ij}f_j (y_j(t,x))\right. \nonumber \\&\quad -\sum \limits _{j=1}^nd_{ij}g_j(y_j(t-\tau (t),x)) -\sum \limits _{j=1}^n\bar{d}_{ij}\int _{t-\mu (t)}^t\bar{g}_j(y_j(s,x))ds\nonumber \\&\quad \left. -\sum \limits _{j=1}^n\tilde{d}_{ij}\int ^t_{-\infty }k_{j}(t-s)\tilde{g}_j(y_j(s,x))ds\right] dt\nonumber \\&\quad +\sum \limits _{j=1}^n\sigma _{ij}(t,y(t,x),y(t-\tau (t),x))dw_j(t),\quad \quad t\ne t_k,\\ y_i(t_k,x)&= y_i(t_k^-,x)+J_{ik}(y_i(t_k^-,x)),\quad t= t_k, x\in \Omega, k\in Z,\nonumber \end{aligned}$$
(21)

where the activation function is described by \(\Omega =\{(x_1,x_2)\mid |x_j|<\sqrt{2},j=1,2\},w_1=w_2=0.05,a_1(s)=a_2(s)=1.5 +0.5sins,b_1(s)=b_2(s)=2.16s,\quad f_1(s)=g_1(s)=\bar{g}_1(s)=\tilde{g}_1(s)=\frac{|s+1|-|s-1|}{20},\quad f_2(s) =g_2(s)=\bar{g}_2(s)=\tilde{g}_2(s)=tanh(s)\), \(t_k-t_{k-1}=0.3, \tau (t)=0.6-0.5sint, \mu (t)=0.06+0.04cost,k_{j}(s)=se^{-s}, \gamma _{ik}=1.5,\)

$$\begin{aligned} C=\left( \begin{array}{cc} 0.01 & -0.03\\ 0.01& 0.03\end{array}\right),\quad D=\left( \begin{array}{cc} 0.06 & 0.07\\ -0.01& 0.09 \end{array}\right),\quad \bar{D}=\left( \begin{array}{cc} 0.03 & 0.01\\ -0.05& 0.06 \end{array}\right),\quad \tilde{D}=\left( \begin{array}{cc} 0.02 & -0.03\\ -0.01& 0.01 \end{array}\right),\\ \Gamma _1=\left( \begin{array}{cc} 1.5 & 0\\ 0& 1.5\end{array}\right),\quad \Gamma _2=\left( \begin{array}{cc} 0.5 & 0\\ 0& 0.5 \end{array}\right). \end{aligned}$$

By simple calculation, we have \(\lambda _1=1,\rho =0.5,\mu =0.1\),

$$\begin{aligned} \overline{A}=\left( \begin{array}{cc} 2 & 0\\ 0& 2 \end{array}\right),\quad \underline{A}=\left( \begin{array}{cc} 1 & 0\\ 0& 1 \end{array}\right),\quad B=\left( \begin{array}{cc} 2.16 & 0\\ 0& 2.16 \end{array}\right),\quad F=L=\bar{L}=\tilde{L}=\left( \begin{array}{cc} 0.1 & 0\\ 0& 1 \end{array}\right). \end{aligned}$$

Using the Matlab LMI Control Toolbox in Matlab to solve the LMI (4), we get

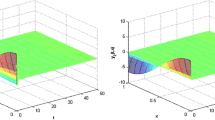
$$\begin{aligned} P=\left( \begin{array}{cc} 6.3180 & 0\\ 0 &6.3180 \end{array}\right), Q=\left( \begin{array}{cc} 4.8411 & -0.0043 \\ -0.0043 & 2.2643 \end{array}\right), \end{aligned}$$
$$\begin{aligned} R=\left( \begin{array}{cc} 4.8650 & -0.0876\\ -0.0876 & 4.8624 \end{array}\right),\quad H=\left( \begin{array}{cc} 3.4671 & 0\\ 0 & 3.4671 \end{array}\right). \end{aligned}$$

Then by Matlab software, we get \(\lambda _{max}(\Xi ^\star )=-2.1396<0\). By Theorem 3.1, the equilibrium point of model (21) is globally stochastically asymptotically stable in the mean square, which is shown in Fig. 1.

Fig. 1
figure 1

Time-space responses of the states \(y_1(t,x)\) (left) and \(y_2(t,x)\) (right)

Full size image

If \(W=0\), we get

$$\begin{aligned} P=\left( \begin{array}{cc} 6.4561 & 0\\ 0 &6.4561 \end{array}\right),\quad Q=\left( \begin{array}{cc} 4.7563 & -0.0067\\ -0.0067 & 2.1702 \end{array}\right),\quad \\ R=\left( \begin{array}{cc} 4.7877 & -0.0979\\ -0.0979 & 4.7873 \end{array}\right),\quad H=\left( \begin{array}{cc} 3.3409 & 0\\ 0 & 3.3409 \end{array}\right). \end{aligned}$$

Then by Matlab software, we get \(\lambda _{max}(\Xi ^\star )=-2.0020<0\). By Corollary 3.4, the equilibrium point of model (21) is globally stochastically asymptotically stable in the mean square, which is shown in Fig. 2.

Fig. 2
figure 2

Time responses curves of \(y_1(t,x)\) and \(y_2(t,x)\) when \(W=0\)

Full size image