Input-to-state stability of impulsive reaction–diffusion neural networks with infinite distributed delays

Abstract

In this paper, we focus on the global existence–uniqueness and input-to-state stability of the mild solution of impulsive reaction–diffusion neural networks with infinite distributed delays. First, the model of the impulsive reaction–diffusion neural networks with infinite distributed delays is reformulated in terms of an abstract impulsive functional differential equation in Hilbert space and the local existence–uniqueness of the mild solution on impulsive time interval is proven by the Picard sequence and semigroup theory. Then, the diffusion–dependent conditions for the global existence–uniqueness and input-to-state stability are established by the vector Lyapunov function and M-matrix where the infinite distributed delays are handled by a novel vector inequality. It shows that the ISS properties can be retained for the destabilizing impulses if there are no too short intervals between the impulses. Finally, three numerical examples verify the effectiveness of the theoretical results and that the reaction–diffusion benefits the input-to-state stability of the neural-network system.

1 Introduction

Due to wide applications in the field of secure communication, image processing, pattern recognition, and machine learning [5, 12, 16, 24, 25], neural networks have attracted much interest of researchers whose intensive efforts are oriented toward the dynamical analysis of neural networks including stability, synchronization, passivity, periodicity, among many others [6, 10, 13, 14]. Such analysis has also been carried on various kinds of neural-network models such as Hopfield neural networks, recurrent neural networks, and complex networks. Among them, the dynamical analysis of impulsive neural networks is one of the common interests since the impulse can either force the neural networks to fall into the desirable pattern or bring fluctuation to the neural networks. How to establish the conditions between the impulse and the continuous neural-network system for desirable properties has ignited plenty of valuable studies [2, 4, 7, 30, 33].

When the electrons are moving in the nonuniform electromagnetic field, the shift trajectory of the electrons may show the diffusion phenomenon, so the reaction–diffusion is introduced into the neural networks and various kinds of reaction–diffusion neural networks (RDNNs) are investigated. For example, the global exponential synchronization in an array of linearly diffusively coupled RDNNs was achieved by the pinning-impulsive controller in [39]. The finite-time passivity and synchronization problems of coupled RDNNs, generalized inertial RDNNs, and memristive RDNNs were addressed in [26, 27, 31]. Recently, the research on genetic regulatory networks with reaction–diffusion terms has obtained many remarkable results such as stability, state estimation, and sampled-data state estimation [17, 28, 42], to name a few. Among the studies of RDNNs, the dynamical analysis of impulsive RDNNs (IRDNNs) is one of the hottest topics and has also got fruitful results such as [5, 9, 18, 19, 22, 36] and references therein.

On the other hand, the time delay is inevitable in the implementation of neural networks, so the dynamical analysis of IRDNNs normally involves the finite delay or infinite distributed delay [4, 5, 11, 19, 22, 23, 34]. For instance, the global exponential stability of Cohen–Grossberg-type IRDNNs with finite-time-varying delays was studied in [19]. The synchronization problems of IRDNNs and stochastic IRDNNs with finite delays and infinite distributed delays were addressed in [5, 22]. In [4], Cao et al. investigated the almost periodicity of fractional-order IRDNNs with time-varying delays and proved the global perfect Mittag–Leffler stability.

In the traditional stability analysis of neural networks, the states are usually designed to converge to the equilibrium point. However, when the neural networks are affected by external input, the stability is hardly achieved [13]. Therefore, the input-to-state stability (ISS), originally proposed by Sontag [29], is employed to measure how the external input influences the stability of the neural networks [1, 13, 40, 44]. For instance, the exponential ISS issues of recurrent neural networks were solved by the Lyapunov–Krasovskii function method and linear matrix inequalities in [40]. The pth moment exponential ISS of recurrent neural networks was established by the vector Lyapunov function in [13]. Note that the above-mentioned works on ISS are concentrated on neural networks without impulses or reaction–diffusion terms both of which can cause non-negligible influence in the neural networks. But there is less relative research on the ISS of IRDNNs, because the IRDNNs, essentially an abstract impulsive differential equation with spatial operator in Hilbert space, may explode at finite time under the spatiotemporal external input; that is, the IRDNNs may not admit a global solution which is fundamental for further dynamical analysis including ISS. Thus, the primary concern of this work is to establish the global existence–uniqueness of the mild solution of IRDNNs. For the ISS analysis of the neural networks [21, 37, 41], most of the existing works address the neural networks with finite delays and the more challenging scenario with infinite distributed delays is rarely treated since the present states of the infinite delayed neural networks depend on all the history information so that the cross-term with infinite distributed delays generated from the Lyapunov function is difficult to handle with the reaction–diffusion and impulses existing in the neural-network model, which further motivates our work.

Motivated by the above discussion, this work investigates the global existence–uniqueness and ISS of the mild solution of IRDNNs with infinite distributed delays. The main contributions of this paper lie in the following three aspects.

• (1) The local existence–uniqueness of the mild solution on impulsive time interval is proven by the Picard sequence and semigroup theory after reformulating the neural-network model in terms of an abstract impulsive functional differential equation in Hilbert space.

• (2) The diffusion–dependent conditions are established to determine the ISS properties of IRDNNs under the spatiotemporal external input and bridge the local existence–uniqueness and the global existence–uniqueness of the mild solution where the cross-term of the infinite distributed delays is solved by the vector Lyapunov function and a novel vector inequality. It shows that the ISS properties can be retained for the destabilizing impulses if there are no too short intervals between the impulses.

• (3) It is of interest to verify in the numerical examples that the reaction–diffusion can force the trajectories of the neural networks to fall into ISS pattern and the ISS properties can be retained under certain impulsive perturbation.

The next sections are structured as follows. In Sect. 2, some lemmas, definitions, and the neural-network model are introduced. In Sect. 3, the well-posedness and ISS of the mild solution are proven. Section 4 proposes the numerical simulation of three examples. Finally, some conclusions are given in Sect. 5.

Notations $\bar{n}=\{1,2,\ldots ,n\}$, $\varvec{a}=(a,a,\ldots ,a)^T$ for $a\in \mathbb {R}$, I is the identity matrix, and $\mathbb {N}$ is the set of positive integers. If A is a vector or matrix, $A\succ 0$ (or $A\succcurlyeq 0$) means that all elements of A are positive (or nonnegative). For $A=(a_{ij})_{n\times n}\in \mathbb {R}^{n\times n}$, we denote $|A|=(|a_{ij}|)_{n\times n}$, $A^*=\text {diag}(a_{11},a_{22},\ldots ,a_{nn})$, $\lfloor A\rceil =A-A^*$, and $\Vert A\Vert _F\triangleq (\text {tr}(AA^T))^{\frac{1}{2}}$. $L^p(J,Y)$ denotes the space of Borel measurable mappings $\{f(t)\}_{t\in J}$ from J to Y with $\int _{t\in J} \Vert f(t)\Vert ^p_Y dt<\infty$ where $J\subset \mathbb {R}$ and $p>0$. $\mathcal {L}\triangleq (L^2(\mathcal {O}))^n$ is a Hilbert space with inner product $\langle z_1,z_2\rangle =\int _{\mathcal {O}} z_1^T(x)z_2(x) dx$ and norm $\Vert z \Vert ^2 = \Vert z \Vert ^2_{\mathcal {L}}=\langle z,z\rangle$, where $\mathcal {O}=\{x|x=(x_1,x_2,\ldots ,x_q)^T, |x_\varsigma |\le \rho _\varsigma ,$ $\varsigma \in \bar{q}\}$. A function f: $J\rightarrow Y$ is piecewise continuous if it has at most a finite number of jump discontinuities on J and $f(t^+)=f(t)$ for all $t\in J$. PC(J, Y) represents the space of piecewise continuous functions from J to Y and $\mathcal {PC}=PC((-\infty ,0],\mathcal {L})$. $\mathcal {PC}^b=\{f|f\in \mathcal {PC} \text { and } f(t) \text { is bounded on } (-\infty ,0]\}$ with norm $\Vert f \Vert _{\mathcal {PC}^b}$ $=\sup _{-\infty < t \le 0}\Vert f(t) \Vert$. A function z(t, x) is said to be piecewise continuous if z(t, x) is piecewise continuous for all $x\in \mathcal {O}$. $\mathcal {K}$ represents the class of continuous strictly increasing function $\kappa :\mathbb {R}_+\rightarrow \mathbb {R}_+$ with $\kappa (0)=0$. $\mathcal {K}_\infty$ is the subset of $\mathcal {K}$ functions that are unbounded. A function $\beta$ is said to belong to the class of $\mathcal {KL}$, if $\beta (\cdot ,t)$ is of class $\mathcal {K}$ for each fixed $t>0$ and $\beta (s,t)$ decreases to 0 as $t\rightarrow +\infty$ for each fixed $s\ge 0$.

2 Model description and preliminaries

Consider the following IRDNNs with infinite distributed delays

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \hat{z}_i(t,x)}{\partial t} = \sum _{\varsigma =1}^q \frac{\partial }{\partial x_\varsigma }\bigg (d_{i\varsigma }\frac{\partial \hat{z}_i(t,x)}{\partial x_\varsigma }\bigg )-a_i \hat{z}_i(t,x) \\ \quad +\sum _{j=1}^n b_{ij}\hat{f}_j(\hat{z}_j(t,x))+\sum _{j=1}^n c_{ij}\hat{f}_j(\hat{z}_j(t-\tau ,x))\\ \quad +\sum _{j=1}^n e_{ij}\int _{-\infty }^t k_{ij}(t-s)\hat{f}_j(\hat{z}_j(s,x))ds+\hat{u}_i(t,x),\\ \quad t\ge 0,\ t\ne t_k,\\ \hat{z}_i(t_k,x) = \hat{z}_i(t_k^-,x) + \hat{I}_{ik}(\hat{z}_i(t_k^-,x)),\ k\in \mathbb {N}, \end{array} \right. \end{aligned}$$

(1)

where $x\in \mathcal {O}$, $i\in \bar{n}$, $\hat{z}_i(t,x)$ is the state variable of the ith neuron at time t and space x, $d_{i\varsigma }$ represents the positive transmission diffusion coefficient of the ith neuron, $\sum _{\varsigma =1}^q \frac{\partial }{\partial x_\varsigma }(d_{i\varsigma }\frac{\partial \hat{z}_i(t,x)}{\partial x_\varsigma })$ represents the reaction–diffusion term, $a_i>0$ stands for the recovery rate, $b_{ij}$, $c_{ij}$, and $e_{ij}$ are the connection weight strengths of the jth neuron on the ith neuron, $\hat{f}_j$ stands for the activation function, the delay kernel $k_{ij}$ is nonnegative continuous function defined on $[0,+\infty )$ and satisfies that $\int _0^{+\infty }k_{ij}(s)ds=1$ and there exists a positive constant $\epsilon$ such that $\int _0^{+\infty } e^{\epsilon s}k_{ij}(s)ds<+\infty$, $\hat{u}_i$ is the external input which satisfies the Dirichlet boundary condition and $\sup _{t\ge 0} \Vert \hat{u}_i(t,x)\Vert ^2<+\infty$, $i,j\in \bar{n}$. To prevent the occurrence of accumulation points, the impulse time sequences are assumed to satisfy $0=t_0<t_1<t_2<\cdots <t_k\rightarrow +\infty$ as $k\rightarrow +\infty$, which are denoted by set $\mathscr {F}_0$. For any $\eta >0$, let $\mathscr {F}(\eta )$ denote the set of all impulse time sequences in $\mathscr {F}_0$ satisfying $t_k-t_{k-1}\ge \eta$ for any $k\in \mathbb {N}$. The impulsive function $\hat{I}_{ik}$ is continuous, $i\in \bar{n}$, $k\in \mathbb {N}$. Then, the neural-network model (1) can be rewritten in terms of the following vector form

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \hat{z}(t,x)}{\partial t} = \nabla \cdot (D\circ \nabla \hat{z}(t,x))-A \hat{z}(t,x) \\ \qquad \quad \quad \ +B\hat{f}(\hat{z}(t,x))+C\hat{f}(\hat{z}(t-\tau ,x))\\ \qquad \quad \quad \ +\int _{-\infty }^t E\circ K(t-s)\hat{f}(\hat{z}(s,x))ds\\ \qquad \quad \quad \ +\hat{u}(t,x),\ t\in [t_{k-1},t_k),\\ \hat{z} (t_k,x) = \hat{z}(t_k^-,x) + \hat{I}_k(\hat{z}(t_k^-,x)),\ k\in \mathbb {N}, \end{array} \right. \nonumber \\ \end{aligned}$$

(2)

where $\nabla \cdot (D\circ \nabla \hat{z}(t,x))=(\sum _{\varsigma =1}^q \frac{\partial }{\partial x_\varsigma }(d_{1\varsigma }\frac{\partial \hat{z}_1(t,x)}{\partial x_\varsigma }),\ldots ,$ $\sum _{\varsigma =1}^q \frac{\partial }{\partial x_\varsigma }(d_{n\varsigma }\frac{\partial \hat{z}_n(t,x)}{\partial x_\varsigma }))^T$, $\hat{z}=(\hat{z}_1,\hat{z}_2,\ldots ,\hat{z}_n)^T$, $A=\text {diag}(a_1,a_2,\ldots ,a_n)$, $B=(b_{ij})_{n\times n}$, $C=(c_{ij})_{n\times n}$, $E=(e_{ij})_{n\times n}$, $K(s)=(k_{ij}(s))_{n\times n}$, $\hat{f}(z)=(\hat{f}_1(z_1),\hat{f}_2(z_2),$ $\cdots ,\hat{f}_n(z_n))^T$, $\hat{u}=(\hat{u}_1,\hat{u}_2,\ldots ,\hat{u}_n)^T$, $\hat{I}_k(\hat{z})=(\hat{I}_{1k}(\hat{z}_1),$ $\hat{I}_{2k}(\hat{z}_2),\ldots ,\hat{I}_{nk}(\hat{z}_n))^T$, and $\circ$ denotes Hadamard product. The Dirichlet boundary condition and initial condition, associated with (1) or (2), are given by

$$\begin{aligned} \begin{array}{l} \hat{z}(t,x)|_{x\in \partial \mathcal {O}}=0,\ t\in \mathbb {R},\\ \hat{z}(t,x)=\hat{\phi }(t,x)\in \mathcal {PC}^b,\ t\le 0,x\in \mathcal {O}. \end{array} \end{aligned}$$

(3)

As standard hypotheses, we assume that

• (H1) there exist positive constants $l_i$ such that

  $$\begin{aligned} |\hat{f}_i(\hat{z}_1)-\hat{f}_i(\hat{z}_2)|\le l_i |\hat{z}_1-\hat{z}_2|, \end{aligned}$$

• (H2) there are positive constants $r_{ik}$ such that

  $$\begin{aligned} |\hat{z}_1+\hat{I}_{ik}(\hat{z}_1)|\le r_{ik}|\hat{z}_1|, \end{aligned}$$

  for any $\hat{z}_1,\hat{z}_2\in \mathbb {R}$, $i\in \bar{n}$, and $k\in \mathbb {N}$.

Define a linear operator

$$\begin{aligned} \mathscr {D}:\ (H_0^1(\mathcal {O}))^n\cap (H^2(\mathcal {O}))^n\rightarrow \mathcal {L},\ \mathscr {D}\hat{z}=\nabla \cdot (D\circ \nabla \hat{z}), \end{aligned}$$

then $\mathscr {D}$ is an infinitesimal generator of a strongly continuous contractive semigroup S(t) on $\mathcal {L}$ [20]. So, the reaction–diffusion with spatial derivative in the neural-network model is treated as a linear operator in Hilbert space, which enables us to reformulate the neural-network model in Euclidean space into an abstract ordinary differential form in Hilbert space. Then, we arrive at an abstract formulation of the neural networks (2)–(3) in the form of an abstract impulsive functional differential equation+

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz(t)}{dt} = \mathscr {D}z(t)-A z(t)+Bf(z(t))\\ \qquad \qquad +Cf(z(t-\tau ))+\int _{-\infty }^t E\circ K(t-s)f(z(s))ds\\ \qquad \qquad +u(t),\ t\in [t_{k-1},t_k),\\ z(t_k) = z(t_k^-) + I_k(z(t_k^-)),\ k\in \mathbb {N},\\ z_0=\phi \in \mathcal {PC}^b, \end{array} \right. \end{aligned}$$

(4)

where $z(t)=\hat{z}(t,x)\in \mathcal {L}$, $f:\mathcal {L}\rightarrow \mathcal {L}$, $u(t)=\hat{u}(t,x)\in \mathcal {L}$, $I_k:\mathcal {L}\rightarrow \mathcal {L}$, $k\in \mathbb {N}$, and $z_0(\theta )=\phi (\theta )=\hat{\phi }(\theta ,x)\in \mathcal {PC}^b$, $\theta \in (-\infty ,0]$.

Definition 1

An $\mathcal {L}$-valued functional z(t) is said to be a mild solution of (4), if z(t) satisfies the following equation

$$\begin{aligned} z(t) =&\ S(t-t_0)\phi (0)-\int _{t_0}^t S(t-s)Az(s)ds\nonumber \\&+\int _{t_0}^t S(t-s)Bf(z(s))ds\nonumber \\&+ \int _{t_0}^t S(t-s)Cf(z(s-\tau ))ds\nonumber \\&+\int _{t_0}^t S(t-s)\int _{-\infty }^s E\circ K(s-r)f(z(r))drds\nonumber \\&+\int _{t_0}^t S(t-s)u(s)ds\nonumber \\&+\sum _{t_0<t_k\le t} S(t-t_k)I_k(z(t_k^-)). \end{aligned}$$

(5)

Definition 2

The mild solution of (4) is said to be

• (i) input-to-state stable (ISS), if there exist functions $\beta \in \mathcal {KL}$ and $\alpha ,\gamma \in \mathcal {K}_\infty$ such that

  $$\begin{aligned} \alpha (\Vert z(t) \Vert ) \le \beta (\Vert \phi \Vert _{\mathcal {PC}^b},t-t_0)+\sup _{t_0\le s\le t} \gamma (\Vert u(s)\Vert ); \end{aligned}$$

• (ii) integral input-to-state stable (iISS), if there exist functions $\beta \in \mathcal {KL}$ and $\alpha ,\gamma \in \mathcal {K}_\infty$ such that

  $$\begin{aligned} \alpha (\Vert z(t)\Vert ) \le \beta (\Vert \phi \Vert _{\mathcal {PC}^b},t-t_0)+\int _{t_0}^t \gamma (\Vert u(s)\Vert )ds; \end{aligned}$$

• (iii) $e^{\lambda t}$-weighted input-to-state stable ($e^{\lambda t}$-ISS), if there exist functions $\alpha _1,\alpha _2,\gamma \in \mathcal {K}_\infty$ and a constant $\lambda >0$, such that

  $$\begin{aligned} \begin{aligned} e^{\lambda (t-t_0)}\alpha _1(\Vert z(t) \Vert ) \le&\ \alpha _2(\Vert \phi \Vert _{\mathcal {PC}^b})\\&+\sup _{t_0\le s\le t} \{e^{\lambda (s-t_0)}\gamma (\Vert u(s)\Vert )\}. \end{aligned} \end{aligned}$$

Remark 1

Note that the IRDNNs (2)–(3) are reformulated in terms of the abstract impulsive functional differential equation (4) defined on Hilbert space after the reaction–diffusion term is represented as the linear spatial operator, so the mild solution and ISS properties are also defined on the Hilbert space, and it is worthwhile to mention that the existence–uniqueness and ISS of (2)–(3) are equivalent to the existence–uniqueness and ISS of (4). Besides, the overhead ISS properties defined on Hilbert space also accord with the ISS properties of impulsive delayed systems on Euclidean space in the existing literature [8, 38].

Definition 3

Given a locally Lipschitz function $V:\mathbb {R}_+\times \mathcal {L}\rightarrow \mathbb {R}_+$, the upper right-hand Dini derivative of V with respect to system (4) is defined by

$$\begin{aligned} D^+V(t,z)= & {} \limsup _{h\rightarrow 0^+}\frac{1}{h}[V(t+h,z+hG(t,z,u))\\&-V(t,z)], \end{aligned}$$

where $G(t,z,u)=\mathscr {D}z(t)-Az(t)+Bf(z(t))+Cf(z(t-\tau ))+\int _{-\infty }^t E\circ K(t-s)f(z(s))ds+u(t)$.

Lemma 1

([3, 13]) If $A=(a_{ij})_{n\times n}\in \mathbb {R}^{n\times n}$ with $a_{ij}\le 0$, $i\ne j$, $i,j\in \bar{n}$, then the following conclusions are equivalent.

• (1) A is a nonsingular M-matrix.

• (2) A is semipositive; that is, there exists $\nu \succ 0$ in $\mathbb {R}^n$, such that $A\nu \succ 0$.

• (3) $A^{-1}$ exists and its elements are all nonnegative.

• (4) All the leading principle minors of A are positive.

Lemma 2

([15]) Let $\mathcal {O}$ be a cube $|x_\varsigma |\le \rho _\varsigma$ ($\varsigma \in \bar{q}$) and let h(x) be a real-valued function belonging to $C^1(\mathcal {O})$, which vanishes on the boundary $\partial \mathcal {O}$, that is, $h(x)|_{\partial \mathcal {O}}=0$. Then,

$$\begin{aligned} \int _{\mathcal {O}} h^2(x)dx \le \rho _\varsigma ^2 \int _{\mathcal {O}}\bigg (\frac{\partial h(x)}{\partial x_\varsigma }\bigg )^2 dx,\ \varsigma \in \bar{q}. \end{aligned}$$

(6)

Lemma 3

For $k\in \mathbb {N}$, the functions $W=(w_1,\ldots ,w_n)^T$, $H=(h_1,\ldots ,h_n)^T\in PC((-\infty ,t_{k-1}],\mathbb {R}^n)$ are continuous on $[t_{k-1},t_k)$ and satisfy the following conditions

$$\begin{aligned} \left\{ \begin{array}{l} D^+W(t) \preccurlyeq \mathfrak {A}W(t)+\mathfrak {B}W(t-\tau )\\ \qquad \qquad \qquad \quad +\int _{-\infty }^t \mathfrak {C}(t-s)W(s)ds,\ t_{k-1}\le t<t_k,\\ D^+H(t) = \mathfrak {A}H(t)+\mathfrak {B}H(t-\tau )\\ \qquad \qquad \qquad \quad +\int _{-\infty }^t \mathfrak {C}(t-s)H(s)ds,\ t_{k-1}\le t<t_k, \end{array} \right. \nonumber \\ \end{aligned}$$

(7)

where $\mathfrak {A}=(\mathfrak {a}_{ij})_{n\times n}$, $\mathfrak {a}_{ij}\ge 0$, $i\ne j$, $\mathfrak {B}=(\mathfrak {b}_{ij})_{n\times n}$, $\mathfrak {b}_{ij}\ge 0$, $i,j\in \bar{n}$, $\mathfrak {C}(s)=(\mathfrak {c}_{ij}(s))_{n\times n}$, $\mathfrak {c}_{ij}(s)\ge 0$, and $\int _{0}^{+\infty } \mathfrak {c}_{ij}(s)ds<+\infty$, $i,j\in \bar{n}$. Then, $W(t)\prec H(t)$ for $t\le t_{k-1}$ implies $W(t)\preccurlyeq H(t)$ for $t_{k-1}\le t<t_k$.

Proof

Suppose that the conclusion is not true, there exist $\check{i}\in \bar{n}$ and $\check{t}\in (t_{k-1},t_k)$ such that

$$\begin{aligned} w_{\check{i}}(\check{t})=h_{\check{i}}(\check{t}),\ D^+w_{\check{i}}(\check{t})>D^+h_{\check{i}}(\check{t}), \end{aligned}$$

(8)

and

$$\begin{aligned} w_i(t)\le h_i(t),\text { for all } t\le \check{t},\ i\in \bar{n}. \end{aligned}$$

(9)

However, it follows from (7) that

$$\begin{aligned} D^+w_{\check{i}}(\check{t})&\le \mathfrak {a}_{\check{i}\check{i}}w_{\check{i}}(\check{t})+\sum _{j\ne \check{i}} \mathfrak {a}_{\check{i}j}w_{j}(\check{t})\nonumber \\&\quad \; +\sum _{j=1}^n (\mathfrak {b}_{\check{i}j}w_j(\check{t}-\tau )\nonumber \\&\quad +\int _{-\infty }^{\check{t}} \mathfrak {c}_{\check{i}j}(\check{t}-s)w_j(s)ds)\nonumber \\&\le \mathfrak {a}_{\check{i}\check{i}}h_{\check{i}}(\check{t})+\sum _{j\ne \check{i}} \mathfrak {a}_{\check{i}j}h_{j}(\check{t})\nonumber \\&\quad \; +\sum _{j=1}^n (\mathfrak {b}_{\check{i}j}h_j(\check{t}-\tau )\nonumber \\&\quad +\int _{-\infty }^{\check{t}} \mathfrak {c}_{\check{i}j}(\check{t}-s)h_j(s)ds)\nonumber \\ =&\ D^+h_{\check{i}}(\check{t}), \end{aligned}$$

(10)

which contradicts (8). Hence, $W(t)\preccurlyeq H(t)$ for $t_{k-1}\le t<t_k$. $\square$

Consider the following inequality

$$\begin{aligned} \left\{ \begin{array}{l} D^+H(t) = \mathfrak {A}H(t)+\mathfrak {B}H(t-\tau )\\ \quad \quad \quad \quad \quad \quad +\int _{-\infty }^t \mathfrak {C}(t-s)H(s)ds,\ t_{k-1}\le t<t_k,\\ H(t) = \delta \varvec{1},\ t\le t_{k-1}, \end{array} \right. \end{aligned}$$

(11)

where $\mathfrak {A}=(\mathfrak {a}_{ij})_{n\times n}$, $\mathfrak {a}_{ij}\ge 0$, $i\ne j$, $\mathfrak {B}=(\mathfrak {b}_{ij})_{n\times n}$, $\mathfrak {b}_{ij}\ge 0$, $i,j\in \bar{n}$, $\mathfrak {C}(s)=(\mathfrak {c}_{ij}(s))_{n\times n}$, $\mathfrak {c}_{ij}(s)\ge 0$, and $\int _{0}^{+\infty } \mathfrak {c}_{ij}(s)ds<+\infty$, $i,j\in \bar{n}$.

Lemma 4

Suppose that there exists a scalar $\sigma \ge 1$ such that

$$\begin{aligned} \left[ \mathfrak {A}^*+\sigma \left( \lfloor \mathfrak {A}\rceil +\mathfrak {B}+\int _{0}^{+\infty }\mathfrak {C}(s)ds\right) \right] \varvec{1}+\frac{\ln \sigma }{t_k-t_{k-1}}\varvec{1}\prec 0, \end{aligned}$$

(12)

then $H(t)\preccurlyeq \delta \varvec{1}$ for $t\in (-\infty ,t_k)$ and $H(t_k^-)\preccurlyeq \frac{\delta }{\sigma } \varvec{1}$.

Proof

From (12), we have

$$\begin{aligned}&\mathfrak {a}_{ii}+\sigma \sum _{j\ne i}\mathfrak {a}_{ij}+\sigma \sum _{j=1}^n\left( \mathfrak {b}_{ij}+\int _{0}^{+\infty }\mathfrak {c}_{ij}(s)ds\right) \nonumber \\&\quad +\,\frac{\ln \sigma }{t_k-t_{k-1}}<0, \end{aligned}$$

(13)

for $\forall i\in \bar{n}$. When $t=t_{k-1}$, a simple computation yields

$$\begin{aligned} D^+h_i(t_{k-1})&=\sum _{j=1}^n\bigg [\mathfrak {a}_{ij}h_j(t_{k-1})+\mathfrak {b}_{ij}h_j(t_{k-1}-\tau )\nonumber \\&\quad +\int _{-\infty }^{t_{k-1}}\mathfrak {c}_{ij}(t_{k-1}-s)h_j(s)ds\bigg ]\nonumber \\&\le \delta \sum _{j=1}^n\bigg [\mathfrak {a}_{ij}+\mathfrak {b}_{ij}\nonumber \\&\quad +\int _{-\infty }^{t_{k-1}}\mathfrak {c}_{ij}(t_{k-1}-s)ds\bigg ]\nonumber \\&= \delta \sum _{j=1}^n\bigg [\mathfrak {a}_{ij}+\mathfrak {b}_{ij}+\int _{0}^{+\infty }\mathfrak {c}_{ij}(s)ds\bigg ]<0, \end{aligned}$$

(14)

for $\forall i\in \bar{n}$. Then, we can conclude that $H(t)\preccurlyeq \delta \varvec{1}$ for $t_{k-1}\le t<t_k$. If it is not true, there exist $\check{i}\in \bar{n}$ and $\check{t}\in (t_{k-1},t_k)$ such that

$$\begin{aligned} h_{\check{i}}(\check{t})=\delta ,\ D^+h_{\check{i}}(\check{t})\ge 0, \end{aligned}$$

(15)

and

$$\begin{aligned} h_i(t)\le \delta ,\text { for all } t\le \check{t},\ i\in \bar{n}. \end{aligned}$$

(16)

However, it follows from (11) that

$$\begin{aligned} D^+h_{\check{i}}(\check{t})=&\ \mathfrak {a}_{\check{i}\check{i}}h_{\check{i}}(\check{t})+\sum _{j\ne \check{i}} \mathfrak {a}_{\check{i}j}h_{j}(\check{t})\nonumber \\&+\sum _{j=1}^n \bigg [\mathfrak {b}_{\check{i}j}h_j(\check{t}-\tau )\nonumber \\&+\int _{-\infty }^{\check{t}} \mathfrak {c}_{\check{i}j}(\check{t}-s)h_j(s)ds\bigg ]\nonumber \\ \le&\ \delta \sum _{j=1}^n\bigg [\mathfrak {a}_{\check{i}j}+\mathfrak {b}_{\check{i}j}+\int _{-\infty }^{\check{t}} \mathfrak {c}_{\check{i}j}(\check{t}-s)ds\bigg ]\nonumber \\ \le&\ \delta \sum _{j=1}^n\bigg [\mathfrak {a}_{\check{i}j}+\mathfrak {b}_{\check{i}j}+\int _{0}^{+\infty } \mathfrak {c}_{\check{i}j}(s)ds\bigg ] < 0, \end{aligned}$$

(17)

which contradicts (15). Hence, $H(t)\preccurlyeq \delta \varvec{1}$ for $t<t_k$.

In the following, we will show that, for $\forall i\in \bar{n}$, $h_i(t_k^-)\le \frac{\delta }{\sigma }$ if $\sigma >1$. For $\forall i\in \bar{n}$, we denote the first time when $D^+h_i(t)\ge 0$ on $(t_{k-1},t_k)$ by $\hat{t}$ and $\hat{t}=t_k$ if $D^+h_i(t)<0$ for all $t\in (t_{k-1},t_k)$. Further, we denote the first time when $h_i(t)\le \frac{\delta }{\sigma }$ on $(t_{k-1},t_k)$ by $\tilde{t}$ and $\tilde{t}=t_k$ if $h_i(t)>\frac{\delta }{\sigma }$ for all $t\in (t_{k-1},t_k)$. Then, we claim that $\hat{t}\ge \tilde{t}$. Suppose that it is not true, there exists $\check{\sigma }\in (1,\sigma )$ such that $D^+h_i(\hat{t})\ge 0$ and $h_i(\hat{t})=\frac{\delta }{\check{\sigma }}$. However, from (11) and $H(t)\preccurlyeq \delta \varvec{1}$ for $t\in (-\infty ,t_k)$, it follows that

$$\begin{aligned}&D^+h_{i}(\hat{t})\nonumber \\&= \mathfrak {a}_{ii}h_{i}(\hat{t})+\sum _{j\ne i} \mathfrak {a}_{ij}h_{j}(\hat{t})\nonumber \\&\quad +\sum _{j=1}^n \bigg [\mathfrak {b}_{ij}h_j(\hat{t}-\tau )+\int _{-\infty }^{\hat{t}} \mathfrak {c}_{ij}(\hat{t}-s)h_j(s)ds\bigg ]\nonumber \\&\le \mathfrak {a}_{ii}\frac{\delta }{\check{\sigma }}+\delta \sum _{j\ne i} \mathfrak {a}_{ij}+\delta \sum _{j=1}^n \bigg [\mathfrak {b}_{ij}+\int _{-\infty }^{\hat{t}} \mathfrak {c}_{ij}(\hat{t}-s)ds\bigg ]\nonumber \\&= \frac{\delta }{\check{\sigma }}\bigg \{\mathfrak {a}_{ii}+\check{\sigma }\bigg [\sum _{j\ne i} \mathfrak {a}_{ij} +\sum _{j=1}^n (\mathfrak {b}_{ij}+\int _{0}^{+\infty } \mathfrak {c}_{ij}(s)ds)\bigg ]\bigg \}\nonumber \\&<0, \end{aligned}$$

(18)

which is contradiction. Hence, $\hat{t}\ge \tilde{t}$. Furthermore, we can show that $h_i(t_k^-)\le \frac{\delta }{\sigma }$ if $\tilde{t}=t_k$. Otherwise, there exists $\check{\sigma }\in (1,\sigma )$ such that $\frac{\delta }{\check{\sigma }}\le h_i(t)\le \delta$ for $t_{k-1}\le t<t_k$ and $h_i(t_k^-)=\frac{\delta }{\check{\sigma }}$. However, for $t_{k-1}\le t<t_k$,

$$\begin{aligned} \begin{aligned}&D^+h_{i}(t)\\&= \mathfrak {a}_{ii}h_{i}(t)+\sum _{j\ne i} \mathfrak {a}_{ij}h_{j}(t)\\&\quad +\sum _{j=1}^n \bigg [\mathfrak {b}_{ij}h_j(t-\tau )+\int _{-\infty }^{t} \mathfrak {c}_{ij}(t-s)h_j(s)ds\bigg ]\\&\le \mathfrak {a}_{ii}h_{i}(t)+\delta \sum _{j\ne i}\mathfrak {a}_{ij} +\delta \sum _{j=1}^n \bigg [\mathfrak {b}_{ij}+\int _{-\infty }^{t} \mathfrak {c}_{ij}(t-s)ds\bigg ]\\&\le h_i(t)\bigg \{\mathfrak {a}_{ii}+\check{\sigma }\bigg [\sum _{j\ne i} \mathfrak {a}_{ij} +\sum _{j=1}^n (\mathfrak {b}_{ij}+\int _{0}^{+\infty } \mathfrak {c}_{ij}(s)ds)\bigg ]\bigg \}, \end{aligned} \end{aligned}$$

(19)

which indicates that

$$\begin{aligned} -\frac{\ln \check{\sigma }}{t_k-t_{k-1}}\le & {} \bigg \{\mathfrak {a}_{ii}+\check{\sigma }\bigg [\sum _{j\ne i} \mathfrak {a}_{ij}\nonumber \\&+\sum _{j=1}^n (\mathfrak {b}_{ij}+\int _{0}^{+\infty } \mathfrak {c}_{ij}(s)ds)\bigg ]\bigg \}. \end{aligned}$$

(20)

Since $\bar{\sigma }<\sigma$, the inequality (20) contradicts with (13). Hence, $h_i(t_k^-)\le \frac{\delta }{\sigma }$ if $\tilde{t}=t_k$. If $\tilde{t}<t_k$, we can also show that $h_i(t)\le \frac{\delta }{\sigma }$ for $[\tilde{t},t_k)$; otherwise, there exists $\check{t}\in [\tilde{t},t_k)$ such that $D^+h_i(\check{t})>0$ and $h_i(\check{t})=\frac{\delta }{\sigma }$. However, from (11) and $H(t)\preccurlyeq \delta \varvec{1}$ for $t\in (-\infty ,t_k)$, it follows that

$$\begin{aligned}&D^+h_{i}(\check{t})\nonumber \\&\quad = \mathfrak {a}_{ii}h_{i}(\check{t})+\sum _{j\ne i} \mathfrak {a}_{ij}h_{j}(\check{t})\nonumber \\&\qquad +\sum _{j=1}^n \bigg [\mathfrak {b}_{ij}h_j(\check{t}-\tau )+\int _{-\infty }^{\check{t}} \mathfrak {c}_{ij}(\check{t}-s)h_j(s)ds\bigg ]\nonumber \\&\quad \le \mathfrak {a}_{ii}\frac{\delta }{\sigma } +\delta \sum _{j\ne i} \mathfrak {a}_{ij}+\delta \sum _{j=1}^n \bigg [\mathfrak {b}_{ij}+\int _{-\infty }^{\check{t}} \mathfrak {c}_{ij}(\check{t}-s)ds\bigg ]\nonumber \\&\quad = \frac{\delta }{\sigma }\bigg \{\mathfrak {a}_{ii}+\sigma \bigg [\sum _{j\ne i} \mathfrak {a}_{ij} +\sum _{j=1}^n (\mathfrak {b}_{ij}+\int _{0}^{+\infty } \mathfrak {c}_{ij}(s)ds)\bigg ]\bigg \}\nonumber \\&\quad <0, \end{aligned}$$

(21)

which is contradiction. Therefore, $h_i(t_k^-)\le \frac{\delta }{\sigma }$ for $\forall i\in \bar{n}$ if $\sigma >1$, that is, $H(t_k^-)\preccurlyeq \frac{\delta }{\sigma }\varvec{1}$. The proof is completed. $\square$

3 Main results

In this section, the global existence–uniqueness and ISS of the mild solution of the IRDNNs (4) are developed by two steps. First, the local existence–uniqueness on the impulsive time interval is established by the Picard sequence. Then, the global existence–uniqueness and ISS are obtained by the vector Lyapunov function, M-matrix, the vector Lemmas 3 and 4.

3.1 Local existence–uniqueness

This subsection mainly concerns the local existence–uniqueness of the mild solution of the IRDNNs (4) on each impulsive time interval. First, let us consider the following auxiliary equation

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz(t)}{dt} =\mathscr {D}z(t)-A z(t)+Bf(z(t))\\ \qquad \qquad +Cf(z(t-\tau ))+\int _{-\infty }^t E\circ K(t-s)f(z(s))ds\\ \qquad \qquad +u(t),\ t\in [t_{k-1},t_k),\\ z_{t_{k-1}}=\phi _{k-1}\in \mathcal {PC}^b, \end{array} \right. \end{aligned}$$

(22)

where $k\in \mathbb {N}$. Accordingly, the mild solution of the overhead auxiliary equation is defined by

$$\begin{aligned} \begin{aligned} z(t) =&\ S(t-t_{k-1})\phi _{k-1}(0)\\&+\int _{t_{k-1}}^t S(t-s)F(s,z(s),u(s))ds, \end{aligned} \end{aligned}$$

(23)

where $t_{k-1}\le t<t_k$, $F(t,z(t),u(t))=-Az(t)+Bf(z(t))$ $+Cf(z(t-\tau ))+\int _{-\infty }^t E\circ K(t-s)f(z(s))ds+u(t)$. Then, we have the following proposition about the existence–uniqueness of the mild solution of the auxiliary Eq. (22).

Proposition 1

If (H1) and (H2) hold, the auxiliary Eq. (22) has a unique continuous mild solution on $[t_{k-1},t_k)$.

Proof

From (H1), for arbitrary $z^1(x),z^2(x)\in \mathcal {L}$, we have

$$\begin{aligned} \begin{aligned}&\Vert f(z^1(x))-f(z^2(x))\Vert ^2\\&\quad = \sum _{i=1}^n \int _\mathcal {O}[\hat{f}_i(z^1_i(x))-\hat{f}_i(z^2_i(x))]^2dx\\&\quad \le \sum _{i=1}^n l_i^2 \int _\mathcal {O}[z^1_i(x)-z^2_i(x)]^2dx\\&\quad \le l^2 \Vert z^1(x)-z^2(x)\Vert ^2, \end{aligned} \end{aligned}$$

(24)

where $l=\max _i\{l_i\}$, which implies that

$$\begin{aligned}&\Vert F(t,z(t),u(t))\Vert ^2 \nonumber \\&\quad \le 5n\Vert A\Vert _F^2\Vert z(t)\Vert ^2+5n\Vert B\Vert _F^2\Vert f(z(t))\Vert ^2\nonumber \\&\qquad +5n\Vert C\Vert _F^2\Vert f(z(t-\tau ))\Vert ^2+5\Vert u(t)\Vert ^2\nonumber \\&\qquad +5\Vert \int _{-\infty }^t E\circ K(t-s)f(z(s))ds\Vert ^2\nonumber \\&\quad \le 5\Vert u(t)\Vert ^2+5n(\Vert A\Vert _F^2+2l^2\Vert B\Vert _F^2)\Vert z(t)\Vert ^2\nonumber \\&\qquad +10nl^2\Vert C\Vert _F^2\Vert z(t-\tau )\Vert ^2+10l^2\Vert E\Vert _F^2 \varTheta (z(t))\nonumber \\&\qquad +10n(\Vert B\Vert _F^2+\Vert C\Vert _F^2+\Vert E\Vert _F^2)\Vert f(0)\Vert ^2, \end{aligned}$$

(25)

where

$$\begin{aligned} \varTheta (z(t))=\sum _{i=1}^n\sum _{j=1}^n \int _{-\infty }^t k_{ij}(t-s)\Vert z_j(s)\Vert ^2ds. \end{aligned}$$

(26)

For any $b\in [t_{k-1},t_k)$, we define the Picard sequence as follows $z_{t_{k-1}}^m=\phi _{k-1}$ for $m=0,1,2,\ldots$, $z^0(t)=\phi _{k-1}(0)$ for $t\in [t_{k-1},b]$, and

$$\begin{aligned} z^m(t) =&\ S(t-t_{k-1})\phi _{k-1}(0)\nonumber \\&+\int _{t_{k-1}}^t S(t-s)F(s,z^{m-1}(s),u(s))ds, \end{aligned}$$

(27)

for $t\in [t_{k-1},b]$ and $m=1,2,\ldots$. When $m=0$, $z^0(t)$ is obviously continuous on $[t_{k-1},b]$ and $\sup _{t_{k-1}\le s\le t}\Vert z^0(s)\Vert ^2$ $\le \Vert \phi _{k-1}\Vert ^2_{\mathcal {PC}^b}$. Combining (25), we obtain

$$\begin{aligned} \begin{aligned} \Vert F(t,z^0(t),u(t))\Vert ^2\le&\ 5n(\Vert A\Vert _F^2+2\kappa l^2)\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2\\&+10n\kappa \Vert f(0)\Vert ^2+5u^*, \end{aligned} \end{aligned}$$

(28)

where $\kappa =\Vert B\Vert _F^2+\Vert C\Vert _F^2+\Vert E\Vert _F^2$ and $u^*=\sup _{t\ge 0}\Vert u(t)\Vert ^2$, which indicates that $F(t,z^0(s),u(s))\in L^2([t_{k-1},b],\mathcal {L})$. Therefore, $z^1(t)$ is continuous and $\sup _{t_{k-1}\le s\le t}\Vert z^1(s)\Vert ^2$ $<\infty$ for $t\in [t_{k-1},b]$. Applying the inequality $(\sum _{i=1}^n a_i)^2$ $\le n\sum _{i=1}^n a_i^2$, the Cauchy–Schwarz inequality, Eq. (28), and the contraction of the semigroup S(t) yields

$$\begin{aligned}&\sup _{t_{k-1}\le s\le t} \Vert z^{1}(s)-z^0(s)\Vert ^2\nonumber \\&\quad \le 2 \sup _{t_{k-1}\le s\le t}\Vert S(s-t_{k-1})\phi _{k-1}(0)-\phi _{k-1}(0)\Vert ^2\nonumber \\&\qquad +2 \sup _{t_{k-1}\le s\le t}\Vert \int _{t_{k-1}}^s S(s-r)F(r,z^0(r),u(r))dr\Vert ^2\nonumber \\&\quad \le 8\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2+2(b-t_{k-1})\nonumber \\&\qquad \times \int _{t_{k-1}}^b \Vert F(s,z^0(s),u(s))\Vert ^2ds\nonumber \\&\quad \le 8\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2+10(b-t_{k-1})^2\nonumber \\&\qquad \times \,[n(\Vert A\Vert _F^2+2\kappa l^2)\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2\nonumber \\&\qquad +2n\kappa \Vert f(0)\Vert ^2+u^*]\nonumber \\&\quad \triangleq C_0, \end{aligned}$$

(29)

In the following, we will show that $z^m(t)$ is continuous on $[t_{k-1},b]$ and

$$\begin{aligned}&\sup _{t_{k-1}\le s\le t} \Vert z^m(s)\Vert ^2<\infty , \end{aligned}$$

(30)

$$\begin{aligned}&\sup _{t_{k-1}\le s\le t} \Vert z^{m+1}(s)-z^m(s)\Vert ^2\le \frac{C_0[M(t-t_{k-1})]^m}{m!}, \end{aligned}$$

(31)

for $m=0,1,2,\ldots$, where $t\in [t_{k-1},b]$, $M=4n(b-t_{k-1})(\Vert A\Vert _F^2+\kappa l^2)$. When $m=0$, $z^0(t)$ has been proved to be continuous, and (30)–(31) hold. Suppose that $z^m(t)$ is continuous and (30)–(31) hold for $m=0,1,2,\ldots ,p-1$, we will show that $z^k(t)$ is continuous and (30)–(31) hold for $m=p$. From (25), we see that

$$\begin{aligned} \begin{aligned}&\Vert F(t,z^{p-1}(t),u(t))\Vert ^2\\&\quad \le 5u^*+5n(\Vert A\Vert _F^2+2l^2\Vert B\Vert _F^2)\Vert z^{p-1}(t)\Vert ^2\\&\qquad +10nl^2\Vert C\Vert _F^2\Vert z^{p-1}(t-\tau )\Vert ^2\\&\qquad +10l^2\Vert E\Vert _F^2 \varTheta (z^{p-1}(t))+10n\kappa \Vert f(0)\Vert ^2\\&\quad \le 5u^*+10n\kappa \Vert f(0)\Vert ^2+10n\kappa l^2\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2\\&\qquad +5n(\Vert A\Vert _F^2+2\kappa l^2)\sup _{t_{k-1}\le s\le t}\Vert z^{p-1}(s)\Vert ^2, \end{aligned} \end{aligned}$$

which indicates that $F(t,z^{p-1}(s),u(s))\in L^2([t_{k-1},b],\mathcal {L})$. Therefore, $z^p(t)$ is continuous on $[t_{k-1},b]$. By the inequality $(\sum _{i=1}^n a_i)^2 \le n\sum _{i=1}^n a_i^2$, the Cauchy–Schwarz inequality, (H2), Eq. (25), and the contraction of the semigroup S(t), we have

$$\begin{aligned}&\sup _{t_{k-1}\le s\le t} \Vert z^{p}(s)\Vert ^2 \nonumber \\&\quad \le 2\sup _{t_{k-1}\le s\le t}\Vert S(s-t_{k-1})\phi _{k-1}(0)\Vert ^2\nonumber \\&\qquad +2 \sup _{t_{k-1}\le s\le t}\Vert \int _{t_{k-1}}^s S(s-r)F(r,z^{p-1}(r),u(r))dr\Vert ^2\nonumber \\&\quad \le 2\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2\nonumber \\&\qquad +2(b-t_{k-1})\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s \Vert F(r,z^{p-1}(r),u(r))\Vert ^2dr\nonumber \\&\quad \le 2\Vert \phi _{k-1}\Vert _{\mathcal {PC}^b}^2+10(b-t_{k-1})^2u^*\nonumber \\&\qquad +20n\kappa (b-t_{k-1})^2\Vert f(0)\Vert ^2\nonumber \\&\qquad +10n(b-t_{k-1})\Vert A\Vert _F^2\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert z^{p-1}(r)\Vert ^2dr\nonumber \\&\qquad +20n(b-t_{k-1})l^2\Vert B\Vert _F^2\nonumber \\&\qquad \sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert z^{p-1}(r)\Vert ^2dr\nonumber \\&\qquad +20n(b-t_{k-1})l^2\Vert C\Vert _F^2\nonumber \\&\qquad \sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert z^{p-1}(r-\tau )\Vert ^2dr\nonumber \\&\qquad +20(b-t_{k-1})l^2\Vert E\Vert _F^2\nonumber \\&\qquad \sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\varTheta (z^{p-1}(r))dr\nonumber \\&\quad \le C_0+10n(b-t_{k-1})^2(\Vert A\Vert _F^2+2\kappa l^2)\nonumber \\&\qquad \sup _{t_{k-1}\le s\le t}\Vert z^{p-1}(s)\Vert ^2\nonumber \\&\quad <\infty , \end{aligned}$$

(32)

$$\begin{aligned}&\sup _{t_{k-1}\le s\le t} \Vert z^{p+1}(s)-z^{p}(s)\Vert ^2\nonumber \\&\quad = \sup _{t_{k-1}\le s\le t}\Vert \int _{t_{k-1}}^s S(s-r)[F(r,z^p(r),u(r))\nonumber \\&\qquad -F(r,z^{p-1}(r),u(r))]dr\Vert ^2\nonumber \\&\quad \le (b-t_{k-1})\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s \Vert F(r,z^p(r),u(r))\nonumber \\&\qquad -F(r,z^{p-1}(r),u(r))\Vert ^2dr\nonumber \\&\quad \le 4(b-t_{k-1})\bigg \{\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert A(z^p(r) -z^{p-1}(r))\Vert ^2dr\nonumber \\&\qquad +\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert B[f(z^p(r))-f(z^{p-1}(r))]\Vert ^2dr\nonumber \\&\qquad +\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert C[f(z^p(r-\tau ))\nonumber \\&\qquad -f(z^{p-1}(r-\tau ))]\Vert ^2dr\nonumber \\&\qquad +\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\Vert \int _{-\infty }^r E\circ K(r-v)\times \nonumber \\&\qquad [f(z^p(v))-f(z^{p-1}(v))]dv\Vert ^2dr\bigg \}\nonumber \\&\quad \le 4(b-t_{k-1})\bigg \{n(\Vert A\Vert _F^2+l^2\Vert B\Vert _F^2+l^2\Vert C\Vert _F^2)\times \nonumber \\&\qquad \int _{t_{k-1}}^t \sup _{t_{k-1}\le v\le r}\Vert z^p(v)-z^{p-1}(v)\Vert ^2dr\nonumber \\&\qquad +l^2\Vert E\Vert _F^2\sup _{t_{k-1}\le s\le t}\int _{t_{k-1}}^s\varTheta (z^{p}(r)-z^{p-1}(r))dr\bigg \}\nonumber \\&\quad \le M \int _{t_{k-1}}^t \sup _{t_{k-1}\le v\le r}\Vert z^p(v)\nonumber \\&\qquad -z^{p-1}(v)\Vert ^2dr\nonumber \\&\quad \le M \int _{t_{k-1}}^t \frac{C_0[M(r-t_{k-1})]^{p-1}}{(p-1)!} dr\nonumber \\&\quad =\frac{C_0[M(t-t_{k-1})]^p}{p!}. \end{aligned}$$

(33)

Hence, (30)–(31) hold for $m=p$. By mathematical induction, $z^m(t)$ is continuous on $[t_{k-1},b]$, and (30)–(31) hold for all $m=0,1,2,\ldots$. Combining $z^m_{t_{k-1}}=\phi _{k-1}$ for all $m=0,1,2,\ldots$, and $\sum _{m=0}^\infty \frac{C_0[M(b-t_{k-1})^m]}{m!}$ $<\infty$, we find that the sums

$$\begin{aligned} z^k(t)=z^0(t)+\sum _{m=0}^{k-1}(z^{m+1}(t)-z^m(t)) \end{aligned}$$

(34)

are convergent uniformly in $t\in (-\infty ,b]$. Denote the limit by z(t), which is clearly continuous on $[t_{k-1},b]$. Note that

$$\begin{aligned}&\left\| \int _{t_{k-1}}^t S(t-s)F(s,z^{m}(s),u(s))ds\right. \nonumber \\&\qquad \left. -\int _{t_{k-1}}^t S(t-s)F(s,z(s),u(s))ds\right\| ^2\nonumber \\&\quad \le 4(b-t_{k-1})\bigg \{\int _{t_{k-1}}^t \Vert A(z^{m}(s)-z(s))\Vert ^2ds\nonumber \\&\qquad +\int _{t_{k-1}}^t \Vert B[f(z^{m}(s))-f(z(s))]\Vert ^2ds\nonumber \\&\qquad +\int _{t_{k-1}}^t \Vert C[f(z^{m}(s-\tau ))-f(z(s-\tau ))]\Vert ^2ds\nonumber \\&\qquad \; +\int _{t_{k-1}}^t \left\| \int _{-\infty }^s E\circ K(s-r)[f(z^{m}(r))\right. \nonumber \\&\qquad \left. -f(z(r))]dr\right\| ^2ds\bigg \}\nonumber \\&\quad \le M(b-t_{k-1})\sup _{t_{k-1}\le s\le t}\Vert z^{m}(s)-z(s)\Vert ^2\rightarrow 0, \end{aligned}$$

(35)

as $m\rightarrow \infty$. Hence we can take $m\rightarrow \infty$ in (27) to obtain the relation

$$\begin{aligned} z(t)= & {} S(t-t_{k-1})\phi _{k-1}(0)\\&+\int _{t_{k-1}}^t S(t-s)F(s,z(s),u(s))ds, \end{aligned}$$

for $t_{k-1}\le t\le b$ as desired. From the arbitrariness of b in $[t_{k-1},t_k)$, z(t) is the unique mild solution of (22) on $[t_{k-1},t_k)$. $\square$

Remark 2

The existence–uniqueness of the mild solution through the bounded initial condition determined by Proposition 1 corresponds to the local existence–uniqueness of the mild solution of (4) on every impulsive time interval, which will be derived in the next subsection. And it is straightforward to have the following results on $[t_0,t_1)$ by Proposition 1 under the fact that $z_0=\phi \in \mathcal {PC}^b$.

Proposition 2

If (H1) and (H2) hold, the IRDNNs (4) have a unique continuous mild solution on $[t_0,t_1)$.

3.2 Global existence–uniqueness and ISS

This subsection will establish the global existence–uniqueness and ISS of the mild solution of the IRDNNs (4). A further assumption is made as follows:

(H3) $f(0)=0$.

Theorem 1

Assume that (H1)–(H3) hold. Then, the IRDNNs with infinite distributed delays (4) have a unique global mild solution and are ISS, iISS, and $e^{\lambda t}$-ISS over the class $\mathscr {F}(\eta )$, if $\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I$ is a nonsingular M-matrix, where $\varLambda =\text {diag}(\sum _{\varsigma =1}^q \frac{d_{1\varsigma }}{\rho _\varsigma ^2},\sum _{\varsigma =1}^q \frac{d_{2\varsigma }}{\rho _\varsigma ^2},\ldots ,\sum _{\varsigma =1}^q \frac{d_{n\varsigma }}{\rho _\varsigma ^2})$, $L=\text {diag}(l_1,l_2,$ $\cdots ,l_n)$, and $\sigma =\max _{i,k}\{r_{ik},1\}$.

Proof

Since $\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I$ is a nonsingular M-matrix, it follows from Lemma 1 that there exists $\nu =(\nu _1,\nu _2,\ldots ,\nu _n)^T\succ 0$ such that $[\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I]\nu \succ 0$. Then, there exist positive constants $p_i=\nu _i/(\min _i(\nu _i))\ge 1$, $i\in \bar{n}$ such that, for $\forall i\in \bar{n}$,

$$\begin{aligned}&\left( -\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma ^2}-a_i+\frac{\ln \sigma }{\eta }+l_i|b_{ii}|\right) p_i\nonumber \\&\quad +\sigma \left( \sum _{j\ne i}l_jp_j|b_{ij}| +\sum _{j=1}^nl_jp_j|c_{ij}|\right. \nonumber \\&\quad \left. +\sum _{j=1}^nl_jp_j|e_{ij}|\right) <0. \end{aligned}$$

(36)

For $\tau >0$, let us consider the following function

$$\begin{aligned} \begin{aligned} \varPi _i(\lambda _i)=&\ \lambda _i-\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma ^2}-a_i+l_i|b_{ii}|+\frac{\ln \sigma }{\eta }\\&+\frac{\sigma }{p_i}\sum _{j\ne i}l_jp_j|b_{ij}|+\frac{\sigma }{p_i}\sum _{j=1}^nl_jp_j|c_{ij}|e^{\lambda _i \tau }\\&+\frac{\sigma }{p_i}\sum _{j=1}^nl_jp_j|e_{ij}|\int _{0}^{+\infty }k_{ij}(s)e^{\lambda _i s}ds, \end{aligned} \end{aligned}$$

(37)

where $i\in \bar{n}$. Combining (36), we obtain that $\varPi _i(0)<0$ and $\varPi _i(\lambda _i)$ is continuous and monotonous on [0, b), furthermore, $\varPi _i(\lambda _i)\rightarrow +\infty$ as $\lambda _i\rightarrow b$ where $b>\epsilon$ is the explosive point or $b=+\infty$. Thus, there exists a constant $\lambda _i^0\in (0,\epsilon )$ such that $\varPi _i(\lambda _i^0)<0$. If we denote $\lambda ^0=\min _i\{\lambda _i^0\}$, then $\varPi _i(\lambda ^0)<0$ for $\forall i\in \bar{n}$, which further implies that

$$\begin{aligned} \begin{aligned}&\bigg [\lambda ^0I -\mathfrak {P}+\mathfrak {Q}^*+\sigma (\lfloor \mathfrak {Q}\rceil +\mathfrak {R}e^{\lambda ^0\tau }\\&\quad +\int _{0}^{+\infty }\mathfrak {K}(s)e^{\lambda ^0s}ds)\bigg ]\varvec{1}+\frac{\ln \sigma }{\eta }\varvec{1}\prec 0. \end{aligned} \end{aligned}$$

(38)

where $\mathfrak {P}=\varLambda +A$, $\mathfrak {Q}=P^{-1}|B|LP$, $\mathfrak {R}=P^{-1}|C|LP$, $\mathfrak {K}(t-s)=P^{-1}|E|LP\circ K(t-s)$, and $P=\text {diag}(p_1,\ldots ,p_n)$.

Given $\phi \in \mathcal {PC}^b$, we write $z(t)=z(t;\phi )$ and define the vector Lyapunov–Krasovskii function candidate by $V(t,z(t))=(V_1(t,z_1(t)),V_2(t,z_2(t)),\ldots ,V_n(t,z_n(t)))^T$ and $V_i(t,z_i(t))=p_i^{-1}\Vert z_i(t)\Vert$. For $t\in [t_{k-1},t_k)$, $k\in \mathbb {N}$, the upper Dini derivative of $V_i^2$ with respect to (4) is calculated by

$$\begin{aligned}&D^+V_i^2(t,z_i(t))\nonumber \\&\quad =2p_i^{-2}\bigg \langle z_i(t),\sum _{\varsigma =1}^q\frac{\partial }{\partial x_\varsigma }\bigg (d_{i\varsigma }\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg )-a_i z_i(t)\nonumber \\&\qquad +\sum _{j=1}^nb_{ij}f_j(z_j(t))+\sum _{i=1}^nc_{ij}f_j(z_j(t-\tau ))\nonumber \\&\qquad +\sum _{j=1}^n e_{ij}\int _{-\infty }^tk_{ij}(t-s)f_j(z_j(s))ds+u_i(t)\bigg \rangle \nonumber \\&\quad \le 2p_i^{-2}\bigg \{\int _{\mathcal {O}}z_i(t;x)\sum _{\varsigma =1}^q\frac{\partial }{\partial x_\varsigma }\bigg (d_{i\varsigma }\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg ) dx\nonumber \\&\qquad +(-a_i)\int _{\mathcal {O}}(z_i(t;x))^2dx\nonumber \\&\qquad +\sum _{j=1}^n b_{ij}\int _{\mathcal {O}}z_i(t;x)f_j(z_j(t;x))dx\nonumber \\&\qquad +\sum _{j=1}^n c_{ij}\int _{\mathcal {O}}z_i(t;x)f_j(z_j(t-\tau ;x))dx\nonumber \\&\qquad +\sum _{j=1}^n e_{ij}\int _{\mathcal {O}}z_i(t;x)\nonumber \\&\qquad \int _{-\infty }^tk_{ij}(t-s)f_j(z_j(s;x))dsdx\nonumber \\&\qquad +\int _{\mathcal {O}}z_i(t;x)u_i(t;x)dx \triangleq 2p_i^{-2}\sum _{m=1}^6 \varTheta _m(z(t)). \end{aligned}$$

(39)

From the Green’s formula, the Dirichlet boundary condition (3), and Lemma 2, we get

$$\begin{aligned} \begin{aligned}&\varTheta _1(z(t))\\&\quad = \int _{\mathcal {O}}z_i(t;x)\nabla \cdot \bigg (d_{i\varsigma }\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg )_{\varsigma =1}^q dx\\&\quad = \int _{\mathcal {O}}\nabla \cdot \bigg (z_i(t;x)d_{i\varsigma }\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg )_{\varsigma =1}^q dx\\&\qquad -\int _{\mathcal {O}}(\nabla \cdot z_i(t;x))\bigg (d_{i\varsigma }\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg )_{\varsigma =1}^q dx\\&\quad = \int _{\partial \mathcal {O}}\bigg (z_i(t;x)d_{i\varsigma }\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg )_{\varsigma =1}^q \cdot \mathbf {n} dx\\&\qquad -\sum _{\varsigma =1}^q \int _{\mathcal {O}}d_{i\varsigma }\bigg (\frac{\partial z_i(t;x)}{\partial x_\varsigma }\bigg )^2 dx\\&\quad \le -\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma ^2}\int _{\mathcal {O}}(z_i(t;x))^2dx, \end{aligned} \end{aligned}$$

(40)

where $\cdot$ stands for the inner product, $\mathbf {n}$ stands for the outward unit normal field of the boundary, and $\nabla$ stands for the gradient operator. By the virtue of Holder inequality, we have

$$\begin{aligned}&\varTheta _3(z(t))\nonumber \\&\quad \le \sum _{j=1}^n |b_{ij}|\int _{\mathcal {O}}|z_i(t;x)||f_j(z_j(t;x))|dx\nonumber \\&\quad \le \sum _{j=1}^n l_j |b_{ij}|\left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad \left( \int _{\mathcal {O}}|z_j(t;x)|^2dx\right) ^{\frac{1}{2}}, \end{aligned}$$

(41)

$$\begin{aligned}&\varTheta _4(z(t))\nonumber \\&\quad \le \sum _{j=1}^n |c_{ij}|\int _{\mathcal {O}}|z_i(t;x)||f_j(z_j(t-\tau ;x))|dx\nonumber \\&\quad \le \sum _{j=1}^n l_j |c_{ij}|\left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad \left( \int _{\mathcal {O}}|z_j(t-\tau ;x)|^2dx\right) ^{\frac{1}{2}}, \end{aligned}$$

(42)

$$\begin{aligned}&\varTheta _5(z(t)) \nonumber \\&\quad \le \sum _{j=1}^n |e_{ij}|\int _{\mathcal {O}}|z_i(t;x)|\nonumber \\&\quad \int _{-\infty }^t k_{ij}(t-s)|f_j(z_j(s;x))|dsdx\nonumber \\&\quad = \sum _{j=1}^n |e_{ij}|\int _{-\infty }^t k_{ij}(t-s)\nonumber \\&\qquad \int _{\mathcal {O}}|z_i(t;x)||f_j(z_j(s;x))|dx ds\nonumber \\&\quad \le \sum _{j=1}^n l_j|e_{ij}| \left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad \times \int _{-\infty }^t k_{ij}(t-s)\left( \int _{\mathcal {O}}|z_j(s;x)|^2dx\right) ^{\frac{1}{2}}ds, \end{aligned}$$

(43)

$$\begin{aligned}&\varTheta _6(z(t)) \nonumber \\&\quad \le \left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\left( \int _{\mathcal {O}}|u_i(t;x)|^2dx\right) ^{\frac{1}{2}}. \end{aligned}$$

(44)

From (39)–(44), we see that

$$\begin{aligned}&D^+V_i^2(t,z_i(t))\nonumber \\&\quad \le 2p_i^{-2}\left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad \times \bigg \{\left( -\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma ^2}-a_i\right) \left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\sum _{j=1}^n l_j|b_{ij}|\left( \int _{\mathcal {O}}|z_j(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\sum _{j=1}^n l_j|c_{ij}|\left( \int _{\mathcal {O}}|z_j(t-\tau ;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\sum _{j=1}^n l_j|e_{ij}|\int _{-\infty }^t k_{ij}(t-s)\nonumber \\&\qquad \left( \int _{\mathcal {O}}|z_j(s;x)|^2dx\right) ^{\frac{1}{2}}ds\nonumber \\&\qquad +\left( \int _{\mathcal {O}}|u_i(t;x)|^2dx\right) ^{\frac{1}{2}}\bigg \}, \end{aligned}$$

(45)

which indicates that

$$\begin{aligned}&D^+V_i (t,z_i(t))\nonumber \\&\quad \le p_i^{-1}\bigg \{\left( -\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma }-a_i\right) \left( \int _{\mathcal {O}}|z_i(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\sum _{j=1}^n l_j|b_{ij}|\left( \int _{\mathcal {O}}|z_j(t;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\sum _{j=1}^n l_j|c_{ij}|\left( \int _{\mathcal {O}}|z_j(t-\tau ;x)|^2dx\right) ^{\frac{1}{2}}\nonumber \\&\qquad +\sum _{j=1}^n l_j|e_{ij}|\int _{-\infty }^t k_{ij}(t-s)\nonumber \\&\qquad \left( \int _{\mathcal {O}}|z_j(s;x)|^2dx\right) ^{\frac{1}{2}}ds\nonumber \\&\qquad +\left( \int _{\mathcal {O}}|u_i(t;x)|^2dx\right) ^{\frac{1}{2}}\bigg \}\nonumber \\&\quad \le p_i^{-1}\bigg \{\left( -\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma }-a_i\right) p_i V_i(t,z_i(t))\nonumber \\&\qquad +\sum _{j=1}^n l_j|b_{ij}|p_j V_j(t,z_j(t))\nonumber \\&\qquad +\sum _{j=1}^n l_j|c_{ij}|p_j V_j(t-\tau ,z_j(t-\tau ))\nonumber \\&\qquad +\sum _{j=1}^n l_j|e_{ij}|p_j \int _{-\infty }^t k_{ij}(t-s) V_j(s,z_j(s))ds\bigg \}\nonumber \\&\qquad +\Vert u_i(t)\Vert , \end{aligned}$$

(46)

Hence,

$$\begin{aligned}&D^+V(t,z(t))\nonumber \\&\quad \preccurlyeq P^{-1}(-\varLambda -A+|B|L)P V(t,z(t))\nonumber \\&\qquad +P^{-1}|C|LP V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +P^{-1}\int _{-\infty }^t |E|LP\circ K(t-s)V(s,z(s))ds\nonumber \\&\qquad +U(t), \end{aligned}$$

(47)

where $U(t)=(\Vert u_1(t)\Vert ,\Vert u_2(t)\Vert ,\ldots ,\Vert u_n(t)\Vert )^T$. When $t=t_k$, $k\in \mathbb {N}$, it follows from (H2) that $V(t_k,z(t_k))\preccurlyeq \sigma V(t_k^-,z(t_k^-))$. Thus,

$$\begin{aligned} \left\{ \begin{array}{l} D^+V(t,z(t))\preccurlyeq (-\mathfrak {P}+\mathfrak {Q})V(t,z(t))\\ \quad +\mathfrak {R} V(t-\tau ,z(t-\tau ))+\int _{-\infty }^t \mathfrak {K}(t-s)V(s,z(s))ds\\ \quad +U(t),\ t\in [t_{k-1},t_k),\\ V(t_k,z(t_k))\preccurlyeq \sigma V(t_k^-,z(t_k^-)), k\in \mathbb {N},\\ V_{t_0}\preccurlyeq \delta _0 \varvec{1}, \end{array} \right. \end{aligned}$$

(48)

where $\delta _0=\max _{i}\{p_i^{-1}\Vert \phi _i\Vert _{\mathcal {PC}^b}\}$.When $t\in [t_0,t_1)$, the unique mild solution of (4), which is continuous on $[t_0,t_1)$, exists from Proposition 2. If we define $W^1(t)=e^{\lambda ^0 t}V(t,z(t))-\int _{t_0}^t e^{\lambda ^0 s}U(s)ds$ for $t_0\le t<t_1$ and $W^1(t)$ $=V(t,z(t))$ for $t\le t_0$, it yields, for $t\in [t_0+\tau ,+\infty )\cap [t_0,t_1)$, that

$$\begin{aligned}&D^+W^1(t)\nonumber \\&\quad = \lambda ^0 e^{\lambda ^0t}V(t,z(t))+e^{\lambda ^0t}D^+V(t,z(t))-e^{\lambda ^0t}U(t)\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0t}V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +e^{\lambda ^0t}\int _{-\infty }^t \mathfrak {K}(t-s)V(s,z(s))ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }e^{\lambda ^0(t-\tau )}V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_0}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\quad = (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})\left[ W^1(t)+\int _{t_0}^t e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }\left[ W^1(t-\tau )+\int _{t_0}^{t-\tau } e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds\nonumber \\&\qquad +\int _{t_0}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}\left[ W^1(s)\right. \nonumber \\&\qquad \left. +\int _{t_0}^s e^{\lambda ^0 r}U(r)dr\right] ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^1(t)+\mathfrak {R}e^{\lambda ^0\tau }W^1(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds\nonumber \\&\qquad +\left[ \lambda ^0I-\mathfrak {P}+\mathfrak {Q}+\mathfrak {R}e^{\lambda ^0\tau }\right. \nonumber \\&\qquad \left. +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}ds\right] \nonumber \\&\qquad \times \int _{t_0}^t e^{\lambda ^0 s}U(s)ds, \end{aligned}$$

(49)

From (38), we get

$$\begin{aligned}&\bigg [\lambda ^0I-\mathfrak {P}+\mathfrak {Q}+\mathfrak {R}e^{\lambda ^0\tau }\nonumber \\&\quad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}ds\bigg ]\varvec{1}\prec 0, \end{aligned}$$

(50)

which further implies that

$$\begin{aligned} D^+W^1(t)&\preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^1(t)\nonumber \\&\quad +\mathfrak {R}e^{\lambda ^0\tau }W^1(t-\tau )\nonumber \\&\quad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds. \end{aligned}$$

(51)

Likewise, for $t\in (-\infty ,t_0+\tau )\cap [t_0,t_1)$,

$$\begin{aligned}&D^+W^1(t)\nonumber \\&\quad = \lambda ^0 e^{\lambda ^0t}V(t,z(t))+e^{\lambda ^0t}D^+V(t,z(t))-e^{\lambda ^0t}U(t)\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0t}V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +e^{\lambda ^0t}\int _{-\infty }^t \mathfrak {K}(t-s)V(s,z(s))ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_0}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\quad = (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})\left[ W^1(t)+\int _{t_0}^t e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }W^1(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds\nonumber \\&\qquad +\int _{t_0}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}\left[ W^1(s)\right. \nonumber \\&\qquad \left. +\int _{t_0}^s e^{\lambda ^0 r}U(r)dr\right] ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^1(t)+\mathfrak {R}e^{\lambda ^0\tau }W^1(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds\nonumber \\&\qquad +\left[ \lambda ^0I-\mathfrak {P}+\mathfrak {Q}+\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}ds\right] \nonumber \\&\qquad \times \int _{t_0}^t e^{\lambda ^0 s}U(s)ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^1(t)+\mathfrak {R}e^{\lambda ^0\tau }W^1(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds. \end{aligned}$$

(52)

Therefore, $W^1(t)$ satisfies the following inequality

$$\begin{aligned} \left\{ \begin{array}{l} D^+W^1(t)\preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^1(t)+\mathfrak {R}e^{\lambda ^0\tau }W^1(t-\tau )\\ \quad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^1(s)ds, t\in [t_0,t_1),\\ W^1_{t_0}\preccurlyeq \delta _0 \varvec{1}. \end{array} \right. \end{aligned}$$

(53)

Based on Lemma 3, we derive the following comparison system

$$\begin{aligned} \left\{ \begin{array}{l} D^+H^1(t)=(\lambda ^0I-\mathfrak {P}+\mathfrak {Q})H^1(t)+\mathfrak {R}e^{\lambda ^0\tau }H^1(t-\tau )\\ \quad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}H^1(s)ds, t\in [t_0,t_1),\\ H^1_{t_0} = (\delta _0+\varepsilon ) \varvec{1}, \end{array} \right. \end{aligned}$$

(54)

where $\varepsilon >0$. From Lemmas 3, 4, and (38), one has that $W^1(t)\preccurlyeq H^1(t)\preccurlyeq (\delta _0+\varepsilon )\varvec{1}$ for $t\in [t_0,t_1)$ and $W^1(t_1^-)\preccurlyeq H^1(t_1^-)\preccurlyeq \frac{\delta _0+\varepsilon }{\sigma }\varvec{1}$. Considering the arbitrariness of $\varepsilon$, we obtain that $W^1(t)\preccurlyeq \delta _0\varvec{1}$ for $t\in [t_0,t_1)$ and $W^1(t_1^-)\preccurlyeq \frac{\delta _0}{\sigma }\varvec{1}$ as $\varepsilon \rightarrow 0$. Therefore,

$$\begin{aligned} V(t,z(t))&\preccurlyeq \delta _0 e^{-\lambda ^0t}\varvec{1}\nonumber \\&\quad +\int _{t_0}^t e^{-\lambda ^0(t-s)}U(s)ds,\quad t\in [t_0,t_1),\nonumber \\ V(t_1^-,z(t_1^-))&\preccurlyeq \frac{\delta _0}{\sigma }e^{-\lambda ^0t_1}\varvec{1}+\int _{t_0}^{t_1} e^{-\lambda ^0(t_1-s)}U(s)ds. \end{aligned}$$

(55)

When $t=t_k$, we have

$$\begin{aligned} V(t_1,z(t_1))\preccurlyeq \delta _0e^{-\lambda ^0t_1}\varvec{1}+\sigma \int _{t_0}^{t_1} e^{-\lambda ^0(t_1-s)}U(s)ds. \end{aligned}$$

(56)

Combining the definition of the mild solution, we have that the mild solution of (4) exists on $[t_0,t_1]$ and satisfies that

$$\begin{aligned} \begin{aligned}&V(t,z(t)) \\&\quad \preccurlyeq \delta _0e^{-\lambda ^0t}\varvec{1}+\sigma \int _{t_0}^{t} e^{-\lambda ^0(t-s)}U(s)ds\\&\quad \preccurlyeq \bigg [\delta _0e^{-\lambda ^0t}+\sigma \int _{t_0}^{t} e^{-\lambda ^0(t-s)}\Vert u(s)\Vert ds\bigg ]\varvec{1}, \end{aligned} \end{aligned}$$

(57)

for $t\in [t_0,t_1]$. Suppose that the mild solution of (4) exists and satisfies (57) on $[t_0,t_m]$, then we will show that the mild solution of (4) exists and satisfies (57) on $[t_0,t_{m+1}]$. From (57), we see that, for $t\in [t_0,t_m]$,

$$\begin{aligned} \begin{aligned} \Vert z_i(t)\Vert&\le p^*\delta _0 e^{-\lambda ^0t}+p^*\sigma \int _{t_0}^t e^{-\lambda ^0(t-s)}\Vert u(s)\Vert ds\\&\le p^*\delta _0 e^{-\lambda ^0t}+\frac{p^*\sigma }{\lambda ^0}\sup _{t\ge t_0}\Vert u(t)\Vert <\infty , \end{aligned} \end{aligned}$$

(58)

where $p^*=\max _i\{p_i\}$, which leads to that

$$\begin{aligned} \Vert z(t)\Vert =\left( \sum _{i=1}^n\Vert z_i(t)\Vert ^2\right) ^{\frac{1}{2}}<\infty ,\ t\in [t_0,t_m]. \end{aligned}$$

(59)

Combining the initial condition $z_{t_0}=\phi \in \mathcal {PC}^b$, we obtain that $z_{t_m}\in \mathcal {PC}^b_{t_m}$. From Definition 1, it follows that the mild solution of (4) on $[t_m,t_{m+1})$ is defined by

$$\begin{aligned} z(t)&= S(t-t_0)\phi (0)\nonumber \\&\quad +\int _{t_0}^t S(t-s)F(s,z(s),u(s))ds\nonumber \\&\quad +\sum _{k=1}^m S(t-t_k)I_k(z(t_k^-))\nonumber \\&= S(t-t_m)\bigg \{S(t_m-t_0)\phi (0)\nonumber \\&\quad +\int _{t_0}^{t_m} S(t_m-s)F(s,z(s),u(s))ds\nonumber \\&\quad +\sum _{k=1}^m S(t_m-t_k)I_k(z(t_k^-))\bigg \}\nonumber \\&\quad +\int _{t_m}^{t} S(t-s)F(s,z(s),u(s))ds\nonumber \\&= S(t-t_m)z_{t_m}(0)\nonumber \\&\quad +\int _{t_m}^{t} S(t-s)F(s,z(s),u(s))ds. \end{aligned}$$

(60)

One can find that the mild solution of (4) on $[t_m,t_{m+1})$ is exactly the mild solution of the auxiliary equation as follows

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz(t)}{dt}=\mathscr {D}z(t)+F(t,z(t),u(s)),\ t\in [t_m,t_{m+1}),\\ z_{t_m}\in \mathcal {PC}^b_{t_m}. \end{array} \right. \end{aligned}$$

(61)

From Proposition 1, the overhead auxiliary Eq. (61) has a unique continuous mild solution on $[t_m,t_{m+1})$; that is, the unique mild solution of (4) exists and is continuous on $[t_m,t_{m+1})$. Define

$$\begin{aligned} \begin{aligned}&W^{m+1}(t)=\\&\left\{ \begin{array}{lcl} V(t,z(t)), &{} \text {for} &{} t\le t_0;\\ e^{\lambda ^0t}V(t,z(t)), &{} \text {for} &{} t_0\le t\le t_m;\\ e^{\lambda ^0t}V(t,z(t))-\int _{t_m}^t e^{\lambda ^0s}U(s)ds, &{} \text {for} &{} t_m\le t< t_{m+1}.\\ \end{array} \right. \end{aligned} \end{aligned}$$

(62)

For $t\in [t_m+\tau ,+\infty )\cap [t_m,t_{m+1})$, we have

$$\begin{aligned}&D^+W^{m+1}(t)\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }e^{\lambda ^0(t-\tau )}V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_0}^{t_m} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_m}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\quad = (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})\left[ W^{m+1}(t)+\int _{t_m}^t e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }\left[ W^{m+1}(t-\tau )+\int _{t_m}^{t-\tau } e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds\nonumber \\&\qquad +\int _{t_0}^{t_m} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds\nonumber \\&\qquad +\int _{t_m}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}[W^{m+1}(s)\nonumber \\&\qquad +\int _{t_m}^s e^{\lambda ^0 r}U(r)dr]ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^{m+1}(t)+\mathfrak {R}e^{\lambda ^0\tau }W^{m+1}(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds. \end{aligned}$$

(63)

For $t\in [t_0+\tau ,t_m+\tau )\cap [t_m,t_{m+1})$, we have

$$\begin{aligned}&D^+W^{m+1}(t)\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }e^{\lambda ^0(t-\tau )}V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_0}^{t_m} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_m}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\quad = (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})\left[ W^{m+1}(t)+\int _{t_m}^t e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }W^{m+1}(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds\nonumber \\&\qquad +\int _{t_0}^{t_m} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds\nonumber \\&\qquad +\int _{t_m}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}\left[ W^{m+1}(s)\right. \nonumber \\&\qquad \left. +\int _{t_m}^s e^{\lambda ^0 r}U(r)dr\right] ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^{m+1}(t)+\mathfrak {R}e^{\lambda ^0\tau }W^{m+1}(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds. \end{aligned}$$

(64)

For $t\in (-\infty ,t_0+\tau )\cap [t_m,t_{m+1})$, we have

$$\begin{aligned}&D^+W^{m+1}(t)\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})e^{\lambda ^0t}V(t,z(t))\nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }V(t-\tau ,z(t-\tau ))\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_0}^{t_m} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\qquad +\int _{t_m}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}e^{\lambda ^0s}V(s,z(s))ds\nonumber \\&\quad = (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})\left[ W^{m+1}(t)+\int _{t_m}^t e^{\lambda ^0 s}U(s)ds\right] \nonumber \\&\qquad +\mathfrak {R}e^{\lambda ^0\tau }W^{m+1}(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^{t_0} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds\nonumber \\&\qquad +\int _{t_0}^{t_m} \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds\nonumber \\&\qquad +\int _{t_m}^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}\left[ W^{m+1}(s)\right. \nonumber \\&\qquad \left. +\int _{t_m}^s e^{\lambda ^0 r}U(r)dr\right] ds\nonumber \\&\quad \preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^{m+1}(t)+\mathfrak {R}e^{\lambda ^0\tau }W^{m+1}(t-\tau )\nonumber \\&\qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds. \end{aligned}$$

(65)

Hence, $W^{m+1}(t)$ satisfies the following inequality

$$\begin{aligned} \left\{ \begin{array}{l} D^+W^{m+1}(t)\preccurlyeq (\lambda ^0I-\mathfrak {P}+\mathfrak {Q})W^{m+1}(t)\\ \qquad \qquad \qquad \qquad +\mathfrak {R}e^{\lambda ^0\tau }W^{m+1}(t-\tau )\\ \qquad \qquad \qquad \qquad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}W^{m+1}(s)ds,\\ \qquad \qquad \qquad \qquad t\in [t_m,t_{m+1}),\\ W^{m+1}_{t_m}\preccurlyeq \delta _m \varvec{1}, \end{array} \right. \nonumber \\ \end{aligned}$$

(66)

where $\delta _m=\delta _0+\sigma \int _{t_0}^{t_m}e^{\lambda ^0s}\Vert u(s)\Vert ds$. Similarly, we derive the following comparison system

$$\begin{aligned} \left\{ \begin{array}{l} D^+H^{m+1}(t)=(\lambda ^0I-\mathfrak {P}+\mathfrak {Q})H^{m+1}(t)\\ \quad +\mathfrak {R}e^{\lambda ^0\tau }H^{m+1}(t-\tau )\\ \quad +\int _{-\infty }^t \mathfrak {K}(t-s)e^{\lambda ^0(t-s)}H^{m+1}(s)ds,\\ t\in [t_m,t_{m+1}),\\ H^{m+1}_{t_m} = (\delta _m+\varepsilon ) \varvec{1}, \end{array} \right. \end{aligned}$$

(67)

where $\varepsilon >0$. Then, it follows from Lemmas 3, 4, and (38) that $W^{m+1}(t)\preccurlyeq H^{m+1}(t)\preccurlyeq (\delta _m+\varepsilon )\varvec{1}$ for $t\in [t_m,t_{m+1})$ and $W^{m+1}(t_{m+1}^-)\preccurlyeq H^{m+1}(t_{m+1}^-)\preccurlyeq \frac{\delta _m+\varepsilon }{\sigma }\varvec{1}$. As $\varepsilon \rightarrow 0$, we see that (57) holds on $[t_m,t_{m+1})$ and

$$\begin{aligned}&V(t_{m+1}^-,z(t_{m+1}^-))\nonumber \\&\quad \le \bigg [\frac{\delta _0}{\sigma } e^{-\lambda ^0 t_{m+1}}+\int _{t_0}^{t_{m+1}} e^{-\lambda ^0(t_{m+1}-s)}\Vert u(s)\Vert ds\bigg ]\varvec{1}. \end{aligned}$$

(68)

Combining Definition 1 and $V(t_{m+1},z(t_{m+1}))\preccurlyeq \sigma V(t_{m+1}^-,z(t_{m+1}^-))$, we have that the mild solution of (4) exists and satisfies (57) on $[t_0,t_{m+1}]$. By the mathematical induction, the IRDNNs with infinite distributed delays (4) have a unique global mild solution, which satisfies (57) for $t\ge t_0$.

Then, we will show that the mild solution of (4) is ISS, iISS and $e^{\lambda t}$-ISS. From (57), a simple computation yields

$$\begin{aligned}&\Vert z_i(t)\Vert ^2\nonumber \\&\quad \le \left( p^*\delta _0 e^{-\lambda ^0t}+p^*\sigma \int _{t_0}^t e^{-\lambda ^0(t-s)}\Vert u(s)\Vert ds\right) ^2\nonumber \\&\quad \le 2(p^*\delta _0)^2 e^{-2\lambda ^0t}\nonumber \\&\qquad +2(p^*\sigma )^2\left( \int _{t_0}^t e^{-\lambda ^0(t-s)}\Vert u(s)\Vert ds\right) ^2. \end{aligned}$$

(69)

Hence,

$$\begin{aligned} \Vert z_i(t)\Vert ^2&\le 2(p^*\delta _0)^2 e^{-2\lambda ^0t}\nonumber \\&\quad \;\, +2(p^*\sigma )^2\left( \int _{t_0}^t e^{-\lambda ^0(t-s)}\sup _{0\le r\le t}\Vert u(r)\Vert ds\right) ^2\nonumber \\&\le 2(p^*)^2\Vert \phi \Vert _{\mathcal {PC}^b}^2 e^{-2\lambda ^0t}\nonumber \\&\quad +\frac{2(p^*\sigma )^2}{(\lambda ^0)^2}\sup _{0\le s\le t}\Vert u(s)\Vert ^2, \end{aligned}$$

(70)

which further implies that the mild solution is ISS with $\alpha (s)=s^2$, $\beta (s,t)=2n(p^*)^2se^{-2\lambda ^0t}$, and $\gamma (s)=\frac{2n(p^*\sigma )^2s^2}{(\lambda ^0)^2}$. Applying the Cauchy–Bunyakovsky–Schwarz inequality to (69) yields

$$\begin{aligned} \Vert z_i(t)\Vert ^2&\le 2(p^*\delta _0)^2 e^{-2\lambda ^0t}\nonumber \\&\quad \;\, +2(p^*\sigma )^2\int _{t_0}^t e^{-2\lambda ^0(t-s)}ds\int _{t_0}^t\Vert u(s)\Vert ^2ds\nonumber \\&\le 2(p^*)^2\Vert \phi \Vert _{\mathcal {PC}^b}^2 e^{-2\lambda ^0t}\nonumber \\&\quad +\frac{(p^*\sigma )^2}{\lambda ^0}\int _{t_0}^t\Vert u(s)\Vert ^2ds, \end{aligned}$$

(71)

which further implies that the mild solution is iISS with $\alpha (s)=s^2$, $\beta (s,t)=2n(p^*)^2se^{-2\lambda ^0t}$, and $\gamma (s)=\frac{n(p^*\sigma )^2}{\lambda ^0}s^2$. Let $\lambda ^0=\lambda ^1+\lambda ^2$, $\lambda _2=(\lambda +\lambda ^*)/2$, and $\lambda ^1,\lambda ^2,\lambda ,\lambda ^*>0$, we can derive that

$$\begin{aligned} \Vert z_i(t)\Vert ^2&\le 2(p^*\delta _0)^2 e^{-2\lambda ^2t}+2(p^*\sigma )^2\nonumber \\&\quad \times \int _{t_0}^t e^{-2\lambda ^1(t-s)}ds\nonumber \\&\quad \int _{t_0}^t e^{-2\lambda ^2(t-s)}\Vert u(s)\Vert ^2ds\nonumber \\&\le 2(p^*\delta _0)^2 e^{-(\lambda +\lambda ^*)t}\nonumber \\&\quad +\frac{(p^*\sigma )^2}{\lambda ^1}\int _{t_0}^t e^{-(\lambda +\lambda ^*)(t-s)}\Vert u(s)\Vert ^2ds, \end{aligned}$$

(72)

which further implies that

$$\begin{aligned} \begin{aligned}&e^{\lambda t}\Vert z_i(t)\Vert ^2 \\&\quad \le 2(p^*\delta _0)^2+\frac{(p^*\sigma )^2}{\lambda ^1}\int _{t_0}^t e^{-\lambda ^*(t-s)}e^{\lambda s}\Vert u(s)\Vert ^2ds\\&\quad \le 2(p^*)^2\Vert \phi \Vert _{\mathcal {PC}^b}^2+\frac{(p^*\sigma )^2}{\lambda ^1\lambda ^*}\sup _{0\le s\le t}\{e^{\lambda s}\Vert u(s)\Vert ^2\}. \end{aligned} \end{aligned}$$

(73)

Hence, the mild solution is $e^{\lambda t}$-ISS with $\alpha _1(s)=s^2$, $\alpha _2(s)=2n(p^*)^2s^2$, and $\gamma (s)=\frac{n(p^*\sigma )^2}{\lambda ^1\lambda ^*}s^2$. The proof is completed. $\square$

Remark 3

Note that many researchers have studied the asymptotic behavior of IRDNNs, such as stability and synchronization [5, 19, 36], based on the assumption of the existence–uniqueness of the solution. From the deduction process of Theorem 1, we see that the global existence–uniqueness of the mild solution is established by the local existence–uniqueness on every impulsive time interval and the moment estimate for the ISS properties on the entire time interval. Therefore, the global existence–uniqueness of the mild solution provides fundamental support for asymptotic analysis of IRDNNs.

Corollary 1

Assume that (H1)-(H3) hold. Then, the IRDNNs with infinite distributed delays (4) have a unique global mild solution and are ISS, iISS, and $e^{\lambda t}$-ISS over the class $\mathscr {F}(\eta )$, if one of the following conditions holds:

• (H4) there exit positive constants $p_i$ such that, for $\forall i\in \bar{n}$,

  $$\begin{aligned}&\left( -\sum _{\varsigma =1}^q \frac{d_{i\varsigma }}{\rho _\varsigma ^2}-a_i+\frac{\ln \sigma }{\eta }+l_i|b_{ii}|\right) p_i\nonumber \\&\quad +\sigma \left( \sum _{j\ne i}l_jp_j|b_{ij}|+\sum _{j=1}^nl_jp_j|c_{ij}|\right. \nonumber \\&\quad \left. +\sum _{j=1}^nl_jp_j|e_{ij}|\right) <0. \end{aligned}$$

• (H5) for $\forall i\in \bar{n}$, $\chi _i=\sum _{\varsigma =1}^q\frac{d_{i\varsigma }}{\rho _\varsigma ^2}+a_i-l_i|b_{ii}|-\frac{\ln \sigma }{\eta }>0$ and

  $$\begin{aligned} \max _{i\in \bar{n}}\frac{\sigma l_i}{\chi _i}\left[ \sum _{j\ne i}|b_{ji}|+\sum _{j=1}^n (|c_{ji}|+|e_{ji}|)\right] <1; \end{aligned}$$

• (H6) for $\forall i\in \bar{n}$, $\chi _i>0$ and

  $$\begin{aligned} \begin{aligned} \frac{\sigma }{2\chi _i}&\bigg [\sum _{j\ne i}(l_j|b_{ij}|+l_i|b_{ji}|) +\sum _{j=1}^n l_j(|c_{ij}|+|e_{ij}|)\\&\quad +\sum _{j=1}^n l_i(|c_{ji}|+|e_{ji}|)\bigg ]<1; \end{aligned} \end{aligned}$$

• (H7) $\varGamma =\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I$, $\varGamma =(\gamma _{ij})_{n\times n}$, $\gamma _{ii}>0$, $\gamma _{ij}\le 0$, $i\ne j$, $\varPi {:}{=}(\varpi _{ij})_{n\times n}$, $\rho (\varPi )<1$, where $\rho (\varPi )$ denotes the spectral radius of $\varPi$, and

  $$\begin{aligned} \varpi _{ij}=\left\{ \begin{array}{ll} 0, &{} i=j,\\ \gamma _{ij}/\gamma _{ii}, &{} i\ne j. \end{array}\right. \end{aligned}$$

Proof

Each of (H4)–(H7) implies that $\varGamma =\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I$ is an M-matrix [32]. $\square$

Remark 4

Note that the ISS conditions of Theorem 1 and Corollary 1 are diffusion–dependent, and the bigger the transmission diffusion coefficient is, the more easily the IRDNNs fall into ISS pattern. This implies that the reaction–diffusion along with the Dirichlet boundary condition benefits the ISS of IRDNNs, which will be also verified by Example 1 and Remark 9.

Remark 5

In most of the existing works on impulsive delayed systems [8, 38] and IRDNNs [5, 22, 33, 41], the scalar Lyapunov function is usually employed to achieve the ISS or stability properties, during which the cross-terms of the present states, the past states, and the external input are inevitably amplified. Here, the cross-terms are handled by vector Lyapunov function and M-matrix method, so the amplification is avoided to reduce conservatism. Compared with the ISS analysis of delayed neural networks via vector Lyapunov function [13], the infinite distributed delays are additionally considered in the neural-network model and effectively handled by a novel vector inequality.

Remark 6

Compared with the existing works on the ISS of neural networks without impulses [13, 40, 44], the established results indicate that the ISS properties can be retained even though certain impulsive perturbation exists in the neural networks, which is also illustrated in Example 2 and Remark 10. Compared with the ISS analysis of IRDNNs [41], the impulses are not restricted to satisfy $\sum _{k=1}^\infty \ln \sigma _k<\infty$ where $\sigma _k$ are the impulsive coefficients. Therefore, the obtained results are more general and efficient.

Remark 7

Note that most of the existing works on ISS analysis of the impulsive nonlinear systems [8, 38, 43] are usually discussed under the condition of average impulsive interval (AII) or average dwell time (ADT). Correspondingly, the established results verify that ISS properties of the IRDNNs can be retained for the destabilizing impulses if there are no too short intervals between the impulses instead of AII or ADT condition, which shows the difference of the results.

When $\hat{u}(t,x)=0$, the IRDNNs with infinite distributed delays (2) become the following system

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \hat{z}(t,x)}{\partial t} = \nabla \cdot (D\circ \nabla \hat{z}(t,x))-A \hat{z}(t,x) \\ \quad +B\hat{f}(\hat{z}(t,x))+C\hat{f}(\hat{z}(t-\tau ,x))\\ \quad +\int _{-\infty }^t E\circ K(t-s)\hat{f}(\hat{z}(s,x))ds,\ t\in [t_{k-1},t_k),\\ \hat{z} (t_k,x) = \hat{z}(t_k^-,x) + \hat{I}_k(\hat{z}(t_k^-,x)),\ k\in \mathbb {N}, \end{array} \right. \end{aligned}$$

(74)

with Dirichlet boundary condition and initial condition (3). The corresponding abstract equation of the neural networks (74) is defined by

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dz(t)}{dt} = \mathscr {D}z(t)-A z(t)+Bf(z(t))+Cf(z(t-\tau ))\\ \quad +\int _{-\infty }^t E\circ K(t-s)f(z(s))ds,\ t\in [t_{k-1},t_k),\\ z(t_k) = z(t_k^-) + I_k(z(t_k^-)),\ k\in \mathbb {N},\\ z_0=\phi \in \mathcal {PC}^b. \end{array} \right. \end{aligned}$$

(75)

Fig. 1

The trajectory evolution of $z(t,1,x_2)$ and $z(t,x_1,1)$ of impulsive reaction–diffusion system (76) in Example 1

Then, the ISS properties degenerate to the following exponential stability of IRDNNs with infinite distributed delays.

Corollary 2

Assume that (H1)–(H3) hold. Then, the IRDNNs with infinite distributed delays (75) have a unique global mild solution and are exponentially stable over the class $\mathscr {F}(\eta )$, if $\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I$ is a nonsingular M-matrix, where $\varLambda =\text {diag}(\sum _{\varsigma =1}^q \frac{d_{1\varsigma }}{\rho _\varsigma ^2},\sum _{\varsigma =1}^q \frac{d_{2\varsigma }}{\rho _\varsigma ^2},\ldots ,\sum _{\varsigma =1}^q \frac{d_{n\varsigma }}{\rho _\varsigma ^2})$, $L=\text {diag}(l_1,l_2,$ $\cdots ,l_n)$, and $\sigma =\max _{i,k}\{r_{ik},1\}$.

Remark 8

Compared with the stability analysis of reaction–diffusion neural networks [15, 23, 32, 35], the impulsive perturbation is considered here. From Corollary 2, we can see that the stability can be retained under certain set of the impulses, which is also illustrated in Example 3 of the next section.

Fig. 2

The surface simulation of impulsive reaction–diffusion system (76) at different times ($t=0.0$, 1.0, 2.0, 2.5, 3.0, 5.0, 6.1, 6.4, 8.0, 9.0, 11.0, 13.0) in Example 1. Zoom in for details of the surface and scalar

4 Numerical examples

This section provides three numerical examples to illustrate the effectiveness and advantage of the theoretical results.

Example 1

Consider the following scalar impulsive reaction–diffusion system with infinite distributed delay on square domain

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial z(t,x_1,x_2)}{\partial t} = d \left( \frac{\partial ^2}{\partial x_1^2}+\frac{\partial ^2}{\partial x_2^2}\right) z(t,x_1,x_2)-a z(t,x_1,x_2)\\ \quad +bf(z(t,x_1,x_2))+cf(z(t-\tau ,x_1,x_2))\\ \quad +e\int _{-\infty }^tk(t-s)f(z(s,x_1,x_2))\\ \quad +u(t,x_1,x_2),\ t\ge 0,\ t\in [t_{k-1},t_k),\\ z(t_k,x_1,x_2) = r z(t_k^-,x_1,x_2),\ k\in \mathbb {N}, \end{array} \right. \end{aligned}$$

(76)

with Dirichlet boundary condition and initial condition $z(t,x_1,x_2)=\cos (\pi x_1/4)\cos (\pi x_2/4)$ for $-5\le t\le 0$ and $z(t,x_1,x_2)=0$ for $t<-5$ where $(x_1,x_2)\in \mathcal {O}$, $\bar{q}=\{1,2\}$, $\rho _1=\rho _2=2$, $d=11/5$, $a=0$, $b=c=1/5$, $e=1/6$, $k(s)=e^{s}$, $f(s)=\tanh (s)$, and $u(t,x_1,x_2)=\sin (t\pi /2)\sin (x_1\pi /2)\cos (x_2\pi /4)$. The impulsive sequence is given by $r=\sqrt{2}$, $t_k=k$, $\eta =1$, $k\in \mathbb {N}$. A simple computation yields

$$\begin{aligned} d\left( \frac{1}{\rho _1^2}+\frac{1}{\rho _2^2}\right) +a-b-r(c+e)-\frac{\ln r}{\eta }>0, \end{aligned}$$

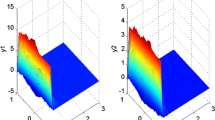
where $|f(s_1)-f(s_2)|\le |s_1-s_2|$. According to Corollary 1, the impulsive reaction–diffusion system with infinite distributed delay (76) has a unique global mild solution and is ISS, iISS, and $e^{\lambda t}$-ISS. Figure 1 presents the trajectory evolution of $z(t,1,x_2)$ and $z(t,x_1,1)$ with time, which shows that the states of the impulsive reaction–diffusion system are bounded with the bounded spatiotemporal external input $u(t,x_1,x_2)$. Figure 2 enumerates the surface simulation of the system on the whole square domain at several moments where we can also observe the boundedness of the surface even though the shape of the surface changes significantly with time. Additionally, see ‘video1.avi,’ ‘video2.avi,’ and ‘video3.avi’ in the supplementary materials for full surface evolution with time. From these figures and videos, we see that the state trajectory of the impulsive reaction–diffusion system (76) falls into ISS pattern.

Remark 9

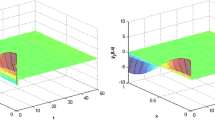
To determine that the reaction–diffusion benefits the ISS of the impulsive reaction–diffusion system, the case of (76) without reaction–diffusion ($d=0$) is considered. From Corollary 1 or the existing results about ISS of impulsive system [8], the ISS conditions are failed so that the ISS properties cannot be ascertained. Figure 3 illustrates the trajectory evolution of impulsive system (76) without reaction–diffusion in terms of $\ln (|z(t,1,x_2)|)$ except the boundary (see ‘video4.avi’ in the supplementary materials for full surface evolution with time). We can see that the trajectory of the impulsive system without reaction–diffusion continues increasing with time under the bounded spatiotemporal external input, which implies the vanishing of the ISS properties. The comparison of Figs. 1 and 3 verifies that the reaction–diffusion along with Dirichlet boundary condition can be regarded as the source to force the impulsive reaction–diffusion system to fall into ISS pattern, which shows the efficiency of the theoretical criteria.

Example 2

Consider the IRDNNs with infinite distributed delays which consist of two neurons on $\mathcal {O}=\{x|-2\le x\le 2\}$, where the parameters are given by

$$\begin{aligned} D= & {} \left( \begin{array}{cc} 0.4 &{}\quad 0\\ 0 &{}\quad 0.5 \end{array} \right) ,\ A=\left( \begin{array}{cc} 1 &{}\quad 0\\ 0 &{}\quad 1.9 \end{array} \right) ,\\&\ B=\left( \begin{array}{cc} -\,0.6 &{}\quad 0.8\\ 0.4 &{}\quad -\,0.4 \end{array} \right) ,\\ C= & {} \left( \begin{array}{cc} 0.1 &{}\quad 0.4\\ 0.4 &{}\quad -\,0.6 \end{array} \right) ,\ E=\left( \begin{array}{cc} 0.4 &{}\quad 0.3\\ 0.5 &{}\quad 0.4 \end{array} \right) , \end{aligned}$$

and $\tau =2$, $k(s)=e^s$, $f(s)=0.2\tanh (s)$. The initial condition is given by

$$\begin{aligned} z_1(t,x)= & {} \left\{ \begin{array}{ll} \frac{1}{10}\cos (\frac{x\pi }{4}), &{} t\in [-\tau ,0],\\ 0, &{} t\in (-\infty ,-\tau ), \end{array}\right. \\ z_2(t,x)= & {} \left\{ \begin{array}{ll} \frac{1}{10}\sin (\frac{x\pi }{2}), &{} t\in [-\tau ,0],\\ 0, &{} t\in (-\infty ,-\tau ), \end{array}\right. \end{aligned}$$

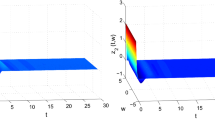
where $x\in \mathcal {O}$. The impulsive sequence is given by $I_k(s)=(\sqrt{3}-1)s$, $t_k=k$, $k\in \mathbb {N}$, and $\sigma =\sqrt{3}$, $\eta =1$. It is easy to check that $\varLambda +A-|B|^*L-\sigma (\lfloor |B|\rceil +|C|+|E|)L-\frac{\ln \sigma }{\eta }I$ is a nonsingular M-matrix. Hence, it follows from Theorem 1 that the global mild solution of the IRDNNs exists and is ISS, iISS, and $e^{\lambda t}$-ISS. Then, we set the external input by $u_1(t,x)=\cos (t\pi /10)\sin (x\pi /2)$ and $u_2(t,x)=(\sin (t\pi /10)+1)\cos (t\pi /4)$. The state trajectories are illustrated in Fig. 4 where we can see that the system with the bounded spatiotemporal external input is also bounded, which corresponds to the ISS properties.

Fig. 3

The trajectory evolution of $\ln (|z(t,1,x_2)|)$ of impulsive system (76) without reaction–diffusion in Remark 9

Fig. 4

The trajectory simulation of IRDNNs with infinite distributed delays in Example 2

Fig. 5

The trajectory simulation of impulsive neural networks in Remark 10

Fig. 6

The trajectory simulation of exponentially stable IRDNNs in Example 3

Remark 10

Here, we consider a special case of the IRDN-Ns with $D=E=0$ in Example 2, that is, impulsive neural networks with finite delay. Similarly, it follows from Theorem 1 that the state trajectories of impulsive neural networks fall into ISS pattern as shown in Fig. 5. Compared with the existing work about ISS of delayed neural networks without impulses [13], especially Example 76 and Remark 10 determined by Theorem 1, the results obtained here mean that the ISS properties can be retained under certain impulsive perturbation. Therefore, we extend part work of [13] to impulsive case.

Example 3

Consider the exponential stability of the IR-DNNs in Example 2, but the parameters are given by

$$\begin{aligned} D= & {} \left( \begin{array}{cc} 2 &{}\quad 0\\ 0 &{}\quad 2 \end{array} \right) ,\ A=\left( \begin{array}{cc} 5 &{}\quad 0\\ 0 &{}\quad 6 \end{array} \right) ,\ B=\left( \begin{array}{cc} -\,0.3 &{}\quad 1\\ 0.5 &{}\quad 0.6 \end{array} \right) ,\\ C= & {} \left( \begin{array}{cc} 0.4 &{}\quad 0.8\\ -\,1 &{}\quad 1.1 \end{array} \right) ,\ E=\left( \begin{array}{cc} -\,0.8 &{}\quad 1\\ -\,0.9 &{}\quad 0.5 \end{array} \right) , \end{aligned}$$

and $\tau =10$, $k(s)=e^s$, $f(s)=\tanh (s)$. The initial condition is given by

$$\begin{aligned} z_1(t,x)= & {} \left\{ \begin{array}{ll} -\frac{1}{4}\cos (\frac{x\pi }{4}), &{} t\in [-\tau ,0],\\ 0, &{} t\in (-\infty ,-\tau ), \end{array}\right. \\ z_2(t,x)= & {} \left\{ \begin{array}{ll} \frac{1}{5}\cos (\frac{x\pi }{2}), &{} t\in [-\tau ,0],\\ 0, &{} t\in (-\infty ,-\tau ), \end{array}\right. \end{aligned}$$

where $x\in \mathcal {O}$. The impulsive sequence is given by $I_k(s)=(e^{1/5}-1)s$, $t_k=0.5k$, $k\in \mathbb {N}$, and $\sigma =e^{1/5}$, $\eta =0.5$. From Corollary 2, it follows that the global mild solution of the IRDNNs exists and is exponentially stable as illustrated in Fig. 6.

Fig. 7

Lena grayscale original image, encrypted image, decrypted image, and their corresponding histograms in Example 4

Remark 11

Compared with the existing work on reaction–diffusion neural networks with infinite distributed delays [23] when the stochastic perturbation is omitted (Example 1 determined by Theorem 1), this example shows that the exponential stability can also be retained under certain impulsive perturbation, which shows the efficiency of the theoretical results.

Example 4

(Application Example) As the major application of RDNNs, the image encryption has been widely studied in recent literature [5, 27, 34], since the pseudorandom number generators can be realized by the complex dynamics of the RDNNs [27]. In [5], the IRDNNs have been successfully used as the pseudorandom number generator for image encryption because of their highly nonlinear characteristics. Thus inspired, we employ the IRDNN in Example 2 for the image cryptosystem proposed in [5]. From Theorem 1 and Corollary 2, the drive system and response system with different initial conditions are ISS and the corresponding error system is exponentially stable, that is the synchronization of the drive signal and response signal which are further used to cipher the Lena grayscale image and decrypt the encrypted image, respectively. The experimental results are shown in Fig. 7 where the encrypted image hides all the information of the original image and the decrypted image is identical with the original image, so the encryption and decryption attempts succeed to show the applicability and practicality of the theoretical results.

5 Conclusion

This paper concerns the global well-posedness and ISS problems of IRDNNs with infinite distributed delays. In light of the semigroup theory, the neural-network model is reformulated in terms of an abstract impulsive functional differential equation, and the criteria for existence–uniqueness and the ISS properties of the mild solution are established by the Picard sequence, vector Lyapunov function, M-matrix, and the vector inequality. The effectiveness and advantage of the theoretical results are verified by three numerical examples. Note that the boundary condition considered here is homogeneous Dirichlet boundary condition that is a special case of Robin boundary condition, so the future work will focus on the ISS analysis of IRDNNs with Robin condition or Neumann condition. On the other hand, the impulsive effects of the neural-network model are viewed as the disturbance factor for the ISS properties. As Refs. [38, 41] suggest, the impulsive effects can also stabilize the unstable nonlinear system, so the ISS analysis of IRDNNs with stabilizing impulses would be another future work.