Introduction

Constitutive models of geomaterials, which relate strains to stresses, are of great importance in geomechanics. Rock mass is a system composed of rock material and rock discontinuities, and hence, is described by discontinuum constitutive models. In this study, a constitutive model for rock discontinuities is developed for rock discontinuities. A large number of research works have been presented in this subject (Jaeger 1959, 1971; Patton 1966; Ladanyi and Archambault 1969; Barton 1972, 1973, 1976; Goodman 1974, 1976; Barton and Choubey 1977; Bandis et al. 1981, 1983; Barton et al. 1985; Desai and Fishman 1987; Aydan et al. 1990; Cundall and Lemos 1990; Gens et al. 1990; Desai and Fishman 1991; Homand et al. 2001; Olsson and Barton 2001; Huang et al. 2002; Zhang and Sanderson 2002; Wang et al. 2003; Grasselli and Egger 2003; Asadollahi and Tonon 2010; Babanouri et al. 2011; Amiri Hossaini et al. 2014; Hou et al. 2016; Azinfar et al. 2016). However, there are generally two approaches used for establishing a model of rock fracture behavior: the empirical approach and theoretical approach (Jing and Stephansson 2007).

In the empirical approach, the model is developed in form of empirical functions best representing the experimental data by means of mathematical regression techniques. No constraint is considered for respecting the second law of thermodynamics in this approach. However, such models can provide agreeable results if the loading conditions and parameter ranges are suitably considered. In contrast, the theoretical approach has the thermodynamic considerations which guarantee the model obeying the second law. Nevertheless, the model parameters may not have clear physical meanings or are difficult to determine by experiments (Jing and Stephansson 2007).

A great number of the constitutive models presented for rock fractures over the years have shed light on the most important aspects of the shear behavior of rock mass. Thus, now there is room to upgrade the classic regression methods to the more robust modeling techniques which better capture the nonlinearity of constitutive response. The power of the today’s computers along with the extreme complexity of shear behavior of rock joints makes it quite reasonable to suggest the application of computational intelligence for constitutive modeling.

The support vector regression (SVR) has been successfully used as a modeling tool in facing a variety of geomechanics problems (Mahdevari et al. 2014; Bagheripour et al. 2015; Elbisy 2015; Chen et al. 2016; Dai et al. 2016; Fattahi 2016; Zhu et al. 2016). However, no attempts have already been made to model the shear behavior of rock fractures using SVR.

In this paper, the support vector regression enhanced with a search algorithm has been employed to construct a constitutive model for rock fractures. A series of 84 direct shear tests was conducted on concrete and plaster replicas of natural rock fractures under different levels of normal stress. The specimens had also different mechanical and morphological characteristics. The SVR constitutive model was developed based on the experimental data. Finally, the results of the proposed model were compared to the performance of Barton–Bandis model for rock fractures.

Experimental study

Sample preparation

To keep mechanical and morphological characteristics of fractures (e.g., wall strength, and roughness) under control, a number of concrete and plaster replicas were constructed from natural rock fractures. Parent rock fractures with different values of the joint roughness coefficient (JRC) were chosen from the Gol-e-Gohar iron ore mine (Iran), and their silicon molds were prepared (Fig. 1a, b). For each of the parent surfaces, 11 digitized roughness profiles along the shear direction were considered to estimate the JRC value (Fig. 1c). Then, the average JRC values of the natural morphologies were calculated as 18.9, 12.4, 7.1, and 4.1, using the following relationship presented by Tse and Cruden (1979):

$${\text{JRC}} = 32.2 + 32.47\log Z_{2} ,$$
(1)

where Z2 is the root mean square (RMS) of the first derivative of the profile, calculated as follows (Myers 1962):

$$Z_{2} = {\text{RMS}} \left( {\frac{{\Delta h}}{{\Delta l}}} \right) = \left( {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\frac{{h_{i + 1} - h_{i} }}{{l_{i + 1} - l_{i} }}} \right)^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,$$
(2)

where N is the number of discrete measurements of profile coordinates (l, h).

Fig. 1
figure 1

Preparing silicon molds of parent rock fracture (a), plaster replicas with different values of JRC (b), location of digitized roughness profiles along the shear direction (c)

Full size image

Several superimposed pairs of each morphology were produced with different concrete and plaster materials. The specimens were cast in a cylindrical shape with a diameter of 60 mm.

To have the plaster samples cured, they were kept in a desiccator at 40 °C for 7 days. The concrete replicas were preserved in a water bath for the same time. Besides the fracture replicas, a number of intact cylindrical specimens from each material were produced. These samples were then used to measure the mechanical properties of the materials used (Fig. 2). Table 1 presents the measured mechanical parameters of the concrete and plaster materials. In this way, a series of fracture replicas with different values of roughness and mechanical properties was prepared.

Fig. 2
figure 2

Measurement of mechanical properties of materials: intact cylindrical specimen (a), uniaxial compressive test (b), tilt test (c)

Full size image
Table 1 Mechanical characteristics of materials
Full size table

Direct shear test

Direct shear testing of fracture replicas was conducted under the constant normal load (CNL) condition. The shear box was wedge type, originally pertaining to a portable shear machine (Fig. 3). Shear and normal actuators worked with two hydraulic pumps equipped with pressure adjustment and relief valves. Each actuator had a loading capacity of 50 kN, and a load cell with an accuracy of 0.04 kN measured its force. One and two LVDTs with an accuracy of 0.03 mm were in charge of measuring the shear and normal displacement, respectively. Shear load was applied to the upper part of the sample at a constant rate of about 0.5 mm/min, while the lower part was kept fixed. During the shear test, the normal displacement, normal force, shear displacement, and shear force were recorded every 0.25 s using a data acquisition system connected to a computer.

Fig. 3
figure 3

Direct shear test apparatus

Full size image

Figure 4 shows shear and dilation curves for a number of the performed direct shear tests. The parameters of peak shear stress (τp), peak shear displacement (δpeak), and dilation angle (d) were extracted from the behavior curves (Fig. 5). Table 2 summarizes the specifications and results of the whole tests.

Fig. 4
figure 4

Behavior curves for three of fracture replicas: shear curve (a), dilation curve (b)

Full size image
Fig. 5
figure 5

Extraction of shear behavior parameters from shear and dilation curves

Full size image
Table 2 Specifications of direct shear tests along with measured values of rock joint shear strength
Full size table

Background theories

The idea behind the proposed model is to optimize values of SVR parameters using a search algorithm. In this section, the SVR technique is explained, followed by describing the employed optimization algorithm.

Support vector regression

The support vector regression (SVR) uses the same principles as the support vector machine (SVM) for classification, with only a few minor differences. In linear SVR, a linear relationship between input data (x) and output data (y) is considered (Fig. 6a):

Fig. 6
figure 6

Support vector regression: linear SVR (a), nonlinear SVR (b) (www.saedsayad.com 2018)

Full size image
$$y = wx + b,$$
(3)

The SVR method aims at minimizing the following term (Hong 2011):

$${\text{Minimize}}\frac{1}{2}||w|| + C\sum\limits_{i = 1}^{N} {\left( {\xi_{i}^{*} ,\xi_{i} } \right),}$$
(4)

with the constraints:

$$\begin{aligned} & y_{i} - wx_{i} - b \le \varepsilon + \xi_{i} , \\ & - y_{i} + wx_{i} + b \le \varepsilon + \xi_{i}^{*} \\ & \xi_{i} ,\xi_{i}^{*} \ge 0. \\ \end{aligned}$$
(5)

The first term of Eq. (4), implying the concept of maximizing the distance of two separated training data, is used to regularize weight sizes, to penalize large weights, and to maintain regression function flatness. The second term penalizes training errors. C is a parameter to trade off these two terms. Training errors above ε are denoted \(\xi_{i}^{{}}\), whereas training errors below − ε are denoted as \(\xi_{i}^{*}\) (Fig. 6a). After the quadratic optimization problem with inequality constraints is solved, the vector w is obtained in terms of two Lagrangian multipliers.

In nonlinear SVR, which is used in this study, the kernel functions transform the data into a higher-dimensional feature space to make it possible to perform the linear separation (Fig. 6b). The value of the kernel equals the inner product of two vectors, xi and xj, in the feature space \(\varphi (x_{i} )\) and \(\varphi (x_{j} )\) as follows (Hong 2011):

$$K\left( {x_{i} ,x_{j} } \right) = \varphi (x_{i} )\varphi (x_{j} ).$$
(6)

There are several types of kernel function, but in this study, we used a most common and powerful of them. This kernel function is called radial basis kernel function (RBF) defined as below:

$$K\left( {x_{i} ,x_{j} } \right) = \exp \left( { -\, \frac{{\left\| {x_{i} - x_{j} } \right\|}}{{2\sigma^{2} }}} \right).$$
(7)

C, σ, and ε are three main parameters of the SVR that are optimized in training state.

BBO search algorithm

The biogeography-based optimization (BBO) is similar to other population-based optimization techniques where population of candidate solutions {x} is represented as a vector of real numbers (Simon 2008). A pseudo-code for the BBO algorithm used in this study is given in Fig. 7. Each element in the solution array is considered as one suitability independent variable (SIV). Fitness of each set of candidate solution is evaluated using a fitness function. The probability of emigration, μ, for each solution is calculated proportionally to its fitness, and the probability of immigration is calculated as λ = 1 − μ.

Fig. 7
figure 7

Pseudo-code for BBO algorithm used in this study (after Wikipedia Contributors 2017)

Full size image

The emigration and immigration probabilities of each solution are used to probabilistically share information between habitats. Using habitat modification probability, each solution is modified based on other solutions. Immigration probability of each solution is used to probabilistically decide whether or not to modify each SIV in that solution. After selecting SIV for modification, emigration probabilities of other solutions are used to probabilistically select which solutions among the population set will migrate. In order to prevent the best solutions from being corrupted by the immigration process, few elite solutions are kept in the BBO algorithm. Like most other evolutionary algorithms, BBO includes mutation of a percent of solutions to increase diversity among the populations. Here, mutation of a selected solution is performed simply by replacing it with randomly generated new solution set. Other than this, any other mutation scheme that has been implemented for genetic algorithm can also be implemented for BBO (Roy et al. 2010).

SVR-BBO constitutive modeling of rock fractures

Inputs and output data

The inputs of the model were once considered to be JRC, joint wall compressive strength (JCS) which is equal to uniaxial compressive strength (σc), Young’s modulus (E), normal stress (σn), and basic friction angle (ϕb), while the outputs were τp, δpeak, and d. Although the basic friction angle of rock fractures has generally a limited range, this parameter plays an important role and cannot be ignored in constitutive modeling of rock joints. The deformability of rock fracture asperities (represented by the Young’s modulus of rock materials in this study) influences the contact area during shearing and consequently affects the shear behavior of fractures. In fact, the incorporation of the Young’s modulus is a step forward in constitutive modeling of rock fractures. However, since the Young’s modulus of rock fracture asperities may not always be measured, the model was construted another time excluding the parameter of E from the inputs. The dataset was randomly divided into two sets of training and testing with 67 and 17 samples, respectively.

Hybrid SVR-BBO model

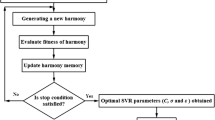
The generalization capability of SVR is extremely dependent upon its learning parameters, i.e., the regularization parameter \(C \in \left[ {2^{ - 5} ,2^{15} } \right]\), the RBF kernel parameter \(\sigma \in \left[ {2^{ - 5} ,2^{3} } \right]\), and the error margin \(\varepsilon \in \left[ {0.01,0.6} \right]\), to be set correctly. Finding the best combination of the hyper-parameters is often troublesome due to the highly nonlinear space of the model performance with respect to these parameters. In this paper, a BBO algorithm was adopted in order to improve the learning procedure of SVR through finding optimal values of its parameters. Figure 8 introduces the flowchart of the hybrid SVR-BBO model used in this study.

Fig. 8
figure 8

Process of optimizing the SVR parameters by BBO

Full size image

Preprocessing of data

In data-driven system modeling methods, some preprocessing steps are commonly implemented prior to any calculations in order to eliminate any outliers, missing values, or bad data. This step ensures that the raw data retrieved from the database are perfectly suitable for modeling. In order for softening the training procedure and improving the accuracy of prediction, all data samples are normalized to adapt to the interval [-1, 1] according to the following linear mapping function:

$$x_{M} = 2\left( {\frac{{x - x_{\hbox{min} } }}{{x_{\hbox{max} } - x_{\hbox{min} } }}} \right) - 1,$$
(8)

where x is the original value from the dataset, xM is the mapped value, and xmin (xmax) denotes the minimum (maximum) raw input values, respectively.

Results

Parameter regularizations for running the optimization models were obtained by trial-and-error procedure (Tables 3, 4, 5). The values of the adjusted parameters \(\left\{ {C,\sigma ,\varepsilon } \right\}\) producing maximal accuracy were considered to be the most appropriate values of the parameters. The best parameter values obtained by each model are presented in Tables 6, 7, 8. The optimal values were then used to retrain the SVR models.

Table 3 Regulated parameters of BBO algorithm for estimation of shear strength
Full size table
Table 4 Regulated parameters of BBO algorithm for estimation of peak shear displacement
Full size table
Table 5 Regulated parameters of BBO algorithm for estimation of dilation angle
Full size table
Table 6 Optimal parameters of SVR obtained by BBO for estimation of shear strength
Full size table
Table 7 Optimal parameters of SVR obtained by BBO for estimation of peak shear displacement
Full size table
Table 8 Optimal parameters of SVR obtained by BBO for estimation of dilation angle
Full size table

Figures 9, 10, and 11 show the performance of the constitutive model with E for the different shear behavior parameters in the training and testing stages. As can be seen, the model has provided agreeable results in both the training and testing phases. The performance of the model in the training phase shows its capability to capture the input–output patterns, and the performance at the testing phase shows the power of the model in facing unseen data.

Fig. 9
figure 9

Performance of SVR constitutive model for shear strength in training stage (a) and testing stage (b)

Full size image
Fig. 10
figure 10

Performance of SVR constitutive model for peak shear displacement in training stage (a) and testing stage (b)

Full size image
Fig. 11
figure 11

Performance of SVR constitutive model for dilation angle in training stage (a) and testing stage (b)

Full size image

Discussion

In order to better evaluate the proposed model, it was compared to the well-known Barton–Bandis (BB) constitutive model for rock fractures. The BB model is a series of empirical relationships developed to describe deformation and strength of rock fractures (Barton 1972, 1973, 1976; Bandis et al. 1981, 1983; Barton et al. 1985). The shear strength, peak shear displacement, and dilation angle are, respectively, estimated as below (Barton 1973, 1976; Barton and Choubey 1977; Barton et al. 1985):

$$\tau_{p} = \sigma_{n} \tan \left[ {\varphi_{b} + {\text{JRC}} \cdot \log_{10} \left( {\frac{\text{JCS}}{{\sigma_{n} }}} \right)} \right],$$
(9)
$$\delta_{\text{peak}} = \frac{{L_{n} }}{500}\left( {\frac{\text{JRC}}{{L_{n} }}} \right)^{0.33} ,$$
(10)
$$d = 0.5{\text{JRC}}_{\text{mob}} \cdot \log \left( {\frac{{{\text{JCS}}_{n} }}{{\sigma_{n} }}} \right),$$
(11)

where Ln is the rock fracture length which is given in meters as well is δpeak.

The BB model does not incorporate Young’s modulus. Therefore, it was compared to the SVR model developed without E. Figures 12, 13, and 14 show the performance of the BB model in comparison with the proposed model for predicting the different parameters. As can be seen, the values of root mean square error (RMSE) indicate significant superiority of the developed model in estimating the shear strength and peak shear displacement, compared to the BB model. Especially, the BB model is unable to provide a good estimation of δpeak and to capture the nonlinearity of the problem. However, in case of the dilation angle, both the models demonstrate the same performance.

Fig. 12
figure 12

Performance of BB model in comparison with proposed model for shear strength

Full size image
Fig. 13
figure 13

Performance of BB model in comparison with proposed model for peak shear displacement

Full size image
Fig. 14
figure 14

Performance of BB model in comparison with proposed model for dilation angle

Full size image

The scale effect is beyond the scope of this research; therefore, the obtained results cannot be directly extended to large scale behavior. However, since the developed model is a JRC–JCS model, it can benefit from the relationships presented for upscaling of JRC and JCS (Bandis et al. 1981; Barton et al. 1985) to consider the effect of scale.

Conclusions

This research developed a constitutive model for rock discontinuities in which the support vector regression was used instead of classic techniques of regression. The model was established based on the results of a systematic set of 84 direct shear tests. The efficiency of SVR in capturing the nonlinear behavior of rock fractures was enhanced through its combination with a search algorithm.

The performance of the developed constitutive model for estimating τp, δpeak, and d based on JRC, JCS, (E), σn, and ϕb was promising in spite of high nonlinearity of shear behavior of rock fractures. The model proved its capability to capture the input–output patterns, and its power when facing unseen data.

On the other hand, comparative investigations revealed that the Barton–Bandis model had a good performance only for estimating the dilation angle and was incapable of modeling the more complicated parameters such as peak shear displacement. Hence, the application of computational intelligence for constitutive modeling is recommended in line with increasing the power of computers.