Introduction

Accurate estimation on the flow behavior of fluid through individual rough fractures in rock is a starting point for a reasonable explanation of water flow process and solute transport in rock aquifers with complex fracture networks, which is of great significance to ensuring the safety and sustainability for numerous environmental geotechnical engineering, such as water resources management and nuclear waste disposal (Berkowitz 2002; Rutqvist and Stephansson 2003; Folch et al. 2011; Huang et al. 2016; Li et al., 2016a; Wang et al. 2016; Ma et al. 2019a; Chen et al. 2019).

For fluid flowing through fractures in the rock, it is generally considered that the flow capacity of water in fractures is several orders of magnitude larger than that of the rock matrix (Cai et al. 2010; Liu et al. 2017). The fluid flowing through a single fracture in rock is popularly approximated by the cubic law. It is obviously deviated from the laminar flow between both perfectly smooth plates separated from each other by a constant opening, which indicates there is a linear relation between the flow rate and pressure gradient (Witherspoon et al. 1980; Brush and Thomson 2003; Xiong et al. 2011; Chen et al. 2015; Zhang et al. 2019). However, in most cases, the natural fractures in rock are commonly characterized by complex surface geometries and asperity contacts, and the existences of contact regions and obstructions cause the variation in the flow directions of fluid along the flow paths, which results in the non-negligible inertial force (Zimmerman and Bodvarsson 1996; Javadi et al. 2014; Zou et al. 2017; Chen et al. 2019; Shi et al. 2020). Another possible reason for the inertial force is the localized eddy flows as the flow velocity is continuously increased (Qian et al. 2011; Chen et al. 2015; Zou et al. 2015). Numerous previous studies have found that the nonlinear flow properties, and the critical Reynolds number denoting the transition of flow, are largely related to the fracture geometry characteristics (Lee et al. 2014, 2015; Liu et al. 2016; Zou et al. 2017; Yin et al. 2019). In situ, the fluid flowing tests under high hydraulic pressure indicated that the flow rate could be nonlinearly related to the pressure drop (Ranjith and Viete 2011; Javadi et al. 2014; Xia et al., 2017; Ma et al. 2019b). In such cases, the linear Darcy’s law is no longer adequate to evaluate the flow behavior of fluid in real rock fractures.

Additionally, due to the various natural and human activities, the real rock fractures are usually subjected to ground stress, there is a strong disturbance in the fracture aperture (Bandis et al. 1983; Min et al. 2004; Cao et al. 2019), thereby causing the great variations in the transmissivity and flow behavior of the fluid (Olsson and Barton 2001; Li et al., 2016b; Zhang and Nemcik 2013; Rong et al. 2016). A lot of experimental and numerical researches indicated that the non-Darcy flow behavior of the fluid in the rock fractures is heavily depended on the changes in the fracture aperture induced by the normal compressive stress (Zhang and Nemcik 2013; Xia et al. 2014; Liu et al. 2016; Yin et al. 2019). Therefore, the quantitative investigation about the flow behavior of fluid in the rough-walled fractures under stress should be further conducted. Consequently, the effects of the fracture surface roughness and loading condition on the nonlinear flow property of the fluid in the rough-walled rock fractures were investigated. A fractal governing function was proposed to establish the fracture profiles with various joint roughness coefficient (JRC) values characterized by the fractal dimension between 1.0 and 1.5. These rough-walled fractures were machined in the plate granite specimens in a size of 495 × 495 × 16 mm containing by using a fully automatic rock carving machine. The hydromechanical tests on these fractured specimens were conducted with respect to the various inlet hydraulic pressures between 0 and 0.6 MPa and the various boundary loads between 7 and 35 kN. The nonlinear flow behavior of fluid in the rock fractures was analyzed, as were the variations in the critical hydraulic gradient, critical Reynolds number, normalized transmissivity, and hydraulic aperture of rock fractures.

Theoretical approach

Assuming that the steady-state fluid flowing through the fracture is incompressible, it governed by the mass conservation equation and the Navier-Stokes equation (Zimmerman and Bodvarsson 1996).

$$ \rho \left(\mathbf{u}\cdot \nabla \right)\mathbf{u}=-\nabla P+\mu {\nabla}^2\mathbf{u} $$
(1)
$$ \nabla \cdot \mathbf{u}=0 $$
(2)

where ρ is the fluid density, u is the flow velocity tensor, P is the hydraulic pressure, and μ is the dynamic viscosity.

In the case of the fluid flowing through the parallel plate with a sufficiently low flow rate, the formula (1) can be rewritten to the cubic law (Witherspoon et al. 1980).

$$ Q=-\frac{{we_{\mathrm{h}}}^3}{12\mu}\nabla P $$
(3)

where Q is the volume flow rate, w is the fracture width, and eh is the hydraulic aperture.

Due to the inertial effect of the fluid flowing in the fracture is not considered, the formula (3) only applies to the hydraulic head that is enough low. Under a high flow rate, the fluid flow deviating from the linear relation between Q and − ∇ P can be obviously observed. Forchheimer’s law is the most extensively used approach for describing this nonlinear flow in fracture (Bear 1972; Chen et al. 2015).

$$ J= aQ+{bQ}^2 $$
(4)

where J is the hydraulic gradient that characterizes the ratio of the hydraulic head difference to the length of a fracture. The parameters of a and b are the linear and nonlinear coefficients that reflect the energy losses caused by the viscous and inertial dissipation mechanisms.

In order to quantitatively analyze the nonlinear flow behavior of the fluid in the rock fracture, a special parameter of E was introduced to judge the flow state of the fluid (Zhang and Nemcik 2013; Javadi et al. 2014).

$$ E=\frac{bQ^2}{aQ+{bQ}^2} $$
(5)

This nonlinear parameter of E denotes the effect of the nonlinear term on the whole hydraulic gradient in the formula (4), from which, the critical hydraulic gradient of Jc that identifies the transition of flow state in rock fracture can be achieved by the combination of the formulas (4) and (5).

The Reynolds number Re characterizes the strength of the inertial force relative to the viscous force, which can be written as follows (Ranjith and Darlington 2007; Zou et al. 2017):

$$ \mathit{\operatorname{Re}}=\frac{\rho Q}{\mu w} $$
(6)

Through the combination of the formulas (5) and (6), the critical Reynolds number Rec can be obtained.

$$ {\mathit{\operatorname{Re}}}_{\mathrm{c}}=\frac{a\rho E}{b\mu w\left(1-E\right)} $$
(7)

The transmissivity T is also an important parameter to describe the hydraulic property that can reflect the flow resistance of the fluid in rock fracture (Olsson and Barton 2001; Wang et al. 2016).

$$ -\nabla P=\frac{\mu }{T}Q $$
(8)

For a significantly low value of J, the intrinsic transmissivity T0 is generally assumed as a constant independent of J. With the continuous increase in J, T can be applied to assess the flow nonlinearity of fluid in rock fracture. Then the normalized transmissivity can be obtained (Liu et al. 2016; Yin et al. 2018).

$$ \frac{T}{T_0}=\frac{1}{1+\beta J} $$
(9)

where β is the dimensionless coefficient.

Materials and methods

Experimental material

The granite was used in this experiment for fluid flow. It is a kind of medium-grained heterogeneous material with the main minerals of feldspar and quartz, obtained from Linyi, Shandong Province, China. Its uniaxial compressive strength was 97.54 MPa, tensile strength was 6.57 MPa, and average density was 2.69 g/cm3. Its natural permeability was in the order of the magnitude of 10−20 m2 (Yin et al. 2017).

Preparation of plate granite specimen with fractures

Before the production of fractures with various surface roughnesses on the specimens, a fractal model for estimating the two-dimensional rough fractures was firstly established according to the modeling method put forward by Ju et al. (2013). The rough morphology of the fractures was evaluated by the fractal dimension of D, which was given by the Weierstrass-Mandelbrot fractal function (Mandelbrot, 1983; Szulga and Molz 2001; Zhang et al. 2015).

$$ W(t)=\sum \limits_{n=-\infty}^{\infty}\left(1-{e}^{ib^nt}\right){e}^{i{\varphi}_n}/{b}_0^{\left(2-D\right)n} $$
(10)

where b0 is a constant larger than 1.0. It indicates that the deviation degree between a fractal curve and a straight curve. According to the reasonable range of b0 suggested by Szulga and Molz (2001), the b0 = 1.4 was used in this paper. φn denotes an arbitrary phase angle. The theoretical bandwidth of fractal dimension is in the range of (1, 2). The real part of the formula (10) obeys the following fractal governing function C(t) (Ju et al. 2013):

$$ C(t)=\sum \limits_{n=-\infty}^{\infty}\left(1-\cos {b}_0^nt\right)/{b}_0^{\left(2-D\right)n} $$
(11)

The formula (11) is a non-differentiable continuous function. The larger the value of fractal dimension, the higher the roughness of a fractal curve (Yin et al. 2017). In order to evaluate the effect mechanism of the surface roughness on the fluid flowing in the fractures, the various values of fractal dimension with 1.0, 1.1, 1.2, 1.3, 1.4, and 1.5 were applied. The corresponding fractal curves were generated using MATLAB programming codes, as presented in Fig. 1. Then, the JRC values of these curves were calculated using the following formulas (12) and (13) proposed by Tse and Cruden (1979), which have been widely adopted (e.g., Liu et al. 2017; Yin et al. 2019).

$$ {Z}_2={\left[\frac{1}{M}\sum {\left(\frac{y_{i-1}-{y}_i}{x_{i-1}-{x}_i}\right)}^2\right]}^{1/2} $$
(12)
$$ \mathrm{JRC}=32.2+32.47\log {Z}_2 $$
(13)
Fig. 1
figure 1

Fracture distribution with different JRCs

Full size image

where xi and yi denote the coordinates of the fracture profile, and M is the number of the sampling points along the fracture.

The calculated JRCs of the fractal curves with a fractal dimension of 1.0, 1.1, 1.2, 1.3, 1.4, and 1.5 are 2.59, 5.79, 8.07, 11.18, 14.10, and 19.31, respectively. In the fractal dimension range of 1.0~1.5, the JRC increases by a factor of approximately 6.46. According to the specimen size in 495 × 495 × 16 mm, two crossed fractures intersected with an angle of 60° were established in Fig. 1, intersecting with the specimen boundaries at the points of A (0, 104.6), B (495, 390.4), A′ (181.2, 495), and B′ (313.8, 0), respectively.

After the fracture profiles with variable surface roughness were determined, the plate granite specimens containing rough-walled fractures were manufactured using the BJD-S325F fully automatic rock carving machine with polycrystalline diamond compact bits moving along the trajectory of a fractal curve, as shown in Fig. 2. The diameter of the bit is 2 mm, and it has a constant spin speed of 18,000 times per minute. During the fracture carving process, the distilled water was utilized for cooling, lubrication, and dust reduction. All fractures were penetrated the specimens thoroughly, and the wall surfaces of the rough fractures appear to match well together without any obvious dislocations, as presented in Fig. 3. It should be noted that this manufacturing method is suitable for making two-dimensional rough fractures but not for three-dimensional rough fractures. The three-dimensional fracture surface is composed of a series of points with three-dimensional coordinates. Therefore, a premise is that the z direction coordinate is not considered to generate two-dimensional rough fractures with different roughnesses in the x-y plane. The two-dimensional rough fractures can be regarded as a contour line with the largest undulation angle in a three-dimensional rough surface. In this case, the permeabilities of the two-dimensional rough fractures were studied.

Fig. 2
figure 2

BJD-S325F fully automatic rock carving machine

Full size image
Fig. 3
figure 3

Plate granite specimens with fractures under different JRCs

Full size image

Experimental system and procedures

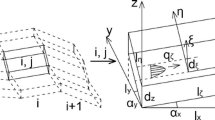
The stress-dependent fluid flow experiments through the rough-walled fractures were conducted using the self-developed flow testing system, as shown in Fig. 4. This system mainly consists of the platform for fluid flowing in fracture networks, hydraulic supply and flow measurement, and pneumatic-hydraulic cylinder. In this test, the water was injected into the fractures through the inflow manifold connected to a water tank with an air compressor that can supply the maximum hydraulic pressure of 2 MPa. Both water inlets along with the directions of x and y evenly equipped with 12 flow distribution chambers. These chambers can be individually switched on or off to guide the fluid flowing, which can achieve a variable but steady flow field. Therefore, the fluid flow paths of x inlet–x outlet, x inlet–y outlet, y inlet–y outlet, and y inlet–x outlet through the rock fractures can be controlled, and the flow paths within fractures are given in Fig. 5 (red arrows). Four hydraulic sensors for measuring hydraulic pressure within 0–2.5 MPa at 0.2% accuracy were arranged at the water inlet and outlet respectively to obtain the osmotic pressure difference under different flow paths. The flow rate of the fluid flowing out the fractures was measured by the glass tube rotameters, which has a measuring range of (0.0004, 11) L/min in the accuracy of 0.0001 L/min. The outflow fluid was collected in a storage tank for treating and recycling. The stress loading of the rock specimen with fracture networks was achieved by the vertical loading (z direction) device and horizontal loading (x and y directions) device in a maximum pressure of 3 MPa.

Fig. 4
figure 4

Stress-dependent fluid flow test system

Full size image
Fig. 5
figure 5

Stress and hydraulic conditions of rock specimen with fractures

Full size image

A rubber sleeve produced by Antell solid waterproof was used to seal the fractured rock specimen, and the void between the specimen and the sleeve filled fully with ethylene propylene diene monomer waterproof rubber for preventing the escape of fluid. It was to note that the fracture should be opened but its edges must be sealed, so the glass glue was evenly coated on the specimen surface to control that. Then the transparent crystal plate in a matching size was attached to the specimen by using the glass glue. The circular holes with a diameter of 10 mm were drilled at the positions of the rubber sleeve that was the inlet and outlet of fluid flowing in the fracture. The horizontal load devices with uniform inlet flow chambers were installed, and then the well-sealed specimen was moved to the fluid flow cell, as presented in Fig. 4. The fractured specimen should be placed on the horizontal plane along x-y direction so that the initial pressure difference between the inlets and outlets could be ignored.

In Fig. 4, for balancing the vertical water pressure in the specimen with the fracture in a certain surface roughness, a vertical load Fz = 20 kN was firstly applied on the upper surface of the specimen. Then both horizontal boundary loads of Fx and Fy were applied and raised stepwise from 7 to 35 kN in an interval of 7 kN, and the condition of Fx = Fy was constant. Under each loading condition, 20 hydraulic tests with various inlet hydraulic pressures in the range of 0 to 0.6 MPa were carried out.

It was assumed that the dense granite matrix is impermeable so that the water only flowed in the voids between both fractures in the specimen. The hydraulic experiments were completed in an isothermal condition with a room temperature of 25 °C. The dynamic viscosity and density of water were μ = 1.0 × 10−3 Pa·s and ρ = 1.0 × 103 kg/m3 in natural states. In this experiment, the fluid flowed into the fracture through the inlet_1. Then both various flow paths of inlet_1–outlet_1 and inlet_1–outlet_2 were separately controlled with Fy = Fx = 7 kN, D = 1.1, and P = 0–0.6 MPa, as presented in Fig. 5, to examine the difference in the responses of hydraulic gradient and flow rate. Then, the fluid flow tests were conducted through the fixed flow path of inlet_1–outlet_1 to estimate the effects of the hydraulic gradient, loading condition, and surface roughness on the nonlinear flow behavior of the real fractured rock.

Results and discussions

Relation between hydraulic gradient and flow rate

Figure 6 shows the relation between hydraulic gradient and flow rate of fluid in rock fractures with a fixed inlet (inlet_1) but different outlets (outlet_1 and outlet_2). Here, the boundary load F denotes the horizontal boundary loads as a result of Fx = Fy. The hydraulic gradient J is defined as the ratio between the hydraulic head difference and the length of the flow path.

$$ J=\frac{P}{\rho gL} $$
(14)
Fig. 6
figure 6

Relation between hydraulic gradient and flow rate under different outlets (F = 7 kN, D = 1.1)

Full size image

where L is the length of the flow path and g is the gravitational acceleration.

Here, the hydraulic head at the water outlet boundary was presumed to be zero. Therefore, as the tested hydraulic pressure drop increased from 0 to 0.6 MPa, the corresponding hydraulic gradient increased from 0 to 123.69, as presented in Fig. 6. It is easy to see that the relation between hydraulic gradient and flow rate can be described by the quadratic function, and the correlation coefficient is larger than 0.99. The fitted regressions are composed of a linear term of aQ and a nonlinear term of bQ2, which characterize the viscous and inertial pressure drops, respectively. The flow transition to nonlinearity in rough fractures arises from the surface roughness, intersection, as well as aperture variation. The above factors render the streamline disorders, preferential paths and localized eddy flows, producing frictional losses of pressures, thereby increasing the hydraulic gradient required to achieve a given flow rate (Chen et al. 2015; Li et al., 2016a; Yin et al. 2019). The flow nonlinearity of fluid in the rock fractures can be enhanced with increasing hydraulic gradient and the variations in streamlines arise from fracture intersection, which results in a larger nonlinear coefficient b and thus a steeper slope of the J–Q fitting curve for fluid flowing through the path from inlet_1 to outlet_2. Additionally, as the hydraulic gradient is sufficiently small (J < 5), the viscous forces are much larger than the inertial forces. The nonlinear term of bQ2 can be ignored, and the fluid flow can be accurately characterized by the linear cubic law. However, with the increase in hydraulic gradient (J > 10), due to the remarkably flow nonlinearity, the cubic law is no longer applicable and the flow follows the Forchheimer’s law.

Forchheimer’s law

All the relations between hydraulic gradient and flow rate of the fluid in rough-walled fractures under different boundary loads and fractal dimensions are given in Fig. 7. The regression line using the best-fit analysis of data indicates that the formula (4) fits the flow data well. The relation of hydraulic gradient and flow rate shifts upwards as the fractal dimension increased, showing a higher resistance of flow due to the increase in the fracture surface roughness. Similarly, for rough-walled fractures with a certain fractal dimension, with an increase in boundary load, the slope of the fitting curves exhibits an increasing trend. Hence, for higher boundary load, to achieve the same flow rate, a larger hydraulic gradient is required.

Fig. 7
figure 7

Relations between hydraulic gradient and flow rate

Full size image

(a) F = 7 kN.

(b) F = 14 kN.

(c) F = 21 kN.

(d) F = 28 kN.

(e) F = 35 kN.

According to formula (4) and experimental results, both linear and nonlinear coefficients a and b under all the experimental conditions can be obtained. Figure 8 presents the effects of fractal dimension and boundary load on linear and nonlinear coefficients. It is easy to see that both coefficients a and b exhibit an increasing trend with an increase in boundary load, while their increase rate steadily diminishes. Taking the fractal dimension of 1.3 as an example, the coefficients a and b increase by a factor of 2.72 and 7.69, respectively, when the boundary load is in the range of 7 to 35 kN. The increase in the coefficient value is caused by the fracture closure induced by the increase in the boundary loads. Additionally, for a certain boundary load, both coefficients a and b also present an increasing trend with fractal dimension. Taking a boundary load of 28 kN as an example, when the fractal dimension is in the range of 1.0 to 1.5, the coefficients a and b show an increase of 30.50% and 77.36%, respectively. The variations in both coefficients a and b are consistent with the experimental results reported in some previous studies (e.g., Zhang et al. 2013; Li et al., 2016a; Liu et al. 2016; Xiong et al. 2018). The linear coefficient a and nonlinear coefficient b characterize the hydraulic drop components caused by linear and nonlinear effects. Zhang and Nemcik (2013) pointed out that the linear coefficient a is negatively related to the fracture permeability, as shown in the formula (15). The larger the coefficient a, the lower the water flow capacity in the fracture. It is easy to understand that the fracture is gradually closed with the increase of the external load, resulting in a decrease in the fracture permeability and an increase in the linear coefficient a.

$$ a=\frac{\mu }{kA} $$
(15)
Fig. 8
figure 8

Fractal dimension and boundary load effect on linear and nonlinear coefficients a and b

Full size image

where k is the fracture permeability, A is the cross area of the fracture perpendicular to the flow direction.

In the view that the variations in a and b are very similar, the relation between a and b is plotted in Fig. 8c. An empirical equation can be used to fit the experimental data as follows, which shows a good agreement with those presentations in some other studies (e.g., Rong et al. 2016; Yin et al. 2018). It also reflects that the reduction of fracture pore size causes an increase in the nonlinearity of water flow in fractures.

$$ b=4.95{a}^{1.69} $$
(16)

(a) Fractal dimension and boundary load effect on linear coefficient

(b) Fractal dimension and boundary load effect on nonlinear coefficient

(c) Relation between linear and nonlinear coefficients

Critical hydraulics

In recent studies, the value of a nonlinear effect factor E for judging the fluid flow regime in fractured/porous media was set as 10% (Zimmerman et al. 2004; Zeng and Grigg 2006; Javadi et al. 2014; Zhou et al. 2015; Yin et al. 2017), in which the nonlinear pressure drop cannot be neglected. Thus, according to the formulas (5), (6), (7), and (14), Fig. 9 illustrates the effect of fractal dimension and boundary load on critical hydraulic gradient and critical Reynolds number. The results present that both critical hydraulic gradient and critical Reynolds number generally decrease with the increase in the fractal dimension for the rock fractures with a certain boundary load. Taking the boundary load of 14 kN as an example, in the fractal dimension range of 1.0 to 1.5, the critical hydraulic gradient and critical Reynolds number decrease by 21.78% and 45.74%, respectively. It can be understood that the flow nonlinearity of fluid in rock fractures can be induced by the increases in the hydraulic gradient and surface roughness. The fluid flowing through the fracture with a larger fractal dimension value is more prone to flow transition from linearity due to the more tortuous flow paths and localized eddy formations induced by the inertial effects of flow (Zhou et al. 2015; Wang et al. 2016; Xiong et al. 2018). For a certain fractal dimension, the critical hydraulic gradient increases with the boundary load. The variation process of the critical hydraulic gradient in terms of the boundary load can be divided into two stages. When the boundary load is smaller than 21 kN, the critical hydraulic gradient varies significantly. When the boundary load is in the range of 21 to 35 kN, the critical hydraulic gradient varies gradually and approaches constant values. Taking the fractal dimension of 1.1 as an example, in the boundary load range of 7 to 21 kN, the critical hydraulic gradient varies significantly from 3.53 to 4.83, increasing by 36.87%. However, in the boundary load range of 21 to 35 kN, the critical hydraulic gradient increases from 4.83 to 4.99, only increasing by 3.32%. It can be understood that the hydraulic aperture sharply decreases with the increase in boundary load. When the increase rate of the critical hydraulic gradient is less than the decrease rate of the cubic power of hydraulic aperture eh3, the critical Reynolds number decreases as shown in formula (17), which leads to opposite variation trends for critical hydraulic gradient and critical Reynolds number of fluid flow in rock fractures as the boundary load increased. For the fluid flowing through the single fracture, the flow rate is proportional to the cubic power of hydraulic aperture eh3, and a small variation in the hydraulic aperture can result in a large variation of flow rate. Additionally, the flow regime in fractures may deviate from linearity as a result of the variation in the flow velocity or direction along the flow paths due to contact regions or obstructions induced by the decrease of hydraulic aperture, thereby affecting the nonlinear flow behavior of fluid in rock fractures (Liu et al. 2016; Yin et al. 2019).

$$ {\mathit{\operatorname{Re}}}_{\mathrm{c}}=\frac{\rho^2{e}_{\mathrm{h}}^3}{12{\mu}^2}{J}_{\mathrm{c}} $$
(17)
Fig. 9
figure 9

Fractal dimension and boundary load effect on critical hydraulic gradient and critical Reynolds number

Full size image

(a) Critical hydraulic gradient Jc

(b) Critical Reynolds number Rec

For comparison with the critical hydraulic gradients, the critical Reynolds numbers under all the experimental cases were calculated. The magnitudes of the critical Reynolds numbers are in the range between 8.41 and 83.73. Table 1 presents the consistencies and differences between the critical Reynolds numbers calculated in this paper and those of other studies. It shows that a wide range of critical Reynolds numbers has been suggested for fractured or porous media. The scope of the critical Reynolds numbers is generally consistent with those reported in some previous studies (e.g., Koyama et al. 2008; Javadi et al. 2014; Yin et al. 2017; Zhou et al. 2015; Wang et al. 2016; Zimmerman et al. 2004; Rong et al. 2016; Zimmerman and Bodvarsson 1996) but shows a large difference with the critical Reynolds number ranges in others (e.g., Brush and Thomson 2003; Chen et al. 2015; Radilla et al. 2013; Qian et al. 2011; Andrade et al. 1999). This is because the ranges of the critical Reynolds number for the onset of nonlinear flow in fractured/porous media might vary with the fracture geometry, pore distribution, applied stress, rock type, as well as the test condition (Liu et al. 2016). It is worth noting that for a certain fractal dimension, the critical hydraulic gradient increases while the critical Reynolds number decreases with an increase in the boundary load. The primary reason is that the hydraulic aperture decreases with the increase in the boundary load. When the increase rate of the critical hydraulic gradient is less than the decrease rate of the cubic power of hydraulic aperture eh3, the critical Reynolds number decreases, which results in the opposite variation trends of the critical hydraulic gradient and critical Reynolds number with the increase of boundary load (Yin et al. 2017).

Table 1 A literature review on the calculated Rec values in previous studies
Full size table

According to the achieved critical hydraulic gradient and critical Reynolds number, the linear and nonlinear flow phases in rough-walled rock fractures can be explicitly identified. Thus, the hydraulic aperture can be calculated by substituting the slope of the linear regression line in − ∇ P versus Q relations into the cubic law in the formula (3). The variations of hydraulic aperture in response to fractal dimension and boundary load are given in Fig. 10. It shows that the hydraulic aperture decreases and exhibits a hyperbolic variation trend as the boundary load increased, which agrees with the results obtained in some other studies (e.g., Bandis et al. 1983; Zhou et al. 2015). In the boundary load range of 7 to 35 kN, the hydraulic aperture decreases by 25.72 to 53.67%, and its decrease rate gradually weakens for fractures with a larger fractal dimension value. Similarly, for a certain boundary load, with an increase in fractal dimension, the hydraulic aperture also decreases. In the fractal dimension range of 1.0 to 1.5, the hydraulic aperture decreases by 8.48 to 42.92%. The variation of hydraulic aperture conducts a significant role in the flow capacity through rock fractures.

Fig. 10
figure 10

Fractal dimension and boundary load effect on hydraulic aperture

Full size image

It is worth noting that the nonlinear coefficient b in the Forchheimer’s law increases with boundary load, as presented in Fig. 8b. However, the hydraulic aperture shows a decreasing trend, which results in a negative correlation between nonlinear coefficient b and hydraulic aperture. In recent studies, for single rough-walled rock fracture, a power-law equation was proposed to describe the relation between nonlinear coefficient b and hydraulic aperture (Chen et al. 2015; Zhou et al. 2015; Yin et al. 2019):

$$ b=\lambda {e_{\mathrm{h}}}^{-\mathrm{m}} $$
(18)

where λ and m are the regression coefficients that are affected by the fracture surface roughness.

Figure 11 presents the variations in b as a function of hydraulic aperture for all the experimental cases. The results show that the formula (18) can fit the experimental data well. The coefficient λ increases but the coefficient m decreases with an increase in the fractal dimension. In the fractal dimension range of 1.0 to 1.5, the coefficient λ varies in a slightly wide range of two orders in the magnitudes of 4.643 × 108 to 1.540 × 1010, while the coefficient m stabilizes in a much narrow range between 3.653 and 5.325.

Fig. 11
figure 11

Relation between nonlinear coefficient b and hydraulic aperture

Full size image

Transmissivity

The transmissivities were calculated by using the formula (8), and all the relations between transmissivities and hydraulic gradients based on the experimental data were plotted in Fig. 12. It indicates that the transmissivity is not a constant value but exhibits a cubic decrease with the increase of hydraulic gradient. This variation trend agrees with the results reported in some previous literature (Zhang and Nemcik 2013; Xia et al., 2017), which further demonstrates the presence of the inertial effects of flow at a high hydraulic gradient or volume velocity. The transmissivity shows a decrease with an increase in the fractal dimension as well as boundary load due to the gradually weakened flow capacity of fluid in rock fractures.

Fig. 12
figure 12

Relation between transmissivity and hydraulic gradient

Full size image

(a) F = 7 kN.

(b) F = 14 kN.

(c) F = 21 kN.

(d) F = 28 kN.

(e) F = 35 kN.

The fitted relations between normalized transmissivity T/T0 and hydraulic gradient were established by using the formula (9). Here, the intrinsic transmissivity T0 represents the transmissivity corresponding to hydraulic gradient J = 0 in Fig. 10, where the flow rate is extremely low and the inertial forces are negligible. Figure 13a displays the regression lines with the best fitting between normalized transmissivity and hydraulic gradient. Obviously, the formula (9) gives a good prediction of the transmissivity, all the corresponding correlation coefficients are larger than 0.99. In the case of hydraulic gradient less than 1, the normalized transmissivity keeps a constant value approaching 1.0, and the fluid flow is linear. Notably, in the condition of hydraulic gradient larger than 1, the normalized transmissivity decreases with an increase in the hydraulic gradient, presenting a slow and then dramatic decrease trend, which further confirms the deviation of fluid flow from linearity to nonlinearity. The experimental results are consistent with the results reported by Zimmerman et al. (2004) and Wang et al. (2016). For the fractures with a certain fractal dimension, at the same hydraulic gradient (J > 1), the nonlinear deviation is less significant as the boundary load increased. However, for a given boundary load, as the fractal dimension increased, the fitting relation between normalized transmissivity and hydraulic gradient generally shifts downwards, indicating a more prone transition of flow regime. The variations of the coefficient β in the formula (9) for rock fractures with various surface roughnesses are shown in Fig. 13b. The magnitudes of β are in the range of 4.51 to 5.73 for all the experimental cases. The coefficient β decreases with the fractal dimension while increases with the boundary load. In the boundary load range of 7 to 35 kN, the coefficient β increases by 18.37% (D = 1.0), 17.10% (D = 1.1), 14.29% (D = 1.2), 15.12% (D = 1.3), 19.57% (D = 1.4), and 12.94% (D = 1.5), respectively.

Fig. 13
figure 13

Fractal dimension and boundary load effect on normalized transmissivity

Full size image

(a) Relation between normalized transmissivity and boundary load

(b) Relation between coefficient β and boundary load

Conclusions

A fractal governing function was proposed to establish the fracture profiles with various JRC values characterized by the fractal dimension between 1.0 and 1.5. These rough-walled fractures were machined in the plate granite specimens in a size of 495 × 495 × 16 mm containing by using a fully automatic rock carving machine. The hydromechanical tests on these fractured specimens were conducted with respect to the various inlet hydraulic pressures between 0 and 0.6 MPa and the various boundary loads between 7 and 35 kN. The nonlinear flow behavior of fluid in the rock fractures was analyzed, as were the variations in the critical hydraulic gradient, critical Reynolds number, normalized transmissivity, and hydraulic aperture of rock fractures.

(1) Forchheimer’s law exactly characterized the fluid flowing through rough-walled fractures, and the flow nonlinearity can be enhanced due to the localized eddy flows and variations in streamlines arisen from fracture intersection. Both linear and nonlinear coefficients increase with the fractal dimension as well as the boundary load. An empirical equation b = 4.95a1.69 was proposed to best fit the relation of nonlinear coefficient as a function of the linear coefficient.

(2) By taking the critical E value of 10%, both the critical hydraulic gradient and critical Reynolds number were achieved. As the fractal dimension increased from 1.0 to 1.5, the critical hydraulic gradient and critical Reynolds number decreased by 3.98%~33.60% and 26.42%~87.65%, respectively. The fluid flow was more prone to transition from linearity. The critical hydraulic gradient increased more for a small boundary load (7 and 14 kN) than for a large load (21, 28, and 35 kN).

(3) The transmissivity of fractures based on the hydraulic gradient could be approximated using a cubic polynomial function, and the transmissivity decreased with both the fractal dimension and boundary load. The fitted curves of normalized transmissivity against hydraulic gradient shifted upwards as the boundary load increased but turn downward with the fractal dimension. As the boundary load increased, the hydraulic aperture presented a hyperbolic decrease, and a power-law equation was proposed to describe the relations between the nonlinear coefficient and hydraulic aperture.