Introduction

The powerful nature of cavitation has long been appreciated. Cavitation-erosion is a well-known, destructive phenomenon often associated with significant damage to ship-based propellers, pumps, and impellers [1,2,3]. Biology displays an equally diverse array of cavitation phenomena, from the prey-stunning capability of the mantis shrimp [4, 5] to cavitation injuries in soft tissues like the liver, kidney, or brain [6, 7]. The rapid expansion and collapse of inertial cavitation bubbles can generate stresses in the surrounding material on the order of GPa with internal bubble pressures and temperatures upon collapse rivaling our sun. For soft matter systems, in particular, understanding the large, high-rate deformation response of the surrounding material during cavitation has become paramount in limiting the collateral damage associated with cavitation-based medical procedures, such as histotripsy [8, 9] and laser-based eye surgeries [10]. Moreover, recent experimental and theoretical investigations have shown that significant, strain-amplifying instability patterns can arise during cavitation depending on the particular boundary and loading conditions [11,12,13]. Strain amplification due to these instabilities has the potential to be even more detrimental to the surrounding material than the deformation fields arising around spherical bubbles. In fact, our recent work has shown that classical rugae instabilities [14, 15], long studied only under quasi-static compressive loading, could also exist under a state of tension when large-scale inertial forces are present [16]. Taken together, these recent discoveries motivate the need for an experimental capability to resolve the existence, spatial variance, and evolution of heterogeneous deformation signatures in the surrounding material during inertial cavitation.

Previous experimental methods focused on providing such full-field information have included background-oriented Schlieren [17,18,19,20], interferometry [21, 22], particle tracking (PT) [23, 24], and particle image velocimetry (PIV) [25,26,27,28,29] methods. While these techniques have provided some information about the deformation fields near a cavitating bubble, they have primarily focused on investigations in liquids and have largely remained qualitative or approximate with generally low spatial information due to several technical challenges. A particular experimental challenge is the non-uniform temporal evolution of an inertially cavitating bubble, featuring intervals of both extremely short (e.g., near the collapse point) and long (e.g., during peak expansion) time windows requiring fast camera frame rates over a long collection window, which is challenging to accomplish with most commercially available camera systems. Measurement difficulties are further exacerbated by the large deformations experienced during cavitation in soft solids, i.e., the maximum circumferential stretch ratio, or the maximum radius ratio, can reach as large as 10 [29, 30]. Furthermore, as the cavitation problem in itself is extremely sensitive to any perturbations in its surroundings, such as changes in impedance due to a free surface [31,32,33] or solid boundaries [34, 35], traditional surface-based DIC or PIV techniques cannot be directly applied. Similarly, due to the fast frame rate requirements and the often small (sub-millimeter) bubble size, volumetric DVC and PIV techniques cannot provide a high enough spatial signal to offer a complete volumetric reconstruction of the surrounding deformation fields [36, 37].

To address some of these challenges, we introduce a new experimental framework to measure the finite deformation fields near inertial microcavitation bubbles inside a gelatin viscoelastic hydrogel. Our method combines and further improves recent advances in adaptive digital image correlation and subsurface speckling methods, namely the SpatioTemporally Adaptive Quadtree mesh Digital Image Correlation (STAQ-DIC) method [38] and the subsurface Embedded Speckle Plane (ESP) patterning method. The advantage of the recently developed STAQ-DIC method is that it allows for the measurement of displacement fields close to boundaries of arbitrary and complex geometries with little user input [38]. Thus, this technique is well-suited for resolving large, evolving deformations near oscillating cavitation bubbles without excessive interface smearing (or intrinsic DIC low pass filtering) [39,40,41]. Leveraging the recently developed ESP patterning method, we provide a straightforward method to selectively pattern at user-specified heights deep within the bulk of a water-based hydrogel specimen [42, 43]. Finally, by combining both of these techniques with our previously established laser-induced cavitation (LIC) system [13, 23, 30], we present the first high-resolution, full-field, high-strain-rate, and large-deformation measurements of highly compliant viscoelastic hydrogel materials during laser-induced inertial microcavitation. As an application of the new experimental method, we examine a key kinematic assumption of Inertial Microcavitation Rheometry (IMR) [13, 23, 30]. IMR is a cavitation-based characterization technique for measuring the viscoelastic mechanical properties of soft materials at high strain rates. Modeling cavitation in soft materials relies on several idealizations to infer the full deformation fields in the material surrounding the bubble from the experimentally measured temporal evolution of the bubble radius. One such assumption in the IMR theoretical modeling framework is that after an LIC event, residual deformation is negligible, and hence that the material surrounding the equilibrium bubble may be idealized as stress-free [30]. Using our new method, we experimentally measure the residual deformation after an LIC event and verify that the residual strain in the surrounding material is minimal in the equilibrium state.

The remainder of this paper is organized as follows. In “Experimental Setup”, we describe the ESP DIC patterning method used to create gelatin hydrogels with embedded speckle planes, our LIC experiments on gelatin, and the subsequent STAQ-DIC post-processing of deformation fields induced during LIC events. In “Results”, we present experimentally measured bubble dynamics and deformation fields in the surrounding material along with the predictions of a theoretical framework based on the idealizations of spherical symmetry and incompressibility. In “Discussion”, we comment on our improved ESP method, experimentally verify the aforementioned key assumption in IMR regarding the equilibrium state, and discuss potential error sources. Finally, we close this paper with some concluding remarks and future directions in “Conclusion and Future Directions”.

Experimental Setup

Creation of Gelatin Hydrogels with Embedded Speckle Planes

Multiple concentrations of gelatin hydrogels were produced using porcine gelatin 300-g bloom (Sigma-Aldrich G1890) mixed with Milli-Q deionized (DI) water. Mass concentrations of 6, 10, and 14 percent were heated above 60 \(^\circ\)C and stirred continuously until all gelatin was dissolved. The gelatin was then pipetted into the bottom of a 14 mm glass-bottom dish (VWR 10810-054) and covered with a polyethylene terephthalate (PET) plastic film to create a horizontal flat surface (Fig. 1(a)). The sample was then placed into an ice bath for 1 hour to allow complete gelation. The PET film was then removed by peeling one end towards the other using the largest possible peeling angle (Fig. 1(b)). Following the successful removal of the film, a speckle pattern was applied to the surface. Here, we quickly sprayed 20 \(\sim\) 30 µm sized inkjet toner particles onto the surface using a high-pressure air stream being careful not to let the gel surface dehydrate. Immediately after the surface was speckled, gelatin heated to a few degrees above its melting temperatureFootnote 1 was added to the sample and allowed to cover the surface (Fig. 1(c)). The exact temperature needed depends on the gelatin type and processing conditions, but for the samples used here, a temperature of approximately 34 \(^\circ\)C was used. After approximately 10 seconds, the sample was then placed in an ice bath to halt further melting of the interface. The intent of this procedure is to melt the gelatin at the speckle interface just enough to create a continuous gel but not enough to cause the speckles to sink or mix. The specific temperature and time needed to fuse the sample together is dependent on many factors and must be determined empirically. After gelation, the sample was placed into a high humidity oven set to just below the melting temperature of the gelatin and allowed to fuse for an additional hour (Fig. 1(d)). Finally, the sample was allowed to hydrate in Milli-Q DI water for two days at 4 \(^\circ\)C (Fig. 1(e)). Before testing, one specimen from each batch was cut perpendicular to the plane, and the gel was pulled away from the speckle plane until failure. A weak interface exists if there is layer separation or if the material fails along the speckle plane. In such a case, the other test samples should be placed into the high humidity oven at a slightly higher temperature. We repeated these testing and heating steps until a test sample confirmed that the layers were fused.

Fig. 1
figure 1

A graphical overview of the fabrication method for embedding a speckle plane within a gelatin hydrogel. (a) Molten gelatin is pipetted into a glass-bottom dish covered by a thin PET membrane. (b) After the gel has set, the thin PET film is removed, revealing a flat surface. (c) A speckle pattern is added to the surface and then covered with molten gelatin heated slightly above its melting temperature. (d) After the gel has been set, the entire sample is heated to the gel transition temperature and allowed to fuse. (e) The sample is placed within a cold water bath to hydrate to equilibrium

Full size image

Quasistatic Shear Moduli Measurements of Gelatin

The quasi-static, ground-state shear modulus of each concentration of gelatin gel was determined using an ARES-G2 rheometer with a 25 mm stainless steel smooth plate force transducer (TA Instruments, DE). First, a strain sweep ranging from 0.01% to 1% strain at a frequency of 2\(\pi\) rad/s was used to determine the linear regime for each of the three gel concentrations. Then, a strain amplitude of 0.5%, which was well within the linear regime of all three gel concentrations, was used in the frequency sweep experiments. The gels were tested at 0.5% strain with a frequency f ranging from 0.01 Hz to 10 Hz. This frequency sweep procedure was iterated four times to ensure repeatable data was achieved and to avoid any Mullins-type effect. The ground-state shear moduli \(G_\infty\) are estimated by extrapolating the measured shear modulus when the frequency \(f \rightarrow 0\), which are \(0.74 \pm 0.02\) kPa, \(3.08 \pm 0.01\) kPa, and \(6.71 \pm 0.03\) kPa for 6%, 10%, and 14% concentration gelatin hydrogels, respectively.

Laser-induced Inertial Microcavitation (LIC)

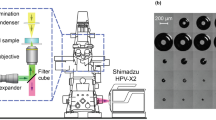
The laser-induced inertial microcavitation platform employed in this work has been described in detail in our previous works [13, 23, 30]. Briefly, a single inertial cavitation event was generated within the speckle plane of each sample through spatially-focused deposition of laser energy within the focal plane of the 3D gelatin gels. A tunable (1-25 mJ) Q-switched Nd:YAG Minilite II laser (Continuum, Milpitas, CA) with a pulse width of \(\sim\)4 ns was frequency-doubled to 532 nm, expanded, and steered into the rear aperture of a Nikon Plan Fluor 20\(\times\)/0.5 NA imaging objective through the backport of a Nikon Ti2-E microscope (Nikon Instruments, Long Island, NY). The expansion, collapse, and subsequent rebounds of each cavitation event were recorded at 2 million frames per second using a Shimadzu HPV-X2 high-speed camera (Shimadzu Corporation, Kyoto, Japan). Pulsed illumination of each frame was achieved through a coupled SILUX640 laser illumination system with a pulse duration of 20 ns (Shimadzu Corporation, Kyoto, Japan) mounted to the collimator of the microscope and triggered by the HPV-X2 ultra-high-speed camera.

Camera Calibration of the Speckle Plane

The optical system needed to guide a laser to an objective lens while simultaneously imaging a 2D speckle plane embedded in a gel perpendicular to the imaging axis requires careful calibration for maintaining collinearity. However, the use of a calibrated inverted microscope simplifies this task greatly since optical plane flatness, and aligned positioning of the object plane are built-in features of commercially available microscope systems. The slope of the 2D speckle plane can be adjusted to be made perpendicular to the optical axis using the leveling screws on the microscope’s mounting plate. Furthermore, great care is taken in the microscope’s optical system to ensure that the warping of the image is minimized. However, since the high-speed camera system used in these experiments is not typically used with these microscope systems, the use of a calibration grid to measure image distortion and pixel to real-world unit conversion is recommended. In our experiments, one pixel corresponds to 1.6 µm in the laboratory frame.

Digital Image Correlation Post-processing

By comparing the image frames during cavitation with the reference frame (e.g., Fig. 2(c:ii-iv) compared to Fig. 2(b:i)) and applying our recently developed SpatioTemporally Adaptive Quadtree mesh Digital Image Correlation (STAQ-DIC) image tracking algorithm [38], we successfully reconstruct the history of full-field material deformations within a planar slice during each LIC event. In STAQ-DIC, we employ an incremental tracking mode where every two consecutive frames are compared to each other to obtain an incremental displacement field. In order to more accurately resolve the displacement and strain fields near boundaries, STAQ-DIC generates an adaptive quadtree mesh based on a binary image mask built from the actual raw image, which is used to adaptively refine the displacement and strain data near the bubble wall. In images Fig. 2(c), black circles are shadowgraphs of the actual laser cavitation bubbles providing a natural and clearly visible boundary between the bubble area and the surrounding material. From Fig. 2(c) and applying image processing, we generated binary mask files to label bubble (black color) and surrounding material (white color) areas as shown in Fig. 2(d:ii-iv) for three time points: 14.0, 26.0, and 125.0 µs, respectively. These binary masks are further used to generate the corresponding quadtree meshes shown in Fig. 2(c:ii-iv) [45, 46]. All of the images are 400 pixels \(\times\) 250 pixels in dimension. The coarsest DIC element size (DIC window spacing) in the generated adaptive quadtree mesh here is 8 pixels \(\times\) 8 pixels while the finest mesh element size is 2 pixels \(\times\) 2 pixels. The displacement for each nodal point in the quadtree mesh is obtained by tracking the local neighboring area – i.e., a square subset whose center point is the tracked nodal point with a subset size of 40 pixels \(\times\) 40 pixels. If a subset crosses the bubble wall, it will be automatically registered and split along the bubble boundary [39]. Only the partial subset for \(r > R\), i.e., the part of the subset outside the bubble wall, is used to determine the deformation of that subset. All the tracked displacement components use a Cartesian coordinate system first, which are then transformed to a polar coordinate system (i.e., the 2D projection of a 3D spherical coordinate system on the center planar slice). The incremental displacement fields are tracked between every two successive frames (e.g., the tracked incremental radial displacements at 14.0 µs compared to 13.5 µs, and 26.0 µs compared to 25.5 µs are shown in Fig. 2(e, f)).

Fig. 2
figure 2

Digital image correlation post-processing for laser-induced inertial cavitation in gelatin hydrogels. (a) A representative measured laser-induced inertial cavitation bubble radius versus time curve in a 10% gelatin hydrogel. (b) The reference virgin material and DIC mesh are shown in a split view bisecting the bubble nucleation site. (c) Insets (ii-iv): deformed raw images split with generated adaptive quadtree meshes at time points 14.0, 26.0, and 125.0 µs, respectively. (d) Examples of binary masks at 14.0, 26.0, and 125.0 µs corresponding to the data are shown in insets (ii-iv). (e–h) Measured incremental and cumulative radial displacements (\(u_r\)) at 14.0 µs and 26.0 µs

Full size image

All the tracked incremental displacement fields are further interpolated at the same set of material points as in the first reference frame and are then added together to obtain the cumulative displacement fields. The resulting cumulative displacements represent the net displacement fields between each of the deformed images during cavitation (e.g., Fig. 2(c:ii-iv)) and the beginning image frame before cavitation (e.g., Fig. 2(b)). For example, the cumulative radial displacement fields at 14.0 µs and 26.0 µs are shown in Fig. 2(g, h). We also note that the radial displacement at the bubble wall is \((R - R_{\text {sf}})\), where \(R_{\text {sf}}\) is the bubble’s stress-free radius, which is very close to bubble’s equilibrium radius \(R_0\). More details about the bubble’s stress-free radius and equilibrium radius will be discussed in “Residual Deformation Fields, Bubble’s Stress-free, and Equilibrium Radii”.

Incremental mode DIC might lead to error accumulation when we interpolate cumulative displacement fields. Here we apply the thin plate interpolation scheme, and our interpolation starts from the last frame’s residual deformation field backward to the very beginning frame. These issues are discussed further in “Potential Error Sources”. After obtaining the cumulative displacement field, the displacement gradient at each nodal point is calculated by employing a local plane fitting method often used in DIC strain calculations [47], which can be used to calculate any finite strain measure. The plane fitting method uses neighboring data points within a user-determined distance. Here, we use 24 pixels or three times the coarsest element size in our DIC post-processing. If a local user-defined fitting plane intersects the bubble wall, there will be no data points available in the bubble shadow area, and its local displacement gradient is computed only using all the available tracked displacement results belonging to the surrounding material. After calculating the cumulative displacement fields, we further compute full-field velocity and acceleration fields using the central difference scheme. For each nodal point i in the DIC mesh, we denote its cumulative displacements at time points \(t_{k-1}\), \(t_k\), and \(t_{k+1}\) as \(\mathbf {u}^{(i)}_{k-1}\), \(\mathbf {u}^{(i)}_{k}\), and \(\mathbf {u}^{(i)}_{k+1}\), respectively. Its velocity, \(\mathbf {v}^{(i)}\), and acceleration, \(\mathbf {a}^{(i)}\), at time \(t_k\) are

$$\begin{aligned} \begin{aligned} \mathbf {v}^{(i)}(t_k)&= \frac{\mathbf {u}^{(i)}_{k+1} - \mathbf {u}^{(i)}_{k-1}}{2 \Updelta t}, \\ \mathbf {a}^{(i)}(t_k)&= \frac{\mathbf {v}^{(i)}_{k+1} - \mathbf {v}^{(i)}_{k-1}}{2 \Updelta t} , \end{aligned} \end{aligned}$$
(1)

where \(\Updelta t\) is the temporal interval in the high-speed camera recorded image sequence and equals 0.5 µs in our LIC experiments. All DIC results are summarized in “Results”.

Results

By combining and improving two recently developed experimental techniques, namely, the Embedded Speckle Plane (ESP) patterning method [43], and the SpatioTemporally Adaptive Quadtree mesh Digital Image Correlation (STAQ-DIC) [38] method, we measure the full-field kinematic deformations of laser-induced inertial cavitation in highly compliant gelatin hydrogels at ultra-high strain rates on the order of \(10^3\) \(\sim\) \(10^6\) s\(^{-1}\)Footnote 2.

Recorded Laser-induced Cavitation Bubble Dynamics

Examples of typical reference and deformed speckle pattern images obtained using the ESP patterning method are shown in Fig. 2(b, c), along with their accompanying binarized image masks in Fig. 2(d) used to generate the adaptive quadtree meshes. At each time step, the bubble radius was determined using Taubin’s method [48]. The experimental measurement of the bubble radius versus time was repeated 3–5 times for each of the three different concentrations of gelatin hydrogel, and the results are summarized in Fig. 3(a–c). For each radius vs time curve, we have shifted the time axis to begin at the moment the cavitation bubble radius reaches \(R_{\text {max}}\) to allow for a visibly simpler comparison between multiple cavitation experiments. The maximum cavitation bubble radii \((R_{\text {max}})\) for 6%, 10%, and 14% gelatin hydrogels are 184.0 ± 18.2 µm, 175.9 ± 21.1 µm, and 171.0 ± 28.2 µm, and their equilibrium radii \((R_0)\) are 52.6 ± 1.3 µm, 48.9 ± 0.7 µm, and 77.1 ± 1.3 µm, respectively. The hoop stretch ratio at the bubble wall (\(\lambda := R/R_0\)) versus normalized time (\(t^* := tU_c/R_{\text {max}}\), where \(U_c=\sqrt{p_\infty / \rho }\) is a characteristic velocity, \(p_{\infty }= 101.3\) kPa is the far-field pressure, and \(\rho =\) 1.016, 1.027, 1.038 g/cm\(^3\) is the mass density of 6%, 10%, and 14% gelatin hydrogels, respectively [49]) curves are summarized in Fig. 3(d–f). The maximum hoop stretches for 6%, 10%, and 14% gelatin hydrogels are 3.29 ± 0.36, 2.99 ± 0.36, and 2.60 ± 0.19, respectively. Alternatively, the bubble radius can also be normalized by the maximum bubble radius \(R_{\text {max}}\), and \(R^*\) (\(R^* := R/R_{\text {max}}\)) vs. \(t^*\) curves for each gelatin hydrogel are shown in Fig. 3(g–i). Interestingly, we find that all the data points for each hydrogel concentration nearly collapse onto a normalized master curve during the first and second expansion and collapse events, a finding that is consistent with our previous work [13, 30].

Fig. 3
figure 3

Results for the measured cavitation bubbles in 6%, 10%, and 14% gelatin hydrogels. (a–c) experimentally measured bubble radii vs. time curves for various gelatin concentrations, (d–f) the corresponding circumferential stretch ratio (\(\lambda := R/R_0\)) vs. normalized time (\(t^* := tU_c/R_{\text {max}}\)) curves, and (g–i) normalized bubble radius (\(R^* := R/R_{\text {max}}\)) vs. normalized time (\(t^*\)) curves. Each gelatin concentration was measured three to five times to obtain statistical information. The time axis is shifted such that \(t=0\) occurs at \(R = R_{\text {max}}\) so the collapse times can be compared

Full size image

DIC Results: Displacement and Strain Fields

Using the DIC post-processing routine as described in “Digital Image Correlation Post-processing”, we obtain displacement fields for all 250 frames of the LIC event.Footnote 3 All events were recorded with a camera frame rate of two million frames per second. Because our LIC events are almost spherically symmetric, DIC-tracked 2D-projected deformation fields on the r-\(\theta\) plane where \(\varphi = \pi /2\) (cf., Fig. 12) are independent of the polar coordinate \(\theta\). We extract a 10-pixel-wide vertical slice of each frame’s full-field results (i.e., \(\theta \sim -\pi\)/2) and concatenate them together to create kymographs to visualize the spatiotemporal evolution of the kinematic fields for each gelatin concentration due to the laser-induced cavitation event as shown in Fig. 4. Results for 6%, 10%, and 14% gelatin hydrogels are summarized in Fig. 4(a), (b), and (c) columns, respectively. The evolution of the radial displacement \(u_r\), radial velocity \(v_r\), radial acceleration \(a_r\), radial logarithmic strain \(E_{rr}\), and circumferential logarithmic strain \(E_{\theta \theta }\) fields for similarly sized bubbles are shown in Fig. 4 rows (i-v). The circumferential displacement component, \(u_{\theta }\), and logarithmic shear strain component, \(E_{r \theta }\), are summarized in Appendix 2, Fig. 13, where \(u_{\theta } < 5\) µm and \(E_{r \theta } < 0.05\). These values are relatively small compared to the corresponding quantities in Fig. 4, where \(u_r\) is up to 60 µm and \(|E_{rr}|\) and \(E_{\theta \theta }\) are up to 0.50 and 0.30, respectively. Based on these observations, we can claim that our LIC events are almost spherically symmetric.

Fig. 4
figure 4

Kymographs of kinematic fields in three concentrations, (a) 6%, (b) 10%, and (c) 14%, of gelatin due to a single laser-induced cavitation bubble. The kymographs are created by taking a 10-pixel-wide vertical slice of the full-field data symmetric about the center of the cavitation bubble for each frame over 250 frames at a camera frame rate of 2 million frames/sec. The resulting (i) radial displacement \(u_r\), (ii) radial velocity \(v_r\), (iii) radial acceleration \(a_r\), (iv) radial logarithmic strain \(E_{rr}\), and (v) circumferential logarithmic strain \(E_{\theta \theta }\) fields are plotted against time for all three gelatin concentrations. In all of these kymographs, the cavitation bubble is shown as the black and grey region at the top of each series

Full size image

One point to note is that the visualized kymographs are created directly from DIC post-processing results without additional smoothing or averaging operations. Inspired by these kymographs and the experimental justification of spherical symmetry in LIC events, in “Circumferentially Averaged Fields”, we circumferentially average the full-field deformation results to examine the radial dependence of each of the tracked kinematic quantities.

Circumferentially Averaged Fields

To further examine the spatial dependence of each of the DIC-derived kinematic quantities, we circumferentially average each quantity noting that the full-field data in Fig. 4 is nearly spherically symmetric. Figure 5 and 6 show the experimentally measured data (colored dots) and the theoretically calculated fields, assuming spherical symmetry and incompressibility, (solid curves) plotted against the radial coordinate normalized by the maximum bubble radius \(R_{\text {max}}\). Details of the theoretical calculations are summarized in Appendix 1. Results for the radial displacement \(u_r\), radial logarithmic strain \(E_{rr}\), and circumferential logarithmic strain \(E_{\theta \theta }\) fields for 10% gelatin LIC experiments are summarized in columns (ii-iv), respectively. Figure 5(a–c) show fields corresponding to the bubble’s first expansion, first collapse, and second expansion regimes; while Fig. 6(a) and (b) show fields corresponding to the first five peaks and collapses. Each subfigure contains results from five representative frames, and the corresponding frame time point for each curve is shown as a circular marker using the same color on the bubble radius vs. time plot in column (i) along the same row.

From Figs. 5 and 6, we further fit the circumferentially averaged experimental measurements using piecewise spline functions and compute differences between experimental results and their theoretical counterparts, which are plotted in Fig. 7. In general, our experimental measurements agree well with theoretical predictions when \(r > 2 R_{\text {max}}\), and the overall maximum displacement and strain differences are smaller than 10 µm and 10%, respectively.

Fig. 5
figure 5

(i) Bubble radius vs. time curves and kinematic fields, (ii) radial displacement \(u_r\), (iii) radial logarithmic strain \((E_{rr})\), and (iv) circumferential logarithmic strain \((E_{\theta \theta })\), are plotted against the radial distance from the center of the cavitation bubble for 10% gelatin. Experimental and theoretical results are plotted in columns (ii-iv) using colored dots and colored solid lines, respectively. The rows (a) first expansion, (b) first collapse, and (c) second expansion each contain data from five representative frames. The corresponding frame time point for each solid curve is shown as a circular marker using the same color on the bubble radius vs. time plot in column (i) in the same row

Full size image
Fig. 6
figure 6

(i) Bubble radius vs. time curves and kinematic fields, (ii) radial displacement \(u_r\), (iii) radial logarithmic strain \((E_{rr})\), and (iv) circumferential logarithmic strain \((E_{\theta \theta })\), are plotted against the radial distance from the center of the cavitation bubble for 10% gelatin. Results are organized as described in Fig. 5 and are presented for frames corresponding to the first five peaks (row (a)) and collapses (row (b))

Full size image
Fig. 7
figure 7

Differences between the experimentally measured kinematic fields and their theoretically calculated counterparts. Differences for (ii) radial displacement \(u_r\), (iii) radial logarithmic strain \((E_{rr})\), and (iv) circumferential logarithmic strain \((E_{\theta \theta })\) are plotted against the radial distance from the center of the cavitation bubble for 10% gelatin. The rows (a) first expansion, (b) first collapse, (c) second expansion, (d) all peaks, and (e) all collapses each contain data from five representative frames. The corresponding frame time point for each curve is shown as a circular marker using the same color on the bubble radius vs. time plot in column (i) in the same row

Full size image

Discussion

Comments on Gelatin Preparation with Embedded Speckle Planes

Previous methods of embedding a speckle plane into a gel used a volumetric 3D printing method that utilizes a granular material as a continuously deformable scaffold [42, 43]. Our improved approach simplifies this process by utilizing the thermal reversibility of gelatin to embed a speckle pattern. This new process does not require specialized equipment or knowledge; however, it can only be used with thermally reversible gels. The use of crosslinking agents such as glutaraldehyde can be used to create a chemically crosslinked gelatin if desired. However, we find that gelatin crosslinked by glutaraldehyde will cause brittle fracture of the gel during cavitation and result in non-spherical deformations.

Experimental Findings vs. Theoretical Predictions

DIC methods can be considered low-pass spatial filters that average the deformation fields over the size of a given DIC subset (40 pixels \(\times\) 40 pixels or 64 µm \(\times\) 64 µm in this study). Although STAQ-DIC can measure displacements very close to complex boundaries, this low pass filtering inherent to DIC will still underestimate the true magnitudes of the displacement and strain fields in the near-field of the bubble wall since deformations change rapidly in this region. When compared to the theoretical predictions we find a difference of up to 10 µm in displacement and up to 10% strain in the strain measurement results (see Fig. 7). The differences between the experimental results and theoretical calculations can also come from approximation errors in the theoretical modeling. For example, we assume that the surrounding deformation field is ideally spherically symmetric and the surrounding material is incompressible. Though, from our measurements, these idealizations still seem to hold true within the aforementioned error bounds (see Appendix 2 Fig. 13 for DIC results on the circumferential displacement and shear logarithmic strain components, \(u_{\theta }\) and \(E_{r \theta }\), respectively).

We also validated our DIC measurements using a synthetic case. First, we numerically simulate the dynamics of laser-induced inertial cavitation following the framework described in Estrada et al. [30]. The simulated bubble radius vs. time curve is plotted in Fig. 8(a) as a black dashed line. All the parameters, including surrounding material properties, cavitation initial conditions, and bubble equilibrium states in the numerical simulation are extracted using the 10% gelatin data sets where the maximum bubble radius, \(R_{\text {max}}\), is 154.1 µm or 96.3 pixels, and the equilibrium radius, \(R_{0}\), is 57.0 µm or 35.6 pixels. Here, we use the same µm to pixel ratio as in our experiments such that 1 pixel corresponds to 1.6 µm. The surrounding material is modeled as a neo-Hookean Kelvin-Voigt material whose dynamic shear modulus is 46.17 kPa and viscosity is 0.088 Pa\(\cdot\)s. From the numerical simulation results, we interpolate a synthetic R-t curve with a sampling frequency of 2 million data points per second to mimic a high-speed camera capturing images, as shown in Fig. 8(a) by the red crosses data points. The displacement at the bubble wall is plotted as yellow circle symbols as \(u_r(R,t) = R(t) - R_0\). The deformation fields in the surrounding material follow (5–6), which are further used to deform the reference image and interpolate the deformed images using a bicubic interpolation scheme. Since the pixel grayscale value interpolation might be inaccurate near the edges, we crop both the reference and deformed images by 10 pixels around all boundaries. The reference image at the final equilibrium and the deformed image corresponding to \(R_{\text {max}}\) are shown in Fig. 8(b:⁎) and (b:⁎⁎), respectively. All the images in the time series have the same dimensions of 380 pixels \(\times\) 230 pixels, with the bubble center located at pixel [190, 10]. We follow the same STAQ-DIC post-processing procedure as described in “Digital Image Correlation Post-processing”, and the reconstructed displacement field (ii) is further compared to the theoretical displacement field (i) and our experimental measurement (iii) in Fig. 8(c). We find that all three displacement fields agree well with each other. It is not surprising that the STAQ-DIC tracked deformation fields underestimate the true displacements near the bubble wall because of its inherent low pass filtering feature. However, this underestimation only exists in a small area where \(u_r > 70\) µm; this border is marked using a white dashed curve in Fig. 8(c:i).

Fig. 8
figure 8

Validation of the DIC post-processing via a synthetic case. (a) One numerically simulated bubble dynamics R-t curve for laser-induced inertial cavitation in a 10% gelatin hydrogel. The radial displacement at the bubble wall is plotted as yellow circles. (b) The reference (⁎⁎) and the deformed (⁎) DIC images at the final equilibrium and the \(R_{\text {max}}\) time points. Two DIC local subsets are zoomed-in to show the DIC speckle pattern. (c) The STAQ-DIC tracked displacement field (ii) is compared to the theoretical, synthetic deformation field (i) and our 10% gelatin experimental results (iii)

Full size image

Residual Deformation Fields, Bubble’s Stress-free and Equilibrium Radii

To experimentally investigate one of the key assumptions in our previously published Inertial Microcavitation Rheology (IMR) technique [13, 23, 30], namely that a stress-free material state exists when the bubble radius reaches its equilibrium point, i.e., at the time when the dynamic cavitation oscillations have fully decayed, we measured the residual deformation fields using DIC by comparing the image frame \(\sim\)30 seconds after the LIC event to the undeformed material frame. In our LIC experiments, the cavitation bubbles reach an equilibrium radius, \(R_0\), after several expansion-collapse cycles (\(\sim\) O(100)µs) followed by a slower diffusion process (\(\sim\) O(100)s) that eventually dissolves the final bubble. Here we focus on the residual deformation fields around the bubble at its equilibrium radius \(R_0\) after cessation of the cavitation dynamics but before the slow diffusion process has sufficient time to affect the bubble radius.

For a material holding a spherical cavity to be stress-free when the naive or virgin state of the material did not possess such a cavity, the volume contained by the spherical cavity must have been consumed during the cavitation process. Therefore, to claim that the material surrounding the cavitation bubble at equilibrium is stress-free, these conditions must be experimentally verified. To directly observe the speckle displacement near the bubble wall, we take the absolute value of the image grayscale value subtraction between the virgin material and the material at equilibrium as shown in Fig. 9(b–d). The white speckles outside of the dashed red line in the breakout of Fig. 9(d) show that the resulting radial displacement of the speckles is very small (i.e \(\sim\) 4 pixels or 6.4 µm). This result can be explained by considering the amount of material that is consumed via chemical reactions and plasma formation during the nucleation stage of the cavitation event. This spherical volume of material should have a radius equivalent to a stress-free material condition as shown in Fig. 9(e:ii). During the inertial dynamics phase, the amount of radial deformation \(u_r\) in the surrounding speckle plane should therefore be measured from this stress-free radius and the measured radius of the cavitation bubble R(t) following (5–6). At the equilibrium radius \(R_0\), any residual stress in the material will cause the cavitation bubble to be slightly larger than the radius of the stress-free material condition.

Fig. 9
figure 9

Two images are selected from (a) the bubble R-t curve, (b) the virgin reference material, and (c) the equilibrium image and are compared via the absolute value of pixel subtraction. (d) The resulting image difference reveals negligible speckle displacement immediately surrounding the equilibrium bubble. (e) This can be explained by considering the ablation of the material caused by the plasma reaction occurring at the time of nucleation (i-ii). During the inertial dynamics phase (iii), all displacement of the speckle pattern \(u_r\) must first take the material ablation into account when comparing the resulting bubble radius measured in each frame R(t) as it reaches an equilibrium radius \(R_0\) (iv) which is assumed to exist in a stress-free condition. The fact that the image difference in (d) shows a minimal shift in the speckle position near the bubble wall adds evidence to the claim that the material is stress-free

Full size image
Fig. 10
figure 10

Residual deformation and strain fields are plotted in the full field as well as radial linescans with gelatin concentrations separated into columns (a) 6%, (b) 10%, and (c) 14%. (row i) Radial displacement \(u_r\); (row ii) Radial logarithmic strain \(E_{rr}\)) as measured \(\sim\)30 seconds after the laser-induced inertial cavitation event; (row iii) Linescans of the radial displacement profile are overlayed with theoretical displacement fields corresponding to various ratios of the stress-free radius \(R_{\text {sf}}\) to the equilibrium radius \(R_0\). The purple dashed lines represent the ratio for the case where no material is ablated, and the green dashed lines represent the condition where the material has no residual stress. The orange dashed line represents the best fit of the data based on the theoretical displacement model. (row iv) This analysis is also plotted for the radial component of the logarithmic strain, with the yellow dashed line representing the fit of the data based on the theoretical field. These experimental results align with a fitted ratio of approximately \(R_{\text {sf}}/R_0 \approx 0.8\) suggesting that the material is indeed approximately stress-free

Full size image

For each concentration of gelatin hydrogel, we analyzed one representative cavitation event and plot its residual displacement and strain fields as shown in Fig. 10(rows i,ii). Since all the residual deformations appear to be spherically symmetric based on our measurements, we further average the residual radial displacement and logarithmic strain fields over the circumferential (hoop) direction (see Fig. 10(rows iii,iv)). We find that there are no significant differences in the residual deformation fields between the different concentrations of our gelatin hydrogels. Furthermore, we fit the stress-free radius using the residual radial displacement and strain measurements in the surrounding material by solving the following optimization problems:

$$\begin{aligned} R_{\text {sf}} = \min _{R_0} \Big \Vert \underbrace{ r - ( r^3 - R(t)^3 + R_0^3 )^{1/3} }_{u_{r,\,\text {model}}(t)} - u_{r,\,\text {exp}}(t) \Big \Vert ^2, \end{aligned}$$
(2)
$$\begin{aligned} R_{\text {sf}} = \min _{R_0} \Big \Vert \underbrace{ -2 \text {ln}(r/( r^3 - R(t)^3 + R_0^3 )^{1/3}) }_{E_{rr,\,\text {model}}(t)} - E_{rr,\,\text {exp}}(t) \Big \Vert ^2. \end{aligned}$$
(3)

The best-fit residual radial displacement and strain results are plotted in Fig. 10(row iii) using red dashed curves and (row iv) using yellow dashed curves, respectively. Experimental results are plotted in gray circles. We also compare these results with two ideal limiting cases: the stress-free radius is equivalent to the equilibrium radius (\(R_{sf}/R_0 = 1\)), and the stress-free radius is zero (\(R_{sf}/R_0 = 0\)). We find that for all three different concentration gelatin hydrogels, the ratios of stress-free radius to equilibrium radius match experimental results (\(R_{sf}/R_0 \sim 0.8-0.9\)) as shown in Fig. 10(rows iii,iv). The maximum, final residual logarithmic strain components, \(E_{rr}\), are about 5% and located adjacent to the bubble wall. These strain magnitudes are small compared to those encountered near peaks or collapses during the cavitation process (see Fig. 6), which supports the idealization of a stress-free equilibrium state invoked in IMR [30].

Potential Error Sources

Many experimental and analytical components are involved in the measurement of spatiotemporal deformation fields (e.g., Figs. 4–6). Each component contributes a potential source of error to our results, so we condition all our findings with the following discussion. First, based on our two-dimensional, projection-based DIC measurements we observe the deformation fields to be nearly spherically symmetric for the given boundary and loading conditions in our experiments. However, in general, the generated 3D cavitation bubbles present out-of-plane motion that may be non-spherical depending on the nucleation and boundary conditions [16, 33, 50].

Second, DIC-induced biasing (low-pass filter) errors due to underresolved displacement field information near the bubble wall can also contribute to systematic error accumulation, particularly when calculating very large strains near an evolving interface, i.e., the bubble wall [38, 39]. For these reasons, we exclude any strain values that are close to the bubble wall, i.e., within a distance equal to the length of one far-field DIC window subset, i.e., 40 pixels \(\times\) 40 pixels or 64 µm \(\times\) 64 µm.

Third, incremental mode DIC might lead to error accumulation when we interpolate cumulative displacement fields. Here, we compare the cumulative mode DIC results (see Fig. 11(i)) and two different interpolation schemes (“Inc-forward” and “Inc-backward”) which transform incremental DIC results into cumulative DIC results. In the “Inc-forward” scheme (see Fig. 11(ii)), incremental DIC results are interpolated from the beginning of the image sequence to the end, and then all the interpolated, incremental displacements at the same set of material points as in the first reference frame are added together to obtain the cumulative displacement. In the “Inc-backward” scheme (see Fig. 11(iii)), we start from the end of the image sequence, i.e., the residual deformation field after LIC, and interpolate and sum back to the very beginning of the image sequence. All of these computed cumulative radial displacement \(u_r\) and logarithmic strain \(E_{rr}\) results are further analyzed and compared. Here, we take an LIC event in a 14% gelatin hydrogel sample as a representative example, as shown in Fig. 11. We find that cumulative mode DIC does not accumulate any errors since all the subsequent frames are always compared with the first undeformed, reference frame. However, cumulative mode DIC only tracks small deformations well (see Fig. 11(i:**)), and it cannot solve large deformation fields near the bubble wall where the hoop stretch ratio can be large during the bubble’s first expansion-collapse cycle (see Fig. 11(i:*)). The “Inc-forward” scheme tracks the first expansion-collapse cycle well, but accumulates large errors after the first violent collapse (see Fig. 11(ii:***)). The “Inc-backward” scheme provides the best overall results since it shows good agreement with the cumulative mode DIC results after the first violent collapse, and it is also able to track extremely large deformations near the bubble wall during the bubble’s first expansion-collapse cycle.

Fig. 11
figure 11

Comparison of three different DIC post-processing schemes to solve for the cumulative deformation fields

Full size image

Conclusion and Future Directions

In this paper, we present full-field in-situ deformation measurements of soft viscoelastic materials at ultra-high strain rates, i.e., on the order of \(10^3\) \(\sim\) \(10^6\) s\(^{-1}\), near an oscillating inertial cavitation bubble. To achieve this, we integrated and advanced our previously developed embedded speckle pattern (ESP) method with our recently developed spatiotemporally adaptive quadtree mesh digital image correlation (STAQ-DIC) technique. By careful comparison of our experimental field measurements with the theoretical kinematics of cavitation in soft matter under the idealizations of spherical symmetry and incompressibility, we find generally good agreement between the experimental measurements and the theoretical predictions. We also find that the use of the quasi-equilibrium bubble radius, \(R_0\), is experimentally justified in the previous Inertial Microcavitation Rheometry (IMR) framework [13, 23, 30, 51], generally incurring no more than 5% residual strain compared to the undeformed material state prior to laser-induced bubble nucleation. Furthermore, the assumption of spherical symmetry within the context of IMR for a sample geometry with dimensions much larger than 2\(\sim\)3 \(R_{\text {max}}\) seems to be justified according to our full-field measurements.

We conclude our paper with some discussion of future research directions. First, our approach shown here opens up exciting new opportunities for examining more complicated and spatially heterogeneous deformation fields within soft materials with full control of the boundary conditions. Specifically, our method can be used to measure cavitation under different external driving forces [6, 52,53,54,55,56] in various material systems and cavitation near different boundary conditions, such as non-spherical cavitation dynamics [12, 16, 57], multi-bubble dynamics [58, 59], cavitation spallation and interfacial cleaning/wear problems [33, 60], cavitation along an impedance-mismatched material interface [25, 34, 61, 62] or in 3D additive manufactured metamaterials.

A clear opportunity exists to utilize our previously developed IMR framework to allow for the simultaneous characterization of material properties while measuring the displacement field due to cavitation. Using a constitutive model, these data can be used to calculate the induced stress and hydrostatic pressure fields. This IMR framework uses the assumption that the surrounding material remains unaffected by cavitation, however, material damage and fatigue can accumulate during the bubble’s expansion-collapse cycles [58, 63, 64]. The measured kinematic results from this method along with known material properties from IMR can be used to develop new constitutive models which quantify cavitation-induced material damage.

Finally, our experimental technique can be easily extended to multiple existing material characterization techniques. The resulting high-resolution full-field measurements can also be integrated into emerging machine learning/data-driven methods to perform computational cavitation simulations with high fidelity [65, 66].