Augmented Lagrangian Digital Volume Correlation (ALDVC)

Abstract

Digital volume correlation (DVC), the volumetric extension of the popular digital image correlation (DIC) technique, is a powerful experimental tool for measuring 3D volumetric full-field displacements and strains. Most current DVC algorithms can be categorized into either local or finite-element-based global methods. As with most experimental approaches, there are drawbacks with each of these methods. In the local method the subvolume deformations are estimated independently and the computed displacement field may not necessarily be kinematically compatible. Thus, the deformation gradients can be noisy, especially when using small volumetric subsets. Although the global method often enforces kinematic compatibility, it generally incurs substantially greater computational costs than its local counterpart, which is especially significant for large volumetric data sets. To address these shortcomings, we present a new hybrid DVC algorithm, called augmented Lagrangian digital volume correlation (ALDVC), which combines the advantages of both the local (fast computation time) and global (compatible displacement field) methods. This new algorithm builds on our recent work on the augmented Lagrangian digital image correlation (2D-ALDIC) technique and solves the general motion optimization problem by using the alternating direction method of multipliers (ADMM). We demonstrate that our ALDVC algorithm has high accuracy and precision while maintaining low computational cost, and is a significant improvement compared to current local and global DVC methods. ALDVC is a computationally efficient algorithm to measure 3D volumetric displacements and strains. An open-source Matlab implementation is freely available.

Introduction

Digital Volume Correlation (DVC) is one of the most popular experimental methods for measuring 3D, volumetric full-field deformations in solid materials. Deformations are computed by tracking motions between successive 3D image volumes. Volumetric images are typically reconstructed from image stacks captured by computed X-ray tomography (CT) [1, 2], magnetic resonance imaging (MRI) [3], 3D confocal microscopy [4, 5], neutron tomography [6], or other 3D volumetric imaging techniques [7]. DVC can be viewed as the volumetric 3D extension of 2D Digital Image Correlation (2D-DIC). In contrast to 2D-DIC, which is limited to measuring 2D in-plane deformations, or 3D-DIC that measures in-plane and out-of-plane displacement on a surface, DVC measures 3D deformations within volumetric images. Although the mathematical formulation of DVC can be derived using the same fundamental minimization process as for 2D-DIC, the computational cost of DVC is dramatically larger due to the additional dimension.

Currently, several algorithms exist to compute full-field displacements via sub-voxel correlative techniques [8,9,10]. Most of these methods are broadly categorized into either local or global methods. In the local methods, the full volume is first divided into a collection of smaller, local subsets, where each local subset is typically assumed to undergo an affine deformation. All of the subset motion field equations are solved independently, i.e., a residual between a given subset image pair containing the reference and deformed bodies is minimized. This has followed from early DVC algorithms, i.e., Bay et al. [1], which were used to measure rigid translations of local subsets. Cross-correlation based implementations are often chosen for simplicity and computational efficiency; however, with large stretches, shears, or rotations, the matching can become degenerate, leading to poor motion reconstruction performance. Bar-Kochba et al. [8, 11] improved the FFT-based method to extend rigid translations to piecewise affine deformations by incorporating correlation filters and an iterative image deformation method (IDM) adapted from the fluid mechanics Particle Image Velocimetry (PIV) community, e.g., Scarano et al. [12].

Besides FFT-based implementations, Gates et al. [9] employed a first order shape function with 12 Degrees of Freedom (DoFs) for each local subset and optimized a similarity matching function approximated by voxel-wise summations of intensities. Although it contains 12 DoFs per subset it is computationally attractive since it can be implemented with an inverse compositional Gauss-Newton (IC-GN) scheme that affords rapid convergence [9, 13]. The voxel-wise IC-GN method can also straightforwardly be extended to higher-order local subset shape functions. For example, recently Wang et al. [14] applied both first and second order shape functions to local subvolumes and established a set of criteria for selecting the order of the shape function in a self-adaptive way.

All of the methods described above are local methods; for each case, the local 3D subvolumes are generally much smaller in size than the full volume. The deformation of each subvolume can be solved relatively quickly and independently, thus scaling via parallelization is easily implementable. However, because the deformation of each subvolume is obtained independently, the individual deformation fields from each subvolume may not be kinematically compatible with each other, which can lead to noise when calculating the strain field. A number of low-pass filtering and smoothing schemes along with other sophisticated regularization schemes have been proposed to address this issue [15,16,17,18]. Regardless of the choice of displacement differentiation scheme and smoothing, the computation of the local strain fields is typically unrelated to the underlying DVC mathematical optimization problem of obtaining the displacement field in the case of the local methods.

When using a global DVC approach, the full deformation field is generally represented using a basis set, often discretized based on a finite element formulation (e.g., 8-node hexahedron (HEX8) elements [10] or 4-node tetragonal (T4) elements [19]), such that the full image domain is analyzed together to obtain the coefficients relative to this basis set. However, this approach is usually computationally expensive and often difficult to implement in parallel, especially for large volumetric data sets. Furthermore, most global DVC algorithms usually provide some level of regularization to further decrease displacement noise and speed up convergence. This can be effective, but spatial dependencies of the displacement and strain fields may become excessively smoothed depending on the level of regularization used. Global DVC approaches therefore often require extreme care in application if inhomogeneous deformations are to be expected, although techniques such as adaptive mesh refinement (e.g., [20]) can ease the process.

Recently, a new hybrid local and global image registration method was developed that matches 2D subsets locally while enforcing full-field kinematic compatibility among all subsets as a global constraint in an augmented Lagrangian form. This technique is called Augmented Lagrangian Digital Image Correlation (ALDIC) [21], and it combines the advantages of both the local (fast and easily parallelized) and the global (guaranteed kinematic compatibility) methods. This method has been shown to work well when combined with image compression techniques [22] and can be easily combined with a self-adaptive meshing algorithms [20]. In this paper, we extend this augmented Lagrangian-method to the 3D volumetric case (ALDVC), assess its performance, and compare it with other popular DVC methods. Specifically, we introduce an auxiliary, globally compatible displacement field and introduce the constraint that this displacement field and its gradients equal the locally correlated displacement values. The augmented Lagrangian approach mentioned above, specifically the alternating direction method of multipliers, has been used previously to solve a variety of constrained minimization problems [23, 24]. It augments the objective functional linear Lagrangian multipliers of the constraints along with quadratic penalties of the constraints for convenient implementation and numerical stability. It generally performs better than the penalty method, which adds quadratic penalties with very large penalty coefficients to guarantee accuracy, risking an ill-conditioned problem.

We implement the formulated augmented Lagrangian DVC optimization problem using the alternating direction method of multipliers (ADMM), which is a form of operator splitting [25, 26]. In each ADMM iteration step, we successively decompose the global optimization problem into two subproblems: the first (subproblem 1) is computed locally and in parallel, and the second (subproblem 2) focuses on solving the auxiliary deformation field, which is computed globally but remains computationally efficient. Penalty coefficients are updated automatically after each ADMM iteration to satisfy optimality conditions.

This paper is structured as follows. We begin by providing the mathematical background and 3D-DVC optimization formulation in the “Problem Formulation” section. Next, we introduce our new augmented Lagrangian DVC, or ALDVC, method and describe its implementation in “Augmented Lagrangian DVC (ALDVC) Method”. We then assess the performance of our new method using both synthetically and experimentally generated homogeneous and inhomogeneous deformation fields. Finally, we provide a brief summary, and address limitations and future directions in the “Conclusions” section.

Problem Formulation

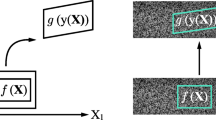
Consider a domain ${\Omega } \in \mathbb {R}^{3}$ undergoing a general deformation $\mathbf {y}: {\Omega } \rightarrow \mathbb {R}^{3}$. As seen in Fig. 1(a), let X denote the reference or undeformed coordinates of any voxel X in Ω and y(X) denote the current image or current voxel position. Suppose we have a speckle pattern with grayscale value f(X) in the reference domain, and the corresponding grayscale value g(y) in the current configuration, the image can be written as

$$ f(\mathbf{X})=g(\mathbf{y}(\mathbf{X})). $$

(1)

The DVC problem is the inverse problem of finding the deformation mapping y(X) that uniquely maps an image in the reference configuration, f(X), to an image in the deformed configuration, g(y). The above inverse problem can be solved by maximizing the cross correlation function (C_CC) or minimizing the sum of squared differences (C_SSD),

$$ C_{\text{CC}} = {\int}_{\Omega} f(\mathbf{X})g(\mathbf{y}(\mathbf{X})) d \mathbf{X} \rightarrow \text{maximize over } \mathbf{y}: {\Omega} \!\rightarrow\! \mathbb{R}^{3}. $$

(2)

$$ \begin{array}{@{}rcl@{}} C_{\text{SSD}} &=& {\int}_{\Omega} \left| f(\mathbf{X}) - g(\mathbf{y}(\mathbf{X})) \right|^{2} d \mathbf{X}\\ &&\rightarrow \text{minimize over } \mathbf{y}: {\Omega} \rightarrow \mathbb{R}^{3}. \end{array} $$

(3)

Fig. 1

(a) Schematic showing a volumetric DVC reference image f(X), with a general speckle pattern, deforming into the deformed image g(y(X)) under some mapping y and the change of variables involved within the IC-GN iteration in the local subvolume DVC method. X and y coordinates are in the reference and deformed images, respectively. z coordinates are in current IC-GN iteration. (Details regarding the local IC-GN method are summarized in Appendix B). (b) A schematic comparison between the local DVC method (left), where all the subvolumes are analyzed independently, and the global DVC method (right), where a global basis set is used to represent the full-field deformation (similarly, see the summary in Appendix C)

Generally, the 3D volume images are in units of voxels taking discrete values, so we can either replace the integrals in equations (2) and (3) with a voxel-wise sum, or interpolate the 3D volume images (typically with tri-cubic polynomials or tri-cubic splines [27]) whenever sub-voxel grayscale values are needed.

In general, most DVC algorithms can be cast into either of two categories, local methods (see Fig. 1(b), left column; Appendices A & B) or global methods (see Fig. 1(b), right column; Appendix C). In the local method, the volume of interest (VOI) is divided into subvolumes and discrete calculation points (usually the center points of the local subvolumes) are first defined in the reference volume images and then tracked in the deformed volume image. As the name “local” indicates, we ignore any connectivity and kinematic compatibility between neighboring subvolumes. Initially, the subvolumes are assumed to have uniform deformation and are tracked independently and in parallel, although initial-guess propagation or a posteriori regularization is possible (e.g. the parallelized 2D implementation of [28]). This process is fast, but the solved deformation field can be incompatible and noisy. In the global DVC method, all the calculation points are solved at the same time and the final deformation field is guaranteed to be kinematically compatible, however, the global method is usually much more computationally expensive. To overcome the kinematic compatibility limitations of the local DVC approaches and the high computational cost associated with the global DVC methods, we introduce a new, hybrid formulation that automatically satisfies the kinematic compatibility of the computed displacement field at computational cost closer to the local DVC methods. We term this the augmented Lagrangian DVC (ALDVC) technique, which can be viewed as the 3D extension of our recently demonstrated 2D-ALDIC method [21].

Augmented Lagrangian DVC (ALDVC) Method

Motion Estimation Formulation via ALDVC

In the local DVC method (see Appendix B (17)) the subset displacements u_i and deformation gradients F_i are generally solved for independently. However, from a global perspective, the full-field displacements should satisfy a kinematic compatibility constraint {F} = D{u}, where D is an appropriate discrete gradient operator. To treat this global constraint efficiently, we introduce an auxiliary compatible global displacement field $\hat {\mathbf {u}}$ that satisfies

$$ \mathbf{F}_{i} = \nabla \hat{\mathbf{u}} (\mathbf{X}_{i0}), \quad \mathbf{u}_{i} = \hat{\mathbf{u}}(\mathbf{X}_{i0}). $$

(4)

where X_i0 is the center point of the local subset Ω_i. Specifically, we apply this global constraint in the augmented Lagrangian form and consider the following correlation functional form

$$ \begin{array}{@{}rcl@{}} \mathcal{L}_{0} &=& \sum\limits_{i} {\int}_{{\Omega}_{i}} \left( \left| f(\mathbf{X}) - g(\mathbf{X}+\mathbf{u}_{i}+ (\mathbf{F}_{i} (\mathbf{X}-\mathbf{X}_{i0}))) \right|^{2}\right.\\ && \left. + \frac{\beta}{2}\left| (\mathbf{D} \hat{\mathbf{u}})_{i} - \mathbf{F}_{i} \right|^{2} + \boldsymbol{\nu}_{i} : ((\mathbf{D} \hat{\mathbf{u}})_{i} - \mathbf{F}_{i})\right.\\ && \left. + \frac{\mu}{2} \left| \hat{\mathbf{u}}_{i} - \mathbf{u}_{i} \right|^{2} + \boldsymbol{\lambda} \cdot (\hat{\mathbf{u}}_{i} - \mathbf{u}_{i}) \right) d \mathbf{X}, \end{array} $$

(5)

where we use the Frobenius norm for matrices $\left | \mathbf {A} \right |^{2} = {\sum }_{i}{\sum }_{j} \left | a_{ij} \right |^{2}$, L₂ norm for vectors $|\mathbf {a}|^{2} = {\sum }_{i} {a_{i}^{2}}$, and : for the double dot product between two matrices $\mathbf {A}:\mathbf {B} = {\sum }_{i}{\sum }_{j} A_{ij}B_{ij}$. Above, {ν_i}, {λ_i} are Lagrange multipliers that enforce the constraint (4). Finally, β and μ are two positive real scalars. It is convenient to set W_i := ν_i/β, v_i := λ_i/μ and simplify (5) as

$$ \begin{array}{@{}rcl@{}} \mathcal{L}_{0} &= & \sum\limits_{i} {\int}_{{\Omega}_{i}} \left( \left| f(\mathbf{X}) - g(\mathbf{X}+\mathbf{u}_{i}+ (\mathbf{F}_{i} (\mathbf{X}-\mathbf{X}_{i0}))) \right|^{2}\right.\\ && \left. + \frac{\beta}{2}\left| (\mathbf{D} \hat{\mathbf{u}})_{i} - \mathbf{F}_{i} + \mathbf{W}_{i} \right|^{2} + \frac{\mu}{2} \left| \hat{\mathbf{u}}_{i} - \mathbf{u}_{i} + \mathbf{v}_{i} \right|^{2} \right) d \mathbf{X}. \\ \end{array} $$

(6)

The Alternating Direction Method of Multipliers

We use the alternating direction method of multipliers (ADMM) allowing us to split the global minimization problem into independently solvable subdomain problems, which can be solved quickly at each global iteration step [26]. Given $\{\mathbf {F}_{i}^{k}\}, \{\mathbf {u}_{i}^{k}\}, \{\hat {\mathbf {u}}_{i}^{k}\}, \{\mathbf {W}_{i}^{k}\},\{\mathbf {v}_{i}^{k}\}$, we find the (k + 1) update using the following steps:

• Subproblem 1: local 1 update. While holding $\{\hat {\mathbf {u}}_{i}^{k}\}$, $\{\mathbf {W}_{i}^{k}\},\{\mathbf {v}_{i}^{k}\}$ fixed, minimize ${\mathscr{L}}$ over {F_i},{u_i}, to obtain $\{\mathbf {F}_{i}^{k+1}\}, \{\mathbf {u}_{i}^{k+1}\}$:

  $$ \{\mathbf{F}_{i}^{k+1}{}\}{\kern-.5pt},{\kern-.6pt} \{\mathbf{u}_{i}^{k+1}{}\}\! = \underset{\{\mathbf{F}_{i}\},\{\mathbf{u}_{i}\}}{\arg\min}~ \mathcal{L}\! \left( {\kern-.5pt}\{\mathbf{F}_{i}{\kern-.5pt}\}{\kern-.5pt},{\kern-.6pt} \{\mathbf{u}_{i}{\kern-.5pt}\}{\kern-.5pt},{\kern-.6pt} \{\hat{\mathbf{u}}_{i}^{k}{\kern-.5pt}\}{\kern-.5pt},{\kern-.6pt} \{\mathbf{W}_{i}^{k}{\kern-.5pt}\}{\kern-.5pt},{\kern-.6pt}\{\mathbf{v}_{i}^{k}{\kern-.5pt}\}{\kern-.5pt} \right)\! . \\ $$

  (7)

  Since $\{\hat {\mathbf {u}}_{i}^{k}\}$ and thus $\{(\mathbf {D} \hat {\mathbf {u}})_{i}^{k}\}$ are known, this problem is broken down into a series of local problems that can be solved independently for each i:

  $$ \begin{array}{@{}rcl@{}} \mathbf{F}_{i}^{k+1} , \mathbf{u}_{i}^{k+1} &=& \underset{\mathbf{F}_{i},\mathbf{u}_{i}}{\text{argmin}} {\int}_{{\Omega}_{i}} \left( \vphantom{\left|\mathbf{v}_{i}^{k} \right|^{2}} | f(\mathbf{X}) \right.\\ && - g(\mathbf{X} + \mathbf{u}_{i} + \left( \mathbf{F}_{i}(\mathbf{X}-\mathbf{X}_{i0})\right))|^{2}\\ &&+ \frac{\beta}{2} \left| (\mathbf{D} \hat{\mathbf{u}})_{i}^{k} - \mathbf{F}_{i} + \mathbf{W}_{i}^{k} \right|^{2} \\ &&+ \frac{\mu}{2} \left| \hat{\mathbf{u}}_{i}^{k}\right.\left.\left.- \mathbf{u}_{i} + \mathbf{v}_{i}^{k} \right|^{2} \right) d \mathbf{X} . \end{array} $$

  (8)

  This is similar to computing the displacement field in the local DVC methods, which can be solved independently for each subset (see Appendix B).

• Subproblem 2: global update. While holding $\{\mathbf {F}_{i}^{k+1}\}$, $\{\mathbf {u}_{i}^{k+1}\}, \{\mathbf {W}_{i}^{k}\},\{\mathbf {v}_{i}^{k}\}$ fixed, we minimize ${\mathscr{L}}$ over $\{ \hat {\mathbf u}_{i}\}$ to obtain $\{\hat {\mathbf u}_{i}^{k+1}\}$:

  $$ \begin{array}{@{}rcl@{}} \{\hat{\mathbf u}_{i}^{k+1}\} &=& \underset{\{ \hat{\mathbf u}_{i}\}}{\text{argmin}} \mathcal{L} \left( \{\mathbf{F}_{i}^{k+1}\}, \{\mathbf{u}_{i}^{k+1}\}, \{\hat{\mathbf{u}}_{i}\}, \{\mathbf{W}_{i}^{k}\},\{\mathbf{v}_{i}^{k}\} \right)\\ &=& \underset{\{ \hat{\mathbf u}_{i}\}}{\text{argmin}} \sum\limits_{i} {\int}_{{\Omega}_{i}} \left( \frac{\beta}{2} \left| (\mathbf{D} \hat{\mathbf{u}})_{i} - \mathbf{F}_{i}^{k+1} + \mathbf{W}_{i}^{k} \right|^{2}\right.\\ && \left. + \frac{\mu}{2} \left| \hat{\mathbf{u}}_{i} - \mathbf{u}_{i}^{k+1} + \mathbf{v}_{i}^{k} \right|^{2} \right) d \mathbf{X} . \end{array} $$

  (9)

  Note that this is a global problem, but it is independent of the images f and g. Indeed, it leads to the linear problem

  $$ \hat{\mathbf{u}}^{k+1} = \left( \beta \mathbf{D}^{T} \mathbf{D} + \mu \mathbf{I} \right)^{-1} \left( \beta \mathbf{D}^{T} \mathbf{a} + \mu \mathbf{b} \right). $$

  (10)

  where $\mathbf {a} {=} \{\mathbf {F}_{i}^{k+1} {-} \mathbf {W}_{i}^{k}\}$ and $\mathbf {b} {=} \{\mathbf {u}_{i}^{k+1} - \mathbf {v}_{i}^{k} \}$. Since β and μ are fixed, the matrix $\left (\beta \mathbf {D}^{T} \mathbf {D} + \mu \mathbf {I} \right )^{-1}$ can be precomputed and stored, and therefore this step becomes a simple matrix-vector multiplication. Further, the matrix D is relatively sparse with the diagonal terms dominating the off-diagonal terms, allowing the matrix-vector multiplication to be computed quickly and efficiently.

• Subproblem 3: Lagrange multiplier update. Finally, we update {W_i},{v_i} as follows

  $$ \begin{array}{@{}rcl@{}} \mathbf{W}^{k+1}_{i} &=& \mathbf{W}^{k}_{i} + \left( (\mathbf{D}\hat{\mathbf{u}})_{i}^{k+1} - \mathbf{F}_{i}^{k+1} \right), \end{array} $$

  (11)
  $$ \begin{array}{@{}rcl@{}} \mathbf{v}^{k+1} &=& \mathbf{v}^{k} + \left( \hat{\mathbf{u}}^{k+1} - \mathbf{u}^{k+1} \right). \end{array} $$

  (12)

• Stopping criterion: The calculations are said to have converged when the L₂ norm between the current and previous displacement iteration, i.e., the norm $\left | \left ({\hat {\mathbf {u}}}^{k+1} - {\hat {\mathbf {u}}}^{k}\right )\right |$, is below a user set threshold tolerance value.

Convergence

We briefly recall some results from Boyd et al. [26] that apply to the ADMM algorithm proposed above. To begin we assume that the following conditions are true:

• Assumption 1: The functional C_i describing the match of intensities in the local subvolume (see Appendix B (18)) or the first term of ${\mathscr{L}}$ can be approximated by a closed, proper, and convex functional near the optimal solution.

• Assumption 2: The Lagrangian ${\mathscr{L}}_{0}$ with β = μ = 0 has a saddle point; i.e., there exist $(\{{\mathbf {F}}_{i}^{*}\}, \{ {\mathbf {u}}_{i}^{*}\}, \{\hat {\mathbf {u}}_{i}^{*}\}, {\{\boldsymbol {\nu }^{*}_{i}\}}$, $\{ \boldsymbol {\lambda }^{*}_{i}\})$ that for all $(\{{\mathbf {F}}_{i}\}, \{ {\mathbf {u}}_{i}\}, \{\hat {\mathbf {u}}_{i}\}, {\{\boldsymbol {\nu }_{i}\}}, \{ \boldsymbol {\lambda }_{i}\})$,

  $$ \begin{array}{@{}rcl@{}} &&\mathcal{L}_{0}(\{{\mathbf{F}}_{i}^{*}\}, \{ {\mathbf{u}}_{i}^{*}\}, \{\hat{\mathbf{u}}_{i}^{*}\}, {\{\boldsymbol{\nu}_{i}\}}, \{ \boldsymbol{\lambda}_{i}\})\\ &\leq& \mathcal{L}_{0}(\{{\mathbf{F}}_{i}^{*}\}, \{ {\mathbf{u}}_{i}^{*}\}, \{\hat{\mathbf{u}}_{i}^{*}\}, {\{\boldsymbol{\nu}^{*}_{i}\}}, \{ \boldsymbol{\lambda}^{*}_{i}\}) \\ &\leq& \mathcal{L}_{0}(\{{\mathbf{F}}_{i}\}, \{ {\mathbf{u}}_{i}\}, \{\hat{\mathbf{u}}_{i}\}, {\{\boldsymbol{\nu}^{*}_{i}\}}, \{ \boldsymbol{\lambda}^{*}_{i}\} ) \end{array} $$

Then, we have the following convergence

• Primal residual convergence: $\left (\mathbf {D}{\hat {\mathbf {u}}}^{k} - {\mathbf {F}}^{k} \right ) {\rightarrow } 0$ and $\left ({\hat {\mathbf {u}}}^{k} - {\mathbf {u}}^{k} \right ) {\rightarrow } 0$ as $k {\rightarrow } \infty$, i.e., the constraints are satisfied asymptotically;

• Dual residual convergence: $\left (\hat {\mathbf {u}}^{k+1} - \hat {\mathbf {u}}^{k} \right )$ → 0 as k → $\infty$, i.e., the dual feasibility is satisfied asymptotically;

• Objective convergence: ${\mathscr{L}}^{k}{\rightarrow } {\mathscr{L}}^{*}$ as $k {\rightarrow } \infty$, i.e., the Lagrangian approaches its optimal value;

• Dual variable convergence: $\mathbf {W}^{k} {\rightarrow } \mathbf {W}^{*}, \mathbf {v}^{k} {\rightarrow } \mathbf {v}^{*}$ as $k {\rightarrow } \infty$, where $\left (\mathbf {W}^{*}, \mathbf {v}^{*}\right )$ is a dual optimal point.

Note that the local functional C_i can be highly oscillatory and is thus not convex. However, if the initial guess for the local variables (i.e., {F_i} and {u_i}) is in the convergence basin of the local subset displacement field, then the first assumption is true. If this assumption is false, then subproblem 1 (7) diverges; this provides a check whether this assumption holds.

To speed up the calculations we simplify subproblem 1 of the ALDVC algorithm. The local problem (8) requires us to minimize over both u_i and F_i, which makes the local problem large and the overall convergence slow. Furthermore, the high dimensionality can lead to local minima and thus poor accuracy. Therefore, we simplify subproblem 1 as follows: in the (k + 1) iteration step, we update F^k+ 1 to be exactly equal to $\mathbf {D} \hat {\mathbf {u}}^{k}$ and only solve for u^k+ 1. We still use the IC-GN iterations to minimize the functional (see Appendix B). A summary of the complete ALDVC technique is given in Algorithm 1.

Assessing the Accuracy and Precision of the ALDVC Algorithm

In this section, we assess both the accuracy and precision of our proposed ALDVC method via both synthetically generated and experimentally applied deformation fields, and compare it to baseline local and global DVC methods. All algorithms are implemented in Matlab.

We use the following parameters unless specified otherwise. We use tri-cubic interpolation for the grayscale values at subvoxel positions.¹ Within the local subset DVC computations, we stop the IC-GN iterations when $\left | d_{i} \right |, \left | e_{jk} \right | < 10^{-4}$. Usually the IC-GN reaches convergence within several iteration steps. In the global DVC computations, we use HEX8 finite elements (linear, fully-integrated, eight-noded bricks) with a trilinear form of the domain’s displacement field approximating the exact displacement fields. We stop the iterations when the mean magnitude of the nodal displacement update is smaller than 10^− 4 voxels. For our ALDVC method, we start W and v from zeros. We choose μ to be $O(10^{-3}) {\sim } O(10^{-1})$ times the diagonal terms of $a^{\prime }_{ip}$. We take β = $\left [ O(10^{-2}) \sim O(10^{1}) \cdot \text {element size}^{2} \cdot \mu \right ]$ to balance the relevant terms. We use the same stopping criteria in subproblem 1 as in the local subvolume DVC ($\left | d^{\prime }_{i} \right | < 10^{-4}$), and we use the central difference operator D or HEX8 finite elements to solve subproblem 2. The ADMM iteration in ALDVC stops when $\left | \hat {\mathbf {u}}^{k+1} - \hat {\mathbf {u}}^{k} \right | < 10^{-4}$ voxels.²

We begin assessing the accuracy and precision of our ALDVC algorithm by employing synthetically generated images where the exact deformation is known. Furthermore, we use the root-mean-square (RMS) error given by

$$ \text{RMS error} \!:=\! \sqrt{\frac{{\sum\limits_{\# \ \text{of nodes}}} \left| \text{Numerical result} - \text{Exact value} \right|^{2}}{\# \ \text{of nodes}}}, $$

(13)

to assess the displacement and strain field reconstruction accuracy of our ALDVC technique.

Method of Obtaining Strain Fields

The complete strain field is an intrinsic output of both our ALDVC algorithm and the local IC-GN-based DVC minimization method, whereas in the global DVC method strains are calculated directly from the finite element mesh. Besides directly solving for the strain fields, it is also common to filter the solved displacement field with a spatial differentiation and smoothing kernel to obtain strain fields in the local DVC methods [8, 29, 30]. However, finding the optimal filter type and size to recover the underlying deformation displacement signal often requires care and experience of the DVC operator. Discussion of strain filters is outside the scope of this paper, but can be found elsewhere [8, 29, 30]. All the computed strains in this paper are in infinitesimal strains (e_xx = u_,x,e_xy = 1/2(u_,y + v_,x),e_yy = v_,y). However, other types of strains can also be easily computed.

Performance Assessment via Homogeneous Deformations

We begin the performance assessment of our new ALDVC technique by benchmarking against synthetically generated uniaxial translation, stretch, and rigid body rotation motion fields. In all the synthetic cases, an 8-bit grayscale reference volume image (image size: 512vx × 512vx × 192vx(vx: voxel) was first generated using a Gaussian-type point spread function (PSF) mimicking typically encountered diffraction-limited volumetric images of spherical fiducial markers acquired via optical 3D imaging (see Appendix D [8]). To generate deformed images accurately and according to the analytically imposed displacement mappings we follow the process of [21] extended to 3D using tri-cubic interpolation (e.g., [27]) to warp the images.

In this section, we set the local subset window size and window spacing to 30vx × 30vx × 30vx. All computations were performed by analyzing the full-field deformation at each increment with respect to the initial, undeformed reference configuration, i.e., cumulative mode. All the solved regions of interest (ROIs) are summarized in the supplementary materials (see Section S1) where only a small portion of the domain near the image borders is not solved due to the loss of information. Specifically, the test cases include:

• (i) Translation. We apply single axis translations in the x-direction with amplitudes ranging from 0 to 1 voxel in increments of 0.1 voxels.

• (ii) Uniaxial Stretch. We apply uniaxial stretches in the x-direction with stretch ratios from 1.0 to 1.3 in increments of 0.05 with no stretch in the y- and z-directions (i.e., zero Poisson’s ratio).

• (iii) Rotation. We apply in-plane rotations about the z-axis with rotation angles ranging from 0^∘ to 25^∘ in increments of 5^∘.

Figure 2 shows root-mean-squared (RMS) displacement and strain errors compared between a local FFT-based algorithm (a simplified³ method derived from [8]), a local IC-GN algorithm, a global algorithm, and our new ALDVC algorithm. These four methods were selected for the homogeneous test case to showcase the differences between the displacement measurement techniques underpinning our algorithm. In the homogeneous deformation cases, the local FFT DVC method has initially small errors that rapidly grow much larger than the other techniques as relative displacements increase – when deformations are small, the local FFT DVC method has high accuracy, however for large deformations the local FFT DVC has rapidly increasing errors. Errors in the global DVC method are also large because we do not use regularization – regularizers typically enforce zero gradients, which artificially forces the desired answer in the translation cases and biases the displacement reconstruction in the uniaxial and planar rotation cases. Our new ALDVC algorithm has the smallest errors in all homogeneous cases, since it provides balance between these error modes.

Fig. 2

Displacement and strain RMS errors of the synthetically applied homogeneous deformations with different DVC algorithms with the undeformed image held as the fixed reference image: local FFT cross-correlation DVC, local IC-GN-based subvolume DVC, finite element-based global DVC, and our new ALDVC method. Evaluated homogeneous deformations are listed by row: (i) x-direction translation from 0 to 1 voxel with 0.1 voxels increments; (ii) Uniaxial stretch with a cumulative stretch ratio varying from 1 to 1.3 in increments of 0.05; (iii) Planar rotations about the z-axis with rotation angles varying from 0^∘ to 25^∘ in increments of 5^∘. (Insets in (c & f) show replotted results of the local, global DVC and ALDVC methods with adjusted vertical axes.) (e & h) Errors of solved uniaxial stretch ratios and rotation angles in the cases (ii-iii)

To close this section, we note that when using synthetic images, a bias can be introduced because of the interpolation used for grayscale values at subvoxels. The subvoxel translation cases showing sinusoidal variation in Fig. 2(a) are a reflection of this bias [27]. Finally, Fig. 3 shows the convergence of both primal and dual residuals (a-b,d) and dual variables (e-f) (without a stopping criterion) for the rigid translation case for ALDVC. We see that, overall, the ALDVC ADMM scheme converges within $3\sim 5$ iterations for this simple case. Primal residuals converge rapidly, usually within the first two to three ADMM iterations, and plateau with further iterations. Both dual residuals and dual variables converge quickly, usually also within the first three ADMM iterations.

Fig. 3

Convergence of the ALDVC method residuals for uniaxial x-translation tests using synthetic volumetric images, see (c). Primal residuals of u (a) and F (b) decrease (rapidly, for the case of the residual of F) in the first three ADMM iterations and plateau with further iterations. (Inset: (a) the replotted results with adjusted vertical axes.) Both the dual residual (d) and dual variables of W (e) and v (f) converge quickly, usually within three ADMM iterations

Performance Assessment via Inhomogeneous Deformation (SEM Challenge Sample 14)

Next, we assess the accuracy and precision of our ALDVC algorithm using a 3D volumetric adaptation of the Society for Experimental Mechanics (SEM) DIC Challenge Sample 14 displacement fields. These are characterized by a sinusoidal displacement field of varying frequency in the x-direction for three different frequency ranges (L1, L3, L5; see supplementary material Fig. S1) at a fixed amplitude [31]. The synthesized 3D volume images of size 2048vx × 192vx × 192vx have the same x-direction deformations as the 2D images of the original challenge and have zero displacements in both the y- and z-directions. We set the local subvolume size (SS) to be 10vx × 10vx × 10vx, and set both the window subset spacing and global element size (ST) to be 5vx × 5vx × 5vx. As before, the ALDVC method converges in about three ADMM iterations. Figures 4 and 5 show the horizontal displacement (u_x) and the horizontal longitudinal infinitesimal strain (e_xx) for the three images and the results of each of the four DVC methods (local FFT+IDM-based⁴ DVC, local IC-GN DVC, FE-based global DVC, and ALDVC), with red dashed lines displaying the exact applied deformations and blue error bars showing mean values and standard deviations of measured u_x and e_xx along the x-axis (i.e., mean ± standard deviation of all y-, z-points as a function of x-location).

Fig. 4

The horizontal displacement (u_x) obtained using four different DVC methods. (a) A local FFT-based implementation with fixed subset size IDM, (b) local IC-GN DVC, (c) FE-based global DVC and (d) our ALDVC method. Images are synthetic volumes with displacement profiles based on the SEM Challenge Sample 14 dataset. This includes three cases with increasing spatial frequency and fixed amplitude: (i) L1, (ii) L3, and (iii) L5. Generally our ALDVC algorithm captures the displacement field accurately, whereas the local techniques produce slightly higher noise and the global technique oversmooths the higher frequencies

Fig. 5

The horizontal infinitesimal longitudinal strain (e_xx) obtained using three different DVC methods. Specifically, (a) local IC-GN DVC, (b) FE-based global DVC and (c) our ALDVC method, using synthetic images based on the three cases of the SEM Challenge Sample 14 dataset: (i) L1, (ii) L3, and (iii) L5

We comment that the local FFT with IDM (for a fixed subset size) has the lowest accuracy of the techniques tested with an RMS error on the displacement field of O(0.1) voxels since IDM performs best for finite deformations with a self-refining subset size. However, the results provided by the local method using IC-GN are also noisy and the associated RMS error of the displacement field is on the order of 0.05 voxel. The global DVC and ALDVC have lower noise signatures than the other methods at O(0.01) voxels. Table 1 provides the computed RMS displacement and strain errors for each DVC method where applicable. Both Figs. 4–5 and Table 1 show that the ALDVC method leads to generally smaller overall errors compared to the three other DVC methods while reconstructing most of the high spatial frequency amplitude data in Figs. 4–5.

Table 1 Comparison of the RMS displacement and strain errors from reconstructing the SEM Challenge Sample 14 (L1, L3, L5) displacement fields using four different DVC methods (subvolume size SS= 10³ voxels, neighboring window distance ST= 5³ voxels)

Regarding the global DVC method results in Figs. 4–5 we have added a gradient regularization term “α|∇u(X)|²” onto (30), where the constant coefficient α is optimized using a line search method.⁵ As the deformation field becomes heterogeneous, the added gradient regularization term helps to decrease noise, but also constrains the magnitude of the deformation gradients. In Fig. 5, for the L3 & L5 cases, the amplitude of the oscillating strain fields is almost constant where x> 1000 voxels; while in Fig. 4 for the L3 & L5 cases, the amplitude of the oscillating displacement fields at the same region decreases approximately linearly with spatial frequency due to the imposed penalty on steep gradients.

Lastly, we examined the effect of changing the subvolume size (SS) on the ALDVC error using the L1 displacement field from the SEM DVC Challenge Sample 14 (see supplementary material Figs. S2-3). The L1 displacement profile is chosen as a typical balance between homogeneity and spatial frequency where a user would be required to carefully select a window size. Table 2 shows the RMS errors in displacement and strain using three different window sizes.

Table 2 DVC displacement and strain RMS errors of Sample 14 L1 with different subvolume sizes (SS) and neighboring window distances (ST)

The errors increase with decreasing window size, due to the reduced amount of spatial filtering during the reconstruction process, which is a well appreciated phenomenon in DIC and DVC.

ALDVC Applied to Experimental Indentation Data

Finally, we apply our new ALDVC algorithm to measure volumetric deformations of a soft polyacrylamide (PA) hydrogel under spherical indentation. Soft hyperelastic materials, such as hydrogels, are often characterized using an atomic force microscope with a calibrated stiffness cantilever and a spherical tip of known diameter, where material properties are extracted via the classical Hertzian [32] or JKR [33] contact models. However, critical parameters such as the contact area of indentation or the contact point of loading are challenging to deduce without having access to full-field data. To address these challenges, methods have been developed using volumetric confocal microscopy to capture 3D images of a spherical indentor on a soft, transparent substrate. These use the known indentation force, radius of the indentor, thickness of the gel, and measured indentation depth to calculate material properties [34, 35]. We employed this type of indentation technique as an experimental test case and compared against a finite element-based analysis using pre-calibrated material properties.

PA hydrogels were formed in individual wells of a glass-bottom 24-well plate. The particular composition of our hydrogels determined by the relative volume fraction of bis-acrylamide to acrylamide was shown to yield an approximate elastic modulus of 480 Pa (see Appendix E). Hydrogels were subsequently allowed to swell in water for 24 hours before being imaged on a Nikon A1 inverted multiphoton microscope. A 1mm diameter magnetic stainless steel sphere with a density of 7.75 g/cm³ (McMaster Carr, NJ) was placed onto the submerged PA hydrogel surface using tweezers. A 3D volumetric image stack containing fluorescent beads to provide contrast for DVC was captured from near the hydrogel surface using multiphoton microscopy and a 25 ×/1.15NA water immersion objective. The bead was then removed without touching the gel surface using a neodymium magnet. A reference, stress-free volumetric image was acquired using the same imaging parameters as before, see Fig. 6. Both volumetric reference and deformed images have the same dimensions of 1024vx × 1024vx × 445vx, and are shown in supplementary materials Section S6. For DVC computation, we set the local subset window sizes to be 32vx × 32vx × 32vx, and set both the subset windows spacing and global element size to be 8vx × 8vx × 8vx. The resulting images (volume of interest: [320,728]vx × [320,728]vx × [20,164]vx selected from within the larger imaging volume) were analyzed. ALDVC iterations converged after 6 ADMM iterations, and the convergence of the ALDVC method is shown in supplementary materials Fig. S4.

Fig. 6

Schematic of the indentation experiment on soft polyacrylamide hydrogels imaged using multiphoton microscopy. Schematic of the experimental conditions (a) before and (b) after the removal of the steel indentor bead with a magnet. (c-1&2), a depiction of x-z projections of the 3D image stacks showing reference and deformed configurations of the gel (not to scale), with the imaging domain used for DVC outlined in cyan. (d) The equivalent computational domain assuming radial symmetry about the central axis of the bead, the rigid shell outline of which is shown in green. The approximate DVC region is highlighted in cyan

The displacement fields obtained using our ALDVC method are shown in Fig. 7 and the accompanying strain fields are shown in Fig. 8.

Fig. 7

ALDVC computed displacement fields from the experimental test case involving indentation of a polyacrylamide hydrogel with a spherical indentor. Surface displacements are shown, (a) u_x, (b) u_y, and (c) u_z components of the solved indentation field. (d) x-z midplane slice of the u_x displacement component at y = 211.7μ m. (e) y-z midplane slice of the u_y displacement component at x = 228.5μ m. (f) y-z midplane slice of the u_z displacement component at x = 228.5μ m. (g) A x-z midplane slice of the computed u_x displacement demonstrating good qualitative comparison with the experimental displacements shown in (d). The full volume has been reconstructed using the symmetry assumptions, and axes are shifted to correspond to the DVC subvolume in the experimental coordinates. (h) An equivalent y-z midplane slice of the computed u_y displacement compares well to the experimental field shown in (e). (i) A y-z midplane slice of the computed u_z displacement, comparable to (f)

Fig. 8

ALDVC solved strain fields for indentation of a soft polyacrylamide hydrogel, where strain fields are intrinsic outputs from ALDVC algorithm. Surface plots are shown for (a) e_xz, (b) e_yz, and (c) e_zz strain components of solved indentation field. (d) x-z midplane slice of the e_xz strain component at y = 211.7μ m. (e) y-z midplane slice of the e_yz strain component at x = 228.5μ m. (f) y-z midplane slice of the e_zz strain component at x = 228.5μ m. (g-i) Abaqus computed strain fields at midplane slices comparable to (d-f)

To match this problem computationally, a domain spanning the entire hydrogel volume was idealized to be axisymmetric and constructed in Abaqus/Standard [36] analogous to prior simulations of spherical indentation [11, 37] using a convergent mesh of 20,000 Abaqus-CAX4RH elements (four-noded, hybrid bilinear axisymmetric quadrilaterals with constant-pressure, reduced integration, and hourglass control). The indentor is modeled as a rigid, frictionless (due to water-mediated contact with minimal adhesion (see [35]), hard-contact acting on the hydrogel through a known resultant force (computed from the known densities using gravitational and buoyant body forces on the steel sphere) exerted perpendicularly to the hydrogel surface. The hydrogel is modeled as a neo-Hookean hyperelastic solid with Young’s modulus E= 480 Pa and Poisson’s ratio ν = 0.495. Boundary conditions imposed were as follows: the bottom surface was set to zero-displacement for each component to match the well-adhered nature of the hydrogel to the glass substrate, the left-hand side of the mesh is coincident with the axis of symmetry and thus the horizontal displacement is fixed, the right-hand boundary abuts the well-plate wall and thus is also modeled with zero horizontal displacement. The axisymmetry of the simulation is used to expand the computational result to match the experimental data. Displacement contours from matching regions of the computational and experimental domains were extracted, where the consistent coordinate basis is that of the full experimental volume. These are plotted in Fig. 7 showing good agreement in both magnitude and spatial distribution between simulated and measured fields.

We also compare our ALDVC results with the other DVC methods (see supplementary materials Section S7). As expected, the ALDVC results are less noisy than the local IC-GN DVC method, and the global DVC seems to oversmooth the deformation field. These findings also agree with the comparison of associated grayscale value SSD errors (see supplementary materials Section S8), where SSD errors in the local IC-GN DVC and ALDVC methods are very similar, but the apparent kinematic compatibility is closer using the ALDVC technique. Furthermore, we compare the SSD errors and gradient regularizers between global DVC and ALDVC. Since gradient regularization is applied to the global DVC, the solved deformation gradients have smaller norms and are oversmoothed. ALDVC does not apply these smoothness penalties and thus has smaller SSD errors and better accuracy (see supplementary materials Table S2).

Computational Cost

All computations are implemented in Matlab (version 2018b, 64-bit) and performed on the same workstation outfitted with an Intel i7-9800X with a base clock of 3.80 GHz (8 threads), 64 GB memory, and run under Windows 10. In both the local DVC and ALDVC the IC-GN iterations used 8 threads via the parallel processing toolbox in Matlab.

We compare the computational cost of the DVC algorithms outlined in “Performance Assessment via Homogeneous Deformations”. The symbols used are listed in Table 3. Since all of our DVC algorithms account for general affine deformations, we minimize for a 12 DoF deformation, i.e., n_L= 12; we use first order, 8 node hexahedron elements in our global DVC and ALDVC methods, and each element has 24 DoFs, i.e., n_G = 24. We estimate the cost of each step in each algorithm [21], and we then use the dominant terms (assuming that k₁≪k₂) to estimate the total cost of computing a pair of volumetric images, and these are listed in the Table 4 (“Theory”).

Table 3 List of symbols used in the analysis of the computational cost estimates for each DVC algorithm

Table 4 Computation time (unit: s) of “Assessing the Accuracy and Precision of the ALDVC Algorithm” case studies using different DVC algorithms

We observe that with the exception of the FFT-based DVC method, the computational costs of the DVC algorithms scale linearly with the size of the image mN. Thus, the differences are in the pre-factors, and these can be significant, as can be seen from the computation times presented in Table 4. The local DVC method is the least expensive, while the global DVC formulation is the most expensive as expected, especially for large images. The computational cost of our ALDVC method is 2 $\sim$ 5 times that of the local IC-GN DVC method, which is much faster than the global DVC method and could decrease the RMS error of displacement field by up to a factor of 10 compared with the local DVC method, see Tables 1–2.

Conclusions

In this paper, we have presented a new augmented Lagrangian digital volume correlation (ALDVC) method that takes advantage of the superior computational speed of local DVC approaches yet produces globally kinematically compatible displacement and strain fields as generally provided by only global DVC methods. We assess the performance of our new ALDVC algorithm by benchmarking it against a series of synthetic and experimental homogeneous and inhomogeneous deformation cases. In general, our ALDVC algorithm provides superior accuracy and spatial reconstruction ability compared with other baseline DVC methods. The RMS error on displacement field reconstruction is up to one order of magnitude lower compared with a general, local IC-GN DVC method. We also show that the computational cost of our ALDVC is only a few times ($2 \sim 5$ times) that of typical local DVC methods and significantly lower than that typical cost of global DVC methods (potentially up to one to two orders of magnitude in computational time faster, especially for large images, see Table 4).

Our ALDVC algorithm correlates subvolumes locally to find the best matching displacement field as in the local subvolume DVC method, but then ties them together by introducing an auxiliary compatible displacement field. The superior accuracy of the ALDVC compared with many other local methods is due to the auxiliary field, which leads to a globally compatible deformation field with less noise than the typical displacement field outputs from the local method alone. In the ALDVC subproblem 1, each ADMM iteration is solved locally, which produces some local points with poor convergence. However, we also solve the global step afterwards and find that a small percentage of poor convergence points typically does not affect the final solution, and the number of local points with poor convergence decreases along with ADMM iterations, see supplementary material Section S5 Fig. S5.

Both ALDVC and global DVC seek to enforce kinematic compatibility of the reconstructed deformation field. Finite-element based global DVC relies on the stiffness operator M (see Appendix C (31)) and external force vector b (see Appendix C (32)), which both depend on the image grayscale values requiring increased computational cost, since classic Gaussian quadrature cannot be used. Instead, ALDVC remains computationally efficient since the global optimization problem has been decomposed into two subproblems. The first subproblem can be further divided into independent local, small problems, which can be solved rapidly and in parallel; while the second global subproblem is also solved efficiently since it does not involve any grayscale values directly. Moreover, the operator M in the global DVC may be poorly conditioned depending on the image and needs to be modified with regularization. This requires sophistication in the implementation since decreasing noise level may also over-smooth the actual deformations, see Figs. 4-5. In contrast, ALDVC does not require explicit smoothness regularization, and can decrease the noise level while resolving the characteristics of the unknown underlying deformation field.

We conclude this paper with a few thoughts on advancing this work. First, in both the local subvolume DVC and subproblem 1 of the ALDVC, the accuracy in the displacements increases with subvolume size. However, the fidelity decreases in regions of large strain or rapidly changing strain (i.e. high spatial frequencies). The ideal strategy is to use an adaptive multiscale approach: large subvolumes in small strain and small strain-gradient areas, and small subvolumes in large strain and large strain-gradient areas and these subvolumes can also be located mesh-adaptively [14, 20, 38, 39]. We shall describe this in a forthcoming work where this new ALDVC technique can be implemented with adaptive meshing capability, which can both reduce computational times and improve overall accuracy near strain localization regions.

Second, since our ALDVC method considers global kinematic compatibility, it is also expected to be robust to artifacts and noise, and the technique can readily be combined with image compression techniques [22].

Third, we have only considered continuous deformations in this paper; however, in principal ALDVC can be improved further to deal with discontinuities. To achieve this, the ADMM subproblem 1 could be solved using a subvolume splitting technique, e.g., [40], and subproblem 2 could be solved globally using, e.g., an extended FEM technique by introducing Heaviside basis functions (X-DVC [41]).

Fourth, digital volume correlation can be viewed as a special case of the Monge-Kantorovich optimal transport problem [42] where we are matching local continuous patches (i.e., subvolumes) and considering global kinematic compatibility with an augmented Lagrangian. More generally, digital volume correlation can also be solved in the discrete formulation by defining and matching discrete features, e.g. particle tracking algorithms [43]. In these cases, the global kinematic compatibility can also be enforced in the form of an augmented Lagrangian to improve the overall accuracy of the reconstructed motion field.

As a final note, we maintain an open-source Matlab implementation of the presented ALDVC⁶ that is freely available for download. To ensure that the reader can fairly compare ALDVC with our global DVC method, we also uploaded the finite element based global DVC codes we used in this paper to our Github page.

Appendices

Appendix A: Local FFT-based and Iterative Image Deformation Method

In the local FFT-based DVC method, the volume of interest (VOI) is divided into local subvolumes (subsets) and the degrees of freedom (DoFs) governing the local deformation of each subvolume are assumed to be represented by a piecewise constant translation

$$ \mathbf{y}(\mathbf{X}) = \mathbf{X}+ \mathbf{u}(\mathbf{X}) = \mathbf{X} + \sum\limits_{i} \left( \mathbf{u}_{i} \right) \chi_{i} (\mathbf{X}), $$

(14)

where u_i is the translation vector of the center of each local subset Ω_i, and χ_i is the characteristic or index function

$$ \chi_{i} = \left\lbrace \begin{array}{ll} &1, \quad \mathbf{X} \in {\Omega}_{i}, \\ &0, \quad \mathbf{X} \notin {\Omega}_{i}. \end{array} \right. $$

(15)

Using this piecewise translation formulation (14), the optimization problem (2) decomposes into a number of independent optimization problems over translation vector variables, where the objective function can be computed very efficiently using the fast Fourier transform (FFT) method [4]

$$ C_{\text{CC}}(\mathbf{u}) = \mathcal{F}^{-1} \left[ \overline{\mathcal{F}(f)} \odot \mathcal{F}(g) \right], $$

(16)

where “$\overline {\ \cdot \ }$” denotes the complex conjugate, and “⊙” is the Hadamard product where multiplication is conducted element-wise. The displacement vector u can be calculated with sub-voxel resolution by fitting the 3³ voxel cross correlation peak to a Gaussian polynomial or a quadratic polynomial [4].

To account for large material deformations including large stretches, rotations, and shear, Bar-Kochba et al. [8] significantly improved on prior local FFT methods by iteratively warping the reference and deformed images using a linearized local displacement field that is interpolated from the current displacement field until the reference and deformed images converge to the same final configuration, while introducing several filtering steps to improve accuracy and convergence. This can be further sped up by using an initial guess transfer scheme [44] and improved by the introduction of quality factors of the cross-correlation space to detect and remove poor FFT results among subvolumes [11].

Appendix B: Non-FFT-based Local IC-GN DVC Method

Similarly to the FFT-based methods, for non-FFT-based DVC methods each subvolume is assumed to be independent (although initial guess propagation is often used, e.g, [28]) with regard to its neighboring subvolumes and the deformation field has the general piecewise affine deformation formulation

$$ \mathbf{y}(\mathbf{X}) = \mathbf{X}+ \mathbf{u}(\mathbf{X}) = \mathbf{X} + \sum\limits_{i} \left( \mathbf{u}_{i} + \mathbf{F}_{i} (\mathbf{X}- \mathbf{X}_{i0} ) \right) \chi_{i} (\mathbf{X}), $$

(17)

where X_i0 is the center point of local subvolume Ω_i, u_i is the displacement of X_i0 and F_i is the affine deformation gradient tensor of Ω_i minus identity.

The optimization problem (3) decomposes into a number of decoupled problems with, typically, twelve degrees of freedom {u_x,u_y,u_z,F_xx,F_xy,F_xz,F_yx,F_yy,F_yz,F_zx, F_zy,F_zz} for the subvolume’s first order shape function and can be solved in parallel. This optimization problem is as follows:

$$ \begin{array}{@{}rcl@{}} C_{\text{SSD} i} &=& {\int}_{{\Omega}_{i}} \left| f(\mathbf{X}) - g(\mathbf{X}+ \mathbf{u}_{i} + \mathbf{F}_{i} (\mathbf{X}- \mathbf{X}_{i0} ) ) \right|^{2} d \mathbf{X}\\ &\rightarrow& \text{minimize over } \lbrace \mathbf{F}_{i}, \mathbf{u}_{i} \rbrace \end{array} $$

(18)

and can be solved efficiently using an inverse compositional Gauss-Newton (IC-GN) scheme. Given the current iteration of the deformation map y^k, we seek the updated deformation map y^k+ 1. It is convenient to define the inverse map φ^k such that φ^k(y^k(X)) = X. We also define the increment ψ^k through y^k+ 1 = ψ^k ∘y^k as shown in Fig. 1(a). At each IC-GN iteration, we make the approximation $\boldsymbol {\psi ^{k}} \approx \mathbf {z} + \mathbf {v} + \mathbf {H}(\mathbf {z}-\mathbf {z}_{0})$, and use a change of variables to minimize the SSD correlation function in the current iteration configuration

$$ \begin{array}{@{}rcl@{}} C_{\text{SSD} i} &=& {\int}_{{{\Omega}_{i}^{k}}} \left| f(\boldsymbol{\varphi}^{k}(\mathbf{z})) - g(\mathbf{z}) - \nabla g(\mathbf{z})\right.\\ &&\left. \cdot \left( \mathbf{v}+ \mathbf{H}(\mathbf{z}-\mathbf{z}_{0}) \vphantom{\boldsymbol{\varphi}^{k}}\right) \right|^{2} d \mathbf{z}. \end{array} $$

(19)

Minimizing over {v,H}, we obtain

$$ \left( \begin{array}{cc} a_{lp} & b_{lqr} \\ b_{mnp} & c_{mnqr} \end{array}\right) \left( \begin{array}{cc} w_{p} \\ H_{qr} \end{array}\right) = \left( \begin{array}{cc} d_{l} \\ e_{mn} \end{array}\right) $$

(20)

where

$$ \begin{array}{@{}rcl@{}} a_{lp} &=& 2 {\int}_{{{\Omega}_{i}^{k}}} g_{,l} g_{,p} d \mathbf{z}, \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} b_{lqr} &=& {\int}_{{{\Omega}_{i}^{k}}} g_{,l}g_{,q}(z_{r} - z_{0r}) d \mathbf{z}, \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} c_{mnqr} &=& 2 {\int}_{{{\Omega}_{i}^{k}}} g_{,m} (z_{n} - z_{0n}) g_{,q} (z_{r} - z_{0r}) d \mathbf{z}, \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} d_{l} &=& {\int}_{{{\Omega}_{i}^{k}}} (f-g) g_{,l} d \mathbf{z}, \end{array} $$

(24)

$$ \begin{array}{@{}rcl@{}} e_{mn} &=& {\int}_{{{\Omega}_{i}^{k}}} (f-g) g_{,m} (z_{n} - z_{0n}) d\mathbf{z} \end{array} $$

(25)

and g_,l = ∂g/∂z_l, etc. We solve (20) for {v,H} to obtain ψ^k. We then obtain the new (inverse) deformation φ^k+ 1 = φ^k ∘ (ψ^k)^− 1. In practice, we compute the integrals (or voxel-wise sums) over the final deformed configuration instead of the intermediate iterating configurations. This significantly decreases computational cost because all the gradients ∇g only need to be computed once and remain unchanged during each IC-GN iteration as summarized in Algorithm 2.

Appendix C: Global DVC Method

For the global DVC method, we represent the global deformation using a global basis set, often based on a finite element formulation, such that the compatibility or continuity of the displacement field is automatically guaranteed (see Fig. 1(b)), i.e.,

$$ \mathbf{y}(\mathbf{X}) = \mathbf{X} + \mathbf{u}(\mathbf{X})=\mathbf{X} + \sum\limits_{p} {u}_{p} \boldsymbol{\psi}_{p} (\mathbf{X}) $$

(26)

where ψ_p(X) are chosen global basis functions and u_p are the unknown degrees of freedom. Thus, equation (3) becomes

$$ \begin{array}{@{}rcl@{}} C_{g} &=& {\int}_{\Omega} \left| f(\mathbf{X}) - g(\mathbf{X} + \sum\limits_{p} {u}_{p} \boldsymbol{\psi}_{p} (\mathbf{X}) ) \right|^{2} d \mathbf{X}\\ &\to& \text{minimize over } \{u_{p}\} . \end{array} $$

(27)

We can solve this problem iteratively by setting u_k+ 1 = u_k + δu and using the first order approximation

$$ g(\mathbf{y}(\mathbf{X})) = g(\mathbf{X}+\mathbf{u}_{k}(\mathbf{X}) + \delta \mathbf{u}) \approx g(\mathbf{X} + \mathbf{u}_{k}(\mathbf{X}) )+ \nabla g \cdot \delta \mathbf{u}(\mathbf{X}) $$

(28)

such that

$$ \begin{array}{@{}rcl@{}} C_{g} &\approx& {\int}_{\Omega} \left|\vphantom{\sum\limits_{p}~} f(\mathbf{X}) - g(\mathbf{X}+\mathbf{u}_{k}(\mathbf{X}))\right.\\ && \left. - \left( \sum\limits_{p} \delta u_{p} \boldsymbol{\psi}_{p} (\mathbf{X}) \right) \cdot \nabla g(\mathbf{X}) \right|^{2} d \mathbf{X}. \end{array} $$

(29)

This leads to a linear equation in δu

$$ M_{pq} \delta u_{q} = b_{p} $$

(30)

where

$$ \begin{array}{@{}rcl@{}} M_{pq} & = & \displaystyle{ {\int}_{\Omega} \boldsymbol{\psi}_{p}^{T} (\mathbf{X}) \left( \nabla g \right) \left( \nabla g \right)^{T} \boldsymbol{\psi}_{q}(\mathbf{X}) d \mathbf{X} }, \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} b_{p} & = & \displaystyle{{\int}_{\Omega} \left( f(\mathbf{X}) - g(\mathbf{X} + \mathbf{u}_{k}(\mathbf{X})) \right) \boldsymbol{\psi}_{p}^{T}(\mathbf{X}) \nabla g (\mathbf{X}) d \mathbf{X} } . \end{array} $$

(32)

In this paper, we use an 8-node hexahedron (HEX8) finite element mesh in our global DVC method, and the algorithm is summarized in Algorithm 3. Alternately, if the displacements are small, we can treat (30) as a linear problem with δu as the incremental displacement.

Global DVC is usually computationally expensive since the size of the linear problem (30) is equal to the number of basis functions or the size of the finite element discretization. While parallel implementation strategies exist, they can be cumbersome to utilize in practice. The problem is exacerbated when analyzing volumetric time-lapse data with multiple image pairs.

Appendix D: Synthetic 3D Volume Images

The synthetic digital volume images in “Assessing the Accuracy and Precision of the ALDVC Algorithm” are generated to mimic actual volumetric experimental images. In each reference volume, isolated spherical beads are randomly seeded using a 3D Gaussian intensity profile as an approximation of a random, isotropic image pattern (e.g., mimicking the point spread function (PSF) of a laser scanning confocal microscope [8, 43]). A typical Gaussian PSF with amplitude A and spread (i.e., standard deviation) σ is expressed as

$$ \text{PSF}(x) = A \exp \left( - \sum\limits_{i=1}^{3} \frac{{x_{i}^{2}}}{2 \sigma^{2}} \right). $$

(33)

A PSF with a spread σ= 1 approximates a spherical particle in the volume image with a diameter of approximately 5 voxels. All the beads are sampled randomly with seeding density 0.006 beads per voxel. To avoid beads overlapping in the synthetic images, a Poisson disc sampling algorithm is used to seed center-point locations in the volume images with a minimum separation distance between particles equal to the particle diameter (see [43]), see Fig. 9. The particle positions in the deformed image are calculated via the imposed displacement field and all the deformed volume images are warped from the reference to deformed configuration using tri-cubic interpolation [27].

Fig. 9

(a) Representative, synthetically generated DVC volume using a typical Gaussian-like point spread function (PSF) mimicking typical diffraction-limited optical systems. (b) Inset from (a)

Appendix E: Indentation Experiment Preparation

In our experiment, polyacrylamide (PA) hydrogels of approximately 400 μm in thickness were polymerized in the well of a glass-bottomed 24-well plate, pre-treated with 0.5% 3-aminopropyl-trimethoxysilane (Sigma-Aldrich, MO) and 0.5% glutaraldehyde (Polysciences, Inc., PA) as described previously [45,46,47]. The hydrogels were fabricated using 3% acrylamide (Bio-Rad, CA) and 0.06% bis-acrylamide (Bio-Rad, CA), following a previously described protocol [45, 46, 48] with an approximate final elastic modulus of 480 Pa. Cross-linking of the PA hydrogels was achieved with the addition of ammonium persulfate (Sigma-Aldrich, MO) and N,N,N,N-tetramethylethylenediamine (ThermoFisher Scientific, MA). Hydrogels were doped with 10% (w/v) 1 μm diameter carboxylate-modified fluorescent microspheres (ThermoFisher Scientific, MA) as fiducial markers. Hydrogels were left to fully swell in deionized water overnight. All the related parameters are summarized in Table 5.

Table 5 Details of hydrogel indentation experiment parameters