Introduction

High-strain rate (\(\dot{\epsilon }>\) 10\(^3\) 1/s) material characterization has remained a formidable challenge for highly compliant materials with shear moduli as low as a few hundred Pascals. Their intrinsic low impedance, slow shear wave speeds, and general strain-rate dependence have largely precluded conventional experimental characterization approaches from successful deployment. Inertial Microcavitation Rheometry (IMR) was recently developed to address this challenge and to characterize the non-linear viscoelastic properties of soft materials at high strain rates [1, 2]. Through the integration of an appropriate theoretical framework, material stresses and strains during cavitation were successfully determined for compliant, homogeneous, isotropic materials [1, 2].

For IMR to robustly determine constitutive properties, the ability to control the magnitude of material deformation, or more specifically, the material stretch, is essential. Assuming bubble sphericity, the material stretch is defined as the ratio of bubble radius at any given time to the long-time bubble radius at mechanical equilibrium. While the development of IMR was a significant milestone in providing experimental access for characterizing highly compliant viscoelastic materials, including bodily tissues, at high to ultra high strain rates (\(O(10^{3}) \sim O(10^{8})\) 1/s), some experimental and theoretical limitations remain. The first is the current reliance on the optical, dielectric breakdown process to nucleate and grow a bubble. As this process is dependent on both the chemical and physical properties of the material and solute under investigation, the maximum deformation reached within each material can change significantly depending on the material and environment. That is contrary to most classical characterization approaches, where the loading (force or kinematic) conditions are independently controlled from the material properties. The second limitation is that for most inertially occurring cavitation events the thermodynamics and material physics can be complex and remain to be fully captured by theoretical models. For example, dynamic fracture or rupture in soft materials under extreme loading rates remains an active area of research [3,4,5,6] that is not captured in the current IMR formulation, which assumes complete, albeit nonlinear, viscoelastic material behavior.

In order to address these limitations and to advance the accuracy and robustness of the IMR technique, this paper presents a new experimental approach for expanding the accessible deformation regime for most hydrogels and biological tissues, while, at the same time, providing a data assimilation approach to (i) more robustly characterize the constitutive properties throughout the cavitation cycle and (ii) identify critical points in the evolution that could benefit from improved physical models (e.g., damage or fracture criteria). The experimental approach to modulate bubble amplitude is twofold. The first technique is to introduce seed particles that serve as nucleation sites so as to minimize the dependence of nucleation on the target material’s properties. The second technique is to nucleate bubbles at several different laser energies. Our experimental results, presented in “Experimental Results”, demonstrate that with these innovations we can successfully modulate bubble amplitude and the resulting imposed material stretch ratios, thus significantly expanding the finite deformation regime. Experimentally accessing such lower stretch regimes is critical in the development of failure models for inertial cavitation as they depend upon proper resolution of the deviation from viscoelastic behavior. The experimental capability to control bubble size and resulting material deformation will ultimately improve constitutive modeling of soft materials to account for bubble non-sphericity, compressibility, damage and failure mechanisms.

Next, we conduct numerical analyses to assess the robustness of the theoretical framework governing IMR across the expanded finite deformation regime. In “Numerical IMR Results”, we use an offline data assimilation (DA) technique to conduct IMR analyses up through the first, second, and third bubble collapse points, comparing experimental data to simulated data. We then report fitted viscoelastic material parameters for a Quadratic law Kelvin-Voigt constitutive model and characterize violent bubble collapses across the significantly expanded finite deformation regime. Finally, we highlight time-varying model uncertainties, particularly at bubble collapse points, of key experimental examples using a quasi-online DA method.

Materials and Methods

Polyacrylamide Hydrogel Preparation

Isotropic polyacrylamide (PA) hydrogels with a concentration of 5/0.03% acrylamide to bisacrylamide solutions (Bio-Rad Laboratories, Hercules, CA) were prepared using previously developed protocols [1, 7]. The nominal quasi-static shear moduli of the samples are \(G_\infty\) = 461 ± 4 Pa and were used as the gel matrix for all samples. A subset of samples was made by suspending three different types of microspheres separately within the volume of a hydrogel: glass, stainless steel, and paramagnetic coated polyethylene particles. These microspheres, hereto referred to as seed particles, are outlined in Table 1. Seed particles were utilized in this study to lower the cavitation nucleation threshold in the gels. To ensure particle suspension long enough to polymerize a PA hydrogel, particles were treated with 2% w/v of Tween 80 in water then centrifuged for 5 minutes at 2500 rpm to ensure particles were evenly coated with tween solution. This final water-based colloidal suspension was used as the water component to make seeded PA hydrogels. Once polymerized, the samples were left to swell in water overnight and tested the next day.

Table 1 Microspheres suspended within a volume of a polyacrylamide hydrogel
Full size table

Laser-induced Cavitation (LIC) Setup

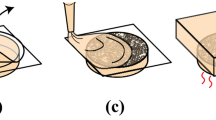
We utilize a similar experimental setup as previously described by Estrada et al., and shown in Fig. 1(a). Briefly, a Q-switched 532 nm Nd:YAG laser (Continuum, San Jose, CA) with 3-5 ns pulse passes through a given neutral density (ND) filter along the optical pathway of the laser and through a beam expander (BE02-05-A, Thorlabs, Newton, NJ), expanding the beam width to five times its original diameter. The beam is then aligned into the back port of a Ti-2 microscope (Nikon, Melville, NY). A dichroic notch filter is used to path the laser into the back aperture of a 10\(\times\)/0.3 NA microscope objective (Nikon, Melville, NY) to focus the beam within the volume of a hydrogel to initiate cavitation. In the case of a seeded hydrogel, the microscope objective was focused onto a single particle before initiating cavitation. Laser energy attenuation was modulated using an assortment of ND filters (Thorlabs, Newton, NJ) along the optical pathway of the laser prior to its entrance into the microscope. At a given energy output through the microscope objective, an EnergyMax Sensor (Coherent, Santa Clara, CA) was placed within the sample holder of the microscope stage. The laser was then pulsed 30 times at each energy level, and the resulting mean laser energies and standard deviations measured out of the microscope objective used in this study were: 18.4 ± 1 \(\mu\)J, 65.0 ± 1 \(\mu\)J, 117.8 ± 1 \(\mu\)J, 254.3 ± 2 \(\mu\)J, 337.2 ± 3 \(\mu\)J, and 449.2 ± 5 \(\mu\)J.

Cavitation kinematics were imaged through the microscope objective using the Hyper Vision HPV-X2 High-Speed Video Camera (Hadland Imaging, Santa Cruz, CA) in HP mode illuminated by a continuous SOLA LED light source (Nikon, Melville, NY) from above. To ensure long-time bubble dynamics of both smaller and larger bubbles were captured, the camera recorded at 0.833 million, 1 million or 1.5 million frames per second (fps). An example cavitation event in PA recorded at 1 million fps, with nominal laser energy 254 \(\mu\)J, is shown in Fig. 1(b).

Fig. 1
figure 1

(a) LIC optical setup (not to scale) (b) Cavitation bubble time lapse (5 \(\mu\)s apart) in PA hydrogel, recorded at 1 million fps, with nominal laser energy 254 \(\mu\)J

Full size image

Experimental Results

Upon bubble nucleation via laser, the bubble rapidly expands to a maximum radius, \(R_{max}\), which we, in-line with prior theoretical treatments, define as time zero. At this point the bubble is idealized as being in thermal equilibrium and mechanical disequilibrium [1, 2, 8]. We assume the bubble contents to consist of a non-condensable gas and water vapor mixture. We define an equilibrium radius, \(R_{o}\), as the long-time radius where the bubble is considered to be in mechanical equilibrium. Finally, we denote the time, t, dependent hoop stretch, \(\lambda (t)\), imposed on the material by the bubble as

$$\begin{aligned} \lambda (t) = \frac{R(t)}{R_{o}} \end{aligned}$$
(1)

and the maximum material stretch as \(\lambda _{max} = R_{max}/R_{o}\).

LIC experiments were performed on a soft polyacrylamide hydrogel at a range of laser energies in both seeded and unseeded samples. This dual experimental approach successfully modulated bubble amplitude and resulting bubble dynamics to vary the maximum bubble radius, \(R_{max}\), the long-time bubble equilibrium radius, \(R_{o}\), and the resulting maximum material stretch, \(\lambda _{max}\), sustained due to bubble formation.

Figure 2 shows representative LIC results from seeded and unseeded PA hydrogels, performed at a constant laser energy (nominally 254.3 ± 2 \(\mu\)J). Figure 2(a) presents a bubble time-lapse where the unseeded sample exhibited the smallest maximum bubble radius and equilibrium radius. For the same laser energy, however, bubbles nucleated on the surface of a seed particle exhibited a larger maximum bubble radius and equilibrium radius. Figure 2(c, e, f) are images of each particle taken on a scanning electron microscope (SEM). The larger views show that the particles are similar orders of magnitude in size and maintain a spherical geometry. The greatest distinction between each particle is the surface roughness. Qualitatively, the paramagnetic coated polyethylene microspheres have the greatest surface roughness, while the stainless steel microspheres have finer inhomogeneity on the particle surface. The glass microspheres have the smoothest particle surface and greatest uniformity of the three particles.

Fig. 2
figure 2

Time lapse images of representative LIC bubbles nucleated in seeded and unseeded PA samples at constant laser energy (nominally 254.3 \(\mu\)J) are shown, with the \(R_{max}\) and \(R_o\) frames outlined in red and blue respectively. (a) In the absence of seed particles, a bubble at the specified energy is shown. SEM images of each particle type were also taken, along with the bubble time lapse for (b, c) glass microsphere, (d, e) stainless steel microsphere, and (f, g) paramagnetic coated polyethylene microsphere cases. (All cavitation events shown here were recorded at 1 million fps)

Full size image

Radius versus time curves in Fig. 3(a) are representative experiments conducted at a constant laser energy of 254.3 \(\mu\)J. Upon bubble nucleation, the bubble rapidly expands to a maximum radius before collapsing, and repeats this oscillatory motion until it reaches its long-time equilibrium radius. Bubbles nucleated on paramagnetic coated polyethylene microspheres exhibited the largest maximum bubble radii, as well as larger subsequent peaks. Similarly, steel and glass particles follow this trend by exhibiting larger bubble amplitudes as compared to bubbles in unseeded hydrogels. In the normalized bubble radius versus time curve (Fig. 3(b)), the first expansion and collapse cycle of all curves overlap, but subsequent peaks show deviations in amplitudes. The time-dependent material stretch is plotted in Fig. 3(c). The maximum material stretch shown at time \(t = 0\) \(\mu\)s, indicated by the dashed vertical line, clearly differs between each cavitation condition. The largest material stretch is exhibited in the unseeded hydrogel of approximately 9, while bubbles nucleated on steel, glass, and paramagnetic coated polyethylene microspheres result in varying maximum stretch ratios down to approximately 5 for the shown examples.

Fig. 3
figure 3

Seeded and unseeded PA samples were tested at a nominal laser energy 254.3 \(\mu\)J. The (a) bubble radius versus time, (b) normalized bubble radius versus time and (c) material stretch versus time plots are shown. (The parameters used to calculate non-dimensionalized time, \(t^*\), are the constant mass density of the surrounding material, \(\rho = 1060\) kg/\(m^3\), and the far-field pressure, \(p_{\infty }= 101.3\) kPa)

Full size image

Figure 4 summarizes the maximum and equilibrium bubble radii, as well as the maximum material stretches imposed by the bubbles, for all sample types across several laser energies. LIC bubbles in PA hydrogels exhibit an increase in \(R_{max}\) and \(R_{o}\) as laser energy increases. Standard error bars where \(\sigma _{err} = \sigma /\sqrt{n}\) are used in the plot. The seed particles were observed to lower the nucleation threshold as bubbles at lower laser energies were successfully nucleated on particles, where it was not possible to nucleate in the lower laser regime otherwise. Additionally, it should be noted that the paramagnetic-coated polyethylene and steel-seeded particles were cavitated at the four lowest energies of this study because cavitating at higher energies resulted in (i) highly energetic bubbles that left the camera field of view and (ii) a lack of temporal resolution to resolve long-time bubble dynamics while adequately capturing short-time bubble dynamics due to a trade-off between the maximum number of recordable camera frames and the total recording duration at ultra high speed. For this reason, the bubbles initiated in seeded samples were in the lower laser energy regime. In the glass microsphere case, it was not possible to consistently and successfully cavitate at the lowest energy recorded in this study.

The range of maximum material stretches measured, using both laser energy modulation and a variety of seed particles as nucleation sites, are summarized in Fig. 4(c). With respect to laser energy, the effective maximum material stretch shows a slight increase, but overall little change in material stretch per type of seeded or unseeded material used. Overall, however, the material deformation regime was successfully expanded from a \(\lambda _{max}\) of 9 (original IMR technique) to a \(\lambda _{max}\) of 4.

Fig. 4
figure 4

Summary of experimental LIC results in seeded and unseeded PA gels where (a) maximum bubble radii, \(R_{max}\), and (b) long-time bubble equilibrium radii, \(R_o\), increase with increased laser energy. The resulting (c) maximum material stretches, \(\lambda _{max}\), achieved across all laser energies define a significantly expanded range of material deformations as compared to the original IMR development. (Each data point is a mean of \(n = 8\) experiments with standard error bars)

Full size image

Numerical IMR results

We implement ensemble-based data assimilation (DA) techniques to fit the hydrogel’s material properties and account for uncertainties in the IMR model. The theoretical background of each framework is briefly summarized here. Following our previous IMR framework we neglect the initial bubble growth phase dominated by plasma physics. Performing a momentum balance in the hydrogel medium, and incorporating slight material compressibility in the far-field [9], the bubble surroundings are governed by the Keller-Miksis equation for one-dimensional spherically symmetric motion [1, 9], namely,

$$\begin{aligned} \left( 1 - \frac{\dot{R}}{c}\right) R \ddot{R} + \frac{3}{2}\left( 1-\frac{\dot{R}}{3c}\right) \ddot{R}^2 = \frac{1}{\rho }\left( 1 + \frac{\dot{R}}{c}\right)\\ \left( p_b - \frac{2\gamma }{R}+ S - p_\infty \right) + \frac{1}{\rho } \frac{R}{c} \dot{\overline{\left( p_b - \frac{2\gamma }{R} + S\right) }}, \end{aligned}$$
(2)

where R, \(\dot{R}\), \(\ddot{R}\) are the radius, velocity, and acceleration of the bubble wall, respectively. c is the constant longitudinal wave speed in the surrounding material, \(\rho\) is the constant mass density of the surrounding material, \(\gamma\) is the surface tension between gaseous bubble contents and surrounding medium, and \(p_\infty\) is the far-field pressure assumed to be atmospheric. For laser-nucleated cavitation events, choosing a two-phase mixture has been shown to be appropriate throughout the literature [1, 2, 8, 10,11,12], where the largest constituent is made up of condensable water vapor and a smaller portion is made up of gases that are non-condensable. This group includes part of the gases that form when the initial bubble is created through the formation of a plasma and vaporization of various other constituents (e.g., parts of the acrylamide polymer). This is homogenized into a general gas cloud with a condensation time scale much longer than the cavitation dynamics. Each gaseous component can be modeled as an ideal gas, and a homobaric idealization is invoked, in which the pressure inside the bubble, \(p_b\), is assumed to be spatially uniform. The vapor concentration field, k(r, t), and the temperature field, T(r, t), inside in the bubble are not spatially uniform and are governed by the balances of mass and energy, respectively, along with Fick’s law for mass transfer and Fourier’s law for heat transfer. The governing equations for the vapor concentration and temperature fields inside the bubble lead to an evolution equation for the time-dependent internal bubble pressure, \(p_b\). Please refer to Estrada et al. for further information [1]. Finally, S is the stress integral of the deviatoric Cauchy stress components. Given spherical symmetry,

$$\begin{aligned} S = \int _{R}^{\infty } \frac{2}{r}(s_{rr} - s_{\theta \theta }) dr, \end{aligned}$$
(3)

where \(s_{rr}\) and \(s_{\theta \theta }\) are the radial and hoop components of the deviatoric stress tensor, respectively. It should be noted that under the model assumptions, heat and mass diffusion in the surrounding material is neglected [1].

This study particularly focuses on cavitation dynamics in polyacrylamide (PA) hydrogels. Following an extensive material fitting study by Yang et al. it was found that polyacrylamide hydrogels at high-strain rate deformations are well characterized by the quadratic law Kelvin-Voigt material model [2]. Given the quasi-static shear modulus \(G_\infty\), strain-stiffening parameter, \(\alpha\), and dynamic viscosity, \(\mu\), of the material, the deviatoric Cauchy stress term for a spherical inertial cavitation bubble is

$$\begin{aligned} S_{Quad} &= \frac{(3\alpha -1)G_\infty }{2} \left[ 5-\left( \frac{R_{o}}{R}\right) ^4 - \frac{4R_{o}}{R}\right] -\frac{4\mu \dot{R}}{R} \\&\quad+ 2\alpha G_\infty \left[ \frac{27}{40} + \frac{1}{8} \left( \frac{R_{o}}{R}\right) ^8 + \frac{1}{5} \left( \frac{R_{o}}{R}\right) ^5 + \left( \frac{R_{o}}{R}\right) ^2 -\frac{2R}{R_{o}}\right] . \end{aligned}$$
(4)

Ensemble-based data assimilation (DA) methods [13, 14], as first implemented for viscoelastic material rheometry by Spratt et al. [15], can help determine bounds of validity of the IMR model. Specifically, we employ an iterative ensemble Kalman smoother (IEnKS) [16,17,18,19] and an ensemble-based 4D-Var (En4D-Var) method [15]. These can estimate material properties of the hydrogels, but in the process also help quantify model and experimental uncertainties. Both methods are similar, the En4D-Var being an offline variant of the IEnKS. The material properties to estimate, in this case the strain stiffening parameter, \(\alpha\), and dynamic viscosity, \(\mu\), are appended to the state vector

$$\begin{aligned} \varvec{x} = \{R, \dot{R}, p_b, S, T, k, \alpha , \mu \}. \end{aligned}$$
(5)

Here, T and k are the temperature and vapor concentration fields inside the bubble, respectively. An initial guess \(\varvec{x}_0\) for these quantities at time \(t=0\) is formulated. Then, an ensemble of state realizations is sampled from a normal distribution with mean \(\varvec{x}_0\) and a given covariance \(\varvec{\mathcal {C}}\) equal to the expected error covariance. In both methods, this full ensemble is stepped through time, and its statistics represent the probability density function of the state dynamics. The IEnKS method comprises of a forecast step and an analysis step. In the forecast step, all ensemble members are stepped forward in time using the physical model only, as \(\hat{x}_{n+1} = f(x_n)\). Experimental data is then introduced in the analysis step, to correct the forecast ensemble. This is done by minimizing the IEnKS cost function

$$\begin{aligned} J(x) = \frac{1}{2} \sum _{i=1}^l \beta _i ||y_{i}-h(f_{i \leftarrow 0}(x))||^2_{\varvec{\mathcal {R}}} + \frac{1}{2}||x-\hat{x}_i||^2_{\varvec{\mathcal {C}}_0}, \end{aligned}$$
(6)

where \(\beta _i\) is a weighting coefficient for each i, y is the measurement vector (in this study just the radius measurement), h is a function mapping the state vector to measurement space, and \(\varvec{\mathcal {R}}\) is the specified measurement covariance. For the IEnKS, l corresponds to the lag of the estimator. That is, the sum in equation (6) will be from \(i = 1\) to l, where l is the number of time steps over which we want to minimize the error. In this study, a lag of 3 was found to provide best results without adding too much computational cost. The IEnKS is thus quasi-online, as estimation lags l timesteps behind the data. After the analysis, a covariance inflation step is necessary to prevent premature convergence of the ensemble, details of which are given by Spratt et al. [15]. The forecast step is then repeated, and so on until the end of the data assimilation window. While the En4D-Var method is fully offline, the cost function is in fact the same (equation (6)), except the sum is now over the whole domain. That is, we set \(l=N\), where N is the last timestep in the DA window. Then, instead of stepping forward in time, only the initial condition is minimized, based on data from the entire time-domain. The offline (En4D-Var) method has proved to be effective in parameter estimation [15, 20]. On the other hand, the quasi-online (IEnKS) method can capture time-dependent behavior because of its quasi-online nature. Both methods will thus be useful for this paper for determining the bubble evolution time points and material deformation regimes when the IMR model deviates from the experimental measurements.

In “Multi-peak Fitting with the Offline (En4D-Var) Method” we perform bubble radius fits using the offline (En4D-Var) method to determine the Quadratic law Kelvin-Voigt material parameters up through the first (1-peak), second (2-peak), and third (3-peak) collapse. Material parameters are then used to calculate the critical Mach numbers for each initial bubble collapse using the IMR framework. For the online method, we assess the time-varying fitted material properties of the quasi-online (IEnKS) method to identify deviations from the model during the bubble time evolution in “Quasi-online (IEnKS) Results”.

Multi-peak Fitting with the Offline (En4D-Var) Method

Numerical results presented in this section use the offline (En4D-Var) method for determining the viscoelastic material parameters in PA. Initial guesses into the solver for viscosity, \(\mu\), and strain stiffening parameter, \(\alpha\), are 0.05 Pa\(\cdot\)s and 0.5 respectively. These are derived from a preliminary run with the former version of IMR using a least squared fitting scheme for fitting material properties [2].

As a measure of the R(t) goodness of fit given the En4D-Var parameter estimates, we use the normalized radius root mean squared error (NRMSE), defined as

$$\begin{aligned} NRMSE = \sqrt{\frac{1}{N}\sum \limits _{i}^{N}\frac{ \Big (R_{sim}(t_i)-R_{exp}(t_i)\Big )^2}{R_{exp}(t_i)^2}}, \end{aligned}$$
(7)

where \(R_{exp}\) and \(R_{sim}\) are the experimental and simulated bubble time histories, respectively. Representative R(t) fits with median NRMSE values for each fitted peak case are shown in Fig. 5. For a cavitation bubble in PA (paramagnetic seed particle), induced at nominal laser energy 117 \(\mu\)J, the 1-peak case has a median NRMSE value of 0.009 (Fig. 5(a)), 2-peak case has a median NRMSE value of 0.027 (Fig. 5(b)), and the 3-peak a median NRMSE value of 0.047 (Fig. 5(c)).

Fig. 5
figure 5

Offline (En4D-Var) method was implemented on experimental curves for 1-, 2- and 3-peak fits. Representative examples of multi-peak fits with median NRMSE values (for PA paramagnetic particles at nominal laser energy 117 \(\mu\)J) are shown for a (a) 1-peak fit (NRMSE = 0.009), (b) 2-peak fit (NRMSE = 0.027), and (c) 3-peak fit (NRMSE = 0.047). While these representative curves show good fit, NRMSE values with respect to maximum material stretch increases as the number of peaks fitted increase (d) 1-peak, (e) 2-peak, and (f) 3-peak fits. In the case of increasing laser energy, NRMSE also increases for all (g) 1-peak, (h) 2-peak, and (i) 3-peak fitting cases

Full size image

We compare R(t) curves obtained with the En4D-Var parameter estimates to experimental data to calculate the NRMSE. Figure 5(d-f) compare \(\lambda _{max}\) to the NRMSE for each peak fit. As the number of fitted peaks increase, the NRMSE also increases. 1-peak fits (Fig. 5(d)) exhibit the lowest NRMSE, with most errors within 0.02. However, the error for the 2-peak fits (Fig. 5(e)) are mostly within 0.05, with some large scatter exhibited by the steel LIC cases. The 3-peak fit case (Fig. 5(f)) NRMSE values are mostly within 0.15, with a few outliers. Given the number of fitted peaks, stretch ratio does not have a noticeable effect on the NRMSE. However, with increasing number of peaks fitted, the NRMSE from the 1- to 3-peak fits increases by almost an order of magnitude. Thus, subsequent oscillatory bubble dynamics beyond the first peak are not as accurately described by the current theoretical IMR framework.

Next, we examine the effect of laser energy on NRMSE. In the 1-peak fit case (Fig. 5(g)), LIC bubbles in PA with no particles have the lowest NRMSE compared to the cases with PA with seed particles. While the general trend indicates increasing NRMSE with increasing laser energy, the bubbles cavitated in PA with seed particles tend to have similar errors at the lowest energies and diverge more with increasing energy. This trend continues in the 2- and 3-peak fit cases, as shown in Fig. 5(h, i). Overall, increasing the laser energy increases the fit error.

For the range of samples and laser energies presented, the strain stiffening parameter, \(\alpha\), and viscosity, \(\mu\), were estimated using the En4D-Var with the IMR framework and Quadratic law Kelvin-Voigt stress integral (equation (4)). A summary of fitted material parameters for all cases are shown in Fig. 6, where the weighted-mean viscosity, \(\mu\), and strain stiffening parameter, \(\alpha\), values are plotted against each other with standard deviation error bars for each experimental condition. (The type of sample is denoted by symbol and energy level denoted by color, in accordance with the color bar shown.) The 1-peak fit case in Fig. 6(a) contains a large cluster of material parameters located within range of \(\mu \approx 0.04 - 0.08\) and \(\alpha \approx\) 0.4 - 0.6 with standard deviation values of \(\sigma _{\mu }=\) 0.008 and \(\sigma _{\alpha }=\) 0.08. A few higher energy cases fall outside of the cluster. However, as the number of fitted peaks increases to 2-peak (Fig. 6(b)) and 3-peak (Fig. 6(c)) fits, an increase in both \(\mu\) and \(\alpha\) values is observed, though the viscosity term is more affected. Another noticeable trend is that the standard deviation of fitted material parameters for a given experimental condition increases with respect to the laser energy. Thus, as energy increases, so does the spread in fitted material parameters, particularly for the 2- and 3-peak fitted cases. Notably though, parameter estimates for lower energy cases remain more clustered, and do not increase as much as more peaks are fitted. This may indicate that the IMR framework remains suitable over multiple peaks for lower laser energies.

Fig. 6
figure 6

The Quadratic law Kelvin-Voigt material model was applied to the IMR framework for fitted material parameters viscosity, \(\mu\), and strain stiffening parameter, \(\alpha\), using En4D-var estimator (offline method). The fitted material parameters for the (a) 1-peak fit are plotted with inset showing a clustering of points at approximately 0.04 - 0.08 Pa\(\cdot\)s for \(\mu\) and 0.4 - 0.6 for \(\alpha\). (b) The 2-peak and (c) 3-peak fits show a larger spread in fitted material parameter values, with a larger effect in the viscosity as number of fitted peaks increases. (The symbols correspond to sample type and the color correspond to laser energy, with associated color bar shown on the far right. Each point is a weighted average of \(n = 8\) experiments where error bars are standard deviation)

Full size image

Upon collapse, inertial cavitation bubbles emit acoustic waves that propagate through the hydrogel matrix. The Mach number, M, over time is a function of the velocity of the bubble wall and the finite wave speed of the material, given by

$$\begin{aligned} M = \dot{R}/c. \end{aligned}$$
(8)

The critical Mach number, \(M_{cr}\), is the maximum Mach number of an inertial bubble, typically occurring at the first bubble collapse. Previous work suggests that \(M_{cr}\) values exceeding 0.08 define the condition for a violent collapse [2], which may introduce additional physical phenomena such as damage and inelastic material behavior. For more details on the IMR theoretical framework, as well as the derivation of non-dimensionalized expressions required for computations, please see Estrada et al. [1].

Given the estimated viscoelastic material parameters, the time evolution of bubble radii is simulated with the IMR frameworkFootnote 1, and the critical Mach number for each experiment are calculated using equation (8). In Fig. 7(a), the critical Mach number, \(M_{cr}\), with respect to each corresponding maximum stretch ratio, \(\lambda _{max}\), is plotted for the 1-peak case and it is found that as the stretch ratio increases, so does the critical Mach number. The 2-peak (Fig. 7(b)) and 3-peak (Fig. 7(c)) cases follow the same trend, though there is an observable increase in scatter, particularly for the steel seed particle case. Thus, there seems to be a dependency of critical Mach number on stretch ratio. Comparing the critical Mach number to laser energy, we refer to Fig. 4(c), where increasing energy only slightly increases the maximum stretch ratio. Given this, we can conclude that the critical Mach number is similarly minimally affected by laser energy.

Fig. 7
figure 7

The critical Mach number, \(M_{cr}\) was deduced from the time evolution of simulated IMR radius curves and plotted with respect to maximum material stretch, \(\lambda _{max}\). Using offline (En4D-Var) method, the (a) 1-peak, (b) 2-peak, and (c) 3-peak fitted solutions show that \(M_{cr}\) increases with increasing \(\lambda _{max}\), and increasing number of fitted peaks decreases the critical Mach number solution. (IMR simulations were run with fitted viscoelastic material parameters)

Full size image

The offline (En4D-Var) method applies the IMR framework to the experimental kinematic bubble radii using the Quadratic law Kelvin-Voigt material model to assess the goodness of the bubble radius history fit and viscoelastic material properties for up to 3-peak fits. The radius fit error, quantified as NRMSE, is generally lower for all cases at lower energy levels, regardless of the number of peaks fitted. However, the radius fit is worse, increasing by almost an order of magnitude, as we increase the DA window from 1- up through 3-peaks with respect to both maximum material stretch and laser energy. While the calculated critical Mach number did not have a noticeable change with respect to input laser energy, it was found that the critical Mach number increases with maximum material stretch ratio, a trend consistent regardless of the number of bubble radius peaks fitted. Lastly, the fitted viscoelastic material properties tend to cluster with a 1-peak fit, but the spread in mean values, as well as the standard deviation of values at a given experimental condition, increases with respect to higher laser energy and number of peaks fitted. The latter particularly affects the fitted viscosity parameter. Critical Mach number increases with respect to material stretch as before, leading to violent collapses at higher material stretches (\(M \ge 0.08\)).

Quasi-online (IEnKS) Results

Next we implement the quasi-online (IEnKS) method, where the estimation trails the simulation by a fixed number of time steps. This is particularly useful because the time-varying estimation provides additional information on IMR model uncertainties. In this section, we will focus on two examples that indicate deviations from the theoretical framework, while comparing cavitation events nucleated under different experimental conditions.

For the first example, we focus on bubbles nucleated in PA (no seed particles) at all four laser energies, ranging from nominal values of 117 \(\mu\)J to 449 \(\mu\)J. In Fig. 8, we plot the ensemble’s variance in these estimates over time. The time evolution of curves span from the first bubble radius peak for all cases, where initial bubble collapse for each example occurs approximately at the normalized time indicated by the dashed vertical lines. For the nominal laser energy of 117 \(\mu\)J case shown in Fig. 8(a), the time-varying \(\alpha\) parameter gradually increases then dips after first bubble collapse. In Fig. 8(b, c), as the laser energy is increased, the \(\alpha\) and \(\mu\) variance have an increased peak. This is even more apparent at the highest laser energy case shown in Fig. 8(d), where at a nominal laser energy of 449 \(\mu\)J, both peak \(\alpha\) and \(\mu\) variances increase almost five times the peak values of the lowest energy case. Thus, as laser energy increases, the quasi-online (IEnKS) method produces more uncertain fitting results. This is most likely due to missing explicit mathematical descriptions accounting for additional physical phenomena that, at present, are not represented in the current IMR theoretical framework.

Fig. 8
figure 8

Quasi-online (IEnKS) fits, with ensemble size of 48, were performed on bubble radius curves in PA (no beads). \(\alpha\) and \(\mu\) variance versus normalized time are plotted at nominal laser energies of (a) \(\sim\) 117 \(\mu\)J, (b) \(\sim\) 254 \(\mu\)J, (c) \(\sim\) 337 \(\mu\)J, and (d) \(\sim\) 449 \(\mu\)J. First bubble collapse occurs at approximately the dashed line for all \(n = 8\) samples per experimental condition

Full size image

The second representative example we present with the quasi-online (IEnKS) method compares a bubble in a PA hydrogel (no seed particles) at the highest energy to a bubble in a PA hydrogel (paramagnetic seed particles) at the lowest energy. The non-dimensionalized time versus radius curves for each case and online estimation are shown in Fig. 9(a, b). These cases have \(\lambda _{max}\) values of 9.5 and 4.7, with low NRMSE values. The data assimilation starts at maximum normalized radius, \(R^* = 1\), and normalized time, \(t^* = 0\). In Fig. 9(c), we consider a time-varying \(\alpha\) of the PA hydrogel (no seed particles) at highest energy first (\(\lambda _{max} = 9.5\)). There is a gradual increase followed by a decrease in \(\alpha\) as the bubble collapses. However, at initial collapse, \(\alpha\) experiences a significant increase. Upon the second peak collapse, we observe another increase in the estimation. The time-varying viscosity (Fig. 9(e)) follows a similar trend, where it maintains a steady value until the first collapse, when a large jump increase is observed. Upon second collapse, the estimator adjusts to a higher viscosity estimate again.

We compare this case to a bubble nucleated within PA on a paramagnetic particle at the lowest laser energy (\(\lambda _{max} = 4.7\)). In this case, \(\alpha\) has no discernible jump at collapse, but instead displays a gradual drop-off in the estimation value over time (Fig. 9(d)). Likewise for the viscosity estimate, we observe relatively constant parameter values in both parameters at collapse, and a slight dip upon first collapse (Fig. 9(f)). It should be noted that while the parameter estimates in subsequent radius peaks are constant, this does not imply a better fit to the model during that portion of the bubble dynamics. Instead, despite using a covariance inflation in the quasi-online method, the ensemble eventually converges when the best estimates are found. Thus, subsequent peaks are not a better fit to the model, but rather, the estimator can no longer improve on its estimates for \(\mu\) and \(\alpha\).

Fig. 9
figure 9

The quasi-online (IEnKS) method (ensemble size of 48) is implemented to compare two extreme cases with normalized radius versus time curves in (a) PA (no beads) at nominal laser energy 449 \(\mu\)J and (b) PA (paramagnetic particles) at nominal laser energy 18 \(\mu\)J. The (c, d) \(\alpha\) and (e, f) \(\mu\) estimates over normalized time for each case are plotted

Full size image

Overall, the low laser energy (paramagnetic seed particle) case exhibits a smoother estimation around first collapse, which is likely due to the smaller exhibited material stretch. This is in stark contrast to the high energy PA (no seed particles) case, with large material stretch, where there is a discernible increase in both parameter estimates and uncertainties at the collapse points. Given the current viscoelastic IMR theoretical framework, the viscosity and strain-stiffening parameters of the surrounding PA hydrogel should be estimated to be the same under both conditions, yet there are observable differences between these cases. These stark contrasts in time-varying material behavior are consistent with previous observations of violent bubble collapses in PA gel. This notion is also reflected by a much higher critical Mach number in the case of no seed particles, compared to that of the paramagnetic particle case (see Fig. 7).

The selected examples described in this section illustrate the time-varying material parameter estimates, as well as the the model uncertainties with respect to material stretch and laser energy. We see the greatest uncertainty in time-varying material parameters at the bubble collapse points, especially at the first inertial collapse. However, we see a convergence in material parameter variation with decreasing energy for a given case, as well as at lower material maximum stretch regimes, indicating that for lower material stretches or nucleation energies, the current IMR framework is appropriate for accurately describing the laser-induced cavitation dynamics.

Discussion

Constitutive material modeling requires controlled loading and unloading techniques to vary the applied strain magnitude and resulting material deformations. While inertial cavitation events provide means of generating high to ultra-high strain rate deformations in soft materials, the IMR framework was developed with access to a limited material deformation regime. Through the use of seed particles and the modulation of laser energies, we successfully expand the deformation regime of a PA hydrogel of given concentration from \(\lambda _{max} \approx 4-9\). Through the use of a recently developed DA technique applied to the IMR framework, we fit a quadratic law Kelvin-Voigt constitutive model to our PA hydrogel and quantified the fitting errors, global material properties, and critical Mach numbers at initial collapse. We continue our analysis by identifying the greatest IMR uncertainties during the time evolution of the cavitation event.

Effects of Laser Energy on Bubble Radius Fits and Material Parameter Variance

Previous studies with lower temporal resolution of bubble kinematics required data fitting of the first 3-peaks [1]. However, with improved high-speed imaging capabilities, the 1-peak approximation was found to provide a more accurate and precise measurement of the intrinsic material properties. It was further found that assuming bubble sphericity, the material incompressibility assumption broke down upon first bubble collapse for a critical Mach number, \(M_{cr} \ge 0.08\) [2]. Our study reaffirms this finding as the 1-peak fits consistently had the lowest NRMSE error regardless of experimental conditions. Though maximum material stretch did not change the goodness of bubble radius fit for a given number of peaks, increasing laser energy increased the NRMSE for all peak-fitting cases (see Fig. 5). This is also reflected in the fitted global material parameters (see Fig. 6), that with increased laser energy, the spread, or uncertainty, of the fitted material parameters also increases. Furthermore, time-varying IMR analysis of PA (no particles) at different laser energies, but relatively constant maximum material stretch, showed higher laser energies resulted in larger material parameter variance, especially around the initial bubble collapse (see Fig. 8).

It should be noted that while laser energies were measured in this study, the values should not be regarded as ground truth bubble energies. Optical breakdown events are characterized by the time evolution of free electron density as a function of input laser pulse parameters, including the excitation of electrons, their interaction with unexcited electrons, and recombination effects with surrounding molecules in the medium. A rate-dependent increase in ionization energy due to these events leads to optical breakdown [21]. While the ionization energy of water is well studied [22, 23], and plasma energy density can be numerically determined to convert to bubble energy, material parameters for ionization thresholds is less known for PA. While laser energy is measured in this study, the energy deposited into the bubble is not quantified and is dependent on laser focusing optics, as well as the physics of dielectric breakdown and nucleation physics specific to the medium. Thus, it is assumed the laser energy measured in this study is a qualitative reference for energy absorbed into the PA hydrogel.

While the IMR model is most accurate up through 1-peak fit, cavitation events nucleated at relatively high laser energies had poor bubble radius fits and large material parameter variance. This deviation from the IMR model may require a potential reevaluation of the current equation of state for the bubble pressure and its underlying thermodynamics, as well as the incorporation of non-spherical bubble geometries, to improve the overall IMR framework.

Increasing Material Stretch Increases Compressibility Effects and IMR Uncertainty

Inertial cavitation collapses with critical Mach numbers, \(M_{cr} < 0.08\) are typically idealized as nearly incompressible [2], where a constant material density is considered without any detrimental loss to accuracy [24]. However, for values exceeding \(M_{cr}>0.08\), it may become necessary to account for more material compressibility by way of density variation in the material [24]. In this study, inertial cavitation bubble collapse became increasingly violent as the maximum material stretch also increased (see Fig. 7). For the low material stretches where the collapse is non-violent and material damage is not expected to occur, the current viscoelastic framework describes the entire cavitation dynamics well, and the error is not expected to grow with the number of data points. For higher material stretches, where violent bubble collapse occurs, the current framework is still an adequate representation of the cavitation dynamics up to the first collapse point after which effects of compressibility and material damage are likely occurring. (For reference, the Rayleigh-Plesset equation to describe inertial cavitation dynamics, mainly in water, assumes material incompressibility [25, 26]. However, the Keller-Miksis approach used in the IMR framework incorporates the material sound speed to account for compressibility in the far-field of the cavitation bubble [1, 9]). While the IMR approach does take into account material compressibility radially from the bubble wall, calculating the critical Mach numbers for the range of bubble amplitudes and material stretches acquired in this study illuminates the need to account for more material compressibility in the IMR framework.

Considering the 1-peak fit case (see Fig. 7(a)), most cavitation events, with the exception of some paramagnetic seed particle cases (\(\lambda _{max} \approx 4\)), have \(M_{cr}> 0.08\). This may be explained by a recent study from Murakami et al. on the effects of gas-vapor bubble dynamics, where the ratio of non-condensible gas to water vapor inside a bubble was varied synthetically, with experimentally verified results. It was found that decreasing the water content of a liquid medium generated more gaseous content inside of a laser-induced bubble, resulting in a damping of oscillatory bubble dynamics [27]. As an example in this study, while paramagnetic particles induced larger bubbles for a fixed laser energy, it is possible more non-condensible gaseous content was also produced, decreasing the maximum material stretch, as well as damping violent bubble behavior. Given the gradual increase of critical Mach number with increased stretch ratio, material compressibility effects may also need to be increasingly accounted for depending on the extent of the material deformation.

Conclusion

We developed a new experimental approach for controlling inertial cavitation bubble amplitudes and resulting maximum material stretches sustained in soft polyacrylamide hydrogels. Through lowering laser energy and embedding seed particles that serve as nucleation sites, we successfully expanded the finite deformation range of PA hydrogel maximum material stretches to span from approximately 4 to 9, representing more than a twofold increase in deformation regime access compared to our previous IMR technique. Numerical ensemble-based data assimilation techniques were implemented to output global and time-varying viscoelastic material properties by means of improved and robust constitutive data fitting, as well as identifying experimental conditions under which the current theoretical framework of IMR might be insufficient for capturing all pertinent cavitation physics.

Finally, the results of this study demonstrate that across a range of material stretches and nucleation energies, purely viscoelastic material behavior is not a sufficient description of bubble dynamics. The current IMR framework performs best when applied to bubbles nucleated under specific experimental conditions, or when applied to only a limited region of the R(t) curve (see [2]). Ideally, bubbles nucleated at low laser energies in samples containing seed particles, to decrease the maximum experienced material stretch, fit the IMR model best. However, our study indicates the physics of inertial cavitation dynamics is richer than our model suggests. Bubble radius fitting using our theoretical framework beyond first bubble collapse is insufficient, likely due to unaccounted physics for material damage sustained from inertial effects of the cavitation event at initial expansion and collapse. Furthermore, material damage sustained beyond the first collapse can also affect the long-term bubble equilibrium radius measurement, and the resulting stress integral within the Keller-Miksis equation (for more information please refer to [1]). To further augment the IMR modeling framework, the future incorporation of non-Newtonian rheological behavior will improve predicted cavitation dynamics, especially over subsequent rebounds and collapses, for all bubble amplitudes. Regarding the contents of the bubble, changes in the underlying thermodynamics including more detailed descriptions of the various molecular constituents as well as a more complex equation of state are another consideration. Furthermore, limited temporal resolution of bubble dynamics at collapse points introduces model uncertainties that also require further investigation. Overall, addressing these challenges leaves much room for further theoretical and experimental development including the introduction of damage mechanisms to describe inelastic material behaviors.