Spatial-temporal fusion graph framework for trajectory similarity computation

Abstract

Trajectory similarity computation is an essential operation in many applications of spatial data analysis. In this paper, we study the problem of trajectory similarity computation over spatial network, where the real distances between objects are reflected by the network distance. Unlike previous studies which learn the representation of trajectories in Euclidean space, it requires to capture not only the sequence information of the trajectory but also the structure of spatial network. To this end, we propose GTS, a brand new framework that can jointly learn both factors so as to accurately compute the similarity. It first learns the representation of each point-of-interest (POI) in the road network along with the trajectory information. This is realized by incorporating the distances between POIs and trajectory in the random walk over the spatial network as well as the loss function. Then the trajectory representation is learned by a Graph Neural Network model to identify neighboring POIs within the same trajectory, together with an LSTM model to capture the sequence information in the trajectory. On the basis of it, we also develop the GTS⁺ extension to support similarity metrics that involve both spatial and temporal information. We conduct comprehensive evaluation on several real world datasets. The experimental results demonstrate that our model substantially outperforms all existing approaches.

1 Introduction

Trajectory similarity computation is a fundamental operation in a wide range of real world applications, such as route search [1,2,3,4,5], route planning [6,7,8], trajectory clustering [9,10,11], trajectory compression [12,13,14], and transportation optimizations [15,16,17]. A trajectory describes the path traced by bodies moving in space over time [18] and is usually represented as a sequence of discrete locations. To measure the similarity between two trajectories, many metrics are proposed in previous studies, such as Dynamic Time Warping [19] (DTW), longest common subsequence [20] (LCSS), edit distance with real penalty [21] (ERP) and edit distance on real sequences [22] (EDR). However, these metrics require quadratic computational complexity ${\mathcal {O}} (n^{2})$, where n is the length of trajectories. As a result, the high computation cost of the above similarity metrics becomes a serious problem when dealing with massive trajectory data. To resolve the problem, some recent studies [6, 23, 24] utilized neural network based models to learn the representation of trajectories. The similarity between trajectories could be measured by that between the low-dimensional embedding vectors, which can be completed in linear time.

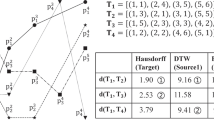
While the above approaches are effective for measuring the trajectory similarity in Euclidean space, they cannot be applied to the problem of trajectory similarity computation over the spatial network, such as road network. In many real application scenarios, objects are moving in spatial networks rather than in Euclidean space. In a spatial network, Euclidean distance may lead to errors when calculating the real distance between objects. Let us consider the example shown in Figure 1. The Euclidean distance between trajectories τ₁ and τ₂ is smaller than that between τ₁ and τ₃. But the distance on the road network between τ₁ and τ₃ is actually much smaller, as there is no passage between τ₁ and τ₂ in the road network.

Fig. 1

Example of Trajectory Similarity Measurement over Spatial Network

There are several previous studies [25,26,27,28] focusing on the computation of trajectory similarity over spatial networks. They proposed hand-crafted heuristic approaches to align the trajectory to the spatial network to compute some user-defined similarity functions, which still suffer from high computational overhead. However, the difficulty in adopting deep learning-based techniques to this problem is two-fold. On the one hand, it is essential to consider the network structure when learning the trajectory embedding, while existing solutions for Euclidean space [6, 23, 24] only capture the sequence information. On the other hand, the learning process suffers from data sparsity: due to the large problem space which is exponential w.r.t. the number of POIs in the spatial network, the coverage of training data might be insufficient to include all possible combinations. As a result, once a trajectory pattern is infrequent or even missing in the training data, the trained model cannot learn a high-quality embedding for it.

To address above issues, in this paper we propose G raph-based approach for measuring T rajectory S imilarity (GTS), a novel framework of trajectory representation learning for similarity computation over spatial networks. GTS consists of three steps, namely measuring trajectory similarity, learning point-of-interest (POI) representation, and generating trajectory embedding. We start from the similarity measurement between trajectories, which is the first step towards a robust framework for learning trajectory embedding. To reflect the relationship between trajectories on the road network as well as the inherited properties of every single trajectory, we define the trajectory similarity from three aspects: POI-wise distance, POI-Trajectory distance, and Trajectory-wise similarity.

Based on such definitions of trajectory similarity over the spatial network, we then learn the trajectory embedding in the following two steps. We first learn the embedding of each POI in the spatial network, which serves as a cornerstone for the embedding of trajectories. While previous works [29,30,31] learn the POI embedding mainly by learning its spatial information, here we need to consider the trajectories along with the topology of the spatial network. To this end, we propose a trajectory-aware random walk algorithm and a new loss function to train a skip-gram model such that POIs co-occurring in these random walks would produce similar embeddings. In the next step, we learn trajectory representation based on such POI embeddings. To overcome the data sparsity problem, we use Graph Neural Network (GNN) to encode the embedding of each POI with its neighbor information. Then a trajectory becomes a sequence of POIs and we can learn its representation with a Long Short-Term Memory (LSTM) network. In this way, the learned representation will contain richer information of the network structure and thus is capable to reflect various trajectory patterns even if they are not explicitly included in the training data.

Moreover, we further take the temporal information in trajectories into consideration and proposed an extended approach GTS⁺ for trajectory similarity computation based on both spatial and temporal information. Specifically, we discretize the time intervals into smaller units and construct the temporal-aware graph of all POIs based on the co-occurrence of their time units. Then we propose a novel LSTM variant termed as ST-LSTM to jointly capture the spatial and temporal information to learn the trajectory embedding.

The main contributions of this paper are summarized as follows:

• We propose a graph-based framework GTS for the problem of trajectory similarity computation over the spatial network. To the best of our knowledge, it is the first work to solve this problem with deep learning techniques.

• We devise a trajectory-aware random walk algorithm with a new loss function to learn the embedding of each POI in the spatial network to integrate the trajectory information with the network structure.

• We further design a GNN-LSTM model which is robust to data sparsity and noisy in given trajectories to learn high-quality trajectory representations.

• We propose the GTS⁺ framework to support trajectory similarity computation with both spatial and temporal information.

• We conduct an extensive set of experiments on popular real-world datasets. The results show that our proposed methods significantly outperform the existing approaches in terms of accuracy.

The rest of the paper is organized as follows: Section 2 surveys the related work. Section 3 introduces necessary background knowledge and problem settings. Sections 4 and 5 propose the techniques to learn the representation of a single location and the whole trajectory, respectively. Section 6 introduces how to extend the above techniques to include temporal information and proposes the GTS⁺ framework accordingly. Section 7 reports the experimental results. Section 8 concludes the paper.

2 Related work

2.1 Non-learning trajectory similarity computation

There are two categories of traditional approaches for trajectory similarity computation. One is grid-based similarity, which uses distances in Euclidean space. Previous studies in this category rely on the distance aggregation over all points on the trajectory to compute the similarity, such as Dynamic Time Warping [19] (DTW), longest common subsequence [20] (LCSS), edit distance with real penalty [21] (ERP), edit distance on real sequences [22] (EDR) and Hausdorff [32]. They are expensive in efficiency even with some optimizations [33] and might suffer from noisy points in trajectories.

The other one is spatial network based similarity [26, 34], where trajectories are first mapped to the spatial network and then the similarity is computed by applying similarity functions on top of the transformed trajectories. Earlier approaches utilized metrics like shortest path and set-based similarity to describe the similarity between trajectories. Shang et al. [26] proposed a joint similarity function to consider both spatial and temporal similarity as well as several indexing and pruning techniques. Wang et al. [35] defined a new function called Longest Overlapping Road Segments to measure the similarity between two transformed trajectories. Unfortunately, existing road-constrained trajectory measures either suffer from the high computation cost or are not capable to satisfy the requirement of real-life applications.

There are many applications regarding trajectory similarity computation. Several previous studies [3, 8, 36] aimed at accelerating the similarity search and join over trajectory data by devising index and pruning techniques following the idea from string similarity search [37,38,39,40]. Specifically, tree-based index structures [22, 27] , such as K-D tree or R-tree are employed to organize the trajectories. Then, bounding-box-based pruning techniques are proposed to eliminate unnecessary computations. Zheng et al. [41] studied the problem of inference hidden route from known trajectories. Song et al. [15] focused on the problem of trajectory compression based on the road network. Han et al. [42] investigated this problem by considering only spatial information.

2.2 Deep learning based approaches

Deep learning techniques have been widely adopted to many problems related to spatial data analysis [29, 42,43,44]. A comprehensive survey is made in [18]. Some existing studies employ neural network models to learn the representation of trajectories and then compute the similarity by measuring that between the embedding vectors. Li et al. [23] adopted an encoder-decoder architecture to obtain trajectory vector representations. Yao et al. [24, 45] further improved the performance by devising new spatial attention mechanism and using pair-wise distance as guidance for learning. Zhang et al. [6] proposed several new loss functions to improve the quality of learned embedding. All the above methods are designed for similarity metrics in Euclidean space and cannot be directly adopted for our problem as they fail to learn the information from the spatial network. Deep learning techniques are also adopted for other related problems, such as clustering [9] and route prediction [25], which have different problem settings from our work.

2.3 Graph neural networks

Recent works on the Graph Neural Network (GNN), especially graph convolutional networks (GCNs) [46] have attracted considerable attention, motivating the remarkable success in various graph mining tasks in multiple domains [47, 48]. GNNs originated from the spectral graph networks [49]. Afterwards, Kipf and Welling [46] further extended it for semi-supervised node classification with concise form and achieved great success. Taking account of large-scale networks, Hamilton et al. [50] approximated GCN by an inductive representation learning framework. Later, the attention mechanism was also introduced to adaptively specify the weights during the training process [51]. Our work took advantage of GNN to obtain neighborhood information of each node in the spatial network so as to overcome the data sparsity problem.

3 Preliminary

3.1 Trajectory with spatial networks

We first describe our data model. The spatial network is represented as an undirected graph G = (V,E). In this graph, each node v ∈ V is a POI in the spatial network, where the representation of a road intersection or a road end with attributes latitude and longitude. Meanwhile, each edge e = 〈v_i,v_j〉∈ E represents the distance between two POIs v_i and v_j. An original trajectory τ = {p₁,p₂,…,p_k} is composed with sequential points with latitude and longitude. Then we mapped them into the POI set V with the nearest distance to generate the corresponding vertex trajectory $\tau = \left \{ v_{n1},v_{n2},\ldots ,v_{nk} \right \}$ and the length of a trajectory (denoted as $\lvert \tau \rvert$) is defined as the number of POIs in it.

3.2 Spatial Similarity between trajectories

Different from previous studies using Euclidean distance, the similarity measurement in our work should not only reflect the property of a trajectory, but also reflect the property of the spatial network. To achieve this goal, we define trajectory similarity by considering the distances from two aspects: POI-wise distance and POI-Trajectory distance.

The POI-wise distance is the distance between two POIs over the road network, which is defined as the length of the shortest path between them. Given two POIs v_i,v_j ∈ V, if v_i is reachable from v_j, we use d(v_i,v_j) to denote the length of shortest path, i.e. the POI-wise distance between them.

Similarly, we define the POI-Trajectory distance as the shortest distance between the POI and the trajectory. However, the computation of the exact value is very expensive as we need to compute distances between the POI and all segments of this trajectory. To reduce the computation overhead, we define the POI-Trajectory distance as the shortest POI-wise distance between the given POI and all POIs in the trajectory. Although the computational complexity of our definition is the same as that of the original method, the cost is much less in practice since the distances between POIs in our definition could be reused for different trajectories and the amortized cost would be rather low. Then given one POI v and trajectory τ, the POI-Trajectory distance d(v,τ) from the POI to the trajectory is formulated as (1):

$$ d(v,\tau) = \min\limits_{v_{i} \in\tau}d(v,v_{i}). $$

(1)

Based on the above definitions, we propose the cornerstone of our learning framework: Trajectory-wise similarity. To define an effective similarity metric, the computation of Trajectory-wise similarity should have the property of commutativity. Moreover, it should also be negatively correlated to the actual distance between trajectories. Based on above consideration, given two trajectories τ₁ and τ₂, we formulate the definition of Trajectory-wise similarity between them (denoted as Sim(τ₁,τ₂)) in (2):

$$ \text{Sim}(\tau_{1},\tau_{2}) = \frac{{\sum}_{v_{i}\in\tau_{1}}e^{-d(v_{i},\tau_{2})}}{\lvert \tau_{1} \rvert} + \frac{{\sum}_{v_{j}\in\tau_{2}}e^{-d(v_{j},\tau_{2})}}{\lvert\tau_{2} \rvert}, $$

(2)

3.3 The GTS framework

With the definition in (2), we can then formally define the problem of trajectory similarity computation over the road network with the learning method formally as Definition 1.

Definition 1

Given a road network G = (V,E) and a trajectory set T = {τ₁,τ₂,…,τ_n}, ∀τ_i ∈T it aims at finding a trajectory τ_j that minimizes Sim(τ_i,τ_j) or Sim_ST(τ₁,τ₂) and i≠j.

To minimize Sim(τ_i,τ_j), we propose a two-step framework GTS shown in Figure 2. Compared with the end-to-end model architecture, the advantage of a two-step framework is that the training process is more stable and interpretable. The two steps will be detailed in Sections 4 and 5, respectively.

Fig. 2

Overall Framework of GTS

There are mainly three challenges in the construction of the trajectory similarity measurement model.

• 1 How to utilize the information of spatial network in the perspective of trajectory, which could be different from grid-based methods.

• 2 How to represent the trajectory should be considered carefully, as the trajectory representations are closely related to the computation of trajectory similarity.

• 3 How to design the objective function to train the models, which should help learn the characteristics of collected trajectory datasets.

4 POI representation learning

In this section, we will introduce a new framework TraNode2Vec for learning the POI representation over the road network. We first give the big picture of the learning objective in Section 4.1 and then provide more technical details in Section 4.2.

4.1 Objective function

Since we targeted learning trajectory similarity over road network, the first step is to learn a high-quality presentation of POIs in the network. To this end, the learning objective should be with physical significance so as to include the information of trajectories into the POI representation. Unlike previous studies that utilized feature engineering methods based on expert knowledge, in our work, we aim at learning trajectory-aware POI embedding via the distance and similarity functions defined in Section 3. As a result, our approach can not only learn the topology of the road network but also fit the distribution of existing trajectories.

The first step towards this goal is to design a proper objective function that is consistent with the goal of learning trajectory similarity. According to our definition of Trajectory-wise similarity, it is essential to know the distance between POIs so as to estimate the similarity. Therefore, we aim at identifying a learning objective to help formulate a representation where the embedding vectors of nearby POIs or belonging to the same trajectories should also be closed to each other. In this target, there are two kinds of relationships between POIs. The first relationship is the topology relationship between POIs in the road network, which will influence the distances between them directly. The second one is whether two POIs belong to the same trajectory. These two relationships could be metaphysically described as the ‘neighbors’ of POIs, in which we can model them with existing embedding methods that are able to capture the property of neighbors.

To capture the property of ‘neighbors’, we could utilize the well-known Skip-gram [52] approach, which is originated in the field of natural language processing. It has been exploited in many applications to learn the representation of basic building blocks, such as the word embeddings in the article. Given the POI set V = {v₁,v₂,…,v_m}, we could get the Skip-gram objective function for our task as (3)

$$ \max\limits_{f}\sum\limits_{v\in V}\log P(N_{s}(v)\lvert f(v)), $$

(3)

where $f:v\rightarrow \mathbb {R}^{d}$ is the encoder to map the POI into d dimension vectors, P(⋅) is probability function and $N_{s}(v)\subseteq V$ is the neighbors of POI v which is obtained via a random walk algorithm described later in Section 4.2. By optimizing this objective function, the learned embedding of given POI will have an explicit connection with those of its neighbors (Figure 3).

Fig. 3

Illustration of the process of random walk with trajectory

One limitation of the above objective function lies in the aspect of computational efficiency. To resolve this problem, we make a trade-off between accuracy and efficiency as follows: For the given POI v, we assume that all its neighbors in $N_{s}(v)\subseteq V$ are independent, which can reduce the computational complexity of the function P(N_s(v)|f(v)). Under this assumption, we have the objective function as (4):

$$ P(N_{s}(v)\vert f(v)) = \prod\limits_{v_{i}\in N_{s}(v)}P(v_{i} \vert f(v)). $$

(4)

Given POIs v_i and v, the value of P(v_i|f(v)) satisfies the following conditions: (i) the value of probability should be ranged in [0,1]; and (ii) the sum of all probabilities for the given POI v should be 1. Thus we employ the softmax function that has been widely used to compute the probability in multiple classification problems. Then we have the explicit formulation of P(v_i|f(v)) as (5)

$$ P(v_{i} \vert f(v)) = \frac{e^{f(v_{i})\cdot f(v)}}{{\sum}_{v_{j}\in V}e^{f(v_{j})\cdot f(v)}}. $$

(5)

However, the computation of ${\sum }_{v_{j}\in V}e^{f(v_{j})\cdot f(v)}$ is time-consuming in the training process. The reason is that function f(⋅) will be updated after every epoch and the computation ${\sum }_{v_{j}\in V}e^{f(v_{j})\cdot f(v)}$ cannot be reused. To solve this problem, the negative sampling method could be utilized to reduce the computation time by pair-wise loss.

4.2 Finding neighbors

Next, we discuss how to generate the set of neighbors N_s(v) of given POI v in the objective function. Previous network embedding approaches, such as node2vec [53], find such neighbors by a random walk algorithm based on the topology structure of the graph. However, in our work, we need to not only consider the topology structure of the road network but also the given existing trajectories.

To address this issue, we employ a random walk algorithm to find N_s(v) for given POI v the topology structure of the road network. Given a starting POI v and the length of walks n_w, the random walks method will generate a random path with starting POI v and n_w nodes. The generation process proceeds node-wise, and every node in the path is dependent on previous nodes. With the starting node c₀ = v, we generate the i-th node c_i for the random path as (6):

$$ P(c_{i} = v_{j} \vert c_{i-1} = v_{k}) = \begin{cases} \frac{\pi_{v_{j}v_{k}}}{Z} &\text{if} (v_{i},v_{j})\in E,\\ 0 &\text{otherwise,} \end{cases} $$

(6)

where $\pi _{v_{j}v_{k}}$ is the transition probability from v_k to v_j and Z is a normalization constant.

As our goal is to learn a trajectory-aware POI representation, we need to reflect the influence of existing trajectories in the definition of transition probability in random walks. The probability of the next node in previous approaches such as node2vec is only decided by the node visited in the previous step. While this approach can capture the topology structure of the graph, it fails to take the trajectories into consideration in our problem setting. To ensure whether two POIs are in the same trajectory, we need to devise a random walk algorithm where the transition probability in each step is also influenced by the starting node of a trajectory.

To reach this goal, a straightforward solution for that is via a sampling-based method. Instead of only considering the last node, we choose the next node according to both the previous node and starting node. The relationship between the next and previous nodes could keep the topology structure of the graph. And the trajectory information will be maintained in the connection between the next and starting nodes.

Based on above discussion, we define the transition probability as $\pi _{v_{j}v_{k}} = \alpha (v_{j},v_{k})\cdot e^{-d(v_{j},v_{k})}$, where the distance in the road network between POIs in incurred in the term d(v_j,v_k). And α(v_j,v_k) is probability of sampling defined in (7):

$$ \alpha(v_{j},v_{k}) = \begin{cases} \frac{1}{p} &\text{if } d_{v_{j}v_{k}} = 0 \text{ and } \{v_{k},v\} \tilde{\in} \tau \\ 1 &\text{if } d_{v_{j}v_{k}} = 1 \text{ and } \{v_{k},v\} \tilde{\in} \tau\\ \frac{1}{q} &\text{if } d_{v_{j}v_{k}} = 2 \text{ and } \{v_{k},v\} \tilde{\in} \tau\\ 0 &\text{otherwise,} \end{cases} $$

(7)

where $d_{v_{j}v_{k}}$ is the path containing the least number of POIs between v_j and v_k, and the operation $\{v_{k},v\}\tilde {\in }\tau$ means there is one trajectory τ ∈ τ that v_k ∈ τ and v ∈ τ.

In this way, we can ensure that all nodes in the path have a direct connection with the starting node v. Moreover, the topology structure of the road network could also be maintained in our sampling method.

5 Graph-based trajectory embedding

In this section, we introduce how to learn the trajectory embedding based on the POI representation learned previously.

5.1 GNN-based representation

Although the POI representation has captured certain information from the spatial network, we still need to incorporate it in the process of learning trajectory embedding. The reason is that we need the information of spatial network from different aspects: In the process of POI representation learning, the spatial network is exploited to make the embedding of connected POIs in the spatial network similar; while in the process of learning trajectory embedding, we need more information about node connections from the spatial network so as to make the trajectory representation more stable and robust.

The main challenge of the trajectory representation is that the search space is the enumeration of combination among all POIs. As a result, we cannot get sufficient training instances to cover all possible trajectory patterns and thus it results in the data sparsity problem. To overcome this problem, we utilize graph neural networks (GNN) to incorporate more information from the spatial network into each trajectory. The reason that we employ GNN here is that its Laplacian regularization term in the objective function of GNN could make the connected nodes keep the same labels and thus help alleviate the sparsity problem. Specifically, the computation of GNN incurs the information of neighbors for the given node.

In our task, we can deal with the sparsity by utilizing more POIs with the same set of trajectories. With the help of GNN, for each POI in one trajectory, we could impose all of its neighboring POIs to generate trajectory embedding. In this way, there will be a larger number of common POIs between similar trajectories. And for a given trajectory, it is easier to find the most similar trajectory in the training set to satisfy our goal in Definition 1.

To this end, we build the graph based on the POIs imposed for each POI in the trajectory as the input graph for GNN. Meanwhile, we could use the spatial network to construct the adjacent graph for GNN where only POIs in the spatial network will be connected in the adjacent graph. In this way, we can directly incorporate the spatial network to compute the trajectory representation.

Given the POIs V = {v₁,v₂,…,v_m} and weights set E, we construct the adjacent graph G as (8):

$$ G_{ij} = \begin{cases} 1 &\text{if } (v_{i},v_{j})\in E\\ 0 &\text{otherwise.} \end{cases} $$

(8)

This adjacent graph G will be symmetric with diagonal element zeros.

Nevertheless, the adjacent graph G in this format still cannot accurately reflect the relationship between POIs. The reason is that values in G are not equal to the influence between the nodes. To address this issue, we construct the Laplacian matrix A in our work with a weight α to control the influence of neighbors as (9)

$$ \mathbf{A} = \mathbf{I} + \alpha \text{Norm}\big(\mathbf{G}\big), $$

(9)

where I is the identity matrix and Norm(G) is the normalization function that every entry will be divided by the ℓ₁-norm of its corresponding row vector. We use P = {p₁,p₂,…,p_n} to denote the POI embeddings V = {v₁,v₂,…,v_n}, where p_i = f(v_i) and f(⋅) is the POI embedding function learned by (3).

As every POI and its neighbors are a subset of V, we only need a subgraph from the graph G to generate the representation by GNN. Here we use the Graph Convolutional Network (GCN) [46] model as the encoder. Given a POI v_i and its neighbors $N(v_{i}) = \{v_{i_{1}},v_{i_{2}},\cdots , v_{i_{k}}\}$, the representation $\tilde {\mathbf {p}}_{i}$ is generated by a 1-layer GCN defined as (10)

$$ \tilde{\mathbf{p}}_{i}= \mathbf{A}_{i} \mathbf{P}_{i} W, $$

(10)

where A_i is the row vector of the adjacent matrix A for the POI v_i, P_i is the stack of features $\{\mathbf {p}_{i},\mathbf {p}_{i_{1}};\mathbf {p}_{i_{2}}; \cdots ;\mathbf {p}_{i_{k}}\}$ for POI v_i and all its neighbors, and W is the learned parameter to project the combined POI features into a new space.

Once the GCN-based embeddings are obtained, we could use them to construct our trajectory embedding with the sequence model. Here we choose LSTM to fulfill this task. Specifically, we use the output of the last time step as the trajectory embedding. Given the network representation $\mathbf {P} = \{\tilde {\mathbf {p}}_{1}, \tilde {\mathbf {p}}_{2}, \ldots , \tilde {\mathbf {p}}_{n}\}$ of a trajectory τ, we generate its embedding E with LSTM as LSTM(P), where LSTM(⋅) is the operation of LSTM which will output the embedding vector in its last timestep.

5.2 Training

With the representation of all trajectories in the training set, we then specify the objective function. According to our definition of Trajectory-wise similarity, the goal of our task is to find the most similar trajectory for a given trajectory. To reach this goal, we use the dot product between the embedding vectors of trajectories to denote the similarity between them. Suppose the embedding vectors of trajectories τ_i and τ_j are E_i and E_j, the similarity score Sim(τ_i,τ_j) can be computed as (11).

$$ \text{Sim} (\tau_{i}\tau_{j}) = E_{i}^{\top} E_{j} $$

(11)

Since we aim at finding the most similar trajectory rather than calculating the exact similarity score, we do not need to perform the actual similarity computation in the process of testing. Therefore, we can decide the objective function in two ways. The first one is to apply the regression loss that uses the true similarity to optimize (11). The second one is using the pair-wise loss that maximizes the similarity between the most similar trajectory and the given one. In our framework, we use pair-wise loss as the objective function, which is also widely used in other ranking-based applications.

Then given the trajectory training set T^tr, we define the loss function as (12).

$$ \max \sum\limits_{\tau_{i}\in T^{tr}, \tau_{j}\in T^{tr}\setminus \{\tau^{\prime}_{i},\tau_{i}\}}\mathbbm{1}(\text{Sim}(\tau_{i},\tau^{\prime}_{i})> \text{Sim}(\tau_{i},\tau_{j})), $$

(12)

where $\tau ^{\prime }_{i}$ is the most similar trajectory for trajectory τ_i. And $\mathbbm {1}$ is the indicator function that equals one if the condition satisfies, otherwise it will be zero.

For a given trajectory in (12), we need to compute similarities between all other trajectories and it. This process would be very time-consuming as the trajectory dataset usually varies largely. To reduce the computation time in the training process, we randomly sample one trajectory instead of traversing all trajectories for the given trajectory.

6 Spatio-temporal trajectory similarity

In this section, we introduce how to learn trajectory embedding based on both spatial and temporal information. We first define the spatio-temporal similarity metric for trajectories in Section 6.1. Next we introduce the way to utilize temporal information in Section 6.2. Finally we propose a spatio-temporal fusion technique to incorporate temporal information into LSTM cells when learning the trajectory representations from the sequence of POIs in Section 6.3.

6.1 Extended similarity with temporal information

For every POI v_i ∈ τ, there is a timestamp v_i.t associated with it which denotes the exact time when the object passed the POI v_i. In many applications, it is essential to also take the temporal information into consideration when We can come up with the temporal-aware POI-Trajectory distance following the idea of Section 3.2 as follows: Given a POI v and a trajectory τ, the definition POI-Trajectory distance between them can be calculated as (13):

$$ d_{T}(v,\tau) = \underset{v_{i} \in\tau}{\min}\|v.t-v_{i}.t\|. $$

(13)

Based on the temporal POI-Trajectory distance, we then propose the temporal Trajectory-wise distance Sim_T(τ₁,τ₂) between trajectories τ₁ and τ₂ as (14).

$$ \text{Sim}_{T}(\tau_{1},\tau_{2}) = \frac{{\sum}_{v_{i}\in\tau_{1}}e^{-d_{T}(v_{i},\tau_{2})}}{\vert \tau_{1} \vert} + \frac{{\sum}_{v_{j}\in\tau_{2}}e^{-d_{T}(v_{j},\tau_{2})}}{ \vert \tau_{2} \vert}. $$

(14)

Finally, by combining the (2) and (14), we could get the spatial-temporal Trajectory-wise distance Sim_ST(τ₁,τ₂) between trajectories τ₁ and τ₂ as (15):

$$ \text{Sim}_{ST}(\tau_{1},\tau_{2}) = \text{Sim}(\tau_{1},\tau_{2}) + \text{Sim}_{T}(\tau_{1},\tau_{2}). $$

(15)

6.2 Temporal-aware graph construction

We propose a new framework GTS⁺ to minimize the value of Sim_ST(τ₁,τ₂) by extending GTS with temporal information. To this end, it requires to first learn the temporal embedding of each POI, and then combine it with POI embedding to learn the representation of the whole trajectory. The first step towards this goal is to identify the temporal embedding of all POIs. To reach this goal, we first build a histogram vector for each POI based on the time it appeared in a trajectory. The closer two histogram vectors are, the more similar two POIs are in the temporal aspect. The first step to build such a histogram is to divide the whole time range into a fixed number of slots. Specifically, there are 24 slots where each slot is corresponding to 1-hour time range of a day. Then the temporal histogram of a POI becomes a 24-dimensional vector. Next we traverse the trajectory collection to build the histogram for all POIs: for each POI on a trajectory, we increase the value of corresponding dimension in the histogram according to its associated timestamp. Finally, we normalize the histogram vector by replacing the value of each dimension to the percentage of occurrence among all the time range, where the sum of values in all dimensions equal to 1. The diagram of this process could be found in Figure 4.

Fig. 4

Example of Temporal Embedding

Next we construct the temporal aware graph based on above temporal histogram of all POIs. In the approach of learning trajectory representation from POI embeddings in Section 4, we construct the adjacent graph G by considering the structure of spatial network and learn the embedding with GNN to address the challenge of data sparsity problem caused by large search space. Following this route, we then construct the temporal-aware adjacent graph so as to identify the neighbors for each POI from the temporal aspect. As the temporal histogram of POI is a fixed-length vector, the similarity between two POIs can be calculated as the cosine similarity between their histogram vectors. Then for each POI v, we add an edge between it and its top-K similarity POIs on the temporal aspect to construct the edge set E_T. The variable K can be regarded as a hyper-parameter and we set it as 20 empirically in this work. And the graph for temporal information G_T = 〈V,E_T〉 can be constructed in the similar way of that in Section 5.1: the set of vertices is the same with G_S and the set of edges is constructed in the way introduced above. Same with G_S, G_T is also symmetric with diagonal element zeros.

Now we have the spatial graph and temporal graph for POIs. Then the next problem is to make use of them to learn the POI embeddings. To solve this problem, we provide a joint training framework GTS⁺ (Joint) that requires only one GNN model to learn the embedding of each POI. Recall that in order to build the graphs G_S and G_T, we need to construct the adjacent matrix M_S and M_T based on the edges in the two graphs, respectively. In the joint training framework, we construct only one graph G with the adjacent matrix M = M_S ⊙ M_T, where ⊙ is the operation of element-wise product. Then we train one GNN model to learn the embedding of each POI based on G using the same way of that in Section 5.1. In this way, the POI embedding learned by the GNN model already carries both spatial and temporal information. Finally, we simple feed the POIs on a trajectory into an original LSTM model as shown in Figure 2 to learn the trajectory representation.

6.3 Fusing spatial and temporal features

Though the effectiveness of GTS⁺ (Joint) framework introduced above, its performance might suffer from the lack of interaction between the spatial and temporal information. To simultaneously learn the characteristics of trajectory from these two kinds of information, we propose a new ST-LSTM model instead of using the original LSTM to generate the trajectory embedding. Specifically, we design a temporal gate to control the influence of temporal information on trajectory representation. In every time step, the temporal gate can select key information in the context according to the current POI embedding input and temporal representations and filter useless information. Meanwhile, the vectors of temporal information can influence the process of sequence modeling and keep the important information in the current hidden states.

To describe the structure of ST-LSTM, we start from reviewing the structure of original LSTM model. In each time step t, it uses the embedding vector x_t of the context POI embedding and temporal embedding vector T_t corresponding to current time step as input. The temporal embedding vector is the one-hot feature which denotes the current time slot of the input. It has three gates: the input gate i_t, forget gate f_t and output gate o_t respectively. The basic update equations of LSTM are as follows:

$$ \begin{array}{@{}rcl@{}} \left( \begin{array}{cc} \text{i}_{t} \\ \text{f}_{t} \\ \tilde{\text{c}}_{t} \end{array} \right) &=& \left( \begin{array}{ccc} \sigma \\ \sigma\\ \tanh \end{array} \right)(\text{W}[\text{h}_{t-1}, \text{x}_{t}] + \text{b}), \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \text{c}_{t} &=& \text{f}_{t} \odot \text{c}_{t-1} + \text{i}_{t} \odot \tilde{\text{c}}_{t}, \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} \text{o}_{t} &=& \sigma(\text{W}_{o}[\text{h}_{t-1}, \text{x}_{t}] + \text{b}_{o}), \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} \text{h}_{t} &=& \text{o}_{t} \odot \tanh(\text{c}_{t}) \end{array} $$

(19)

where h_t and c_t are the cell states.

Based on above update operations of LSTM, we add a temporal gate to each LSTM cell and propose the ST-LSTM model as shown shown in Figure 5. The temporal gate is computed by a POI’s spatial embedding x_t and its temporal embedding T_t. It controls the influence of temporal specificity on trajectory representation for the current input x_t. It can be formalized as follows:

$$ \boldsymbol{g}_{t} = \sigma(\boldsymbol{W}_{xg}[\boldsymbol{x}_{t} \| \boldsymbol{T}_{t}] + \boldsymbol{b}_{g}) $$

(20)

where [⋅∥⋅] is the operation of concatenation, T_t ∈ R^dt is temporal embedding; W_xg ∈ R^d×(dx+dt) is the weighted matrix to be learned; b_g ∈ R^dx+dt is bias. Parameter dt stands for the dimension of temporal vector. dx is the dimension of POI embedding and d is the dimension of hidden layer.

Fig. 5

The Structure of ST-LSTM Cell

Correspondingly, we replace (17) and (18) with (21) and (22) in a cell of ST-LSTM.

$$ \begin{array}{@{}rcl@{}} \boldsymbol{c}_{t} &=& \boldsymbol{f}_{t} \odot \boldsymbol{c}_{t-1} + \boldsymbol{i}_{t} \odot \boldsymbol{g}_{t} \odot \Tilde{\boldsymbol{c}_{t}}, \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} \boldsymbol{o}_{t} &=& \sigma(\boldsymbol{W}_{o}[\boldsymbol{h}_{t-1}, [\boldsymbol{x}_{t}\|\boldsymbol{T}_{t}]] + \boldsymbol{b}_{o}). \end{array} $$

(22)

To apply ST-LSTM in the framework, we just need to use two separate GNN model to learn the spatial and temporal embedding of each POI, respectively. Then we replace the LSTM in Figure 2 with ST-LSTM and use above spatial and temporal embedding of POIs on a trajectory as input.

7 Experiments

In this section, we will demonstrate the effectiveness of our proposed methods by conducting an extensive set of experiments. The experiment setup is introduced in Section 7.1. Results and the corresponding analysis are presented by comparing with 4 state-of-the-art baselines in Section 7.2. Moreover, we conduct an ablation study as well as parameter analysis in Sections 7.3 and 7.4. Finally, the results of spatio-temporal trajectory similarity computation are reported in Section 7.5.

7.1 Experiment setup

7.1.1 Dataset

For the road network, we use two spatial networks from different cities. One is from the city of Beijing, namely the Beijing Road Network (BRN). The other is from the city of New York, namely the New York Road Network (NRN)¹. There are 28,342 POIs and 27,690 edges in the BRN dataset; and 95,581 POIs and 260,855 edges in the NRN dataset.

For trajectories in BRN, we use the taxi driving data [54] from the T-drive project². The taxi trajectories in BRN are collected by taxi id, and the time range of one trajectory may last several days. So we split these trajectories by hour, then we could get 5,621,428 trajectories in total. The average length of these trajectories is 25 by filtering the abnormal ones. For trajectories in NRN, we use the taxi driving data from New York. There are 697,622,444 trips in the original dataset, and we randomly sample a subset of them to generate the trajectory dataset. After pre-processing, there are 10,541,288 trajectories in our experiments and the average length of them is 38. The details are summarized in Table 1. For both trajectory datasets, we randomly split them into training, evaluation, and testing set with the ratio 20%, 10%, and 70%.

Table 1 Statistics of datasets

To evaluate the spatio-temporal based similarity measurement, we still use the above two datasets but perform pre-processing to incorporate temporal information as following: we create the ground truth based on the similarity calculated from (2) and (14) that takes both spatial and temporal information into consideration.

7.1.2 Parameter setting

The details of the hyper-parameter setting are as follows. The dimension of POI embedding is set as 128. And the parameters p and q in the sampling strategy proposed in Section 4.2 are both set as 1. We conduct a grid search to decide on the following hyper-parameters: The dimension of GNN embedding is selected from the range {32,64,128,256}; The dimension of trajectories is also from the range {32,64,128,256} in a similar manner to select the dimension of GNN embedding. The parameter α to control the influence of neighbors in GNN is selected from the range of [0 : 0.1 : 1]. We use Adam [55] as the optimizer to train our proposed methods. The learning rate of Adam is set as 0.001.

7.1.3 Evaluation metric

Following previous studies, we use the hitting ratio in the top K list (HR@K) as the metric in our experiments to show the performance of different methods. The definition of HR@K is set as (23)

$$ HR@K = \frac{1}{\vert T^{te} \vert}\sum\limits_{\tau\in T^{te}}\frac{\vert L_{\tau}^{T}@K\cap L_{\tau}^{R} \vert}{\vert L_{\tau}^{R} \vert} $$

(23)

where T^te is the test set of trajectories, |⋅| is the set cardinality, $L_{\tau }^{T}@K$ is the list of predicted most similar trajectories for a given trajectory τ with length K, and $L_{\tau }^{R}$ is the set of most similar trajectory in the training set for the given trajectory τ where $L_{\tau }^{R} = \{\tau '\}$.

7.1.4 Baseline

As our work is the first deep learning-based method for trajectory similarity over the spatial network, we extend four state-of-the-art methods to similar research problems in our experiments as baselines to show the performance of our method. The details of these methods are summarized as follows:

• Traj2vec [9]: They use a sequence-to-sequence model to learn the representation of the trajectory. Mean square error is utilized as the loss function to optimize their method.

• Siamese [56]: This method is a time series learning approach based on the Siamese network. They use the cross-entropy as the objective function to train the framework. We set the backbone of their Siamese network with LSTM and use the similar setting as [24] to support trajectory similarity computation.

• NeuTraj [24]: This method revised the structure of LSTM to learn the embeddings of the grid in the process of training their framework. To support our task, we replace the grid with POIs in their framework.

• Traj2SimVec [6]: This method employs a new loss for learning the trajectory similarity by point matching. We apply their model to the road network in a similar way to learn the similarity between trajectories.

For the evaluation of spatio-temporal based similarity measurement, we extend the above approaches in a similar way: we initialize the temporal embedding with one-hot representation and feed it into an MLP layer. Then we concatenate the output of the MLP layer with that of the POI embedding to formulate the input of the above models.

7.2 Experimental results

The experiment results on the two datasets could be found in Tables 2 and 3. From these results, we present our observations and corresponding analysis as follows.

Table 2 Results on Beijing dataset (Bold numbers indicate the best performance.)

Table 3 Results on New York dataset (Bold numbers indicate the best performance.)

Firstly, our method outperforms all other methods on all metrics and this could verify the superiority of our method. The main reason is that our framework can utilize the information from the road network, where others only consider the information of the grid.

Specifically, our method significantly outperforms NeuTraj. The improvements come from two aspects: (i) The embedding generation of POIs is independent from the trajectory similarity learning in our method, where NeuTraj learns them simultaneously; and (ii) NeuTraj utilizes the regression loss to learn the actual similarity between two trajectories, while GTS can learn the partial ordering relationship between trajectories. These two factors both improve the performance of trajectory similarity computation.

Moreover, one additional reason why GTS is better than Traj2SimVec is that we use the dot product of embedding vectors to compute the similarity between two trajectories, where Traj2SimVec uses the L₂-norm of absolute the difference between embedding vectors. Using dot product to compute the similarity is inspired by collaborative filtering in the field of recommendation, which has been proved more effective than the linear operation as it could propagate the information between indirectly connected samples efficiently.

Finally, the advantage of GTS over Siamese lies in that the cross-entropy loss in Siamese cannot learn the partial ordering relationship between similar and dissimilar trajectories. And the objective of Siamese is to make the similarity between the similar trajectories as large as possible. Nevertheless, this optimization process will lead to overfitting. At the same time, the loss function of GTS can avoid this problem as its value will be zero if the predicted similarity between similar trajectories is larger than that between dissimilar ones.

7.3 Ablation study

The main components and contributions of our work are that we propose a new way to generate the POI embeddings and utilize GNN to learn the trajectory embeddings. To show the effects of these two techniques in our framework, we give the ablation experiment in Table 4. The settings of these methods are summarized as follows:

• GTS/POI: In this method, we did not utilize our POI embedding as the input for the trajectory similarity model. The embedding matrix is randomly initialized and trained along with other components in the framework.

• GTS/GNN: Instead of applying GNN on POIs for further encoding, we just use our POI embedding as the input for the LSTM to get the trajectory embedding.

Table 4 Ablation Experiment (Bold numbers indicate the best performance.)

From the results in Table 4, we can obtain the following conclusions and analysis:

First, we find that utilizing our POI embedding could significantly improve the performance. As the objective function of the trajectory, similarity cannot directly constrain the POI embedding in GTS/POI, and the POI embedding learned in this process will be random without explainable physical significance. Then the relationship between POI embeddings will be uncertain, and the combinations of POIs cannot reflect the spatial topology of existing trajectories on the spatial network. The two-step strategy for the trajectory similarity learning in our framework could address this problem: The POI embedding learned in the first step would include the information of both the spatial network and existing trajectories in the training data. Then the combinations of them will lead to more reasonable trajectory patterns.

Moreover, we observe that the GNN can definitely improve the performance of our framework. By applying GNN on POI embeddings, it provides richer information of the spatial network. The reason is that the adjacent graph in GNN has the same topology structure as the spatial network. Moreover, the data sparsity problem in the trajectory dataset can also be alleviated with the help of GNN. For each node in the network, the GNN can help impose all of its connected POIs to generate trajectory embedding. In this way, the number of common POIs between similar trajectories will be larger. For a given trajectory, it is easier to find its most similar trajectory in the training set.

7.4 Parameter analysis

We also conduct the parameter analysis to provide more insights into some components in our framework. From the results in Figure 6, we have the following observations:

Fig. 6

Results of different parameters

As shown in Figure 6(a), we could see that the results vary greatly with different values of parameter α. This serves as evidence that the usage of GNN has a significant influence on the performance of learning trajectory similarity. GNN would incur the information of neighbors for the given sample. The performance is the best when α = 0.1, which means the relationship between a given POI and its neighbors achieves the best state for the trajectory similarity learning. When α = 0.0, the GNN will be equivalent to MLP, where there are no neighbors for any given POI. By comparing the results between α = 0.1 and α = 0.0, we could conclude that for a given POI, gathering its neighborhood information in an appropriate way will help improve the performance. However, when the value of α is too large, the performance will become worse. The main reason is that in this case, the weights in the adjacent graph cannot reflect the actual relationship between POIs.

The effect of the trajectory embedding dimension could be found in Figure 6(b). It is obvious that the dimension of trajectory embedding decides how much information they can contain in the training process. If the dimension is too small, it will lead to the underfitting problem, where the model cannot fit the training dataset well. Meanwhile, if the value is too large, it may cause the overfitting problem, where the model cannot achieve good performance on the test dataset. The overfitting problem could be resolved by many other technologies, such as our pair-wise loss and GNN component. And that’s the reason why we could obtain a good performance when the dimension of trajectory embedding is large.

7.5 Evaluate the GTS ⁺ framework

Finally, we report the results of computing trajectory similarity-based both spatial and temporal information. Based on the techniques introduced in Section 6, we proposed 3 approaches:

• GTS⁺ (Concat) is the method that first learns the temporal embedding of each POI with GAT based on the graph constructed in Section 6.2 and then composes the embedding of each POI by concatenating its spatial and temporal embeddings. Finally, the trajectory representation is learned with the original LSTM network.

• GTS⁺ (Joint) is the method that jointly learns the spatial and temporal information of each POI with one GAT network introduced in the last paragraph of Section 6.2.

• GTS⁺ (ST-LSTM) is the method that uses spatial and temporal embedding of each POI as the input and employs a ST-LSTM network introduced in Section 6.3 to learn the trajectory representation.

The experimental results are shown in Table 5. We have the following observations: Firstly, the three GTS⁺ based approaches have a better overall performance than state-of-the-art methods. The reason is that previous approaches fail to capture both the structure of the spatial network and temporal representation. Meanwhile, with our graph-based method, GTS⁺ can learn such information in the learned trajectory embedding. Thus it can achieve promising results in spatial-temporal based trajectory similarity computation.

Table 5 Evaluation Results: Spatial and Temporal Information (Bold numbers indicate the best performance.)

Secondly, GTS⁺ (Contact) performs the worst among the three approaches. The reason is that it cannot properly merge spatial and temporal information. Since the two embeddings are learned in two different vector spaces, directly concatenating them might lead to some noises. The GTS⁺ (ST-LSTM) and GTS⁺ (Joint) methods significantly outperform GTS⁺ (Contact) as they employ reasonable approaches for information fusion. For example, on the New York dataset for the results of HR@50, the results of Concat, ST-LSTM and Joint is 43.07, 46.53, 46.88, respectively.

Thirdly, the performance of GTS⁺ (ST-LSTM) is comparable with that of GTS⁺ (Joint). But the overall performance of GTS⁺ (Joint) is slightly better. The reason might be that although ST-LSTM can effectively make use of the spatial and temporal embedding of POIs, such embeddings are still learned from two different GAT models. Due to the potential issues in data sparsity and vector space alignment, the quality of spatial and temporal embedding themselves is somewhat limited. At the same time, GTS⁺ (Joint) can combine the spatial and temporal information with only one GAT in an earlier stage when learning the POI embedding. It is proved to be a simple but effective approach for this kind of task.

8 Conclusion

In this paper, we proposed the first deep learning-based framework for trajectory similarity computation over the spatial network. Compared with existing approaches, our framework is able to capture underlying route information of the trajectories by considering the structure of the spatial network, thus being robust to the number of available training instances and noisy points introduced by system errors. To this end, our GTS framework first employs a trajectory-aware random walk scheme to learn the representation of each POI in the spatial network. Then it utilizes a GNN-based model combined with LSTM to learn the trajectory representation for similarity computation. We further extend the framework to incorporate temporal information into the similarity computation and design a joint training approach. Experimental results on several popular real-life datasets show the superiority of our framework in terms of effectiveness.