1 Introduction

Deep learning (DL) adopts a deep neural network (DNN) to encapsulate data representations at various layers, which could be facilitated through a diverse array of machine learning (ML) techniques such as supervised ML, unsupervised ML, and reinforcement learning. One of the most remarkable DL paradigms in communication systems is the DNN-based codec (i.e., encoder and decoder) presented in [23], which harnesses inherent expressiveness of deep architectures to exhibit competitive system performance to the result driven by communication theory-based algorithms. As a remarkable instance, a data-driven DNN model proposed in [32] indirectly addresses the challenges posed by multipath fading in Orthogonal Frequency Division Multiplexing (OFDM) systems while simultaneously recovering the transmitted symbols, in contrast with the inevitability of channel state information estimation in conventional communication systems receivers; indeed, the findings from extensive simulations highlight that the DNN-based receiver exhibits performance comparable to that of the minimum mean-square error (MMSE) estimator. Alternatively, a model-driven DL approach was presented in [7], where the receiver architecture is composed of two primary entities—a channel estimation subnet and an OFDM signal detection subnet—both realized through DNNs. Further exploration of the DL realm extends to the integration of a deep unfolding approach, as elucidated in [33], demonstrating the effectiveness of applying DL to realize an equalizer in underwater acoustic OFDM systems. An analogous neural networking receiver to tackling issues such as limited pilots and short cyclic prefixes (CPs) was laid out in [17]. A robust DNN-based precoder in massive Multiple Input Multiple Output (MIMO) systems was introduced in [26] to effectively mitigate the harmful effects stemming from imperfect channel state information (CSI).

The quest for optimal performance in communication systems is often hindered by the complex nature of ambient noise present in real-world physical channels. This complexity arises from the difficulty in accurately modeling such noise, leading to received signals of substantial magnitude and unpredictability [5, 21, 24, 31]. The presence of non-Gaussian impulse noise further compounds this challenge, jeopardizing the guaranteed quality of service typically established under the assumption of a stationary Gaussian random process as the predominant source of interference. A notable example of combatting impulse noise is the application of a fuzzy median filter, as demonstrated in millimeter wave MIMO systems [21]. Adding to that challenge is the inherent vulnerability of DNNs to rare adversarial perturbations [11], including impulse noise. This prompts a rigorous study on how DNNs can be harnessed to effectively address the negative impact of non-Gaussian noise in communication systems. Drawing inspiration from the domain of image processing, an innovative approach was introduced in [2], leveraging Artificial Intelligent Neural Networks so as to expand feature dimensions to train a fully connected (FC) neural network for binary classification—specifically detecting impulse occurrences in OFDM blocks. Unlike this approach, our proposed DNN-based receiver, following the pioneering work of [32], obviates the need for the otherwise inevitable multipath fading channel estimation, thereby focusing on the process of explicit data recovery. The realm of OFDM channel estimation under impulsive noise scenarios was explored through a denoising autoencoder DNN in [18]. Additionally, the synergy of a Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) was harnessed in [19] to estimate communication channels within spatio-temporal impulsive noise channels; however, enhanced reliability in this context often yields at the cost of using partial channel statistics. In the domain of power line communication systems, [25] introduced a DNN-based approach for evaluating model parameters, albeit with the inadvertent assumption of an impulse noise model as a Gaussian mixture model (GMM). Analogously, [6] proposed a GMM-based wireless channel estimator trained on imperfect training data. Furthermore, a notable investigation by He et al. [13] delved into a CNN-based learning algorithm tailored for OFDM systems, with an aim at estimating parameters crucial for impulsive noise suppression. Going beyond the scope of FC neural network models, the field of Polar codes drove the application of an LSTM neural network decoder in [30]. This decoder adeptly addresses memory impulse noise, exhibiting superior system performance and latency results compared to established decoding techniques. Notably, multipath fading channels were not considered in those systems studied in [13, 25, 30].

This paper presents an in-depth analysis of the impact of impulse noise on the bit error rate (BER) performance of a DNN-based receiver in OFDM systems undergoing multipath fading channels. Notably, the DNN-based receiver operates without prior knowledge of impulse statistics, fading coefficients, or the Signal-to-Noise Ratio (SNR) level. Our approach involves a two-stage training process: the initial stage involves modeling OFDM signaling within fading channels, simulated based on specific channel statistics in AWGN. The subsequent stage fine-tunes the model by integrating training data infused with impulse noise. This sophisticated DNN model aims to mitigate the detrimental impact of impulse noise across all subcarriers, a challenge often overlooked yet critical for robust data recovery. Remarkably, even in the face of inherent disparities between training and testing datasets, our experimental outcomes substantiate the efficacy of our approach in combating the adverse effects of impulse noise on data recovery. This further reinforces the resilience of our proposed DNN-based receiver. Beyond harnessing the power of deep learning for targeted impulse noise attenuation, our work importantly establishes a crucial connection between optimal clipping thresholds—quintessential in governing the BER performance of clipping-featured receivers facing impulse noise—and a computationally efficient resolution of this challenge via second-order cone programming (SOCP) formulation. To pursue this optimization solution in a distributed manner, we employ the consensus alternating direction method of multipliers (ADMM) algorithm [3]. Particularly noteworthy is the fact that the conventional clipping-featured receiver relies on the SNR level to calibrate the clipping threshold judiciously. However, as highlighted in [28], its efficacy in suppressing impulse noise becomes compromised when the threshold is measured amidst substantial deviations from the true SNR value. In contrast, our subsequent BER performance comparison—benchmarked against the performance achieved through convex programming introduced in [4]—serves as a compelling evidence to the effectiveness of our DNN-based receiver. Intriguingly, our DNN-based receiver excels while circumventing the reliance on assumed SNR levels and CSI, thereby emphasizing its pragmatic adaptability.

The contribution of this paper is highlighted in the following list:

  • In pursuit of a versatile model adaptable to diverse real-world scenarios, we advance the training paradigm of a pre-trained DNN by incorporating the principles of representation learning. This strategic enhancement entails refining the model’s efficacy through the integration of impulse noise-laced training data in the secondary training stage. This innovation empowers the DNN’s adaptability to unforeseen impulse noise challenges, a cornerstone for robust communication performance.

  • Diverging from the system described in [32], we judiciously incorporate inter-block interference into the framework via an additional CP. This strategic inclusion underpins our effort to synergize impulse noise mitigation with OFDM data detection, which we ingeniously formulate as a convex optimization problem. This formulation culminates in the emergence of a second-order cone programming approach, elegantly addressing the impulse noise corruption.

  • Building on the above formulation, our research contributes a meticulous exposition of the consensus ADMM algorithm’s application. Our approach harnesses the efficiency of this algorithm to derive optimal solutions.

  • We rigorously subject the trained DNN-based receiver to diverse impulse noise contexts, revealing its robustness against the challenges posed by impulse noise and noise model mismatches under specific conditions. Notably, the BER performance of our DNN receiver closely aligns with its conventional clipping-featured counterpart, a benchmark receiver assuming the knowledge of critical impulse noise model parameters.

This paper is organized as follows: the problem statement and the system framework are reviewed in Sect. 2 subsequently, and the details of the proposed schemes are manifested in Sect. 3. Section 4 will present the simulation results, in terms of bit error rate, and a conclusion is drawn in Sect. 5.

Notation: The Hermitian operator is denoted by \((\cdot )^{H}\). For a complex-valued x, the real and imaginary parts are defined as \(\Re \{x\}\) and \(\Im \{x\}\), respectively. The indicator function \(\mathbbm {1}(y)\) returns one if the condition y is satisfied and zero otherwise. The \(\ell _2\)-norm of an N-by-1 vector \({\varvec{x}}\) is expressed as \(\Vert {\varvec{x}}\Vert _2 = (\sum _{k=1}^N |x_k|^2)^{\frac{1}{2}}\). Referencing the i-th element of vector \({\varvec{u}}\) is conventionally accomplished by using \(({\varvec{u}})_i\).

2 System Model

2.1 OFDM Block Formation and Fading Channel Modeling

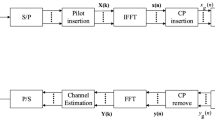
The input bit stream is initially divided into groups based on the alphabet size of Quadrature Phase Shift Keying (QPSK) modulation, assuming Gray mapping. These partitions are then passed through the QPSK modulator, resulting in output symbols denoted as \(X_m\). Here, the superscript m signifies the QPSK symbol index, which corresponds to two-bit partition \({\varvec{u}}_m = [({\varvec{u}}_m)_2\ \ ({\varvec{u}}_m)_1]\). Refer to Fig. 1 for a visual representation of the process. Once N modulated symbols are collected, they are arranged into a vector \({{\varvec{X}}} = [X_0, X_1, \ldots , X_{N-1}]^T\). Let us define \(\omega _N = e^{-j2\pi /N}\), where j is the imaginary unit. The Fast Fourier Transform (FFT) matrix \({\varvec{F}}\) (of size \(N\times N\)) is formulated as follows:

$$\begin{aligned} {\varvec{F}}= \begin{bmatrix} 1 &{} 1 &{} 1 &{} \dots &{} 1 \\ 1 &{} \omega _N &{} \omega _N^2 &{} \dots &{} \omega _N^{N-1} \\ 1 &{} \omega _N^2 &{} \omega _N^4 &{} \dots &{} \omega _N^{2(N-1)} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \omega _N^{N-1} &{} \omega _N^{2(N-1)} &{} \dots &{} \omega _N^{(N-1)^2} \end{bmatrix}~. \end{aligned}$$
(1)

After undergoing an Inverse FFT (IFFT), the time-domain signal block \({\varvec{x}}= [x_0, x_1, \ldots , x_{N-1}]^T\) can be written as follows:

$$\begin{aligned} {\varvec{x}}= {\varvec{F}}^{H}{\varvec{X}}~. \end{aligned}$$
(2)

Specifically, the element \(x_k\) is expressed by the following:

$$\begin{aligned} x_k = \frac{1}{\sqrt{N}}\sum _{m=0}^{N-1}X_m e^{j\frac{2\pi mk}{N}}~, \ \ k\in \{0,1,\ldots , N-1\}~, \end{aligned}$$
(3)

where m is the sub-carrier index for the IFFT implementation (over which the symbol \(X_m\) is transported) and N is the IFFT size. For a sufficiently large IFFT size N, the temporal sequence \(x_k\ (0\le k \le N-1)\) is modeled by an independent, identically distributed (i.i.d.) Gaussian random vector, with each entry \(x_k\) characterized by a mean of zero and a variance of \(E_s\)–which is identical to the modulated symbol energy, i.e., \(E(|X_m|^2)\) for all m–by invoking the central limit theorem.

Fig. 1
figure 1

OFDM System model

Full size image

To preempt inter-block interference, the insertion of a CP is executed at the output of the parallel-to-serial converter. This CP, with a length denoted as \({\mathcal {L}}_p\), is intentionally chosen to exceed the delay spread of the multipath fading channel, ensuring \({\mathcal {L}}_p\ge L\). The Channel Impulse Response (CIR) characterizing the effect on the OFDM symbol is succinctly encapsulated by a CIR vector, represented as follows

$$\begin{aligned} {{\varvec{h}}}= [h_0, h_1, \ldots , h_{L-1}]~. \end{aligned}$$
(4)

Given the premise of precise time and frequency synchronization at the receiver, the intricate time-domain representation of the received signal sequence, after removal of the CP, can be elegantly captured as:

$$\begin{aligned} r_k = h_k\otimes x_k =r_{k_I}+j r_{k_{Q}} \ (0\le k\le N-1)~. \end{aligned}$$
(5)

In this context, the operator \(\otimes\) is used to denote the N-point circular convolution. At each discrete time instance indexed by k, the in-phase and quadrature-phase components of the received signal \(r_k\) are represented as \(r_{k_I}\) and \(r_{k_{Q}}\), respectively. To account for the additive interference, the sequence of received signals is expressed as \(y_k = h_k\otimes x_k +\eta _k~.\) The term \(\eta _k\) encompasses noise contributions originating from diverse sources, as elaborated upon in the following:

$$\begin{aligned} \eta _k= i_k+\xi _k~. \end{aligned}$$
(6)

Here, \(\xi _k\) symbolizes the AWGN, characterized by a flat single-sided power spectral density (PSD) with amplitude \(N_0\). Moreover, the subsequent subsection delves into the formulation of the remaining impulse noise term \(i_k\).

2.2 Memoryless Impulse Noise Modeling

One of the most popularly used statistical models to construct the memoryless impulse noise is the GMM. For instance, Bernoulli-Gaussian (B-G) model [8], where, in addition to AWGN, the impulse occurrence \(i_k = b_k{\tilde{i}}_k\) is taken into account and characterized by an inherent Bernoulli random variable \(b_k\in \{0,1\}\) with the probability of impulse occurrence denoted by \(P(b_k= 1) = p_b\). Further, the impulse noise sequence \({\tilde{i}}_k\ (k =0, \ldots ,{N-1})\) is also an independent and identically distributed (i.i.d.) Gaussian random process with mean zero and variance \(\frac{N_0}{2}\Gamma\) (per dimension), where the impulse-to-Gaussian ratio \(\Gamma\), a strength indicator of the impulse noise, is the mean power ratio between the impulse noise \({\tilde{i}}_k\) and the AWGN noise \(\xi _k\), and abbreviated by IGR. As a consequence, the probability density function (PDF) of the noise sample \(\eta _k\) (a two-state Gaussian mixture model) is written as follows:

$$\begin{aligned} P^{BG}_{\eta _k}(x) = (1-p_b)\ \mathcal{C}\mathcal{N}\left( x;0,{N_0}\right) +p_b\ \mathcal{C}\mathcal{N}\left( x;0,{N_0}(1+\Gamma )\right) ~, \end{aligned}$$
(7)

where

$$\begin{aligned} \mathcal{C}\mathcal{N}\left( z;\mu _z,\sigma _z^2\right) =\frac{1}{\pi \sigma _z^2}e^{-\frac{|z-\mu _z|^2}{\sigma _z^2}} \end{aligned}$$

is the PDF of a circular symmetric Gaussian random variable z, the mean and variance of which are denoted by \(\mu _z\) and \(\sigma _z^2\), respectively. From the description of the noise model in (7), it is worth noting that sophisticated receivers require precise knowledge of the underlying model parameters such as \(p_b\), \(\Gamma\), and \(N_0\) to realize system performance gain. Another widely adopted GMM but with infinite states is Middleton Class-A (MC-A) noise model [20]. The PDF of the i.i.d. noise sample \(\eta _k\) is expressed as follows:

$$\begin{aligned} {P}_{MC-A}(x) = \sum _{\ell =0}^{\infty } \alpha _{\ell }\ \mathcal{C}\mathcal{N}(x;0,\varphi _{\ell })~, \end{aligned}$$
(8)

where \(\alpha _\ell = e^{-A}\frac{A^\ell }{\ell !}\) and \(\varphi _{\ell } = N_0(1+\frac{\ell }{\Lambda A})\). Typically, A is referred to as the impulsive index and \(\Lambda\) is the ratio between the AWGN’s mean power, and that of the impulsive noise.

Aside from the aforementioned Gaussian mixture models, the symmetric alpha-stable (\(S\alpha S\)) distribution [22], defined by the following characteristic function

$$\begin{aligned} \varphi (t) = e^{-\gamma \vert t\vert ^{\alpha }}~, \end{aligned}$$
(9)

is commonly used as well, where the characteristic exponent \(\alpha\) \((0<\alpha \le 2)\) intimates the degree of impulsiveness: the PDF induced by the \(S\alpha S\) distribution is yielded by the inverse Fourier transform of (9), as expressed in the following:

$$\begin{aligned} P(x;\alpha ,\gamma ) = \frac{1}{2\pi }\int _{-\infty }^{\infty } \varphi (t) e^{-jtx} dt = \frac{1}{2\pi }\int _{-\infty }^{\infty } e^{-(\gamma \vert t\vert ^{\alpha } +j t x)}dt~. \end{aligned}$$
(10)

Empirically, a smaller \(\alpha\) signifies more impulsive behavior and vice versa. The particular case with \(\alpha = 2\) corresponds to Gaussian distribution while Cauchy distribution is associated with the special setting of \(\alpha = 1\). A scale parameter \(\gamma\) \((\gamma >0)\) is in regards to driving the dispersion; for instance, the variance of Gaussian distribution (\(\alpha = 2\)) is measured by \(2\gamma\). Since the variance of this impulse noise distribution is infinite–thanks to its heavy tails in the context of \(\alpha <2\), the geometric signal-to-noise ratio (G-SNR), defined as

$$\begin{aligned} \text{ G-SNR } = \frac{1}{2C_g}\left( \frac{A_0}{C_g^{\frac{1}{\alpha } -1}\gamma ^{\frac{1}{\alpha }}}\right) ^2~, \end{aligned}$$
(11)

is a metric substituting for SNR. Moreover, \(A_0 =1\) and \(C_g\approx 1.78\) are used in (11) [10].

It is imperative to stress that the proposed DNN-based receiver, devoid of prior knowledge regarding the specific impulse noise model under consideration, is purposefully subjected to testing. This approach, resonant with real-world scenarios, underscores the resilience of our receiver against the unexpected variability in impulse noise models. Subsequently, the entailing BER performance results (refer to Sect. 4) reinforce its remarkable adeptness in mitigating the adverse effects of impulse noise, notwithstanding the pervasive presence of model mismatches.

2.3 Compressive-Sensing Based Receiver

This subsection initiates by shedding light on the viability of a benchmark receiver rooted in compressive sensing, strategically applied within impulse-corrupted OFDM systems. A notable facet of this benchmark involves harnessing consensus Alternating Direction Method of Multipliers (ADMM), a paradigm of distributed processing. Delving into the mechanics of this framework, we subsequently elucidate its derivation. Notably, the efficacy of this benchmark receiver thrives contingent upon the availability of CSI and SNR level-a caveat intrinsic to this compressive-sensing based receiver. Ultimately, we will assess the efficacy of our proposed DNN-based receiver through extensive computer simulations. We will compare its performance with that of the compressive-sensing based counterpart in terms of BER.

In accordance with established conventions (cf. (6)), the impulse noise instances are collated and structured into a vector format denoted as \({\varvec{i}}= [i_0, i_1, \ldots , i_{N-1}]^T\). Similarly, the AWGN noise samples are organized as \(\varvec{\xi }= [\xi _0,\ldots ,\xi _{N-1}]^T\). Successively, the vector form of the received signal sequence can be analogously written as follows:

$$\begin{aligned} {\varvec{y}}= {{\varvec{H}}}{\varvec{x}}+\varvec{\eta }~, \end{aligned}$$
(12)

where the composite non-Gaussian interference vector is represented by

$$\begin{aligned} \varvec{\eta }= {\varvec{i}}+\varvec{\xi }~, \end{aligned}$$
(13)

and \({\varvec{H}}\) denotes an N-by-N circulant matrix with the transposed form of \({{\varvec{h}}}\) (cf. (4)) serving as its first column. The concatenated output of the IFFT is represented as \({\varvec{x}}= [x_0,\ldots ,x_{N-1}]^T\). It is crucial to emphasize that achieving robust OFDM detection against gross errors through \(\ell _1\)-\(\ell _2\) optimization [4] cannot be guaranteed solely based on an isolated OFDM block (subsequent to CP removal). This limitation emerges due to the inherent deficiency in the rank of the N-by-N matrix \({\varvec{H}}\), which is formed using elements that are randomly generated. Furthermore, in contrast to the strategy presented in [1], which relies on null subcarriers exclusively reserved for sparse signal recovery as a means to overcome this dimensional challenge, the proposed benchmark receiver directly addresses the broader context of impulse noise mitigation in generic OFDM transmission. Of paramount importance, the proposed approach does not hinge on a specific estimation phase and is not contingent upon the use of reserved null subcarriers, as highlighted in [1].

Recall that the DNN receiver developed in [32] considers a data transmission frame comprising two distinctive OFDM blocks. The first block is exclusively composed of pilot symbols, while the second is allocated for the transmission of actual data. Importantly, the CIR is assumed not to vary within the time span of a frame. However, rather than discarding the potentially valuable information embedded within, the innovative impulse noise mitigation approach introduced in this paper takes a step further by exploiting the corrupted CP-length signals situated between the two OFDM blocks. This strategic incorporation serves as a countermeasure against the rank deficiency challenges typically encountered in compressive sensing scenarios. It is worth noting that a similar mechanism was employed in [27], although its application was limited to scenarios involving AWGN. In congruence with the architecture outlined in [27], and harnessing this additional CP segment to avert rank deficiency issues, it is of utmost significance to underscore that this section of the paper (distinctively disregarded in preceding studies such as [27]) is dedicated to the realization of impulse noise mitigation through the prism of convex programming. Notably, the forthcoming passages provide a meticulous delineation of the relevant mathematical notations.

The p-th transmission frame is defined by two consecutive OFDM blocks: \({\varvec{X}}(2p)\) and \({\varvec{X}}(2p+1)\), identified by their indices as (2p) and \((2p+1)\), respectively. Analogously, the (2p)-th received signal block, subsequent to CP removal, is expressed as follows:

$$\begin{aligned} {\varvec{y}}(2p) = {\varvec{H}}_{\scriptscriptstyle T}{\varvec{I}}_{\scriptscriptstyle E}{\varvec{x}}(2p) +\varvec{\eta }(2p)~, \end{aligned}$$
(14)

where the time-domain signal vector is encapsulated as \({\varvec{x}}(2p) = {\varvec{F}}^{H}{\varvec{X}}(2p)\), and the matrix \({\varvec{H}}_{\scriptscriptstyle T}\) is structured as a N-by-\((N+{\mathcal {L}}_p)\) Toeplitz matrix, with the first row corresponding to the CIR vector–\([{{\varvec{h}}}, 0, \ldots , 0]\), while the first column marked by \([h_0, 0, \ldots , 0]^T\). To seamlessly integrate the concept of CP insertion with the underlying OFDM block, a crucial step entails the construction of the \((N+{\mathcal {L}}_p)\)-by-N matrix \({\varvec{I}}_{\scriptscriptstyle E}\). This is accomplished by appending a submatrix \({{{\tilde{{\varvec{I}}}}}}_{{\mathcal {L}}_p}\) beneath an N-by-N identity matrix \({\varvec{I}}_{N}\), where \({{{\tilde{{\varvec{I}}}}}}_{{\mathcal {L}}_p}\) is crafted through the extraction of the initial \({\mathcal {L}}_p\) rows from \({\varvec{I}}_N\). This intricate process culminates in the synthesis of the composite matrix \({\varvec{I}}_{\scriptscriptstyle E} = [{\varvec{I}}_N^T\ \ {{{\tilde{{\varvec{I}}}}}}^T_{{\mathcal {L}}_p}]^T\) in (14).

As opposed to the utilization of a single OFDM block-time observation, as implicated in (14), this paper considers the signal sequence with respect to the p-th transmission frame, which now extends in length to \(M \triangleq 2N+{\mathcal {L}}_p\) instead of 2N. This sequence is expressed in vector form as follows:

$$\begin{aligned} {\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)= & {} {\overline{{\varvec{H}}}}_{\scriptscriptstyle T}{\overline{{\varvec{I}}}}_{\scriptscriptstyle E} {\overline{{\varvec{x}}}}(p) + {\overline{\varvec{\eta }}}(p) \nonumber \\= & {} \varvec{\Xi }\ {\overline{{\varvec{x}}}}(p) + {\overline{\varvec{\eta }}}(p)~, \end{aligned}$$
(15)

where the matrix \({\overline{{\varvec{H}}}}_{\scriptscriptstyle T}\) takes on the form of a \(M\times (M+{\mathcal {L}}_p)\) Toeplitz matrix. The first row is represented by \([{{\varvec{h}}}, 0, \ldots , 0]\) of size M, and first column adopts the configuration \([h_0, 0, \ldots , 0]^T\) of size \((M+{\mathcal {L}}_p)\). Simultaneously, the matrix \({\overline{{\varvec{I}}}}_{\scriptscriptstyle E} = {\varvec{I}}_2\otimes {{\varvec{I}}}_{\scriptscriptstyle E}\) is an expansion of \({{\varvec{I}}}_{\scriptscriptstyle E}\) as defined in (14)), encompassing a two-by-two identity matrix \({\varvec{I}}_2\) and the Kronecker product denoted by \(\otimes\). Stacking two transmitted signal blocks yields a tall vector \({\overline{{\varvec{x}}}}(p) = [{\varvec{x}}^T(2p+1)\ \ {\varvec{x}}^T(2p)]^T\); accordingly, the additive noise sequence in regards to the p-th frame can be represented as another tall vector \({\overline{\varvec{\eta }}}(p)\), which is further decomposed into \({\overline{\varvec{\eta }}}(p) = {\overline{{\varvec{i}}}}(p)+{\overline{\varvec{\xi }}}(p)\).

Crucially, in the absence of interference, the composite channel matrix (presented as a tall matrix) denoted by \(\varvec{\Xi }= {\overline{{\varvec{H}}}}_{\scriptscriptstyle T}{\overline{{\varvec{I}}}}_{\scriptscriptstyle E}\) enables the representation of the received sequence as a simple product of \(\varvec{\Xi }\) and the transmission frame \({\overline{{\varvec{x}}}}(p)\) (refer to (15)). This lays the groundwork for the formulation of the subsequent convex optimization problem. Of notable significance is the incorporation of inter-block interference amidst two consecutive OFDM block-time observations, a distinct hallmark setting the formation (15) apart from the architecture presented in [32]. This distinctive inclusion essentially paves the way for the implementation of a compressive sensing-based receiver in the ensuing discourse.

Leveraging the underpinning structure outlined in (15) and and its resonance with sparse impulse noise (gross errors), a strategy rooted in second order cone programming (SOCP) strategy [4] is harnessed to facilitate the recovery of the transmitted signal vector \({\overline{{\varvec{x}}}}(p)\). This task can be expressed by the subsequent formulation:

$$\begin{aligned} \begin{aligned} \min _{\tilde{{\overline{{\varvec{x}}}}}(p),\tilde{{\overline{\varvec{\xi }}}}(p)}&\quad \Vert {\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-\varvec{\Xi }\ \tilde{{\overline{{\varvec{x}}}}}(p) -\tilde{{\overline{\varvec{\xi }}}}(p)\Vert _1 \\ \text{ subject } \text{ to }&\quad \Vert \tilde{{\overline{\varvec{\xi }}}}(p)\Vert _{2}\le \lambda ;\ \ {\varvec{\Xi }}^{H}\tilde{{\overline{\varvec{\xi }}}}(p) = \textbf{0}~.\\ \end{aligned} \end{aligned}$$
(16)

Given the potential proliferation of the unknown variables at hand, the endeavor to estimate the OFDM signal vector \({\overline{{\varvec{x}}}}(p)\) in conjunction with the AWGN noise vector \({\overline{\varvec{\xi }}}(p)\) can be a computationally demanding task. To alleviate this computational burden, a series of mathematical transformations are invoked, as detailed in the following discourse.

It becomes evident that the null space of the tall matrix \(\varvec{\Xi }\) featured in (15) is indeed present. From this perspective, the column space of \(\varvec{\Xi }\) is effectively denoted as \({{\varvec{U}}}\), while the complementary orthogonal space is represented as \({{\varvec{U}}}^{\perp }\). Furthermore, the establishment of an orthobasis for the column space \({{\varvec{U}}}^{\perp }\) manifests as the matrix \({{\varvec{Q}}}\). In consequence, the orthonormal projector onto \({{\varvec{U}}}^{\perp }\) can be succinctly expressed as \({{\varvec{P}}}_{{{{\varvec{U}}}}^{\perp }}={{{\varvec{Q}}}}{{{\varvec{Q}}}}^{H}\). In this regard, the SOCP (as presented in (16)) can be alternatively formulated as follows:

$$\begin{aligned} \begin{aligned} \min _{\tilde{{\overline{{\varvec{i}}}}}(p)}&\quad \Vert \tilde{{\overline{{\varvec{i}}}}}(p)\Vert _1 \\ \text{ subject } \text{ to }&\quad \Vert {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-\tilde{{\overline{{\varvec{i}}}}}(p))\Vert _{2}\le \lambda ~. \end{aligned} \end{aligned}$$
(17)

Notably, the equivalence between (16) and (17) hinges on the deliberate pursuit of impulse noise mitigation. This is predominantly realized through the initial step of pre-multiplying the received signal vector \({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)\) by the matrix \({{{\varvec{Q}}}}^{H}\). The resolution of the SOCP problem depicted in (16) can be facilitated by employing the widely utilized CVX [12] software package, as exemplified in [29]. In marked contrast, this paper focuses on incorporating the consensus ADMM-based distributed optimization algorithm [3] as the backbone for implementing impulse noise suppression. This novel approach harnesses its inherent parallelism to enhance convergence speed by strategically decomposing the optimization problem into a series of sub-problems. The ensuing mathematical derivation intricately unfolds in the following passages.

In the first hand, two auxiliary variables \({\varvec{z}}_1\) and \({\varvec{z}}_2\) are introduced to enable the parallelism for solving (17), as written in the following:

$$\begin{aligned} \begin{aligned} \min _{\tilde{{\overline{{\varvec{i}}}}}(p)}&\quad \Vert \tilde{{\overline{{\varvec{i}}}}}(p)\Vert _1 \\ \text{ subject } \text{ to }&\quad \Vert {\varvec{z}}_1\Vert _2 \le \lambda \\&\quad {\varvec{z}}_1 = {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2) \\&\quad {\varvec{z}}_2 = \tilde{{\overline{{\varvec{i}}}}}(p)~. \end{aligned} \end{aligned}$$
(18)

Given the global variable \({\varvec{z}}_2\), the local variables \(\{\tilde{{\overline{{\varvec{i}}}}}(p),{\varvec{z}}_1\}\) are considered as a group to be optimized, reflecting the essence of implementing the consensus ADMM. In regards to the newly formulated optimization problem by (18), the augmented Lagrangian is laid out as follows:

$$\begin{aligned} L_{\rho }(\tilde{{\overline{{\varvec{i}}}}}(p),{\varvec{z}}_1,{\varvec{z}}_2,\varvec{\mu }_1,\varvec{\mu }_2)= & {} \Vert \tilde{{\overline{{\varvec{i}}}}}(p)\Vert _1+{\varvec{\mu }_1}^H({\varvec{z}}_1-{{\varvec{Q}}}^{H} ({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2) ) \nonumber \\{} & {} +\frac{\rho }{2}\Vert {\varvec{z}}_1-{{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2)\Vert _2^2 + {\varvec{\mu }_2}^H ({\varvec{z}}_2-\tilde{{\overline{{\varvec{i}}}}}(p))\nonumber \\{} & {} +\frac{\rho }{2}\Vert {\varvec{z}}_2-\tilde{{\overline{{\varvec{i}}}}}(p) \Vert _2^2~, \end{aligned}$$
(19)

where \(\rho > 0\) is the penalty parameter, and \(\varvec{\mu }_1\) and \(\varvec{\mu }_2\) are dual variables.

The scaled dual form of ADMM execution is carried out by setting \(\varvec{\omega }_i = \varvec{\mu }_i/\rho\) for \(i \in \{ 1, 2\}\). After \(\gamma\) iterations (a positive integer \(\gamma \ge 1\)), the update for the i-th entry of impulse noise vector estimate \(\tilde{{\overline{{\varvec{i}}}}}(p)\), i.e., \((\tilde{{\overline{{\varvec{i}}}}}(p))_i\) for \(i\in \{ 1, 2, \ldots , M\}\) is yielded–in closed form–by the following:

$$\begin{aligned} {(\tilde{{\overline{{\varvec{i}}}}}^{\gamma +1}(p))_i} = \max \left\{ 0, |({\varvec{z}}_2^{r}+\varvec{\omega }_2^{\gamma })_i|-\frac{1}{\rho }\right\} \frac{({\varvec{z}}_2^{\gamma }+\varvec{\omega }_2^{\gamma })_i}{|({\varvec{z}}_2^{\gamma }+\varvec{\omega }_2^{\gamma })_i|}~, \end{aligned}$$
(20)

Successively, the update for \({\varvec{z}}_1\)–by minimizing (19) while subjecting \(\Vert {\varvec{z}}_1\Vert _2\) to within the Euclidean ball \(\Vert {\varvec{z}}_1\Vert _2\le \lambda\)–can be yielded in closed formed, and the result is expressed as follows:

$$\begin{aligned} {\varvec{z}}_1^{\gamma +1} = \left\{ \begin{array}{ll} {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma })-\varvec{\omega }_1^{\gamma }~, &{} \text{ if } \Vert {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma })-\varvec{\omega }_1^{\gamma }\Vert _2 \le \lambda \\ \lambda \frac{{{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma })-\varvec{\omega }_1^{\gamma }}{\Vert {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma })-\varvec{\omega }_1^{\gamma }\Vert _2}~, &{} \text{ if } \Vert {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma })-\varvec{\omega }_1^{\gamma }\Vert _2 > \lambda \end{array} ~.\right. \end{aligned}$$
(21)

With the availability of updates \({\tilde{{\overline{{\varvec{i}}}}}^{\gamma +1}(p)}\) as well as \({\varvec{z}}_1^{\gamma +1}\), the proceeding of ADMM is carried out continually and the global variable \({\varvec{z}}_2\) is updated by the following:

$$\begin{aligned} {\varvec{z}}_2^{\gamma +1} = ({{\varvec{Q}}}{{\varvec{Q}}}^{H}+{\varvec{I}})^{-1}\left( {{\varvec{Q}}}({{\varvec{Q}}}^{H}{\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_1^{\gamma +1})+{\tilde{{\overline{{\varvec{i}}}}}^{\gamma +1}(p)} -{{\varvec{Q}}}\varvec{\omega }_1^{\gamma }-\varvec{\omega }_2^{\gamma } \right) ~, \end{aligned}$$
(22)

where the local variables \(\{\tilde{{\overline{{\varvec{i}}}}}(p),{\varvec{z}}_1\}\) are updated by the latest iterates, as shown in (20) and (21), respectively. Finally, the two dual variables \(\varvec{\omega }_1\) and \(\varvec{\omega }_2\) are updated in the following:

$$\begin{aligned} \varvec{\omega }_1^{\gamma +1}= & {} \varvec{\omega }_1^{\gamma }+({\varvec{z}}_1^{\gamma +1}-{{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma +1}))\end{aligned}$$
(23)
$$\begin{aligned} \varvec{\omega }_2^{\gamma +1}= & {} \varvec{\omega }_2^{\gamma }+({\varvec{z}}_2^{\gamma +1}-{(\tilde{{\overline{{\varvec{i}}}}}(p))_i}^{\gamma +1}) \end{aligned}$$
(24)

Denote the primal solutions by \({\tilde{{\overline{{\varvec{i}}}}}}^{*}(p)\), \({\varvec{z}}_1^{*}\) and \({\varvec{z}}_2^{*}\); likewise, the dual solutions are indicated by \(\varvec{\omega }_1^{*}\) and \(\varvec{\omega }_2^{*}\). As expressed by the following, the necessary and sufficient optimality condition for the ADMM problem (17) are primal feasibility:

$$\begin{aligned} \begin{aligned}&{\varvec{z}}_1^{*} - {{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{*}) = 0\ \ \; \text{ where }\ \ \ \Vert {\varvec{z}}_1^{*}\Vert _2\le \lambda \\&{\varvec{z}}_2^{*} - {\tilde{{\overline{{\varvec{i}}}}}}^{*}(p) = 0~, \end{aligned} \end{aligned}$$
(25)

and dual feasibility:

$$\begin{aligned} \begin{aligned} \textbf{0}&\in \partial \Vert \tilde{{\overline{{\varvec{i}}}}}(p)\Vert _1 - \rho \varvec{\omega }_2^{*}~, \\ \textbf{0}&\in {{\varvec{Q}}}\varvec{\omega }_1^{*}+\varvec{\omega }_2^{*} \end{aligned} \end{aligned}$$
(26)

where \(\partial (\cdot )\) indicates the subdifferential operator.

The stopping criterion for the consensus ADMM is contrived by first measuring the primal and dual residuals; in a fashion similar to [3], one can obtain the primal residual as follows:

$$\begin{aligned} \begin{aligned} {\zeta }_1^{\gamma }&= {\varvec{z}}_1^{\gamma }-{{\varvec{Q}}}^{H}({\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p)-{\varvec{z}}_2^{\gamma }) \\ {\zeta }_2^{\gamma }&= {\varvec{z}}_2^{\gamma }-{(\tilde{{\overline{{\varvec{i}}}}}(p))_i}^{\gamma } \end{aligned} \end{aligned}$$
(27)

Noteworthily, the iterate \({\varvec{z}}^{\gamma +1}_2\) aims to minimize \(L_{\rho }(\tilde{{\overline{{\varvec{i}}}}}^{\gamma +1}(p),{\varvec{z}}^{\gamma +1}_1,{\varvec{z}}_2,\varvec{\mu }^{\gamma }_1,\varvec{\mu }^{\gamma }_2)\), and, to attain that goal, it can be verified that the following condition always holds:

$$\begin{aligned} \textbf{0} \in {{\varvec{Q}}}\varvec{\omega }_1^{\gamma +1}+\varvec{\omega }_2^{\gamma +1}~, \end{aligned}$$
(28)

indicating that \(\varvec{\omega }_1^{\gamma +1}\) and \(\varvec{\omega }_2^{\gamma +1}\) satisfy (26) all the time. Furthermore, the dual residual, after a few mathematical derivations, is yielded to be

$$\begin{aligned} \begin{aligned} {\zeta }_3^{\gamma +1}&= -(\varvec{\omega }_1^{\gamma }-{{\varvec{Q}}}^H({\varvec{z}}_2^{\gamma +1}-{\varvec{z}}_2^{\gamma })) \\ {\zeta }_4^{\gamma +1}&= -\rho \left( ({\varvec{z}}_2^{\gamma +1}-{\varvec{z}}_2^{\gamma })-(\varvec{\omega }_2^{\gamma +1}-\varvec{\omega }_2^{\gamma })\right) ~. \end{aligned} \end{aligned}$$
(29)

The termination criterion is employed as follows:

$$\begin{aligned} (\Vert {\zeta }_1^{\gamma }\Vert _2^2+\Vert {\zeta }_2^{\gamma } \Vert _2^2)^{\frac{1}{2}} \le \epsilon ^{pri}\ \ \text{ and } \ \ (\Vert {\zeta }_3^{\gamma }\Vert _2^2+\Vert {\zeta }_4^{\gamma } \Vert _2^2)^{\frac{1}{2}} \le \epsilon ^{dual}~, \end{aligned}$$
(30)

where \(\epsilon ^{{pri}}\) and \(\epsilon ^{{dual}}\) are feasibility tolerances for the primal and dual feasibility conditions (25) and (26), respectively. These tolerances are designed to vary with iterations such as

$$\begin{aligned} \begin{aligned} \epsilon ^{pri}&= \sqrt{{\mathcal {L}}_p}\epsilon ^{abs} + \epsilon ^{rel}\text{ max }\{\Vert {\varvec{z}}^{\gamma }_1\Vert _2,\Vert -{{\varvec{Q}}}^H{\overline{{\varvec{y}}}}_{\scriptscriptstyle F}(p) \Vert _2,\Vert {{\varvec{Q}}}^H{\varvec{z}}^{\gamma }_2\Vert _2 \} \\ \epsilon ^{dual}&= \sqrt{{\mathcal {L}}_p}\epsilon ^{abs} + \epsilon ^{rel}(\Vert \rho \varvec{\omega }^{\gamma }_1\Vert _2^2+\Vert \rho \varvec{\omega }^{\gamma }_2\Vert _2^2)^{\frac{1}{2}}~, \end{aligned} \end{aligned}$$
(31)

where an absolute and relative criterion is used for adapting feasibility tolerances. The absolute tolerance \(\epsilon ^{abs}\) is set to be \(10^{-4}\) whereas the relative stopping criterion \(\epsilon ^{rel}\) is chosen at \(10^{-2}\) in the following simulations.

It is worth noting that setting the parameter value of \(\lambda\) in (17)–while attempting to minimize the \(\ell _1\)-norm of impulse noise estimate \(\tilde{{\overline{{\varvec{i}}}}}(p)\)–critically impacts the governance of clipping, which in turn affects the BER performance. The optimal value of \(\lambda\) can however be empirically searched as this compressive sensing-based receiver, serving as a benchmark receiver, assumes not only the SNR level but also the statistics of impulse noise as well.

3 Neural Network Receiver

In this research endeavor, we emphasize harnessing the potential of artificial intelligence for the development of DNN-based receivers, eliminating the need to assume the prior knowledge of impulse noise models, related statistics, or SNR levels. This approach obviates the need to assume impulse noise models, associated statistics, or SNR levels. The subsequent section will provide an elaborate account of the architecture of our enhanced OFDM model, complete with pertinent mathematical representations. By capitalizing on proliferative training data generated through simulation processes, the DNN model is trained by treating OFDM modulation, multipath fading channels, and impulse noise as black boxes. Ultimately, the DNN model demonstrates its capability to effectively recover binary data sequences in real-world scenarios. The efficacy of this novel approach is substantiated by a meticulous comparative analysis, specifically evaluating the BER performance of our designed DNN-based receiver against a benchmark counterpart. Section 4 elaborates on the detailed insights of this assessment through the presentation of experimental outcomes

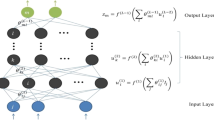
The DNN architecture comprises an input layer, multiple hidden layers, and an output layer, where neurons are fully connected between consecutive layers. The activation function employed at the output of the preceding hidden layer is the Rectified Linear Unit (ReLU) function, mathematically represented as follows:

$$\begin{aligned} \text{ ReLU }(x) = \max (0,x)~. \end{aligned}$$
(32)

Remarkably, the ReLU operation bears resemblance to soft thresholding, a technique commonly employed in signal processing and optimization tasks. This similarity becomes apparent, especially when disregarding the implicit sign implementation in (20), highlighting the intriguing connection between deep learning and signal processing paradigms. The Sigmoid function, serving as the nonlinear activation function at the output layer, is expressed as

$$\begin{aligned} \sigma (x) = \frac{1}{1+e^{-x}}~. \end{aligned}$$
(33)

Referring to the weight matrix connecting the i-th and \((i+1)\)-th layers as denoted by \(\varvec{\theta }^{(s)}_{i+1,i}\), the output of the \((i+1)\)-th layer is formulated as follows:

$$\begin{aligned} {{\varvec{u}}}_{i+1}^{(s)} = f^{(i)}\left( \varvec{\theta }^{(s)}_{i+1,i}{\varvec{u}}_i^{(s)}\right) ~, \ \ i\in \{1,2,\ldots , L_D-1\}\ \text{ and }\ s\in \{1,2,\ldots ,N_s\}~, \end{aligned}$$
(34)

where \({\varvec{u}}_i^{(s)}\) signifies the input of the i-th layer, \(L_D\) denotes the total number of layers in the DNN, and \(N_{s}\) represents the number of sub-systems. Figure 2 provides a visual representation where the DNN encompasses a total of five layers, with three hidden layers and eight sub-systems. It is noteworthy that each of these eight sub-systems processes identical received samples (following the removal of Cyclic Prefix) which spans a temporal duration equivalent to twice the length of an OFDM block, as input. Utilizing the notation delineated in (34), this alignment is denoted as \({\varvec{u}}^{(1)}_1 = {\varvec{u}}^{(2)}_1 = \ldots = {\varvec{u}}^{(8)}_1\), indicating the synchrony in their input sources. Furthermore, the activation functions \(f^{(i)}(\cdot )\), where \(i\in \{1,\ldots ,L_D-2\}\), are element-wise ReLU (32), while \(f^{(L_D-1)}(\cdot )\) employs the element-wise Sigmoid function. Finally, the collective vector \([({\varvec{u}}_{L_D}^{(1)})^T \ ({\varvec{u}}_{L_D}^{(2)})^T\ \ldots ({\varvec{u}}_{L_D}^{(N_s)})^T]^T\), namely the output of the DNN, represents the estimation of the transmitted OFDM data block. The parameter set for which the DNN is trained, optimizing the specified metric (as detailed in the following passage), is succinctly summarized as \(\{\varvec{\theta }^{(s)}_{i+1,i}\}\), where \(i\in \{1,2,\ldots , L_D-1\},\ \text{ and }\ s\in \{1,2,\ldots ,N_s\}\).

In contrast to the employed mean-squares error (MSE) loss function, namely \(L_2 = \sum _{k=1}^{N_{{\textit{Train}}}}\Vert {\hat{{\varvec{X}}}}^{(k)}-{\varvec{X}}^{(k)}\Vert _2^2/N_{{\textit{Train}}}\) as employed in [32], where \(N_{{\textit{Train}}}\) represents the scale of the training dataset, \({\hat{{\varvec{X}}}}^{(k)}\) signifies the prediction generated by our proposed DNN, and \({\varvec{X}}^{(k)}\) indicates the ground truth corresponding to training dataset k , we opt for the cross-entropy loss function as the focal point of the cost function in this paper. The choice of the cross-entropy loss function is motivated by its suitability for classification tasks, as underscored in prior research [9]. Additionally, our simulation results, as presented in the following, validate its superiority—particularly when faced with instances of unforeseen impulse noise occurrences.

Fig. 2
figure 2

DNN model

Full size image

For the sake of conciseness and notational clarity, we omit the superscript \({}^{(k)}\) which corresponds to the training dataset index in the subsequent discussions. The ultimate layer, which is fully connected, directs crucial output information to an In-phase and Quadrature-phase (I/Q) softmax layer. This specialized layer computes probabilities for each transmitted two-bit binary partition and adopts a vector configuration (specifically, a four-by-one vector), as elaborated in the ensuing description:

$$\begin{aligned} {[}P(({\hat{{\varvec{u}}}}_m)_1 = 1)\ \ P(({\hat{{\varvec{u}}}}_m)_1 =0)\ \ P(({\hat{{\varvec{u}}}}_m)_2 = 1)\ \ P(({\hat{{\varvec{u}}}}_m)_2 = 0)]^T~. \end{aligned}$$
(35)

In the context of QPSK modulation demapped using Gray mapping, the probabilities associated with the I/Q components can be derived from the aforementioned equation (35), presented here in the subsequent vectorized form:

$$\begin{aligned} \left[ P\left( \Re \{{\hat{X}}_m\} = \frac{-E_s}{\sqrt{2}}\right) \ \ P\left( \Re \{{\hat{X}}_m\} = \frac{E_s}{\sqrt{2}}\right) \ \ P\left( \Im \{{\hat{X}}_m\} = \frac{-E_s}{\sqrt{2}}\right) \ \ P\left( \Im \{{\hat{X}}_m\} = \frac{E_s}{\sqrt{2}}\right) \right] ^T~. \end{aligned}$$
(36)

Guided by standard practices, the process of normalization ensures that the subsequent summations attain a unity value: \(P(({\hat{{\varvec{u}}}}_m)_1 = 1)+P(({\hat{{\varvec{u}}}}_m)_1 =0) = 1\), and similarly, \(P(({\hat{{\varvec{u}}}}_m)_2 = 1)+P(({\hat{{\varvec{u}}}}_m)_2 = 0) = 1\). In the context of each trained OFDM block, the adeptness of our DNN model in minimizing the cross-entropy loss function is succinctly demonstrated, as articulated in the subsequent expression:

$$\begin{aligned} L_{c} = \displaystyle -\frac{1}{N}\sum _{m=0}^{N-1} \sum _{q = 0}^1 \left[ \mathbbm {1}(({{\varvec{u}}}_m)_1 = q)\log P(({\hat{{\varvec{u}}}}_m)_1 = q) + \mathbbm {1}(({{\varvec{u}}}_m)_2 = q)\log P(({\hat{{\varvec{u}}}}_m)_2 = q) \right] ~. \end{aligned}$$
(37)

Derived from the cross-entropy loss function \(L_c\) outlined in (37), the evolution of the weights and biases within the DNN model transpires through the realization of a stochastic gradient descent method, or its relevant extension, operating on incoming batches of the training dataset. The initial phase of training the DNN model is characterized by the pursuit of minimizing the loss function \(L_c\), amid the presence of data-corrupting interference solely attributed to AWGN.

However, in response to the challenge posed by non-Gaussian impulse noise, this study, following the lead of [14], undertakes a refinement of the previously established DNN model. This evolution involves strategically interleaving the training data with instances of impulse noise subsequent to the initial training phase. This strategic interleaving enables the systematic fine-tuning of the parameters of the DNN model. This iterative process continues until the value of the loss function (37) reaches a point of marginal diminishment, indicating the enhanced robustness of the proposed DNN model to non-Gaussian disturbances.

It is noteworthy that the learning rate, which is subject to experimentation in the subsequent section, is deliberately decreased over the course of training. This deliberate reduction in the learning rate is driven by the objective of attaining convergence toward an optimal solution within the intricate domain of DNN modeling, wherein the interplay between model complexity and convergence efficiency is meticulously balanced.

4 Simulation Results

The simulations adopt the B-G and \(S\alpha S\) impulse noise models (as described in Sect. 2.2). In contrast to previous studies, such as the work in [28], we vary the IGR within the range of SNR values relevant to our investigation. The DNN’s input consists of received data from a frame, comprising one pilot block and one data block. Each block contains 64 QPSK symbols, aligned with an FFT/IFFT size of \(N = 64\). The pilot symbols remain fixed during training and validation. As in [32], the CP length is set to \({\mathcal {L}}_p = 16\). Moreover, the wireless channel dataset is generated following the new radio model (WINNER II [16]), resulting in a multipath channel with 24 paths, which varies from one frame to another. Notably, the received signal, conditioned on channel gains \(h_k^{(i)}\), where \(k\in \{0,1,\ldots ,L-1\}\), derived from the i-th channel realization, where \(i\in \{1,2,\ldots , N_d\}\), in a dataset of size \(N_d\), follows a Gaussian distribution with a mean of zero and a variance of \(\sigma _{r_i}^{2} = \left( \sum _{k=0}^{L-1}|h_k^{(i)}|^2\right) E_s\). In this regard, signal-to-Noise ratio (SNR) is defined as the ratio of the averaged received signal power over the dataset of interest to the variance of AWGN, namely \((\frac{1}{N_d}\sum _{i=1}^{N_d}\sigma _{r_i}^{2})/{N_0}\). SNR values are expressed in decibels (dB) for the following simulations. It is pivotal to highlight that while the compressive sensing-based receiver leverages channel state information and AWGN power levels to generate BER curves, our DNN-based receiver operates without presuming any prior knowledge of these parameters.

Figure 3 presents the BER performance outcomes of the trained model, building upon experiments from [32]. In contrast to their study, which focused exclusively on AWGN, we extend our investigation to incorporate moderate impulse noise, characterized by a probability of impulse occurrence \(p_b = 0.001\) with variances ranging from 0.02 to 2.5. The DNN model is composed of five layers, with neurons allocated as follows: 256, 500, 250, 120, and 16. Notably, every 16 bits of the transmitted data are independently predicted prior to concatenation as a whole (128 bits.) Training involves 5,000 epochs, each comprising 50 batches (with 500 training realizations per batch). We employed the Adam optimizer [15] with a learning rate of \(10^{-4}\). For specific system parameter values, please refer to Table 1. Analyzing Fig. 3 reveals that as \(\sigma ^2_I\), representing impulse noise power, grows, the BER performance stabilizes at lower SNR values; for instance, at \(\sigma ^2_I = 2.5\), the BER curve becomes notably flat from as early as 15-dB SNR. Conversely, the curve for \(\sigma ^2_I = 0.02\) exhibits gradual tilting. However, even in the latter scenario—moderate impulse probability coupled with minimal power intensity—the BER remains significantly higher than \(10^{-3}\). This performance gap persists even as SNR ascends to 30 dB (see solid line marked by “\(\square\)”). Our experimental insights underscore a critical point: although the trained model excels in the presence of AWGN only—where the BER declines to less than \(10^{-3}\) at SNR levels below 30 dB—its effectiveness diminishes when faced with the unforeseen presence of impulse noise. This observation highlights the formidable challenge of mitigating the impact of impulse noise without enhancements to the model. Notably, the dash-dotted line marked by “\(\circ\)” aligns with findings in [32], revealing BER performance comparable to that of the MMSE receiver.

Fig. 3
figure 3

BER performance of the DNN model (trained in the context of AWGN only) in the B-G model (\(p_b = 0.001\))

Full size image

In response to this shortcoming, we adopt a successive fine-tuning approach for the trained model parameters. This strategy is employed once the value of the loss function (37) has reached a plateau, and no further decline can be achieved by increasing the number of training epochs. In our study, this point is observed at 5,000 epochs. Beginning with the model parameters obtained from the initial structure, this enhanced method yields a refined DNN model through fine-tuning. This process occurs at a fixed training SNR level of 25 dB.

The fine-tuning process incorporates the following key adjustments: the learning rate is reduced to one-fifth of its most recent value after every 25 epochs, eventually reaching a minimum value of \(10^{-5}\). Simultaneously, the training dataset, distinct from the previous experiment, considers impulse occurrences with a probability set at 0.005 and an average power of 0.2. The outcomes of these refinements under error-prone conditions are displayed in Fig. 4. In comparison to the original DNN model, the BER curves derived from the incorporation of fine-tuning (indicated by solid lines) exhibit an earlier descent than their counterparts (represented by dash-dotted lines) across a comprehensive range of \(\sigma _I^2\) strengths. For instance, considering the instance where \(\sigma _I^2 = 0.02\) (highlighted by “\(\square\)” on the curves), a noteworthy SNR improvement of over 10 dB is evidenced. This observation underscores the affirmative impact of incorporating the fine-tuning technique into the DNN model. The discerned superiority of the refined DNN model over the original version can be attributed to the transfer of knowledge from the pre-trained model—leveraging learned parameters as initializations—which is then subjected to fine-tuning for tackling more intricate learning tasks, such as addressing anomalous attacks.

Furthermore, the receiver employing clipping (indicated by the dashed line marked with “\(\circ\)” in Fig. 4), with an optimal threshold determined via linear programming (as discussed in Sect. 2.3) through an exhaustive exploration of the parameter \(\lambda\) in (16), slightly outperforms the refined DNN-based receiver. However, it is worth noting that the clipping-featured receiver necessitates the assumption of known SNR values. In contrast, the refined DNN receiver does not assume knowledge of the impulse noise statistics or SNR values from the testing data.

Fig. 4
figure 4

BER performance of the refined DNN model (with fine-tuning) in the B-G model (\(p_b = 0.001\))

Full size image

Notably, even under relatively mild conditions, such as \(p_b = 0.001\) and \(\sigma _I^2 = 0.02\), the achieved BER performance in the preceding experimental findings reaches a saturation point around 30-dB SNR. This is particularly significant when considering the instances where \(p_b\) is substantially elevated, highlighting the limitations of the preceding DNN model. This issue is prominently depicted in Fig. 5, where the DNN model encounters heightened instances of anomalous occurrences, notably at \(p_b = 0.01\) across the entire range of presented \(\sigma _I^2\) magnitudes. This is observable through the consistent BER levels (indicated by the dash-dotted lines) that persist even as the SNR value surpasses 25 dB. This behavior indicates that the DNN-based receiver becomes overwhelmed by the influx of impulse arrivals within the data frame duration.

To overcome this shortcoming, we enhance the DNN model by augmenting the network depth from five to six layers. Additionally, we meticulously determine the number of neurons in each layer empirically as follows: 256, 550, 832, 280, 128 and 16. The fine-tuning process remains consistent with the strategy outlined earlier. The resulting BER outcomes are depicted in Fig. 5, with each solid line corresponding to a distinct \(\sigma _I^2\) level. A noteworthy observation emerges: the lower the average power of the impulse noise, the earlier the departure of BER curves between the two compared DNN models as the SNR grows. Strikingly, for \(\sigma _I^2\) values of 0.1 and 0.02, the ’deeper’ neural network model induces a consistent downward trajectory of BER curves as SNR progressively increases.

Of notable significance, the BER performance achieved remarkably converges with outcomes obtained from the clipping-featured receiver (as indicated by the dashed line marked by “\(\circ\)”), attesting the efficacy of our proposed DNN framework against impulse noise, even in hostile scenarios. In summation, this notable performance enhancement is adapted through a strategic trade-off, judiciously balancing computational complexity to enrich the prowess of representation learning.

Fig. 5
figure 5

BER performance of the proposed DNN model (with fine-tuning) in the B-G model with a growing \(p_b\) at 0.01

Full size image

To further amplify the robustness claims of our proposed DNN-based receiver—relaxing its assumptions on the specifics of the driving impulse noise model—we carry out a pivotal experiment. In this experiment, we intentionally replace the interference model in the testing phase with the symmetric alpha-stable distribution (as defined in (9)), thereby introducing a deliberate model mismatch. This strategic maneuver investigates the efficacy of the receiver in the face of variations stemming from the impulsiveness of interference. This exploratory path involves a meticulous modulation of the magnitude of the \(\alpha\) parameter, as delineated in (10). Specifically, we scrutinize the outcomes for varying values of \(\alpha\), specifically 1.4, 1.6, and 1.8, throughout our simulations, as detailed below. Notably, the performance outcomes detailed within Fig. 6 unequivocally resonate with our central assertion: the devised DNN model consistently outperforms its counterpart. This superiority becomes particularly evident as the performance loss incurred by the clipping-featured receiver—developed based on assuming the Gaussian mixture noise model—becomes substantial due to its susceptibility to a model mismatch. The stark divergence from the assumed \(S\alpha S\) model becomes an essential factor responsible for this phenomenon. This disparity is acutely illustrated when considering an instance with \(\alpha\) set at 1.8: the BER performance curve dictated by the clipping-featured receiver (as denoted by the dash-dotted line marked by “\(\square\)”) exhibits minimal downward movement, starkly contrasting with the trajectory observed with our proposed DNN model. As the BER derived from our DNN receiver steadily declines amidst growing G SNR values, the gap in performance loss with regard to the clipping-featured counterpart magnifies significantly.

Fig. 6
figure 6

BER performance comparison of the trained DNN model (with fine-tuning) and a clipping-featured receiver in realistic scenarios in the presence of model mismatch, where \(\alpha\) values in the \(S\alpha S\) model are varied

Full size image

In pursuit of a comprehensive assessment, we extend our evaluation by comparing our DNN-based receiver with a peer model proposed in [2], which enhances performance through the integration of convolutional coding. To facilitate a thorough, equitable comparative analysis, we conduct simulations within a coded OFDM framework encompassing 1,024 sub-carriers, out of which 256 are dedicated to pilots. The code rate is set at 1/2, with a constraint length of 7 and generator matrix defined by \([171\ 133]\). Channel decoding is implemented via a Viterbi decoder. Further augmenting the simulation settings is the channel model, which comprises ten paths with path arrival times conforming to a Poisson distribution with a mean of 1 ms, whereas the path amplitudes follow the Rayleigh fading distribution, reflecting an exponentially decreasing average power profile. It is noteworthy that the same strategy is employed, enabling the retraining of our proposed DNN to adapt to the unique characteristics of this channel model. The performance disparity between our DNN receiver and the counterpart in [2], within the B-G model, is depicted in Fig. 7. Notably, across all scenarios, the divergence between comparative curves becomes more pronounced as the SNR value grows. A discernible 0.5 dB SNR gain (see those lines marked by “\(\times\)”) is observed at a BER level of \(10^{-4}\) when \(p_b = 0.06\). Their performance loss can be attributed to the quality of channel estimation—a crucial factor impacting zero-forcing frequency domain equalization, known for its susceptibility to noise enhancement. This is corroborated by our observation that the solid line representing our DNN-based receiver consistently falls below the dash-dotted line, even when limited to the AWGN scenario (marked by “\(\square\)”). The impact of adopting blanking operation there in scenarios with higher \(p_b\) values, such as 0.1, can further contribute to a degraded BER performance.

Fig. 7
figure 7

BER performance comparison of the trained DNN model with the one proposed in [2] at \(\text{ SIR } = 0 \,\text{ dB }\)

Full size image

Our exploration further extends to the MC-A model, the outcomes of which are plotted in Fig. 8. The BER performance aligns with the trends exhibited in Fig. 7. Particularly notable is its marginal yet consistent superiority compared to the counterpart across various impulsive indices A, especially when the power ratio between AWGN and moderate impulse noise remains constant (e.g., \(\Lambda = 0.5\)). This persistence in performance gain further solidifies the versatility and efficacy of our DNN-based receiver across diverse impulsive environments.

Fig. 8
figure 8

BER performance comparison of the trained DNN model with the one proposed in [2] in the MC-A model with \(\Lambda = 0.5\)

Full size image

5 Conclusion

In summary, we have delved into the formidable implications of impulse noise on the bit error rate (BER) performance of a deep neural network (DNN) receiver tailored for Orthogonal Frequency Division Multiplexing systems in the presence of multipath fading. Notably, our study encompasses a scenario where the precise impulse noise statistics remain elusive to the DNN receiver, mirroring real-world uncertainties, and extends to instances where the ambient noise power level remains unchartered. Empirical revelations emphasize the vulnerability of a DNN model exclusively trained to contend with additive white Gaussian noise, rendering it susceptible to the covert yet detrimental anomalies introduced by impulse occurrences. Consequently, a critical facet of this study emerges—enriching the DNN’s capacity for representation learning by enabling adaptive responses to nuanced data variations, effectively rejuvenating the initial training model. In this endeavor, the prominent clipping-featured receiver, emanating from the compressive sensing paradigm, emerges as a pertinent benchmark for BER performance comparison against our DNN receiver. Of paramount significance, our investigation unveils a pivotal nexus between optimal clipping thresholds—a cornerstone of the compressive sensing-based clipping-featured receiver—and the efficient resolution of this task through a second-order cone programming realized by the consensus alternating direction method of multipliers (ADMM). Nonetheless, it is imperative to acknowledge that the conventional clipping-featured receiver’s efficacy in setting the clipping threshold is engaged with an assumption about the signal-to-noise ratio level-a presumption that our proposed DNN receiver manages to circumvent. Our simulation results elegantly demonstrate the prowess of the proposed DNN receiver, aligning it commendably with its clipping-featured peer in moderate environments and even surpassing it slightly in more hostile scenarios. Moreover, our DNN receiver underscores robustness in the face of impulse noise model mismatches, further attesting to its practicality and adaptability.

Table 1 The hyperparameters of the DNN
Full size table