1 Introduction

Polar code was proposed in [1]. It, concatenated with Cyclic Redundancy Check (CRC), is adopted as the channel code of the 5G control channel [2]. Its decoding methods include Successive Cancellation (SC) [1], Belief Propagation (BP) [3] and Successive Cancellation list (SCL) [4]. SC decoding is simpler but it does not have parallel structure. BP decoding is an iterative message passing procedure and has parallel structure and doesn’t need many iterations. In addition to the additive white Gaussian noise (AWGN) considered in most Polar code decoding papers, the non-Gaussian noise such as the impulse noise has a more serious impact on communication systems.

The impulse noise exists in wired and wireless communications channels by experimental measurements [5,6,7] such as urban outdoor/indoor mobile [8, 9], power-line communications [10, 11] because of man-made electromagnetic interference etc.

The impulse noise is different from the AWGN. The energy of impulse noise is often tens of times that of the AWGN. Impulse noise models can be divided into memory noise channels like Markov-Gaussian channel models [10, 12,13,14,15], and memoryless noise channels like Bernoulli-Gaussian (BG) [16,17,18] and Additive White (Middleton) Class A Noise (AWAN) [19,20,21,22]. The works on the Polar code decoding in the impulse noise channels are [19, 23, 24]. Tseng et al. [19, 23] used SC to decode the Polar code in the memoryless impulse noise channels with different cases like known statistical features, position or not [24]. Compared the SC and BP on Polar code with memoryless impulse noise with different situation like [23].

Deep learning is popular in many areas like image classification [25], speech recognition [26], and radio resource allocation [27, 28]. Machine learning needs separate feature extraction. Deep learning has embedded feature extraction and uses deep nueural network (DNN) composed of multiple layers of nonlinear processing units. The DNN learns data representation with multiple abstraction levels. Deep learning can learn complex structures in training sets to adjust the neuron weights [29]. There are special cases of DNN. The convolutional neural network (CNN) realizes spatial correlations [30, 31]. The recurrent neural network (RNN) [32] realizes the temporal correlations and is suited to sequential data [33]. To solve the gradient explosion problem of RNN, a Long Short-Term Memory (LSTM) model [34] that can be remembered for a long time emerges from RNN.

Recent years, many researchers try to use deep learning for channel coding [35,36,37,38,39,40,41]. Kim et al. [35] used RNN and Neural Recursive Systematic Convolutional (N-RSC) to train convolutional codes and Turbo codes on the AWGN channel and test it on the non-AWGN channel which show better performance than convolutional Turbo decoder. Liang et al. [36] proposed LDPC decoder using BP-CNN, CNN extracts the feature of the color noise (correlated noise is similar to spatial correlation of an image) and removes the BP decoding error in a way similar to image denoising. It showed BP-CNN is better than the BP decoder under the general color noise environment. Cammerer et al. [37] partitioned the 128 bit long Polar code encoding graph in to blocks and trained separately. These neural network decoders are connected to BP decoding. Gruber et al. [38] used deep neural network for decoding Polar and random code with 16–64 bit codeword length and showed the performance of Polar code is better than random code. Irawan et al. [39] extended [38] to fading channels for (16, 8) Polar code. Lyu et al. [40] compared DNN, CNN, and RNN for Polar code decoding. Gross et al. [41] proposed to partition Polar encoding graph too but to connect to SC decoding instead. It showed the same performance and 43.5% reduction in latency than [37] for a (128, 64) Polar code. The above deep learning Polar cod decoding papers, however, did not consider the impulse noise.

The main objective or research problem that this paper want to address is deep learning based Polar code decoding in the memeory impulse noise channels. We considered short Polar code (16,8), the same as the prior works [38, 39] for comparison. For longer code length, we could add more layers in DNN/CNN, or stack more LSTM cells in every time step [40]. The impulse channels exist in realistic environment [5,6,7,8,9,10,11] but it requires more complicated statistics for Polar code decoding like known statistical features (average number of impulses in a code word), the positions of the impulses in a codeword, the state transition probability to and from the states with the impulse noise or not, etc. [15, 19, 23], so the other existing works do not consider the impulse noise channel.

The reasons why deep learning or LSTM is selected for Polar code decoding are as follows. First, non-deep learning-based Polar code decoding required iterative operations and has no parallel structure, so it has high computation complexity and thus high decoding latency [38]. The deep learnning for Polar code decoding has inherently parallel structure and is a one-shot operation [38]. That is, there is no iterative steps and thus reduce the complexity by 30% or more [42, 43]. Second, Polar decoding is a sequential decoding problem [43]. That is, there is long time dependency within the codeword [44] and LSTM is built for exploiting the temporal correlation. Finally, the memory impulse noise we considered in this paper has temporal memory, this is one more reason to select LSTM which is naturally fit to deal with temporal correlation for Polar code decoding.

In this paper, we propose LSTM (deep learning) based decoder for Polar code in the memory impulse noise channel. The contribution is as follows:

  1. 1.

    Previous papers [19, 23, 24] which did not use deep learning only considered the memoryless impulse noise and AWGN.

  2. 2.

    Previous papers [38,39,40,41,42,43,44] which decoded using deep learning didn’t consider the impulse noise.

  3. 3.

    We find the optimal training SNR value 4.5 dB in the memory impulse channel, which is different from that 1.5 dB in the AWGN channel in [38, 40]. Based on the optimal training SNR value we found, the bit error probabilityt of the proposed LSTM-based decoding method is one third of that of the previous non-deep-learning based schemes for the testing SNR range 0 ~ 6 dB.

  4. 4.

    The proposed LSTM-based method is 5 ~ 12 times less and thus has much less decoding latency than that of SC/BP/SCL methods because the proposed LSTM-based method has inherently parallel structure and has one shot operation- no iterative operations.

2 System Model

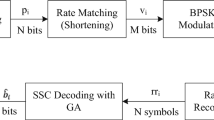
The Polar code encoder and decoder block diagram is shown in Fig. 1. The decoder is replaced by LSTM based Polar coder decoder.

Fig. 1
figure 1

Polar code decoder system model

Full size image

2.1 Markov-Gaussian (MG) Impulse Noise Channel Model

The MG noise model is shown in Fig. 2. The MG channel is a hybrid two state Markov chain and generated by a Gaussian process, while state1 (j = 1) represents the Gaussian noise only, state2 (j = 2) represents the impulse noise. MG channel model describes the burst channel, we assume that the received signal:

$$y = x + \omega$$
(1)

where \(x\) is the transmitted signal with bit energy \({E}_{b}\), \(\omega\) is the noise, and it has two states, \({state}_{1}\) is the AWGN, and \({state}_{2}\) is the impulse noise. Then, the probability density functions (PDF) of \(\upomega\) is:

$$P{(}\omega {|} state_{1} ) = \frac{1}{{\sqrt {2\pi \sigma_{G}^{2} } }}exp\left\{ {\frac{{\left| \omega \right|^{2} }}{{2\sigma_{G}^{2} }}} \right\}$$
(2)
$$P{(}\omega {|} state_{2} ) = \frac{1}{{\sqrt {2\pi R\sigma_{G}^{2} } }}exp\left\{ {\frac{{\left| \omega \right|^{2} }}{{2R\sigma_{G}^{2} }}} \right\}$$
(3)

where \({\sigma }_{G}^{2}\) is the variance of the Gaussian noise, and \(R\) is the impulse noise power over the Gaussian noise power. The SNR is defined as \(\frac{{E}_{b}}{{\sigma }_{G}^{2}}\).

Fig. 2
figure 2

State diagram of Markov-Gaussian noise model

Full size image

The channel state transition probabilities are expressed as:

$$\begin{gathered} P_{{state^{*} |state}} = P\left( {state^{*} {|}state} \right) \hfill \\ state,state^{*} \in \left\{ {state_{1} ,state_{2} } \right\} \hfill \\ \end{gathered}$$
(4)

\({state}^{*}\) is the next state.

The state transition probability matrix of the MG impulse noise channel is as follows:

$${\text{M}} = \left[ {\begin{array}{*{20}c} {P_{state1|state1} } & {P_{state2|state1} } \\ {P_{state1|state2} } & {P_{state2|state2} } \\ \end{array} } \right]$$
(5)

The matrix element must satisfy:

$$P_{state1|state1} + P_{state2|state1} = 1$$
(6)
$$P_{state1|state2} + P_{state2|state2} = 1$$
(7)

and \({P}_{state1}\), \({P}_{state2}\) can be expressed as:

$$P_{{state_{1} }} = \frac{{P_{state1|state2} }}{{P_{state2|state1} + P_{state1|state2} }}$$
(8)
$$P_{{state_{2} }} = \frac{{P_{state2|state1} }}{{P_{state2|state1} + P_{state1|state2} }}$$
(9)

According to [12, 15, 16], we set the matrix M as:

$${\text{M}} = \left[ {\begin{array}{*{20}c} {0.99} & {0.01} \\ {0.2} & {0.8} \\ \end{array} } \right]$$
(10)

2.2 Polar Code

The Binary Discrete Memoryless Channel (B-DMC) is assumed channel splitter and channel combining to make channel polarization [1]

2.2.1 Channel Polarization

Channel polarization is the repeated use of any B-DMC in a recursive manner, and through channel splitting and channel combination. The original independent B-DMC is turned into a polarized channel with a certain relationship, and so many the sub -channels will have different reliabilities. When the encoding length N is larger, the more polar sub-channels, the channel capacity of some polar sub-channels will approach 1 and become the perfect channel. The rest sub-channels are the opposite. Their channel capacity will approach zero, making it a poor channel for pure noise. The transmission of the polarization code is to use the channel whose channel capacity is close to 1 to transmit the message, and the channel closer to 0 will transmit the frozen bits.

2.2.2 Encoder

The encoder is to form a butterfly architecture for channel merging and select a sub-channel with better channel capacity for message transmission. The polarization code encoding method with length N which is u through the generator matrix form \({G}_{N}\) and then through each channel:

$${\text{d}} = {\text{u}}G_{N}$$
(11)

\({G}_{N}\) is the matrix with code length N, \({G}_{N}\) is generated using the matrix \(\mathrm{F}=[\begin{array}{cc}1& 0\\ 1& 1\end{array}]\) via Kronecker power:

$$G_{N} = F^{ \otimes n}$$
(12)

\({F}^{\otimes n}\) Kronecker power is define as:

$$A_{m*n} \otimes {\text{B}} = { }\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{11} B \ldots A_{1n} B} \\ { \vdots \ddots \vdots } \\ \end{array} } \\ {A_{m1} B \ldots A_{mn} B} \\ \end{array} } \right]$$
(13)

Only the sub-channel with the better channel capacity is selected for transmission, and the remaining sub-channels transmit frozen bits known in advance by the encoding and decoding end, so (11) can be rewritten in more details:

$$\begin{gathered} {\text{d}} = u_{A} G_{N} \left( {\text{A}} \right) + u_{{A^{c} }} G_{N} \left( {A^{c} } \right) \hfill \\ {\text{u}} = \left( {u_{A} ,u_{{A^{c} }} } \right) \hfill \\ \end{gathered}$$
(14)

A is the set of original signals, \({A}^{c}\) is set of frozen bits (= zeros).

2.2.3 Decoder

Assume a parameter (N, K, A, \({A}^{c}\)), The encoder makes \({\mathrm{u}}_{i}\) into \({\mathrm{d}}_{i}\) and transmits it through the channel C. The decoder uses the two parameters known in advance with the encoder, The first one is the transmits message A, the second is the frozen bit \({A}^{c}\), and estimate \({\mathrm{u}}_{i}\) with the received signal \({\mathrm{y}}_{i}\), then get the predicted result \(\widehat{{u}_{i}}\). The decoder has already known the location and information of the frozen bit, so the \({\widehat{u}}_{{A}^{c}}\) must be equal to \({u}_{{A}^{c}}\), we only need to estimate the remaining information to get \({\widehat{u}}_{A}\).

Three common decoding methods will be used in this work to compare: Successive Cancellation (SC), Belief Propagation (BP), Successive Cancellation List (SCL).

Due to the limitation of space, we only describe SC in details. Please refer to references [3, 4] for details of BP and SCL.

SC decoding method was proposed in [1]. It can be known from the encoding principle that the construction of the Polar code is the choice of the channel, and this selection method is selected according to the optimal SC performance as the standard. The channel has the channel reliability, SC decoding is to judge the log likelihood ratio (LLR) of each bit from small to large, each step of decoding will need to use the previous results, so under the condition of correct decoding, the channel capacity will be reached, and the longer the Polar code, the easier the channel capacity is reached.

$$\widehat{{u_{i} }} \triangleq \left\{ {\begin{array}{*{20}c} { u_{i} , i \in A^{C} } \\ { h_{i} \left( {y_{1}^{N} ,\hat{u}_{1}^{i - 1} } \right) , i \in A} \\ \end{array} } \right.$$
(15)

The estimated value \(\widehat{{u}_{i}}\) during decoding will be determined according to (15).\({y}_{1}^{N}\) is the first bit of receive signal with length N. As mentioned before, when it is a frozen bit, \({u}_{i}\) must be equal to \(\widehat{{u}_{i}}\). Where \({h}_{i}\) is the decision equation decoded for this:

$$h_{i} \left( {y_{1}^{N} ,\hat{u}_{1}^{i - 1} } \right) \triangleq \left\{ {\begin{array}{*{20}c} {0 , L_{1,i} \ge 0} \\ { 1 , otherwise} \\ \end{array} } \right.$$
(16)

\({L}_{1,i}\) is the LLR of \(\widehat{{u}_{i}}\):

$$LLR\left( y \right) = ln\frac{{W({\text{y}}|{\text{u}} = 0)}}{{W({\text{y}}|{\text{u}} = 1)}}$$
(17)

W is the set of channel after channel polarization, \(W(\mathrm{y}|\mathrm{u}=0)\) is the channel transmission probability.

The SC decoding recursion can be expressed as (18):

$$L_{j,i} = \left\{ {\begin{array}{*{20}c} {2tanh^{ - 1} \left[ {\tanh \left( {\frac{{L_{j + 1,i} }}{2}} \right)\tanh \left( {\frac{{L_{{j + 1,i + 2^{j - 1} }} }}{2}} \right)} \right] , \frac{i - 1}{{2^{j - 1} }}mod2 = 0 \left( {18a} \right)} \\ {\left( {1 - 2\hat{u}_{{j,i - 2^{j - 1} }} } \right)\left( {L_{{j + 1,i - 2^{j - 1} }} } \right) + L_{j + 1,i} , otherwise \left( {18b} \right)} \\ \end{array} } \right.$$
(18)

L is LLR, \({\mathrm{L}}_{\mathrm{j},\mathrm{i}}\)’s j and i respectively represent the jth recursion in the coding structure and the ith bit in this structure. \(1\le \mathrm{j}\le \mathrm{n}, 1\le \mathrm{i}\le \mathrm{N}\).

We define two functions:

$${\text{f}}\left( {{\text{x}},{\text{ y}}} \right) \, = {\text{sign}}\left( x \right){\text{sign}}\left( y \right){\text{min}}\left( {\left| x \right|,\left| y \right|} \right)$$
(19)
$${\text{g}}\left( {{\text{x}},{\text{ y}},{\text{ z}}} \right) \, = \left( { - 1} \right)^{z} *x + y$$
(20)

and (18) can be rewritten as:

$$L_{{j,i{ }}} \approx \left\{ {\begin{array}{*{20}c} {f\left( {L_{j + 1,i} , L_{{j + 1,i + 2^{j - 1} }} } \right)} \\ {g\left( {L_{{j + 1,i - 2^{j - 1} }} ,L_{j + 1,i} ,\hat{u}_{{j,i - 2^{j - 1} }} } \right)} \\ \end{array} } \right. = \left\{ {\begin{array}{*{20}c} {sign\left( {L_{j + 1,i} } \right)sign\left( {L_{{j + 1,i + 2^{j - 1} }} } \right)\min \left( {\left| {L_{j + 1,i} } \right|,\left| {L_{{j + 1,i + 2^{j - 1} }} } \right|} \right), \frac{i - 1}{{2^{j - 1} }}mod 2 = 0 \left( {21a} \right)} \\ {\left( { - 1} \right)^{{\hat{u}_{{j,i - 2^{j - 1} }} }} \left( {L_{{j + 1,i - 2^{j - 1} }} } \right) + L_{j + 1,i} , otherwise \left( {21b} \right)} \\ \end{array} } \right.$$
(21)

when (18) updates, it is estimated one by one, and the result of previous bit will use in the next bit.

$${\text{S}}_{{{\text{i}} + 1,{\text{j}}}} \triangleq {\text{ S}}_{{{\text{i}},{\text{j}}}} \otimes {\text{S}}_{{{\text{i}},{\text{j}} + 2^{{{\text{i}} - 1}} }} { },{ }\frac{{{\text{i}} - 1}}{{2^{{{\text{j}} - 1}} }}{\text{mod}}2 = 0$$
(22)
$${\text{S}}_{{{\text{i}},{\text{j}} + 2^{{{\text{i}} - 1}} }} { } \triangleq {\text{ S}}_{{{\text{i}},{\text{j}}}}$$
(23)

After receiving \({y}_{1}^{N}\), the decoder can first calculate the initial LLR \({L}_{n,i}\), and it is updated by the operation of (18) to obtain \({L}_{1,i}\) and use (15, 16) to estimate \(\widehat{{u}_{i}}\). After estimating \(\widehat{{u}_{i,j}}= {\mathrm{S}}_{\mathrm{i},\mathrm{j}}\), The decoder could use (22, 23) to push back \({\mathrm{S}}_{\mathrm{i}+1,\mathrm{j}}\) and \({\mathrm{S}}_{\mathrm{i},\mathrm{j}+{2}^{\mathrm{i}-1}}\),. After the calculation and update of formula (18), the decoder could calculate \({L}_{1,i}\) of the next message, and use (15) and (16) to estimate the next \(\widehat{{u}_{i}}\).

As shown in Fig. 3, first go the orange line using f function defined in (19) with \({L}_{\mathrm{1,1}}\) and \({L}_{\mathrm{1,2}}\) to calculate the LLR of \(\widehat{{u}_{1}}\) and use (15), (16) to estimate the \(\widehat{{u}_{1}}\). Next, we go the blue line using g function defined in (20) with \(\widehat{{u}_{1}}\) and \({L}_{\mathrm{1,1}}\) and \({L}_{1,2}\) to get the LLR of \(\widehat{{u}_{2}}\), then put it to (15), (16) to estimate \(\widehat{{u}_{2}}\).

Fig. 3
figure 3

Unit structure SC decoding

Full size image

3 The Proposed Deep-learning Based Decoding for Polar Code

3.1 Long Short-Term Memory(LSTM)

In this work, we use a 2-layer LSTM with a hidden layer size set to 256 and use sigmoid as the output process as shown in Fig. 4. \({Y}^{t}\) is the training data (the received signal after impulse noise, and the orginal imformation bit) with different SNR and t is the time. A LSTM cell in Fig. 4 is shown in Fig. 5.

Fig. 4
figure 4

Two layer LSTM model

Full size image
Fig. 5
figure 5

LSTM cell model

Full size image

\({C}_{0}^{t}\) is the value in the memory cell (cell state) of the first layer LSTM cell in the time t which is a vector, \({h}_{0}^{t}\) is the first output solution of first LSTM cell (hidden state) in the time t. Next, \({C}_{0}^{t}\) and \({h}_{0}^{t}\) will put into second layer of LSTM Cell to help training. \({h}_{0}^{t}\) size is (128,256) which mean the size of data 128 and the hidden layer size of prediction output 256.

Finally, We get the hidden state output\({h}_{1}^{T}\), T mean the final time of t. We do the matrix multiplication with \({h}_{1}^{T}\) and put it to the sigmoid to get the the\(\widehat{u}\), which is (128, 8).

$$\sigma \left( Z \right) = \frac{1}{{1 + e^{ - z} }}$$
(24)

This is sigmoid function, the output is 0 ~ 1.

$${\text{Z }} = weight_{{h^{t - 1} }}^{{y^{t} }} = \left[ {W,U} \right]*\left[ {h^{t - 1} ,y^{t} } \right] + bias$$
(25)

Z is the real input of LSTM, which is y and h multipe with weight W and weight U and add bias.

$${\text{G}}\left( {\text{Z}} \right) = {\text{tanh}}\left( {weight_{{h^{t - 1} }}^{{y^{t} }} } \right) = tanh\left( {\left[ {W,U} \right]*\left[ {h^{t - 1} ,y^{t} } \right] + bias} \right)$$
(26)

G(Z) is the value into the input gate.

$${\text{S}}\left( {Z^{i} } \right) = \sigma (inputweight_{{h^{t - 1} }}^{{y^{t} }} ) = \sigma \left( {\left[ {W_{i} , U_{i} } \right]*\left[ {h^{t - 1} ,y^{t} } \right] + bias_{i} } \right)$$
(27)

\({Z}^{i}\) is the control value, which decide whether G(Z) can put in memory cell, the value of \(\mathrm{S}({Z}^{i})\) will approximate 0 or 1

$${\text{S}}\left( {Z^{o} } \right) = \sigma (outputweight_{{h^{t - 1} }}^{{y^{1} }} ) = \sigma \left( {\left[ {W_{o} , U_{o} } \right]*\left[ {h^{t - 1} ,y^{1} } \right] + bias_{o} } \right)$$
(28)

\({Z}^{o}\) is the control value, which decide whether the tanh multiply memory cell value can be output, the value of \(\mathrm{S}({Z}^{o})\) will approximate 0 or 1

$${\text{S}}(Z^{f} ) = \sigma (forgetweight_{{h^{t - 1} }}^{{y^{t} }} ) = \sigma \left( {\left[ {W_{f} , U_{f} } \right]*\left[ {h^{t - 1} ,y^{t} } \right] + bias_{f} } \right)$$
(29)

\({Z}^{f}\) is the control value, which decide whether the value can be forgot or not, the value of S(\({Z}^{f})\) will approximate 0 or 1

$$c^{t} = \left( {\left( {S\left( {Z^{f} } \right)} \right)*c^{t - 1} } \right) + \left( {S\left( {Z^{i} } \right)*G\left( Z \right)} \right)$$
(30)

(30) is the value in the memory cell, cell state, we can see if S(\({Z}^{f})=0\), then the value of input will replace the value of cell (forget), if S(\({Z}^{f})=1\) it will add up with input become new value.

$$h^{t} = S\left( {Z^{o} } \right)*{\text{tanh}}\left( {c^{t} } \right)$$
(31)

(31) is the hidden state output, which is the real output, it is control by \({Z}^{o}\) if \(S({Z}^{o})\) is 0, then we can’t transmit the output.

3.2 Training Data

The purpose of the decoding is to find the optimal map function, \({f}^{*}=Y\to X\), Y is the set of all possible y and U is the set of all possible of u. \({f}^{*}\) should satisfy maximum a posteriori (MAP) criterion:

$$\begin{aligned} f^{*} & = argmax \quad P{(}u{|}y) \\ & {\text{u}} \in {\text{U}} \\ \end{aligned}$$
(32)

In deep learning, if want to train the neural network, we need a lot of data and then define the loss function.

  1. I.

    Generating training samples: To train the NN, we generate a large number of received signals y, and the real information bits x. The received vector y is x plus the impulse noise. Taking y as the training data and x as the labeled output to train the model to estimate y to obtain \(\widehat{{u}_{i}}\).

  2. II.

    Loss function: It is a very important parameter in NN. It measures the difference between the labeled output and the neural network (NN) output. In this paper, we define loss function as:

    $$L_{MSE} = \frac{1}{K}\mathop \sum \limits_{i = 0}^{K - 1} \left( {u_{i} - \hat{u}_{i} } \right)^{2}$$
    (33)

    where \(u_{i} = \left\{ {0,1} \right\}\) is the i-th labeled output (correct information bit). \(\hat{u}_{i}\) is the i-th of NN output (estimated information bit).

3.3 Validation

During training, the signal-to-noise ratio (SNR) \({\rho }_{t}\) during training must be defined. Because in the actual decoding stage, the SNR is unknown and will change with time, the performance of our NN decoder will be greatly affected by the SNR during training, so we use a performance metric—the normalized validation error (NVE) [38]

$$NVE\left( {\rho_{t} } \right) = \frac{1}{S}\mathop \sum \limits_{S = 1}^{S} \frac{{BER_{NN} \left( {\rho_{t} ,\rho_{v,s} } \right)}}{{BER_{MAP} \left( {\rho_{v,s} } \right)}}$$
(34)

where \({\rho }_{v,s}\) represents the s-th SNR in a set of S different verification samples, \({BER}_{NND}({\rho }_{t},{\rho }_{v,s})\) represents the BER obtained by NN decoder training SNR \({\rho }_{t}\). \({BER}_{MAP}({\rho }_{v,s})\) is the BER of MAP decoding at the SNR \({\rho }_{v,s}\). The intention of this method is measuring the performance of NN decoder trained on a specific SNR compared to MAP decoding in different ranges of SNR. From (34), we can know that the less the NVE, the better the NN decoder, and there will be an optimal \({\rho }_{t}\). So, we train the NN decoder with datasets of different \({\rho }_{t}\) in our work, and choose the optimal \({\rho }_{t}\) which results in the least NVE.

In Fig. 6, we can see the SNR of 4.5 dB has the best performance, we choose this SNR as our NN decoder’s training SNR, so there is only one NN model and training data are of SNR 4.5 dB, and testing data are of SNR in 0 ~ 6 dB (13 different SNR values). The optimal training SNR in the impulse noise channel is different from that in the AWGN channel. In the prior work [38], the optimal training SNR is 1.5 dB, not 4.5 dB, for the same testing SNR range 0–6 dB.

Fig. 6
figure 6

NVE training \({E}_{b}/{N}_{0}\) for 16 bit length codes in impulse noise

Full size image

4 The Numerical Results

4.1 Setting Environment of the Proposed Method and Comparing Methods

We compare the following schemes: NN (proposed), SC (comparing), BP (comparing), SCL (comparing), MAP (comparing). The common setting environment/ parameters of all schemes are listed in Table 1. We use the same (16,8) Polar code as prior works without impulse noise [38, 39].

Table 1 Common setting environment of the proposed (NN) and comparing methods (SC, BP, SCL, MAP)
Full size table

The unique setting environment/ parameters for each method is as follows. The number of iterations for BP method is 100. We try 50,100, 200 iterations [24] and found 100 and 200 iterations have similar performance, so we set 100 iterations for BP method. The list size for SCL method is 2. We try list size 2,4,8,16 [4] and find they have similar performance so I select list size 2 for SCL method. In this work we don’t set the CRC for SCL. The hyperparameters for the proposed NN method are listed in Table 2.

Table 2 The hyperparameters of the proposed method (NN)
Full size table

One important finding is that the optimal training SNR in the impulse noise channel is different from that in the AWGN channel. In the prior work [38], the optimal training SNR is 1.5 dB, not 4.5 dB in Fig. 6, for the same testing SNR range 0–6 dB (Table 1).

4.2 Simulation Results

4.2.1 In the AWGN

Figure 7 shows the BERs of the proposed deep learning based decoding scheme (NN) and previous non-deep-learning based schemes SC/BP/SCL and the MAP bound are close to each other’s.

Fig. 7
figure 7

AWGN

Full size image

4.2.2 In the Impulse Noise

For Markov Gaussian memory impulse noise channel with state transition matrix in (10), we compare the BERs of the proposed deep learning based decoding scheme (NN) and previous non-deep-learning based schemes SC/BP/SCL and the MAP bound in Fig. 8.

Fig. 8
figure 8

Impulse noise

Full size image

We can see all decoders under the impulse noise has a BER gap with the MAP bound, but the BER of proposed NN decoder is about one third of that of SC, SCL, and BP. One finding is that the NN decoder could learn to a degree the memory impulse noise. For comparison SC/BP/SCL/MAP perform poorly when the noise model in not exactly AWGN. Thus, the proposed NN decoded is more suited to memory impulse noise channel than previous SC/BP/SCL decoding schemes.

Another finding is that the proposed LSTM-based method is 5 ~ 12 times less and thus has much less decoding latency than that of SC/BP/SCL methods because the proposed LSTM-based method has inherent parallel structure and has one shot operation- no iterative operations.

5 Conclusion

Deep learning-based Polar code decoding method has parallel structure in nature and has lower execution time and thus decoding latency. However, prior works do not consider memory impulse channels which has more complicated statistical model about average number of impulses in a codeword and the positions of the impulses in a codeword etc. In this paper, we propose the use LSTM for the Polar code decoding under the Markov Gaussian memory impulse noise channels. For the SNR range 0 ~ 6 dB, we find the optimal SNR value 4.5 dB, which is different from the 1.5 dB in the AWGN channel found in [38, 40]. The data set with training SNR 4.5 dB is used to train the proposed LSTM-based Polar code decoding method. The bit error probability of the proposed LSTM-based method is only one-third that of the conventional SC/BP/SCL decoding schemes under Markov Gaussian channels, and 5 ~ 12 times faster in execution time and decoding latency.