1 Introduction

Reconfigurable Intelligent Surface (RIS) play a pivotal role in advancing wireless communication for the next generation [1]. RIS can efficiently manage dynamic wireless environments and provide additional transmission gains, particularly when a direct source-to-destination connection faces obstruction [2]. With the help of passive metamaterial reflective elements, RIS introduces controllable phase shifts to incident electromagnetic waves through a controller connected between the RIS and the source [3]. These intelligent phase shifts constructively enhance the signal-to-noise ratio (SNR) at the desired user, transforming the random wireless channel into a deterministic entity and allowing RIS to create a truly smart radio environment [1, 4].

1.1 Related Works

In the literature, extensive studies on single RIS-aided systems have proven that RIS is a potential energy-efficient technology [5,6,7,8,9,10,11]. RIS-assisted single input single output (SISO) system will provide a low bit error rate even in low SNR regimes and outperforms the conventional relay schemes in terms of SER and outage probability [5, 6]. Extensive research has delved into the application of RIS to enhance energy efficiency (EE) across various communication scenarios, including broadcast and multi-user uplink systems [7]. RIS has proven beneficial in supporting ultra-reliable, low-latency scenarios with reduced energy requirements, extended coverage, and minimized latency [8]. Integration with multiple access schemes, such as rate-splitting multiple access and non-orthogonal multiple access (NOMA), has been explored to enhance overall throughput, secrecy and energy efficiency [9,10,11].

Recent research has highlighted the superior capacity of multi-RIS systems compared to single RIS systems while the configurations with a direct link between source and destination in multi RIS systems show further increase in average achievable rate gains and improved outage probabilities compared to single RIS setups [12,13,14]. However, practical scenarios may not guarantee such direct links. In [15], the authors have focused on improving outage probability by selecting the RIS with the highest instantaneous SNR among multiple RIS, but the selection strategy of RIS and location of RIS were not covered. Moreover, a multi-RIS aided system will also enhance the physical layer security [16]. However, resource allocation and energy efficiency become significant concerns when using multiple RISs to meet the desired Quality of Service (QoS) [17] and challenges such as reliable channel status information and increased computational complexity with a growing number of RIS were noted [18]. In response to these considerations, a novel double-RIS-assisted system was introduced, placing one RIS near the source and another near the destination [19]. This configuration demonstrated higher beamforming gain and improved wireless communication system secrecy compared to single RIS-assisted systems [20]. However, the double-RIS-assisted system in [19, 20] suffered from high path loss due to double reflection, potentially deteriorating signal power and overall performance. To overcome this issue, we propose a parallel double-RIS system, where two RISs aid communication simultaneously.

Motivated by the above considerations, in this paper, we consider a double RIS-assisted wireless system where two RISs aid communication simultaneously, with R1 placed near the source and R2 placed near the destination, without a direct link between the source and destination. The proposed system addresses challenges associated with double reflection, offering promising prospects for practical deployment. For the proposed system, MGF-based SER analysis is developed and a simple expression in terms of Q-function is derived to calculate OP. Additionally, our study considers the dissipated power at the transceivers and RIS circuitry to perform energy consumption gain analysis and showcases the superiority of the proposed double RIS system compared to a baseline single RIS system. All analytical results undergo rigorous verification through Monte Carlo simulations, ensuring the robustness and reliability of our findings.

The next section introduces the system model under consideration. Section 3 presents the analysis of SER and the outage probability of the proposed system. Section 4 provides theoretical and simulation results. Finally, Sect. 5 concludes the paper. The list of symbols and parameters used in the paper are given in Table 1.

Table 1 List of symbols and parameters
Full size table

2 System Model

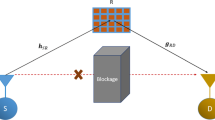
As shown in Fig. 1, we consider a double-RIS-assisted system consisting of a single antenna source (S) that communicates with a single antenna destination (D), with the assistance of R1 and R2. The number of reflecting elements in R1 and R2 are N1 and N2 respectively. The reflecting elements of each RIS are programmable with the help of RIS controller and it communicates with the source through a separate backhaul link to coordinate transmission and information exchange, such as channel state information and RIS phase shifts. The direct link between source and destination is blocked due to obstacles. The source and destination are in the far field of R1 and R2 [8]. It is assumed that the fading channel is quasi-static and flat, with no interference [1]. Further, we assume that the cascaded links from source to destination via each RIS are independent.

Fig. 1
figure 1

Proposed Double RIS-assisted wireless communication system

Full size image

Then, the received signal at the destination via two independent paths (S-R1-D and S-R2-D) is expressed as follows:

$$y=\sqrt{P}\left[\sum_{i=1}^{{N}_{1}}{h}_{1,i}{e}^{{j\phi }_{1,i}}{g}_{1,i}+\sum_{k=1}^{{N}_{2}}{h}_{2,k}{e}^{{j\phi }_{2,k}}{g}_{2,k}\right]x+n.$$
(1)

For simplicity, we assume that each RIS have the same number of elements, i.e., N1 = N2 = \({N}_{d}\), then Eq. (1) modified as:

$$y=\sqrt{P}\left[\sum_{i=1}^{{N}_{d}}{h}_{1,i}{e}^{{j\phi }_{1,i}}{g}_{1,i}+\sum_{i=1}^{{N}_{d}}{h}_{2,i}{e}^{{j\phi }_{2,i}}{g}_{2,i}\right]+n.$$
(2)

In Eq. (2), \({\phi }_{1,i}\) and \({\phi }_{2,i}\) are the phase shift introduced by the \(i\) th element of RIS-1(R1) and RIS-2(R2) respectively; P is the transmit power of the source, \(x\) denotes the transmitted signal and n ~ CN (0, \({\sigma }_{D}^{2}\)) stands for additive white Gaussian noise. The channels from S to the \(i\) th element of R1 and \(i\) th element of R1 to D are \({h}_{1,i}={d}_{{SR}_{1,i}}^{-\mathrm{\varrho }/2}{\alpha }_{1,i}{e}^{{-j\theta }_{1,i}}\) and \({g}_{1,i}= {{d}_{{R}_{1,i}D}^{-\varrho /2}\beta }_{1,i}{e}^{{-j\psi }_{1,i}}\) respectively. Similarly, \({h}_{2,i}={d}_{{SR}_{2,i}}^{-\mathrm{\varrho }/2}{\alpha }_{2,i}{e}^{{-j\theta }_{2,i}}\) and \({g}_{2,i}={{d}_{{R}_{2,i}D}^{-\varrho /2}\beta }_{2,i}{e}^{{-j\psi }_{2,i}}\) are the channels from S to \(i\) th element of R2 and \(i\) th element of R2 to D respectively. Here\({\alpha }_{1,i}\),\({\alpha }_{2,i}\), \({\beta }_{1,i}\) and \({\beta }_{2,i}\) denotes the amplitudes of channel coefficients and\({\theta }_{1,i}\), \({\theta }_{2,i}\), \({\psi }_{1,i}\) and \({\psi }_{2,i}\) denotes the phase of the corresponding channel, and denotes the path loss coefficient. The distances from S to the \(i\) th element of R1 and R2 are denoted as \({d}_{{SR}_{1,i}}\) and \({d}_{{SR}_{2,i}}\) respectively. Similarly, the distances from \(i\) th element of R1 and R2 to D are denoted as \({d}_{{R}_{1,i}D}\) and \({d}_{{R}_{2,i}D}\) respectively. Then the Eq. (2) can be written as,

$$\gamma =\frac{P{\left|\sum_{i=1}^{{N}_{d}}{{d}_{{SR}_{1,i}}^{-\mathrm{\varrho }/2}\alpha }_{1,i}{{d}_{{R}_{1,i}D}^{-\mathrm{\varrho }/2}\beta }_{1,i}{e}^{j\left({\phi }_{1.i}-{\theta }_{1,i}-{\psi }_{1,i}\right)}+\sum_{i=1}^{{N}_{d}}{{d}_{{SR}_{2,i}}^{-\mathrm{\varrho }/2}\alpha }_{2,i}{d}_{{R}_{2,i}D}^{-\mathrm{\varrho }/2}{\beta }_{2,i}{e}^{j\left({\phi }_{2,i}-{\theta }_{2,i}-{\psi }_{2,i}\right)}\right|}^{2}}{{\sigma }_{D}^{2}}$$
(3)

Under the far-field assumption we can write\({d}_{{SR}_{1,i}}={d}_{{SR}_{1}}\), \({d}_{{SR}_{2,i}}={d}_{{SR}_{2}}\) \(,{d}_{{R}_{1,i}D}={d}_{{R}_{1}D}\) and\({d}_{{R}_{2,i}D}={d}_{{R}_{2}D}\). Moreover, in the proposed system, R1 and R2 are deployed symmetrically such that \({d}_{{SR}_{1}}={d}_{{R}_{2}D}\) and\({d}_{{SR}_{2}}={d}_{{R}_{1}D}\), then we have\({d}_{S{R}_{1}}{d}_{{R}_{1}D}={d}_{S{R}_{2}}{d}_{{R}_{2}D}={d}_{t}\). By assuming that the perfect knowledge of CSI at each RIS [13], i.e., \(\phi_{1.i} = \theta_{1,i} + \psi_{1,i}\) and \(\phi_{2,i} = \theta_{2,i} + \psi_{2,i}\) then Eq. (3) is modified as Eq. (4).

$$\gamma =\frac{P{\left(\sum_{i=1}^{{N}_{d}}{\alpha }_{1,i}{\beta }_{1,i}+\sum_{i=1}^{{N}_{d}}{\alpha }_{2,i}{\beta }_{2,i}\right)}^{2}}{{\sigma }_{D}^{2}{{d}_{tol}}^{\varrho }}= {(A+B)}^{2} \overline{\gamma }={C}^{2}\overline{\gamma }.$$
(4)

Here \(, C=A+B ,A=\sum_{i=1}^{N}{\alpha }_{1,i}{\beta }_{1,i} ,B=\sum_{i=1}^{N}{\alpha }_{2,i}{\beta }_{2,i}\) and \(\overline{\gamma }=\frac{P}{{\sigma }_{D}^{2}{{d}_{tol}}^{\varrho }}\) stands for average SNR.

3 Performance Analysis

This section focuses on deriving mathematical expressions for the symbol error rate (SER) and outage probability (OP) of the proposed system. The analysis considers independent and identical fading for each communication channel. It begins with assumption of a RicianFootnote 1 distribution for all communication links, and subsequently adjusts the derived expressions to accommodate the RayleighFootnote 2 fading scenario.

3.1 SER analysis

In preparation for the analysis of SER of the proposed system, it is essential to compute the statistical parameters of received SNR for Rician and Rayleigh fading scenarios. In Eq. (4), \({\alpha }_{1,i}\) and \({\beta }_{1,i}\) follows Rician distribution with mean and variance given by \( E[a_{{(1,i)}} ] = E[({\text{ }}\beta )_{{(1,i)] = v(p/2)}} s(L)_{{(1/2)}} ( - v^{2} /(2s^{2} )) \) and \( V[a_{{(1,i)}} ] = V\left[ {(\beta )_{{(1,i)}}^{2} } \right] = v^{2} + 2s^{2} - p/2s^{2} (L_{{(1/2)}} ( - v^{2} /(2s^{2} ))) \)

Where \(K=\frac{\mathrm{Power in line of sight }({\text{LoS}})\mathrm{ component}}{\mathrm{Power in non}-\mathrm{LoS }({\text{NLoS}})\mathrm{ component }}=\frac{{v}^{2}}{2{\sigma }^{2}}\) denotes the shape parameter and the statistical parameters of product of \({\alpha }_{1,i },{ \beta }_{1,i}\) and all other random variables are obtained in Table 2.

Table 2 The derivation of statistical Parameters of random variables \(A, B\) and \(C\)
Full size table

The mean and variance of the product of independent and identical distributed Rican random variables\({\alpha }_{1,i}\), \({\beta }_{1,i}\) and\({\alpha }_{2,i}\), \({\beta }_{2,i}\) follows Rician distribution with statistical properties as shown in Table 2. With the assumption of\({N}_{d}\gg 1\),\(A\), B follows Gaussian distribution as per central limit theorem and C = \(A+B\), also follows Gaussian with statistical mean and variance as shown in Table 2. Then \(\gamma \), the square Gaussian random variable\(C\), follows a non-central chi-square distribution with one degree of freedom (DoF) [21] and the MGF of \(\gamma \) is given as [22],

$${M}_{\gamma }\left(s\right)={\left(\frac{1}{1-2s{\mathbb{V}}\left[C\right]\overline{\gamma }}\right)}^\frac{DoF}{2}\times exp\left(\frac{s{t}^{2}}{1-2s{\mathbb{V}}\left[C\right]\overline{\gamma }}\right),$$
(5)

In Eq. (5), \(t=\sqrt{{{\mathbb{E}}\left[C\right]}^{2}}={N}_{d}\pi {\sigma }^{2}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{2}\) denotes the non-centrality parameter of the NCCS. Now the MGF of received SNR for the proposed system is written as,

$${M}_{\gamma }\left(s\right)={\left(\frac{1}{1-{\text{s}}\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}\right)}^\frac{1}{2} \times exp\left(\frac{s{{N}_{d}}^{2}{\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\overline{\gamma }}{1-{\text{s}}\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}\right)$$
(6)

From (5), the average SER of M-ary phase shift keying (MPSK) signaling is calculated as [22]:

$${P}_{e}=\frac{1}{\pi }{\int }_{0}^{\left(M-1\right)\pi /M}{M}_{\gamma }\left(\frac{-{{\text{sin}}}^{2}\left(\pi /M\right)}{{{\text{sin}}}^{2}\eta }\right)d\eta $$
(7)

By substituting Eq. (6) in Eq. (7) the closed form expression for the for average SER of MPSK can be given as

$${P}_{e}=\frac{1}{\pi }{\int }_{0}^{\left(M-1\right)\pi /M}{\left(\frac{1}{1+\frac{{sin}^{2}\left(\pi /M\right)\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}{{sin}^{2}\eta }}\right)}^\frac{1}{2} \times exp\left(\frac{\frac{-{sin}^{2}\left(\pi /M\right){{N}_{d}}^{2}{\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\overline{\gamma }}{{sin}^{2}\eta }}{1+\frac{{sin}^{2}\left(\pi /M\right)\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}{{sin}^{2}\eta }}\right)d\eta .$$
(8)

By substituting \(\eta =\left(M-1\right)\pi /M\) in Eq. (8), we will get the upper bound of \({P}_{e}\) as follows:

$${P}_{e}\le \frac{(M-1)}{M}{\left(\frac{1}{1+\frac{{{\text{sin}}}^{2}\left(\pi /M\right){N}_{s}{\Omega }^{\frac{4}{\beta }}\left({\left(\Gamma \left(1+2/\beta \right)\right)}^{2}-{\Gamma \left(\left(1+1/\beta \right)\right)}^{4}\right)\overline{\gamma }}{{sin}^{2}(\left(M-1\right)\pi /M)}}\right)}^\frac{1}{2}\times {\text{exp}}\left(\frac{\frac{-{{\text{sin}}}^{2}\left(\pi /M\right){{N}_{d}}^{2}{\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\overline{\gamma }}{{sin}^{2}(\left(M-1\right)\pi /M)}}{1+\frac{{{\text{sin}}}^{2}\left(\pi /M\right)\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{2}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}{{sin}^{2}(\left(M-1\right)\pi /M)}}\right),$$
(9)

for binary PSK (BPSK), i.e. for M = 2, Eq. (8) and Eq. (9) are simplified to Eq. (10) and Eq. (11) which will give expressions to evaluate the average SER and upper bound of SER respectively.

$${P}_{e}=\frac{1}{\pi }{\int }_{0}^{\pi /2}{\left(\frac{1}{1+\frac{\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}{{{\text{sin}}}^{2}\eta }}\right)}^\frac{1}{2}\times {\text{exp}}\left(\frac{\frac{-{{N}_{d}}^{2}{\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\overline{\gamma }}{{{\text{sin}}}^{2}\eta }}{1+\frac{\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}{{{\text{sin}}}^{2}\eta }}\right)d\eta ,$$
(10)

By substituting \(\eta =1/2\) in Eq. (10), we will get the upper bound of \({P}_{e}\) for BPSK signaling scheme as follows:

$${P}_{e}\le \frac{1}{2}{\left(\frac{1}{1+\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}\right)}^\frac{1}{2}\times {\text{exp}}\left(\frac{-{{N}_{d}}^{2}{\pi }^{2}{\sigma }^{4}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\overline{\gamma }}{1+\left({N}_{d}{v}^{2}+8{N}_{d}{\sigma }^{2}-{{N}_{d}\pi }^{2}{\sigma }^{2}{\left({L}_{1/2}\left(-\frac{{v}^{2}}{2{\sigma }^{2}}\right)\right)}^{4}\right)\overline{\gamma }}\right).$$
(11)

For the Rayleigh fading scenario one can get the expressions for SER by simply substituting \({v}^{2}=0\), \({\sigma }^{2}=\frac{1}{2}\) in Eq. (7). For an instance the expression to evaluate average SER of M-ary phase shift keying (PSK) signaling is given as,

$${P}_{e}=\frac{1}{\pi }{\int }_{0}^{\left(M-1\right)\pi /M}{\left(\frac{1}{1+\frac{{sin}^{2}\left(\pi /M\right){N}_{d}\left(16-{\pi }^{2}\right)\overline{\gamma }}{4{sin}^{2}\eta }}\right)}^\frac{1}{2}exp\left(\frac{-\frac{{sin}^{2}\left(\pi /M\right){{N}_{d}}^{2}{\pi }^{2}\overline{\gamma }}{4{sin}^{2}\eta }}{1+\frac{{sin}^{2}\left(\pi /M\right){N}_{d}\left(16-{\pi }^{2}\right)\overline{\gamma }}{4{sin}^{2}\eta }}\right) d\eta $$
(12)

3.2 Outage Probability Analysis:

The probability that the received SNR is less than a specified threshold \({\gamma }_{th}\) is known as outage. As we mentioned, in previous section, \(\gamma \) follows a \(NCCS\) distribution and hence outage probability can be expressed as [15]:

$${P}_{out}={\text{Pr}}(\upgamma <{\gamma }_{th})=1-{Q}_\frac{1}{2}\left(\sqrt{\frac{{t}^{2}}{{\mathbb{V}}\left[C\right]}},\sqrt{\frac{{\gamma }_{th}}{\overline{\gamma }{\mathbb{V}}\left[C\right]}}\right)$$
(13)

The closed form expression for the outage probability for a threshold \({\gamma }_{th}\) in terms of Q-functionFootnote 3 with integer order of 1 is given as [27],

$${P}_{out}=1-\left(Q\left(\sqrt{\frac{{\gamma }_{th}}{\overline{\gamma }{\mathbb{V}}\left[C\right]}}-\sqrt{\frac{{t}^{2}}{{\mathbb{V}}\left[C\right]}}\right)+\left(\sqrt{\frac{{\gamma }_{th}}{\overline{\gamma }{\mathbb{V}}\left[C\right]}}+\sqrt{\frac{{t}^{2}}{{\mathbb{V}}\left[C\right]}}\right)\right)$$
(14)

Substituting the corresponding values of \({\mathbb{V}}\left[C\right]\), \(t\) gives the closed-form expressions to evaluate outage probability.

4 Simulation Results

In this section, we present theoretical and simulation results of SER and outage probability for the single and proposed double RIS system with same number of RIS element in both systems i.e., \(N={N}_{1}+{N}_{2}\) to validate the analytical framework. The path-loss at a reference distance of one meter for a carrier frequency of 3 GHz is, \(\alpha ={\left(\lambda /4\pi \right)}^{2}=\) −42 dB and the noise power at destination is set as \({\sigma }_{D}^{2}=\)−94 dBm, and the path loss exponent for all the link is set to 3. The values of \({P}_{i},{P}_{c}^{S}\) and \({P}_{c}^{D}\) are set as 7.8, 10 and 10 milliwatt respectively [12]. The simulation setup for the single RIS and proposed system are shown in Fig. 2. In both systems, source and destination are separated by \(d=100\) metre apart and \(h=5\) meter. In the single RIS, \({d}_{1}\) is fixed at \(50\) metre and for proposed system, \({d}_{1},{d}_{2}\) are fixed as \({d}_{1}={d}_{2}=5\) metre in such a way that \({d}_{S{R}_{1}}{d}_{{R}_{1}D}={d}_{S{R}_{2}}{d}_{{R}_{2}D}\). The Path loss exponent set \(\varrho =3\) and \({\gamma }_{th}=10 dB\)[14] and system operates at a bandwidth (BW) of 10 M Hz.

Fig. 2
figure 2

Simulation Setup: a Single RIS b Double RIS

Full size image

In Fig. 3, we plot BER of the proposed system under BPSK signalling scheme while varying the parameter N and fixed Rician K factor (K = 0) using Eq. (10). Where the solid curves and markers represents the theoretical and simulations respectively. The results unequivocally demonstrate a substantial enhancement in error performance compared to a single RIS system. For example, achieving a target BER of 10–6 with a single RIS system demands transmission powers (P) of approximately 47 dBm, 42 dBm, and 36 dBm for corresponding values of N set at 64, 128, and 256. In contrast, in the double RIS system, the same BER of 10–6 attainable with lower transmission powers of 35 dBm, 28 dBm, and 22 dBm for N values of 64, 128, and 256, respectively. This observation underscores the superiority of the proposed system in achieving superior BER performance compared to the base line single RIS system, demanding significantly reduced transmission power. Moreover, the figure also confirms that the special case of Rician channel with \(K=0\) is equivalent to Rayleigh fading scenario.

Fig. 3
figure 3

Bit error rate of single RIS and proposed double RIS system versus \(P\) for varying \(N\) and \(K=0\) assuming BPSK

Full size image

In Fig. 4, we examine the influence of the Rician K factor on the BER performance of the proposed system. The simulations are performed with a fixed number of reflecting elements, N = 128, and \({\sigma }^{2}=1/2\). As the Rician K factor, representing the power in the LoS component, increases, the severity of fading diminishes, resulting in an enhancement of BER performance, as visually depicted in Fig. 5. The plotted results illustrate that, for a fixed K value, an incremental increase in the transmitted power corresponds to a gradual reduction in the BER. This observation aligns with the expected behavior, indicating that higher transmit power contributes to improved communication reliability, particularly in scenarios characterized by Rician fading.

Fig. 4
figure 4

BER performance of proposed double RIS systems versus \(P\) with varying \(K\) assuming BPSK

Full size image
Fig. 5
figure 5

Symbol error rate of proposed double RIS systems versus \(P\) for different modulation order in M-ary PSK \(K=1\), N = 128

Full size image

Figure 5 illustrates the Symbol Error Rate (SER) of the proposed system as a function of \(P\) for different M-ary PSK signaling schemes, incorporating simulations with N = 128, \(K=1\) using Eq. (10). The simulations are conducted with. The results demonstrate that, with increasing modulation order (M), the SER performance deteriorates. This behavior aligns with the expectations observed in conventional wireless systems without RIS. In general, higher modulation orders entail a greater sensitivity to channel impairments, leading to increased symbol error rates.

In Fig. 6, we compare the outage probability of both systems with \(K=0\), while varying the parameter N. It can be inferred from Fig. 6 that the theoretical results match with simulation counterparts. As anticipated, in both systems, there is a notable reduction in outage probability for a fixed N as \(P\) increases, we observe sharp decrease in outage probability. For example, for \(N\) = 128, in the single RIS system, the outage probability decreases by a factor of 10 as P transitions from 29 to 31 dBm, and by a factor of 100 as \(P\) changes from 32 to 33 dBm. In the proposed system, under the same \(N\), the outage probability decreases by a factor of 10 from 16 to 18 dBm and by a factor of 100 from 20 to 21 dBm. The presented results underscore the efficiency of the proposed system, which exhibits a more pronounced reduction in outage probability for the same changes in transmitted power, particularly in comparison to the single RIS system. Moreover, in Fig. 6, \(K=0\) in a Rician channel mimics Rayleigh fading behaviour.

Fig. 6
figure 6

Outage probability of single RIS and proposed double RIS systems versus \(P\) for varying , \(K=0\)

Full size image

Figure 7 shows the impact of Rician K factor on the outage probability of proposes system for \(N=128\) and \({\sigma }^{2}=1/2\). Notably, as we maintain a fixed transmission power \(P\), the outage probability consistently decreases with an escalation in the Rician K factor. This trend suggests that higher K values, indicative of a strong Line-of-Sight (LoS) component, improves the system's resilience against fading conditions.

Fig. 7
figure 7

Outage probability of proposed double RIS systems versus \(P\) for varying \(K\), \(N=128\)

Full size image

4.1 Analysis of Energy Consumption Gain (\({{\varvec{G}}}_{{\varvec{E}}}\)):

Energy consumption gain (\({G}_{{\text{E}}}\)), serves as a valuable metric to assert the energy efficiency of the proposed system in comparison to a baseline system. In order to substantiate a claim of enhanced energy efficiency, \({G}_{{\text{E}}}\) should exceed one. The definition of \({G}_{{\text{E}}}\), as outlined in reference [25], involves the ratio of energy consumed by the baseline system to achieve a target BER and the energy consumed by the proposed system to achieve the same BER. and expressed as follows:

$${G}_{{\text{E}}}=\frac{{E}_{single RIS}}{{E}_{double RIS}}$$

The energy consumed by the system is calculated using the formula, \({P}_{total}/R\) [26]. In the context of an RIS-aided system, \({P}_{Total}=P+N{P}_{i}+{P}_{c}^{S}+{P}_{c}^{D}\) is the total amount of power consumed by the system to achieve a target BER, where R= \(b\times B\) is the rate at which bits are transmitted, \(b\) is denoting the bits per symbol (for BPSK, \(b=1\)) and \(B\) representing the system's bandwidth.

Table 3, clearly highlights the enhanced energy efficiency of the proposed system compared to the single RIS system across all values of N. However, as N increases, there is a noticeable decrease in \({G}_{E}\). This decline is attributed to the concurrent rise in power consumption (\(N{P}_{{\text{i}}}\)) associated with the increasing number of reflecting elements.

Table 3 Evaluation of \({G}_{{\text{E}}}\)
Full size table

5 Conclusion

In conclusion, this paper introduces and analyses the double RIS-assisted system. By strategically placing the first RIS (R1) near the source and the second RIS (R2) near the destination, both independently contribute to communication improvement, especially in scenarios without a direct line between the source and destination. The analysis incorporates moment generating function (MGF)-based symbol error rate (SER) evaluations for Rician and Rayleigh fading channels. A simplified closed-form expression for outage probability (OP) is derived using the Q-function. Through rigorous comparative evaluations, considering an equal number of RIS elements in single and double RIS systems, the proposed approach demonstrates superior performance in terms of SER and OP, all validated through Monte Carlo simulations. Additionally, an in-depth exploration of energy consumption gain reveals that the proposed system outperforms the single RIS system in terms of energy efficiency also.