1 Introduction

The reconfigurable intelligent surfaces (RISs), built using multiple passive metamaterial reflective elements can convert the dynamic wireless propagation medium into a controllable entity with the assistance of a controller, are one among the prime contenders for developing next-generation wireless communication systems [1]. With huge number of reflective elements whose electromagnetic response (e.g., phase shifts) can be programmable, the RIS can steer the incident signal toward the desired user and provide additional transmission gain when a direct link from source to destination is obstructed [2].

The numerous analyses of single RIS-assisted systems show that the RIS is an energy and spectral efficient technique. The spectrally effective RIS-aided SISO system outperforms both amplify-and-forward (AF) and decode-and-forward (DF) relays in terms of outage probability and offers low bit error rates [3, 4]. It is worth noting that the reconfigurable intelligent surface (RIS) has been demonstrated to have more energy efficiency (EE) than the AF and DF relay [4, 5].

The use of RIS has been investigated extensively in the literature for improving EE in various communication scenarios, such as broadcast and multi-user uplink systems. For example, studies have shown that RIS-assisted broadcast communication can significantly improve EE compared to traditional broadcast communication without RIS [6]. Moreover, the EE-SE tradeoff in the RIS-assisted multi-user uplink system can be optimized by designing the phase shift and covariance matrix [7]. The EE can also be improved by jointly optimizing the active and passive beamforming matrices at the base station and RIS respectively [8]. On the other hand, RIS supports ultra-reliable low latency scenarios with fewer energy requirements, increases coverage, and minimizes latency [9]. The amalgamation of RIS with multiple access schemes like rate-splitting multiple access and non-orthogonal multiple access (NOMA) will also increase the overall throughput and energy efficiency [10, 11].

However, the works mentioned above focus on a single RIS-aided system. Recently, a plethora of research works has shown that the multi-RIS system achieves higher capacity than a single RIS system [12,13,14,15]. Multi-RIS system with a direct link between transceivers outperforms the single RIS-assisted system [12] and outperforms relay-assisted system in terms of average sum rate, but in practical scenarios the direct link between transceivers cannot be guaranteed. In [13], authors show improved outage probability by selecting the RIS with highest instantaneous signal-to-noise ratio (SNR) out of multiple RIS. However, neither the location of RISs nor how to choose a RIS with a high SNR are covered. The authors [14] proposed a distributed on–off approach to increase the energy efficiency of multi-RIS systems which requires reliable channel status information (CSI), which is practically impossible when several RISs are deployed. In [15], authors proposed deep learning and convex optimization-based solution to optimize the energy efficiency of multi-RIS system. But the solution is sub-optimal and the computational complexity and resource allocation will increase with increase in number of RIS. Therefore, EE and resource allocation are crucial when employing a large number of RIS to provide the appropriate Quality of Service (QoS).

Inspired by this, the authors [16] presented a double-RIS-assisted system, with one RIS near the source and another RIS near the destination, to assist the communication between transceivers and show that a double RIS-assisted system achieves higher beamforming gain than a single RIS-assisted system. In addition, a double-RIS-assisted system can also enhance the secrecy of the wireless communication system [17]. Although the prior works on double-RIS-assisted systems have provided remarkable insights, the considered domino patterned system suffers from high path loss due to double reflection, which will deteriorate the received signal power and overall performance. Motivated by the above considerations and to overcome the issue of double reflection in the previous works, we consider a double RIS-assisted system where two RISs will aid communication between transceivers parallelly. Further, we have assumed the practical scenario of direct link blockage between source and destination. The proposed double-RIS system can be used in smart buildings to enhance indoor wireless coverage and improve energy efficiency and it can be used in RIS-assisted-NOMA networks, where the RIS-1 and RIS-2 can assist the near and far users respectively.

1.1 Motivation and contribution

Motivated by the above considerations, in this paper, we provide a comprehensive performance analysis of a double RIS-assisted system in comparison with a single RIS-assisted system. The main contribution of the paper is summarized as follows:

  • Analyzed the single RIS and double RIS-assisted systems over Weibull fading channels for the first time.

  • We calculate the mean, variance, and second-order moment of received SNR for both systems using the central limit theorem, and thereby closed-form equations for the upper and lower bounds of ergodic capacity and outage probability are obtained.

  • Furthermore, the theoretical results are verified through Monte-Carlo simulations, and we provide the comparison between S-RIS and double-RIS systems.

  • In addition, by considering circuit dissipated power at the source, RIS, and destination, we present the energy efficiency analysis as a function of spectral efficiency.

  • Finally, the impact of RIS locations on the ergodic capacity and energy efficiency of both systems were simulated using the theoretical framework.

1.2 Paper organization

The remainder of the paper is structured as follows. The system model and related channel models of single-RIS and double-RIS-assisted systems are introduced in Sect. 2. The mathematical expressions for the lower, upper bounds of ergodic capacity and outage probability are derived in Sect. 3. In Sect. 4, we present the theoretical and simulation results, and we show the impact of RIS location on ergodic capacity and energy efficiency in Sect. 5. Finally, we draw the conclusions in Sect. 6.

1.3 Notations

Vectors and matrices are denoted using boldface lowercase and boldface uppercase letter respectively. \(diag\left({\varvec{p}}\right)\) represents a diagonal matrix with each diagonal element being the corresponding element in \({\varvec{p}}\), \({(.)}^{T}\) stands for transposition, and \(\mathrm{Pr}\left(.\right)\) defines the probability of an event. The operators \({\mathbb{E}}\left[ a\right]\), \({\mathbb{V}}ar\left[ a\right],\) and \({\mathbb{E}}\left[ {a}^{2}\right]\), denote the mean, variance, and second-order moment of random variable \(a\) respectively, \(\Gamma \left(.\right)\) is the Gamma function.

2 System model

2.1 Single RIS-assisted system

We will start with a single RIS-assisted (S-RIS) SISO system in which RIS (R) with \({N}_{S}\) reflecting elements is placed in the mid-way between the source (S) and destination (D) as illustrated in Fig. 1. Since the direct link between transceivers is blocked due occlusion, S transmits the signal to D through S-R-D link. Then the signal received at D is given by

$${y}_{1}=\sqrt{{P}_{S}}\left({{\varvec{g}}}_{RD}^{T}{\varvec{\Phi}}{{\varvec{h}}}_{SR}\right)x+{n}_{D},$$
(1)

where \({P}_{S}\) is the transmit power of S, \(x\) is the unit energy signal transmitted by S, and \({n}_{D}\) is the additive white Gaussian noise at destination with mean zero and variance \({\sigma }_{D}^{2}\), i.e., \({n}_{D}\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_{D}^{2}\right)\). The channels of S → R, R → D are denoted by \({{\varvec{h}}}_{SR}\in {\mathbb{C}}^{N\times 1}\), \({{\varvec{g}}}_{RD}\in {\mathbb{C}}^{N\times 1}\) respectively. Also, \({\varvec{\Phi}}\in {\mathbb{C}}^{N\times N}\) is the phase shift matrix of R. Under the assumption of unit gain reflection coefficient, \({\varvec{\Phi}}\) can be expressed as \({\varvec{\Phi}}=diag\left({e}^{{\phi }_{1}}, {e}^{{\phi }_{2}}, ... , {e}^{{\phi }_{N}}\right)\) [18]. The elements of \({{\varvec{h}}}_{SR}\), \({{\varvec{h}}}_{RD}\) are represented as

Fig. 1
figure 1

Single RIS-assisted wireless communication system

Full size image
$$h={d}^{-\frac{\eta }{2}} a{e}^{j\psi }.$$
(2)

In Eq. (2) \(h\in \left\{{h}_{i} ,{g}_{i}\right\}\) denotes the complex fading channel coefficients of S → R, R → D links for the \(i\)-th element of R, \(\eta\) is the path loss exponent (PLE) of the corresponding channel. The distances from S to the \(i\)-th element of R and \(i\)-th element of R to D are denoted as \(d\in \left\{{d}_{{SR}_{i}}, {d}_{{R_i}{D}}\right\}\), \(\psi \in \left\{{\psi }_{i} ,{\varphi }_{i}\right\}\) indicates the phase of the corresponding channel and is uniformly distributed over\([-2\pi /\beta ,2\pi /\beta ]\). The absolute value of the corresponding channel is denoted by \(a\in \left\{\left|{h}_{i}\right|, \left|{g}_{i}\right|\right\}\) and follows the Weibull distribution with probability density function (PDF) as follows [18]

$${f}_{A}\left(a\right)=\frac{\beta }{\Omega }{a}^{\beta -1}exp\left(-\frac{{a}^{\beta }}{\Omega }\right),$$
(3)

where \(\Omega ={\mathbb{E}}\left[{a}^{\beta }\right]=\) \({\left(\frac{{\mathbb{E}}\left[{a}^{2}\right]}{\Gamma \left(1+\frac{2}{\beta }\right)}\right)}^{\frac{\beta }{2}}\) is the scale parameter, which characterizes the average fading power, and \(\beta\) is the shape parameter that indicates the fading severity. As the value of \(\beta\) decreases, fading severity decreases. The mean, \(n\)-th order moment, and variance of the Weibull distribution are \({\mathbb{E}}\left[a\right]={\Omega }^{\frac{1}{\beta }}\Gamma \left(1+\frac{1}{\beta }\right)\), \({\mathbb{E}}\left[{a}^{n}\right]={\Omega }^{\frac{n}{\beta }}\Gamma \left(1+\frac{n}{\beta }\right)\), and \({\mathbb{V}}ar\left[a\right]={\Omega }^{\frac{2}{\beta }}\left\{\Gamma \left(1+\frac{2}{\beta }\right)-{\left[\Gamma \left(1+\frac{1}{\beta }\right)\right]}^{2}\right\}\) respectively.

We assume S and R have perfect channel state information (CSI). We rely on channel estimation methodologies provided in [19, 20]. Then the maximum SNR at the destination can be written as [21]

$${\gamma }_{D,1}=\frac{{\left(\sum_{i=1}^{{N}_{S}}{d}_{{SR}_{i}}^{-\frac{\eta }{2}}{d}_{{R}_{i}D}^{-\frac{\eta }{2}}\left|{g}_{i}\right|\left|{h}_{i}\right|\right)}^{2}{P}_{S}}{{\sigma }_{D}^{2}},$$
(4)

similar to [6], we assume that our system belongs to the far-field case, then \({d}_{{SR}_{i}}={d}_{SR}\), \({d}_{{R}_{i}D}={d}_{RD}\) and Eq. (4). can be written as

$${\gamma }_{D,1}=\frac{{\left(\sum_{i=1}^{{N}_{S}}\left|{g}_{i}\right|\left|{h}_{i}\right|\right)}^{2}{P}_{S}}{{\sigma }_{D}^{2}{d}_{SR}^{\eta }{d}_{RD}^{\eta }}={{Z}_{1}}^{2}{\gamma }_{1}.$$
(5)

In Eq. (5)\({Z}_{1}=\sum_{i=1}^{{N}_{S}}\left|{g}_{i}\right|\left|{h}_{i}\right|\), \({\gamma }_{1 }=\frac{{P}_{S}}{{\sigma }_{D}^{2}{d}_{SR}^{\eta }{d}_{RD}^{\eta }}\) denotes the transmit SNR.

2.2 Double RIS-assisted system

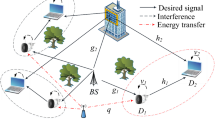
Now we consider a double-RIS-aided wireless communication system as illustrated in Fig. 2. Since there is no direct link, S transmits the signal to D through RIS-1 (R1) with \({N}_{1}={N}_{S}/2\) elements is placed near S and RIS-2 (R2) with \({N}_{2}={N}_{S}/2\) elements is placed near to D. The signal received at the D from both S-R1-D and S-R2-D links is given by

$${y}_{2}=\sqrt{{P}_{S}}\left({{\varvec{g}}}_{{R}_{1}D}^{T}{{\varvec{\Phi}}}_{1}{{\varvec{h}}}_{{SR}_{1}}+{{\varvec{g}}}_{{R}_{2}D}^{T}{{\varvec{\Phi}}}_{2}{{\varvec{h}}}_{{SR}_{2}}\right)x+{n}_{D},$$
(6)

where\({P}_{S}\),\(x\), and \({n}_{D}\) are same as S-RIS system. The channels of S → R1, R1 → D, S → R2, and R2 → D are defined as \({{\varvec{h}}}_{{SR}_{1}}\in {\mathbb{C}}^{{N}_{1}\times 1}\), \({{\varvec{g}}}_{{R}_{1}D}\in {\mathbb{C}}^{{N}_{1}\times 1}\), \({{\varvec{h}}}_{{SR}_{2}}\in {\mathbb{C}}^{{N}_{2}\times 1}\), and \({{\varvec{g}}}_{{R}_{2}D}\in {\mathbb{C}}^{{N}_{2}\times 1}\) respectively. Similar to S-RIS system, the phase shift matrices of R1 and R2 can be expressed as \({{\varvec{\Phi}}}_{1}=diag\left({e}^{{j\phi }_{\mathrm{1,1}}}, {e}^{{j\phi }_{\mathrm{1,2}}}, ... , {e}^{{j\phi }_{1,{N}_{1}}}\right)\) and \({{\varvec{\Phi}}}_{2}=diag\left({e}^{{j\phi }_{\mathrm{2,1}}}, {e}^{{j\phi }_{\mathrm{2,2}}}, ... , {e}^{{j\phi }_{2,{N}_{2}}}\right)\) respectively. The elements in \({{\varvec{h}}}_{{SR}_{1}}\), \({{\varvec{h}}}_{{R}_{1}D}\), \({{\varvec{h}}}_{{SR}_{2}}\), and \({{\varvec{h}}}_{{R}_{2}D}\) are represented as in Eq. (2).

Fig. 2
figure 2

Double RIS-assisted wireless communication system

Full size image

Where the complex fading channel coefficients of S → R1, R1 → D, S → R2, R2 → D links for the \(i\)-th and \(j\)-th elements of R1 and R2 are denoted by\(h\in \left\{{h}_{1,i} ,{g}_{1,i},{h}_{2,j},{g}_{2,j}\right\}\), \(\eta\) denotes PLE. The distance of corresponding links are denoted as \(d\in \left\{{d}_{{SR}_{1,i}}, {d}_{{R}_{1,i}D},{d}_{{SR}_{2,j}}, {d}_{{R}_{2,j}D}\right\}\), where \({d}_{{SR}_{1,i}}\) is the distance from S to \(i\)-th element of R1,\({d}_{{R}_{1,i}D}\) is the distance from \(j\)-th element of R1 to D. Similarly, \({d}_{{SR}_{2,j}}\) is the distance from S to \(j\)-th element of R2 and \({d}_{{R}_{2,j}D}\) is the distance from \(j\)-th element of R2 to D, \(\psi \in \left\{{\psi }_{1,i}, {\varphi }_{1,i},{\psi }_{2,j},{\varphi }_{2,j}\right\}\) denotes the phase and is uniformly distributed over \([-2\pi /\beta ,2\pi /\beta ]\) and \(a\in \left\{\left|{h}_{1,i}\right|, \left|{g}_{1,i}\right|, \left|{h}_{2,j}\right|,\left|{g}_{2,j}\right|\right\}\) is the absolute value of the corresponding channel and follows the Weibull distribution similar to Eq. (3).

With the assumption of having perfect CSI at both R1 and R2 [21], the maximum SNR at the destination in double-RIS system can be obtained as

$${\gamma }_{D,2}=\frac{{\left(\sum_{i=1}^{{N}_{1}}{d}_{{SR}_{1,i}}^{-\frac{\eta }{2}}{d}_{{R}_{1,i}D}^{-\frac{\eta }{2}}\left|{g}_{1,i}\right|\left|{h}_{1,i}\right|+\sum_{j=1}^{{N}_{2}}{d}_{{SR}_{2,j}}^{-\frac{\eta }{2}}{d}_{{R}_{2,j}D}^{-\frac{\eta }{2}}\left|{g}_{2,j}\right|\left|{h}_{2,j}\right|\right)}^{2}{P}_{S}}{{\sigma }_{D}^{2}},$$
(7a)

similar to S-RIS system we placed R1 and R2 under far-field propagation, hence\({d}_{{SR}_{1,i}}={d}_{{SR}_{1}}\),\({d}_{{R}_{1,i}D}={d}_{{R}_{1}D}\),\({d}_{{SR}_{2,j}}={d}_{{SR}_{2}}\), \({d}_{{R}_{2,j}D}={d}_{{R}_{2}D}\), and by assuming, \({N}_{1}=\) \({N}_{2}={N}_{D}\) where \({N}_{D}={N}_{S}/2\) then Eq. 7(a) can be written as

$${\gamma }_{D,2}=\frac{{\left({d}_{{SR}_{1}}^{-\frac{\eta }{2}}{d}_{{R}_{1}D}^{-\frac{\eta }{2}}\sum_{i=1}^{{N}_{D}}\left|{g}_{1,i}\right|\left|{h}_{1,i}\right|+{d}_{{SR}_{2}}^{-\frac{\eta }{2}}{d}_{{R}_{2}D}^{-\frac{\eta }{2}}\sum_{i=1}^{{N}_{D}}\left|{g}_{2,i}\right|\left|{h}_{2,i}\right|\right)}^{2}{P}_{S}}{{\sigma }_{D}^{2}},$$
(7b)

in the double-RIS system, we deployed R1 and R2 in such a way that, the product \({d}_{{SR}_{1}}\), \({d}_{{R}_{1}D}\) is same as the product of \({d}_{{SR}_{2}}\), \({d}_{{R}_{2}D}\), i.e., \({d}_{S{R}_{1}}{d}_{{R}_{1}D}={d}_{S{R}_{2}}{d}_{{R}_{2}D}={d}_{tol}\) then,

$${\gamma }_{D,2}=\frac{{\left(\sum_{i=1}^{{N}_{D}}\left|{g}_{1,i}\right|\left|{h}_{1,i}\right|+\sum_{i=1}^{{N}_{D}}\left|{g}_{2,i}\right|\left|{h}_{2,i}\right|\right)}^{2}{P}_{S}}{{\sigma }_{D}^{2}{{d}_{tol}}^{\eta }}={\left(A+B\right)}^{2}{\gamma }_{2}={{Z}_{2}}^{2}{\gamma }_{2}.$$
(8)

In Eq. (8)\({Z}_{2}=A+B\), \(A=\sum_{i=1}^{{N}_{D}}\left|{g}_{1,i}\right|\left|{h}_{1,i}\right|\), \(B=\sum_{i=1}^{{N}_{D}}\left|{g}_{2,i}\right|\left|{h}_{2,i}\right|\) and \({\gamma }_{2 }=\frac{{P}_{S}}{{\sigma }_{D}^{2}{{d}_{tol}}^{\eta }}\) denotes the transmit SNR.

3 Performance analysis

This section is devoted to the analysis of ergodic capacity and outage probability of both S-RIS and double-RIS systems. Before analyzing these metrics first, we need to evaluate mean, variance, second order moment of \({\gamma }_{D,1}\) and \({\gamma }_{D,2}\).

3.1 Mean, second order moment, variance of \({\gamma }_{D,1}\)

In Eq. (5), the product of independent and identically distributed Weibull random variables \(\left|{g}_{i}\right|\), \(\left|{h}_{i}\right|\) also follows Weibull distribution with mean \({\Omega }^{\frac{2}{\beta }}{\left(\Gamma \left(1+1/\beta \right)\right)}^{2}\) and variance \({\Omega }^{\frac{4}{\beta }}\left({\left(\Gamma \left(1+2/\beta \right)\right)}^{2}-{\Gamma \left(\left(1+1/\beta \right)\right)}^{4}\right)\)[22, 23]. With the assumption of having a sufficient number of reflecting elements in R, to obey the central limit theorem (CLT), i.e.,\({N}_{S}\gg 1\), \({Z}_{1}\) follows Gaussian distribution with mean \({N}_{S}{\Omega }^{\frac{2}{\beta }}{\left(\Gamma \left(1+1/\beta \right)\right)}^{2}\) and variance \({N}_{S}{\Omega }^{\frac{4}{\beta }}\left({\left(\Gamma \left(1+2/\beta \right)\right)}^{2}-\Gamma {\left(\left(1+1/\beta \right)\right)}^{4}\right)\). Then \({ \gamma }_{D,1}\) follows a non-central chi-square (NCCS) distribution with one degree of freedom [24].

Theorem 1: The mean, variance, and second-order moment of \({\gamma }_{1}\) can be obtained as

$${\mathbb{E}}\left[{ \gamma }_{D,1 }\right]={N}_{S}{\Omega }^{\frac{4}{\beta }}\left[\left({N}_{S}-1\right){\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}+{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}\right]{\gamma }_{1},$$
(9a)
$$\begin{aligned}{\mathbb{E}}\left[{{ \gamma }_{D,1 }}^{2} \right] &={{N}_{S}}^{2}{\Omega }^{\frac{8}{\beta }}\left[\left({{N}_{S}}^{2}-6{N}_{S}+3\right)\left({\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{8}\right)\right. \\ &\quad +\left(6{N}_{S}-6\right)\left({\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}\right)\\ &\quad +\left. 3{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{4}\right]{\gamma }_{1}^{2}, \end{aligned}$$
(9b)
$$\begin{aligned}{\mathbb{V}}ar\left[{ \gamma }_{D,1 }\right]&=2{{N}_{S}}^{2}{\Omega }^{\frac{8}{\beta }}\left[\left(1-2{N}_{S}\right)\left({\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{8}\right) \right. \\ &\quad +\left(2{N}_{S}-2\right)\left({\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}\right)\\ &\quad \left.+{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{4}\right]{\gamma }_{1}^{2},\end{aligned}$$
(9c)

Proof

Please refer to Appendix A.

3.2 Mean, second order moment, variance of \({\gamma }_{D,2}\)

In Eq. (8) the mean and variance of the product of \(\left|{g}_{1,i}\right|\),\(\left|{h}_{1,i}\right|\) and \(\left|{g}_{2,i}\right|\),\(\left|{h}_{2,i}\right|\) which are independent and identically distributed Weibull random variables, is given as [22, 23]

$${\mathbb{E}}\left[\left|{g}_{1,i}\right|\left|{h}_{1,i}\right|\right]={\mathbb{E}}\left[\left|{g}_{2,i}\right|\left|{h}_{2,i}\right|\right]={\Omega }^{\frac{2}{\beta }}{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{2},$$
(10a)
$${\mathbb{V}}ar\left[\left|{g}_{1,i}\right|\left|{h}_{1,i}\right|\right]={\mathbb{V}}ar\left[\left|{g}_{2,i}\right|\left|{h}_{2,i}\right|\right]={\Omega }^{\frac{4}{\beta }}\left[{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}-\Gamma {\left(\left(1+\frac{1}{\beta }\right)\right)}^{4}\right].$$
(10b)

By adopting the similar assumption as in the S-RIS system, i.e.,\({N}_{D}\gg 1\), \(A\) and \(B\) follow Gaussian distribution with equal mean and variance as follows,

$${\mathbb{E}}\left[A\right]={\mathbb{E}}\left[B\right]={N}_{D}{\Omega }^{\frac{2}{\beta }}{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{2} ,$$
(11a)
$${\mathbb{V}}ar\left[A\right]={\mathbb{V}}ar\left[B\right]={N}_{D}{\Omega }^{\frac{4}{\beta }}\left[{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}-{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}\right],$$
(11b)

since \(A\) and \(B\) are independent, their sum \({Z}_{2}\) also follows Gaussian distribution with mean \(2{N}_{D}{\Omega }^{\frac{2}{\beta }}{\left(\Gamma \left(1+1/\beta \right)\right)}^{2}\) and variance \(2{N}_{D}{\Omega }^{\frac{4}{\beta }}\left[{\left(\Gamma \left(1+2/\beta \right)\right)}^{2}-{\left(\Gamma \left(1+1/\beta \right)\right)}^{4}\right]\). Then \({\gamma }_{D,2}\) follows NCCS distribution with one degree of freedom [24].

Theorem 2: The mean, variance, and second order moment of \({\gamma }_{D,2}\) can be obtained as

$$\begin{aligned}{\mathbb{E}}\left[{\gamma }_{D,2}\right]&=2{N}_{D}{\Omega }^{\frac{4}{\beta }}\left[\left(2{N}_{D}-1\right)\left({\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}\right)\right. \\ &\quad +\left.{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}\right]{\gamma }_{2},\end{aligned}$$
(12a)
$${\mathbb{E}}\left[ {\gamma _{{D,2}} ^{2} } \right] = 4N_{D} ^{2} \Omega ^{{\frac{8}{\beta }}} \left[ \begin{aligned}& \left( {4N_{D} ^{2} - 12N_{D} + 3} \right)\left( {\Gamma \left( {1 + \frac{1}{\beta }} \right)} \right)^{8} \hfill \\ &+ \left( {12N_{D} - 6} \right)\left( {\Gamma \left( {1 + \frac{2}{\beta }} \right)} \right)^{2} \left( {\Gamma \left( {1 + \frac{1}{\beta }} \right)} \right)^{4} \hfill \\& + 3\left( {\Gamma \left( {1 + \frac{2}{\beta }} \right)} \right)^{4} \hfill \\ \end{aligned} \right]\gamma _{2}^{2} ,$$
(12b)
$${\mathbb{V}}ar\left[ {\gamma _{{D,2}} } \right] = 8N_{D} ^{2} \Omega ^{{\frac{8}{\beta }}} \left[ \begin{aligned} & \left( {1 - 4N_{D} } \right)\left( {\Gamma \left( {1 + \frac{1}{\beta }} \right)} \right)^{8} \hfill \\ & + \left( {4N_{D} - 2} \right)\left( {\Gamma \left( {1 + \frac{2}{\beta }} \right)} \right)^{2} \left( {\Gamma \left( {1 + \frac{1}{\beta }} \right)} \right)^{4} \hfill \\ & + \left( {\Gamma \left( {1 + \frac{2}{\beta }} \right)} \right)^{4} \hfill \\ \end{aligned} \right]\gamma _{2}^{2} ,$$
(12c)

Proof

Please refer to Appendix A.

3.3 Ergodic capacity

The ergodic capacity of both systems is expressed as \({C}_{n}={\mathbb{E}}\left[{\mathrm{log}}_{2}\left(1+{\gamma }_{D,n}\right)\right]\), while \(n=1\) and \(n=2\) denotes the S-RIS and double-RIS system respectively. As we mentioned in earlier, \({\gamma }_{D,n}\) follows NCCS distribution with one degree of freedom and whose cumulative distribution is mathematically intractable, hence it is difficult to characterize the exact ergodic capacity. Therefore, by utilizing Jensen’s inequality, we provide upper and lower bounds of ergodic capacity as [25],

$${C}_{l{b}_{n}}\le C\le {C}_{{ub}_{n}}.$$
(13)

In Eq. (13), \({C}_{lb}\) and \({C}_{ub}\) are defined as [26],

$${C}_{u{b}_{n}}={\mathrm{log}}_{2}\left(1+{\mathbb{E}}\left[{\gamma }_{D,n}\right]\right),$$
(14a)
$${C}_{l{b}_{n}}={\mathrm{log}}_{2}\left(1+\frac{{\mathbb{E}}\left[{\gamma }_{D,n}\right]^3}{{\mathbb{E}}\left[{\gamma }_{D,n}\right]^2}\right),$$
(14b)

by substituting mean and second order moments of \({\gamma}_{D,1}\) in Eq. 14(a) and Eq. 14(b) the closed-form expressions to compute \({C}_{{ub}_{1}}\) and \({C}_{{lb}_{1}}\) for the S-RIS containing only elementary functions are given as

$$\begin{aligned} {C}_{{ub}_{1}}&={\mathrm{log}}_{2}\left(1+{\gamma }_{1}{N}_{S}{\Omega }^{\frac{4}{\beta }}\left[\left({N}_{S}-1\right){\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}\right.\right. \\ &\quad +\left. \left.\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)^{2}\right]\right),\end{aligned}$$
(15)
$${C}_{l{b}_{1}}={\mathrm{log}}_{2}\left(1+\frac{{\gamma }_{1}{\left({N}_{S}{\Omega }^{\frac{4}{\beta }}\left[\left({N}_{S}-1\right){\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}+{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}\right]\right)}^{3}}{{{N}_{S}}^{2}{\Omega }^{\frac{8}{\beta }}\left[\left({{N}_{S}}^{2}-6{N}_{S}+3\right){\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{8}+\left(6{N}_{S}-6\right){\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}+{3\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{4}\right]}\right).$$
(16)

Similarly, by substituting mean and second order moments of \({\gamma }_{D,2}\) in Eqs. 14(a) and 14(b) the closed-form expressions to compute \({C}_{u{b}_{2}}\) and \({C}_{l{b}_{2}}\) for the double-RIS containing only elementary functions are given as

$$C_{{ub_{2} }} = {\text{log}}_{2} \left( {1 + \gamma _{2} 2N_{D} \Omega ^{{\frac{4}{\beta }}} \left[ \begin{aligned}& \left( {2N_{D} - 1} \right)\left( {\left( {\Gamma \left( {1 + \frac{1}{\beta }} \right)} \right)^{4} } \right) \hfill \\ & + \left( {\Gamma \left( {1 + \frac{2}{\beta }} \right)} \right)^{2} \hfill \\ \end{aligned} \right]} \right),$$
(17)
$${C}_{l{b}_{2}}={\mathrm{log}}_{2}\left(1+\frac{{\gamma }_{2}{\left[2{N}_{D}{\Omega }^{\frac{4}{\beta }}\left[\left(2{N}_{D}-1\right)\left({\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}\right)+{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}\right]\right]}^{3}}{4{{N}_{D}}^{2}{\Omega }^{\frac{8}{\beta }}\left[\left(4{{N}_{D}}^{2}-12{N}_{D}+3\right){\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{8}+\left(12{N}_{D}-6\right){\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{2}{\left(\Gamma \left(1+\frac{1}{\beta }\right)\right)}^{4}+3{\left(\Gamma \left(1+\frac{2}{\beta }\right)\right)}^{4}\right]}\right).$$
(18)

3.4 Outage probability

In this section, we derive the outage probability of S-RIS and double-RIS system, which is defined as the probability that the received SNR falls below a specified threshold \({\gamma }_{th}\) [9], i.e.

$${P}_{out}=\mathrm{Pr}\left({\gamma }_{D,n}<{\gamma }_{th}\right),$$
(19)

or equivalently

$${P}_{out}={F}_{{\gamma }_{D,n}}\left({\gamma }_{th}\right).$$
(20)

As we mentioned in the previous section, \({\gamma }_{n}\) follows NCCS distribution, and by using the cumulative distribution function of \({\gamma }_{D,n}\) the outage probability is expressed as [9]

$${P}_{o,n}=\mathrm{Pr}\left({\gamma }_{D,n}<{\gamma }_{th}\right)=1-{Q}_{\frac{1}{2}}\left(\sqrt{\frac{{\lambda }_{n}}{{{\sigma }_{n}}^{2}}},\sqrt{\frac{{\gamma }_{th}}{{{\gamma }_{D,n}^{2}{\sigma }_{n}}^{2}}}\right),$$
(21)

in Eq. (21) \({Q}_{\frac{1}{2}}\left(x,\mathrm{y}\right)\) is the Generalized Marcum Q-function with fractional order \(1/2\) and can be expressed as [27],

$${Q}_{\frac{1}{2}}\left(x,\mathrm{y}\right)=Q\left(y-x\right)+Q\left(y+x\right),$$
(22)

by exploiting Eq. (22), the closed-form expression to evaluate outage probability for the S-RIS and double-RIS system are given as

$${P}_{o,n}=1- \left(Q\left(\sqrt{\frac{{\gamma }_{th}}{{{\gamma }_{D,n}^{2}{\sigma }_{n}}^{2}}}-\sqrt{\frac{{\lambda }_{{Z}_{n}}}{{{\sigma }_{{Z}_{n}}}^{2}}}\right)+Q\left(\sqrt{\frac{{\gamma }_{th}}{{{\gamma }_{D,n}^{2}{\sigma }_{n}}^{2}}}+\sqrt{\frac{{\lambda }_{{Z}_{n}}}{{{\sigma }_{{Z}_{n}}}^{2}}}\right)\right),$$
(23)

where \({\lambda }_{{Z}_{1}}={{N}_{S}}^{2}{\Omega }^{\frac{4}{\beta }}{\left(\Gamma \left(1+1/\beta \right)\right)}^{4}\), \({{\sigma }_{{Z}_{1}}}^{2}={N}_{S}{\Omega }^{\frac{4}{\beta }}\left({\left(\Gamma \left(1+2/\beta \right)\right)}^{2}-{\Gamma \left(\left(1+1/\beta \right)\right)}^{4}\right)\) for S-RIS system and \({\lambda }_{{Z}_{2}}=4{{N}_{D}}^{2}{\Omega }^{\frac{4}{\beta }}{\left(\Gamma \left(1+1/\beta \right)\right)}^{4}\), \({{\sigma }_{{Z}_{2}}}^{2}=2{N}_{D}{\Omega }^{\frac{4}{\beta }}\left[{\left(\Gamma \left(1+2/\beta \right)\right)}^{2}-{\left(\Gamma \left(1+1/\beta \right)\right)}^{4}\right]\) for double RIS-system.

4 Simulation results

In this section, we present the simulation results of S-RIS and double-RIS systems to verify the analytical framework presented in the preceding sections. In addition, we compare both systems in terms ergodic capacity, outage probability and energy efficiency by varying the location RISs. To have a fair comparison, we consider an equal number of reflecting elements in both systems, i.e., \({N}_{S}={2N}_{D}=N\), outage threshold SNR \({\gamma }_{th}=\) 10 dB. In addition, the set of parameters given in Table 1 are used in the simulations.

Table 1 Simulation parameters
Full size table

Figure 3 illustrates the ergodic capacity of the S-RIS system with the varying number of reflecting elements \(N\), Weibull shape parameter \(\beta =1,\) and scale parameter \(\Omega =1\). The figure shows that, for a fixed N as the transmit power \({P}_{S}\) increases, the ergodic capacity of the system also increases. This is because higher transmit power results in a stronger signal at the receiver, which in turn increases the amount of information that can be reliably transmitted. For example, for \(N=32\), as \({P}_{S}\) increases from 0 to 5 dBm, the ergodic capacity increases by 89.2 \(\%\). In addition, we observe that for a fixed \({P}_{S}\), as \(N\) increases, the ergodic capacity also increases. For instance, for \({P}_{S}=\) 5 dBm, as \(N\) changes from 32 to 64, the ergodic capacity increases by 69.64%.

Fig. 3
figure 3

Simulated Ergodic Capacity, upper and lower bounds of S-RIS system versus transmit power of the source (\({P}_{S}\)) for varying \(N\), \(\beta =1\), \(\Omega =1\)

Full size image

Similarly, Fig. 4 illustrates the ergodic capacity of the double-RIS system with varying \(N\),\(\beta =1\), and \(\Omega =1\). Similar to the S-RIS system we observe an increase in the ergodic capacity as \({P}_{S}\) increases for fixed \(N\) and for fixed \({P}_{S}\), ergodic capacity increases with \(N\) for fixed \({P}_{S}\), as \(N\) doubles, we observe an improvement of 2 b/s/Hz in EC for S-RIS and double RIS systems. Finally, from Figs. 3 and 4, we observe the tightness of upper and lower bounds as the value of \(N\) increases which indicates the accuracy of closed-form expressions (\({C}_{{ub}_{n}}\), \({C}_{l{b}_{n}}\)) derived in previous section.

Fig. 4
figure 4

Simulated Ergodic Capacity, upper and lower bounds of double-RIS system versus transmit power of the source (\({P}_{S}\)) for varying \(N\), \(\beta =1\) and \(\Omega =1\)

Full size image

Figure 5 compares the ergodic capacity of S-RIS and double-RIS systems for varying \(N\) by fixing the Weibull shape and scale parameters equal to \(1\). Double-RIS system shows significant improvement in ergodic capacity with the same number of reflecting elements for a fixed \({P}_{S}\). For instance, when \({P}_{S}\) is fixed at 5 dBm double-RIS system with \(N=32\) shows an improvement of 6 b/s/Hz over the S-RIS system with \(N=32\). Finally, it is observed that when \({P}_{S}\) is varying from -30 dBm to 10 dBm for a double RIS-system with \(N=64\), shows an approximate improvement of 0.5 to 2 b/s/Hz over an S-RIS system with \(N=256\).

Fig. 5
figure 5

Ergodic Capacity Comparison of S-RIS and double-RIS system versus transmit power of the source (\({P}_{S}\)) for varying \(N\), \(\beta =1\) and \(\Omega =1\)

Full size image

Figure 6 shows the impact of Weibull shape parameter \(\beta\) on the ergodic capacity of S-RIS and double-RIS systems for \(N=32\) and \(\Omega =1\). As mentioned in the previous section, fading severity decreases with an increase in \(\beta\). Consistent with this, the results indicate that increasing \(\beta\) leads to an increase in the ergodic capacity of the system. As can be seen, for a fixed \(\beta\) as, \({P}_{S}\) increases the ergodic capacity increases monotonically. It is worth noting that \(\beta\) =2 corresponds to the Rayleigh fading scenario, which is a special case of the Weibull distribution.

Fig. 6
figure 6

Simulated Ergodic Capacity of S-RIS and double-RIS system versus transmit power of the source (\({P}_{S}\)) for varying \(\beta\), \(N=32\) and \(\Omega =1\)

Full size image

In Fig. 7, we compare the outage probability of both systems with \(\beta =1\) and \(\Omega =1\). It can be inferred from Fig. 7 that the theoretical results match with simulation counterparts. As expected, in both systems, for a fixed \(N\), as \({P}_{S}\) increases, we observe sharp decrease in outage probability. For example, for \(N\) = 64, OP decreases by 10 times as \({P}_{S}\) changes from 5 to 6 dBm in S-RIS system whereas in double-RIS system, for \(N\) = 64, OP decreases by 10 times as \({P}_{S}\) changes from − 11 to − 10 dBm. In addition, the rate of decrease is faster with a larger \(N\).

Fig.7
figure 7

Outage probability comparison of S-RIS and double-RIS system versus transmit power of the source (\({P}_{S}\)) for varying \(N\), \(\beta =1\) and \(\Omega =1\)

Full size image

Figure 8 shows the impact of Weibull shape parameter \(\beta\) on the outage probability of S-RIS and double-RIS system for \(N=32\) and \(\Omega =1\), where \(\beta =2\) denotes the Rayleigh fading. For fixed \({P}_{S}\), we observe an improvement in the outage probability as \(\beta\) increase. In addition, we observe that for a fixed \(\beta\) as, \({P}_{S}\) increases the outage probability decreases at faster rate.

Fig. 8
figure 8

Outage Probability of S-RIS and double-RIS system versus transmit power of the source (\({P}_{S}\)) for varying \(\beta\),\(N=32\) and \(\Omega =1\)

Full size image

In Fig. 9, taking the total power consumed by the source, destination nodes and RIS elements into account, we evaluate the energy efficiency (EE) of the S-RIS and double-RIS systems as a function of target spectral efficiency (R). The EE of a RIS-aided system can be defined as \(EE={BW}_{T}\times R/{P}_{Total}\) [Mbit/Joule] [4], \({P}_{Total}\) is the total power consumed by the system and calculated as,\({P}_{Total}={P}_{S}+N{P}_{i}+{P}_{c}^{S}+{P}_{c}^{D}\). Double-RIS system shows higher energy efficiency than the S-RIS system. When \(R\le \widetilde{R}=\) 17.5 b/s/Hz, the double-RIS system with \(N=\) 64 surpasses system with \(N=\) 128 in terms of EE. Similarly, when \(R\le \widetilde{R}=\) 12.5 b/s/Hz, S-RIS system with \(N=\) 64 achieves higher energy efficiency system with \(N=\) 128 where \(\widetilde{R}\) is the transition point as indicated in Fig. 9. The above phenomenon is due to the fact that, the \({P}_{Total}\) increases linearly and \(R\) increases logarithmically with \(N\).

Fig. 9
figure 9

The energy efficiency of S-RIS and double-RIS system as a function of target SE (\(R\))

Full size image

The same can be observed from Table 2. For instance, when the target SE is \(R\)=4, D-RIS system can enhance the EE 94 by up to 94.65% and 96.23% for \(N\)=64 and \(N\)=128 respectively compared to S-RIS system. Similarly, for \(R\)=6, D-RIS system can enhance the EE by up to 100.16% and 114.21% for \(N\)=64 and \(N\)=128 respectively compared to S-RIS system.

Table 2 Evaluation metrics
Full size table

5 Impact of RISs location on the ergodic capacity and energy efficiency

To gain further insights about the considered system we compared the proposed D-RIS system with S-RIS system by varying the location of RISs and analyzed the ergodic capacity and energy efficiency.

Figure 10 depicts the impact of changing the horizontal distance \({x}_{R}\in (\mathrm{0,200})\) on the ergodic capacity. In S-RIS system, we observed the improved performance in ergodic capacity when RIS is in the vicinity of either source or destination node when varying the position of RIS since the double fading problem is minimum which is directly proportional to the product of \({d}_{SR}=\sqrt{{{x}_{R}}^{2}+{{y}_{R}}^{2}}\) and \({d}_{RD}=\sqrt{{\left({{d}_{SD}-x}_{R}\right)}^{2}+{{y}_{R}}^{2}}\). Similarly, for the proposed D-RIS system we simulated the ergodic capacity by changing the location of RIS’ for two different scenarios without altering the far-field assumption: (i) \({R}_{1}\) and \({R}_{2}\) placed closer to the S and D, (ii) \({R}_{1}\) and \({R}_{2}\) placed midway between the S and D. From the figure it is observed that the proposed D-RIS system \(\left(\left({x}_{{R}_{1}},{y}_{{R}_{1}}\right) =(\mathrm{5,10}) , \left({x}_{{R}_{2}},{y}_{{R}_{2}}\right)=(\mathrm{195,10})\right)\) outperforms the S-RIS system in terms of ergodic capacity but when the single RIS is placed nearer to S or D, it achieves high ergodic capacity compared to that of the D-RIS system \(\left(\left({x}_{{R}_{1}},{y}_{{R}_{1}}\right) =(\mathrm{95,10}) , \left({x}_{{R}_{2}},{y}_{{R}_{2}}\right)=(\mathrm{105,10})\right)\).

Fig. 10
figure 10

Impact of location of RISs on Ergodic capacity of the S-RIS and D-RIS system for varying \(N\), \(\beta =1\),\(\Omega =1\) and \({P}_{S}= 10 dBm\)

Full size image

In Fig. 11, we analyze the EE of S-RIS system by placing the RIS nearer to the S, D, and middle of S-D link, and compare it with two different scenarios of D-RIS system. From Figs. 9 and 11 it is observed, that the S-RIS system with RIS placed either near to S or D achieved same ergodic performance and energy efficiency which outperforms the S-RIS system with RIS placed in the middle S-D link and D-RIS system of scenario (ii). However, the proposed D-RIS system with R1 and R2 placed near to source and destination respectively, shown superior performance than the above mentioned systems with same number of reflecting elements. Figures 10 and 11 clearly reveal that D-RIS with optimally positioned RISs outperforms S-RIS system with same number of reflecting elements. Thus, the positioning of RISs in a D-RIS or multiple-RIS is an important factor in optimizing the performance gains.

Fig. 11
figure 11

Impact of RISs location on the energy efficiency of S-RIS and double-RIS system as a function of target SE (\(R\)) for \(N\) = 64, \(\beta =1\), \(\Omega =1\)

Full size image

6 Conclusion

In this paper, we analyze the ergodic capacity and outage probability of single-RIS, double-RIS assisted systems over Weibull fading channels. Relying on central limit theorem, we derive the statistical parameters such as mean, variance and second order moment of received SNR for both systems. Thereby, we derived the closed-form expression for the lower, upper bounds of ergodic capacity and outage probability. The theoretical results are validated through Monte-Carlo simulations with various system parameters and found that the bounds are tight for larger number of reflecting elements. In addition, we compare the performance of both systems with equal number of reflecting elements and found that the proposed double-RIS system with R1 and R2 placed near to source, and destination respectively outperforms the S-RIS system. Also, we provide the energy efficiency analysis as a function of required spectral efficiency, from the analysis we found that, double-RIS assisted systems is energy-efficient than single-RIS. At the end we simulate the impact of RISs placement on the ergodic capacity of double-RIS system in comparison with the single-RIS system. Finally, we conclude that instead of deploying single RIS in the midway between source–destination link, placing two RIS, in the vicinity of source and destination with overall number of reflecting elements equal to single-RIS is an energy-efficient solution to improve the overall performance. It is worth noting that the EE of the systems will mainly depend on the target SE (R), number of reflecting elements (N) and location of the RIS. Hence, the D-RIS system that switches between single-RIS and double-RIS modes can help to minimize transmit power and maximize EE, especially in cases where the target SE is not too high. Evaluating the performance of the proposed system when transceivers are in the near-field regime of RISs with appropriate channel models can be considered as future works.