Physical Layer Security of Non Orthogonal Multiple Access Using Reconfigurable Intelligent Surfaces

Abstract

In this paper, we propose to improve the physical layer security of non orthogonal multiple access (NOMA) using reconfigurable intelligent surfaces (RIS). RIS is decomposed in different sets of reflectors dedicated to NOMA users. As reflections reach the ith user with the same phase, the transmitter can reduce its power so that the eavesdropper cannot detect its signal. We derive the secrecy outage probability and the Strictly positive secrecy capacity (SPSC) for NOMA systems using RIS for Rayleigh fading channels.

1 Introduction

Reconfigurable intelligent surfaces (RIS) allow to improve the performance of wireless systems and are a good candidate for 6G communications [1, 2]. RIS can be implemented as a reflector between the transmitter and receiver. All reflections have the same phase at the receiver. Therefore, the receiver output is similar to that of the maximum ratio combiner (MRC) [3]. The phase of kth reflector depends on channel phase between transmitter and RIS as well as channel phase between RIS and receiver [4]. The number of RIS reflectors can be varied between $N=8$ and $N=512$. RIS offers 10–40 dB gain with respect to conventional wireless systems without RIS [5, 6]. RIS can also be implemented at the transmitter to improve the throughput [1]. When RIS is implemented as a transmitter, the phase of reflector depends on channel phase between RIS and receiver. RIS implemented as a transmitter offers 1 dB with respect to RIS implemented as a reflector [1]. However, RIS implemented as a transmitter cannot be used in Non Orthogonal Multiple Access (NOMA) systems since multiple users should be served. In NOMA systems, RIS should be implemented as a reflector where subsets of reflectors are dedicated to the different users [7].

Physical layer security of orthogonal multiple access (OMA) has been evaluated in [8, 9]. SOP and SPSC of NOMA systems were computed in [10,11,12,13]. Security of energy harvesting systems was studied in [14]. PLS of free space optical (FSO) communications was studied in [15]. SOP and SPSC of Multiple Multiple Output (MIMO) systems were evaluated in [16,17,18,19,20]. In this paper, we propose the use of reconfigurable intelligent Surfaces (RIS) to improve the Physical Layer Security (PLS) of Non Orthogonal Multiple Access (NOMA) systems by evaluating the SOP and SPSC. RIS is decomposed in K sets of reflectors serving K users. Each set of reflectors reflects signals towards a given user. RIS contains $N_i$ reflectors dedicated to user i. When RIS is used, all reflections reach the ith user with the same phase. RIS has not been yet used to improve the physical layer security in NOMA systems where the transmitter sends a combination of symbols dedicated to K users and in the presence of an eavesdropper. The ith user $U_i$ has to detect the symbols of remaining $K-i$ users. It performs Successive Interference Cancelation and detects first the symbol of weakest user. Then, it removes the signal of weakest user and detect that of second weakest user. The process is continued until $U_i$ detects its own symbol. We derive the secrecy outage probability (SOP) and the probability of strictly positive secrecy capacity (SPSC) of NOMA systems using reconfigurable intelligent surfaces (RIS). We show that the use of RIS improve the security of physical layer by 10–40 dB with respect to conventional NOMA without RIS.

The contributions of the paper are

• Security enhancement of physical layer of NOMA systems using Reconfigurable Intelligent Surfaces (RIS).

• Derivation of the Secrecy Outage Probability (SOP) and the probability of Strictly Positive Secrecy Capacity (SPSC) of NOMA when RIS is deployed as a reflector.

• Comparison of the SOP and SPSC of NOMA systems when RIS is deployed to conventional NOMA without RIS. We show that the use of RIS improves the security of NOMA systems by 20-30 dB with respect to conventional wireless systems without RIS [10,11,12,13].

Next section describes the system model. Section 3 and 4 derive the SOP and SPSC in the presence of two and multiple users. Section 5 describes the theoretical and simulation results. Section 6 compares our results to the current literature. Section 7 concludes the paper.

2 System Model

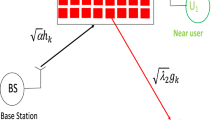
As shown in Fig. 1, we consider a network containing a Base Station (BS), strong and weak NOMA users $U_1$ and $U_2$. Let $\sqrt{\beta }h_k$ be the channel gain between BS and the kth reflector of RIS, $\beta =\frac{1}{d^{ple}}$, d is the distance from BS to RIS and ple is the path loss exponent. For Rayleigh channels, $h_k$ is a zero mean complex Gaussian random variable. Let $h_k=a_k e^{-jb_k}$ where $a_k=|h_k|$ and $b_k$ is the phase of $h_k$. For Rayleigh channels, $a_k$ is Rayleigh distributed with mean $E(a_k)=\frac{\sqrt{\pi }}{2}$ and $E(a_k^2)=1$ where E(.) is the expectation operator. Let $\sqrt{\beta _i}g_k$ be the channel gain between kth reflector of RIS and $U_i$ where $\beta _i=\frac{1}{d_i^{ple}}$, $d_i$ is the distance from RIS to $U_i$. Let $g_k=c_k e^{-je_k}$, $c_k=|g_k|$ and $e_k$ is the phase of $g_k$. For Rayleigh channels, $c_k$ is Rayleigh distributed with $E(c_k)=\frac{\sqrt{\pi }}{2}$ and $E(c_k^2)=1$. Let $\sqrt{\beta _E}t$ be the channel coefficient between the source and eavesdropper where $\beta _E=\frac{1}{d_E^{ple}}$ and $d_E$ is the distance between source S and E.

Fig. 1

NOMA using reconfigurable intelligent surfaces (RIS)

RIS adjusts the phase $v_k$ of kth reflector as follows [1]

$$ v_{k} = b_{k} + e_{k} . $$

(1)

Figure 1 shows that $N_1$ reflectors are dedicated to user $U_1$ and $N_2$ reflectors for user $U_2$. $N=N_1+N_2$ is the total number of RIS reflectors. $I_1$ and $I_2$ are the set of reflectors dedicated respectively to $U_1$ and $U_2$. The received signals at $U_1$ and $U_2$ are expressed as

$$ r_{1} = {\text{ }}s\sqrt {2E_{s} \beta \beta _{1} } \sum\limits_{{k \in I_{1} }} {h_{k} } g_{k} e^{{jv_{k} }} + n_{1} , $$

(2)

$$ r_{2} = s\sqrt {2E_{s} \beta \beta _{2} } \sum\limits_{{k \in I_{2} }} {h_{k} } g_{k} e^{{jv_{k} }} + n_{2} , $$

(3)

where $E_s$ is the symbol energy of BS, s is the transmitted NOMA symbol and $n_1$, $n_2$ are Gaussian noises with variance $N_0$.

The BS transmits a combination of two symbols $s_1$ and $s_2$ dedicated to strong and weak users:

$$ s = \sqrt {P_{1} } s_{1} + \sqrt {P_{2} } s_{2} , $$

(4)

where $0<P_i<1$ is the power allocated to $U_i$, $P_1+P_2=1$. More power is allocated to weak user $U_2$: $0<P_1<P_2<1$.

Using (1)–(3), we obtain

$$ r_{1} = {\text{ }}s\sqrt {2E_{s} \beta \beta _{1} } \sum\limits_{{k \in I_{1} }} {a_{k} } c_{k} + n_{1} , $$

(5)

$$ r_{2} = s\sqrt {2E_{s} \beta \beta _{2} } \sum\limits_{{k \in I_{2} }} {a_{k} } c_{k} + n_{2} , $$

(6)

Therefore, we have

$$ r_{1} = \sqrt {A_{1} } s + n_{1} , $$

(7)

$$ r_{2} = \sqrt {A_{2} } s + n_{2} , $$

(8)

where

$$ A_{1} = {\text{ }}2E_{s} \beta \beta _{1} W_{1}^{2} , $$

(9)

$$ A_{2} = 2E_{s} \beta \beta _{2} W_{2}^{2} , $$

(10)

$$\begin{aligned} W_1 &= {} \sum _{k\in I_1}a_kc_k, \end{aligned}$$

(11)

and

$$\begin{aligned} W_2=\sum _{k\in I_2}a_kc_k \end{aligned}$$

(12)

Using (4-6), we have

$$\begin{aligned} r_1 &= {} \sqrt{A_1}\left[ \sqrt{P_1}s_1+\sqrt{P_2}s_2\right] +n_1, \end{aligned}$$

(13)

$$\begin{aligned} r_2&= {} \sqrt{A_2}\left[ \sqrt{P_1}s_1+\sqrt{P_2}s_2\right] +n_2. \end{aligned}$$

(14)

3 SOP and SPCS

Weak user detects its symbol $s_1$ with Signal to Interference plus Noise Ratio (SINR) given by

$$\begin{aligned} \gamma _2=\frac{P_2A_2}{P_1A_2+N_0}. \end{aligned}$$

(15)

Strong user $U_1$ demodulates $s_2$ since it is transmitted with a larger power. The SINR at $U_1$ to detect $s_2$ is equal to

$$\begin{aligned} \gamma _{1\rightarrow 2}=\frac{P_2A_1}{P_1A_1+N_0}. \end{aligned}$$

(16)

Then, strong user removes $s_1$ and detects $s_2$ with SINR

$$\begin{aligned} \gamma _{1\rightarrow 1}=\frac{P_1A_1}{N_0}. \end{aligned}$$

(17)

The SINR at $U_1$ is the minimum of $\gamma _{1\rightarrow 1}$ and $\gamma _{1\rightarrow 2}$

$$\begin{aligned} \gamma _1=min\left( \gamma _{1\rightarrow 1},\gamma _{1\rightarrow 2}\right) \end{aligned}$$

(18)

The outage probability at $U_2$ is expressed as

$$\begin{aligned} P^{outage,2}\left( \gamma _{th}\right) =P_{\gamma _2}\left( \gamma _{th}\right) =P_{A_2}\left( \frac{N_0\gamma _{th}}{P_2-P_1\gamma _{th}}\right) \end{aligned}$$

(19)

where $P_{A_2}(x)$ is the Cumulative Distribution Function of $A_2$ given by

$$\begin{aligned} P_{A_2}(x)=P\left( A_2\le x\right) =P\left( -\sqrt{\frac{x}{2E_s\beta \beta _2}} \le W_2 \le \sqrt{\frac{x}{2E_s\beta \beta _2}}\right) \end{aligned}$$

(20)

Using the Central Limit Theorem (CLT), we approximate $A_i$ by a Gaussian r.v. with mean $m_{W_i}=\frac{N_i\pi }{4}$ and variance $\sigma _{W_i}^2=N_i(1-\frac{\pi ^2}{16})$ [1].

Therefore, we have

$$\begin{aligned} P_{A_2}(x)\simeq 0.5erfc\left( \frac{-\sqrt{\frac{N_0x}{2E_s\beta \beta _2}}-m_{W_2}}{\sqrt{2}\sigma _{W_2}}\right) \nonumber \\&-0.5erfc\left( \frac{\sqrt{\frac{N_0x}{2E_s\beta \beta _2}}-m_{W_2}}{\sqrt{2}\sigma _{W_2}}\right) \end{aligned}$$

(21)

There is no outage at user $U_1$ when SINRs $\gamma _{1\rightarrow 1}$ and $\gamma _{1\rightarrow 2}$ are larger than $\gamma _{th}$

$$\begin{aligned} P^{outage,1}\left( \gamma _{th}\right)&= P_{\gamma _1}\left( \gamma _{th}\right) =1-P\left( \gamma _{1\rightarrow 1}>\gamma _{th},\gamma _{1\rightarrow 2}>\gamma _{th}\right) \nonumber \\&= {} P_{A_1}\left( max\left[ \frac{N_0\gamma _{th}}{P_2-P_1\gamma _{th}},\frac{N_0\gamma _{th}}{P_1}\right] \right) , \end{aligned}$$

(22)

where $P_{A_1}(x)$ is the CDF of $A_1$ equal to

$$\begin{aligned} P_{A_1}(x) &\simeq 0.5erfc\,\left( \frac{-\sqrt{\frac{N_0x}{2E_s\beta \beta _1}}-m_{W_1}}{\sqrt{2}\sigma _{W_1}}\right) \nonumber \\&-0.5erfc\left( \frac{\sqrt{\frac{N_0x}{2E_s\beta \beta _1}}-m_{W_1}}{\sqrt{2}\sigma _{W_1}}\right) \end{aligned}$$

(23)

Let $\gamma _E$ be the SNR at Eavesdropper expressed as

$$\begin{aligned} \gamma _E=E_S\beta _E\frac{|t|^2}{N_0} \end{aligned}$$

(24)

For Rayleigh channels, $\gamma _E$ is exponentially distributed with PDF expressed as [21]

$$\begin{aligned} p_{\gamma _E}(x)=\frac{N_0e^{-\frac{xN_0}{E_S\beta _E}}}{E_S\beta _E} \end{aligned}$$

(25)

The secrecy capacity of the user $U_1$ is expressed as

$$\begin{aligned} C_1=0.5ln\left( \frac{1+\gamma _1}{1+\gamma _E}\right) \end{aligned}$$

(26)

where $\gamma _1$ is the SINR of user $U_1$ given in (16-18).

The Secrecy Outage Probability (SOP) of user $U_1$ is computed as

$$\begin{aligned} SOP&= {} P\left( C_1<R_1\right) =P\left( 0.5ln\left( \frac{1+\gamma _1}{1+\gamma _E}\right)<R_1\right) \nonumber \\&= {} P\left( 1+\gamma _1<\left[ 1+\gamma _E\right] e^{2R_1}\right) . \end{aligned}$$

(27)

where $R_1$ is the transmission rate of $U_1$.

We deduce the SOP as follows

$$\begin{aligned} SOP_1&= {} \int _0^{+\infty }P\left( \gamma _1<[1+x]e^{2R_1}-1\right) p_{\gamma _E}(x)dx\nonumber \\&= {} \int _0^{+\infty }P_{\gamma _1}\left( (1+x)e^{2R}-1\right) p_{\gamma _E}(x)dx. \end{aligned}$$

(28)

where $P_{\gamma _1}(x)$ is the CDF of SNR at $U_1$ given in (22) while $p_{\gamma _E}(x)$ is the PDF of SNR at eavesdropper given in (25).

The Probability of Strictly Positive Secrecy Capacity (SPSC) of user $U_1$ is computed as

$$\begin{aligned} SPSC_1&= {} P(C_1>0)=P\left( \gamma _1>\gamma _E\right) \nonumber \\&= {} \int _0^{+\infty }P\left( \gamma _1\ge x\right) p_{\gamma _E}(x)dx\nonumber \\&= {} \int _0^{+\infty }\left[ 1-P_{\gamma _1}(x)\right] p_{\gamma _E}(x)dx \end{aligned}$$

(29)

The secrecy capacity of user $U_2$ is expressed as

$$\begin{aligned} C_2=0.5ln\left( \frac{1+\gamma _2}{1+\gamma _E}\right) \end{aligned}$$

(30)

where $\gamma _2$ is the SINR at user $U_2$ given in (15).

Similarly, the SOP of user $U_2$ is computed as follows

$$\begin{aligned} SOP_2&= {} \int _0^{+\infty }P\left( \gamma _2<[1+x]e^{2R_2}-1\right) p_{\gamma _E}(x)dx \nonumber \\&= {} \int _0^{+\infty }P_{\gamma _2}\left( (1+x)e^{2R_2}-1\right) p_{\gamma _E}(x)dx. \end{aligned}$$

(31)

where $R_2$ is the rate of user $U_2$, $P_{\gamma _2}(x)$ is the CDF of SNR at $U_1$ given in (19) while $p_{\gamma _E}(x)$ is the PDF of SNR at eavesdropper given in (25).

The Probability of Strictly Positive Secrecy Capacity (SPSC) of user $U_2$ is computed as

$$\begin{aligned} SPSC_2&= {} P\left( C_2>0\right) =P\left( \gamma _1>\gamma _E\right) \nonumber \\&= {} \int _0^{+\infty }\left[ 1-P_{\gamma _2}(x)\right] p_{\gamma _E}(x)dx \end{aligned}$$

(32)

4 NOMA with Multiple Users Using RIS

Figure 2 shows the network model with K NOMA users. $N_i$ reflectors of RIS refelect signals to user $U_i$. The total number of RIS reflectors is $N=\sum _{i=1}N_i$. $I_i$ is the set of reflectors dedicated to user $U_i$. The BS transmits a linear combination of K symbols $s_1,s_2,...,s_K$ to K users:

$$\begin{aligned} s=\sum _{i=1}^K\sqrt{P_i}s_i, \end{aligned}$$

(33)

where $\sum _{i=1}^KP_i=1$ and $0<P_1<P_2<...<P_K<1$ are powers allocated to users $U_1$, $U_2$,...$U_K$.

Fig. 2

NOMA with K users using reconfigurable intelligent surfaces (RIS)

The received signal at $U_i$ is equal to

$$\begin{aligned} r_i=s\sqrt{KE_s\beta \beta _1} \sum _{k\in I_i}a_kc_k+n_i, \end{aligned}$$

(34)

We deduce

$$\begin{aligned} r_i&= {} s\sqrt{A_i}+n_i, \end{aligned}$$

(35)

where

$$\begin{aligned} A_i&= {} KE_s\beta \beta _2W_i^2, \end{aligned}$$

(36)

$$\begin{aligned} W_i&= {} \sum _{k\in I_i}a_kc_k, \end{aligned}$$

(37)

$U_i$ detects $s_K$ since $P_K>P_{K-1}>...>P_i$. The SINR at $U_i$ to detect $s_K$ is expressed as

$$\begin{aligned} \gamma _{i\rightarrow K}=\frac{A_iP_K}{N_0+A_i\sum _{j=1}^{K-1}P_j} \end{aligned}$$

(38)

$U_i$ removes the contribution of $s_K$ and detects $s_{K-1}$ with SINR

$$\begin{aligned} \gamma _{i\rightarrow K-1}=\frac{A_iP_{K-1}}{N_0+A_i\sum _{j=1}^{K-2}P_j} \end{aligned}$$

(39)

The process is continued until $U_i$ detects $s_i$. The SINR at $U_i$ to detect $s_q$, $i\le q\le K$, is expressed as

$$\begin{aligned} \gamma _{i\rightarrow q}=\frac{A_iP_{q}}{N_0+A_i\sum _{j=1}^{q-1}P_j}, i\le q\le K, \end{aligned}$$

(40)

There is no outage at $U_i$ if SINRs $\gamma _{i\rightarrow K}$, $\gamma _{i\rightarrow K-1}$,..., $\gamma _{i\rightarrow i}$ are greater than $\gamma _{th}$.

The SINR at $U_i$ is equal to

$$\begin{aligned} \gamma _i=min\left[ \gamma _{i\rightarrow K}, \gamma _{i\rightarrow K-1},..., \gamma _{i\rightarrow i}\right] \end{aligned}$$

(41)

We deduce the outage probability at $U_i$

$$\begin{aligned} P^{outage,i}\left( \gamma _{th}\right) =P_{\gamma _i}\left( \gamma _{th}\right) \nonumber \\&= {} 1-P\left( \gamma _{i\rightarrow K}>\gamma _{th},\gamma _{i\rightarrow K-1}>\gamma _{th},...,\gamma _{i\rightarrow i}>\gamma _{th}\right) \nonumber \\&= {} P_{A_i}\left( \underset{i\le q\le K}{max}\left( \frac{N_0\gamma _{th}}{P_q-\gamma _{th}\sum _{j=1}^{q-1}P_j}\right) \right) , \end{aligned}$$

(42)

where

$$\begin{aligned} P_{A_i}(x) & \simeq 0.5erfc\,\left( \frac{-\sqrt{\frac{N_0x}{KE_s\beta \beta _i}}-m_{W_i}}{\sqrt{2}\sigma _{W_i}}\right) \nonumber \\&-0.5erfc\left( \frac{\sqrt{\frac{N_0x}{KE_s\beta \beta _i}}-m_{W_i}}{\sqrt{2}\sigma _{W_i}}\right) \end{aligned}$$

(43)

The secrecy capacity of the user $U_i$ is expressed as

$$\begin{aligned} C_i=0.5ln\left( \frac{1+\gamma _i}{1+\gamma _E}\right) \end{aligned}$$

(44)

where $\gamma _i$ is the SINR at user $U_i$ defined as the minimum of SINRs of all detected symbols:

$$\begin{aligned} \gamma _i=min\left[ \gamma _{i\rightarrow K}, \gamma _{i\rightarrow K-1},..., \gamma _{i\rightarrow i}\right] \end{aligned}$$

(45)

Similarly, the SOP of user $U_i$ is computed as follows

$$\begin{aligned} SOP_i=\int _0^{+\infty }P_{\gamma _i}\left( (1+x)e^{2R_i}-1\right) p_{\gamma _E}(x)dx. \end{aligned}$$

(46)

where $R_i$ is the rate of user $U_i$, $P_{\gamma _i}(x)$ is the CDF of SNR at $U_i$ given in (42-43) while $p_{\gamma _E}(x)$ is the PDF of SNR at eavesdropper given in (25).

The Probability of Strictly Positive Secrecy Capacity (SPSC) is computed as

$$\begin{aligned} SPSC_i=\int _0^{+\infty }\left[ 1-P_{\gamma _i}(x)\right] p_{\gamma _E}(x)dx \end{aligned}$$

(47)

5 Theoretical and Simulation Results

Figures 3 and 4 depict the SOP at strong and weak users when there are two NOMA users. The distances are $d_1=1$, $d_2=1.5$ and $d_E=3$. The path loss exponent is three. We observe that the proposed RIS offers 22, 28 and 34 dB gain with respect to conventional NOMA without RIS for a number of reflectors $N_1=N_2=8,16,32$. We notice a good accordance between theoretical and simulation results.

Fig. 3

SOP of strong user: NOMA with two users

Fig. 4

SOP of weak user: NOMA with two users

Figures 5, 6 and 7 depict the SOP at three NOMA users located at $d_1=0.8$, $d_2=1$ and $d_3=1.5$. The Eavesdropper is located at $d_E=3$. We observe a significant enhancement on the physical layer security of NOMA using RIS. RIS offers 20, 30 dB gain with respect to conventional NOMA without RIS for a number of reflectors $N_1=N_2=N_3=8,16$.

Fig. 5

SOP of strongest user: NOMA with three users

Fig. 6

SOP of middle user; NOMA with three users

Fig. 7

SOP of weak user : NOMA with three users

Figures 8and 9 depict the SPSC for NOMA with and without RIS when there are two users. The distances are $d_1=1$, $d_2=1.5$ and $d_E=3$. We notice that RIS improves the physical layer security of NOMA systems.

Fig. 8

SPSC of strong user : NOMA with two users

Fig. 9

SPSC of weak user : NOMA with two users

6 Comparison with Current Literature

The main contribution of the paper is to improve the physical layer security of NOMA systems using RIS. We derived both the Secrecy Outage Probability (SOP) and the Strictly Positive Secrecy Capacity (SPSC) of NOMA using RIS. When there are two users, the proposed RIS improves the physical layer security by 22, 28 and 34 dB with respect to conventional NOMA without RIS [11, 12] for a number of reflectors $N_1=N_2=8,16,32$. When there are three users, RIS offers 20, 30 dB gain with respect to conventional NOMA without RIS [11, 12] for a number of reflectors $N_1=N_2=N_3=8,16$ per user.

7 Conclusions

In this paper, we improved the physical layer security of NOMA systems using Reconfigurable Intelligent Surfaces (RIS). When RIS is employed, the base station can reduce its power since all reflected signals have the phase phase at different NOMA users. We have compared the SOP and SPSC of NOMA systems when RIS is deployed to conventional NOMA without RIS. We have shown that the use of RIS improve the security of NOMA systems by 20-30 dB with respect to conventional wireless systems without RIS [10,11,12,13].