1 Introduction

In the past two decades, a great deal of attention is devoted by the researchers to the area of uncertain nonlinear discrete-time systems such as robot manipulators, servo motor, and underwater vehicle systems [1,2,3]. Due to the development of technology control devices and objects are becoming more complex and not possible to control via a linear control model [4, 5]. Therefore the control of nonlinear systems is becoming much more challengeable since not all states are measurable and it becomes more difficult in the presence of disturbances and hence drawing a lot of attention from researchers [6,7,8,9]. Due to uncertainty and disturbances, it has been acknowledged that the methodologies to control uncertain nonlinear systems are comparatively more difficult than the linear control [10]. Bounded disturbances often exist in many practical problems and become the cause of the instability of control systems. Therefore, designing an efficient control scheme and its stability attract the attention of researchers. However, due to limitations in modeling, measurement and observations many physical systems are affected by parameter uncertainties.

Uncertain systems appear very often in the numerous practical plants, in this connection the adaptive neural network (ANN) control and the control based on fuzzy logic systems (FLS) have achieved extensive accomplishments and improvements to approximate nonlinear functions present in such systems [11,12,13,14]. Many methods were developed like back-stepping, sliding mode control, observer-based system, and robust control which are used to tackle such nonlinear systems [15,16,17,18]. An adaptive tracking control methodology was discussed for uncertain nonlinear single-input and single-output (SISO) systems [19] and multi-input and multi-output (MIMO) systems in [17, 20, 21]. Tracking control of uncertain systems is more difficult in presence of diverse forces which may interfere with the systems [22]. Among many diverse forces, the dead zone is one force that is symmetric and asymmetric in nature [23]. Adaptive tracking control is developed for switching systems with non-symmetric dead-zone [24], in addition to this, observer-based adaptive control and some fuzzy based adaptive control techniques addressing nonlinear systems with discrete-time and bounded disturbances with dead-zone are presented in [25,26,27,28] while nonlinear time-delay problem with unknown nonlinear dead-zone is presented in [27, 29, 30].

In the assessment with continuous systems, discrete-time systems have more practical consequences. Although a large number of the real-time processes are continuous in nature, they are demonstrated mostly utilizing discrete-time as they are effectively feasible [31]. Keeping into view this advantage, the discrete-time systems are taken into consideration. Many adaptive control techniques were developed to approximate the unknown functions for nonlinear discrete-time systems [23, 30, 32, 33]. The time-changing parameters in the systems may cause major challenges in tracking performance. Another important issue is time-delay input for nonlinear systems which usually makes a system complicated. Back-stepping based adaptive control design employing intelligent systems like neural networks or fuzzy logic systems (FLS) gives more fruitful results for nonlinear systems [17, 34,35,36].

Motivated by the aforementioned discussion, it has been noticed that an adaptive control strategy based on NN or FLS, ensured the basic system stability, but how to attain the preferred trajectory remains to be studied additionally. To enhance the theory of adaptive control, especially for nonlinear systems with discrete-time, we propose an adaptive controller for uncertain nonlinear systems with discrete-time on the basis of a hybrid neural network. In the proposed hybrid neural network controller, we use the evolutionary differential evolution method to initialize the weight and biases of the neural network with mean square error (MSE) as the fitness function. In this work, we address HNN adaptive controller to attain the reference signal for uncertain nonlinear systems with discrete-time having bounded disturbances and immersion of utterly unknown functions.

The primary endowments of this work are summed up as follows:

  1. (1)

    An evolutionary method named differential evolution is used for the initialization of the weight vector of the neural network. Employing the HNN and feedback approach, the proposed control scheme is capable of successfully tracking the reference signal. The considered adaptive HNN is used to approximate unknown functions involving dead-zone.

  2. (2)

    The proposed adaptive control scheme surmounts the requirements of affine form and linear parametric situation, i.e. it is not required to be assumed that the nonlinear uncertainties are needed to be linear with unknown parameters.

  3. (3)

    By the use of the Lyapunov method, the semi-global uniformly ultimate boundedness (SGUUB) of the system is verified. The unknown functions are be approximated by the proposed HNN controller and the error signal converges in a compact set containing zero, which is shown and verified by the using simulation examples.

The remaining part of this paper has been structured in the following manner. The formulation of the problem for uncertain nonlinear systems with discrete-time having dead-zone and preliminaries is presented in Sect. 2. In Sect. 3, the HNN controller is discussed, and Sect. 4 deals with the stability analysis of the system using the Lyapunov method. Section 5 provides the simulation results and description, and the conclusion of this paper carries out in Sect. 6.

Notation: Following are the notations that will be used throughout this paper.

In the whole of the article, all work is done using standard notations. \({\mathfrak{R}}^{m}\) denotes an m-dimensional Euclidean space; \(\overline{\zeta }_{i} (k)\) stands for the ith state of the system and \(\overline{\zeta }_{i} (k) = \left[ {\zeta_{1} (k),\,\zeta_{2} (k),\, \cdots \,,\,\zeta_{i} (k)} \right]^{T} \in \Re^{i}\) represents state vector where T is the transpose of vector/matrix and \({\overline{}}_{s}\left(\mathrm{k}\right)\) be the supremum of \(\zeta\)\(\left(\bullet \right)\); \(\varepsilon \left(k\right)\) represents tracking error; \(\varepsilon \left(\right)\) represents approximation error for NN and \(\varepsilon\) is a constant. \(y\left(k\right)\) and \({y}_{d}(k)\) represents obtained and the desired trajectory respectively.

2 Problem Formulation and Preliminaries

Let us take into consideration the under mentioned nonlinear stochastic pure-feedback systems as follows:

$$\left\{ \begin{gathered} \zeta_{1} (k + 1) = \,\psi_{1} \left( {\zeta_{1} (k)} \right) + \phi_{1} \left( {\zeta_{1} (k)} \right)\zeta_{2} (k) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \hfill \\ \zeta_{n - 1} (k + 1) = \,\psi_{n - 1} \left( {\zeta_{1} (k), \cdots ,\zeta_{n - 1} (k)} \right) + \phi_{n - 1} \left( {\zeta_{1} (k), \cdots ,\zeta_{n - 1} (k)} \right)\zeta_{n} (k) \hfill \\ \zeta_{n} (k + 1) = \psi_{n} \left( {\zeta_{1} (k), \cdots ,\zeta_{n} (k)} \right) + \phi_{n} \left( {\zeta_{1} (k), \cdots ,\zeta_{n} (k)} \right)\tau (k) + d(k) \hfill \\ y(k) = \zeta_{1} (k) \hfill \\ \end{gathered} \right.$$
(1)

where, \(\overline{\zeta }_{i} (k) = \left[ {\zeta_{1} (k),\,\zeta_{2} (k),\, \cdots \,,\,\zeta_{i} (k)} \right]^{T} \in \Re^{i}\), where \(i = 1,2,\, \cdots \,,\,n\),\(\tau (k) \in \,\,\Re\) and \(y(k) \in \,\,\Re\) be the state vector, input and output of the system respectively;\(d(k) \in \,\Re^{m} \,\) stand for external bounded disturbances such that \(\left\| {d(k)} \right\|\, \le d_{M}\), and \(\psi_{i} (\zeta (k));\,\forall i = 1,2, \cdots ,n\) and \(\phi_{i} (\zeta (k));\forall i = 1,2, \cdots ,n\) are unknown smooth and bounded functions with all its partial derivatives are also continuous. The dead zone function \(\tau (k)\) in Eq. (1) is defined as:

$$\tau (k) = \left\{ \begin{gathered} \varphi_{r} (\upsilon (k)):\,\,\,\,\upsilon (k) \ge b_{r} \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,:\,\,\,\,b_{l} < \upsilon (k) < b_{r} \hfill \\ \varphi_{l} (\upsilon (k)):\,\,\,\,\upsilon (k) \le - b_{l} \hfill \\ \end{gathered} \right.$$
(2)

where\(\upsilon (k) \in \Re\) is known as dead zone for the input, \(b_{l} < 0\) and \(b_{r} > 0\) be the unknown dead zone parameters while \(\varphi_{r}\) and \(\varphi_{l}\) are the unknown smooth nonlinear function. The functions \(\varphi_{r} (\upsilon (k))\) and \(\varphi_{l} (\upsilon (k))\) are smooth functions.

$$\tau (k) = \left[ {C_{r} (\upsilon (k)),\,C_{l} (\upsilon (k))} \right]\,\left[ {\hbar_{r} (\upsilon (k)),\,\hbar_{l} (\upsilon (k))} \right]^{T} \upsilon (k) + \,p(\upsilon (k))$$
(3)

where

$$C_{r} (\upsilon (k)) = \left\{ \begin{gathered} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\upsilon (k) \le b_{l} \,\,\,\, \hfill \\ \varphi_{{_{r} }}^{^{\prime}} (b_{r} ),\,\,\,\,\,\,\,\,\,\,b_{l} \, < \upsilon (k) < b_{r} \,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \varphi_{{_{r} }}^{^{\prime}} (\eta_{r} (\upsilon (k))),\,\,b_{r} \, \le \upsilon (k) < \infty \hfill \\ \end{gathered} \right.,\;\;C_{l} (\upsilon (k)) = \left\{ \begin{gathered} \varphi_{l}^{^{\prime}} (\eta_{l} (\upsilon (k))),\,\, - \infty < \upsilon (k) \le b_{l} \hfill \\ \varphi_{{_{l} }}^{^{\prime}} (b_{l} ),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b_{l} < \upsilon (k) < b_{r} \,\,\,\, \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\upsilon (k) \ge b_{r} \,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right.$$
$$\hbar_{r} (\upsilon (k)) = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\upsilon (k) > b_{l} \,\,\, \hfill \\ 0,\,\,\,\,\,\,\upsilon (k) \le b_{l} \,\, \hfill \\ \end{gathered} \right.,\;\;\hbar_{l} (\upsilon (k)) = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\upsilon (k) < b_{r} \,\,\, \hfill \\ 0,\,\,\,\,\,\,\upsilon (k) \ge b_{r} \,\, \hfill \\ \end{gathered} \right.\,\,,\;\;\eta_{r} (\upsilon (k) \in (b_{r} ,\infty )\;\;{\text{and}}\;\;\eta_{l} (\upsilon (k) \in ( - \infty ,b_{l} )$$

Let \(y_{d} (k)\) be the reference signal for the system (1) and \(y(k)\) is the calculated output of the system (1). Then our objective is to minimize the usual quadratic cost function given in (4):

$$E = \frac{1}{2}\sum\limits_{k = 1}^{n} {\left( {y(k) - y_{d} (k)} \right)^{2} }$$
(4)

Definition

[37]

The Nussbaum gain \(N\left( {\zeta (k)} \right)\) of a discrete sequence \(\left\{ {\zeta (k)} \right\}\) for discrete time satisfy following properties:

$$\zeta (0) = 0,\;\;\zeta (k) \ge 0\;\;{\text{and}}\;\;\Delta \zeta (k) = \left| {\zeta (k + 1) - \zeta (k)} \right| < \varepsilon ;\forall k$$

where,\(\varepsilon\) is constant.

Then \(N\left( {\zeta (k)} \right)\) defined as follows:

$$N\left( {\zeta (k)} \right) = \zeta_{s} (k)H\left( {\zeta (k)} \right)$$
(5)

where, \(\zeta_{s} (k) = \mathop {\sup }\limits_{k^{\prime} \le k} \left\{ {\zeta (k^{\prime})} \right\}\) and \(H\left( {\zeta (k)} \right)\) is defined as:

$$H\left( {\zeta (0)} \right) = 1\;\;{\text{for}}\;\;k = k_{1}$$
$${\text{If}}\;\;H\left( {\zeta (k_{1} )} \right) = 1,\;{\text{then if}}\;\;\sum\limits_{k^{\prime} = 0}^{{k_{1} }} {N\left( {\zeta (k^{\prime})} \right)} \,\Delta \zeta (k^{\prime}) > \zeta_{{_{s} }}^{3/2} (k_{1} )$$

In this case, \(H\left( {\zeta (k_{1} + 1)} \right) = - 1\;\;{\text{otherwise}}\;\;H\left( {\zeta (k_{1} + 1)} \right) = 1\).

If \(H\left( {\zeta (k_{1} )} \right) = - 1\), then if \(\sum\limits_{k^{\prime} = 0}^{{k_{1} }} {N\left( {\zeta (k^{\prime})} \right)} \,\Delta \zeta (k^{\prime}) < - \zeta_{{_{s} }}^{3/2} (k_{1} )\).

In this case, \(H\left( {\zeta (k_{1} + 1)} \right) = 1\;\;{\text{otherwise}}\;\;H\left( {\zeta (k_{1} + 1)} \right) = - 1\).

Result [37] If \(\zeta_{s} (k)\) holds uniform boundedness, then same is true for \(\left| {H\left( {\zeta (k)} \right)} \right|\) and if \(\zeta_{s} (k)\) is unbounded then \(\left| {H\left( {\zeta (k)} \right)} \right|\) oscillates between -∞ and + ∞. Using this result we establish lemma 1.

Lemma 1

[37] If the function \(V(\zeta )\) is such that it is positive definite and \(N(\zeta )\) is Nussbaum gain defined in Eq. (5) and if inequality (6) holds:

$$V(k) \le \sum\limits_{k^{\prime} = 0}^{{k_{1} }} {\left( {c_{1} + \lambda N\left( {\zeta (k^{\prime})} \right)} \right)} \Delta \zeta (k^{\prime}) + c_{2} \zeta (k) + c_{3}$$
(6)

where \(c_{1}\), \(c_{2}\) and \(c_{3}\) are constants then \(V(k)\),\(\zeta (k)\) and RHS of Eq. (6) must be bounded.

NN Approximation

In the control theory, there are several well-formulated methods for unknown function approximations namely the polynomial method, fuzzy logic, and neural network, etc. In this work we use a neural network as an unknown function approximator. The basic universal approximation result says that any smooth function \(\psi (\zeta )\) can be approximated arbitrarily on a closed compact set with appropriate weight adjustment using NN. If \(\psi (\zeta )\) be an unknown smooth function can be written as:

$$\psi (\xi ) = W^{T} \sigma \left( \xi \right) + \varepsilon (\xi )$$
(7)

where, \(\varepsilon (\xi )\) is known as NN function approximation error and bounded by \(\overline{\varepsilon }\) i.e. \(\left\| {\varepsilon (\xi )} \right\| \le \overline{\varepsilon }\). The error function defined in Eq. (3) can be minimized via choosing optimal weight vector \(W\), for this let us consider Lyapunov function as:

$$V = \frac{1}{2}e(k)e^{T} (k)$$
(8)

where \(e(k) = y(k) - y_{d} (k)\) and Lyapunov function defined above is same as the usual quadratic cost function. The derivative of Eq. (8) is given by:

$$\dot{V} = - e^{T} \frac{\partial e}{{\partial W}}\dot{W}\;\;{\text{or}}\;\;\dot{V} = - e^{T} J\dot{W}$$
(9)

where \(J = \frac{\partial e}{{\partial W}}.\) If arbitrary initial weight \(W(0)\) is updated by the rule

$$W(t_{1} ) = W(0) + \int\limits_{0}^{{t_{1} }} {\dot{W}dt} \dot{W} = \frac{{\left\| e \right\|^{2} }}{{\left\| {J^{T} e} \right\|^{2} }}J^{T} e$$
(10)

where error \(e\) converges to zero under the condition that \(\dot{W}\) exist along the convergence trajectory. Using Eq. (10), Eq. (6) yields: \(\dot{V} = - \left\| e \right\|^{2} \le 0\) and \(\dot{V} < 0\) if \(e \ne 0\). The difference equation representation of weight updating algorithm based on Eq. (10) is given by:

$$W(t + 1) = W(t) + \alpha \dot{W}(t)$$
(11)

where\(\alpha\) is known as learning rate.

The structure of the hybrid neural network proposed in this work can be seen in Fig. 1, where \(\left[ {x_{1} , \, x_{2} , \, ..., \, x_{n} } \right]\) is the input state vector and \(\left[ {y_{1} , \, y_{2} , \, ..., \, y_{m} } \right]\) is the initial weight matrix defined by using differential evolution, \(\sigma\) is the activation function and \(V_{jk}\) is the weight matrix from hidden to output layer and \(\left[ {y_{1} , \, y_{2} , \, ..., \, y_{m} } \right]\) is the output vector.

Fig. 1
figure 1

Neural network

Full size image

3 Adaptive Controller Design

In this part of paper, we will use pure feedback technique to design an adaptive controller \(\tau (k)\) in Eq. (1) or \(\upsilon (k)\) which is defined in Eq. (3). The detail system transformation, design procedure and stability analysis are described below:

Step 1: Let first design the virtual controller \(\upsilon (k)\) as defined in Eq. (3), start the virtual control design to stabilize the first part of Eq. (1) as follows:

$$\zeta_{2\psi } (k) = - \frac{1}{{\phi_{1} \left( {\zeta_{1} (k)} \right)}}\left[ {\psi_{1} \left( {\zeta_{1} (k)} \right) - y_{r} (k + 1)} \right]$$
(12)

Similarly the virtual control design to stabilize the second part of Eq. (1) as follows:

$$\zeta_{3\psi } (k) = - \frac{1}{{\phi_{2} \left( {\zeta_{1} (k),\zeta_{2} (k)} \right)}}\left[ {\psi_{2} \left( {\zeta_{1} (k),\zeta_{2} (k)} \right) - \zeta_{2\psi } (k + 1)} \right]$$
(13)

Repeat the above procedure to get the final control \(\tau (k)\), by examine the first (n-1) equation of system (1). For this let us denote:

$$\zeta_{i} (k + 1) = \,\rho_{i} \left( {\zeta_{i + 1} (k)} \right);\,\forall i = 1, \cdots ,n - 2$$
(14)

where\(\rho_{i} \left( {\overline{\zeta }_{i + 1} (k)} \right) = \psi_{i} \left( {\zeta_{1} (k + 1),\, \cdots ,\zeta_{i} (k + 1)} \right) + \phi_{i} \left( {\zeta_{1} (k + 1),\, \cdots ,\zeta_{i} (k + 1)} \right)\zeta_{i + 1} (k + 1)\)

Therefore:

$$\overline{\zeta }_{i} (k + 1) = \left[ \begin{gathered} \zeta_{1} (k + 1) \hfill \\ \,\,\,\,\,\,\, \vdots \hfill \\ \zeta_{i} (k + 1) \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \rho_{1} \left( {\overline{\zeta }_{1 + 1} (k)} \right) \hfill \\ \,\,\,\,\,\,\, \vdots \hfill \\ \rho_{i} \left( {\overline{\zeta }_{i + 1} (k)} \right) \hfill \\ \end{gathered} \right] = \Psi_{i} \left( {\overline{\zeta }_{i + 1} (k)} \right) \in \Re^{i} ;\,\forall i = 1,2, \cdots ,n - 1$$

After moving one step ahead system (1) can be expressed as:

$$\begin{gathered} \zeta_{i} (k + 2) = \,\psi_{i} \left( {\zeta_{1} (k + 1),\, \cdots ,\zeta_{i} (k + 1)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \quad + \phi_{i} \left( {\zeta_{1} (k + 1),\, \ldots ,\zeta_{i} (k + 1)} \right) \times \zeta_{i + 1} (k + 1);\,\forall i = 1, \ldots ,n - 2 \hfill \\ \end{gathered}$$
(15)
$$\zeta_{n - 1} (k + 2) = \,\psi_{n - 1} \left( {\zeta_{1} (k + 1),\, \ldots ,\zeta_{n - 1} (k + 1)} \right) + \phi_{n - 1} \left( {\zeta_{1} (k + 1),\, \ldots ,\zeta_{n - 1} (k + 1)} \right) \times \zeta_{n} (k + 1)$$
(16)

Equations (15, 16) can be rewritten as:

$$\begin{aligned} \zeta_{i} (k + 2) &= \,\rho_{i} \left( {\overline{\zeta }_{i + 2} (k)} \right);\;\;{\text{for all}}\;\;i = 1, \cdot ,n - 2 \\ \zeta_{n - 1} (k + 2) &= \,\Psi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right) + \Phi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right) \times \zeta_{n} (k + 1)\end{aligned}$$
(17)

where

$$\begin{aligned} \rho_{i} \left( {\overline{\zeta }_{i + 2} (k)} \right) &= \psi_{i} \left( {\Psi_{i} \left( {\overline{\zeta }_{i + 1} (k)} \right)} \right) + \varphi_{i} \left( {\Psi_{i} \left( {\overline{\zeta }_{i + 1} (k)} \right)} \right) \times \rho_{i + 1} \left( {\overline{\zeta }_{i + 2} (k)} \right), \\ \Psi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right) &= \psi_{n - 1} \left( {\Psi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right)} \right), \quad \Phi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right) = \varphi_{n - 1} \left( {\Psi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right)} \right)\end{aligned}$$

Using Eq. (15) and moving one step ahead the first (n-2) terms at the (k + 2)th step in (17) we have:

$$\overline{\zeta }_{i} (k + 2) = \left[ \begin{aligned} \zeta_{1} (k + 2) \hfill \\ \,\,\,\,\,\,\, \vdots \hfill \\ \zeta_{i} (k + 2) \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} \rho_{1} \left( {\overline{\zeta }_{1 + 1} (k + 1)} \right) \hfill \\ \,\,\,\,\,\,\, \vdots \hfill \\ \rho_{i + 1} \left( {\overline{\zeta }_{i + 1} (k + 1)} \right) \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} \rho_{1} \left( {\Psi_{2} \left( {\overline{\zeta }_{3} (k)} \right)} \right) \hfill \\ \,\,\,\,\,\,\, \vdots \hfill \\ \rho_{i} \left( {\Psi_{i + 1} \left( {\overline{\zeta }_{i + 2} (k)} \right)} \right) \hfill \\ \end{aligned} \right]$$

From Eq. (15) it is clear that

$$\overline{\zeta }_{i} (k + 2) = \Psi_{i} \left( {\overline{\zeta }_{i + 2} (k)} \right);\,{\text{for all}}\;\;i = 1,2, \cdots ,n - 2$$
(18)

Similar way to above process, we have

$$\begin{aligned} \zeta_{1} (k + n - 1) &= \rho_{1} \left( {\overline{\zeta }_{n} (k)} \right) \\ \zeta_{2} (k + n - 1) &= \,\Psi_{2} \left( {\overline{\zeta }_{n} (k)} \right) + \Phi_{2} \left( {\overline{\zeta }_{n} (k)} \right) \times \zeta_{3} (k + n - 2)\end{aligned}$$
(19)

where \(\rho_{1} \left( {\overline{\zeta }_{n} (k)} \right) = \psi_{1} \left( {\Psi_{1} \left( {\overline{\zeta }_{n - 1} (k)} \right)} \right) + \varphi_{1} \left( {\Psi_{1} \left( {\overline{\zeta }_{n - 1} (k)} \right)} \right) \times \psi_{2} \left( {\overline{\zeta }_{n} (k)} \right)\) and

$$\Psi_{2} \left( {\overline{\zeta }_{n} (k)} \right) = \psi_{2} \left( {\Psi_{2} \left( {\overline{\zeta }_{n} (k)} \right)} \right)$$
$$\Phi_{2} \left( {\overline{\zeta }_{n} (k)} \right) = \varphi_{2} \left( {\Psi_{2} \left( {\overline{\zeta }_{n} (k)} \right)} \right)$$

Now at the nth step, we have

$$\zeta_{1} (k + n) = \,\Psi_{1} \left( {\overline{\zeta }_{n} (k)} \right) + \Phi_{1} \left( {\overline{\zeta }_{n} (k)} \right)\zeta_{2} (k + n - 1)$$
(20)

where \(\Psi_{1} \left( {\overline{\zeta }_{n} (k)} \right) = \psi_{1} \left( {\rho_{1} \left( {\overline{\zeta }_{n} (k)} \right)} \right)\;\;{\text{and}}\;\;\Phi_{1} \left( {\overline{\zeta }_{n} (k)} \right) = \varphi_{1} \left( {\rho_{1} \left( {\overline{\zeta }_{n} (k)} \right)} \right)\).

From Eqs. (16) to (20), Eq. (1) can be re-casted as:

$$\left\{ \begin{gathered} \zeta_{1} (k + n) = \,\Psi_{1} \left( {\overline{\zeta }_{n} (k)} \right) + \Phi_{1} \left( {\overline{\zeta }_{n} (k)} \right) \times \zeta_{2} (k + n - 1) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \hfill \\ \zeta_{n - 1} (k + 2) = \,\Psi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right) + \Phi_{n - 1} \left( {\overline{\zeta }_{n} (k)} \right) \times \zeta_{n} (k + 1) \hfill \\ \zeta_{n} (k + 1) = \psi_{n} \left( {\overline{\zeta }_{n} (k)} \right) + \phi_{n} \left( {\overline{\zeta }_{n} (k)} \right) \times \tau (k) + d(k) \hfill \\ y(k + n) = \zeta_{1} (k + n) \hfill \\ \end{gathered} \right.$$
(21)

From Eq. (19) to (20), we have

$$\zeta_{1} (k + n) = \,\Psi_{1} (k) + \Psi_{2} (k) \times \Phi_{1} (k) + \Phi_{1} (k) \times \Phi_{2} (k) \times \zeta_{3} (k + n - 2)$$
(22)

Repeating above process, until \(\tau (k)\) appears

$$\zeta_{1} (k + n) = \,\Psi \left( {\overline{\zeta }_{m} (k)} \right) + \Phi \left( {\overline{\zeta }_{m} (k)} \right) \times \tau (k) + d_{1} (k)$$
(23)

where \(\Psi \left( {\overline{\zeta }_{m} (k)} \right) = \Psi_{1} (k) + \Psi_{2} (k) \times \Phi_{1} (k) + \cdots + \Psi_{n - 1} (k) \times \prod\limits_{i = 1}^{n - 2} {\Phi_{j} (k)} + \psi_{n} (k) \times \prod\limits_{i = 1}^{n - 2} {\Phi_{j} (k)}\)

$$\Phi \left( {\overline{\zeta }_{m} (k)} \right) = \varphi_{n} (k) \times \prod\limits_{i = 1}^{n - 1} {\Phi_{j} (k)}$$
$$d_{1} (k) = d(k) \times \prod\limits_{i = 1}^{n - 1} {\Phi_{j} (k)}$$

Then the output of the re-casted system is given as:

$$y(k + n) = \,\Psi \left( {\overline{\zeta }_{m} (k)} \right) + \Phi \left( {\overline{\zeta }_{m} (k)} \right) \times \tau (k) + d_{1} (k)$$
(24)

Let us define tracking error \(\varepsilon (k) = y(k) - y_{d} (k)\), from Eq. (24) error is:

$$\varepsilon (k + n) = \,\Psi \left( {\overline{\zeta }_{m} (k)} \right) + \Phi \left( {\overline{\zeta }_{m} (k)} \right)\tau (k) + d_{1} (k) - y_{d} (k + n)$$
(25)

Since, the dead zone \(\tau (k)\) defined in Eq. (2) is containing unknown variables, therefore \(\tau (k)\) can be used for controller in terms of Eq. (3):

$$\varepsilon (k + n) = \,\Psi \left( {\overline{\zeta }_{m} (k)} \right) + \Phi \left( {\overline{\zeta }_{m} (k)} \right)\left[ {C^{T} (\upsilon (k))\hbar_{r} (\upsilon (k))\upsilon (k) + \,p(\upsilon (k))} \right] + d_{1} (k) - y_{d} (k + n)$$
(26)

where, \(C^{T} (\upsilon (k)) = \left[ {C_{r} (\upsilon (k)),\,C_{l} (\upsilon (k))} \right]\).

For simplification let us denote:

$$\Gamma \left( {\overline{\zeta }_{m} (k),\upsilon (k)} \right) = \Psi \left( {\overline{\zeta }_{m} (k)} \right) + \Phi \left( {\overline{\zeta }_{m} (k)} \right) \times C^{T} (\upsilon (k)) \times \hbar_{r} (\upsilon (k))\upsilon (k)$$

Then Eq. (26) becomes

$$\varepsilon (k + n) = \,\Gamma \left( {\overline{\zeta }_{m} (k),\upsilon (k)} \right) - y_{d} (k + n) + \Phi \left( {\overline{\zeta }_{m} (k)} \right) \times p(\upsilon (k)) + d_{1} (k)$$
(27)

By using implicit theorem, find the required control input \(\upsilon^{*} (k)\) such that following holds

$$\Gamma \left( {\upsilon^{*} (k),\overline{\zeta }_{m} (k)} \right) - y_{d} (k + n) = 0$$
(28)

With the neural network approximation as in Eq. (7), we get

$$\upsilon^{*} (k) = W^{*T} \sigma \left( {\upsilon (k)} \right) + \varepsilon^{*} (\upsilon (k))$$
(29)

where,\(\sigma \left( {\upsilon (k)} \right)\) is the bounded input to the hidden layer and \(\varepsilon^{*} (\upsilon (k))\) error after approximation which is to be minimized, for this let us assume \(\hat{W}\) is the approximation of \(W^{*}\) and \(\overline{W} = \hat{W} - W^{*}\). Using this construct HNN controller for \(\upsilon (k)\) as

$$\upsilon (k) = \hat{W}^{T} \sigma \left( {\upsilon (k)} \right) + \hat{\varepsilon }(\upsilon (k))$$
(30)

where, \(\hat{\varepsilon }\) is the estimation of \(\varepsilon^{*}\) and \(\overline{\varepsilon } = \hat{\varepsilon } - \varepsilon^{*}\). Using mean value theorem and Eq. (28), (27) can be further written as:

$$\begin{gathered} \varepsilon (k + n) = \,\Gamma \left( {\overline{\zeta }_{m} (k),\upsilon (k)} \right) - \Gamma \left( {\overline{\zeta }_{m} (k),\upsilon^{*} (k)} \right) + d_{1} (k) + \Phi \left( {\overline{\zeta }_{m} (k)} \right)p(\upsilon (k)) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad= \,g\left( {\overline{\zeta }_{m} (k),\upsilon^{\# } (k)} \right)\left( {\upsilon (k) - \upsilon^{\# } (k)} \right) + d_{1} (k) + \Phi \left( {\overline{\zeta }_{m} (k)} \right)p(\upsilon (k)) \hfill \\ \end{gathered}$$
(31)

where \(\upsilon^{\# } (k) \in \left[ {\min \left\{ {\upsilon^{*} (k),\upsilon (k)} \right\},\,\max \left\{ {\upsilon^{*} (k),\upsilon (k)} \right\}} \right]\)

Using Eqs. (29, 30, 31) becomes.

$$\begin{gathered} \varepsilon (k + n) = \,g\left( {\overline{\zeta }_{m} (k),\upsilon^{\# } (k)} \right) \times \left( {\overline{W}^{T} \sigma \left( {\upsilon (k)} \right) + \hat{\varepsilon }(\upsilon (k)) - \overline{\varepsilon }(\upsilon (k))} \right) + \tau_{1} (k) + \Phi \left( {\overline{\zeta }_{m} (k)} \right) \times p(\upsilon (k)) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ = \,g\left( {\overline{\zeta }_{m} (k),\upsilon^{\# } (k)} \right) \times \left( {\pi (k) + \varepsilon^{*} (\upsilon (k))} \right) + d_{0} (k) \hfill \\ \end{gathered}$$

where \(\pi (k) = \overline{W}^{T} \sigma \left( {\upsilon (k)} \right)\;{\text{and}}\;d_{0} (k) = g\left( {\upsilon^{\# } (k),\overline{\zeta }_{m} (k)} \right) \times \overline{\varepsilon }(\upsilon (k)) + d_{1} (k) + \Phi \left( {\overline{\zeta }_{m} (k)} \right)p(\upsilon (k))\).

Now, the parameter adjustment regulation are designed as

$$\hat{W}\left( {k + 1} \right) = \hat{W}\left( {k_{1} } \right) - \kappa N\left( {\zeta (k)} \right)\sigma \left( {\upsilon (k_{1} )} \right)\frac{\alpha (k)\chi (k + 1)}{{B(k)}}$$
(32)
$$\hat{\varepsilon }\left( {k + 1} \right) = \hat{\varepsilon }\left( {k_{1} } \right) - \left( {\chi (k + 1)} \right) \times \kappa \frac{{N\left( {\zeta (k)} \right) \times \alpha (k)}}{B(k)}$$
(33)

where, \(\kappa\) is positive adaptation gain constant, \(\alpha (k)\) is augmented error and \(k_{1} = k - n + 1\).

$$\chi (k + 1) = \kappa \left( {\frac{\varepsilon (k + 1)}{{1 + \left| {N\left( {\zeta (k)} \right)} \right|}}} \right)$$
$$B(k) = 1 + \chi^{2} (k + 1) + \left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\| + N\left( {\zeta (k)} \right)$$
$$\alpha (k) = \left\{ \begin{gathered} 1,\,\,\,\left| {\chi (k + 1)} \right| > \kappa \hfill \\ 0,\,\,otherwise \hfill \\ \end{gathered} \right.$$

\(\Delta \zeta (k) = \zeta (k + 1) - \zeta (k) = \frac{{\alpha (k) \times \left( {1 + \left| {N\left( {\zeta (k)} \right)} \right|} \right) \times \chi^{2} (k + 1)}}{B(k)}\). For the design of controller, the sequence \(\left\{ {\zeta (k)} \right\}\) must satisfy \(\zeta (0) = 0,\) \(\zeta (k) \ge 0\) and \(\Delta \zeta (k) = \left| {\zeta (k + 1) - \zeta (k)} \right| < \varepsilon ;\) for all k.

The overall working of the control process can be well understood through Figs. 2 and 3.

Fig. 2
figure 2

Working process of the Controller

Full size image
Fig. 3
figure 3

Flow Chart for the Algorithm

Full size image

Algorithm

A step-by-step procedure of detailed implementation of the controller is as follows:

  1. 1.

    Select initial state and parameters.

  2. 2.

    Construct HNN and evaluate error, y(k) – yd(k).

  3. 3.

    Update the weight. Calculate the controller and construct equation

  4. 4.

    Use the controller υ(k) for the given system.

  5. 5.

    Go to step 3 for next updation.

4 Analysis of Stability

Theorem: If a nonlinear system of the type (1) with dead zone. To construct the HNN controller with parameter adaption law defined in Eqs. (32, 33) with appropriate design parameters, the feedback systems guarantee that system possess semi-global uniformly ultimate boundedness.

Proof: Let us consider the Lyapunov function:

$$V\left( k \right) = V_{1} \left( k \right) + V_{2} \left( k \right)$$

where, \(V_{1} \left( k \right) = \sum\nolimits_{j = 0}^{n - 1} {\overline{W}^{T} \left( {k_{1} + j} \right)} \,\overline{W}\left( {k_{1} + j} \right)\;\;{\text{and}}\;\;V_{2} \left( k \right) = \sum\nolimits_{j = 0}^{n - 1} {\overline{\varepsilon }^{2} \,\left( {k_{1} + j} \right)} \,\)

$$\begin{aligned} \overline{W}\left( {k + 1} \right) & = \overline{W}\left( {k_{1} } \right) - \kappa \times N\left( {\zeta (k)} \right) \times \left( {\frac{\alpha (k)}{{B(k)}}} \right) \times \sigma \left( {\upsilon (k_{1} )} \right) \times \chi (k + 1) \\ \Delta V_{1} \left( k \right) & = V_{1} \left( {k + 1} \right) - V_{1} \left( k \right) \\ & = \overline{W}^{T} \left( {k + 1} \right) \times \overline{W}\left( {k + 1} \right) - \overline{W}^{T} \left( {k_{1} } \right) \times \overline{W}\left( {k_{1} } \right) \\ & = \left( {\overline{W}^{T} \left( {k + 1} \right) - \overline{W}^{T} \left( {k_{1} } \right)} \right)^{T} \times \left( {\overline{W}^{T} \left( {k + 1} \right) - \overline{W}^{T} \left( {k_{1} } \right)} \right) + 2\overline{W}^{T} \left( {k_{1} } \right) \times \left( {\overline{W}\left( {k + 1} \right) - \overline{W}\left( {k_{1} } \right)} \right) \end{aligned}$$
(34)

From Eq. (34), we have

$$\begin{gathered} \Delta V_{1} \left( k \right) = \left( { - \kappa N\left( {\zeta (k)} \right)\sigma \left( {\upsilon (k_{1} )} \right)\frac{\alpha (k)\chi (k + 1)}{{B(k)}}} \right)^{T} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\left( { - \kappa N\left( {\zeta (k)} \right)\sigma \left( {\upsilon (k_{1} )} \right)\frac{\alpha (k)\chi (k + 1)}{{B(k)}}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,2\overline{W}^{T} \left( {k_{1} } \right)\left( { - \kappa N\left( {\zeta (k)} \right)\sigma \left( {\upsilon (k_{1} )} \right)\frac{\alpha (k)\chi (k + 1)}{{B(k)}}} \right) \hfill \\ \end{gathered}$$
$$\begin{gathered} \Delta V_{1} \left( k \right) = \left( {\kappa^{2} N^{2} \left( {\zeta (k)} \right) \times \left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\|^{2} \times \left( {\frac{{\alpha^{2} (k)}}{{B^{2} (k)}}} \right) \times \chi^{2} (k + 1)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\left( { - 2\kappa N\left( {\zeta (k)} \right)\overline{W}^{T} \left( {k_{1} } \right)\sigma \left( {\upsilon (k_{1} )} \right) \times \left( {\frac{{\alpha^{2} (k)}}{{B^{2} (k)}}} \right) \times \chi (k + 1)} \right) \hfill \\ \end{gathered}$$
(35)
$$\overline{\varepsilon }\left( {k + 1} \right) = \overline{\varepsilon }\left( {k_{1} } \right) - \kappa \times \left( {\frac{\alpha (k)}{{B(k)}}} \right) \times N\left( {\zeta (k)} \right) \times \chi (k + 1)$$
$$\Delta V_{2} \left( k \right) = V_{2} \left( {k + 1} \right) - V_{2} \left( k \right) = \overline{\varepsilon }^{2} \,\left( {k + 1} \right) - \overline{\varepsilon }^{2} \,\left( {k_{1} } \right)$$
$$\Delta V_{2} \left( k \right) = \left( {\overline{\varepsilon }\,\left( {k + 1} \right) - \overline{\varepsilon }\,\left( {k_{1} } \right)} \right)^{2} + 2\overline{\varepsilon }\left( {k_{1} } \right)\left( {\overline{\varepsilon }\,\left( {k + 1} \right) - \overline{\varepsilon }\,\left( {k_{1} } \right)} \right)$$
$$\Delta V_{2} \left( k \right) = \left( { - \kappa N\left( {\zeta (k)} \right) \times \left( {\frac{\alpha (k)}{{B(k)}}} \right) \times \chi (k + 1)} \right)^{2} + 2\overline{\varepsilon }\left( {k_{1} } \right)\left( { - \kappa N\left( {\zeta (k)} \right) \times \left( {\frac{\alpha (k)}{{B(k)}}} \right) \times \chi (k + 1)} \right)$$
$$= \kappa^{2} \frac{{N^{2} \left( {\zeta (k)} \right)\alpha^{2} (k)}}{{B^{2} (k)}}\chi^{2} (k + 1) - 2\overline{\varepsilon }\left( {k_{1} } \right)\kappa \frac{{N\left( {\zeta (k)} \right)\alpha (k)}}{B(k)}\chi (k + 1)$$
(36)
$$\Delta V\left( k \right) = \left( {\kappa^{2} N^{2} \left( {\zeta (k)} \right)\left( {\left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\|^{2} + 1} \right)\frac{{\alpha^{2} (k)\chi^{2} (k + 1)}}{{B^{2} (k)}}} \right)$$
$$\begin{aligned} &- 2\kappa N\left( {\zeta (k)} \right)\overline{W}^{T} \left( {k_{1} } \right)\sigma \left( {\upsilon (k_{1} )} \right)\frac{\alpha (k)\chi (k + 1)}{{B(k)}}\, \\ &- 2\overline{\varepsilon }\left( {k_{1} } \right)\kappa \frac{{N\left( {\zeta (k)} \right)\alpha (k)}}{B(k)}\chi (k + 1)\end{aligned}$$
$$\Delta V\left( k \right) = \left( {\kappa^{2} \times \chi^{2} (k + 1) \times N^{2} \left( {\zeta (k)} \right) \times \left( {\left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\|^{2} + 1} \right) \times \left( {\frac{{\alpha^{2} (k)}}{{B^{2} (k)}}} \right)} \right)$$
$$- 2\kappa N\left( {\zeta (k)} \right) \times \chi (k + 1) \times \left( {\frac{\alpha (k)}{{B(k)}}} \right) \times \left( {\pi (k) + \overline{\varepsilon }(k_{1} )} \right)$$
(37)

From Eq. (37) we get, \(\varepsilon (k + 1) = \,g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)\left( {\pi (k_{1} ) + \overline{\varepsilon }(k_{1} )} \right) + d_{0} (k_{1} )\)where,\(k_{1} = k - n + 1\) and \(g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)\) is not zero therefore multiplying both side by \(g^{ - 1} \left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)\), we get

$$\pi (k) + \overline{\varepsilon }(k_{1} ) = \frac{{\varepsilon (k + 1) - \tau_{0} (k)}}{{g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)}}$$
(38)

Using Eqs. (38, 37) yields

$$\begin{aligned}\Delta V\left( k \right) &= \left( {\kappa^{2} N^{2} \left( {\zeta (k)} \right) \times \chi^{2} (k + 1) \times \left( {\left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\|^{2} + 1} \right)\left( {\frac{{\alpha^{2} (k)}}{{B^{2} (k)}}} \right)} \right) \\ &\quad - 2\kappa N\left( {\zeta (k)} \right) \times \left( {\frac{\alpha (k)}{{B(k)}}} \right) \times \left( {\frac{{\varepsilon (k + 1) - \tau_{0} (k)}}{{g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)}}} \right) \times \chi (k + 1) \end{aligned}$$

Since,\(\chi (k + 1)1 + \left| {N\left( {\zeta (k)} \right)} \right| = \kappa \varepsilon (k + 1)\) we have

$$\begin{aligned}\Delta V\left( k \right) &= \left( {\kappa^{2} N^{2} \left( {\zeta (k)} \right) \times \chi^{2} (k + 1) \times \left( {\left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\|^{2} + 1} \right) \times \left( {\frac{{\alpha^{2} (k)}}{{B^{2} (k)}}} \right)} \right) \\ &\quad+ \frac{{2N\left( {\zeta (k)} \right)}}{{g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)}}\left[ { - \frac{{\alpha (k)\chi (k + 1)\chi (k + 1)\left( {1 + \left| {N\left( {\zeta (k)} \right)} \right|} \right)}}{B(k)} + 2\kappa \frac{{\alpha (k)\chi (k + 1)\tau_{0} (k)}}{B(k)}} \right]\end{aligned}$$
(39)

By the use of Young’s inequality \(xy \le \frac{1}{2}(x^{2} + y^{2} )\), we get

$$\frac{{2\kappa N\left( {\zeta (k)} \right)\alpha (k)\chi (k + 1)d_{0} (k)}}{{B(k)g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)}} \le \frac{{\kappa^{2} N^{2} \left( {\zeta (k)} \right)\alpha^{2} (k)\chi^{2} (k + 1)}}{{B^{2} (k)}} + \frac{{\left( {d_{0} (k)} \right)^{2} }}{{\left( {g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)} \right)^{2} }}$$
$$\begin{aligned} &\le \frac{{\kappa^{2} N\left( {\zeta (k)} \right)}}{B(k)}\Delta \zeta (k) + \frac{{\left( {d_{0} (k)} \right)^{2} }}{{\left( {g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)} \right)^{2} }} \\& \le \kappa^{2} \Delta \zeta (k) + \frac{{\left( {d_{0} (k)} \right)^{2} }}{{\left( {g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)} \right)^{2} }}\end{aligned}$$

and \(\kappa^{2} N^{2} \left( {\zeta (k)} \right)\left( {\left\| {\sigma \left( {\upsilon (k_{1} )} \right)} \right\|^{2} + 1} \right)\frac{{\alpha^{2} (k)\chi^{2} (k + 1)}}{{B^{2} (k)}} \le \frac{{\kappa^{2} \alpha (k)\left( {1 + \left| {N\left( {\zeta (k)} \right)} \right|} \right)\chi^{2} (k + 1)}}{B(k)}\)

$$\le \kappa^{2} \Delta \zeta (k)$$

and hence we have from Eq. (39)

$$\Delta V(k) \le - \frac{{2N\left( {\zeta (k)} \right)}}{{g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)}}\Delta \zeta (k) + 2\kappa^{2} \Delta \zeta (k) + \frac{{\left( {d_{0} (k)} \right)^{2} }}{{\left( {g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)} \right)^{2} }}$$
(40)

Taking, summation on of Eq. (40), we get

$$V(k) \le - 2\sum\limits_{k^{\prime} = 0}^{k} {\frac{{N\left( {\zeta (k^{\prime})} \right)}}{{g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)}}\Delta \zeta (k^{\prime}) + 2\kappa^{2} \zeta (k^{\prime}) + \frac{{\left( {d_{0} (k^{\prime})} \right)^{2} }}{{\left( {g\left( {\overline{\zeta }_{m} (k_{1} ),\upsilon^{\# } (k_{1} )} \right)} \right)^{2} }}}$$

Since, \(\hat{W}(k),\,\hat{\varepsilon }(k),\,\zeta (k)\) and \(N\left( {\zeta (k)} \right)\) are bounded and hence \(1 + \left| {N\left( {\zeta (k)} \right)} \right|\) is also bounded. Since, \(\Delta \zeta (k) = \frac{{\alpha (k)\left( {1 + \left| {N\left( {\zeta (k)} \right)} \right|} \right)\chi^{2} (k + 1)}}{B(k)} \ge 0\), and bounded which concludes that \(\alpha (k) = \frac{\kappa \varepsilon (k)}{{\left( {1 + \left| {N\left( {\zeta (k)} \right)} \right|} \right)}}\) is bounded and hence \(\varepsilon (k) = \frac{1}{\kappa }\alpha (k)\left( {1 + \left| {N\left( {\zeta (k)} \right)} \right|} \right)\) is also bounded and since \(\varepsilon (k) = y(k) - y_{d} (k)\) where \(y_{d} (k)\) is bounded and hence output of the HNN \(y(k)\) is also bounded.

5 Simulation Examples

In this part of paper, two examples with simulation are provided to demonstrate the validity of the designed controller.

Example 1: Consider the below mentioned stochastic nonlinear system

$$\left\{ \begin{gathered} \zeta_{1} (k + 1) = \frac{{1.4\zeta_{{_{1} }}^{2} (k)}}{{1 + \zeta_{{_{1} }}^{2} (k)}} + 0.3\zeta_{2} (k) \hfill \\ \zeta_{2} (k + 1) = \frac{{\zeta_{{_{1} }}^{2} (k)}}{{1 + \zeta_{{_{1} }}^{2} (k) + \zeta_{{_{1} }}^{2} (k)}} + \tau (k) + 0.1 \times \cos (0.05k)\times \cos (\zeta_{1} k) \hfill \\ y(k) = \zeta_{1} (k) \hfill \\ \end{gathered} \right.$$

where \(\tau (k) = \left\{ \begin{gathered} 0.3\,\left( {\upsilon^{2} (k) - 0.5} \right),\,\,\,\,\,\,\upsilon (k) \ge 0.5 \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 0.6 < \upsilon^{2} (k) < 0.5\,\, \hfill \\ 0.2\,\left( {\upsilon^{2} (k) + 0.6} \right),\,\upsilon (k) < - 0.6 \hfill \\ \end{gathered} \right.\) and reference trajectory is given by:\(y_{d} (k) = 0.7 + 0.5sin\left( {{\raise0.7ex\hbox{${kT\pi }$} \!\mathord{\left/ {\vphantom {{kT\pi } 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}} \right) + 0.5cos\left( {{\raise0.7ex\hbox{${kT\pi }$} \!\mathord{\left/ {\vphantom {{kT\pi } {10}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${10}$}}} \right)\;\;{\text{where}},\;\;T = 0.05.\)

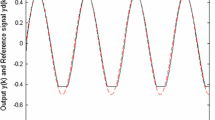
By employing the proposed HNN controller, the system is capable of successfully tracking the reference trajectory with error quickly converging to a small neighborhood of zero. The tracking performance of the controller can be seen in Figs. 4 and 5 where Fig. 4 shows the tracking performance for tracking the reference trajectory and Fig. 5 shows the tracking error. The performance of the proposed controller is compared with existing methods as shown in the Figs. 4 and 5. From Fig. 5, it can be clearly observed that the tracking error for the proposed controller is smaller than the other ones, and hence better results are obtained.

Fig. 4
figure 4

Tracking of desired trajectory yd (red line) using Hybrid NN (blue line)

Full size image
Fig. 5
figure 5

Error measured by hybrid model (blue line) and Neuro-fuzzy model (red line)

Full size image

Example 2: Consider the below mentioned stochastic nonlinear system

$$\left\{ \begin{gathered} \zeta_{1} (k + 1) = 0.2\zeta_{1} (k)cos\zeta_{1} (k) + 0.1\zeta_{1} (k)sin\zeta_{1} (k) + 3\zeta_{2} (k) \hfill \\ \zeta_{2} (k + 1) = 0.3\zeta_{2} (k)\frac{{\zeta_{1} (k)}}{{1 + \zeta_{{_{1} }}^{2} (k)}} - 0.6\frac{{\zeta_{{_{2} }}^{3} (k)}}{{2 + \zeta_{{_{2} }}^{2} (k)}} - 0.1\tau (k) \hfill \\ y(k) = \zeta_{1} (k) \hfill \\ \end{gathered} \right.$$

and reference trajectory is given as \(y_{d} (k) = 1.5 sin\left( {{\raise0.7ex\hbox{${kT\pi }$} \!\mathord{\left/ {\vphantom {{kT\pi } 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}}} \right) + 1.5 cos\left( {{\raise0.7ex\hbox{${kT\pi }$} \!\mathord{\left/ {\vphantom {{kT\pi } {10}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${10}$}}} \right)\;{\text{where}}\;T = 0.05\)

By choosing initial states as [1, 1], the tracking performance of the proposed controller can be seen in Figs. 6 and 7. From Fig. 6, it can be clearly observed that the controller has successfully tracked the reference trajectory with a very small error rapidly converging to zero. Fig. 7 shows the tracking error of the proposed controller in comparison with the existing controllers and it can be clearly seen that the proposed controller has achieved a better performance than the existing ones.

Fig. 6
figure 6

Tracking of desired trajectory yd (red line) using Hybrid NN y (blue line)

Full size image
Fig. 7
figure 7

Error measured by hybrid model (blue line) and Neuro-fuzzy model (red line)

Full size image

6 Conclusion

In this work, an HNN is used as a controller for nonlinear discrete-time systems in presence of a nonlinear dead zone. This HNN is designed on the basis of one-step advanced state prediction of higher-order nonlinear discrete-time systems. The discrete Nussbaum function is used in order to counter the knowledge of control directions. Also, it is verified that the feedback systems possess semi-globally ultimate uniform boundedness and output tracking errors converge in the closed neighborhood of zero. The performance of the HNN model is envisaged by the two simulation examples. Results show that the HNN control model by the use of Nussbaum gain works as predicted in the analysis.