AFMBC for a Class of Nonlinear Discrete-Time Systems with Dead Zone

Abstract

This paper is fretful about an adaptive fuzzy model-based controller (AFMBC), which is studied and implemented for class of nonlinear discrete-time system with dead zone. Due to immeasurable states and the presence of symmetric/non-symmetric dead zones, design of controller becomes more challenging. AFMBC is design for approximation of such nonlinear system to a relative degree of accuracy, which can be used for adaptation of nonlinear discrete-time systems with or without the presence of symmetric/non-symmetric dead zones. AFMBC employs as a reference model which is useful to closed-loop pure feedback form of fuzzy controller. AFMBC provides approximation of immeasurable states and minimizes effects of unknown bounded disturbances in the system. Based on Lyapunov method, it is proved that proposed scheme for discrete-time nonlinear systems is asymptotically stable. Hence, not only stability of proposed system is assured, but it is also shows that tracking error of model lies in closed neighbourhood of zero after sufficient number of iterations, i.e. tracking error $(e(t) \to 0\;{\text{as}}\;t \to \infty )$. The feasibility of the AFMBC is demonstrated by well-known direct current (DC) motor example and other nonlinear discrete-time problem through simulation.

1 Introduction

Famous Stone–Weierstrass theorem says that any real function $f(x)$ on a closed and bounded set can be uniformly approximated via some set of basis functions $f(x,\alpha )$ where $\alpha \in \varOmega^{k}$ and $\varOmega^{k} \subseteq R^{k}$ to a certain/arbitrary degree of accuracy [1]. The exact mathematical model of plant or industrial systems is not always possible to design and solve. Due to uncertain nature of these industrial systems, soft computing techniques employ on such type of systems. Neural networks (NN) and fuzzy logic systems (FLS) are example of such cases. In a finite-dimensional normed vector space, an uncertain nonlinear system can be approximated to a certain extent with artificial neural network (ANN) [2,3,4]. Approximation of nonlinear model is a more challenging comparison to linear model, and these challenges increase in the presence of dead zone or bounded disturbances. Adaptive techniques are passable to use for handling approximation of these unwanted uncertainties arising in the plant/system. Fuzzy model-based controller and adaptive neural network are adequate to be used for handling these uncertainties. Certain specific adaptive techniques like FLS and NN [5,6,7,8,9] for approximation of multiple-input multiple-output (MIMO) with actuator nonlinearities, multiple-input single-output (MISO) and single-input single-output (SISO) nonlinear systems were discussed. But, the above said systems does not deal about immeasurable states and dead-zone effects, which affects the many physical system, and its presence may give the instability of systems [10].

Last few years, many researchers work in the area of adaptive computational techniques for approximation of discrete-time nonlinear systems [11, 12]. Based on FLS and ANN model, many nonlinear control systems have been developed with uncertainty [13, 14]. Consequently, adaptive intelligent control design for pure feedback systems [15] and fuzzy counter propagation network for uncertain nonlinear discrete-time systems was implemented [16, 17]. Neural network has been widely used for approximation of unknown systems [18, 19], and many control systems like back-stepping control [20,21,22,23], sliding mode control [24, 25] and control using flexible computing [26] have been designed by progressing attention among researchers. Unwanted disturbances like dead zone, hysteresis, backlash and bounded difference frequently occur in every field of engineering. Various soft computing techniques like neural network, fuzzy logic and hybrid approaches (neuro-fuzzy) method have been modelled and implemented for control of discrete-time systems in various domains. The adaptive control model was developed [27,28,29] for some real applications, which have more practically used in industries. In addition, some NN and FLS applications were given for an active suspension vehicle [30], heat-exchanger pilot plant [31], air-conditioning systems [32] a flexible crane output constraint system [33] and control of non-holonomic chained systems [34].

Above-mentioned applications do not take into account the effect of input nonlinearities such as backlash, hysteresis and dead zone. The existence of these nonlinearities may affect that the system becomes unstable. Some adaptive trajectory control techniques [35,36,37,38,39,40,41] for unmanned surface vehicles, fully actuated marine surface vehicles and complex surface vehicle system have been designed for nonlinear system with symmetric/non-symmetric dead zones; for example, motion control system with dead-zone compensation and dynamic surface control for servo systems with unknown were developed [17, 42, 43]. An adaptive critic-based neural network [44] has been investigated for pure feedback systems. Adaptive systems like fuzzy tracking control and ANN were developed for fully unknown parametric dynamics with uncertainties and uncertain nonlinear systems [45,46,47] for nonlinear stirred tank reactor with the presence of unknown disturbances. Observer-based fuzzy output feedback control [48] was proposed for SISO nonlinear system with input nonlinearities, and later on, this idea has been extended for MIMO [49]. However, at the present stage, no effective methods work for discrete-time nonlinear systems with disturbances like backlash, hysteresis and dead zone.

Motivated by aforementioned work, our study is focused on adaptive fuzzy model-based control of discrete-time nonlinear systems with immeasurable states and dead-zone nonlinearity. Lyapunov function has been used to prove that system is asymptotically stable and tracking error converges on a compact set in neighbourhood of zero. The contribution of this paper is focused on an adaptive control method for discrete-time systems with input nonlinearities, if no prior knowledge is available about the system. To design such fuzzy model, some basis functions for higher dimensional spaces are used to approximate nonlinear functions. Further, it is proved that designed system is asymptotically stable. This paper will help for approximation of discrete-time nonlinear systems with disturbances like dead zone. The viability and efficiency of proposed method are shown by two simulation results.

Remaining part of the paper is organized as follows. Section 2 contains problem formulation and system description with some basic lemmas/theorems and definitions. Adaptive fuzzy-based model and Lyapunov function-based stability analysis are described in Sect. 3. Section 4 contains the simulation examples of nonlinear systems, and Sect. 5 contains conclusion of paper followed by the future work.

2 Problem Formulation

Consider general form of nonlinear discrete-time systems with input nonlinearities like dead zone [5, 50]:

$$ \left\{ \begin{aligned} & \alpha_{1} (t + 1) = \alpha_{2} (t) \\ & \ldots \\ & \alpha_{n} (t + 1) = f(\alpha (t)) + g(\alpha (t)) + \varGamma (\upsilon (t)) + \delta (t) \\ & y(t) = \alpha_{1} (t) \\ \end{aligned} \right. $$

(1)

where $\alpha (t) = [\alpha_{1} (t),\alpha_{2} (t), \ldots ,\alpha_{n} (t)]^{T}$ is a $n \times 1$, column state vector s.t. tuples of $\alpha (t)$ are known as immeasurable states; $y(t) \in R$ is output of the system; $f(\alpha (t))$ and $g(\alpha (t))$ are smooth nonlinear functions $\delta (t)$ is unknown bounded differences; $\varGamma (\upsilon (t))$ is the dead zone and $\upsilon (t)$ is the input to dead zone. Dead zone $\varGamma (\upsilon (t))$ can be defined as:

$$ \varGamma (\upsilon (t)) = \left\{ {\begin{array}{*{20}l} {m_{r} \left( {\upsilon (t) - b_{r} } \right):} \hfill & {\upsilon (t) \ge b_{r} } \hfill \\ {0:} \hfill & { - b_{l} \le \upsilon (t) \le b_{r} } \hfill \\ {m_{l} \left( {\upsilon (t) + b_{l} } \right):} \hfill & {\upsilon (t) \le - b_{l} } \hfill \\ \end{array} } \right. $$

(2)

where $m_{r}$ and $m_{l}$ are right and left slope of dead zone, respectively; $b_{r}$ and $b_{l}$ are right and left break points, respectively, and all are positive constant. The dead zone can be represented as:

$$ \varGamma (\upsilon (t)) = m(t)\upsilon (t) + b(t) $$

(3)

where

$$ m(t) = \left\{ \begin{aligned} & m_{r} \upsilon (t):\upsilon (t) > 0 \\ & m_{l} \upsilon (t):\upsilon (t) \le 0 \\ \end{aligned} \right. $$

(4)

$$ b(t) = \left\{ {\begin{array}{*{20}l} { - m_{r} b_{r} :} \hfill & {\upsilon (t) \ge b_{r} } \hfill \\ { - m(t)\upsilon (t):} \hfill & { - b_{l} \le \upsilon (t) \le b_{r} } \hfill \\ {m_{l} b_{l} :} \hfill & {\upsilon (t) \le - b_{l} } \hfill \\ \end{array} } \right. $$

(5)

It is obvious to know that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} = \hbox{min} \{ m_{r} ,m_{l} \}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{m} = \hbox{max} \{ m_{r} ,m_{l} \}$. The objective of this paper is to find the approximate solution of nonlinear discrete-time system [Eq. (1)] using AFMBC, so that (1), all the signals obtained via AFMBC are bounded and (2) the system output converges reference signal $y_{r} (t)$, where $y_{r} (t)$ is bounded (3) also, AFMBC is asymptotically stable. Discrete-time system with dead zone is making stable using FLS’s and NN’s [7,8,9,10,11,12,13]. In this paper, we focus on adaptive controller based on fuzzy logic techniques for immeasurable states and discrete-time nonlinear systems. Many practical applications or problems can be converted into form of Eq. (1), as shown in Example 2.

Assumption 1

Let us suppose that $f(\alpha (t))$ and $g(\alpha (t))$ are nonzero and bounded s.t. $0 < \left\| {f(\alpha (t))} \right\| \le \bar{f}$ and $0 < \left\| {g(\alpha (t))} \right\| \le \bar{g}$, where $\bar{f}$ and $\bar{g}$ are positive constants.

2.1 System Description

In this section, we studied some basic definitions of functions, lemma and theorems related to nonlinear function approximation [1, 5, 6, 11]. Let us define some basic definitions:

Definition 1

Let $\varGamma = \left\{ {f(x,\alpha ):\,\alpha \in \varOmega^{k} ,\,k \ge 1} \right\}$ be a class of functions of the form $f(x,\alpha )$ where $\alpha \in \varOmega^{k}$ and $\varOmega^{k} \subseteq R^{k}$ may be uniformly approximated on $\varOmega$ by set of functions $\varGamma$ if for any $\varepsilon$ > 0 there exist some $f(x) \in \varGamma$ such that $\sup_{x \in \varOmega } \left| {f(x) - F(x)} \right|\, < \, \in$. Also is said to be $f(x)$step function if it takes only a finite number of distinct values, with each values assigned in one or more non-overlapping intervals and class of step functions is denoted by $\varGamma_{s}$.

Definition 2

Let $\varGamma_{1}$ be a class of functions said to be universal approximation of class of functions of class $\varGamma_{2}$ if for each $f(x) \in \varGamma_{2}$ may be uniformly approximated by $\varGamma_{1}$.

Lemma 1

Class of step functions$\varGamma_{s}$is universal approximation of set of scalar-valued continuous functions$f(x) \in \varGamma_{cb}$defined on a compact set$\varOmega = [a,b]$. If$f(x)$is continuous on compact set$\varOmega$, therefore$f(x)$is uniformly continuous on$\varOmega$, so for given$\varepsilon$ > 0,$\exists$a$\delta > 0$s.t.$\left| {f(x) - f(y)} \right|\, < \,\varepsilon$whenever$\,\left| {x - y} \right| < \delta$.

Proof

Let $f(x)$ is continuous function on $\varOmega$, then $f(x)$ is uniformly continuous. Therefore, for given $\varepsilon > 0$, there exists a $\delta > 0$ such that whenever $\,\left| {x - y} \right| < \delta$, then $\left| {f(x) - f(y)} \right|\, < \varepsilon$. Divide the interval $\varOmega$ into k non-overlapping intervals of equal lengths, i.e. $h = (b - a)/k$ as follows:

$I_{1} = [a,\,a + h]$, $I_{2} = (a + h,\,a + 2h]$,$\ldots$,$I_{k} = (b - h,\,b]$. Choose sufficiently large k s.t. $h < \delta$ for given $\varepsilon > 0$; so that magnitude of the difference between any two values of $f(x)$ in $I_{k}$ is less than $\varepsilon$. Define a step function $s(x) = f(a + (r - 1)h)$ on $x \in (a + (r - 1)h,\,a + rh]$. Since the value of step function on an interval is simply the value of $f(x)$ at left end points of the interval, $\left| {f(x) - f(y)} \right|\, < \,\varepsilon$.

Theorem 1

If $f \in \varGamma_{cb}$ be a nonlinear function, then $\exists$ fuzzy membership functions which act as basis become universal approximations for $f.$

Theorem 2

Fuzzy model-based systems containing basis functions as$\phi :R \to [0,1]$are universal approximation for$f \in \varGamma_{cb}$.

Proof

Since $\Omega$ is a compact set, and $f,\phi$ are continuous on $\Omega$, there are $x_{0} \in\Omega$, $y_{0} \in \Omega$, satisfying $f\left( {x_{0} } \right)$ = ${\bigvee }_{x \in \varOmega } \left\{ {f\left( x \right)} \right\},\phi \left( {y_{0} } \right) = {\bigvee }_{x \in \varOmega } \left\{ {g\left( x \right)} \right\}$. If $\left| {f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right)} \right| \ge \varepsilon$, we have $f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right) \le - \varepsilon$ or $f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right) \ge \varepsilon$.

To the first case of above equation, considering $f\left( {y_{0} } \right) \le f\left( {x_{0} } \right)$, we obtain

$$ f\left( {y_{0} } \right) - \phi \left( {y_{0} } \right) \le f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right) \le - \varepsilon \Rightarrow \left| {f\left( {y_{0} } \right) - \phi \left( {y_{0} } \right)} \right| \ge \varepsilon , $$

which contradicts the assumption $\left| {f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right)} \right| \ge \varepsilon ,$ since $\left( {x_{0} } \right) \le f\left( {y_{0} } \right)$, it follows that

$$ f\left( {x_{0} } \right) - \phi \left( {x_{0} } \right) \ge f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right) \ge \varepsilon , \Rightarrow \left| {f\left( {x_{0} } \right) - \phi \left( {x_{0} } \right)} \right| \ge \varepsilon , $$

which also contradicts assumption $\left| {f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right)} \right| \ge \varepsilon$.

Thus, $\left| {f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right)} \right| \ge h$ does not hold, that is, $- \varepsilon < f\left( {x_{0} } \right) - \phi \left( {y_{0} } \right) < \varepsilon$, so | $f\left( {x_{0} } \right) - \phi \left( {x_{0} } \right)$ | $< \varepsilon$, i.e. $\left| {{\bigvee }_{x \in \varOmega } \left\{ {f\left( x \right)} \right\} - {\bigvee }_{x \in \varOmega } \left\{ {\phi \left( x \right)} \right\}} \right| < \varepsilon$.

3 Description of Adaptive Fuzzy Model

To develop the framework of adaptive fuzzy model presented in Fig. 1, for the approximation of nonlinear discrete-time systems, the generalization of fuzzy model is based on many linguistic rules. To track the reference signal proposed model based on the following task (1) Track set point trajectory (2) immeasurable states or uncertainty of system parameters and (3) uncertainty due to disturbances. Before going to formulation of fuzzy model-based controller, we present the basic terminology of fuzzy logic.

Fig. 1

Framework of adaptive fuzzy model

3.1 Fuzzy Logic

Fuzzy logic is a multivalued logic which makes use of linguistic variables, fuzzy sets and membership functions. Linguistic variable is used to define different fuzzy sets and membership functions are some curves that use to assign input domain to fuzzy set ranges over [0, 1]. The fuzzy rule constitutes the database and rule base, which is known as knowledge base. Fuzzy If–Then rules are as follows:

$$ {\text{IF}}\;X_{1} \;{\text{is}}\;M_{1}\; {\text{AND}}\;X_{2} \;{\text{is}}\;M_{2} \;{\text{THEN}}\;Y = aX_{1} + bX_{2} + c\;{\text{is}}\;N $$

where $X_{1}$, $X_{2}$ and $Y$ are linguistic variable ranges over $M_{1}$, $M_{2}$ and $N$, respectively. IF part of the rule is known as antecedent and THEN part is known as consequent. Fuzzy inference system comprises of some functional blocks as shown in Fig. 2.

Fig. 2

Block diagram of fuzzy inference system

• 1. Fuzzification interface is transforming the crisp values into linguistic variables.

• 2. Decision-making unit is performing the interface on different fuzzy IF–THEN rules.

• 3. Combination of database and rule base is known as knowledge base, where database defines different fuzzy membership functions and rule base comprises different IF–THEN rules.

• 4. Defuzzification interface is transforming the fuzzy values to crisp values.

In this paper, fuzzy model-based approximation has been developed using inference engine, and whole system dynamics can be represented by subjective mean of linear sub-systems. The nonlinear characteristic has been extracted and resolved via sector nonlinearities. For a nonlinear system, two ways to construct fuzzy model: (1) It can be obtained by use of system identification algorithms or (2) derive the mathematical equations for nonlinear systems to weighted sum of linear systems. Adaptive fuzzy model consists of a number of linguistic rules, i.e. fuzzy IF–THEN rules base consisting two parts (1) antecedents represent a subset of model variables into fuzzy sets and (2) consequents of each rule are a functional representation [35, 36]. Nonlinear system dynamics can be represented by weighted sum of linear sub-systems. The proposed model is based on rule base and input–output relation of nonlinear systems. Input of nonlinear system depends on the initial condition, e.g. $\alpha_{1} (0) = 0$, $\alpha_{2} (0) = 0$, and output of system is reference signal.

3.2 Fuzzy Rule Model

Let $r$ be the number of fuzzy IF–THEN rules, to represent nonlinear system and ith rule is described as follows:

$$ \begin{aligned} & {\mathbf{rule}}\;{\mathbf{1}}:\;{\text{IF}}\;g_{1} (z(t))\;{\text{is}}\;M_{1}^{1} \;{\text{AND}} \ldots {\text{AND}}\;g_{r} (z(t))\;{\text{is}}\;M_{1}^{r} \;{\text{THEN}}\;\left\{ \begin{aligned} &\dot{z}(t) = A_{1} z(t)\, + \,B_{1} u(t) \hfill \\ &y_{1} (t) = C_{{_{1} }}^{T} z(t) \hfill \\ \end{aligned} \right. \\ & {\mathbf{rule}}\;{\mathbf{2}}:\;{\text{IF}}\;g_{2} (z(t))\;{\text{is}}\;M_{2}^{1} \;{\text{AND}} \ldots {\text{AND}}\;g_{r} (z(t))\;{\text{is}}\;M_{2}^{r} \;{\text{THEN}}\;\left\{ \begin{aligned} &\dot{z}(t) = A_{2} z(t)\, + \,B_{2} u(t) \hfill \\ &y_{2} (t) = C_{2}^{T} z(t) \hfill \\ \end{aligned} \right. \\ & \ldots \\ & {\mathbf{rule}}\;{\mathbf{i}}:\;{\text{IF}}\;g_{1} (z(t))\;{\text{is}}\;M_{i}^{1} \;{\text{AND}} \ldots {\text{AND}}\;g_{r} (z(t))\;{\text{is}}\;M_{i}^{r} \;{\text{THEN}}\;\left\{ \begin{aligned} &\dot{z}(t) = A_{i} z(t)\, + \,B_{i} u(t) \hfill \\ &y_{i} (t) = C_{i}^{T} z(t) \hfill \\ \end{aligned} \right., \\ \end{aligned} $$

where $A_{i} \in R^{n \times n}$, $B_{i} \in R^{n \times m}$ and $C_{i} \in R^{1 \times n}$ with $z(0) = 0$ as initial condition, for all $i = 1,2, \ldots ,n$ and $M_{{_{i} }}^{j}$; $j = 1,2, \ldots ,r$ are fuzzy sets and state vector $z(t)\, \in \,R^{n}$, input vector $u(t)\, \in \,R^{m}$, also $(A_{i} ,B_{i} )$ are known as system and input matrix pair and $z_{1} (t), \ldots ,z_{r} (t)$ are fuzzy variables.

3.3 Fuzzy Controller

The control algorithm uses adaptive fuzzy model with state vector $z(t)$ and input vector $u(t)$; then, the whole system dynamics are represented as:

$$ \dot{z}(t) = \mathop \Sigma \limits_{i = 1}^{r} w_{i} (z(t))\left( {A_{i} z(t) + B_{i} u(t)} \right) $$

(6)

where

$$ w_{i} \left( {z(t)} \right) = \frac{{\mathop \Pi \limits_{l = 1}^{n} \mu_{{M_{l}^{i} }} g_{l} (z(t))}}{{\mathop \Sigma \limits_{k = 1}^{r} \mathop \Pi \limits_{l = 1}^{n} \mu_{{M_{l}^{k} }} g_{l} (z(t))}},\forall i $$

(7)

$\mu_{{M_{l}^{i} }} (g_{l} z(t))$ be the membership function corresponding to fuzzy set $M_{l}^{i}$. It is assumed that $w_{i} \left( {z(t)} \right) \ge 0$ where $i = 1,2, \ldots ,n$ and $\mathop \sum \nolimits_{i = 1}^{r} w_{i} \left( {z(t)} \right) = 1$.

Similarly, another fuzzy model can be described using number of fuzzy rules for fuzzy controller; the jth rule is defined as:

$$ {\mathbf{rule}}\;{\mathbf{j:}}\;{\text{IF}}\;f_{1} (z(t))\;{\text{is}}\;N_{j}^{1} \;{\text{AND}} \ldots {\text{AND}}\;f_{p} (z(t))\;{\text{is}}\;N_{j}^{p}\;{\text{THEN}}\;u(t) = G_{j} z(t),\;{\text{and}}\;x(0) = 0 $$

(8)

where $N_{j}^{q}$ is fuzzy set corresponding to jth rule and function $f_{q} (z(t))$ and $G_{j} \in R^{m \times n} ;$$j = 1,2, \ldots ,p,$

where

$$ u(t) = \mathop \Sigma \limits_{j = 1}^{p} m_{j} (z(t))G_{j} (z(t)) $$

(9)

and $m_{j} (z(t)) \ge 0,\,\forall j$$\mathop \Sigma \limits_{j = 1}^{p} m_{j} (z(t)) = 1$

$$ m_{j} (z(t)) = \frac{{\mathop \Pi \limits_{l = 1}^{n} \mu_{{N_{l}^{j} }} (g_{l} z(t))}}{{\mathop \Sigma \limits_{k = 1}^{r} \mathop \Pi \limits_{l = 1}^{n} \mu_{{N_{l}^{k} }} (g_{l} z(t))}},\forall j $$

(10)

$\mu_{{N_{l}^{i} }} (f_{l} z(t))$ be the membership function corresponding to fuzzy set $N_{l}^{i}$.

Fuzzy model-based control system is given by

$$ \begin{aligned} \dot{z}(t) & = \mathop \Sigma \limits_{i = 1}^{r} w_{i} (z(t))\left( {A_{i} z(t) + B_{i} \mathop \Sigma \limits_{j = 1}^{p} m_{j} (z(t))G_{j} z(t)} \right) \\ \dot{z}(t) & = \,\mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{p} w_{i} (z(t))m_{j} (z(t))\left( {A_{i} + B_{i} G_{j} } \right)z(t) \\ \end{aligned} $$

(11)

Remark 1

Let us assume that $f(\alpha )$ is discrete-time function defined on a compact set $\varOmega$; then, there exist fuzzy logic systems in the form of Eq. (11), we have $\left\| {f(\alpha ) - z(\alpha )} \right\| < \varepsilon$ where $\varepsilon > 0$. Then, $f(\alpha )$ can be written as $f(\alpha )$ = $f(\alpha ) = \eta^{*} (\alpha ) + e^{*} (\alpha )$, where $\eta^{*}$ represents optimal fuzzy parameter vector s.t. $e^{*} (\alpha )$ is error close to zero and $\exists$; two positive constants $\bar{\eta }$ and $\bar{e}$ satisfy $\left\| {\eta^{*} } \right\| \le \bar{\eta }$ and $\left\| {e^{*} } \right\| \le \bar{e}$.

Definition 3

(Lyapunov function) A function $V:R^{n} \to R$ defined on a compact set $\varOmega \subseteq R^{n}$ with continuous partial derivatives is known as Lyapunov function for nonlinear system if it satisfies the following conditions (1) $V(\alpha )$ is positive definite and (2) $\dot{V}(\alpha )$ is negative definite $\forall \alpha \in \varOmega$.

Definition 4

(Asymptotically stable) A system is said to be asymptotically stable if $\exists$ a Lyapunov function $V(\alpha )$ if $\dot{V}(\alpha ) \le 0$, $\forall \alpha \in \varOmega$.

Theorem 3

A fuzzy model-based control for nonlinear discrete-time system represented by Eq. (8) or Eq. (11) is asymptotically stable if there exists constant scalar s.t. $\tau_{j} > 0$ and $\beta_{j}$ satisfying $m_{j} - \tau_{j} w_{j} + \beta_{j} \ge 0$; there exist matrices $H_{ij} = H_{{_{ji} }}^{T} \in R^{n \times n}$, $E_{ij} = E_{{_{ji} }}^{T} \in R^{n \times n}$, $\varLambda_{j} = \varLambda_{j} \in R^{n \times n}$ and $V_{ij} = V_{ij} \in R^{n \times n}$ s.t. $H < 0$ and $E < 0$ given by $H = \left[ {\begin{array}{*{20}c} {H_{11} } & {H_{12} \cdots } & {H_{1p} } \\ \begin{aligned} H_{21} \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} H_{22} \cdots \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} H_{2p} \hfill \\ \vdots \hfill \\ \end{aligned} \\ {H_{p1} } & {H_{p2} \cdots } & {H_{pp} } \\ \end{array} } \right]\;{\text{and}}\;E = \left[ {\begin{array}{*{20}c} {E_{11} } & {E_{12} \cdots } & {E_{1p} } \\ \begin{aligned} E_{21} \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} E_{22} \cdots \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} E_{2p} \hfill \\ \vdots \hfill \\ \end{aligned} \\ {E_{p1} } & {E_{p2} \cdots } & {E_{pp} } \\ \end{array} } \right].$

3.4 Stability Analysis of Fuzzy Model

To discuss the stability of proposed adaptive fuzzy model for the approximation of nonlinear systems, we have to discuss about stability control based on Lyapunov theory. Let us consider fuzzy model-based control system, given in Eq. (11). Consider Lyapunov function:

$$ V(k) = \alpha (k)^{T} P\alpha (k) $$

(12)

$P \in R^{n \times n}$ is symmetric positive definite matrix. Differentiating Eq. (18), we have

$$ \begin{aligned} \dot{V}(k) & = \dot{\alpha }(k)^{T} P\alpha (k) + \alpha (k)^{T} P\dot{\alpha }(k) \\ V(k) & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{p} w_{i} m_{j} \alpha^{T} (k)\left( {(A_{i} + \,B_{i} G_{j} )^{T} P + P(A_{i} + \,B_{i} G_{j} )} \right)\alpha (k) \\ V(k) & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{p} w_{i} m_{j} z(k)^{T} \left( {X(A_{i} + \,B_{i} G_{j} )^{T} P + P(A_{i} + \,B_{i} G_{j} )X} \right)z(k) \\ V(k) & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{p} w_{i} m_{j} z(k)^{T} Q_{ij} z(k) \\ \varTheta_{ij} & = X\left( {A_{i} + \,B_{i} G_{j} } \right)^{T} P + P\left( {A_{i} + \,B_{i} G_{j} } \right)X \\ \end{aligned} $$

(13)

Lyapunov stability theory says that fuzzy model-based controller is asymptotically stable if $V(k) > 0$ and $\dot{V}(k) < 0$. Let $X = P^{ - 1}$, $z(k) = X^{ - 1} \alpha (k)$ and $G_{j} = N_{j} X^{ - 1}$

To relax the stability conditions, some slack variables are introduced by considering the equation given below:

$$ \begin{aligned} & \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} (w_{j} - m_{j} )\varLambda_{i} \\ & = \mathop \Sigma \limits_{i = 1}^{r} w_{i} \left( {\mathop \Sigma \limits_{j = 1}^{r} w_{j} - \mathop \Sigma \limits_{j = 1}^{r} m_{j} } \right)\varLambda_{i} = 0 \\ \end{aligned} $$

(14)

$$ \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \tau_{j} w_{j} \left( {V_{ij} - V_{ij} } \right) = 0 $$

(15)

where $\varLambda_{i} > 0,\,\varLambda_{i} \in R^{n \times n}$ and $\varLambda_{i} = \varLambda_{i}^{T}$ also $V_{ij} = V_{ij}^{T}$.

From (13), (14) and (15), we have

$$ \begin{aligned} \dot{V}(k) & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} m_{j} z(k)^{T} \varTheta_{ij} z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {w_{j} - m_{j} } \right)z(k)^{T} Q_{ij} z(k) \\ & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} m_{j} z(k)^{T} \varTheta_{ij} z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {w_{j} - m_{j} + \tau_{j} w_{j} - \tau_{j} w_{j} } \right)z(k)^{T} \varTheta_{ij} z(k) \\ & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} m_{j} z(k)^{T} \varTheta_{ij} z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {w_{j} - \tau_{j} w_{j} } \right)z(k)^{T} \varTheta_{ij} z(k) \\ & \quad - \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {m_{j} - \tau_{j} w_{j} } \right)z(k)^{T} \varTheta_{ij} z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \tau_{j} w_{j} z(k)^{T} \left( {V_{ij} - V_{ij} } \right)z(k) \\ \end{aligned} $$

(16)

where scalars $\tau_{j} > 0,$$j = 1,2,\, \cdots \,,\,r$ define a $\beta_{j}$ s.t. $m_{j} - \tau_{j} w_{j} + \beta_{j} \ge 0$

These additional scalars and matrices are further reducing the conservativeness of stability criteria. From Eq. (16), we have

$$ \begin{aligned} \dot{V}(k) & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} z(k)^{T} \left( {w_{i} + \tau_{j} w_{j} - \tau_{j} w_{j} } \right)\varTheta_{ij} z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {w_{j} - \tau_{j} w_{j} } \right)z(k)^{T} \varTheta_{ij} z(k) \\ & \quad - \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {m_{j} - \tau_{j} w_{j} } \right)z(k)^{T} \varTheta_{ij} z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \tau_{j} w_{j} z(k)^{T} V_{ij} z(k) - \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \tau_{j} w_{j} z(k)^{T} V_{ij} z(k) \\ & = \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} w_{j} z(k)^{T} \tau_{j} \left( {\varTheta_{ij} - \varLambda_{i} - V_{ij} } \right)z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {m_{j} - \tau_{j} w_{j} } \right)z(k)^{T} \left( {\varTheta_{ij} - \varLambda_{i} } \right)z(k) \\ & \quad + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} w_{j} z(k)^{T} \left( {\varLambda_{i} + \tau_{j} V_{ij} } \right)z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {\beta_{j} - \beta_{j} } \right)z(k)^{T} \left( {Q_{ij} - \varLambda_{i} } \right)z(k) \\ & = \,\mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} w_{j} z(k)^{T} \left( {\tau_{j} \left( {\varTheta_{ij} - \varLambda_{i} - V_{ij} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {Q_{ik} - \varLambda_{i} } \right)} \right)z(k) \\ & \quad + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} \left( {m_{j} - \tau_{j} w_{j} + \beta_{j} } \right)z(k)^{T} \left( {\varTheta_{ij} - \varLambda_{i} } \right)z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} w_{j} z(k)^{T} \left( {\varLambda_{i} + \tau_{j} V_{ij} } \right)z(k) \\ \end{aligned} $$

(17)

$$ {\text{From}}\;m_{j} - \tau_{j} w_{j} + \beta_{j} \ge 0,\;\forall j\;{\text{and}}\;x(t),\;{\text{we}}\;{\text{have}}\;(\varTheta_{ij} - \varLambda_{i} ) < 0,\,\forall i,j $$

(18)

$$ \begin{aligned} \dot{V}(k) & \le \,\mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} w_{j} z(k)^{T} \left( {\tau_{j} \left( {\varTheta_{ij} - \varLambda_{i} - V_{ij} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {Q_{ik} - \varLambda_{i} } \right)} \right)z(k) \\ & \quad + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{j = 1}^{r} w_{i} w_{j} z(k)^{T} \left( {\varLambda_{i} + \tau_{j} V_{ij} } \right)z(k) \\ & = \mathop \Sigma \limits_{i = 1}^{r} w_{{_{i} }}^{2} z(k)^{T} \left( {\tau_{i} \left( {\varTheta_{ii} - \varLambda_{i} - V_{ii} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {\varTheta_{ik} - \varLambda_{i} } \right)} \right)z(k) \\ & \quad + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{i < j} w_{i} w_{j} z(k)^{T} \left( {\tau_{j} \left( {\varTheta_{ij} - \varLambda_{i} - V_{ij} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {\varTheta_{ik} - \varLambda_{i} } \right)} \right. \\ & \quad + \left. {\,\tau_{i} \left( {\varTheta_{ji} - \varLambda_{j} - V_{ji} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {\varTheta_{ik} - \varLambda_{i} } \right)} \right)z(k) \\ & \quad + \mathop \Sigma \limits_{i = 1}^{r} w_{{_{i} }}^{2} z(k)^{T} \left( {\varLambda_{i} + \tau_{i} V_{ii} } \right)z(k) + \mathop \Sigma \limits_{i = 1}^{r} \mathop \Sigma \limits_{i < j} w_{i} w_{j} z(k)^{T} \left( {\varLambda_{i} + \tau_{j} V_{ij} + \varLambda_{j} + \tau_{i} V_{ji} } \right)z(k) \\ \end{aligned} $$

(19)

Let $H_{ij} = H_{{_{ji} }}^{T} \in R^{n \times n}$ and $E_{ij} = E_{{_{ji} }}^{T} \in R^{n \times n}$

$$ H_{ii} > \tau_{j} \left( {\varTheta_{ij} - \varLambda_{i} - V_{ij} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {\varTheta_{ik} - \varLambda_{i} } \right)\,\forall i; $$

(20)

$$ \begin{aligned} & H_{ij} + H_{{_{ij} }}^{T} > \tau_{j} \left( {\varTheta_{ij} - \varLambda_{i} - V_{ij} } \right) - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {\varTheta_{ik} - \varLambda_{i} } \right) + \tau_{i} \left( {\varTheta_{ji} - \varLambda_{j} - V_{ji} } \right) \\ & - \mathop \Sigma \limits_{k = 1}^{r} \beta_{k} \left( {\varTheta_{jk} - \varLambda_{j} } \right)\;\forall j;\;{\text{and}}\;i < j \\ \end{aligned} $$

(21)

$$ E_{ii} > \left( {\varLambda_{i} + \tau_{i} V_{ii} } \right)\;\forall i; $$

(22)

$$ E_{ij} + E_{{_{ij} }}^{T} > \left( {\varLambda_{i} + \tau_{j} V_{ij} } \right) + \left( {\varLambda_{j} + \tau_{i} V_{ji} } \right)\;\forall j;\;{\text{and}}\;i < j $$

(23)

Using Eqs. (20), (21), (22) and (23), Eq. (19) becomes

$$ \dot{V}(k) \le \,z(k)^{T} (H + E)z(k) $$

(24)

where $Z(k) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {w_{1} z(k)} \\ {w_{2} z(k)} \\ \begin{aligned} \,\,\,\,\, \vdots \hfill \\ w_{r} z(k) \hfill \\ \end{aligned} \\ \end{array} } \\ {} \\ \end{array} } \right]$, $H = \left[ {\begin{array}{*{20}c} {H_{11} } & {H_{12} \cdots } & {H_{1p} } \\ \begin{aligned} H_{21} \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} H_{22} \cdots \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} H_{2p} \hfill \\ \vdots \hfill \\ \end{aligned} \\ {H_{p1} } & {H_{p2} \cdots } & {H_{pp} } \\ \end{array} } \right]$ and $E = \left[ {\begin{array}{*{20}c} {E_{11} } & {E_{12} \cdots } & {E_{1p} } \\ \begin{aligned} E_{21} \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} E_{22} \cdots \hfill \\ \vdots \hfill \\ \end{aligned} & \begin{aligned} E_{2p} \hfill \\ \vdots \hfill \\ \end{aligned} \\ {E_{p1} } & {E_{p2} \cdots } & {E_{pp} } \\ \end{array} } \right]$

Based on Lyapunov theory, Definitions 3 and 4 show that $V(k) > 0$ and $\dot{V}(k) < 0$, $\forall \alpha (k) \ne 0$, i.e. system is asymptotically stable for $\alpha (k) \to 0$ as $k \to \infty$.

4 Simulation Results

To express the effectiveness of proposed adaptive fuzzy model-based controller, two nonlinear discrete-time systems with nonlinearity input as dead zone are considered and discussed. MATLAB 7.13.0 (R2013a) with 1 GB RAM, Intel Pentium 4, 2.81 GHz processor and 200 GB hard disc are used for simulation.

Example 1

The proposed approach is used for following nonlinear system with dead zone:

$$ \left\{ \begin{aligned} & \alpha_{1} (t + 1) = \alpha_{2} (t) \\ & \alpha_{2} (t + 1) = f(\alpha (t)) + g(\alpha (t))\varGamma (\upsilon (t)) + \delta (t) \\ & y(t) = \alpha_{1} (t) \\ \end{aligned} \right. $$

(25)

where, $\alpha (t) = [\alpha_{1} (t),\,\alpha_{2} (t)]^{T}$; the system state vector and unknown functions $f(\alpha (t))$ and $g(\alpha (t))$ are given by:

$$ \begin{aligned} f(\alpha (t)) & = \frac{{\alpha_{{_{1} }}^{2} (t)}}{{1 + \alpha_{{_{1} }}^{2} (t) + \alpha_{{_{2} }}^{2} (t)}} \\ g(\alpha (t)) & = 0.3 \\ \end{aligned} $$

(26)

External bounded disturbance is $\delta (t) = 0.1\cos (0.5t)\cos (\alpha_{1} (t))$ such that $0 \le \left| {{\text{d}}(t)} \right| \le \bar{b}$ and $u(t) = \varGamma (\upsilon (t))$ be the dead zone described as:

$$ \varGamma (\upsilon (t)) = \left\{ \begin{aligned} & 0.3^{*}(\upsilon (t) - 0.5):\,\upsilon (k) \ge 0.5 \\ & 0:\, - 0.6 \le \upsilon (t) \le 0.5 \\ & 0.2^{*}(\upsilon (t) + 0.6):\,\upsilon (t) \le - 0.6 \\ \end{aligned} \right. $$

(27)

The adaptive fuzzy model is based on rule base and input–output relation of nonlinear systems. Input of nonlinear system Eq. (25) depends on the initial condition $\alpha_{1} (0) = 0$, $\alpha_{2} (0) = 0$, and output of system is $y(k)$. The objective is to design fuzzy controller, such that (i) output $y(k)$ track the reference signal $y_{r} (t) = 0.25\sin (tT\pi /2.5) + 0.25\cos (tT\pi ),\,T = 0.01$ to small bounded compact set and (ii) tracking error lies in the neighbourhood of zero. Let us choose some fuzzy membership functions for $\alpha (t)$ as follows: $\mu_{{\phi_{i}^{1} }} (x_{i} ) = \exp [ - (x_{i} + 2)^{2} /3]$, $\mu_{{\phi_{i}^{2} }} (x_{i} ) = \exp [ - (x_{i} + 1)^{2} /3]$, $\mu_{{\phi_{i}^{3} }} (x_{i} ) = \exp [ - x_{i}^{2} /3]$, $\mu_{{\phi_{i}^{4} }} (x_{i} ) = \exp [ - (x_{i} - 1)^{2} /3]$ and $\mu_{{\phi_{i}^{5} }} (x_{i} ) = \exp [ - (x_{i} - 2)^{2} /3]$.

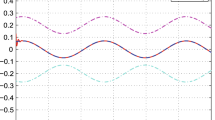
By using fuzzy model-based controller to the nonlinear systems with dead zone (27), the simulation curves are shown in Fig. 3. Figure 3 shows the system tracking trajectories and it reflects that good tracking performance by proposed model in comparison with neuro-fuzzy and ANN. Figure 3 shows that tracking error trajectories of AFMBC, neuro-fuzzy and ANN lies on a compact set.

Fig. 3

Reference signal $y_{r} (k)$ (black dashed) and AFMBC, Neuro-fuzzy and ANN (blue, green and red dashed line), respectively

It can be seen from Table 1 that the different error parameters are small as compared with neuro-fuzzy and ANN. It is noticed that from Fig. 4, error obtained via AFMBC is minimum than neuro-fuzzy and ANN.

Table 1 Calculated various errors for Example 1

Fig. 4

Error trajectories via AFMBC, Neuro-fuzzy and ANN (blue, green and red dashed line), respectively, show that error bounded in $[0,\,7 \times 10^{ - 3} ]$

Example 2

To further demonstrate the effectiveness of proposed model, consider nonlinear system as DC motor, which described and transformed into nonlinear discrete-time system as follows:

$$ \left\{ \begin{aligned} & \dot{q}_{1} = q_{2} \\ & Jq_{2} + f\dot{q}_{1} + T_{f} + \delta (t) = u \\ & y = q_{1} \\ \end{aligned} \right.(t) $$

(28)

where $q_{1}$ is motor angular position; $J$ is the known inertia; $f$ unmeasured viscous and $T_{f}$ nonlinear friction; $\delta (t) = 0.05\sin t$ is the bounded disturbance $u(t)$ or $\varGamma (\upsilon (t))$ is motor torque. Let us define new variables $\alpha_{1} = q_{1}$ and $\alpha_{2} = q_{2}$; corresponding difference equation of (28) is written as:

$$ \left\{ \begin{aligned} & \alpha_{1} (t + 1) = \alpha_{2} (t)*\Delta T \\ & \alpha_{2} (t + 1) = \alpha_{2} (t) + [(u(t) - f(\alpha_{2} (t)) - T_{f} - \delta (t) \\ & y = \alpha_{1} (t) \\ \end{aligned} \right.)/J]\Delta T $$

(29)

Objective is that to design controller for system (29) such that output $y$ is driven to track reference signal, $y_{r} (t) = 0.3\sin (0.5t\pi /50 + \pi /4)$. Initial condition for system (29) is $\alpha_{1} (0) = - 1$, $\alpha_{2} (0) = 1$. Fuzzy model-based controller to the nonlinear systems with dead zone (27), the simulation curves are shown in Fig. 5. From Fig. 5, it is clear that good tracking trajectory has been obtained and Fig. 5 shows that tracking error lies in the neighbourhood of zero.

Fig. 5

Reference signal $y_{r} (k)$ (black dashed) and AFMBC, Neuro-fuzzy and ANN (blue, green and red dashed line), respectively

It can be seen from Table 2 that the different error parameters are small as compared with neuro-fuzzy and ANN. It is noticed that from Fig. 6, error obtained using AFMBC is minimum in comparison with neuro-fuzzy and ANN.

Table 2 Calculated various errors for Example 2

Fig. 6

Error trajectories via AFMBC, Neuro-fuzzy and ANN (blue, green and red dashed line), respectively, show that error bounded in $[0,\,4.5 \times 10^{ - 3} ]$

5 Conclusion

An adaptive fuzzy model-based controller is proposed for approximation of class discrete-time nonlinear system or a dynamical system which is transformed to nonlinear discrete-time system with dead-zone nonlinearities. AFMBC is focused to measure immeasurable states and approximation of unknown functions. AFMBC is employed on FLS-based controller of unknown functions with external bounded disturbances. AFMBC is also useful to approximate the physical problem like DC motor (which is transform to discrete form). Stability of AFMBC is studied and analysed by Lyapunov theory and shown that system is asymptotically stable. Figures 3, 4, 5 and 6 show that simulation results obtained using AFMBC give better results in comparison with neuro-fuzzy and ANN. Trajectories of actual signal are much closer to the AFMBC output; different error parameters are also discussed and shown that tracking errors lie in the bounded neighbourhood of zero with sufficient number of iterations. Two examples have been illustrated that AFMBC gives good approximation. In future, noncanonical and stochastic nonlinear systems will be used for approximation using some adaptive techniques.