1 Introduction

With the heuristics of the biological nervous system, neural networks (NNs) have been proven to be the key to solving various difficult problems in many fields [1,2,3,4,5]. The response of the NNs to the weak envelope modulation signal formed by the superposition of two periodic signals with different frequencies was studied in [6]. Artificial NNs, as a method of local search heuristics, [7] proposed differential evolutionary hybridization algorithms to predict the optimal strategy or to generate better offspring from a set of differential evolutionary strategies. In order to improve the classification accuracy of diabetes diagnosis, [8] used Watts-Strogatz small-world feedforward NNs (SWFNNs) and Newman-Watts SWFNNs for analysis, and proved that Newman-Watts SWFNNs analysis method can obtain the best output error parameters and the highest output correlation.

In practical engineering, the communication time and the switching speed of the amplifiers may be limited between neurons. Since the existence of time delays is frequently a source of instability, weak performance [9,10,11]. And the stability of the system is one of the prerequisites to study the performance of the system. Therefore, the stability analysis of DNNs is important theoretical significance and practical value [12,13,14].

In the natural and artificial world, only a few networks can adjust their system parameters to achieve stability. In order to overcome this problem, most networks need to rely on some external force, that is, controllers [15]. Thus, various control methods have been introduced to stabilize the DNNs, such as intermittent control [16], sliding mode control [17, 18], state feedback control [19, 20], event-trigger-ed control [21], impulsive control [22,23,24,25], sampled-data control [26,27,28,29]. Among these commonly used control methods, discontinuous control (including impulsive control and intermittent control), are more effective than other control methods in terms of reducing control costs. The control mechanism of these two discontinuous control methods is: intermittent control is activated within a certain time interval, that is, intermittent control controls the state of the system within a specific interval, while impulsive control is only activated at discrete instants.

Obviously, the impulsive control mechanism is less cost than intermittent control mechanism [30]. In addition, for many real networks, the state of nodes is often disturbed instantaneously, and there will be sudden changes at some instants. These sudden changes may be produced by sudden noises, frequency changes or other switching phenomena. In other words, there exists impulsive effects [31, 32]. Therefore, impulsive control is the most consistent with the actual situation and more effective in reducing the control cost. Generally, in the dynamic analysis of the DNNs, there are two types of impulses: stable impulses and unstable impulses. If the impulsive effects can destroy the stability of DNNs, then the impulse sequence is called unstable impulse. Meanwhile, if the corresponding impulsive effects can promote the stability of DNNs, the impulse sequence is called stable impulse. What’s more, when the impulsive effects are unstable impulse, the impulse should not occur too frequently in order to achieve the goal of stability. Similarly, when the impulsive effects are stable impulse, the impulsive interval should not be too long, otherwise it will affect the stability of the DNNs. To solve this difficulty, many literatures used the upper and lower bounds of the impulsive interval to control the frequency of impulses occurring [33,34,35,36,37]. In [22], authors proposed a unified criterion to investigative the synchronization of impulsive dynamical networks. Unfortunately, using the upper or lower bounds to characterize the impulses frequency may lead to conservative results. Thus, in order to get less conservative results, what can we do to obtain more relax results for the occurrence of the impulse and not even impose any restrictions on the impulse? and it works for both stable impulses and unstable impulses.

In most studies, the traditional Lyapunov functional is used to obtain the stability/synchronization of the impulsive systems. However, the drawback of the classical Lyapunov theory is that the constructed functional must satisfy the positive definiteness characterization in the whole impulsive interval, which will cause the result to be quite conservative. Thus, a looped-functional method (LFM) was developed [38] in order to get a less conservative result. It’s shown that the LFM satisfies the positive definiteness at the sampling instants, which not only reduces the conservatism, but also obtains a larger sampling interval. Then on this basis, many studies used the LFM to study the asymptotic stability of the SDSs [39, 40]. In [41,42,43,44], LFM was applied to the impulsive systems, but these papers have the following shortcomings: (1) The systems they studied were linear impulse systems, and only studied the asymptotic stability of system. (2) Due to the constructed one-sided looped-functional, the information of the impulsive instant was not fully utilized, resulting in a certain conservatism. Hence, the stability problem of impulsive DNNs based on bilateral looped-functional has not been fully investigated, and it is still an open and challenging problem.

Motivated by the above analysis, the positive effects and negative effects of impulses for DNNs are analyzed in this work. When the impulse has a negative effect for DNNs, the linear feedback control in the hybrid controller can be used to balance the negative effect, and then the system stability can be obtained by using the IBBLF method. On the contrary, if the impulse plays a positive role in the stability of the DNNs, then only the impulsive controller can achieve the expected results under IBBLF.

The main highlights of this work are shown as follows:

  1. (1)

    In order to consider both stable and unstable impulses at the same time, a hybrid controller is developed, in which the feedback controller is used to coordinate the impulsive controller.

  2. (2)

    An improved IBBLF is constructed, which relaxes the requirement of positive definiteness. In addition, the functional introduces the cross-terms of the state and the integral of impulsive instants and takes the information on both impulsive instants \(z(t_k^{+})\) and \(z(t_{k+1})\) into account.

  3. (3)

    A novel lemma is presented by using Cauchy-Schwarz inequality and Gronwall-Bellman inequality. Furthermore, discrete-time exponential stability conditions are derived based on the constructed IBBLF method, and less conservative exponential stability criteria are obtained in the light of linear matrix inequalities (LMIs).

  4. (4)

    The exponential stability results of impulsive systems are applied to SDSs with variable sampling and time-varying delay, and compared with the Refs. [28, 45, 46], one can obtain a larger allowable upper bound.

Table 1 Notations
Full size table

2 Preliminaries and problem statement

The following DNNs with external input are considered:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{z}}(t)={\mathcal {A}}z(t)\!+\!{\mathcal {B}}g(z(t))\!+\!{\mathcal {C}}h(z(t\!-\!\tau (t)))\!+\!u(t),\\ {}&z(s)=\varphi (s), \quad s\in [-\tau ,0], \end{aligned}\right. \nonumber \\ \end{aligned}$$
(1)

where the state vector \(z(t)\!=\!\mathrm{col}\big \{z_1(t), z_2(t),...,z_n(t)\big \}\!\!\in {\mathcal {R}}^n\), \({0\le \tau (t)\le \tau }\) denotes the time-varying delay and satisfies \({\dot{\tau }}(t)\le \mu \le 1\), \(g(z(t))=\mathrm{col}\big \{g_1(z_1(t)),g_2(z_2(t)),...,g_n(z_n(t))\big \}\in {\mathcal {R}}^n\) and \(h(z(t-\tau (t)))=\mathrm{col}\big \{ h_1(z_1(t-\tau (t))),h_2(z_2(t-\tau (t))),...,h_n(z_n(t-\tau (t)))\big \}\in {\mathcal {R}}^n\) are the activation functions and satisfy \(g_i(0)=h_i(0)=0\). \({\mathcal {A}}=\mathrm{diag}\big \{a_1, a_2,..., a_n\big \}\in {\mathcal {R}}^{n\times n}\) denotes the self-inhibition matrix, where \(a_i<0\) (\(i=1,2,...,n\)), \({\mathcal {B}},{\mathcal {C}}\in {\mathcal {R}}^{n\times n}\) represent the connection weight of the activation functions \(g(\cdot ), h(\cdot )\), \(u(t)\in {\mathcal {R}}^n\) is the control input to be designed.

Assumption 1

[47]. The \(g_i(\cdot )\), \(h_i(\cdot )\) are Lipschitz’s continuous activation functions, and there are constants \({\mathcal {G}}_i>0\), \({\mathcal {H}}_i>0\), such that

$$\begin{aligned}&0\le \frac{g_i(\mu _1)-g_i(\mu _2)}{\mu _1-\mu _2}\le {\mathcal {G}}_i,\;\;\\&0\le \frac{h_i(\mu _1)-h_i(\mu _2)}{\mu _1-\mu _2}\le {\mathcal {H}}_i, \end{aligned}$$

where \(i=1,2,...,n\), \(\mu _1\ne \mu _2\).

For system (1), the following hybrid control strategy is considered:

$$\begin{aligned}&u(t)=u_1(t)+u_2(t),\nonumber \\&u_1(t)=-\Gamma z(t),\,u_2(t)=\sum _{k=1}^{\infty }{\mathscr {Q}}z(t)\delta (t-t_k), \end{aligned}$$
(2)

where \(\Gamma =\mathrm{diag}\big \{\gamma _1, \gamma _2,...,\gamma _n\big \}\ge 0\) is the feedback gain, \({\mathscr {Q}}\) means the strength of impulse, \(\delta (\cdot )\) is the Dirac function and \(\big \{t_k\big \}_{k=1}^{\infty }\), \(\lim _{k\rightarrow \infty }t_k=\infty \) is the impulsive sequence. The impulsive interval is defined as \({\mathcal {T}}_k=t_{k+1}-t_k\in [{\mathcal {T}}_{m},{\mathcal {T}}_{M}]\). z(t) is supposed to be left-continuous (that is: \(z(t_k)=z(t_{k}^{-})\)) and has right-limits.

Substituting (2) into (1), one has

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{z}}(t)\!=\!({\mathcal {A}}\!\!-\!\!\Gamma )z(t)\!\!+\!\!{\mathcal {B}}g(z(t))\!\!+\!{\mathcal {C}}h(z(t\!-\!\!\tau (t))), t\!\ne \!t_k,\\ {}&\Delta z(t_k)={\mathscr {Q}}z(t_k), \quad t=t_k, \;\;k\in {\mathbb {N}}^{+},\\ {}&z(s)=\varphi (s),\quad s\in [-\tau , \;0], \end{aligned}\right. \end{aligned}$$
(3)

where \(\Delta z(t_k)=z(t_k^{+})-z(t_k^{-})\). Next, some effective lemmas and definition are introduced.

Definition 1

[41]. The functional f satisfies the following mapping

$$\begin{aligned} \begin{aligned} f:[0, {\mathcal {T}}_{M}]\times {\mathbb {K}}_{[{\mathcal {T}}_{m}, {\mathcal {T}}_{M}]}\times [{\mathcal {T}}_{m}, {\mathcal {T}}_{M}]\rightarrow {\mathcal {R}}, \end{aligned} \end{aligned}$$

where \(0<\epsilon \le {\mathcal {T}}_{m}\le {\mathcal {T}}_{M}<+\infty \). If the following conditions are satisfied, then the functional f is called looped-functional.

  1. 1.

    f satisfies the characteristics of periodic

    $$\begin{aligned} \begin{aligned} f(0,x,{\mathcal {T}}_k)=f({\mathcal {T}}_k, x, {\mathcal {T}}_k), \end{aligned} \end{aligned}$$
    (4)

    for \(\forall x\in C([0, {\mathcal {T}}_k], {\mathcal {R}}^n)\subset {\mathbb {K}}_{[{\mathcal {T}}_{m}, {\mathcal {T}}_{M}]}\) , \({\mathcal {T}}_k\in [{\mathcal {T}}_{m}, {\mathcal {T}}_{M}]\).

  2. 2.

    It’s differentiable with respect to the first variable.

Lemma 1

[48]. Constants \(T>0\), \(c\ge 0\), \(r\ge 0\). Let u(t) be a Borel measurement bounded nonnegative function on \([t_0, T]\), and g(t) be a nonnegative integral function on \([t_0,T]\). If

$$\begin{aligned} u(t)\le c+\int _{t_0}^{t}[g(s)u(s)+r]\mathrm{d}s,\quad \mathrm {for}\;\;\forall t_0\le t\le T, \end{aligned}$$

then

$$\begin{aligned} u(t)\le [c+r(t-t_0)]\exp \bigg (\int _{t_0}^{t}g(s)\mathrm{d}s\bigg ). \end{aligned}$$

Lemma 2

For system (3), the following inequality holds for \(t\in (t^{+}_k,t_{k+1}]\):

$$\begin{aligned} \begin{aligned} \Vert z(t)\Vert ^2\le \theta _1\Vert z(t_k)\Vert ^2+\theta _2\int _{t_k-\tau (t_k)}^{t_k}\Vert z(s)\Vert ^2\mathrm{d}s, \end{aligned} \end{aligned}$$
(5)

where

$$\begin{aligned}&{\mathcal {G}}=\mathrm{diag}\big \{{\mathcal {G}}_1, {\mathcal {G}}_2,...,{\mathcal {G}}_n\big \},\\&{\mathcal {H}}=\mathrm{diag}\big \{{\mathcal {H}}_1, {\mathcal {H}}_2,..., {\mathcal {H}}_n\big \}, \\&\theta _1=4e^{\sigma }\Vert I+{\mathscr {Q}}\Vert ^2, \\&\theta _2=\frac{4}{1-\mu }e^{\sigma }{\mathcal {T}}_M\Vert {\mathcal {C}}\Vert ^2\Vert {\mathcal {H}}|^2, \\&\sigma =4T_M^2(\Vert {\mathcal {A}}-\Gamma \Vert ^2+\Vert {\mathcal {B}}\Vert ^2\Vert {\mathcal {G}}\Vert ^2 \\&\quad +\frac{\Vert {\mathcal {C}}\Vert ^2\Vert {\mathcal {H}}\Vert ^2}{1-\mu }). \end{aligned}$$

Proof

From system (3), we can obtain

$$\begin{aligned} z(t)&=z(t_{k}^{+})+\int _{t_k}^{t}({\mathcal {A}}-\Gamma )z(s)\mathrm{d}s \\ \nonumber&\quad +\int _{t_k}^{t}{\mathcal {B}}g(z(s))\mathrm{d}s \\ \nonumber&\quad +\int _{t_k}^{t}{\mathcal {C}}h(z(s-\tau (s)))\mathrm{d}s. \end{aligned}$$
(6)

According to inequalities \(\Vert {\mathcal {B}}g(z(t))\Vert ^2\!\!\le \!\!\Vert {\mathcal {B}}\Vert ^2\Vert {\mathcal {G}}\Vert ^2\Vert z(t)\Vert ^2\), \(\Vert {\mathcal {C}}h(z(t-\tau (t)))\Vert ^2\le \Vert {\mathcal {C}}\Vert ^2\Vert {\mathcal {H}}\Vert ^2\Vert z(t-\tau (t))\Vert ^2\), and by using Cauchy-Schwarz inequality, one can derive

$$\begin{aligned}&\Vert z(t)\Vert ^2\nonumber \\&\le 4\Vert z(t^{+}_{k})\Vert ^2+4\bigg \Vert \int _{t_k}^{t}({\mathcal {A}}-\Gamma )z(s)\mathrm{d}s\bigg \Vert ^2 \nonumber \\ {}&+4\bigg \Vert \!\int _{t_k}^{t}{\mathcal {B}}g(z(s))\mathrm{d}s\!\bigg \Vert ^2\!\!+\!\!4\bigg \Vert \!\int _{t_k}^{t}{\mathcal {C}}h(z(s\!\!-\!\!\tau (s)))\mathrm{d}s\!\bigg \Vert ^2\nonumber \\ {}&\le 4\Vert I\!+\!{\mathscr {Q}}\Vert ^2\Vert z(t_{k})\Vert ^2\!+\!4{\mathcal {T}}_{M}\Vert {\mathcal {A}}\!-\!\Gamma \Vert ^2\int _{t_k}^{t}\big \Vert z(s)\big \Vert ^2 \mathrm{d}s\nonumber \\ {}&+4{\mathcal {T}}_{M}\Vert {\mathcal {B}}\Vert ^2\Vert {\mathcal {G}}\Vert ^2\int _{t_k}^{t}\Vert z(s)\Vert ^2\mathrm{d}s+4{\mathcal {T}}_{M}\Vert {\mathcal {C}}\Vert ^2\Vert {\mathcal {H}}\Vert ^2 \nonumber \\ {}&\times \int _{t_k-\tau (t_k)}^{t}\Vert z(s)\Vert ^2\mathrm{d}s\nonumber \\ {}&=4\Vert I\!+\!{\mathscr {Q}}\Vert ^2\Vert z(t_{k})\Vert ^2\!+\!4{\mathcal {T}}_{M}\bigg (\Vert {\mathcal {A}}\!-\!\Gamma \Vert ^2\!+\!\Vert {\mathcal {B}}\Vert ^2\Vert {\mathcal {G}}\Vert ^2 \nonumber \\ {}&+\frac{\Vert {\mathcal {C}}\Vert ^2\Vert {\mathcal {H}}\Vert ^2}{1-\mu }\bigg )\int _{t_k}^{t}\Vert z(s)\Vert ^2\mathrm{d}s+\frac{4{\mathcal {T}}_{M}\Vert {\mathcal {C}}\Vert ^2\Vert {\mathcal {H}}\Vert ^2}{1-\mu } \nonumber \\ {}&\times \int _{t_k-\tau (t_k)}^{t_k}\Vert z(s)\Vert ^2\mathrm{d}s. \end{aligned}$$
(7)

Then, for \(t\in (t^{+}_k,t_{k+1}]\), applying Lemma 1, one has

$$\begin{aligned} \begin{aligned} \Vert z(t)\Vert ^2\le \theta _1\Vert z(t_k)\Vert ^2+\theta _2 \int _{t_k-\tau (t_k)}^{t_k}\Vert z(s)\Vert ^2\mathrm{d}s. \end{aligned} \end{aligned}$$
(8)

3 Main results

3.1 The analysis of exponential stability based on an IBBLF approach

For convenience, one will use the following notations in Theorem 1.

$$\begin{aligned} \begin{aligned}&\pi _1(t)=\frac{1}{t\!-\!t_k}\int _{t_k}^{t}z(s)\mathrm {d}s,\\ {}&\pi _2(t)=\frac{1}{t_{k+1}\!-\!t}\int _{t}^{t_{k\!+\!1}}\!z(s)\mathrm {d}s,\\ {}&\eta _1(t)=\mathrm {col}\big \{z(t_k^{+}),\;z(t_{k+1})\big \},\\ {}&\eta _2(t)=\mathrm {col}\big \{z(t)-z(t_k^{+}),\;z(t)-z(t_{k+1})\big \},\\ {}&\eta _3(t)\!=\!\mathrm {col}\big \{(t_{k+1}\!-\!t)(z(t)\!\!-\!\!z(t_k^{+})),(t\!\!-\!\!t_k)(z(t)\!\!-\!\!z(t_{k+1}))\big \},\\ {}&\eta _4(t)=\mathrm {col}\big \{z(t),\;z(t_k),\;z(t_{k+1})\big \},\\ {}&\eta _5(t)=\mathrm {col}\big \{\pi _1(t),\pi _2(t),g(z(t)),h(z(t\!-\!\tau (t)))\big \},\\ {}&\xi (t)=\mathrm {col}\big \{z(t),z(t\!-\!\tau (t)),z(t_k),z(t_{k+1}),{\dot{z}}(t),\eta _5(t)\big \},\\ {}&e_j=[0_{n\times (j-1)n},I_{n\times n}, 0_{n\times (j-1)n}],\; j=1,2,...,9. \end{aligned} \end{aligned}$$

Theorem 1

Given constants \({\mathcal {T}}_{m}>0\), \({\mathcal {T}}_{M}>0\), \(\alpha >0\), the system (3) is exponential stable if there exist matrices \(P_j>0\), \(X_j>0\), \(M_1>0\), \(N_1>0\), diagonal matrices \(\Lambda _j>0\), symmetric matrix S and arbitrary appropriate dimensions matrices \(Q_j\), R, \(L_j\), \({\mathcal {D}}_j\), \(Y_\iota \), \(Z_\iota \) \(M_\kappa \), \(N_\kappa \), \(j=1,2\), \(\iota =1,2,3\), \(\kappa =2,3\), such that the following LMIs hold:

$$\begin{aligned}&\begin{bmatrix} P_1 &{} (I+{\mathscr {Q}})P_1 \\ {\star } &{} P_1\end{bmatrix}>0,\end{aligned}$$
(9)
$$\begin{aligned}&{\mathcal {L}}_1=\begin{bmatrix} X_1 &{} L_1 \\ {\star } &{} X_2\end{bmatrix}>0, \end{aligned}$$
(10)
$$\begin{aligned}&{\mathcal {L}}_2=\begin{bmatrix} 3X_1 &{} L_2 \\ {\star } &{} 3X_2\end{bmatrix}>0,\end{aligned}$$
(11)
$$\begin{aligned}&\Omega _1({\mathcal {T}}_k)=\Xi _1+{\mathcal {T}}_k\Xi _2<0,\end{aligned}$$
(12)
$$\begin{aligned}&\Omega _2({\mathcal {T}}_k)=\Xi _1+{\mathcal {T}}_k\Xi _3<0, \end{aligned}$$
(13)

where \(\Xi _1\), \(\Xi _2\) and \(\Xi _3\) are defined in Appendix A.

Proof

Construct the following time-dependent IBBLF:

$$\begin{aligned} {\mathcal {W}}(t)={\mathcal {V}}_1(t)+{\mathcal {V}}_2(t),\;\; t\in (t^{+}_k,t_{k+1}], \end{aligned}$$
(14)

where \({\mathcal {V}}_1(t)=V_1(t)+V_2(t)\), \({\mathcal {V}}_2(t)=\sum _{i=3}^{7}V_{i}(t)\) and

$$\begin{aligned} V_1(t)\mathrm {d}&=z^T(t)P_1z(t),\\ V_2(t)&=\int _{t-\tau (t)}^{t}e^{2\alpha (s-t)}z^T(s)P_2z(s)\mathrm {d}s,\\ V_3(t)&=2\eta ^T_3(t)[Q_1\eta _1(t)+Q_2\eta _2(t)],\\ V_4(t)&=2[z(t)-z(t_k^{+})]^TR[z(t)-z(t_{k+1})],\\ V_5(t)&=(t_{k+1}-t)(t-t_k)\eta _1^T(t)S\eta _1(t),\\ V_6(t)&=(t_{k+1}-t)(t_{k+1}-t_k)\int _{t_k}^{t}e^{2\alpha (s-t)}{\dot{z}}^T(s)X_1{\dot{z}}(s)\mathrm {d}s\\ {}&\quad -(t-t_k)(t_{k+1}-t_k)\int _{t}^{t_{k+1}}e^{2\alpha (s\!-\!t)}{\dot{z}}^T(s)X_2{\dot{z}}(s)\mathrm {d}s,\\ V_7(t)&=(t_{k+1}-t)\int _{t_k}^{t}e^{2\alpha (s-t)}\eta ^T_4(s){\mathscr {M}}\eta _4(s)\mathrm {d}s \\ {}&\quad -(t-t_k)\int _{t}^{t_{k+1}}e^{2\alpha (s\!-\!t)}\eta ^T_4(s){\mathscr {N}}\eta _4(s)\mathrm {d}s, \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&Q_1\!\!=\!\!\begin{bmatrix} Q_{11} &{} Q_{12} \\ Q_{13} &{} Q_{14}\end{bmatrix}, Q_2\!\!=\!\!\begin{bmatrix} Q_{21} &{} Q_{22} \\ Q_{23} &{} Q_{24}\end{bmatrix}, S\!\!=\!\!\begin{bmatrix} S_{11} &{} S_{12} \\ {\star } &{} S_{22} \end{bmatrix},\\ {}&{\mathscr {M}}=\begin{bmatrix} M_1 &{} Y_1 &{} Y_2\\ {\star } &{} M_2 &{} Y_3 \\ {\star } &{} {\star } &{} M_3\end{bmatrix},\; {\mathscr {N}}=\begin{bmatrix} N_1 &{} Z_1 &{} Z_2 \\ {\star } &{} N_2 &{} Z_3 \\ {\star } &{} {\star } &{} N_3\end{bmatrix}. \end{aligned} \end{aligned}$$

Taking the derivative of \({\mathcal {W}}(t)\), one obtains

$$\begin{aligned}&{\dot{V}}_1(t)+2\alpha V_1(t) \nonumber \\ {}&=\xi ^T(t)He\big \{e^T_1P_1e_5+\alpha e^T_1P_1e_1\big \}\xi (t), \end{aligned}$$
(15)
$$\begin{aligned}&{\dot{V}}_2(t)+2\alpha V_2(t)\nonumber \\ {}&\le \xi ^T(t)\big \{e^T_1P_2e_1-(1-\mu )e^{-2\alpha \tau }e^T_2P_2e_2\big \}\xi (t), \end{aligned}$$
(16)
$$\begin{aligned}&{\dot{V}}_3(t)+2\alpha V_3(t)\nonumber \\ {}&=\xi ^T(t)He\big \{\Sigma _6^TQ_1\Sigma _1+\Sigma _6^TQ_2\Sigma _2+(t-t_k)(\Sigma ^T_8\nonumber \\ {}&\times Q_1\Sigma _1+\Sigma ^T_8Q_2\Sigma _2+ \Sigma ^T_5Q_2\Sigma _3+2\alpha \Sigma ^T_5Q_1\Sigma _1\nonumber \\ {}&+2\alpha \Sigma ^T_5 Q_2\Sigma _2)\!+\!(t_{k\!+\!1}\!-\!t)(\Sigma ^T_7Q_1\Sigma _1+\Sigma ^T_7Q_2\Sigma _2\nonumber \\ {}&+\Sigma ^T_4Q_2\Sigma _3+2\alpha \Sigma ^T_4Q_1\Sigma _1 +2\alpha \Sigma ^T_4Q_2\Sigma _2)\big \}\xi (t), \end{aligned}$$
(17)
$$\begin{aligned}&{\dot{V}}_4(t)+2\alpha V_4(t)\nonumber \\ {}&=\xi ^T(t)He\big \{e^T_5R(e_1-e_4)+(e_1-(I+{\mathscr {Q}})e_3)^T\nonumber \\ {}&\times \!Re_5+2\alpha (e_1-(I+{\mathscr {Q}})e_3)^TR(e_1-e_4)\big \}\xi (t), \end{aligned}$$
(18)
$$\begin{aligned}&{\dot{V}}_5(t)+2\alpha V_5(t)\nonumber \\ {}&=\xi ^T(t)\big \{(t_{k+1}-t)\Sigma _1^TS\Sigma _1-(t-t_k)\Sigma _1^TS\Sigma _1\nonumber \\ {}&+2\alpha (t_{k+1}-t)(t-t_k)\Sigma ^T_1S\Sigma _1\big \}\xi (t), \end{aligned}$$
(19)
$$\begin{aligned}&{\dot{V}}_6(t)+2\alpha V_6(t)\nonumber \\ {}&\le \xi ^T(t)\big \{(t_{k+1}\!-\!t){\mathcal {T}}_ke^T_5X_1e_5\big \}\xi (t)-{\mathcal {T}}_k\int _{t_k}^{t}e^{\!-\!2\alpha {\mathcal {T}}_M}\nonumber \\ {}&\times {\dot{z}}^T(s)X_1{\dot{z}}(s)ds+\xi ^T(t)\big \{(t-t_k){\mathcal {T}}_ke^T_5X_2e_5\big \}\nonumber \\ {}&\times \xi (t)-{\mathcal {T}}_k\int _{t}^{t_{k+1}}{\dot{z}}^T(s)X_2{\dot{z}}(s)ds, \end{aligned}$$
(20)
$$\begin{aligned}&{\dot{V}}_7(t)+2\alpha V_7(t)\nonumber \\ {}&\le \!-e^{\!-\!2\alpha {\mathcal {T}}_M}\!\!\int _{t_k}^{t}\!\!z^T(s)M_1z(s)ds+(t\!-\!t_k)\xi ^T(t)\Phi _1\xi (t)\nonumber \\ {}&+(t_{k+1}\!-\!t)\xi ^T(t)\Phi _2\xi (t)-\int _{t}^{t_{k+1}}z^T(s)N_1z(s)ds\nonumber \\ {}&+(t-t_k)\xi ^T(t)\Phi _3\xi (t)+(t_{k+1}-t)\xi ^T(t)\Phi _4\xi (t). \end{aligned}$$
(21)

For the integral terms of (20) and (21), one has

$$\begin{aligned}&\!-\!{\mathcal {T}}_k\int _{t_k}^{t}\!\!e^{\!-\!2\alpha {\mathcal {T}}_M}{\dot{z}}^T(s)X_1{\dot{z}}(s)ds\!\!-\!\!{\mathcal {T}}_k\int _{t}^{t_{k+1}}\!\!{\dot{z}}^T(s)X_2{\dot{z}}(s)ds \nonumber \\ {}&\le \xi ^T(t)\big \{-\Phi ^T_5{\mathcal {L}}_1\Phi _5-\Phi ^T_6{\mathcal {L}}_2\Phi _6\big \}\xi (t), \end{aligned}$$
(22)
$$\begin{aligned}&\!-\!e^{-2\alpha {\mathcal {T}}_M}\!\!\int _{t_k}^{t}z^T(s)M_1z(s)ds\!-\!\int _{t}^{t_{k+1}}\!\!z^T(s)N_1z(s)ds\nonumber \\ {}&\le \xi ^T(t)\big \{-(t-t_k)e^{-2\alpha T_M}e^T_6M_1e_6-(t_{k+1}-t)\nonumber \\ {}&\times e^T_7N_1e_7\big \}\xi (t). \end{aligned}$$
(23)

Therefore, one obtains

$$\begin{aligned}&{\dot{V}}_6(t)+2\alpha V_6(t)\nonumber \\ {}&\le \xi ^T(t)\big \{(t_{k+1}-t){\mathcal {T}}_Me^T_5X_1e_5+(t-t_k){\mathcal {T}}_Me^T_5X_2e_5\nonumber \\ {}&-\Phi _5{\mathscr {L}}\Phi _5-\Phi ^T_6{\mathcal {L}}_2\Phi _6\big \}\xi (t), \end{aligned}$$
(24)
$$\begin{aligned}&{\dot{V}}_7(t)+2\alpha V_7(t)\nonumber \\ {}&\le \xi ^T(t)\big \{(t-t_k)(\Phi _1+\Phi _3-e^{2\alpha T_M}e^T_6M_1e_6)\nonumber \\ {}&+(t_{k+1}-t)(\Phi _2+\Phi _4-e^T_7N_1e_7)\big \}\xi (t). \end{aligned}$$
(25)

In addition, for any diagonal matrices \(\Lambda _1>0\), \(\Lambda _2>0\), the following inequalities hold:

$$\begin{aligned} \begin{aligned}&\xi ^T(t)\mathrm{He}\big \{e^T_8\Lambda _1({\mathcal {G}}e_1-e_8)\big \}\xi (t)\ge 0,\\ {}&\xi ^T(t)\mathrm{He}\big \{e^T_9\Lambda _2({\mathcal {H}}e_2-e_9)\big \}\xi (t)\ge 0. \end{aligned} \end{aligned}$$
(26)

For any matrices \({\mathcal {D}}_1\in {\mathcal {R}}^{n\times n}\), \({\mathcal {D}}_2\in {\mathcal {R}}^{n\times n}\), one can get:

$$\begin{aligned} \begin{aligned} \xi ^T(t)He\big \{\Phi ^T_7\Phi _8\big \}\xi (t)=0. \end{aligned} \end{aligned}$$
(27)

From (15–28), the estimation of \(\dot{{\mathcal {W}}}(t)+2\alpha {\mathcal {W}}(t)\) will be obtained:

$$\begin{aligned}&\dot{{\mathcal {W}}}(t)+2\alpha {\mathcal {W}}(t)\nonumber \\ {}&w1q\le \xi ^T(t)\big \{\Xi _1+(t-t_k)\Xi _2+(t_{k+1}-t)\Xi _3\big \}\xi (t). \end{aligned}$$
(28)

Then, one obtains

$$\begin{aligned}&\dot{{\mathcal {W}}}(t)+2\alpha {\mathcal {W}}(t)\nonumber \\ {}&\le \xi ^T(t)\bigg \{\frac{t-t_k}{{\mathcal {T}}_k}\Omega _1({\mathcal {T}}_k)+\frac{t_{k+1}-t}{{\mathcal {T}}_k}\Omega _2({\mathcal {T}}_k)\bigg \}\xi (t). \end{aligned}$$
(29)

Therefore, based on conditions (12) and (13), one obtains

$$\begin{aligned} \begin{aligned} \dot{{\mathcal {W}}}(t)+2\alpha {\mathcal {W}}(t)<0, \quad t\in (t^{+}_k,t_{k+1}]. \end{aligned} \end{aligned}$$
(30)

Pre- and post-multiply inequality (9) by \(diag\big \{I,P^{-1}\big \}\),

$$\begin{aligned} \begin{aligned} \begin{bmatrix} P_1 &{} I+{\mathscr {Q}} \\ {\star } &{} P_1^{-1}\end{bmatrix}>0. \end{aligned} \end{aligned}$$
(31)

Hence, one can derive

$$\begin{aligned} \begin{aligned} {\mathcal {W}}(t_k^{+})&={\mathcal {V}}_1(t_k^{+})+{\mathcal {V}}_2(t_k^{+})\\ {}&\le z^T(t_k)P_1z(t_k)+{\mathcal {V}}_2(t_k^{-})\\ {}&={\mathcal {W}}(t_k), \end{aligned} \end{aligned}$$
(32)

which means that the jumps of \({\mathcal {W}}(t)\) at every impulse instant are decreasing, that is, \({\mathcal {W}}(t_k^{+})<{\mathcal {W}}(t_k)\).

For \(t\in (t^{+}_k,t_{k+1}]\), it follows from Lemma 1 that

$$\begin{aligned}&{\mathcal {W}}(t)\le e^{-2\alpha (t-t_k)}{\mathcal {W}}(t_k)\nonumber \\ {}&\quad \quad \; \le e^{-2\alpha (t-t_{k-1})}{\mathcal {W}}(t_{k-1})\nonumber \\ {}&\quad \quad \; \le ...\nonumber \\ {}&\quad \quad \; \le e^{-2\alpha t}{\mathcal {W}}(0). \end{aligned}$$
(33)

On the one hand, we can know

$$\begin{aligned} {\mathcal {W}}(0)&=z^T(0)P_1z(0)+\int _{-\tau (t)}^{0}e^{2\alpha s}z^T(s)P_2z(s)\mathrm{d}s \nonumber \\ {}&\le \theta _3\sup _{s\in [-\tau ,0]}\Vert \varphi (s)\Vert ^2, \end{aligned}$$
(34)

where \(\theta _3=\lambda _\mathrm{max}(P_1)+\tau \cdot \lambda _\mathrm{max}(P_2)\).

On the other hand, from Lemma 2 and (34), one gets

$$\begin{aligned}&\Vert z(t)\Vert ^2\nonumber \\ {}&\le \theta _1\Vert z(t_k)\Vert ^2+\theta _2 \int _{t_k-\tau (t_k)}^{t_k}\Vert z(s)\Vert ^2\mathrm{d}s\nonumber \\ {}&<\max \bigg \{\frac{\theta _1}{\lambda _\mathrm{min}(P_1)},\;\;\frac{\theta _2 e^{2\alpha \tau }}{\lambda _\mathrm{min}(P_2)}\bigg \}{\mathcal {W}}(t_k)\nonumber \\ {}&<\max \bigg \{\frac{\theta _1}{\lambda _\mathrm{min}(P_1)},\;\;\frac{\theta _2 e^{2\alpha \tau }}{\lambda _\mathrm{min}(P_2)}\bigg \}e^{-2\alpha t_k}{\mathcal {W}}(0)\nonumber \\ {}&\le e^{2\alpha {\mathcal {T}}_M}\max \bigg \{\frac{\theta _1}{\lambda _\mathrm{min}(P_1)},\;\;\frac{\theta _2 e^{2\alpha \tau }}{\lambda _\mathrm{min}(P_2)}\bigg \}e^{-2\alpha t}{\mathcal {W}}(0)\nonumber \\ {}&\le e^{2\alpha {\mathcal {T}}_M}\max \bigg \{\frac{\theta _1}{\lambda _\mathrm{min}(P_1)},\frac{\theta _2 e^{2\alpha \tau }}{\lambda _\mathrm{min}(P_2)}\bigg \}\theta _3\nonumber \\ {}&\times e^{-2\alpha t}\sup _{s\in [-\tau ,0]}\Vert \varphi (s)\Vert ^2. \end{aligned}$$
(35)

Thus, we can obtain

$$\begin{aligned} \begin{aligned} \Vert z(t)\Vert \le \epsilon e^{-\alpha t}\sup _{s\in [-\tau ,0]}\Vert \varphi (s)\Vert , \end{aligned} \end{aligned}$$
(36)

where

$$\begin{aligned} \epsilon =e^{\alpha {\mathcal {T}}_M}\sqrt{\max \bigg \{\frac{\theta _1}{\lambda _\mathrm{min}(P_1)},\;\;\frac{\theta _2 e^{2\alpha \tau }}{\lambda _\mathrm{min}(P_2)}\bigg \}\theta _1}. \end{aligned}$$

Then, the exponential stabilization of system (3) can be achieved. This completes the proof.

Remark 1

Although the Lyapunov functional \({V}_1(t)\) and \(V_2(t)\) are positive definite, the IBBLF \({\mathcal {W}}(t)\) may not be so. Therefore, the IBBLF approach relaxes the requirement of positive definiteness and it only satisfies \({\mathcal {W}}(t)\) is positive at the moment of impulsive \(t=t_k\;(t=t_k^{-})\). In addition, \(\dot{{\mathcal {W}}}(t)<0\) can be obtained by using IBBLF, it is obvious that one can ensure \({\mathcal {W}}(t)\) is decreasing on the impulsive instants.

Remark 2

In (14), the IBBLF \(\sum _{l=3}^{7}V_l(t,z(t))\), takes full advantage of the state information from \(z(t_k^{+})\) to z(t) and z(t) to \(z(t_{k+1})\), which not only can obtain less conservative results, but also improve the interval \([{\mathcal {T}}_m, {\mathcal {T}}_M]\) of allowable aperiodic impulses compared with the LFM in Refs. [28, 45, 46].

3.2 Application: exponential stability of SDSs with variable sampling

According to system (1), we consider the following SDSs:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{z}}(t)={\mathcal {A}}z(t)\!+\!{\mathcal {B}}g(z(t))\!+\!{\mathcal {C}}h(z(t\!-\!\tau (t)))\!+\!u_c(t),\\ {}&z(s)=\varphi (s), \quad s\in [-\tau ,0], \end{aligned}\right. \end{aligned}$$
(37)

where \(u_c(t)={\mathcal {K}}z(t_k)\), and the other notations have the same meaning as Theorem 1. In order to use the results of Theorem 1, the SDSs can be written as an impulsive system with state \(\omega (t):=col\big \{z(t),x(t)\big \}\) and \(x(t):=z(t_k)\), \(t\in (t_k,t_{k+1}]\) and \({\mathcal {T}}_k=t_{k+1}-t_k\in [{\mathcal {T}}_{m},{\mathcal {T}}_{M}]\). The dynamics of system (38) can be written as

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{\omega }}(t)\!=\!{\mathfrak {A}}\omega (t)\!+\!{\mathfrak {B}}{\tilde{g}}(\omega (t))\!+\!{\mathfrak {C}}{\tilde{h}}(\omega (t\!-\!\tau (t))), t\!\ne \!t_k,\\ {}&\omega (t_k^{+})=\begin{bmatrix} z(t^{-}_k) \\ z(t^{-}_k) \end{bmatrix},\quad t=t_k,\;\forall k\in {\mathbb {N}}^{+}, \end{aligned}\right. \end{aligned}$$
(38)

where

$$\begin{aligned}&{\mathfrak {A}}=\begin{bmatrix} {\mathcal {A}} &{} {\mathcal {K}} \\ 0 &{} 0 \end{bmatrix},\; {\mathfrak {B}}=\begin{bmatrix} {\mathcal {B}} &{} 0 \\ 0 &{} 0 \end{bmatrix},\; {\mathfrak {C}}=\begin{bmatrix} {\mathcal {C}} &{} 0 \\ 0 &{} 0 \end{bmatrix},\\ {}&{\tilde{g}}(\omega (t))\!=\!\begin{bmatrix} g(z(t)) \\ g(x(t)) \end{bmatrix},{\tilde{h}}(\omega (t\!-\!\tau (t)))\!=\!\begin{bmatrix} h(z(t\!-\!\tau (t))) \\ h(x(t\!-\!\tau (t)))\end{bmatrix}. \end{aligned}$$

and the initial condition \(z(s)=\varphi (s), s\in [-\tau ,0]\).

Between the impulses z(t), x(t) evolve according to (37) and at the impulse instant \(t_k\), the value of z(t) before and after \(t_k\) remains unchanged, but the value of x(t) is updated by \(x(t_k^{-})\). Then exponential stability of SDSs (38) can be obtained as follows:

Theorem 2

Given constants \({\mathcal {T}}_{m}>0\), \({\mathcal {T}}_{M}>0\), \(\alpha >0\), \(\varepsilon _1\), \(\varepsilon _2\), if there exist matrices \({P}_j>0\), \({X}_j>0\), \(M_1>0\), \(N_1>0\), diagonal matrices \({\Lambda }_j>0\), symmetric matrix S and arbitrary matrices \({Q}_j\), R, L, \({\mathcal {D}}_j\), \(Y_\iota \), \(Z_\iota \) \(M_\kappa \), \(N_\kappa \), \(j=1,2\), \(\iota =1,2,3\), \(\kappa =2,3\), such that conditions (10) (11) of the Theorem 1 and following LMIs hold for \({\mathcal {T}}_k\in [{\mathcal {T}}_{m},{\mathcal {T}}_{M}]\):

$$\begin{aligned}&{\tilde{\Omega }}_1(T_k)={\tilde{\Xi }}_1+{\mathcal {T}}_k{\tilde{\Xi }}_2<0, \end{aligned}$$
(39)
$$\begin{aligned}&{\tilde{\Omega }}_2(T_k)={\tilde{\Xi }}_1+{\mathcal {T}}_k{\tilde{\Xi }}_3<0. \end{aligned}$$
(40)

Then, the system (38) is exponential stable and the gain matrix can be obtained by \({\mathcal {K}}=(\mathcal {D^T})^{-1}\tilde{{\mathcal {K}}}\). The process of proof is shown in Appendix B, C.

Remark 3

What’s worth noting here is that \({\mathcal {W}}(t)\) is strictly monotonically decreasing due to \(\dot{{\mathcal {W}}}(t)<0\), \((t^{+}_k,t_{k+1}]\). In [38], discrete Lyapunov stability theory and discrete integral method was proposed to prove the asymptotically stable of linear SDSs. Unfortunately, these analysis methods cannot be used to discuss nonlinear SDSs. However, to bridge the generation gap, discrete-time Lyapunov theorem and Lemma 2 are developed to derive the exponential stability conditions.

4 Numerical simulations

The point of this part is that we use two numerical examples to illustrate the less conservatism and effectiveness of the proposed approach in this work.

4.1 Example 1

For comparison with the Ref. [41], the system is reduced to a linear impulsive system as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{z}}(t)={\mathcal {A}}z(t),\;t\ne t_k,\\ {}&z(t^{+}_k)={\mathscr {Q}}z(t_k),\;t=t_k. \end{aligned}\right. \end{aligned}$$
(41)

Namely, for system (3), the matrices \({\mathcal {B}}={\mathcal {C}}=\Gamma =0\). We consider the asymptotically stable of the system (42) in the following two cases.

Case 1 When \({\mathcal {A}}\) and \({\mathscr {Q}}\) are set to the following matrices:

$$\begin{aligned} \begin{aligned} {\mathcal {A}}=\begin{bmatrix} -3.5 &{} 0.3 \\ 0.1 &{} 0.6\end{bmatrix}, \quad {\mathscr {Q}}=\begin{bmatrix} 1.3 &{} 0.1 \\ 0.1 &{} 0.01\end{bmatrix}. \end{aligned} \end{aligned}$$

One can know that the eigenvalues of \({\mathcal {A}}\) are \(-3.50489\) and 0.6049, meanwhile, the eigenvalues of \({\mathscr {Q}}\) are 1.3077 and 0.0023. The impulsive system can’t achieve stable if the impulsive interval is too small or too large. Thus, \({\mathcal {T}}_k\) plays a vital part for the stability of system (42). By using the theoretical results of Theorem 1, the allowable impulsive interval is listed in Table 1 compare with Refs. [41,42,43,44]. From Table 1, it is obviously that the impulsive interval obtained by Theorem 1 is better than Refs. [41,42,43,44], which indicates that the results of Theorem 1 is less conservative. However, the cost of computational complexity is large than Refs. [41,42,43] (Note: The presence of “NDVs” in Table 2 means the number of decision variables).

Table 2 Allowable intervals \([{\mathcal {T}}_m, {\mathcal {T}}_{M}]\) with aperiodic impulses
Full size table

Case 2 When we set the matrices \({\mathcal {A}}\) and \({\mathscr {Q}}\) as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {A}}=\begin{bmatrix} 1 &{} 3 \\ -1 &{} 2\end{bmatrix},\quad {\mathscr {Q}}=\begin{bmatrix} 0.5 &{} 0 \\ 0 &{} 0.5 \end{bmatrix}. \end{aligned} \end{aligned}$$

\({\mathcal {A}}\) is anti-Hurwitz and \({\mathscr {Q}}\) is Schur, the dwell-time \({\mathcal {T}}_k\) should be small enough to guarantee the stability of system (42). When the dwell-time \({\mathcal {T}}_k<{\mathcal {T}}\), the impulsive system is asymptotical stable, where \({\mathcal {T}}\) denotes the maximal dwell-time. Further, by using Theorem 1, \({\mathcal {T}}\) can be obtained (See Table 3). It is clear that \({\mathcal {T}}\) obtained by this work is larger than Refs. [41,42,43], thus the results of Theorem 1 has less conservatism than [41,42,43].

Table 3 Maximal dwell-time \({\mathcal {T}}_k\) with aperiodic impulses
Full size table

4.2 Example 2

Consider the DNNs with the following parameters:

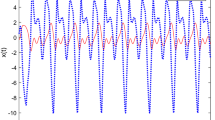
$$\begin{aligned} {\mathcal {A}}=\begin{bmatrix} -1 &{} 0 &{} 0\\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -1\end{bmatrix}, {\mathcal {B}}=\begin{bmatrix} 0 &{} 8 &{} 0\\ 1 &{} 0 &{} 1 \\ 0 &{} -11 &{} 1\end{bmatrix}, {\mathcal {C}}=\begin{bmatrix} 2 &{} 0 &{} 0 \\ 0.2 &{} 0.1 &{} 0 \\ 9 &{} 0 &{} 0.1\end{bmatrix}. \end{aligned}$$

Select \(\tau (t)=0.3+0.2sint\), \(g(z(t))=z(t)\), \(h(z(t))=0.5(|z+1|-|z-1|)\), thus \({\mathcal {G}}={\mathcal {H}}=diag\big \{1,1,1\big \}\). Figure 1 draws the state trajectory z(t) without controller under the initial condition \(\varphi (s)=[-2,1,-2]^T\), \(s\in [-0.5,0]\). Obviously, system (1) is unstable without controller.

Fig. 1
figure 1

State trajectory of system (1) without any controller

Full size image
Fig. 2
figure 2

State trajectory of system (1) with stable impulses

Full size image

Next, we will use these parameters to analyze the impulsive DNNs and SDSs, respectively.

Case 1: Impulsive DNNs (3) We verify the relation of the exponential rate \(\alpha \) and \({\mathcal {T}}_M\) under different impulse strength. Table 4 shows the maximum allowable bound for \({\mathcal {T}}_M\) with \({\mathcal {T}}_m=0.001\). Figure 2 depicts the state trajectory of DNNs with stable impulse.

Table 4 Allowable upper bound \({\mathcal {T}}_M\) when \({\mathcal {T}}_m=0.001\) for different \(\alpha \)
Full size table

Remark 4

Fig. 3 describes the state trajectory of system (1) with unstable impulsive. As can be seen from the Fig. 3 (where \({\mathscr {Q}}=diag\big \{0.2,0.2,0.2\big \}\), that is \(z(t^{+}_k)=1.2z(t_k)\)), the system can still achieve stability under the action of the impulsive controller (2). The reason of this stability is that the feedback term is incorporated into the controller. Namely, the feedback controller plays a meaningful role when the unstable impulses are activated. But in Refs. [25, 49], when the unstable impulses was activated, they can’t obtain the expected results because the feedback control was not considered. Thus, the hybrid controller presented in this work is more general than the previous works. In order to verity the influence of \(u_1(t)\) in the hybrid controller (2), we set \(\Gamma =0\) when \({\mathscr {Q}}=0.1I\). From Fig. 4, the exponential stability can’t be achieved, which further demonstrates the feedback control \(u_1(t)\) in hybrid controller (2) has an important significance in the exponentially stable.

Fig. 3
figure 3

State trajectory of system (1) with unstable impulses

Full size image
Fig. 4
figure 4

State trajectory of system (1) with unstable impulses

Full size image

Case 2: SDSs (38) Firstly, in (39), the controller \(u_c(t)={\mathcal {K}}z(t_k)\) and the delay \(\tau (t)=\tau \) is constant delay. To describe the validity of the results of Theorem 2, the comparisons results are obtained. The maximum allowable bound for \({\mathcal {T}}_M\) with \({\mathcal {T}}_m=10^{-5}\) is shown in Table 5. Additionally, the number of decision variables are also compared, which is a measure of computational complexity. Therefore, Table 5 displays that when the computational complexity increases, a relatively conservative result is obtained than those Refs. [28, 45, 46].

Table 5 The maximum allowable upper bound \({\mathcal {T}}_M\) with \({\mathcal {T}}_m=10^{-5}\)
Full size table

Secondly, set \(\alpha =0.8\), \({\mathcal {T}}_m=0.001\), \({\mathcal {T}}_M=0.3790\), then the feasible solution of Theorem 2 can be got by MATLAB LMI Toolbox, and the following gain matrix \({\mathcal {K}}\) can be obtained

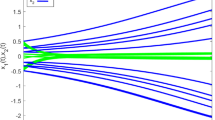
$$\begin{aligned} \begin{aligned} {\mathcal {K}}=\begin{bmatrix} -0.6212 &{} -0.2322 &{} -0.3941 \\ 0.0311 &{} -0.3344 &{} -0.1689\\ 1.0447 &{} 0.6187 &{} -3.2544 \end{bmatrix}. \end{aligned} \end{aligned}$$

And consider \(\varphi (s)=[-2,1,-2]^T\), \(s\in [-0.5,0]\). The state trajectory z(t), sampled-data state \(z(t_k)\), and sampling instants and sampling periods under aperiodic sampling is described in Figs. 5 and 6, respectively, which shows the exponentially stable can be achieved by the sampled-data controller.

Fig. 5
figure 5

State trajectory of system (1) with sampled-data controller

Full size image
Fig. 6
figure 6

Sampling instants and sampling periods

Full size image

5 Conclusion

This work studies the analysis of the exponential stability for DNNs based on a hybrid control strategy, where unstable and stable impulses have all been considered. An exponential stability criterion for DNNs by employing an improved IBBLF with discontinuity at the impulses instant has been obtained. Then, sufficient conditions have been obtained on the ranged dwell-time, which is the result of stability in discrete-time, but expressed in continuous-time. Lastly, the derived results have also been applied to SDSs and the corresponding stability results are also obtained. In our future work, the following topics will be considered: 1. Consider the case that the delay-impulses between two consecutive impulsive instants based on the IBBLF method. 2. Design a novel event-triggered control with the aid of IBBLF, where the impulsive sequence is unknown sequence and determined by the event-triggered condition.