1 Introduction

Flood routing is one of the important topics to design water structures in water resources engineering. There are two main approaches in flood routing: the hydrological and hydraulic approaches. In the hydrological approaches, the flow rate calculated as a function of time. These methods are based on storage-continuity equation in the specific location. In the hydraulic approaches the flow rate determines as a function of both time and location. These methods are based on the Saint-Venant equations. There are other approaches which need more data and parameters for solving their models. One of the popular hydrological methods is Muskingum method, which frequently used in flood routing that first, the U.S. Army Corps of Engineers developed this model.

The linear Muskingum model is based on two main equations: continuity equation and storage equation (Gill 1978; Tung 1985; Yoon and Padmanabhan 1993; Mohan 1997; Kim et al. 2001; Geem 2006; Al-Humoud and Esen 2006):

$$ \frac{d{s}_t}{dt}={I}_t-{O}_t $$
(1)
$$ {S}_t=K\left[x{I}_t+\left(1-x\right){O}_t\right] $$
(2)

Where, S t , I t and O t are storage, inflow and outflow magnitude, respectively at time t. K is storage-time constant that may be considered as an approximation of travel time through the reach; x is a weighting factor which is usually between 0 and 0.5 for reservoirs storage and between 0 and 0.3 for stream channel (Mays 2010). The dimensions of O and I are (L3T−1) similar; x is dimensionless, S is L3 and K is T. In the linear Muskingum model, the parameters K and x usually estimate graphically by a trial and error procedure. First x assumed and the values of [xI t  + (1 − x)O t ] compute by using observed data and plotted against S t . If the value of x can reduce width of the plotted loop then the value of x right selected. K is equal to the slope of the straight fitted line through the loop (Barati 2011). K and x expect to capture the flood propagating characteristics of the reach in its entirety, and no additional topography information of the channel is required for flood routing (Yoon and Padmanabhan 1993). As said before, the linear Muskingum is based on graphical methods, which can make errors in visual judgments. Nevertheless, in some reaches of rivers the linear Muskingum routing is not suitable. As a result, the performance of nonlinear of Muskingum model is more appropriate (Mohan 1997). Two forms of nonlinear Muskingum models have been recommended [Eqs. (3)-(5)] in the previous researches to improve the fitness of nonlinear relationships (Gill 1978; Mohan 1997; Luo and Xie 2010).

$$ {S}_t=K{\left[x{I}_t+\left(1-x\right){O}_t\right]}^m $$
(3)
$$ {S}_t=K\left[x{I_t}^m+\left(1-x\right){O_t}^m\right] $$
(4)

These models have an additional parameter (m), which used as power exponents to improve the relation between accumulated storage and weighted flow. The linear model considers a special case of nonlinear models when m is equal to one. Unlike the linear model, in the nonlinear models K has the dimension of [L3(1-m) Tm] and does not describe the travel time of flood wave. Also, x does not to be the same as in the linear model. A graphical method that is used from historical inflow and outflow hydrographs is inappropriate for nonlinear Muskingum models. Hence, the determination of correct values of K and x is difficult and needs advanced methods (Gill 1978; Tung 1985; Yoon and Padmanabhan 1993; Mohan 1997; Kim et al. 2001; Das 2004, 2007; Geem 2006; Chu 2009; Chu and Chang 2009; Luo and Xie 2010; Barati 2011, 2013; Xu et al. 2011; Karahan et al. 2012).

Several previous researches on parameter estimation of the Muskingum method have been applied to finding the values of the parameters in the nonlinear Muskingum model. The mathematical techniques include segmented least squares method (S-LSM) (Gill 1978), nonlinear least squares (NONLR) (Yoon and Padmanabhan 1993), Lagrange multiplier (LMM) (Das 2004), the Broyden-Fletcher-Goldfarb-Shanno method (BFGS) (Geem 2006), Nelder-Mead simplex (NMS) method (Barati 2011), and the generalized reduced gradient (GRG) (Barati 2011) were used to solve the nonlinear forms of the Muskingum models.

In addition, various heuristic algorithms such as genetic algorithm (GA) (Mohan 1997), harmony search (HS) (Kim et al. 2001), immune clonal selection algorithm (ICSA) (Luo and Xie 2010), differential evolution (DE) (Xu et al. 2011), parameter setting free harmony search (PSF-HS) algorithm (Geem 2010), particle swarm optimization (PSO) (Chu and Chang 2009), simulated annealing (SA) algorithm, and shuffled frog leaping algorithm (SFLA) (Orouji et al. 2013) have been developed in order to search optimum parameters in nonlinear models.

Das (2007) suggested a chance-constrained optimization-based model for estimating the Muskingum model parameters. This model determined the parameters of the Muskingum model using minimizing the SSQ of difference between the observed and estimated outflows. Also, the new model is very complex and requires massive computation to estimate parameters of the Muskingum model (Luo and Xie 2010). Chu (2009) determined the parameters of the Muskingum model by a Neuro-Fuzzy approach, which has no physical basis. The mentioned method can be an alternative in the application of the Muskingum model (Barati 2013). Niazkar and Afzali (2014) applied the modified honey bee mating optimization (MHBMO) algorithm along the modified routing procedure to estimate the Muskingum parameters using two different objective functions. The results demonstrated that the MHBMO algorithm not only converged faster, but it also captured the best optimal parameters values. Latt (2015) examined the application of artificial neural network (ANN) approach based on the Muskingum equation, and compared the feedforward multilayer perceptron (FMLP) models to other reported methods. The FMLP model showed a clear-cut superiority over other methods in flood routing of well-known benchmark data.

The previous studies showed that the particle swarm optimization (PSO) was used to determine the three parameters in nonlinear Muskingum models, but in this paper the PSO algorithm is applied to estimate the parameters of a new nonlinear Muskingum model which consist of four parameters and was developed by Easa (2011). The PSO algorithm is a population-base evolutionary algorithm and already applied in Civil Engineering and Water Resources Engineering optimization problems such as reservoir operation (Nagesh Kumar and Janga Reddy 2007), water quality management (Afshar et al. 2011; Lu et al. 2002; Chau 2005), Basin wide water resources management (Shourian et al. 2008), flood control management (Meraji 2004). To check the performance of the new method, four real examples have assessed. The results showed the PSO is a simple and clear algorithm for understanding. Also, it does not need an initial guess for its correspondent parameters unlike other previous methods. Although the new four-parameter nonlinear Muskingum model is more complicated, but it can improve the routed flow better than the three-parameter nonlinear Muskingum, particularly in the multiple-peak hydrograph.

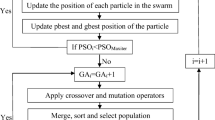
2 Particle Swarm Optimization (PSO)

Particle swarm optimization (PSO) is a meta-heuristic optimization technique, which first introduced by Eberhart and Kennedy (1995). This algorithm is a member of the category of swarm intelligence that inspired from the flocking and schooling of birds and fishes. All possible solutions for a problem in PSO are in a search framework that called solution space. Each individual in this swarm is called a particle. Each particle represents a solution for the problem in optimization in each iteration, which flies in the location space. In each iteration, the result of three vectors defines moving each particle. One of them is velocity vector that is a randomly vector and other vectors are produced based on the best position of particles are found to now (Kuo et al. 2010). Each particle keeps track of its position vector, pbest,which has obtained best fitness function, so far. The position vector, gbest,which is the best value of fitness function achieved so far considering all the particles is also memorized. The position vectors of the particles update from velocity vector. These updated positions in PSO algorithm evaluate with an objective or fitness function in the each iteration and pbest and gbest are updated. The particle velocities V ij t and position X ij t calculate in the iteration number t using following equations (De Moura Meneses et al. 2009),

$$ {V}_{ij}^{{}^{t+1}}={W}^t{V}_{ij}^t+{c}_1{r}_1^t\left(\boldsymbol{pbest}\left(i,j\right)-{X}_{ij}^t\right)+{c}_2{r}_2^t\left(\boldsymbol{gbest}(j)-{X}_{ij}^t\right) $$
(5)
$$ {X}_{ij}^{t+1}={X}_{ij}^t+{V_{ij}}^t $$
(6)

Where, i = [1, 2, …, P] and J = [1, 2, …, n]. The c 1 and c 2 are acceleration constant that change between [2, 4]. The r 1, r 2 are random numbers between [0,1]. The gbest and pbest call global and particle best position, respectively. The W is an initial weight which represent the exploration and exploitation properties of algorithm and changes between [0.4–0.9]. The characteristics of exploration algorithm will increase if W closes to 0.9, otherwise, its exploitation properties increases. In this stage, a new modified factor which is called W damp used in the each iteration based on Eq. (7) to increase exploration characteristics in the final steps. (Hossein Zaji and Bonakdari 2014). The value of W damp factor used in this paper was 0.998, which reduces the W and particle movement in the each iteration.

$$ W=W\times {W}_{damp} $$
(7)

3 New Non-Linear Muskingum Model

In this paper, the new non-linear Muskingum model has been used, which introduced first by Easa (2013). The new method considers the four parameters to determine. The new four-parameter non-linear Muskingum model is given by the following equation:

$$ {S}_t=K{\left[x{I}_t^a+\left(1-x\right){O_t}^a\right]}^m $$
(8)

In fact, the new model is similar to the Eq. (3). However, in the proposed model m corresponds to the non-linear form of the storage equation, while in the Eq.(3) m is related to the assumed linear form of it (Easa 2013).

The Eq. (8) is a general model, which can cover all of previous developed models e.g. (Eqs. 2–4) by considering a = m = 1 in linear model (Eq. 2) and a = 1 or m =1 in non-linear models (Eqs. 3–4). The dimension of K in the proposed model is not the same as the linear model. Although, the new proposed model is more complex than previous model, but the optimization models such as PSO can compute the best values for its parameters at less time. The extra parameter in new model causes to improve fitting between routed and observed outflow especially in multi-peak hydrograph examples. The proof and details of the derivation of Eq. (8) presented by Easa (2013).

3.1 Routing Procedure of the Nonlinear Muskingum Model

By rearranging Eq. (8), the routed outflow can be expressed as,

$$ {O}_t={\left[\left(\frac{1}{1-x}\right){\left(\frac{S_t}{K}\right)}^{1/m}-\left(\frac{x}{1-x}\right){I}_t^a\right]}^{1/a} $$
(9)

The first term in bracket of Eq. (9) should be greater than the second term so that the routed outflow not be negative value. By considering mentioned condition, the relation between the four parameters can be expressed as,

$$ \frac{1}{m}>\frac{ \ln \left(x{I}^a\right)}{ \ln \left({S}_t/K\right)} $$
(10)

By substituting Eq. (9) in Eq. (1), the time rate of changes volume the storage can be obtained as,

$$ \frac{\Delta {S}_t}{\Delta t}={I}_t-{\left[\left(\frac{1}{1-x}\right){\left(\frac{S_t}{K}\right)}^{1/m}-\left(\frac{x}{1-x}\right){I}_t^a\right]}^{1/a} $$
(11)

As well, the next accumulated storage can be rewritten as,

$$ {S}_{t+1}={S}_t+\Delta {S}_t $$
(12)

The routing procedure for the nonlinear model includes the following steps (Tung 1985; Kim et al. 2001; Geem 2006, 2010; Chu and Chang 2009; Karahan et al. 2012; Barati 2013):

  1. 1.

    Determination the hydrologic parameters (K, x, a, m) using the PSO algorithm. PSO select randomly the initial values of parameters based on the specified bounds.

  2. 2.

    Calculation the time rate of change of the storage volume by using Eq. (11). Here in the first time step initial outflow is the same as the initial inflow

  3. 3.

    Estimation the next accumulated storage using Eq. (12)

  4. 4.

    Calculation the outflow in the next time using Eq. (9)

  5. 5.

    Repetition steps 2–4 for all time steps

This procedure should be repeated with different parameters values several times so that the best fit between routed and observed outflow achieve.

4 The Objective Functions

The objective function of the optimization model minimizes the sum of the squared deviations between the observed and estimated outflows,

$$ Minimize\kern0.5em SSQ={{\displaystyle \sum_{t=1}^n\left({O}_t-{\overset{\frown }{O}}_t\right)}}^2 $$
(13)

Where, SSQ is the sum of the squared deviations between the observed and estimated outflows; O t is the observed outflow at time t; Ȏ t is the estimated outflow at time t that calculated by Eq. (9) and n is the number of time steps in flood routing. Also, the other objective function can be introduced to minimize the sum of absolute deviation between the observed and estimated outflows,

$$ Minimize\kern0.5em SAD={\displaystyle \sum_{t=1}^n\left|{O}_t-{\overset{\frown }{O}}_t\right|} $$
(14)

Where, SAD is the sum of absolute deviation between the observed and estimated outflows and |.| denotes = absolute value.

4.1 Error of Peak Discharge

The error of peak discharge (EQ p ) provides a deviation of peak of observed and routed outflows (Latt 2015). EQ p is given as,

$$ E{Q}_p=\frac{\left|{O}_{observed}^{peak}-{O}_{routed}^{peak}\right|}{O_{observed}^{peak}} $$
(15)

Where, O peak observed is the peak of observed outflow and O peak routed is the peak of routed outflow. A lower absolute value of EQ p implies a more accurate model.

4.2 Error of Time to Peak

The error of time to peak (ET p ) provides a deviations of peak time of observed and routed outflows (Latt 2015). ET p is given as,

$$ E{T}_p=\left|{T}_{observed}^{peak}-{T}_{routed}^{peak}\right| $$
(16)

Where, T peak observed is the time of peak of observed outflow and T peak routed is the time of peak of routed outflow. A smaller value of ET p implies a more accurate prediction of occurrence of peak outflow.

4.3 Mean Absolute Relative Error Consideration

The mean absolute relative error (MARE) between the observed and routed outflows is considered as the error mode (Toprak 2009). MARE is given as,

$$ MARE=\frac{1}{N}{\displaystyle \sum_{i=1}^N\frac{\left|{O}_{observed}^t-{O}_{routed}^t\right|}{O_{observed}^t}} $$
(17)

4.4 Variance Explained

The closeness of shape and size of the hydrograph can be measured using the criterion of variance explained as advocated by Je and Sutcliffe (1970) and recommended by the ASCE Task Committee on Difinition of Criteria for Evaluation of Watershed Models of the Watershed Management Committee, Irigation and Drainage Division (1993) (McCuen et al. 2006; Perumal and Sahoo 2007; Barati 2013, Niazkar and Afzali, 2014). The variance explained in percentage (VarexQ) is given as

$$ VarexQ=\left[1-\frac{{\displaystyle \sum_{i=1}^N{\left({O}_{observed}^t-{O}_{routed}^t\right)}^2}}{{\displaystyle \sum_{i=1}^N{\left({O}_{observed}^t-{O}_{observed}^{mean}\right)}^2}}\right]\times 100 $$
(18)

Where, O mean observed = mean of observed outflows.

5 Application of the Routing Techniques

5.1 Numerical Experiment 1

In this example, the inflow–outflow hydrograph data of Wilson (1974) have been employed. The previous researches have applied the various optimization methods to estimate the Muskingum parameters by using these data. Table 1 shows the inflow and routed outflow of Wilson (1974), which calculated by new four-parameter Muskingum model and other methods.

Table 1 Comparison of the observed and best-routed outflows for Wilson data
Full size table

In this paper, the objective functions SSQ and SAD have utilized to estimate the parameters. According to Table 2, the PSO method calculated the SSQ and SAD values 8.82 and 9.77, respectively, which were much smaller than another model. As well, SSQ and SAD values that presented by Easa were 7.67 and 10.31, respectively which used the generalized reduced gradient method with Solver associated in Excel.

Table 2 Comparison of the routing results of the different methods
Full size table

Additionally, at the Table 2 the parameters EQ p , ET p , MARE and VarexQ compared between the previous methods and the presented method. Since the occurrence of the predicted peak outflow happen at the same time with that of the observed maximum outflow, ET p values are zero for all methods exept the NONLR method. The EQ p obtained 0.0001, which was less than all of applied methods except LMM (Das 2004) . Although, Easa used the four-parameter non-linear model, but the EQ p value achieved 0.0037 and as a result the proposed method can make 96.7 % improvement in this term. Also the PSO algorithm can produce as well results as the most accurate procedures in terms of both MARE and VarexQ.

Figure 1 shows the observed and estimated outflow of the best five methods presented in the Table 2 respect to the proposed method. Moreover, Fig. 2 illustrates a comparison between the observed and the routed outflows.

Fig. 1
figure 1

Inflow, observed and computed outflows hydrographs with different methods by using the Wilson data

Full size image
Fig. 2
figure 2

Comparison the difference between the routed and observed outflows with various methods by using the Wilson data

Full size image

The optimal parameters of the proposed model are K = 0.1659, x =0.2981, m =3.6830 and a = 0.4689. The optimization processes performed in 200 iteration that after several times of trial and error the best value of the PSO algorithm parameters was selected so that initial population = 100, c 1 = c 2 =2.05, W =0.4 and W damp =0.998.

5.2 Numerical Experiment 2

The data of this example firstly have recorded by Karahan et al. (2012) from the 1960 flood of the River Wye in the United Kingdom. The 69–75 km stretch of the River Wye from Everwood to Belmont has no tributaries and very small lateral flow (NERC 1975). It is, thus, an excellent example to demonstrate the use of flood-routing techniques (Bajracharya and Barry 1997). The inflow data, estimated outflow by O’Donnell (O’DONNELL 1985), HS-BFGS (Karahan et al. 2012), GRG (Easa 2013) and proposed method presented in the Table 3.

Table 3 Comparison of the observed and best-routed outflows by using the River Wye data
Full size table

As shown in Table 3, by PSO algorithm the value of SSQ and SAD computed 31,099.52, 695.77, respectively which is better than all of methods. Also the PSO can obtained the less value than O’Donnell and HS-BFGS method in term of EQ p . Moreover, the PSO can determinated 0.09 and 98.12 % for MARE and VarexQ, respectively, which are in acceptable range rather to other methods in the Table 3. The Fig. 3 described comparison between the observed and computed hydrographs by applying methods. In addition, Fig. 4 shows a comparison of the difference between the observed and the estimated outflows by applied methods. It can be understand from Fig. 4 the low swing in the PSO model chart.

Fig. 3
figure 3

Inflow, observed and computed outflows hydrographs with different methods by using the River Wye data

Full size image
Fig. 4
figure 4

Comparison the difference between the routed and observed outflows with various methods by using the River Wye data

Full size image

The estimated Muskingum parameters by proposed model are K =0.612, x =0.401, a =1.133 and m =1.363. These values achieved by PSO optimization processes after only 30 iterations. The initial population, W, W damp were selected 200, 0.5, 0.998 respectively and c 1 = c 2 =2.05.

5.3 Numerical Experiment 3

In this example, the Viessman and Lewis (2003) data have been applied to estimate the new Muskingum parameters. This example is one of multi-peak hydrographs, which inflow and observed outflow data shown in the Table 4. The PSO algorithm computed the SSQ =74,812.30 that indicate about 2 % reduction in comparison with the Easa method (SSQ = 76,785). In addition, in this example, the EQ p , ET p , MARE and VarexQ was determinated 0.0358, zero, 0.067 and 98.27 %, respectively by PSO method. In this example there are not the more datails of routed flow by Easa method to compare the results in terms of EQ p , ET p , MARE and VarexQ. The inflow, observed and estimated hydrograph by the PSO algorithm shown in Fig. 5. It is obvious that the new applied method yields a considerable improvement in fitting multi-peak hydrographs. The optimal values of K, x, a and m are equal to 0.0605, 0.1310, 0.3213 and 4.574 respectively, which obtained after 500 iterations. The PSO parameters were obtained similar to Example 2.

Table 4 Comparison of the observed and best-routed outflows for Viessman and Lewis
Full size table
Fig. 5
figure 5

Inflow, observed and computed outflows hydrographs for Viessman and Lewis

Full size image

5.4 Numerical Experiment 4

This example is about the Karoon River in Iran, which firstly have been gathered by Orouji et al. (2013). Karoon River is one of the great rivers in the southwest of Iran that supply urban, agricultural and industrial demand in the area. The applied data recorded by two hydrometric stations, Godar and Gotvand (Orouji et al. 2013). They applied SFLA and SA optimization techniques based on non-linear Muskingum (3 parameters) and reported the best values of SSQ and SAD 130,928.6 and 1835.6, respectively. The proposed method computed these parameters 68,790.84 and 1067.102, respectively, which indicate 47 % and 42 % improvement, respectively.

Table 5 and Fig. 6 present the results of estimated outflow respect to inflow and observed outflow by using proposed method and previous methods. Also, the PSO can calculated the EQ p , MARE and VarexQ equal to 0.0132, 0.03 and 98.05 %, respectively, which have the more improvement than SA and SFLA methods.

Table 5 Comparison of the observed and best-routed outflows for Karoon River
Full size table
Fig. 6
figure 6

Inflow, observed and computed outflows hydrographs for Karoon river

Full size image

The optimal values of K, x, a and m computed 7740.68, −0.0527, 0.1786 and 0.9911, respectively. In addition, the maximum number of iterations was 300. In this study, only the initial population set to 500 and other parameters did not change.

6 Conclusions

Most of the researcher in the past only focused on robust optimization algorithms to improve the fitting performance of the nonlinear Muskingum model, which considered as an exponent parameter of the weighted storage. However, the resulted achievements in this field were not very considerable. In this paper, the four new non-linear Muskingum model that has introduced firstly by Easa (2013) to compute the routed outflow at a reach of river has used. The new Muskingum model which was based on power function of weighted storage was more suitable than linear function. The new Muskingum model considers more complex than previous models. But, it is not a non solver problem with recent advances in modern optimization algorithms which can find the optimal parameters for all of highly non-linear and non-convex problems.

In this research, the PSO algorithm has employed to estimate the parameters in the new non-linear Muskingum model. The performance of these algorithms compared with other techniques in literature based on minimizing the two objective functions, SSQ and SAD. In this regards, three benchmark examples and one real case in Iran were investigated. The results showed the PSO algorithm which uses the four-parameter in the Muskingum model, can compute the best values of SAD factor rather than all used other techniques in the examples. The SSQ factor improved in all studied cases except the Wilson example. On the other hand, the SAD, EQ p , ET p , MARE and VarexQ were acceptable in Wilson example.

The results confirmed that the PSO algorithm estimated the four parameters in the new Muskingum model with high accuracy along with a fast rate of convergence. In addition, the PSO method does not necessary assumption of initial values of the model parameters and no derivative. PSO can be achieved the nearly global optimum solution in lowest iterations by setting right the its parameters. The other experiences of PSO applications have shown that the main and sensitive parameters in this algorithm are c 1 and c 2 which can set c 1 = c 2 =2.05 presented the best answer (Carvalho and Ludermir 2006; Prakash and Sydulu 2007; Li et al. 2010). These values are similar to the results of the present research. Consequently, by using the PSO with new four-parameters Muskingum models improved the outflow forecasting, significantly.